Perspectives for hybrid ab initio/molecular mechanical simulations of solutions: from complex chemistry to proton-transfer reactions and interfaces

Introduction

Theoretical approaches have been of important relevance in chemistry for a long time [1–14] and due to the continuous development of computational resources have enjoyed increasing interest during the last few decades. A consequence of the still-improving capabilities of computational resources results in a heightened accuracy of the computations as well as the possibility to treat systems of increasing size. While quantum chemistry [5–10] is essentially treating the molecules in a vacuum environment, the development of statistical simulation methods [11–14] of the Monte Carlo (MC) and molecular dynamics (MD) type in conjunction with a periodic treatment of the system (corresponding to the treatment of a quasi-crystalline representation) enables accurate studies of chemical phenomena occurring in the bulk of a liquid. Although such methods have been in use for a number of decades, the accuracy of this type of simulation was, and still is, strongly dependent on the employed interaction potentials, commonly referred to as molecular mechanics (MM) or force fields (FFs) [1–4]. The simplest, yet most widely employed approach is the application of the atomic interaction via Coulombic plus Lennard–Jones potentials for intermolecular particle pairs, while the intramolecular contributions are models via harmonic bond and angle potentials (a spring-like description corresponding to Hooke’s law) and cosine expressions for intramolecular bond rotations. Inclusion of polarization effects [15], e.g., via induced dipoles or charge-on-spring models, results in general in an improved description of the systems’ interactions, but also dramatically increases the computational effort and thus limits the treatable systems size and the achievable simulation length. Although the importance of including these effects in simulation studies has been recognized for a long time, they are still rarely employed in simulation approaches to date.

A particular obstacle in the development of FFs is the balancing of the respective parameters, which due to the complex interactions is, in general, tedious and time-consuming. While a number of FFs are available for systems composed of rather simple elements such as organic molecules [16], ionic liquids [17–19], biomolecules (such as peptides and nucleic acids) [20–26], as well as minerals [27] and metallic systems [28–30], the parameterization for metal-containing systems is often a great challenge. This is due to the complex interactions of metals and metal ions with their immediate surrounding resulting from the intricate electronic structure present in these systems. Naturally, a description taking the quantum mechanical nature of electrons into account is highly desirable to describe the interactions within such systems, and the development of approaches combining statistical simulation methods with a quantum chemical description of the system proved to be of great value. Two main classes of methods are employed to achieve this goal, namely, Car–Parrinello (CP)-type approaches [31, 32] and hybrid quantum mechanical/molecular mechanical (QM/MM) techniques [33–40]. While in the first approach the system size is reduced to treat the entire system via a quantum chemical approach, typically in the context of density functional theory (DFT) at the generalized-gradient approximation (GGA) level [41, 42], the latter methods divide the system into a high- and a low-level region. While the chemically most relevant part located in the high-level zone is treated on a quantum mechanical (QM) basis, molecular mechanical (MM) potentials are considered to be sufficiently accurate to model the interactions in the remaining part of the system.

The recent awarding of the Nobel prize in chemistry to Martin Karplus, Michael Levitt, and Arieh Warshel for the development of multiscale models for complex chemical systems [43] can be interpreted to include QM/MM techniques to a large extent. While the research conducted by the three Nobel laureates focused on the development and application of uncountable techniques in computational chemistry, their studies marking milestones in the field of chemical simulations (e.g., the first simulation studies of biomolecular systems [44–46]), all three scientists made substantial contributions to the field of QM/MM simulations [33, 34] which were found to be ground-breaking in that they managed to make Newton’s classical physics work side-by-side with the fundamentally different quantum physics [47].

Both, the CP and the QM/MM approach, have been employed with huge success during the past decades to model systems being of relevance for solution chemistry, such as pure water as well as solvated species [48–55]. A particular limitation in conventional QM/MM approaches is the fact that in order to describe the interaction between QM and MM particles, FF expressions have to be used, implying that an adequate set of potential parameters for the Coulombic plus non-Coulombic potentials is required. This prerequisite might become a limiting step for systems exhibiting complex interactions with the environment, since the corresponding potentials are difficult and in some cases impossible to obtain. However, since in QM/MM approaches the applied QM method is not limited to the DFT level, simulations employing correlated ab initio methods [5–10], taking also the influence of electron correlation into account, are feasible. Since the application of these methods is highly desirable, the formulations of improved hybrid QM/MM approaches enjoyed increased interest.

During the last decades, QM/MM techniques have been successfully applied in studies of hydration phenomena in our lab as well, increasing both the complexity of the investigated systems as well as the details of the theoretical level employed in the investigations. Based on the experience of a number of simple systems, the quantum mechanical charge field (QMCF) approach [39, 56] was developed. Since non-Coulombic interactions are known to be short-ranged, they are negligible when considering the distances between a solute located at the center of the QM region and particles located in the MM part. Consequently, the application of a solvent–solute non-Coulombic potential is not required, provided that the size of the QM region is sufficiently large (typically 0.55–0.6 nm or beyond), which offers the unique possibility to investigate the solvation of any kind of solute via a QM/MM approach.

A further significant improvement of the QMCF ansatz compared to conventional QM/MM techniques is the inclusion of the partial charges of the MM atoms surrounding the high-level region as a perturbation potential into the QM treatment. It was shown that this measure leads to a substantial improvement in the quality of results in QMCF-type simulations. The reason for this lies in the nature of the QM treatment: after assignment of the molecules to the QM region, the respective computation considers the system as an isolated cluster of nuclei and electrons in vacuo.

As a consequence, all properties obtained for the particles within the QM region do not correspond to the situation as if the cluster was part of the bulk. However, if the QM treatment also considers the influence of the effective MM charges in the vicinity of the QM region (being, e.g., –0.8476 and 0.4238 a.u. for oxygen and hydrogen atoms in the extended simple point charge charge (SPC/E) water model [57]), the influence of the surrounding bulk structure is taken into account. In case a negatively charged particle is located close to the QM/MM interface, the electron density is repelled compared to the in vacuo treatment, while the presence of a positively charged atom will lead to an attraction of the electron density [55]. Since the influence of the surrounding point charges improves the entire electron density, the embedding technique does not only account for the QM/MM interactions, but also improves the accuracy of forces acting between particles within the QM region. Thus, the use of the embedding technique [40, 58, 59] is of significant benefit for QM/MM techniques. Since the potential of these partial charges enters the less-demanding one-electron contributions, the associated increase in computation time is moderate, irrespective of the rather large number of point charges compared to the number of atoms included in the QM region. Hence, this electrostatic embedding approach enables a substantial improvement of the accuracy (e.g., an improved description of hydrogen bonds penetrating the QM/MM interface), while the computational effort remains manageable. The use of an enlarged buffer region for the QM treatment was shown to further improve the results in hybrid QM/MM simulations [60]. Figure 1 depicts the separation of the system into QM and MM region in a QMCF simulation study of a uranyl carbonate complex in aqueous solution, the QM region embedded in the field of MM point charges is shown in Fig. 1b.

Fig. 1

(a) Separation of system into the individual regions used in the QMCF approach. (b) Embedding of the QM region indicated by the sphere in the field of surrounding partial charges of the respective MM atoms.

The usefulness of a QM description becomes evident when treating systems exhibiting an anisotropic potential such as the transition-metal ions copper(II) [61], palladium(II) [62], and platinum(II) [63] and systems carrying lone-electron pairs, e.g., germanium(II) [64], tin(II) [65], and lead(II) [66] (see Fig. 2a and b). In order to accurately model these systems on the basis of purely classical simulation approaches, sophisticated intermolecular potential functions are required, which is in many cases a limiting factor due to the tedious and time-consuming parametrization of these models. Although classical studies of such systems have been successfully performed, one has to be aware that a classical description of these system via empirical models implies a prebiasing of the interaction, e.g., by assuming the presence of four ligands arranged in a square planar arrangement at close distances in the first shell of aqueous palladium(II) and platinum(II). A quantum description on the other hand does not introduce any biasing of the interaction, since it considers only the interaction associated with the nuclei and electrons (modulated by the presence of external point charges as outlined above). For example, in the case of QM/MM simulations of aqueous palladium(II) and platinum(II), the presence of the four first-shell water molecules at close distance arranged in a square plane is a direct consequence of the computation and not the result of an assumption made prior to the set-up of the simulation.

Fig. 2

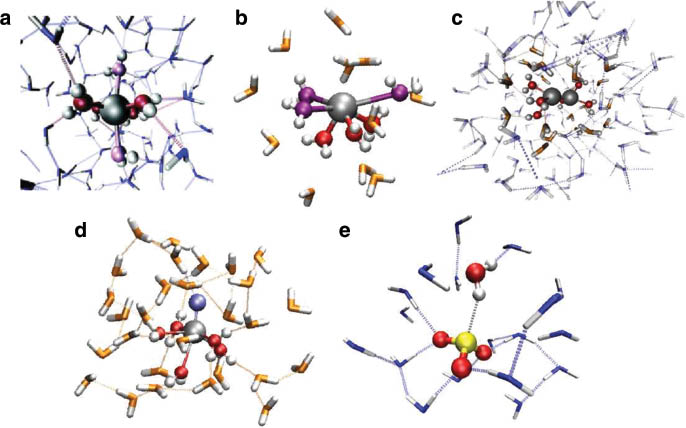
Snapshots obtained from QMCF MD simulations of (a) palladium(II), (b) germanium(II), (c) the dipositive dimeric mercury ion (d) titanyl(IV), and (e) sulfite in aqueous solution.

Composite solutes such as the dipositive dimeric mercury ion [67], titanyl(IV) [68], and uranyl(V/VI) [69, 70] exhibit also an (effectively) anisotropic potential resulting in an anisotropic hydration pattern (see Fig. 2c and d). Since, as mentioned earlier, the QMCF approach does not require non-Coulombic solute–solvent potentials, these systems can be treated in the same way as monoatomic species. The successful extension of the QMCF methodology to oxoanions [71–73] such as and (Fig. 2e), further demonstrated the versatility of QM/MM techniques such as the QMCF approach for the study of hydration phenomena.

At this point, it remained to be seen whether this method is also able to yield data of similar accuracy for organic solutes and a number of investigations studying the hydration properties of organic systems has been carried out. Typical examples are species such as N-methylformamide [74], guanidinium [75], formaldehyde [76], urea [77], and glycine [78] (see Fig. 3). For all systems, structural and dynamical data in good agreement with available experimental and other theoretical data has been obtained from the QMCF MD simulations. A particular advantage of the knowledge of the time evolution of the microscopic properties of the systems (i.e., position and velocities of all atoms as a function of time) is the possibility to investigate the properties of individual groups. A typical example is the characterization of different hydrogen bond sites within a solute as, for example, present in N-methylformamide, urea, and glycine.

Fig. 3

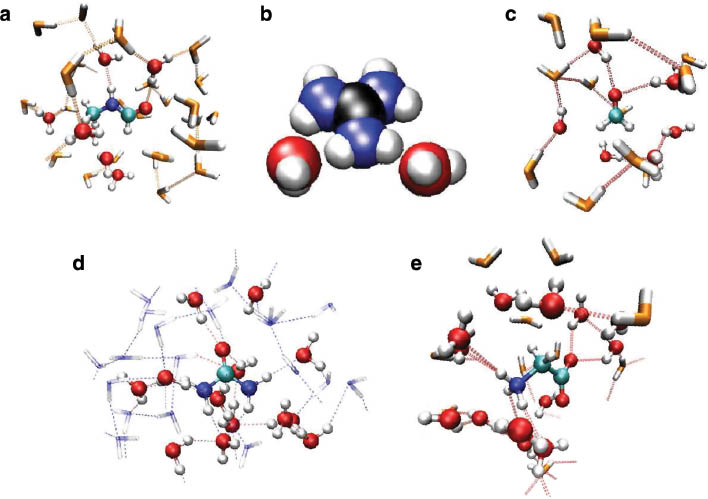
Snapshots obtained from QMCF MD simulations of (a) N-methylformamide, (b) guanidinium, (c) formaldehyde, (d) urea, and (e) glycine.

With the possibility of accurately describing both metallic aquo-complexes as well as organic compounds on the basis of first principles, it appeared promising to combine these classes to investigate the properties of coordination complexes in solutions. Despite the size of these composite systems, the capacities of modern computational facilities made the execution of such simulations feasible. A joint experimental and theoretical investigation of the inertness against racemization of cis- and trans-bis-(glycinato) copper(II) complexes [79] in aqueous solution marked the first application of the QMCF technique to a metal-organic system. While it was known for some time, that the associated crystals of those two isomers are stable and do not show racemization over time at temperatures below 180–210 °C [80], it was still an open question whether this is also true for the complexes in solution [81–84].

Figure 4 depicts the time series of the in-plane dihedral angle φ for cis- and trans-bis(glycynato) copper(II) in aqueous solution observed in the QMCF MD simulations at room temperature. It can be seen that while the cis-isomer shows a planar configuration for most of the simulation time, long periods showing out of plane motion occur in the trans case. However, neither of the isomers show an inversion of this dihedral angle along the simulation time, which implies that no interconversion of the species takes place. The conclusion drawn from the simulation results, that no racemization of bis-glycynato copper(II) complexes takes place at room temperature, was further examined via a series of spectroscopic investigations. The fact that the mid-infrared spectra of pure cis- and trans-bis(glyinato) copper(II) solutions were found to show noticeable differences supports the findings of the theoretical investigations [79]. Quantitative partial least-square regression (QPLSR) analysis used in addition to the pure solutions samples containing isomeric mixtures (20, 40, 60, and 80 %) resulted in a clear separation of the pure samples from each other and the mixtures, thus confirming the previous findings. The QPLSR model was further verified using both conventional cross-validation as well as test set validation. Heating of a pure cis-bis(glycynato) copper(II) solution in a Teflon-lined Parr bomb over a range of 90–180 °C indicated that a temperature of 150 °C or higher is required for the liquid-state isomerization to take place.

Fig. 4

Time evolution of the in-plane dihedral angle φ obtained for a QMCF MD simulation of cis- and trans-bis-glycynato copper(II) in aqueous solution.

Another example of the successful application of the QMCF methodology to complex chemistry is the investigation of different uranyl(VI) carbonates. The ion is considered the most abundant form of uranium in the environment [85–87], and although the ion has a very low diffusivity, its mobility can be dramatically increased via complexation. Since carbonate is a potent complexation agent occurring with high abundance in the environment [88–91], investigations focusing on uranyl carbonates in aqueous solution attracted increased interest in recent years [92–96], motivated strongly by the increasing number of radioactive incidents that occurred in recent years.

Figure 5 depicts screenshots obtained from the QMCF MD simulation of the three different [UO₂(CO₃)_n]²–²ⁿ complexes. In all cases, coordination number five was retained for the uranium atom (not considering the covalently bound oxygen atoms), which coincides with the coordination number observed for the aqueous uranyl(V/VI) species [69, 70]. The coordinating atoms are located in a planar arrangement with respect to the main axis of the 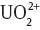ion. In general, the carbonate ions prefer a bidentate coordination, which cannot be realized for the third 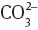ion in the case of the uranyl tricarbonate system – the third ligand coordinates only via a single oxygen atom. This implies that the hydration of the coordinating carbonate ions and, thus, their physicochemical properties are different in the uranyl(VI) tricarbonate species.

Fig. 5

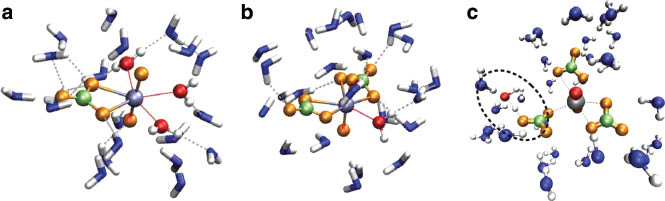
Snapshots obtained from QMCF MD simulations of (a) uranyl(VI) carbonate, (b) uranyl(VI) dicarbonate, and (c) uranyl(VI) tricarbonate. In the latter case, hydrolysis of a water molecule coordinating to one of the carbonate ions accompanied with a proton transfer is observed, thereby increasing the charge of the complex.

While in the case of the bidentately coordinated ligands the uranium atom can attract a significant amount of the ion’s electron density, this effect can be assumed to be less pronounced for the monodentate carbonate. Considering the overall charge of the uranyl(VI) tricarbonate complex of –4 a.u., it was not too surprising to observe a proton transfer event between a water molecule and the monodentate carbonate ion in the QMCF MD simulation, thereby reducing the total charge of the solute. Due to its negative charge, the newly generated hydroxyl ion was repelled by the [UO₂(HCO₃)(CO₃)₂]^3– complex and quickly migrated into the low-level region. At this point, the simulation had to be considered complete since the employed MM potential is not capable of properly describing a hydroxyl ion and the associated occurrence of proton-transfer events in aqueous solution. Thus, in order to investigate the properties of the resulting [UO₂(HCO₃)(CO₃)₂]^3– complex, a separate simulation had to be performed, this time employing the protonated system in the initial configuration.

Nevertheless, this simulation study provided important insights into the properties of uranyl(VI) carbonates in aqueous solution. Since the quantum chemical treatment is capable of describing the formation and cleavage of chemical bonds, species included in the high-level region are able to undergo chemical reactions in order to adopt a more favorable chemical composition. This is not possible for the majority of FF approaches, where the topology of the system remains constant throughout the simulation: existing bonds can never be cleaved and particles that are not bonded in the initial state cannot form a bond in later stages of the simulation. This property of classical simulation approaches may become a problem in those investigations where the correct composition of the species is not exactly known as it has been the case in MM simulation studies of uranyl(VI) carbonate complexes carried out in the past [92]. In this and similar investigations the presence of three carbonate species has been assumed, different protonation states have not been considered, and consequently, the simulations have been carried out with a different composition. The authors [92] have been aware of the problem arising from the use of empirically derived potentials in MD simulations, however, and pointed out that quantum chemically derived potentials can be assumed to yield more reliable results.

At present, the required computational effort of hybrid ab initio/MM simulations is too demanding to study dynamical properties occurring beyond the picosecond timescale via molecular dynamics as, for example, ligand exchange reactions involving the carbonate ions [97–99]. In order to study such phenomena in simulations, methods biasing the potential energy surface towards the occurrence of rare events have been developed [100–104]. By considering the dynamics of the simulation in context of the biasing potentials it is possible to obtain detailed information on the characteristics of rare events. Although the application of such methods have not been the focus of the work presented in the manuscript, it is planned to employ such techniques in the future to obtain information on kinetic properties beyond the achievable time-scale of unbiased MD simulations.

Another aspect of the observed proton-transfer event between water and one of the carbonate ions is the importance to also include solvent molecules into the quantum chemical treatment. In most QM/MM protocols, only the atoms of the solute species are included into the high-level zone, in which case the water molecule cannot be deprotonated and the proton-transfer event cannot take place.

To the best of knowledge, this QMCF MD study was the first to investigate uranyl carbonates using a QM/MM simulation approach, which highlighted the advanced capabilities of improved QM/MM methods such as the QMCF approach. Despite the impressive ability to account for proton-transfer events within the QM region, the imperative to stop the simulation as soon as the hydroxyl-ion migrates into the low-level region is still a major drawback. The reason to discontinue the simulation stems from the fact that in order to adequately describe the presence of hydroxyl or oxonium ions in the MM zone, the respective potential model has to be able to adequately describe proton-transfer events. The different description of intra- and intermolecular potentials employed in classical FFs and the application of a harmonic spring formulation to describe bonding interactions prevent the description of proton-transfer events by the majority of classical FF models. However, in recent years the development of reactive FF techniques [105–109] has enjoyed increasing interest. In addition to the widely used multistate empirical valence bond (MS-EVB) approaches [110–114], a number of dissociate FF descriptions treating intra- and intermolecular contributions on the same footing have been developed, among which the model of Garofalini and co-workers [107, 115, 116] proved to be particularly useful for the application in the context of a QM/MM simulation.

Here the difficulty arises that in order to assign molecules to either the QM or MM zone, the topology of the molecular units (i.e., which atoms form a water, hydroxide, oxonium, etc.) at each step of the simulation has to be known. Since this topology can change over time as protons are transferred between the individual species, the simulation software has to automatically monitor all occurring proton-transfer events and update the respective topology accordingly. In order to achieve this in molecular simulations, a simple yet effective update criterion has been proposed [117]. First, the component of the donor hydrogen distance r_DH parallel to the donor–acceptor distance r_DA is computed via vector projection:

Next, the ratio ρ between and r_DA is computed.

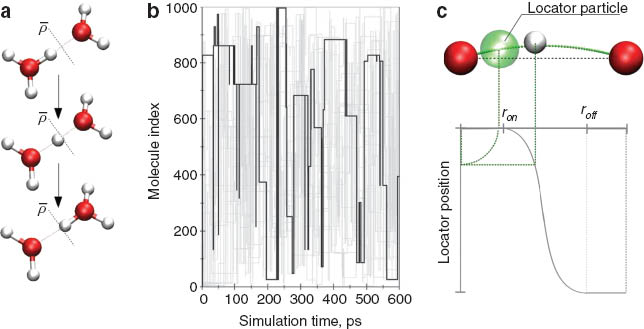
If this ratio exceeds a preset threshold 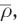the proton is assigned to the acceptor molecule (see Fig. 6a). It should be stressed at this point that although this procedure leads to a discontinuous assignment of the molecular topology, the underlying potential energy surface (i.e., the potential energy of the system and the resulting forces) remain continuous. This is achieved by treating all intra- and intermolecular contributions with identical potential functions. Due to the simple formulation of this update criterion avoiding angular and dihedral expressions, it can also be applied to monitor proton-transfer events between simple species such as:

Fig. 6

(a) Threshold criterion for the determination of proton-transfer events. If the projected donor–hydrogen distance with respect to the donor–acceptor distance exceeds the threshold 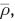the event is considered as successful exchange event. (b) Proton-transfer mapping monitoring all proton-transfer events obtained from a MD simulation of 1 M HCl. The path of one selected proton is highlighted. (c) In order to link subsequent proton-transfer events into a single diffusive entity, a locator particle smoothly connecting the donor and acceptor atoms is used. The respective position is determined via a switching function, using the projected donor–hydrogen distance as variable.

In addition, the lack of time-dependence in the criterion (e.g., the proton has to remain beyond the threshold for preset time interval t* prior to considering the event as an actual proton transfer) enables the application of this criterion in investigations that do not propagate the system via equation of motion as it is the case in Monte Carlo simulations and geometry optimizations.

By probing the number of registered proton-transfer events as a function of the threshold 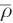in simulations of an excess proton in aqueous solution and 1 M HCl, an optimal threshold 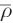in the range between 0.58 and 0.60 was determined [117]. This implies that the proton has to travel about 60 % of the donor–acceptor distance to consider the event as sustained proton transfer, while proton migrations remaining below are considered as short-time fluctuations. The resulting time-dependent molecular topology can then be depicted via a proton-transfer mapping, monitoring the index of the molecular unit currently carrying the proton as a function of time. In Fig. 6b, the proton-transfer map obtained from a simulation of 1 M HCl (17 HCl molecules in 1000 water molecules) using the Garofalini model for all 17 protons is depicted, highlighting the proton-transfer map of one particular proton. Each vertical line corresponds to a registered proton-transfer event, while the horizontal lines correspond to time intervals where the proton remains bound. Knowledge of the number of exchange events per time interval enabled the computation of the average proton-hopping rate as 0.25 ps^–1, i.e., on average one proton-transfer event occurs per 4 ps. While this number is smaller compared to the experimental estimation of 0.75 ps^–1, it is well within the range reported from various MS-EVB investigations as 0.16–0.5 ps^–1.

The deviation from the experimental value can result from inaccuracies of both computational models as well as in the experimental proton-hopping rate, which was determined from the experimentally determined (NMR) mean residence time of an excess proton in water [118] being approximately 1.33 ps [119]. However, since classical MD frameworks do not take nuclear quantum effects into account, tunneling contributions are not considered in the simulation studies. Consequently, the proton-hopping rate determined via classical MD has to be lower than the experimental one, irrespective of any inaccuracies in the theoretical and experimental techniques.

Knowledge of all molecules participating in the respective proton-transfer events enables the determination of the corresponding diffusion coefficient. At this point, it should be noted that proton migration does not correspond to the migration of an individual hydrogen atom: as long as the proton is bound to a water molecule, the diffusion is governed by the heavy oxygen atom. This motion is regularly interrupted by proton-transfer events, in which a hydrogen atom travels a rather large distance in a short time interval, thus leading to a large contribution to the overall diffusion coefficient. Wraight [119] estimated the latter based on the average oxygen-oxygen distance in pure water of 0.255 nm and the mean proton lifetime of 1.33 ps [118] as D_H+ = 8.1‧10^–9 m² s^–1. Due to their similar size, Wraight approximated the diffusion coefficient of the H₃O⁺ as that of the sodium ion D_Na+ = 1.3‧10⁻⁹ m² s^–1. Adding both values results in a “good, but perhaps fortuitous, agreement” [119] with the experimental value reported as 9.3‧10^–9 m² s^–1 [120, 121].

In order to apply this concept in the analysis of MD trajectories, subsequent proton-transfer events have to be linked into a single diffusive entity, which can be achieved by using a locator particle (green particle in Fig. 6c) [117]. As long as all hydrogen atoms of a H₃O⁺ are bound to the oxygen atom, the position of the locator particle corresponds to the latter. Upon transfer of any of the protons, an interpolation scheme is invoked to determine the coordinates of the locator, however, this interpolation is only applied if the projected donor–hydrogen distance r_DH is within the boundaries r_on and r_off. To ensure that oscillations of the hydrogen atom about its equilibrium position are not considered as diffusion, the boundaries are set to a distance of approx. 0.1 nm from the donor and acceptor atom, respectively. Once the proton transfer is complete, the locator position coincides with the coordinates of the acceptor atom and the procedure is repeated in the next proton-transfer event. The determination of the overall diffusion coefficient can then be easily performed over the trajectory of the locator particle using the Einstein relation

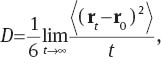
where r_t and r₀ are the position of the locator particle at times t and the time origin, respectively. By performing extensive tests of this procedure [117], it could be shown that the diffusion coefficient is largely independent of the settings for r_on/r_off and the threshold ratio as long as they are chosen in a reasonable chemical range. Not surprising, too low values for r_on and r_off result in a contamination of the locator trajectory due to the vibrational motion of the hydrogen atoms, which is reflected in a strong dependence of the resulting diffusion coefficient. Values above approx. 0.13 nm also result in notable change of the diffusion coefficient, because the interpolation is essentially disabled and the change in position of the locator particle upon proton migration corresponds to a step function (i.e., the position of the locator particle is instantaneously transferred from the donor to the acceptor oxygen). Different settings for the threshold 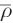do not result in any notable difference in the diffusion coefficient, if the boundaries r_on/r_off are set into the valid interval discussed above (approx. 0.1–0.13 nm).

The diffusion coefficients determined for an excess proton in water treated with the Garofalini model were found as 3.9·10^–9 m² s^–1, which again is well within the range determined by different MS-EVB models [110–114] being 2.9–8.3‧10^–9 m² s^–1. Again, the deviation to the experimental value determined as 9.3‧10^–9 m² s^–1 [120, 121] can be explained by inaccuracies in the model as well as the inability of classical MD simulations to include nuclear quantum effects.

With the implementation of the outlined framework, automatically detecting proton-transfer events to update the time-dependent topology, it recently became possible to apply the dissociative model of Garofalini in the context of QMCF MD simulations [117]. The advantage of this methodical extension is the possibility to continue QM/MM simulations whenever a hydrolysis reaction takes place in the QM region and the resulting (de-)protonated water molecule migrates into the low-level region. Furthermore, since parameters for Na⁺ and Cl^– have been developed in the context of this water model [115], it is also possible to describe HCl and NaOH solutions. This enables the execution of QM/MM studies at different pH values, a feature of which only a few simulation approaches are capable. Combined with the capabilities of the QMCF procedure, any kind of solute can be included in a system at a given pH value, and it is thus possible to study proton- and hydroxide-induced reactions with this approach and test simulations have already confirmed the applicability of this novel simulation technique [117].

With the successful application of QM/MM techniques for the study of hydrated species, the extension of this method to more complex scenarios appears highly desirable. A particularly challenging topic in solution chemistry is the study of interfaces near liquid systems. Due to their importance in fields such as heterogeneous catalysis as well as electrochemistry, solid/liquid interfaces have obtained a prominent role in research focused on solution chemistry. While cluster models [122–124], treating a small island of the surface and bound molecules on a quantum chemical basis, have proven to be versatile QM/MM approaches for the study of surface phenomena in the past, the capacities of modern computational facilities provide the means to include entire layers of the system in a 2d-periodic QM/MM description. Figure 7a depicts a possible partitioning of a MgO/H₂O surface into a high- and low-level zone. In this example, two layers of a 8 × 8 atom slab of the solid plus one whole layer of solvent molecules is included in the QM regions, while the remaining particles are included in the MM region. While the solid can be expected to remain bulk-like if a sufficient number of layers is included in the MM part (early test indicated that approx. 10–20 MM layers are sufficient), a boundary region employing a constraining potential similar as in simulations using spherical boundary conditions is required to avoid the evaporation of particles.

Fig. 7

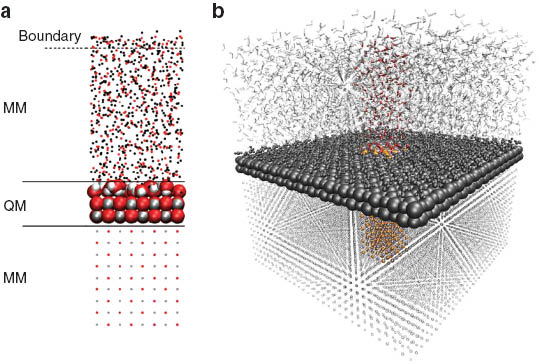
By utilizing a 2d-periodic quantum chemical description, the extension of the QMCF approach to interface systems can be achieved. (a) Sketch of the different regions for the example of the MgO/H₂O interface. (b) The simulation system shown in color acts as unit cell for the 2d-periodic treatment, periodic replicas are depicted in gray.

The point charge embedding technique outlined earlier can be used to modulate the electron density in this case as well. Similar as in the case of the QMCF approach, this methodology will provide the possibility to investigate interface phenomena without the requirement of accurate solid/liquid non-Coulombic potentials. In addition, the interaction between solute molecules in contact with the surface can be expected to be different from the interaction between molecules in the bulk. While this influence is in general not considered in classical, pairwise additive potentials, the QM treatment takes these effects into account as well. Furthermore, the QM treatment provides the means to describe proton-transfer events between the solid and molecules of the liquid from first principles. A combination of the outlined QM/MM procedure for proton transfer with a 2d-periodic description is thus a very promising approach for a computational investigation of surface phenomena.

Although present computational facilities might not provide the means to treat a system as outlined in Fig. 7a, investigations of solid/gas interfaces employing this simulation framework are already feasible. Figure 7b depicts a snapshot of a QM/MMMD simulation of a MgO covered by a water monolayer. Only the atoms depicted in color are considered in the actual QM/MM simulation (i.e., the 2d unit cell), whereas particles depicted in gray correspond to periodic images. Two layers of the MgO system and all water molecules are included in the quantum chemical treatment, the remaining 10 layers of the solid are included in the MM region. This system can be seen as a primer for more advanced investigations of this system in contact with bulk water.

Although the treatment of metal surfaces is conceptually very similar to the example presented above, a number of difficulties have to be addressed to apply the QM/MM scheme to metal/liquid interfaces. In particular, since the point charge embedding technique cannot be employed to modulate the electron density at the QM/MM interface within the solid part, the pseudo-potential approach [125, 126], an effective potential mimicking the presence of an atom, provides a promising alternative route. Although pseudo-potentials are widely used in electronic structure calculations, they have to be newly constructed in order to be compatible with the QM/MM protocol, which is a highly nontrivial task. Nevertheless, future applications of the outlined methodology could not only provide the means to compute solid/liquid interfaces, but can also be extended for the treatment of solid/solid contacts as well as the treatment of metal oxide supported atomic (mono)layers in contact with a gaseous or liquid system, thus providing the means to investigate a broad spectrum of chemical systems relevant for various disciplines in science and engineering.

In summary, the novel developments discussed in this contribution can be expected to significantly enhance the capabilities of QM/MM approaches for the treatment of liquids and solutions and related areas such as surface and interface chemistry already in the near future. These developments became possible due to the continuous evolving capacities of computational infrastructure, which is reflected by the possibility to treat systems of increasing size with increasing accuracy. Since at the same time the benefit/cost ratio of computational resources is continuously increasing as well, theoretical methods are already considered as an indispensible tool providing an alternative route to study chemical phenomena, complementing experimental approaches. Since the acceleration of theoretical methods via linear scaling techniques [127–134] and the implementation of algorithms in the context of graphical processing unit (GPU) [135–142] enable a further dramatic increase in the capabilities of computational methods, these trends can be expected to persist and even accelerate within the next decades.