Kinetic studies on cyclopalladation in palladium(II) complexes containing an indole moiety

Introduction

Cyclopalladation has been intensely studied not only for the coordination and organometallic chemistry but also for the importance of Pd–C intermediates in catalytic organic syntheses. Many Pd–C bond formations including cyclopalladation have been widely developed to date, affording deep insights into the reaction mechanisms for many useful homogeneous catalytic reactions [1–10]. Especially Pd–C binding complexes, which are becoming important intermediates in catalytic systems, have been formed in general by the oxidative insertion of the organic substrates or by the reaction with the C–H activated species [1–10].

On the other hand, the indole ring of the tryptophyl side chain residue having the highest hydrophobicity among natural α-amino acids [11] is known to provide a hydrophobic microenvironment for enzyme catalysis, protein stability, specific binding of molecules, etc. [12–15]. It is involved in electron-transfer pathways, and formation of the indolyl radical at a tryptophyl residue has been established for the intermediate, compound I, formed in the catalytic cycle of cytochrome c peroxidase (CcP) [15–19]. It is known to form covalent bonds with Pd(II), etc. through the nitrogen and carbon atoms [20–30] besides π–π interactions with aromatic nitrogen donors in metal complexes [30–34]. The pendent indole ring in metal complexes of tripodal ligands was found to bind to Cu(I) by η² coordination of the C2=C3 bond to form a tetrahedral structure [20]. Similar η² coordination has been recently detected in biological systems for a Cu chaperone CusF [21, 22]. On the other hand, Yamauchi et al. reported Pd(II)–C3 bond formation in complexes with indole derivatives [23–25]. Kostić et al. developed unique artificial peptidases using Pd(II) and Pt(II), which recognize the indole moiety and cleave the adjacent amide or peptide bond specifically [26–29].

With these points in mind, we have synthesized and characterized Pd(II)–indole C2 bonding complexes and analyzed their Pd–indole carbon bond formation through cyclopalladation [30, 35–38]. We present here our recent studies on reversible Pd–indole C2 carbon bond formations in complexes of 2N1O-donor ligands with an indole and phenol moiety [35–37] and on a low concentration-favored Pd–C bond formation of the complex with a 2N-donor ligand with an indole moiety (Scheme 1) [38]. These results may be important for deeper understanding of the reaction mechanism of the catalytic conversion for the organic substrates having Pd–C intermediate as well as the significance of metal–indole complexes in biological systems.

Scheme 1

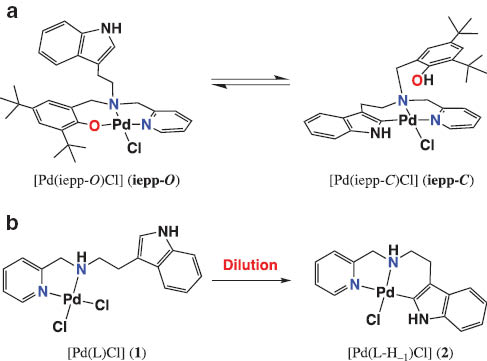
Reversible Pd–indole C2 carbon bond formations: (a) a complex of 2N1O-donor ligand with an indole and phenol moiety; (b) low concentration-favored Pd–C bond formation of the complex with a 2N-donor ligand with an indole moiety.

Cyclopalladation of Pd(II) complexes with 2N1O-donor ligand with an indole ring: interconversion between phenolate complex and indole-binding complex

The pendent indole ring in the Pd(II) complex of a 2N1O-donor ligand involving a phenolate, a pyridine, and a tertiary amine as metal binding sites ([Pd(iepp-O)Cl] in Scheme 1a) replaced the phenolate group under suitable conditions to form a complex with a direct Pd–C2 bond ([Pd(iepp-C)Cl] in Scheme 1a) [35]. In this Pd–C bond formation mechanism, the proton dissociated from the indole ring binds to the phenolate moiety. The conversion property depends on the nature not only of the O-donor but also of the aromatic N-donor atoms.

Effect of N-donor properties on cyclopalladation

In order to understand the participation of the pendent indole ring of Pd(II) complexes in Pd–C(indole) bond formation, we synthesized the Pd(II) complexes of 2N1O-donor tridentate ligands having a different aromatic N-donor such as imidazole (Hieip) and methyl-substituted imidazole and pyridine derivatives (HMe₃-ieip and HMe-iepp, respectively) as a substitute for the pyridine ring in ligand Hiepp (Fig. 1) [35]. Among the methyl-substituted pyridines as aromatic N-donors, 2-methylpyridine has been reported to show weaker donor properties than pyridine itself due to steric requirement [36, 39]. However, the steric effect in 4,5-dimethylimidazole is smaller in comparison to that in pyridine due to a larger N–C–Me angle in the pentagonal ring.

Fig. 1

Structures of 2N1O-tridentate ligands with a pendent indole moiety and various aromatic nitrogen donors.

The X-ray structures of the phenolate complexes (Fig. 2) revealed the square-planar four-coordinated Pd(II) complexes. However, the Pd–N bond length and the distortion from the coordination plane depended on the N-donor properties. The Pd–aromatic nitrogen (N_arom) bond length in this series was found to be longer for the methyl-substituted complexes, the order being ieip-O (1.986(4) Å) < iepp-O (2.011(4)) < Me₃-ieip-O (2.015(7)) < Me-iepp-O (2.050(2)), while the Pd–tertiary amine nitrogen (N_amine) bond length showed the opposite characteristics [36]. The results suggest that the methyl-substituted pyridine and imidazole are weaker N-donors than unsubstituted ones. Further, the angles of O–Pd–N_arom and Cl–Pd–N_amine are affected by the methyl-substituted aromatic nitrogen ligand; for example, the Cl–Pd–N_amine angles are distorted from 180° in the order ieip-O (176.9(1)°) ≤ iepp-O (176.2(1)°) ≤ Me₃-ieip-O (175.2(2)°) < Me-iepp-O (170.47(6)°). Thus, the methyl substituent on the aromatic N-donor causes distortion from the square plane due to its steric hindrance [36, 39].

Fig. 2

Molecular structures of Pd(II)–phenolato complexes: (a) [Pd(iepp-O)Cl] (iepp-O), (b) [Pd(ieip-O)Cl] (ieip-O), (c) [Pd(Me₃-ieip-O)Cl] (Me₃-ieip-O), and (d) [Pd(Me-iepp-O)Cl] (Me-iepp-O).

The indole-binding complexes (Fig. 3) revealed different structural features from the phenolate complexes (Fig. 2); the Pd–C bond length in these complexes is affected by the methyl substituent of the aromatic N-donor, as observed for the Pd–C bond length of ieip-C (1.972(3) Å) and of Me₃-ieip-C (2.005(6) Å). In comparison to the phenolate complexes, all of the indole–binding complexes have a longer Pd–N bond, suggesting that the carbanion donor of the indole moiety is more donating to the Pd ion. On the other hand, the differences in the angles of C–Pd–N_arom and Cl–Pd–N_amine in indole-binding complexes are rather small in comparison to the phenolate complexes, indicating that the Pd–indole bond requires a “flat” geometry [39]. It is interesting to note in Fig. 3 that the OH group of the phenol moiety in complex iepp-C is directed toward the center of the Pd–C bond with weak interaction, while that in Me₃-ieip-C is directed toward the outside of the molecule. Complexes ieip-C and Me-iepp-C were revealed to be a 1:1 mixture of the structures with these different OH group directions, and as a result, the phenol OH group was disordered. These structural differences suggest that the electron density of the Pd–C bond may be ordered as Me₃-ieip-C < ieip-C = Me-iepp-C < iepp-C, which may correlate with the Pd–O to Pd–C conversion rate and the stability of the indole-binding complexes.

Fig. 3

Molecular structures of Pd–indole binding complexes: (A) [Pd(iepp-C)Cl] (iepp-C), (B) [Pd(ieip-C)Cl] (ieip-C), (C) [Pd(Me₃-ieip-C)Cl] (Me₃-ieip-C), and (D) [Pd(Me-iepp-C)Cl] (Me-iepp-C). (a) and (b) are the structures of two isomers with a different OH direction and observed as disordered.

All of the phenolate complexes convert to the indole-binding complexes with a color change from orange to pale yellow, in which typical absorption bands of the phenolato complexes gradually decreased with a new band appearing with isosbestic points [36]. Such spectral changes were also observed in the ¹H NMR spectra; the signals of the phenolate complexes gradually disappeared, and those of the indole-binding complexes appeared without proton signals of any other products. Further, the formation ratio from the phenolate to indole-binding species depends on the temperature. These results suggest reversible conversion and an intramolecular process, which is expressed by the following equation:

where k₁ and k_–1 denote the rate constants of the forward and backward processes, respectively, and the equilibrium constant is expressed by K = k₁/k_–1 = [indole-binding complex]/[phenolate complex]. All the reversible conversions could be analyzed by the first-order kinetics, and the observed first-order rate constant k_obs is expressed by k_obs = k₁ + k_–1 [40, 41]. From the dependences of K and k_obs on temperature, the thermodynamic parameters (ΔH° and ΔS°) and activation parameters (ΔH₁^‡ and ΔS₁^‡ for k₁ path, and ΔH_–1^‡ and ΔS_–1^‡ for k_–1 path, respectively) for all the complexes in this study were determined as shown in Table 1.

Table 1

Thermodynamic and activation parameters for interconversion between phenolate and indole-binding species [36].

Complex	K		k 1 path		K – 1 path		Temperature range
	ΔH°/kJ mol–1	ΔS°/J mol–1K–1	ΔH1‡/kJ mol–1	ΔS1‡/J mol–1 K–1	ΔH–1‡/kJ mol–1	ΔS–1‡/J mol–1 K–1
iepp	1	1	99 ± 2	–47 ± 7	98 ± 2	–47 ± 6	60–90 °C
ieip	12	23	100 ± 5	–51 ± 15	88 ± 6	–74 ± 16	60–90 °C
Me3-ieip	11	23	104 ± 1	–39 ± 1	94 ± 1	–61 ± 1	60–90 °C
Me-iepp	10	27	102 ± 2	–26 ± 7	92 ± 1	–54 ± 4	50–80 °C

In comparison to the iepp complex system, all the other complexes showed large ΔH° and ΔS° values, which indicates that the formation ratio of the indole-binding species increases with the increase of the reaction temperature. The iepp and Me-iepp complex systems showed that the thermodynamic parameters are significantly different due to the effect of steric hindrance, while the ieip and Me₃-ieip systems showed very similar thermodynamic parameters.

The activation enthalpies (ΔH₁^‡) of all the complexes are estimated to be ca. 100 kJ mol^–1, which suggest that the sum of the binding energy changes with the conversion in all the complexes is similar. On the other hand, the negative activation entropies (ΔS₁^‡) indicate that the mechanism of the conversion upon achieving the transition state is associative, that is, the five-coordinated intermediate is preferred in the conversion [42–44]. Further, the order of the ΔS₁^‡ value is as follows: Me-iepp (ΔS₁^‡ = –26 J mol^–1 K^–1) > Me₃-ieip (–39) > iepp (–47) > ieip (–51), which agrees well with the order of the distortion from the square plane of the Pd coordination sphere in the phenolate complexes. The ΔS₁^‡ indicates the changes of the freedom of the structural change upon achieving the transition state [41], and therefore the ΔS₁^‡ is affected by the distortion of the Pd coordination sphere. Thus, the steric hindrance is more effective in comparison to the basicity of the nitrogen donors in the conversion to the indole-binding species.

Effect of O-donor properties on cyclopalladation

For further understanding of the interconversion between the phenolate and the indole-binding complexes having a 2N1O-donor ligand, it is important to investigate the effect of the O-donor property on the reactivity. We have prepared a series of indole-containing ligands with various substituted phenol moieties or carboxylic acid having a different acidity (Fig. 4).

Fig. 4

Structures of 2N1O-tridentate ligands with a pendent indole moiety for investigating the effect of O-donor properties.

X-ray crystal structure analysis revealed that these structures (Fig. 5) are very similar to those of complex iepp-O and its derivatives (Fig. 2) [35, 36]. The Pd–O bond length increased in the order iepp-MeO-O (1.989(2) Å) < iepp-NO₂-O (2.009(8) Å) < iepc-O (2.026(2) Å). This tendency is in agreement with the order of the pK_a value of the O-donor [45, 46].

Fig. 5

Structures of Pd(II)–phenolato complexes: (a) [Pd(iepp-MeO-O)Cl] (iepp-MeO-O), (b) [Pd(iepp-NO₂-O)Cl] (iepp-NO₂-O), and (c) [Pd(iepc-O)Cl] (iepc-O).

When complex iepp-MeO-O in DMSO and DMF was kept at 50 °C for a few days, a color change from orange to yellow occurred to give the indole-binding complexes [37]. The formation ratio of the indole-binding complex to the phenolate complex was higher for the complexes of the ligands with a higher pK_a value of the conjugate acid of O-donor in the order, iepp-MeO > iepp > iepp-NO₂ > iepc [37]. The results indicate that the complex of the ligand having a more basic O-donor shows higher formation ratio. The ratio of the phenolate complex to the indole-binding complex was temperature-independent in the range from 40 to 80 °C, i.e., ΔH° ~ 0 kJ mol^–1.

All the conversions from the phenolate complex to the indole-binding complex could be analyzed by the first-order kinetics, suggesting a reversible reaction and an intramolecular process. Therefore, the activation parameters for the conversion were determined from the dependence of the observed first-order rate constants (k_obs) on temperature, and listed in Table 2.

Table 2

Activation parameters for formation of the indole-binding Pd(II) complexes of 2N1O-donor ligand having a different O-donor moiety in DMF [37].

Complex	ΔH‡/kJ mol–1	ΔS‡/J mol–1 K–1	104kobs333/s–1a	Temperature range
iepp	92 ± 4	–64 ± 10	0.122	40–70 °C
MeO-iepp	96 ± 2	–51 ± 6	0.122	40–70 °C
NO2-iepp	72 ± 1	–94 ± 3	3.64	40–70 °C
iepc	38 ± 2	–170 ± 6	107	30–60 °C

^aThe k_obs value at 60 °C estimated from the activation parameters.

The observed first-order rate constants at 60 °C (k_obs³³³ in Table 2) indicate that the conversion rate for the indole-binding Pd(II) species also depends on the O-donor properties; for the complexes of the ligands with a lower pK_a value of the conjugate acid of O-donor exhibited a faster rate of conversion to the indole-binding species in the order iepp-MeO < iepp < iepp-NO₂ < iepc. The plot of the activation energy vs. the pK_a value of the conjugate acid of oxygen donor is shown in Fig. 6. This result clearly indicates that the barrier of the conversion correlates with the O-donor ability. In other words, the barrier correlates with the bond strength of Pd–O, the order of which is MeO-phenol < NO₂-phenol < COO^–. The rate-determining step of the conversion from the phenolate complex to the indole-binding complex may involve the Pd–O bond cleavage besides the C–H bond cleavage process.

Fig. 6

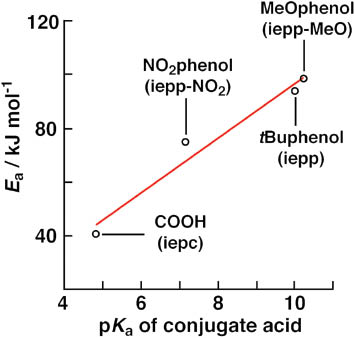
Activation energies (E_a) as a function of the pK_a values of conjugate acids of the ligand O-donor groups.

It is generally agreed that cyclopalladation reactions of aryl compounds proceed by an electrophilic substitution by Pd(II) ions [9, 42–44, 47–53]. The electrophilicity of the Pd(II) center to the indole moiety should increase with the decreasing pK_a value of the ligand OH group, and our experiments have shown that the reaction rates are in the order iepp-MeO-O < iepp-O < iepp-NO₂-O < iepc-O (Table 2), which is in agreement with the decreasing order of the pK_a values of the corresponding ligands. On the other hand, the formation ratio of the indole-binding complex to the O-donor complex was higher for the complexes of the ligands with a higher pK_a value in the order iepp-MeO-O > iepp-O > iepp-NO₂-O > iepc-O. Further, the addition of a base enhanced the formation of the indole-binding complex, which indicates that basic conditions are favorable for the present cyclopalladation [37]. Thus, the O-donor to C-donor conversion reaction may be explained by a mechanism involving a five-coordinate intermediate [36, 37, 42–44].

Cyclopalladation of Pd(II) complexes with 2N-donor ligands with a pendent indole ring: low concentration-favored cyclopalladation

As mentioned in the above section, the complexes of 2N1O-donor ligands having both a phenol and an indole moiety are interconvertible in solution between the Pd(II)–phenolate and Pd(II)–indole complexes [35]. The conversion kinetics of the similar geometry depend on the aromatic N-donors and the O-donor properties [36, 37], and especially the pK_a value of the O-donor is very important for conversion to the indole-binding species [37]. The results may suggest that the role of exogenous donors, such as solvent molecules, is important for formation of the Pd–C bond via Pd–O intermediate. In order to understand the mechanisms of the interconversion between the Pd(II)–phenolate and Pd(II)–indole complexes in detail, we synthesized the Pd(II) complex of a simple 2N-donor ligand containing a pendent indole moiety and investigated conversion of the dichloro complex to the indole-binding complex in DMSO. From the detailed reaction analyses, we concluded that conversion to the indole-binding complex depends on the concentration of its solution, that is, a low concentration-favored the Pd–C bond formation (Scheme 1) [38].

The Pd(II) complex of a 2N-donor ligand, [Pd(L)Cl₂] (1), where L is 3-(2-pyridylmethylamino)ethylindole (L), has a square-planar geometry with the pyridine and amine nitrogen atoms and two chloride ions (Fig. 7). The indole-binding species of the ligand L could be also isolated as [Pd(L-H_–1)Cl] (2) by addition of 1 equiv of triethylamine [38], and was supported by X-ray crystal structure and physicochemical measurements. Complex 2 exhibited the characteristic UV-vis absorption band for the indole-binding species at 307 nm, which is in good agreement with the other indole-binding species [54]. The conversion from 1 to 2 could not be detected in DMSO-d₆ (0.1 M solution) at 60 °C, which was different from the observation on the complexes of the previous 2N1O donor-ligands.

Fig. 7

Formation reactions and molecular structures of Pd(II) complexes with a 2N-donor ligand (L) having an indole moiety; [Pd(L)Cl₂] (1) and [Pd(L-H_–1)Cl] (2).

However, at a lower concentration of 1 (< ca. 10 mM), some proton signals of new species (2) appeared with concomitant disappearance of the signals of 1 even at room temperature. The results in Fig. 8 clearly show the concentration dependent conversion from 1 to 2 without any decomposition. The low concentration-favored conversion of [Pd(L)Cl₂] (1) to [Pd(L-H_–1)Cl] (2) in DMSO can be expressed by the following equation:

Fig. 8

¹H NMR spectra in DMSO-d₆ at room temperature (a) and the absorption spectra in DMSO at 25 °C (b) at various initial concentrations (C_Pd) of complex 1. The filled and open circles in (a) denote the signals of complexes 1 and 2, respectively.

The equilibrium constant K = [2][H⁺][Cl^–]/[1] could be determined to be K = 5 × 10^–8 M² from the ¹H NMR spectral data (cf. Fig. 8a). This K value was also estimated to be in the order of 10^–8 M² from the UV-vis spectral data (cf. Fig. 8b) [38].

The initial rates analyses [41, 55] for this conversion by dilution of 1 revealed that the initial rate (v) linearly depended on both the initial concentration of 1 (C_Pd) and the inverse of the concentration of Cl^– (1/C_Cl), i.e., v = kC_Pd/C_Cl, but the v was independent of the proton concentration [38]. The results suggest that the reversible dissociation of a coordinated Cl^– ion from 1 is involved in the forward reaction via a solvated complex, such as [Pd(L)Cl(DMSO)]⁺ [40, 56–60] as shown in Scheme 2.

Scheme 2

Proposed conversion mechanism of Pd(II) complexes [Pd(L)Cl₂] (1) and [Pd(L-H_–1)Cl] (2) without base in DMSO. The rate constants were estimated by the kinetic analyses for the 2-to-1 conversion under the pseudo first-order conditions (C_HCl′ >> C_Pd).

The conversion of 2 to 1, that is, the backward reaction in eq. 2 could be kinetically analyzed under the pseudo first-order conditions; [H⁺] and [Cl^–] (= C_HCl′) are much higher than C_Pd: the decrease of 2 was expressed by –d[2]/dt = k_obs[2] at C_HCl′ >> C_Pd, where k_obs is the conditional pseudo first-order rate constant. The dependence of k_obs on C_HCl′ was successfully analyzed by applying the steady-state approximation [40, 41] for the intermediate I in the reverse reaction mechanism of the 1-to-2 conversion (Scheme 2) [38]. Thus, the 2-to-1 conversion was also found to proceed via the solvated intermediate, [Pd(L)Cl(DMSO)]⁺.

The reaction mechanism of the low concentration-favored 1-to-2 interconversion involves the solvated intermediate [Pd(L)Cl(DMSO)]⁺ (Scheme 2). On the contrary, no intermediate was involved in the phenolate-to-indole conversion in Pd(II) complexes of 2N1O-donor ligands, which intramolecularly proceeded via a five-coordinated transition state [36, 37]. It is noted that the 1-to-2 conversion is initiated by the Cl^– interchange with DMSO in 1. This reaction step does not occur in all the phenolate-to-indole conversion system of the complexes of 2N1O-ligands mentioned in the above section [35–37]. The reaction step of the [Pd(L)Cl(DMSO)]⁺ intermediate to give 2 (k₂ and k_–2 paths in Scheme 2) may correspond to “overall” phenolate-to-indole conversion of the 2N1O-donor ligand complexes, because both these reactions involve three steps; C–H bond cleavage, Pd–C bond formation, and the dissociation of one coordinated ligand. The rate constant k₂ for the indole-binding process of [Pd(L)Cl(DMSO)]⁺ was estimated to be >> 7.6 × 10^–3 s^–1 (Scheme 2), which is much larger than the rate constant for the phenolate-to-indole conversion system [36, 37]. The difference can be ascribed to the difference of the pK_a values, that is, the proton affinity of DMSO is much lower than that of the phenolate moiety.

This concentration-dependent conversion can be assigned to the concentration-dependent 1-to-2 conversion consisting of two successive thermodynamically controlled processes. Both processes prefer lower concentrations of dissociated free ions such as Cl^– and H⁺, which is just the case of lowering the concentration of the precursor complex 1. This is the reason why the 1-to-2 conversion is low concentration-favored.

Summary

This review is focused on characterization of Pd(II) complexes having a pendent indole moiety and their conversion mechanism to indole-binding species. The conversion between the phenolate and indole-binding complexes is dependent on some important factors. One of them is the N-donor property of the ligands and especially the steric requirement of the N-donor, which can cause distortion of the Pd(II) complexes from the square-planar structure, and both these factors affect the kinetics of conversions. On the other hand, the pK_a value of the O-donor is also important especially for deprotonation of the O–H bond and protonation of the coordinated O-donor concomitant with the indole C–H bond cleavage. Further, the concentration-dependent Pd–C bond formation in the Pd(II) complex of a 2N-donor ligand was also described. It can be understood on the basis of the above fundamental results from the 2N1O-donor systems. These studies further suggest that in some cases the Pd-catalyzed cross-coupling reaction may proceed through possible formation of a solvated complex intermediate at low concentrations. Thus, the present findings may be important for understanding the reaction mechanism of the catalytic conversion for the organic substrates having Pd–C intermediate and construction of highly efficient catalytic systems.