Normal and shear delamination of paperboards

2.1 DCB and SDCB specimens

Figures 1 and 2 show the schematics of the DCB and the SDCB, respectively. As seen in the figures, both specimens involve two beams with a strip of paperboard glued between them. In addition, the direction of loading and the parameters recorded during experiments are also visible in Figures 1 and 2. The DCB and SDCB substrates are made of a steel sheet and an aluminum rectangular tube, respectively. Table 2 lists the configurations for each specimen. Due to practical considerations, the paperboard strip length was set to 280 mm instead of the 300 mm proposed by Ebrahimijamal et al. (2025) for SDCB while maintaining the same total length of specimens and initial crack length. As a result, the far 20 mm end of the SDCB specimens did not include any paperboard.

Figure 1:

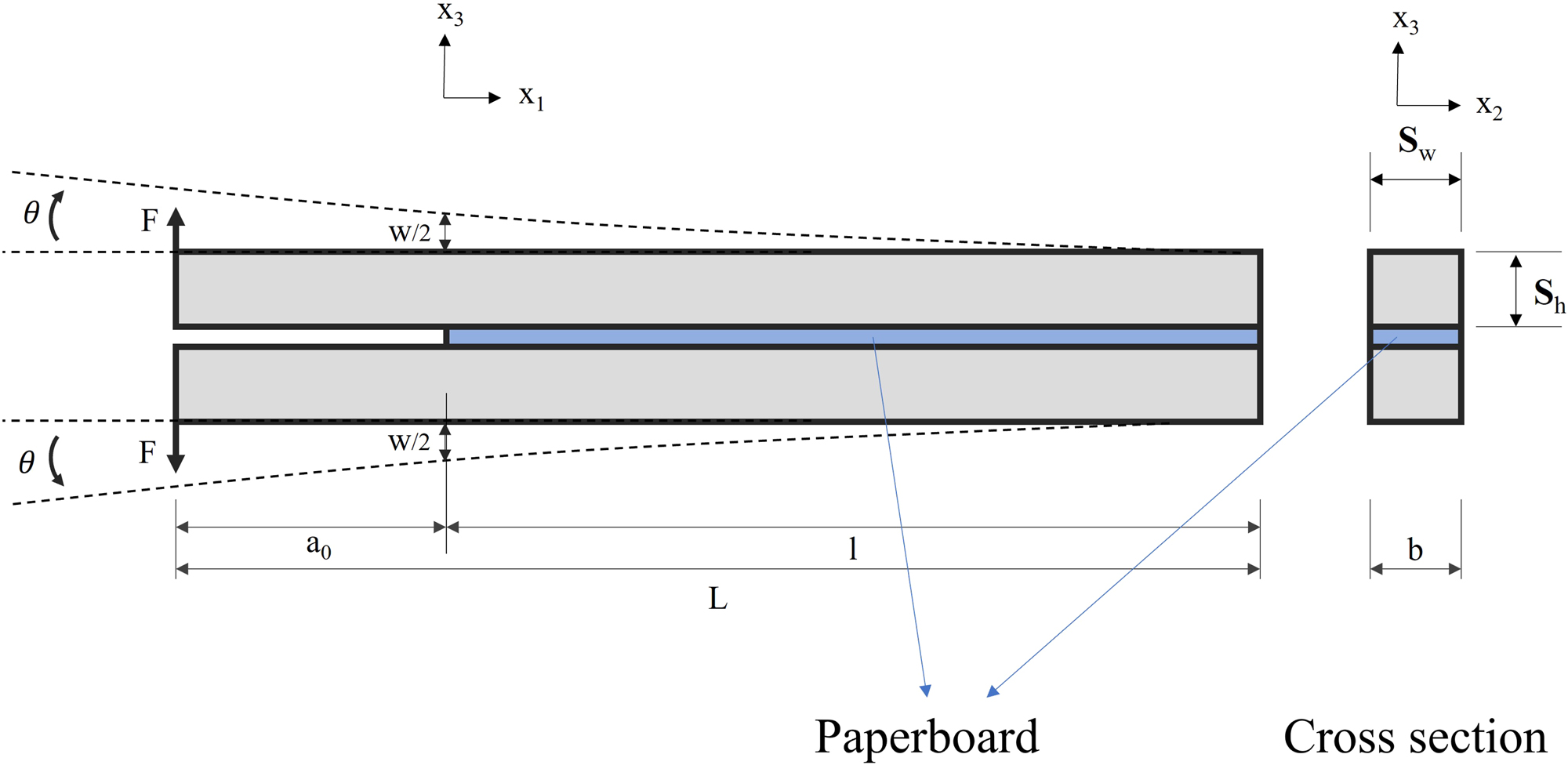
A schematic of DCB. Displacement and rotation are exaggerated.

Figure 2:

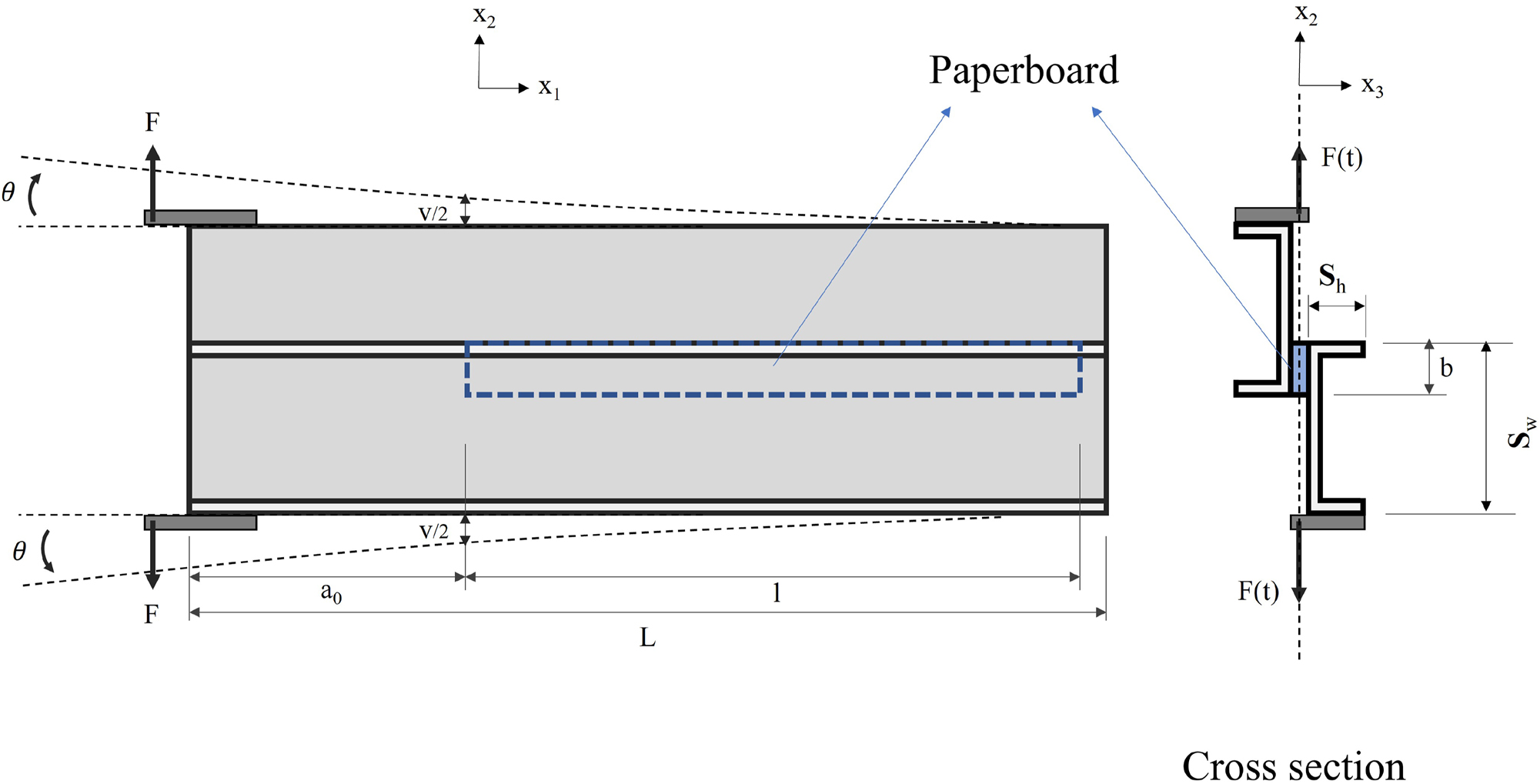
A schematic of SDCB. Displacement and rotation are exaggerated.

2.2 Specimen fabrication

In this work, a similar manufacturing procedure as Biel et al. (2022); Ebrahimijamal et al. (2025) is used. Fabricating DCB and SDCB specimens entails a few general steps. First, the beams must be polished for better adhesion and to avoid crack growth at the interface between the paperboard and the beams. Second, the paperboard and dry-mount tissue are cut into suitable sizes, generally wider than the final width. Third, two beams, two layers of dry-mount tissue, and a paperboard strip are placed and fixed in clamps before being transported into the oven. Considering the easier geometry to handle, ordinary commercial clamps are sufficient for DCB specimens. However, for SDCB specimens, the same custom-designed clamps as in Ebrahimijamal et al. (2025) are used to ensure consistency in width and pressure during curing and among specimens. It is worth mentioning that the C-shaped beams were cut from a single rectangular tube with a wall-thickness of 4 mm. Fourth, all specimens are cured in an oven heated to 90 °C for at least 30 min. At this temperature, the dry-mount tissues are activated, and our experience showed that at least 30 min of curing is necessary for successful adhesion. Fifth, the specimens are immediately transferred into a climate room with a humidity of 50 % ± 2 % and a temperature of 23 °C ± 1 °C. Lastly, the excessive or overlapping portions of the paperboard and dry-mount tissue are trimmed to the final width as specified in the specimen design. This overlapping ensures complete and consistent adhesion along the length of the specimen, which is required to achieve accurate results. At least five DCB and ten SDCB experiments were conducted on each paperboard.

2.3 Test procedure

The same testing machine and equipment as used by Biel et al. (2022); Ebrahimijamal et al. (2025) were used in this research, where the specimens were installed vertically, and the displacement was applied horizontally (see Figure 3). A shaft encoder, two LVDTs, and a load cell on the machine were used to record the rotation at the machine heads, the deformation at the crack tip termed as “separation”, and the corresponding force during the testing process. Unlike the DCB specimens, the weight of the SDCB specimen is considerable. As a result, their weight were balanced out with a few rubber-bands attached to the upper end of the specimens. All specimens were kept in the climate room for at least 24 hours before testing to ensure they reached equilibrium with the room’s climate conditions. The fracture surfaces of specimens were monitored after each experiment to ensure that the crack had initiated and grown inside the thickness of the paperboard, not the gluing interface.

Figure 3:

Test procedure. a) DCB test procedure; b) SDCB test procedure.

Figure 4 shows post-mortem fracture surfaces from the DCB and SDCB specimens. Paperboards 1, 3, and 4 exhibit similar fracture surfaces in both shear and normal modes. However, Paperboard 2 shows delamination between the middle (brown) and bottom (brown) plies in SDCB tests, while in DCB tests, delamination occurs between the top (white) and middle (brown) plies.

Figure 4:

Fracture surfaces. a) DCB fracture surfaces; b) SDCB fracture surface.

ZDT experiments were conducted to supplement the DCB tests; see the ZDT delamination surfaces in Figure 5. For paperboards 1, 3 and 4, ZDT delamination is similar to that observed in the DCB tests, as expected. However, a discrepancy arose in the fracture surfaces between the DCB and ZDT tests for Paperboard 2, which both tests measure normal mode delamination. DCB tests show delamination between the top and middle plies, while ZDT tests align with SDCB results and show delamination between the middle and bottom plies. This difference may be attributed to the higher test speed of ZDT and the increased brittleness of paperboard at higher displacement rates.

Figure 5:

ZDT fracture surfaces.

A digital microscope was positioned in front of the DCB test specimens to observe fiber deformation and delamination in the paperboard, facilitating a better understanding of fracture mechanisms during testing. However, conducting a microstructural study on the SDCB specimens was not feasible due to the asymmetry of the specimen geometry and limited microscope access, which prevented reliable imaging of the paperboard. When it comes to high-framerate, high-resolution microscopy, saving each photo introduces latency and larger time intervals as the photo count increases. Thus, resolution and time intervals were determined through trials. Our optimized microscope setting captures a photo every 4 s at a resolution of 2,048×1,536, synchronized with the testing machine so that the initial image is taken before any displacement is applied.

2.4 Experimental data

As mentioned above, the separation, the reaction force, and the rotation of the beams were recorded during the experiments. Note that other parameters have been recorded as well, but they are not part of this analysis. The reaction force-separation and rotation-separation curves for all experiments in both normal and shear mode experiments, DCB and SDCB, respectively, are presented in Figures 6 and 7. The reaction force-separation and rotation-separation trends are similar in both normal and shear modes, but the magnitude differs considerably. Later in this paper, these experimental data are used to derive the traction-separation laws and calibrate our model.

Figure 6:

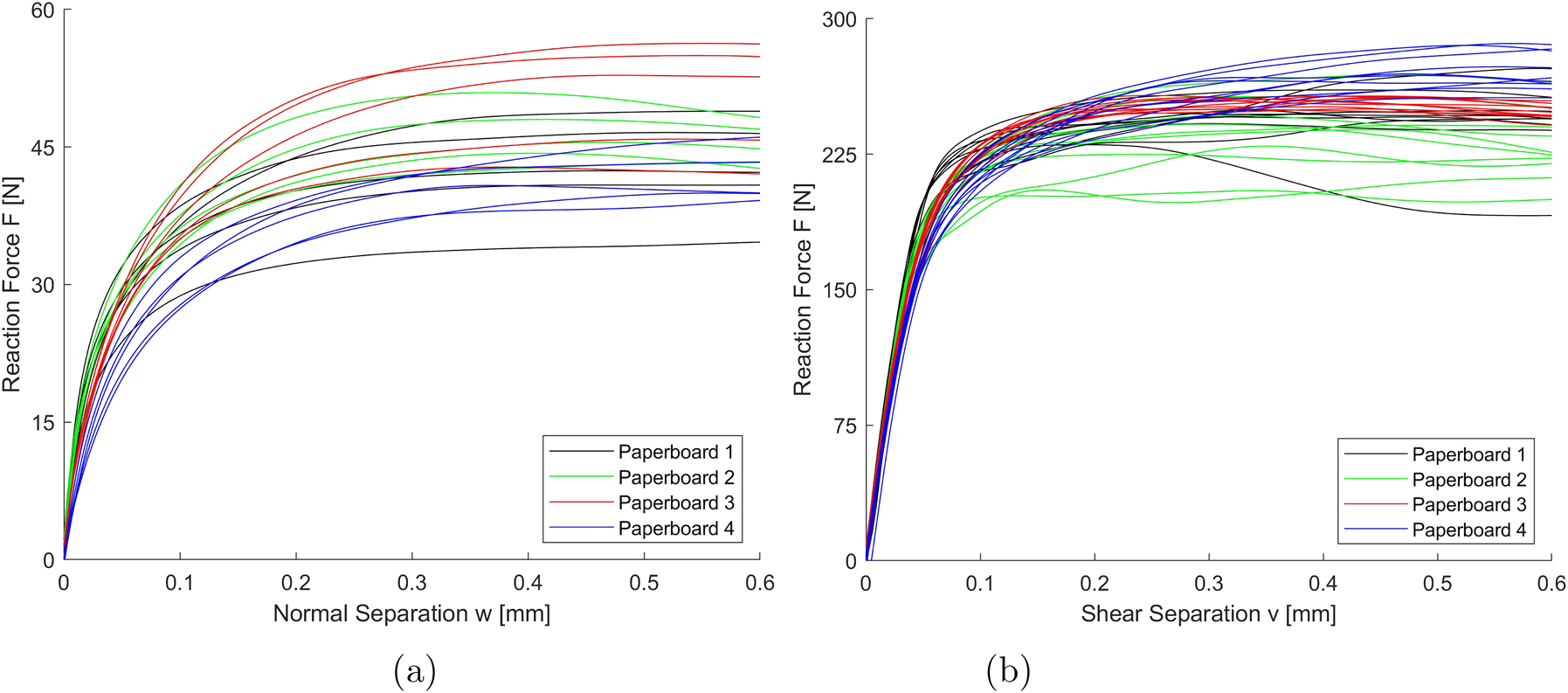
Reaction force-separation curves from all experiments. a) Normal mode (DCB); b) Shear mode (SDCB)..

Figure 7:

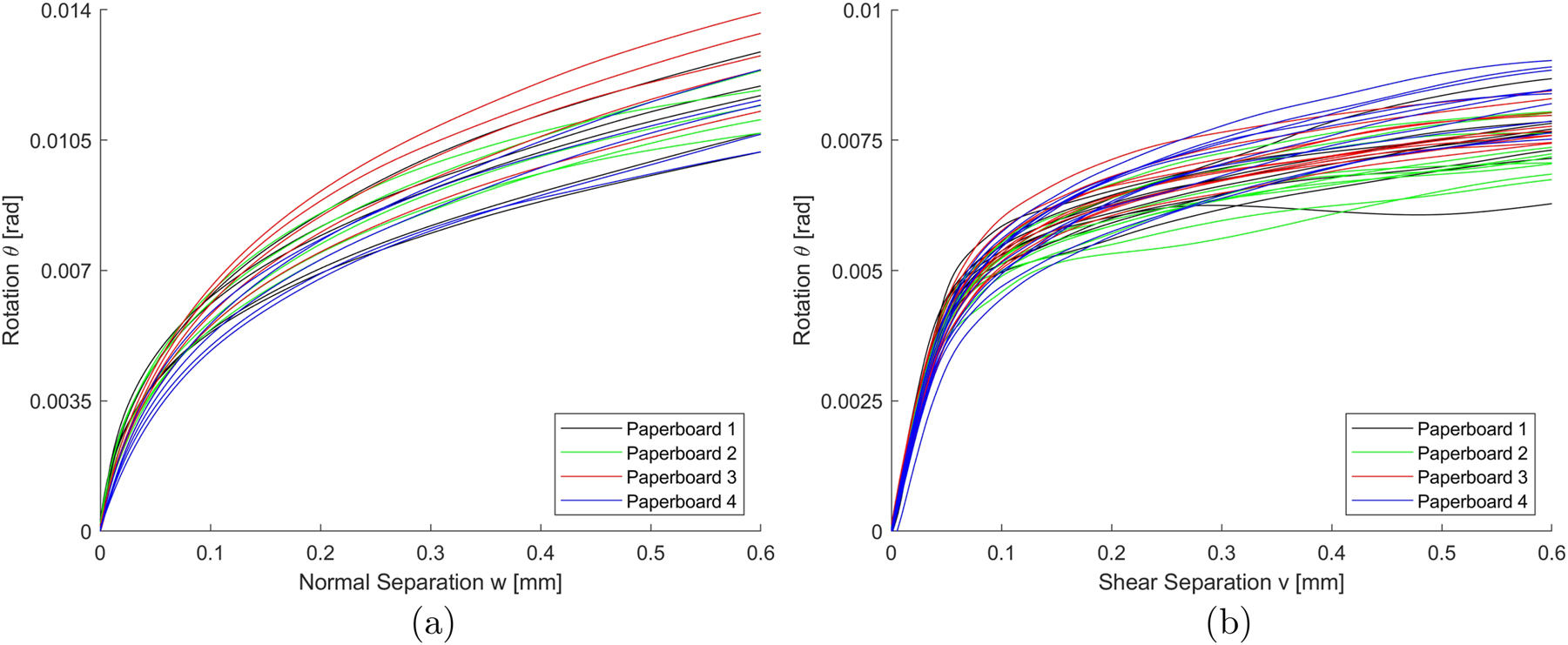
Rotation-separation curves from all experiments. a) Normal mode (DCB); b) Shear mode (SDCB).

2.5 Fracture analysis and calibration

The measurements’ results are analyzed using a fracture resistance approach and a cohesive zone model, complemented by a calibration procedure. The calibration procedure is used to fine-tune the model parameters, ensuring that the predicted behavior aligns with the experimental data.

2.6 Experimental fracture resistance

Fracture resistance data for the normal opening mode (Mode I) were obtained from DCB specimens, while data for the shear sliding mode (Mode III) were derived from SDCB specimens.

For the normal opening mode, the normal fracture resistance J _I from DCB specimens can be expressed as¹³

where F is the applied force, θ is the rotation at the applied force, and b is the width of the paperboard.

Similarly, for the shear mode, the shear fracture resistance J _III from SDCB specimens is presented by Biel et al. (2022) as

In Equation (2), F is the applied force, θ is the rotation at the applied force position, b is the paperboard width, and k₁ is the initial shear stiffness. The first term in Equation (2) represents the combined contribution from shear stresses τ₁ and τ₂, while the second term adjusts the τ₁ contribution within the first term to accurately account for the influence of shear stress τ₂. The formula assumes a linear relationship between shear stress and shear separation, i.e., τ₁ = k₁v₁.

The cohesive law for normal and shear stresses is derived by taking the derivative of the fracture resistance in (1) and (2), respectively with respect to the separation at the crack tip, see Rice (1968).

2.7 Nonlinear cohesive zone model

A theoretical model valid for normal and shear modes is proposed, with material parameters to be determined from experimentally obtained fracture resistance. The primary objective is to identify the optimal material parameters for the theoretical model that minimize the discrepancy between model predictions and experimental observations for both loading conditions.

The traction-separation law is derived by differentiating the fracture resistance with respect to the separation. A schematic traction-separation law is depicted in Figure 8. In Figure 8, the blue curve represents the fracture resistance-separation which is determined from the experimental data, and the red curve shows the derived traction-separation law. The experimental fracture resistance transitions from a convex to a concave curve. The convex portion (δ ≤ δ_max) corresponds to an ascending traction-separation response, termed the elastic traction-separation. It must be noted that from a modeling perspective, we assume this concave portion to be non-linearly elastic, as we do not have any unloading data. In contrast, the concave portion (δ > δ_max) represents a descending traction-separation response, termed the cohesive traction-separation. During the cohesive fracture, delamination initiates, progresses, and ultimately separates the paperboard into two distinct plies connected by single fibers. Hence, the two fracture resistance sections are mathematically described as follows;

Figure 8:

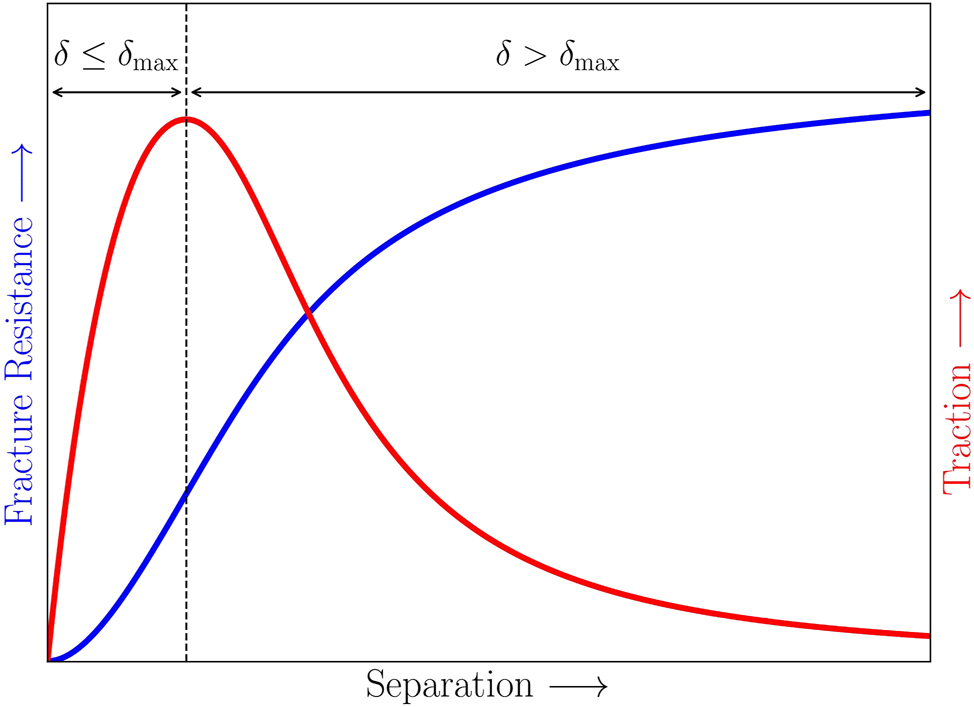
A schematic example of cohesive law derivation. The blue curve shows the fracture resistance-separation, and the red curve shows the traction-separation.

Elastic traction-separation, (δ ≤ δ_max): For separation values less than or equal to the threshold δ_max (where δ = w for normal mode and δ = v for shear mode), the model uses a normalized non-linear elastic relation f _e (ϵ ^e ) in the interval ϵ ^e ∈ [0, 1], with the following criteria: The function is monotonic increasing ( f e ′ ( ϵ e ) > 0 ) , has a concave shape ( f e ″ ( ϵ e ) < 0 ) , and satisfies the boundary conditions f _e (0) = 0, f _e (1) = 1, f e ′ ( 0 ) > 1 , and f e ′ ( 1 ) = 0 .

A rational function that meets these criteria (Carpinteri et al. 2011) is

The dimensionless parameter a = kδ_max/T, where k is the initial stiffness and T is the traction at δ_max. The elastic energy function g _e (ϵ ^e , a), representing the convex section of the fracture resistance, is given by the integration of (3) as

Cohesive traction-separation, (δ > δ_max): For separation values greater than δ_max, the model uses a normalized nonlinear cohesive relation f(ϵ) over the interval ϵ ∈ [0, ∞), with the following criteria: the function is monotonically decreasing (f′(ϵ) ≤ 0), has one inflection point where f′(ϵ) = −1, and satisfies the boundary conditions f (0) = 1 and lim_ϵ→∞f(ϵ) = 0. A rational function that meets these criteria (Biel et al. 2022; Tryding and Ristinmaa 2017) is

where

In (6), the parameter 0 < c < 1 controls the curvature of the nonlinear response, α(c) ensures the fulfillment of the boundary condition f′(ϵ) = −1, and δ _N is a normalizing length measure determined by the ratio of the cohesive strength (maximum cohesive traction) and the maximum negative slope of the cohesive traction-separation curve (Biel et al. 2022). The cohesive energy function g (ϵ, c) is the normalized fracture resistance obtained by integration of (5) as (Alzweighi et al. 2023; Biel et al. 2022; Tryding and Ristinmaa 2017)

In Eq. (7), ₂F₁ • , • ; • ; • is the Gauss’s hypergeometric function of the strain measure ϵ and the shape parameter c. The normalized fracture function g (ϵ; c) is an increasing monotonic function. The function g (ϵ, c) starts linearly with ϵ as ϵ increases from zero. As ϵ increases to infinity, g obtain a maximum value that depends only on the shape parameter c as^12,20,

The normalized fracture energy, g_max(c), is a U-shaped function within the interval 0 < c < 1 of the shape parameter c. The function reaches its minimum value at g_max (0.413) = 0.973 and tends to infinity as c approaches zero and one.

The nonlinear elastic and cohesive relations are combined into a fracture resistance model to fit the experimental fracture resistance data, determining the optimal parameters a, c, δ_max, T, and δ _N , which are used for both normal and shear modes. The calibrated parameters minimize the discrepancy between the model and observations, ensuring the model accurately reflects the material’s physical behavior. Combining both regimes, the fracture resistance model is given by

where δ represents w for normal mode or v for shear mode. In (9b), Tδ_max g _e (1, a) is a constant denoting the onset of cohesive fracture resistance. The traction-separation relation is given by the derivatives of (9) as,

where f _e (ϵ ^e , a) and f (ϵ, c) are given by (3) and (5), respectively.

2.8 Calibration procedure

The Calibration process seeks to determine the set of parameters θ = [a, δ _N , c] for both normal and shear modes by minimizing the sum of squared errors (SSE) between the theoretical model predictions and the experimental fracture resistance data. The SSE is calculated using SSE ( θ ) = ∑ i Data i − Model i ( θ ) 2 , where Model _i (θ) is the predicted fracture resistance from the theoretical model for the i-th data point, and Data _i is the corresponding experimental measurement. For each dataset and mode, values of separation (δ) and fracture resistance (J) were extracted from the experimental data, limited to separation values up to 0.6 mm to capture the fracture resistance within this range. The Sequential Least Squares Programming (SLSQP) algorithm calibrates both modes.

The normal and shear mode parameters θ = [a, δ _N , c] are calibrated by minimizing the SSE measure for fracture resistance, with T and δ_max values derived directly from the experimental data. Following this, the root mean square error (RMSE) is calculated to assess the quality of the fit.

First, the model was calibrated for each individual experiment to determine θ = [a, δ _N , c]. To ensure that the solution remains within physically realistic ranges, bounds are applied to θ. Initial guesses for shear parameters are [ k t , δ N t , c ] = [ 98,0.04 , 0.86 ] with bounds [(10, 130), (0.01, 0.10), (0.40, 1.0)], and for normal parameters [ k n , δ N n , c ] = [ 98,0.3 , 0.86 ] with bounds [(10, 130), (0.01, 1.00), (0.40, 1.0)]. Second, the parameters for normal and shear modes were compared to test the hypothesis by Biel et al. (2022), suggesting that the normalized cohesive fracture energy g in (9b) is identical for both modes. Third, the shape parameters c from each experiment’s calibration in both modes were used to calculate a median c for each of the four paperboards. Fourth, experimental curves for each mode were averaged, and the recalibration of these averages used the median c as fixed, determining [a, δ _N ] by minimizing the SSE for fracture resistance with c held constant. Parameters T and δ_max were derived from the corresponding experimental average curve.

3.1 CZM calibration

The parameters θ = [a, δ _N , c] for both the normal and shear modes were calibrated independently for each measured sample. Figure 9 shows boxplots of the calibrated δ _N and c values from the data.

Figure 9:

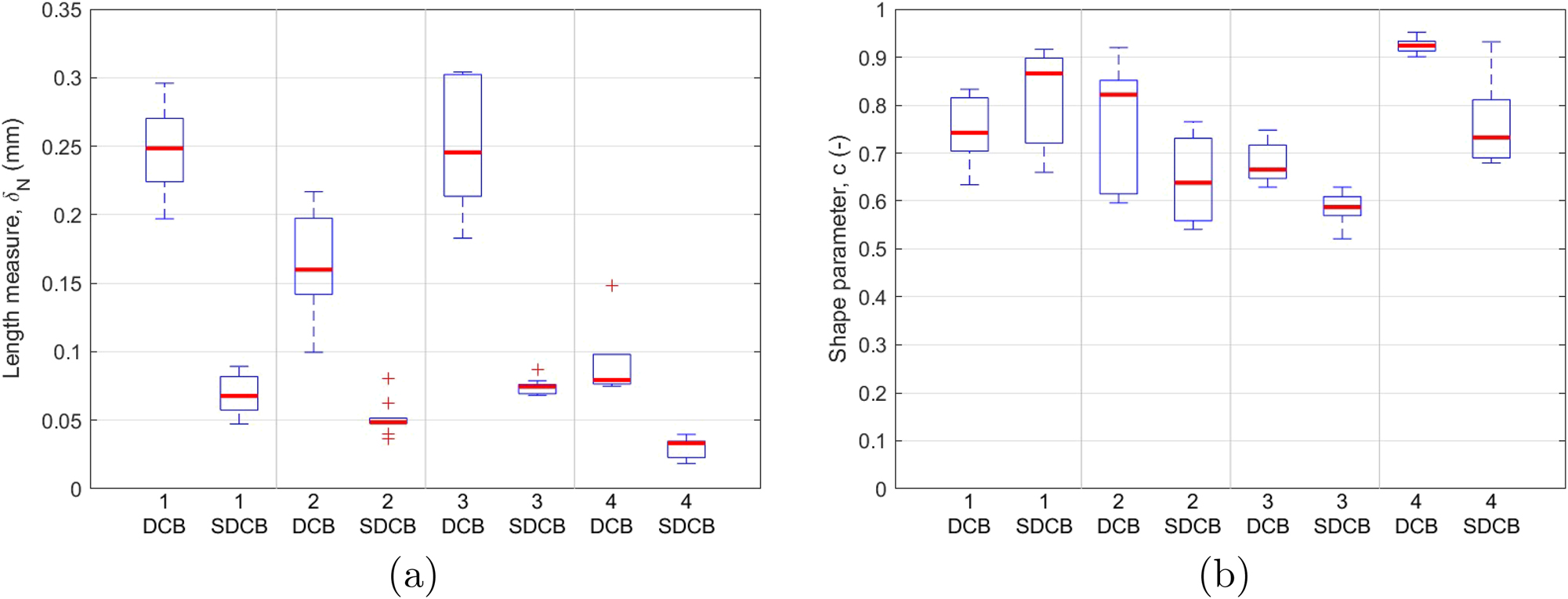
A boxplot with subgroups of paperboard and specimen types. a) Length measure δ _N ; b) Shape parameter c. The median values are highlighted by a bold red line. Values that reach the boundary are excluded from the boxplot.

Figure 9a shows a boxplot comparing the length measure δ _N across various paperboard qualities. The vertical axis shows length in millimeters (mm), ranging from 0 to 0.35 mm, while the horizontal axis categorizes paperboard from 1 to 4, with each number representing two specimen subcategories: “DCB” and “SDCB.” In Paperboard 1, the DCB specimen has a higher median length measure (around 0.25 mm) and a slightly wider interquartile range, with some outliers above the box. The SDCB specimen shows a lower median measure (just below 0.07 mm) with a narrow interquartile range and some outliers below the box. For Paperboard 2, the DCB median is lower (around 0.16 mm), while the SDCB median is very low (below 0.05 mm), with several outliers below the box. In Paperboard 3, the DCB specimen exhibits a median comparable to Paperboard 1 (close to 0.25 mm) and a large interquartile range. Conversely, the SDCB median with a narrow spread is slightly below 0.08 mm. Finally, in Paperboard 4, the DCB median is around 0.08 mm, showing some variability, while the SDCB specimen has the lowest range and median measure, just above 0.03 mm. The boxplot indicates that the DCB specimens have higher length measures than the SDCB specimens across all paperboard categories, with notable variability in median and interquartile ranges.

Figure 9b shows a boxplot comparing the shape parameter, denoted as c, across different paperboard qualities. The vertical axis represents the shape parameter c, ranging from 0 to 1. The horizontal axis categorizes the paperboards from 1 to 4. In Paperboard 1, the DCB specimen has a median shape parameter close to 0.75 with a relatively narrow interquartile range, while the SDCB specimen has a higher median, around 0.85, with a larger spread. In Paperboard 2, the DCB median is around 0.8, showing a wide interquartile range, while the SDCB median is around 0.65, with a slightly lower spread. For Paperboard 3, the DCB median is just above 0.66, with a narrow spread, whereas the SDCB median is slightly below 0.6, with a narrow interquartile range. In Paperboard 4, the DCB median is slightly above 0.9, with the narrowest interquartile range among all groups, while the SDCB specimen has a median above 0.7 with a similar spread as the SDCB of Paperboard 1 and 2. The boxplot indicates that the DCB and SDCB specimens generally have distinct medians and variability in the shape parameter across paperboards, with the DCB specimen in Paperboard 4 exhibiting the lowest spread.

Figure 9a shows an anisotropy variation between the normal (DCB) and shear (SDCB) loading compared to Figure 9b, which shows a more isotropic behavior in the normal (DCB) and shear (SDCB) loading. The RMSE mean values of the fit to the fracture resistance for the normal and shear modes are < 1.3 × 1 0 − 3 and < 2.3 × 1 0 − 3 , respectively.

Based on experimental observations that the shape parameter c is nearly isotropic, the hypothesis proposed by Biel et al. (2022) is investigated, suggesting that this parameter remains isotropic, i.e., consistent in both normal and shear modes. The median values of c calibrated for all individual experiments in the normal and shear modes, as shown in Figure 9b, are recorded for paperboards 1 to 4 as 0.815, 0.640, 0.609, and 0.849, respectively. With c fixed, the remaining parameters were re-calibrated using the reduced parameter set θ = [a, δ _N ]. The reduced parameter set was calibrated to fit the mean experimental fracture resistance data achieving RMSE mean values of < 1.3 × 1 0 − 3 and < 2.3 × 1 0 − 3 in the normal and shear modes, respectively.

Figures 10 show that the theoretical model accurately captures the behavior observed in the experimental data for both modes, with low RMSE values (<2.3 × 10⁻³) indicating a good fit. In addition, the traction–separation curves are plotted in Figure 11 to visualize the response of both modes. Table 3 presents the calibrated parameters for normal and shear fracture modes across four qualities of paperboard: 1, 2, 3, and 4

Figure 10:

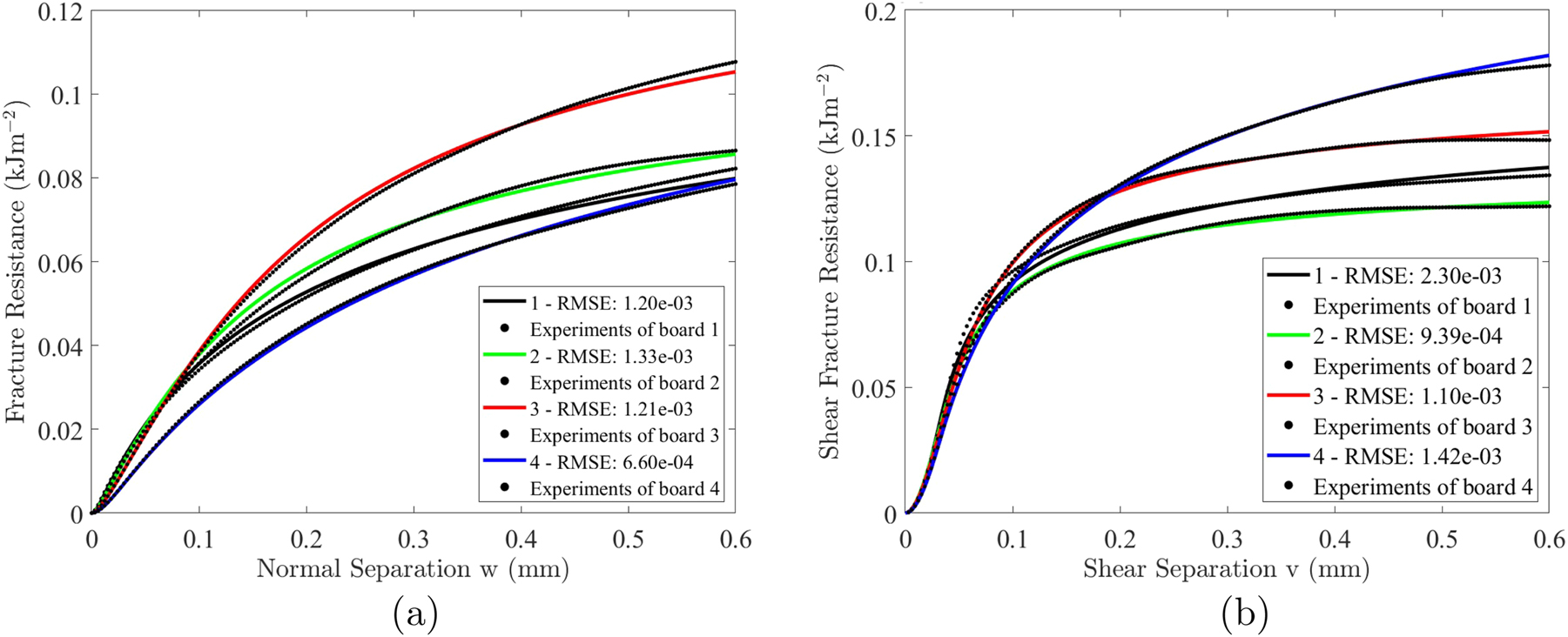
Fracture resistance-separation curves for each paperboard quality. a) Normal mode; b) Shear mode. Solid lines represent calibrated curves, while the experimental curves are depicted as filled black circles.

Figure 11:

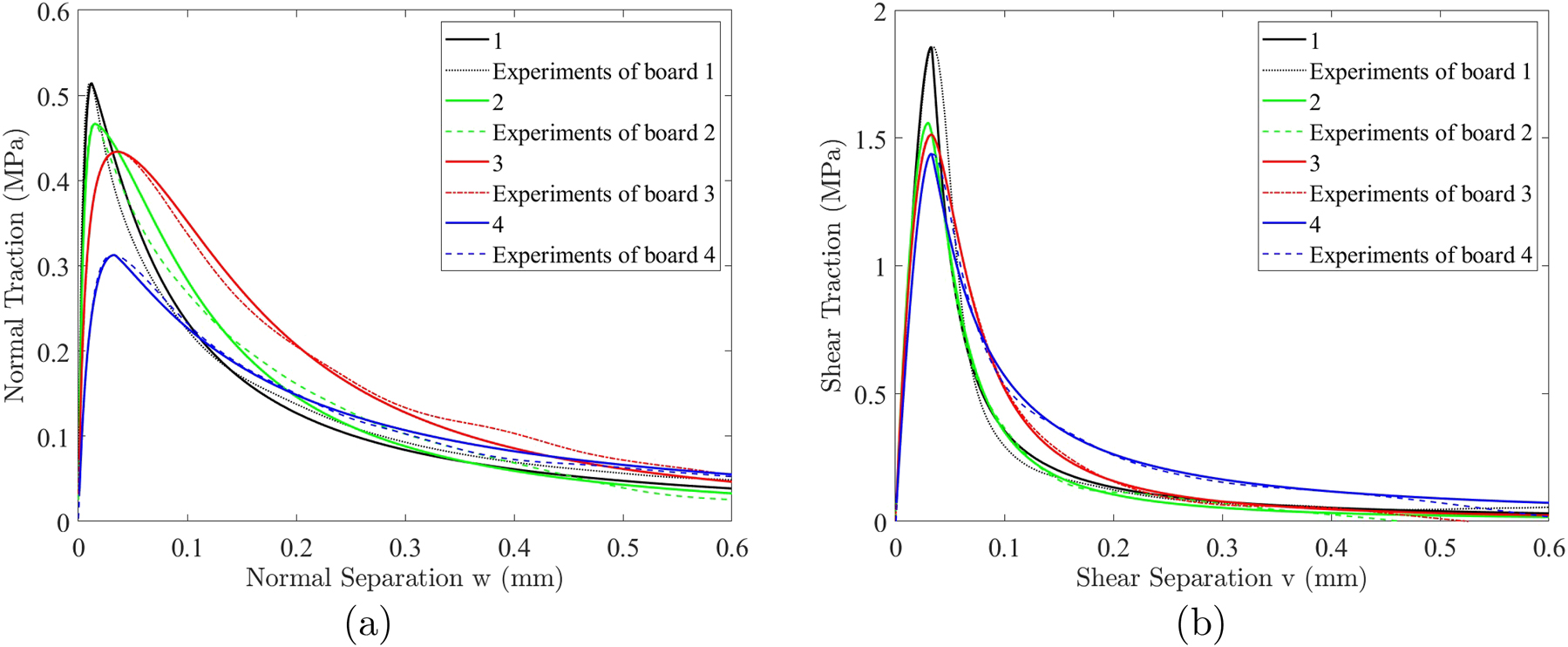
Traction-separation curves for each paperboard quality; a) Normal; b) Shear. Experimental curves are depicted as dashed lines, while solid lines represent calibrated curves.

Figure 11 shows the normal and shear traction versus displacement for both the model and the mean curves from the experiments, represented by solid and dashed curves, respectively. The model is derived using the parameters from Table 3 in (10). The figure demonstrates that the model (solid curves) closely matches the experimental results (dashed curves), as expected since the fitted reduced parameter set (k, δ _N ) for the fracture resistance data yielded low RMSE values (see Figure 10).

A comparison of the shape parameter values in Table 3 and Figure 9b shows that the median values for each mode are fairly similar, except for the normal mode (DCB) in paperboards 1 and 4, which differ noticeably. Despite this discrepancy, the fitted data closely matches the experimental data in Figure 11a for the normal mode in paperboards 1 and 4, with RMSE values lower for these two paperboards than the others.

3.2 Fracture energy, cohesive strength, and initial stiffness

In the normal mode, as presented in Figure 12, the fracture energy, cohesive strength, and initial stiffness of four paperboard qualities were evaluated. The fracture energy is defined as the maximum value of the fracture resistance. The fracture energy mean values for paperboards 1 through 4 were measured at 0.082, 0.086, 0.108, and 0.078 kJm⁻², respectively, with corresponding standard deviations of 0.017, 0.007, 0.021, and 0.011 kJm⁻². For cohesive strength, the mean values recorded for paperboards 1 through 4 were 0.514, 0.467, 0.434, and 0.313 MPa, with standard deviations of 0.010, 0.068, 0.046, and 0.049 MPa, respectively. As seen in Table 1 and Figure 12, the cohesive strength values from the ZDT and DCB experiments, respectively, are in the same range for Paperboard 1, 3, and 4. However, the results for Paperboard 2 are considerably different, which could be attributed to the delamination position shift, visible in Figures 4 and 5, as a result of the considerably faster ZDT test speed. Initial stiffness measurements revealed mean values of 91, 84, 45, and 29 MPamm⁻¹ for the respective paperboards, with standard deviations of 31, 25, 11, and 12 MPamm⁻¹. These results indicate variability in mechanical performance among the paperboards under normal loading conditions, with Paperboard 3 exhibiting the highest fracture energy and Paperboard 1 showing the highest cohesive strength and initial stiffness.

Figure 12:

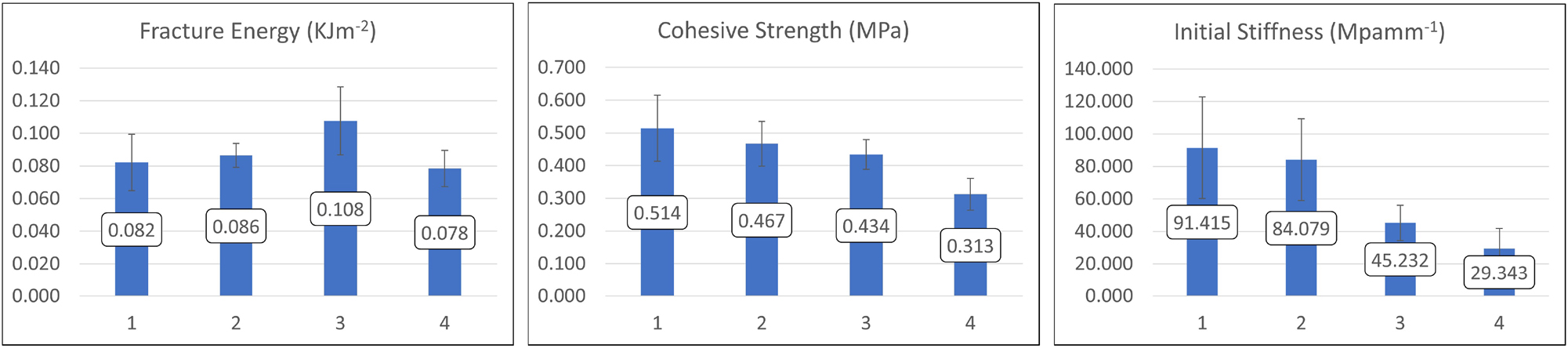
Fracture energy, cohesive strength, and initial stiffness of paperboards in the normal direction.

In the shear mode, illustrated in Figure 13, fracture energy, cohesive strength, and initial stiffness were assessed for the same paperboards. The fracture energy mean values increased to 0.134, 0.122, 0.148, and 0.178 kJm⁻² for paperboards 1 through 4, respectively, with standard deviations of 0.018, 0.019, 0.006, and 0.014 kJm⁻². Cohesive strength measurements were significantly higher in shear mode, recorded at 1.856, 1.559, 1.513, and 1.438 MPa for paperboards 1 through 4, with standard deviations of 0.122, 0.131, 0.070, and 0.095 MPa. Initial stiffness mean values, except for paperboard 1, were also elevated measured at 78, 85, 85, and 76 MPamm⁻¹ for the respective paperboards, with standard deviations of 19, 15, 7, and 6 MPamm⁻¹. These findings demonstrate that the paperboards exhibit enhanced mechanical properties under shear loading, with paperboards 1 and 4 showing the highest cohesive strength and fracture energy, respectively, in this mode.

Figure 13:

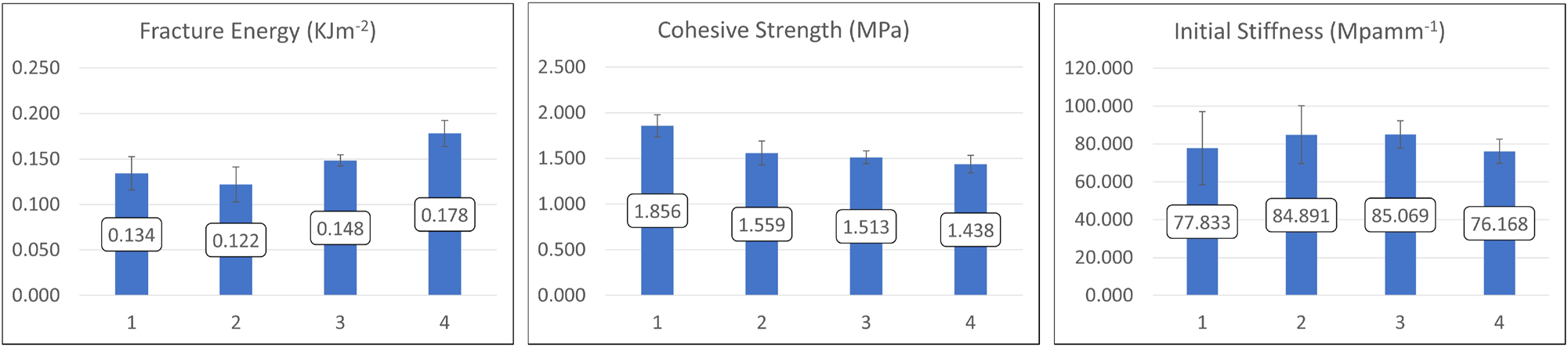
Fracture energy, cohesive strength, and initial stiffness of paperboards in the shear direction.

The comparative analysis between normal and shear modes reveals that all paperboards demonstrate greater fracture energy and cohesive strength when subjected to shear loading. This suggests that the mechanical performance of the paperboards is mode-dependent, with shear mode inducing more substantial material responses than normal mode across all tested paperboard types.

In the normal mode, the calibrated initial stiffness reached the upper bound of 130 MPamm⁻¹ for Paperboards 1 and 2, whereas, for Paperboards 3 and 4, the calibrated initial stiffness values were 85 and 38 MPamm⁻¹, respectively. However, the upper bound constraint on the initial stiffness of Paperboards 1 and 2 has, if any, only a minor effect on the fit, as indicated by the low RMSE shown in Figure 10a. For the shear mode, the calibrated initial stiffness values were 86, 100, 96, and 72 MPamm⁻¹ for paperboards 1 through 4, respectively. Evidently, the initial stiffness values obtained from direct measurements, denoted as K, differ from those determined by the calibration fit (k) for both the normal and shear modes. The calibrated initial stiffness k was measured from the initial linear stress-separation relationship; using the relation a = kδ_max/T from (3), the initial stiffness is calculated and denoted as k. A linear regression analysis comparing the different initial stiffness measures was performed, yielding K = 0.88k with an R² value of 98 %. Values at the boundary were excluded from the analysis. The high coefficient of determination indicates a strong correlation between the two initial stiffness measures, with k showing higher stiffness than the direct measure K. Despite these differences, Figure 11 demonstrates that the traction versus separation curves for each paperboard quality in normal and shear modes exhibit a good fit between the model and the experimental data.

3.3 Microstructural observations

Figures 14 and 15 show microscopic photos of the DCB specimens at 0, 0.1, 0.3, and 0.6 mm separation levels. Figure 11 shows that the peak load for all four paperboards is reached before 0.1 mm of separation. At 0.1 mm separation, the delamination is visible as is illustrated in Figures 14 and 15. Furthermore, it can be seen in Figure 14 that the delamination in Paperboard 1, a single-layer paperboard, exhibits multiple delaminations as microcracks, forming and growing in the core of the paperboard. Similarly, Paperboards 3 and 4, as shown in Figure 15, display distributed delamination through the thickness, although they include multiple plies. Since microcracks are highly distributed between the plies in Paperboards 3 and 4, it is unclear whether the main delamination occurs within the plies or at the interfaces between them. Nevertheless, it can be assumed that the interfaces have similar strength since the microcracks in the delaminated structure do not favor a distinct crack path for initiation and growth. In contrast, Paperboard 2, as seen in Figure 14, composed of two brown (mid and bottom plies) and white (top ply) plies, shows a distinct crack delamination between the mid and top ply interface. It is further observed that the brown fibers are stretched toward the white ply, with no white fibers stretching toward the brown ply.

Figure 14:

Microscopic photos of the DCB specimens made of Paperboard 1 and 2 at different separation levels.

Figure 15:

Microscopic photos of the DCB specimens made of Paperboard 3 and 4 at different separation levels.

3.4 Mode-independent shape parameter and near-symmetry

Biel et al. (2022) hypothesized that this shape parameter is the same for normal and shear loading modes. Our experimental data and subsequent calibration support this hypothesis. For each paperboard quality, the calibrated shape parameter c is consistent in both modes, reinforcing the notion of a unified fracture mechanism that governs normal and shear delamination. A mode-independent c for different paperboard qualities can reduce the complexity of the calibration process for predictive models.

The calibration results in Table 3 provide crucial parameters for modeling the fracture behavior of these paperboards under different loading conditions. Understanding these parameters allows us to predict how each material will respond to mechanical stresses, which is essential for applications where material failure could be critical. The calibration process, which aligns the model parameters closely with the experimental data, ensures that simulations and analyses based on these parameters will be accurate and reliable.

Based on the experimental data, Biel et al. (2022) utilized the strain measure ϵ and found that the normalized fracture resistance data for normal g _n and shear loading g₂ closely follow each other. This observation is supported by the analysis conducted on the four paperboard qualities. To validate the calibrated data presented in Table 3, derived using the traction-separation law in (10), the fracture-energy normalization method for DCB and SDCB tests described by Biel et al. (2022) is employed. Figure 16 shows the experimental mean curves of the normalized fracture resistance, g = J − J 0 / ( T δ N ) , plotted against the normalized cohesive separation, ϵ = (δ − δ_max)/δ _N , for paperboards 1 through 4. Solid curves represent normal-mode loading data, and dashed curves represent shear-mode loading data. Although slight deviations occur between the two modes, the curves closely align, confirming that normalization using δ _N and cohesive strength T provides a consistent fracture response independent of the loading mode. Hence, the normalized fracture resistance is most likely independent of the loading direction as

This suggests that g is an invariant parameter, implying that the normalized fracture resistance of the paperboards studied is a material property unaffected by the type of loading applied, whether normal or shear. The experiments further indicate that each paperboard has its unique value of g, but all paperboards obey the relation in (11).

Figure 16:

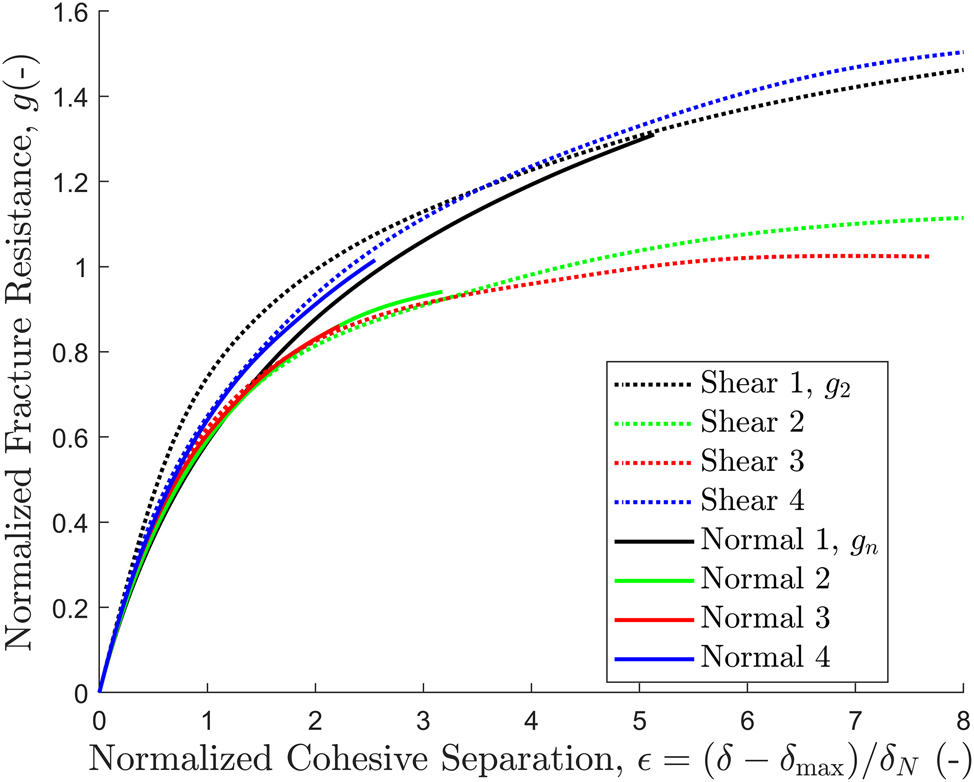
The mean curves of the normalized fracture resistance g = J − J 0 / ( T δ N ) plotted against the normalized cohesive separation ϵ = (δ − δ_max)/δ _N , for the paperboards 1 to 4.

The potential near-symmetry between shear and normal cohesive parameters was assessed through analysis of the parameter ratios T t / δ N n and T n / δ N t . Experimental values for the four investigated paperboard grades, including mean and standard deviations, are summarized in Table 4.

Figure 17 illustrates a strong linear correlation between the ratios T t / δ N n and T n / δ N t , depicted as light blue circles with error bars corresponding to the standard deviations. The regression analysis yields the relationship, T t / δ N n = 1.17 ⋅ T n / δ N t , with a coefficient of determination R² = 0.97, demonstrating that the regression model effectively captures the variability in the data. The minor deviation of the slope from unity indicates slight anisotropy, likely attributed to fiber orientation from paperboard manufacturing processes. The fitted regression line is shown as a solid green line.

Figure 17:

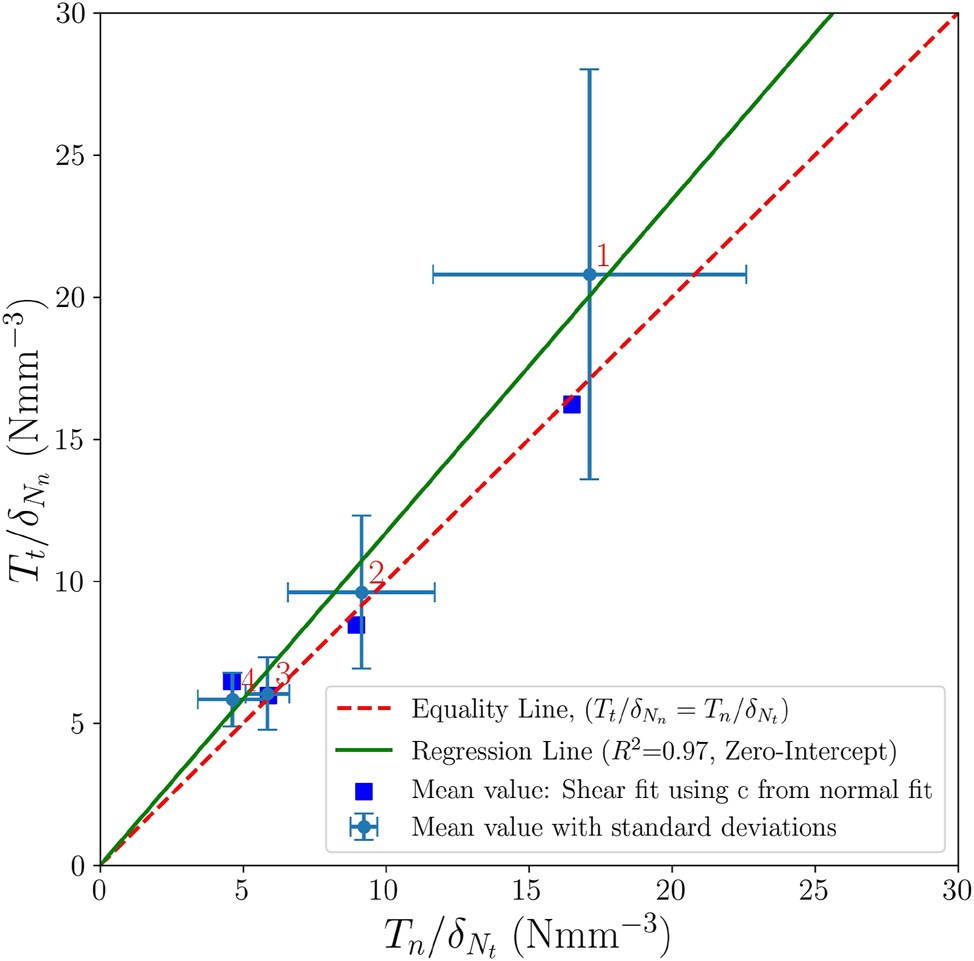
Comparison of T t / δ N n and T n / δ N t for four paperboard grades. Data labels correspond to paperboard samples 1–4. Error bars indicate standard deviations.

Additionally, Figure 17 includes corresponding ratios from Table 3, marked by blue cubes, closely aligned with the red dashed equality line T t / δ N n = T n / δ N t . Thus, the shape parameter enforcing symmetry between the normal and shear modes also imposes symmetry between the ratios, consistent with the data.

The observed proportional relationship simplifies parameter calibration significantly, enabling estimation of shear parameters from normal-mode tests or vice versa. Despite inherent variability in experimental measurements, as represented by the error bars, the consistent linear trend supports material near-symmetry. Hence, the ten parameters needed for calibrating the CZM model reduces to an eight-parameter CZM model.

3.5 Rationale for the selected CZM

In this study, the cohesive zone model (CZM) proposed in (10) was selected due to its demonstrated capability in accurately representing the experimental behavior of paperboard delamination. To validate this selection, a comparative analysis was performed with two alternative CZM approaches: the three-parameter model proposed by Li et al. (2018) and the two-parameter model introduced by Xu and Needleman (1994).

The models developed by Li et al. and Xu and Needleman apply separate parameter sets for normal and shear loading conditions, requiring six and four parameters, respectively. Conversely, the CZM formulation described in (10) employs eight parameters, reduced from ten by using the same shape parameter for both modes and leveraging near-symmetry between the normal and shear loading modes.

Model performance was assessed through root mean square error (RMSE) comparisons. The CZM by Biel et al. yielded maximum RMSE values of 1.2 × 10⁻³ for normal-mode and 2.3 × 10⁻³ for shear-mode fracture resistance. In contrast, the Li et al. model produced RMSE values up to 4.7 × 10⁻³ and 1.5 × 10⁻², and the Xu and Needleman model generated RMSE values of 8.6 × 10⁻³ and 1.5 × 10⁻², for normal and shear fracture resistance, respectively.

These findings indicate that the CZM approach in (10) significantly better represents the experimental data. Despite having more parameters, this model effectively captures the tail behavior of the experimental fracture resistance and traction–separation curves. Although simpler, the alternative models fail to represent the complete experimental behavior accurately, particularly in the cohesive response’s tail region. The nearly one-to-one fitting accuracy and lower RMSE values provided by the selected CZM, alongside its capacity to capture inherent symmetry and tail behavior of the delamination process, demonstrate its effectiveness in reproducing the experimental data. Thus, the selected CZM provides an accurate and physically consistent representation of paperboard delamination behavior.