Abstract
An analysis has been carried out to study the effect of nonlinear thermal radiation on slip flow and heat transfer of fluid particle suspension with nanoparticles over a nonlinear stretching sheet immersed in a porous medium. Water is considered as a base fluid with dust particles along with suspended Aluminum Oxide (Al2O3) nanoparticles. Using appropriate similarity transformations, the coupled nonlinear partial differential equations are reduced into a set of coupled nonlinear ordinary differential equations. The reduced equations are then solved numerically using Runge-Kutta-Fehlberg45 order method with the help of shooting technique to investigate the impact of various pertinent parameters for the velocity and temperature fields. The obtained results are presented in tabular form as well as graphically and discussed in detail. Effect of different parameters on skin friction coefficient and Nusselt number are also discussed.
1 Introduction
Heat, mass and momentum transfer in the laminar boundary layer flow over a stretching sheet is relevant to several industrial and engineering processes in the field of metallurgy and chemical engineering processes. These applications involve the cooling of continuous strips or filaments by drawing them through a quiescent fluid. The steady two dimensional boundary layer flow of Newtonian fluid over a stretching surface has been studied by Crane [1]. Chen [2] presented the laminar mixed convection in boundary layers adjacent to a vertical, continuously stretching sheet. The problem of laminar fluid flow which results from the stretching of a flat surface in a nanofluid has been investigated numerically by Khan and Pop [3]. After this pioneering work the flow field over a stretching surface has drawn considerable attention and a good amount of literature has been generated on this problem [4–9]. Sulochana et al. [10] analyzed the three-dimensional magnetohydrodynamic Newtonian and non-Newtonian fluid flow, heat and mass transfer over a stretching surface in the presence of thermophoresis and Brownian motion. Recently Gireesha et al. [11] numerically investigate the effect of thermal stratification on MHD flow and heat transfer of dusty fluid over a vertical stretching sheet embedded in a thermally stratified porous medium in the presence of uniform heat source and thermal radiation.
However, all these studies are restricted to linear stretching of the sheet. It is worth mentioning that the stretching is not necessarily linear. The problem of heat and mass transfer of both Newtonian and non-Newtonian fluids flow over non-linear stretching sheet has been studied by different researchers. Abbas and Hayat [12] carried out the Stagnation slip flow and heat transfer characteristics of a viscous fluid over a nonlinear stretching surface. Abel et al. [13] discussed the effects of Buoyancy, viscous and joule dissipation on MHD flow and heat transfer over a nonlinear vertical stretching sheet with partial slip. Rana and Bhargava [14] has investigated the steady, laminar boundary fluid flow which results from the non-linear stretching of a flat surface in a nanofluid. Mandal and Mukhopadhyay [15] presented the flow and heat transfer of an exponentially stretching porous sheet with the effect of magnetic field. Khan et al. [16] have been applied both analytical and numerical method in examining the two-dimensional boundary layer flow and heat transfer to Sisko nanofluid over a non-linearly stretching sheet under the influences of the thermophoresis and Brownian motion. The boundary layer flow and heat transfer of Carreau fluid over a nonlinear stretching surface is discussed by Khan and Hashim [17]. Krishnamurthy et al. [18] have studied the effects of thermal radiation and chemical reaction on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet. Recently Hayat et al. [19] observed the phenomenon of steady flow of an Oldroyd-B fluid induced by an exponentially stretched surface.
A nanofluid is a new class of heat transfer fluids that contain a base fluid and nanoparticles. Nanofluids are innovative coolant with more effective cooling properties compared to the conventional fluids such as water and oil. Unfortunately the viscosity of the nanofluid is higher than the base fluid. The viscosity affects directly the pressure drop and pumping consumption of the system. Greater thermal conductivities, excellent stability and negligible increasing pressure loss are some important characteristics of the nanofluids that are mentioned in the literature. A comprehensive survey of convective transport in nanofluids was made by Buongiorno [19]. The Buongiorno model [20] has also been used by Khan and Pop [21] to study the boundary layer flow of a nanofluid past a stretching sheet. Later on the different aspects of nanofluid model was extensively used by many researchers [22–25]. Prasannakumara et al. [26] discussed the effect of chemical reaction on flow, heat, and mass transfer of Williamson nanofluid over a stretching sheet. Recently Nandeppanavar [27] describe the boundary layer flow and heat transfer of a nanofluid due to a vertically stretching sheet under the influence of uniform transverse magnetic field with partial slip.
In various industrial processes, slip effects can arise at the boundary of pipes, walls, and curved surfaces, for example. An usual approach in studying the slip phenomena is the Navier velocity slip condition. Thermal slip and solutal slip conditions may also arise in many industrial processes. A boundary layer slip flow problem arises in polishing of artificial heart valves and internal cavities. The effects of slip at the boundary on the flow of Newtonian fluid over a stretching sheet were studied by Anderson [28]. The magnetohydrodynamic flow under slip condition over a permeable stretching surface is solved analytically by Fang and Yao [29]. Ibrahim and Makinde [30] examines the effect of slip and convective boundary condition on magnetohydrodynamic (MHD) stagnation point flow and heat transfer due to Casson nanofluid past a stretching sheet. Khader and Megahed [31] give the numerical solution for the flow of a Newtonian fluid over an impermeable stretching sheet with a power-law surface velocity, slip velocity, and variable thickness. The steady, two dimensional, non-linear, hydromagnetic laminar flow of an incompressible, viscous and electrically conducting fluid over a stretching sheet with variable thickness in the presence of variable magnetic field and slip flow regime is studied by Anjali and Prakash [32]. Hayat et al. [33] examines the hydromagnetic three-dimensional flow induced by a stretched surface. Recently Shaw et al. [34] investigate the effects of momentum, thermal, and solute slip boundary conditions on nanofluid boundary layer flow along a permeable surface.
Two-phase particulate suspension flows containing discrete particle phase and the continuous fluid phase have several engineering applications. Study of boundary layer flow and heat transfer in dusty fluid is very constructive in understanding of various industrial and engineering problems concerned with powder technology, rain erosion in guided missiles, sedimentation, atmospheric fall-out, combustion, fluidization, electrostatic precipitation of dust, nuclear reactor cooling, waste water treatment, acoustics batch settling, aerosol and paint spraying and etc. Saffman [35] initially described the fluid dust particle system, who derived the motion of gas equations carrying the dust particles. Heat transfer effects on dusty gas flow past a semi-infinite isothermal inclined plate are investigated by Palani and Ganesan [36]. Recently several attempts have been made to analyze the flow and heat transfers of dusty fluid under various physical situations are reported by [37–39].
Main motivation of the problem is to discuss about the enhancement in the heat transfer of dusty fluid after saturating the nanoparticles. Moreover, we have considered the nonlinear thermal radiation effect on slip flow of dusty fluid having suspended Al2O3 nanoparticles over a nonlinear stretching sheet through a porous medium. Constructed nonlinear partial differential equations concerning to the model have been converted into a system of nonlinear ordinary differential equations with the implication of similarity transformations and then solved numerically using Runge–Kutta–Fehlberg method after converting the system of boundary value problem into initial value problem with the help of a shooting technique. The behaviors of each of the nondimensional quantities are exposed graphically for all the fluid parameters. Comparison of the present article with the available literature is presented through tables.
2 Mathematical formulation
Consider a steady, laminar, two-dimensional boundary layer flow and heat transfer of an incompressible dusty fluid combined with Al2O3 nanoparticles over a stretching sheet embedded in a porous medium. The sheet coincides with the plane y = 0 and the flow is confined to y > 0. The flow is generated due to linear stretching of the sheet caused by the simultaneous applications of two equal and opposite forces along the x–axis as shown in the Fig. 1. A uniform magnetic field B0 is assumed to be applied in the y -direction. Keeping the origin fixed, the sheet is then stretched with a velocity Uw(x) = axn where a > 0 the stretching rate is and x is the coordinate measured along the stretching surface. The fluid is a water based dusty fluid containing Al2O3 nanoparticles. The nanoparticles are assumed to have a uniform shape and size. Moreover, it is assumed that both the fluid phase and nanoparticles are in thermal equilibrium state.
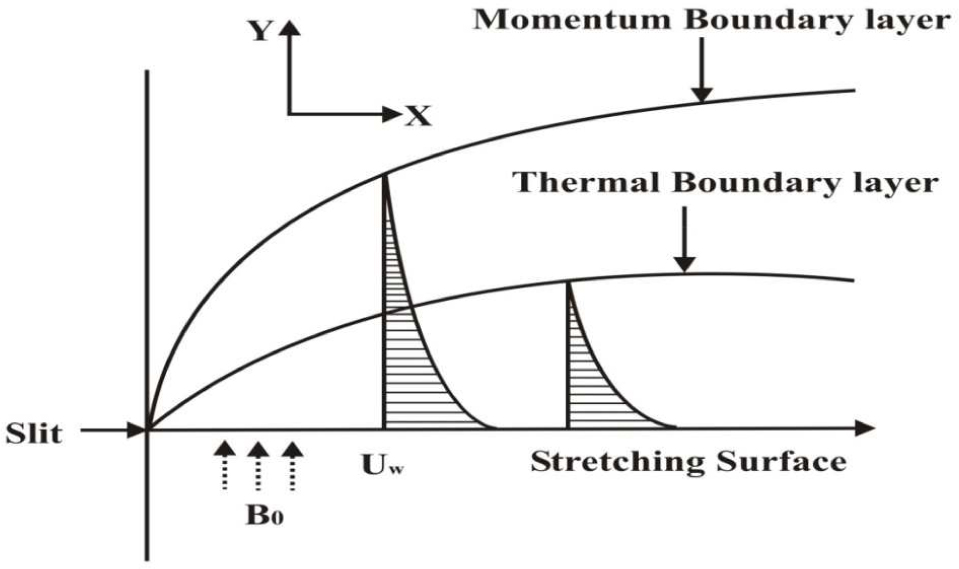
Schematic representation of the flow diagram.
Under usual boundary layer approximations, the flow governing equations of nanofluid phase and dust phase are given by,
where x and y respectively represents coordinate axes along the continuous surface in the direction of motion and perpendicular to it. (u, v) and (up, vp) denotes the velocity components of the nanofluid and dust phases along the x and y directions respectively, k′ is the permeability of the porous medium, N is the number density of dust particle, K = 6πμnfr is the Stokes drag constant, r is the radius of dust particle, σ is the electrical conductivity, m is the mass concentration of dust particles. ρnf is the effective density of nanofluid, μnf is the effective dynamic viscosity of nanofluid which are given by [38],
where ϕ is the solid volume fraction of nanofluid, ρf is the density of base fluid, ρs is the density of nanoparticle and μf is the dynamic viscosity of base fluid.
In equations (5) and (6), T and Tp are represents the temperatures of the fluid and dust particles inside the boundary layer cpf and cmf are the specific heat of fluid and dust particles, τT is the thermal equilibrium time i.e., the time required by a dust cloud to adjust its temperature to the fluid, τv is the relaxation time of the dust particle, that is, the time required by a dust particle to adjust its velocity relative to the fluid, knf is the thermal conductivity and (ρcp)nf is heat capacity of the nanofluid, which are given by [38],
where (ρcp)f is the heat capacity of base fluid, (ρcp)s is the heat capacity of nanoparticle, kf is the thermal conductivity of base fluid and ks is the thermal conductivity of nanoparticle.
The corresponding boundary conditions are given by,
Using Rosseland approximation for radiation, the nonlinear radiative heat flux qr is simplified as,
where σ∗ is the Stefan–Boltzmann constant and k∗ is the mean absorption coefficient. Here energy equation take the form as follows;
To convert the governing equations into a set of similarity equations, introduce the following similarity transformation as,
with
The corresponding boundary conditions will takes the following form,
where a prime denotes differentiation with respect to η and
The physical quantities of interest are the skin friction coefficient (Cf) and the local Nusselt number (Nux), which are defined as,
where the surface shear stress τw and the surface heat flux qw are given by,
with μnf and knf being the dynamic viscosity and thermal conductivity of the nanofluids, respectively. Using the similarity transformation (12), we obtain,
where
3 Numerical Method and accuracy
In the first step, a set of non-linear ordinary differential equations (13)–(16) with boundary conditions (17) are discretized to a system of nine simultaneous differential equations of first order by introducing new dependent variables. In order to integrate these equations as an initial value problem, one requires nine initial conditions. Out of required nine initial conditions, three are known and remaining initial conditions are accessed with the help of shooting technique. Afterward, a finite value for η∞ is chosen in such a way that all the far field boundary conditions are satisfied asymptotically. Our bulk computations are considered with the value at η∞ = 6, which is sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters are considered.
After fixing finite value for η∞, integration is carried out with the help of Runge-Kutta-Fehlberg-45 order method. At each step, two different approximations for the solution are made and compared. If the two answers are in close agreement, the approximation is accepted otherwise, the step size is reduced until to get the required accuracy. For the present problem, we took the step size Δη = 0.001, η∞ = 6 and accuracy to the fifth decimal places. The CPU time is 1.855 seconds.
4 Results and discussions
In this section, the behaviors of pertinent parameters on the velocity and temperature distributions are carefully examined through graphical and numerical results. The fluid flow and heat transfer analysis has been carried out for two phases namely fluid phase and dust phase. We have considered dusty fluid as a base fluid with suspended Al2O3 nanoparticles. We have considered the range of nanoparticle fraction as 0 ≤ ϕ ≤ 02. It is worth mentioning that the present flow system reduces to the classical viscous nano fluid when ϕ = l = 0 and also it reduces to dusty viscous fluid when ϕ = 0. In order to get physical insight of the problem, a parametric study has been made and results are presented through graphs and tables.
Figure 2 illustrate the effect of velocity slip parameter A on velocity profile for both nanofluid and dust phases. It is observed that, increasing value of velocity slip parameter reduces the thickness of momentum boundary layer and results in decrease of velocity of both phases. This is because, the slip at the surface wall get increases with increase in slip parameter and thus a smaller amount of penetration due to the stretching surface into the fluid.
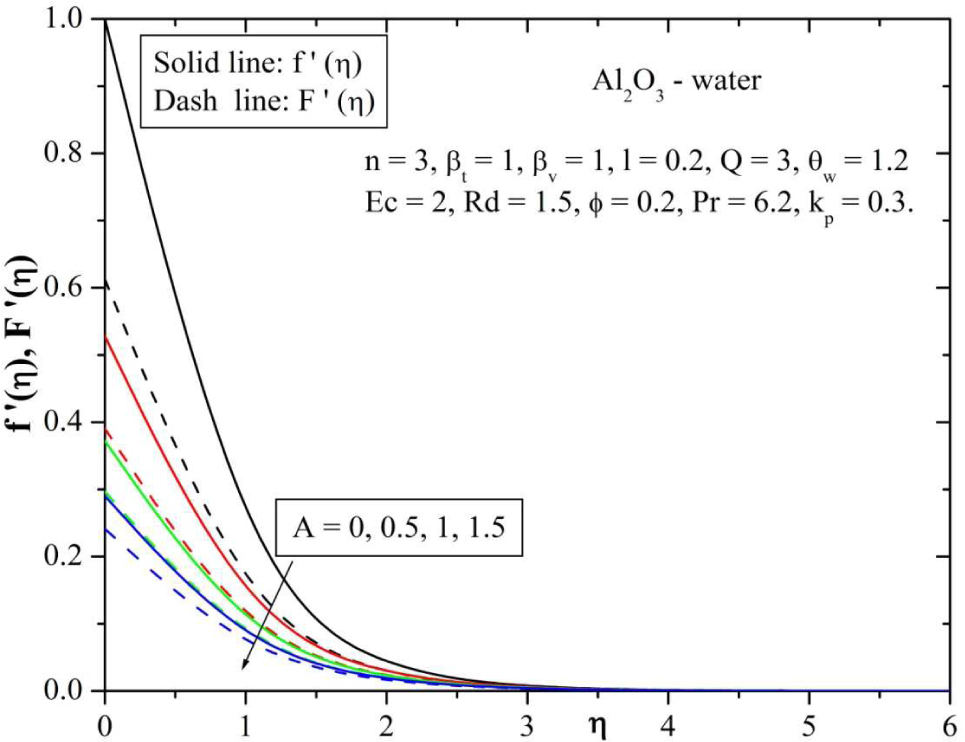
Behavior of velocity for varying values of Slip parameter(A).
Figure 3 and 4 shows the velocity and temperature profile for various values of magnetic parameter (Q). It is observed that, the velocity profile decreases and temperature profile increases for increasing the values of Q. Since the effect of magnetic field on an electrically conducting fluid results a resistive type of force called as Lorentz force, which has tendency to decrease the fluid velocity and to increase the temperature field. Due to this fact, magnetic field effect has many possible control-based applications like MHD ion propulsion, electromagnetic casting of metals, in MHD power generation and etc.
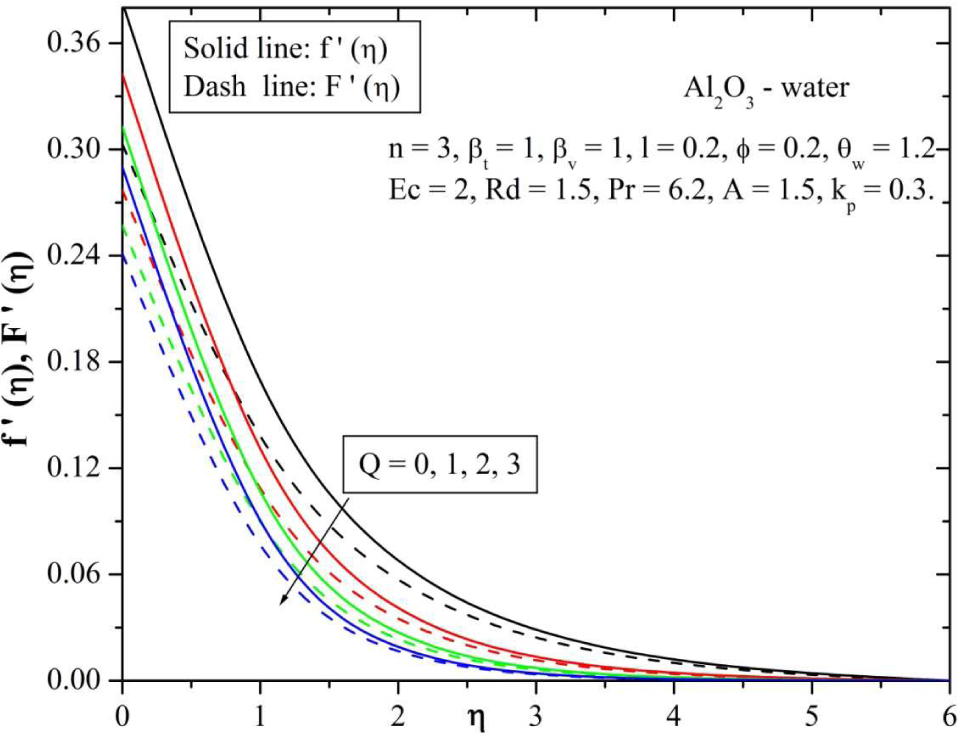
Behavior of velocity for varying values of magnetic parameter (Q).
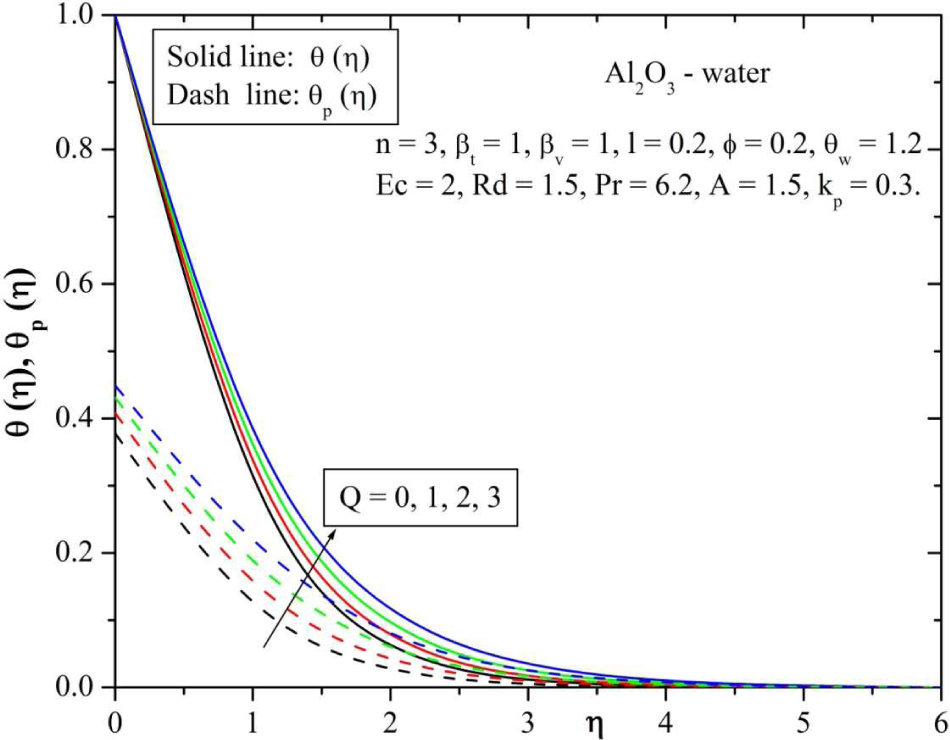
Behavior of temperature for varying values of magnetic parameter (Q).
The velocity distribution for fluid particle interaction parameter of velocity (βv) is shown in Figure 5. It is observed that an increase in fluid-particle interaction parameter, the thickness of momentum boundary layer decreases for fluid phase and this phenomena is opposite for the dust phase and which is as shown in Figure 5. From these figures observed that, the fluid phase velocity decreases and dust phase velocity increases for increasing the values of βv.
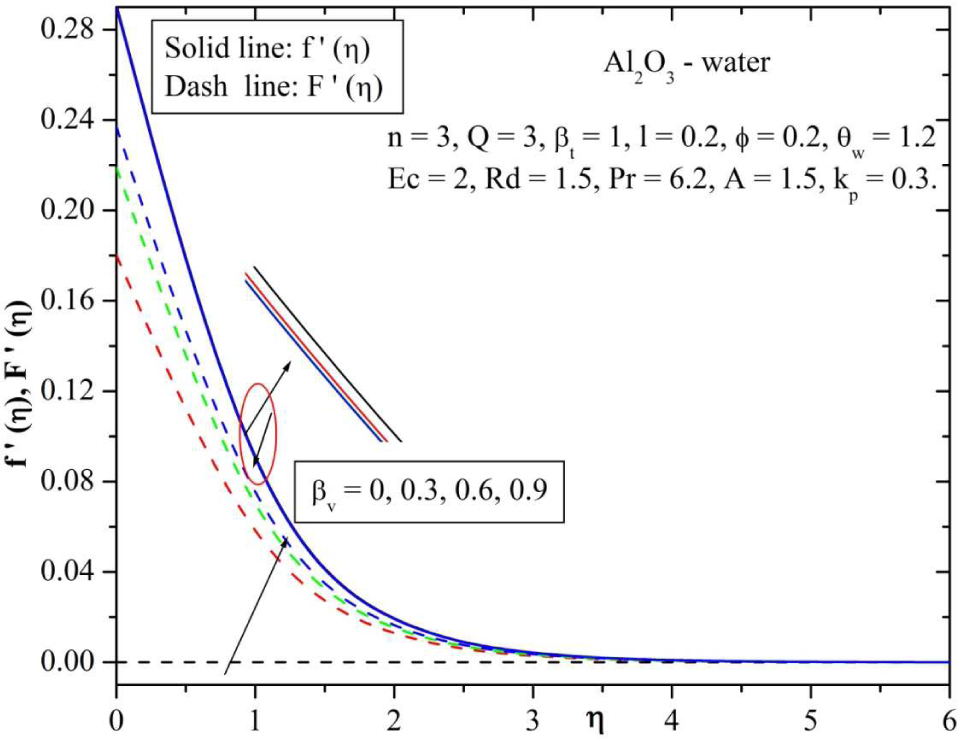
Behavior of velocity for varying values of velocity fluid particle interaction parameter (βv).
Figure 6 and 7 depicts the velocity and temperature profile of both fluid and dusty phases for various values of mass concentration parameter (l). In this figure, it is observed an increase in mass concentration of the particles decreases the momentum boundary layer for both the phases. Figures 8 and 9 represents the variation of velocity and temperature distributions for different values of permeability parameter kp. It is obvious that the presence of porous medium causes higher restriction to the fluid flow which causes the fluid to decelerate. Therefore, with an increase in impermeability parameter causes the resistance to the fluid motion and hence velocity decreases of both the phases. The effect of increasing values of permeable parameter contributes to the thickening of thermal boundary layer, which is shown in Figure 9. This is evident from the fact that, the porous medium opposes the fluid motion. The resistance offered to the flow is responsible in enhancing the temperature.
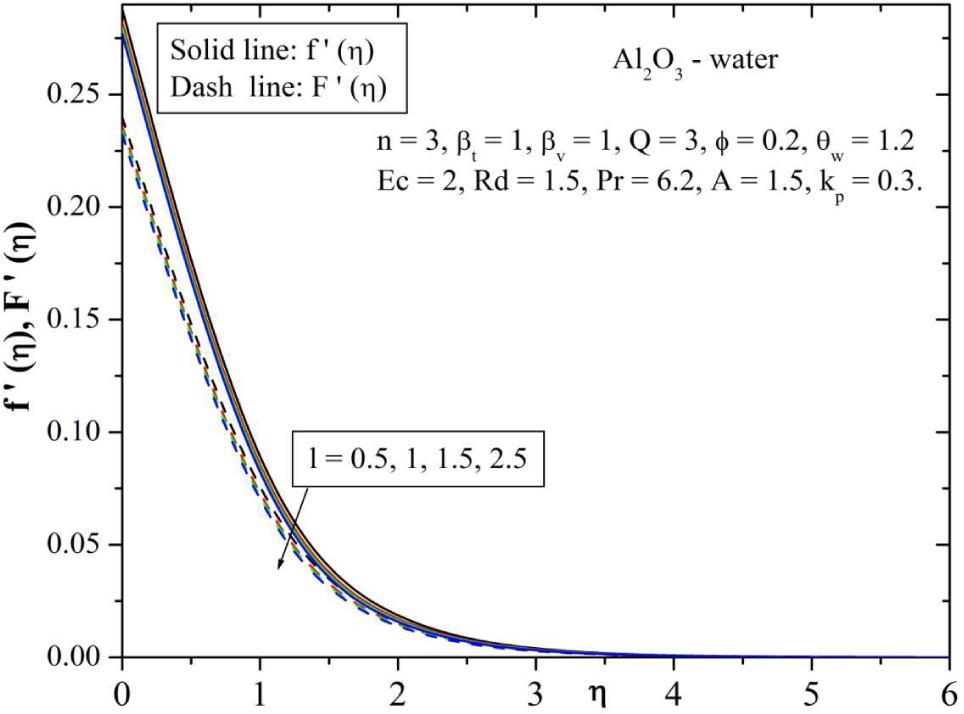
Behavior of velocity for varying values of mass concentration particle parameter (l).
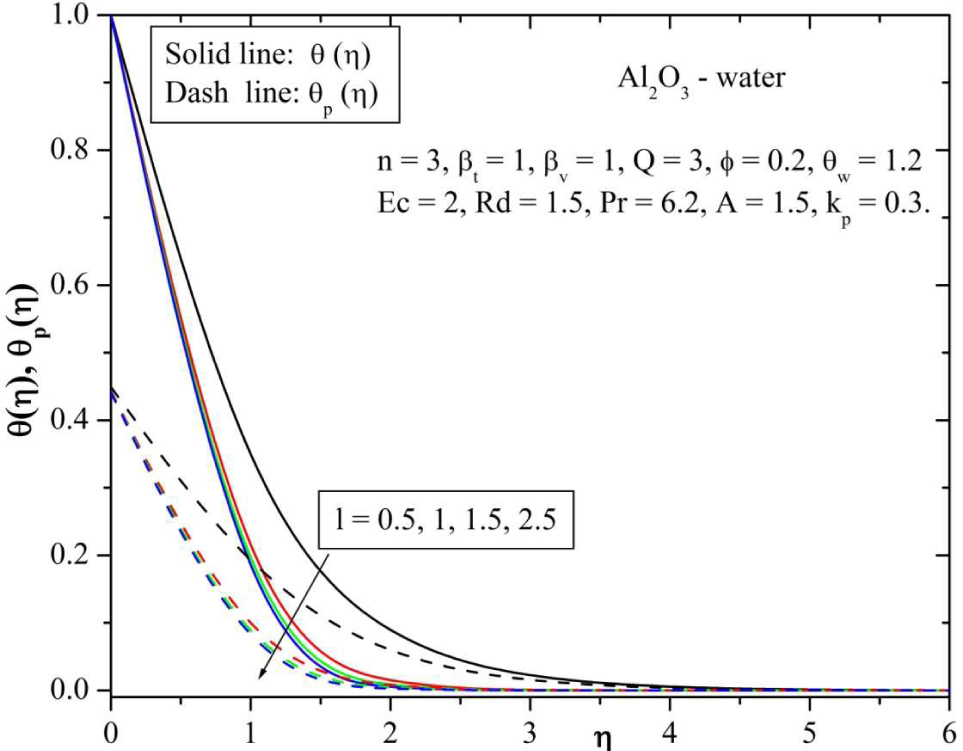
Behavior of temperature for varying values of mass concentration particle parameter (l).
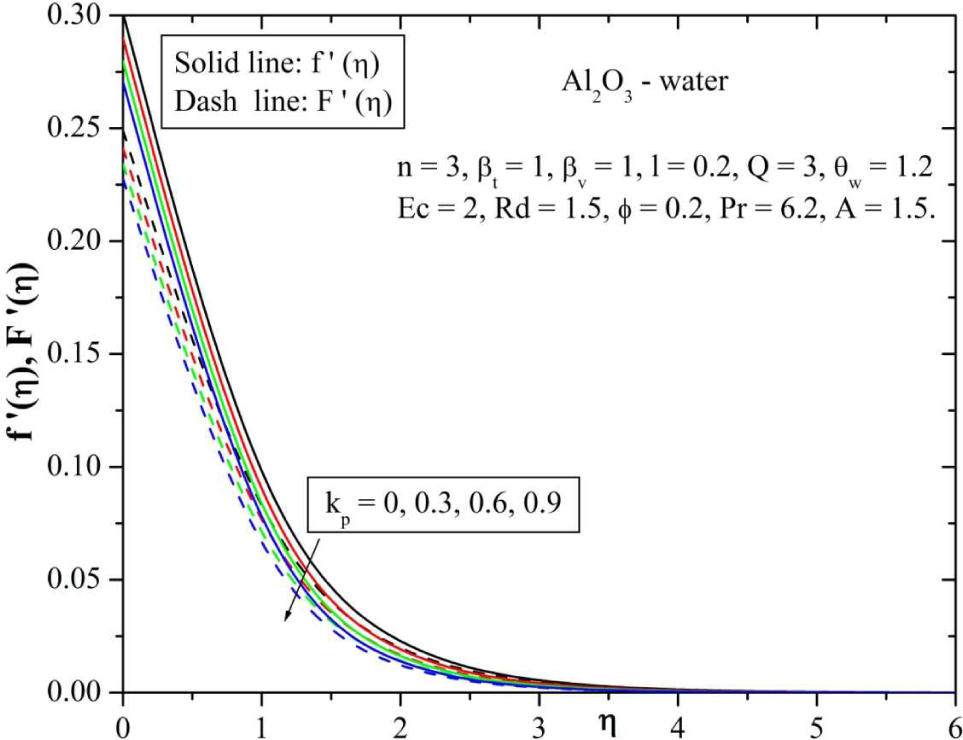
Behavior of velocity for varying values of permeability parameter (kp)
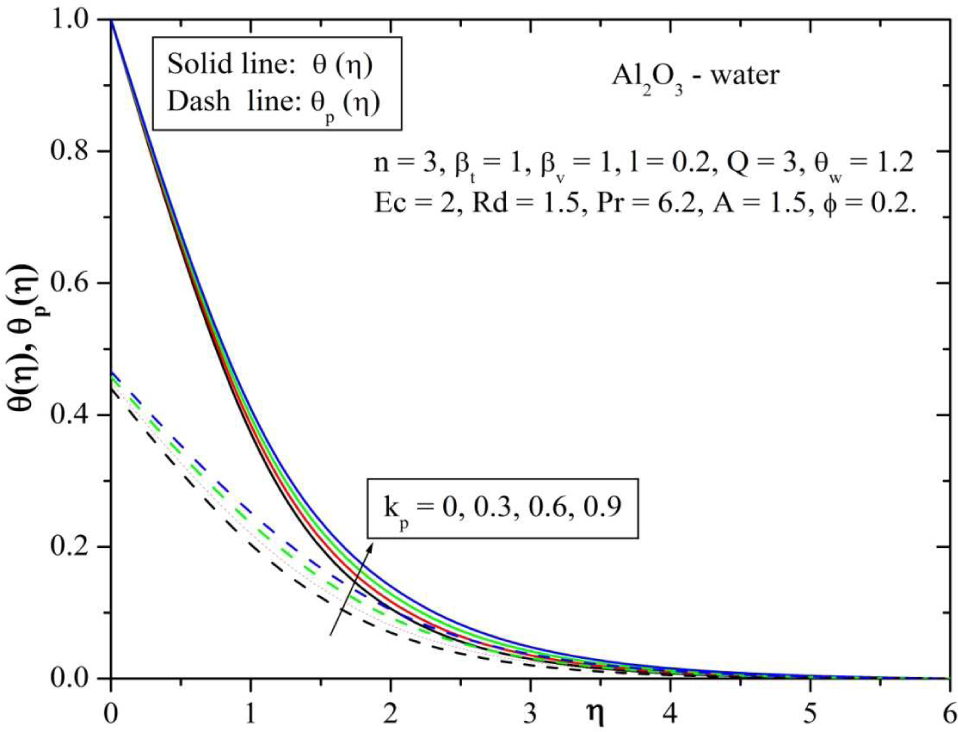
Behavior of temperature for varying values of permeability parameter (kp).
Figures 10 and 11 depicts the effect of nanoparticle volume fraction ϕ on the velociy and temperature distributions. From these graphs, it is clear that, with increase in the volume fraction of nanoparticle the velocity increases throughout the boundary layer region for both fluid and dust phase. Figure 11 shows that the effect of an increasing values of nanoparticle volume fraction, the temperature profile of both the phases increases throughout the boundary layer region. These figures illustrate this agreement with the physical behavior. When the volume fraction of nanoparticle increases, the thermal conductivity increases, this leads to increase in thermal boundary layer thickness.
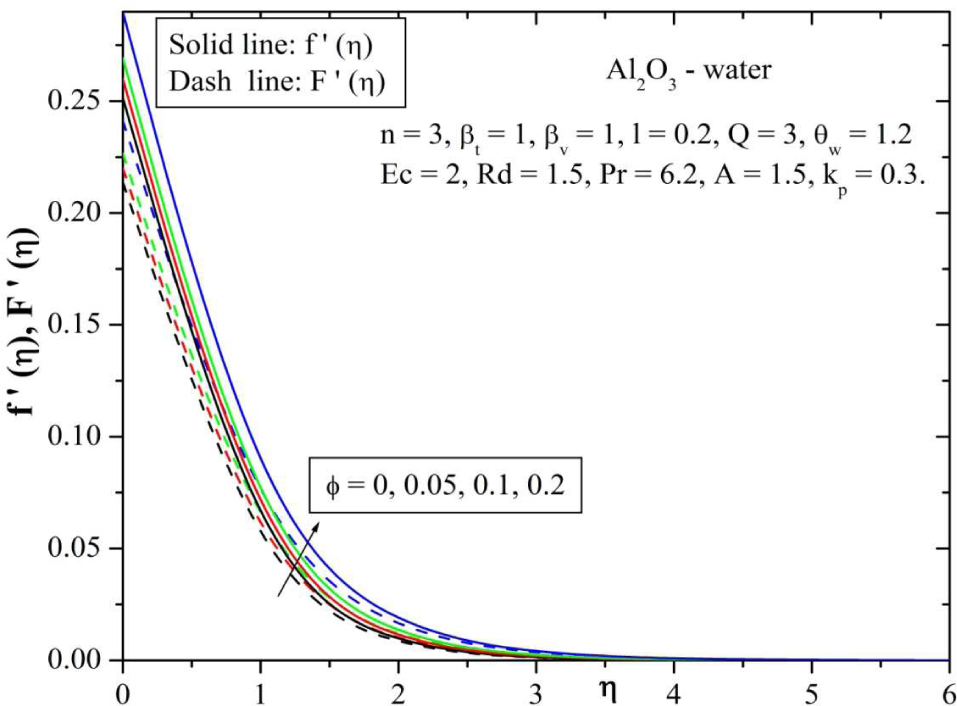
Behavior of velocity for varying values of solid volume fraction parameter (ϕ).
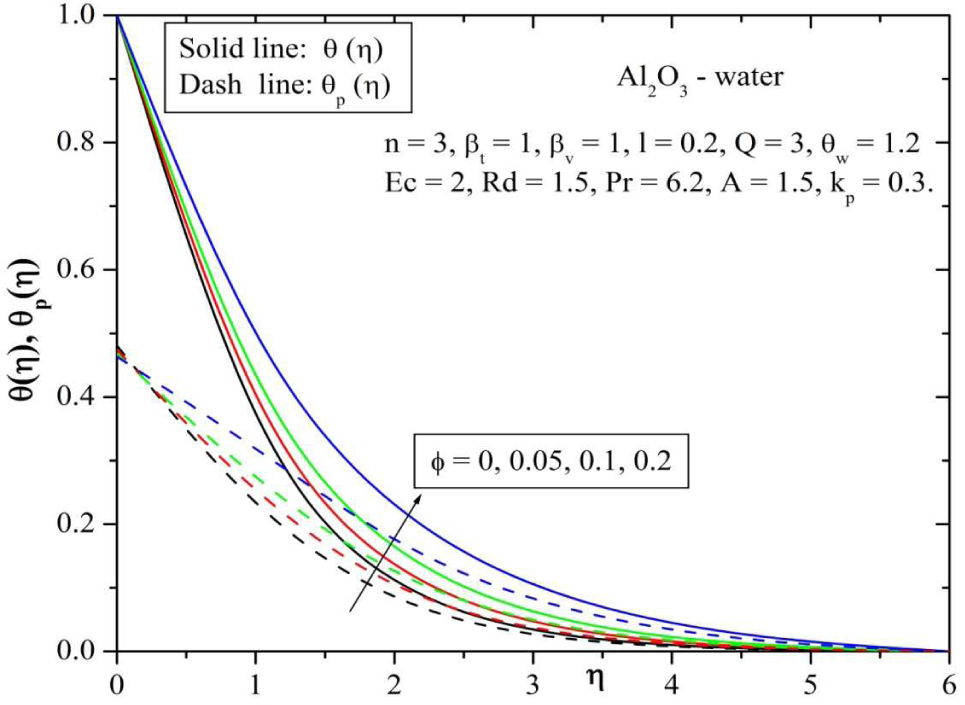
Behavior of temperature for varying values of solid volume fraction parameter (ϕ).
The effect of Eckert number (Ec) for temperature distribution was shown in Figure 12. From this figure it is observed that the temperature profiles increases for both fluid and dust phases with increasing values of Ec. It is because heat energy is stored in the liquid due to frictional heating and this is true in both the cases.
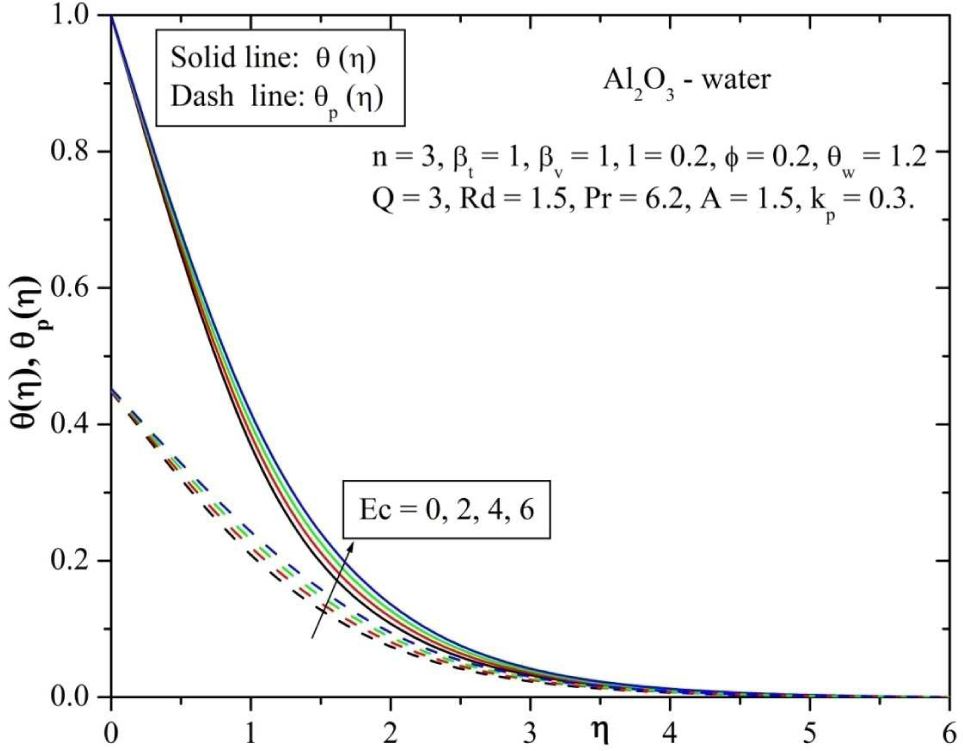
Behavior of temperature for varying values of Eckert number (Ec).
Figures 13 and 14 shows the temperature profile for various values of radiation parameter (Rd) and temperature ratio parameter θw respectively. From the Figure 13 it is observed that, the temperature profile increases for increasing values of Rd. This is due to the fact that an increase in radiation parameter provides more heat to fluid that causes an enhancement in the temperature and thermal boundary layer thickness. Form the Figure 14 it is observed that, the increase in temperature ratio parameter increases the thermal state of the fluid, and it results in increase of temperature profiles of both phases.
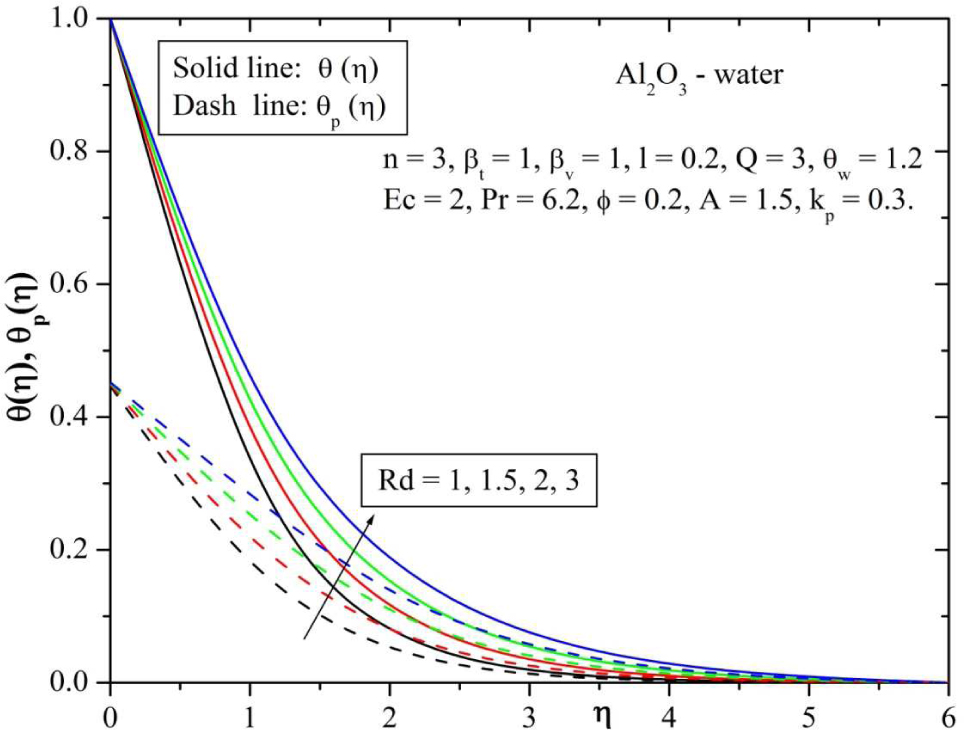
Behavior of temperature for varying values of radiation parameter (Rd).
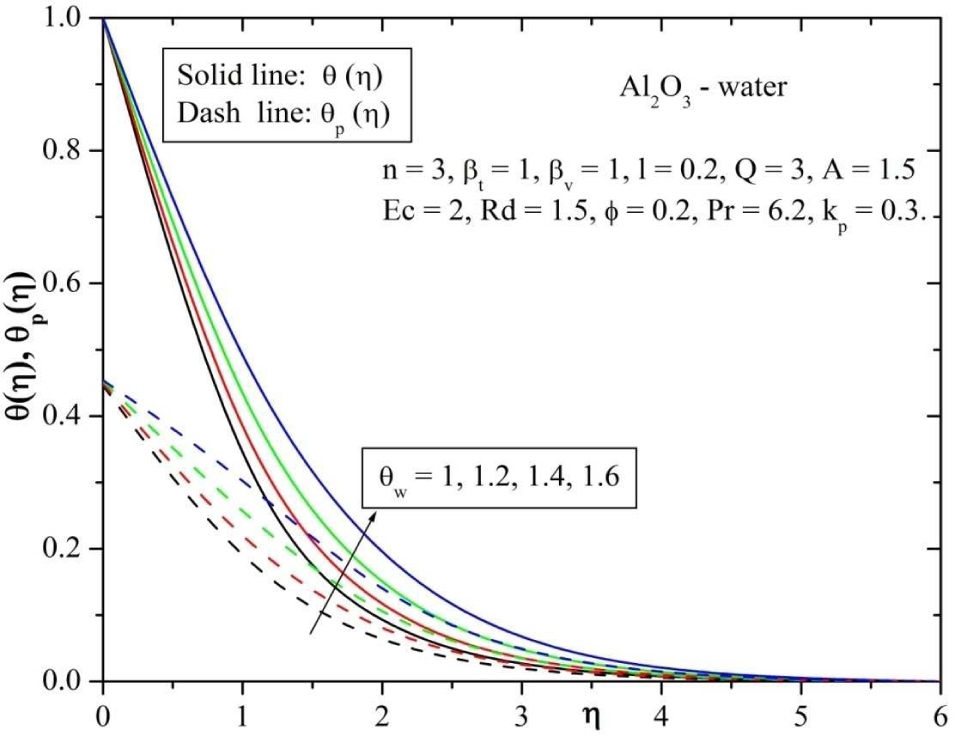
Behavior of temperature for varying values of temperature ratio parameter (θw).
The effect of Prandtl number on the heat transfer is shown in Figure 15. The relative thickening of momentum and thermal boundary layers is controlled by Prandtl number (Pr). Since small values of Pr will possess higher thermal conductivities, so that heat can diffuse from the sheet very quickly compared to the velocity. From this figure, it reveals that the temperature decreases with increase in the value of Pr. Hence Prandtl number can be used to increase the rate of cooling. By analyzing the graph it reveal that the effect of increasing the Pr is to decrease the temperature distribution in the flow region, and also it is evident that large values of Prandtl number results in thinning of thermal boundary layer. From this figure we observed that both the profiles decreases for increasing the values of Pr.
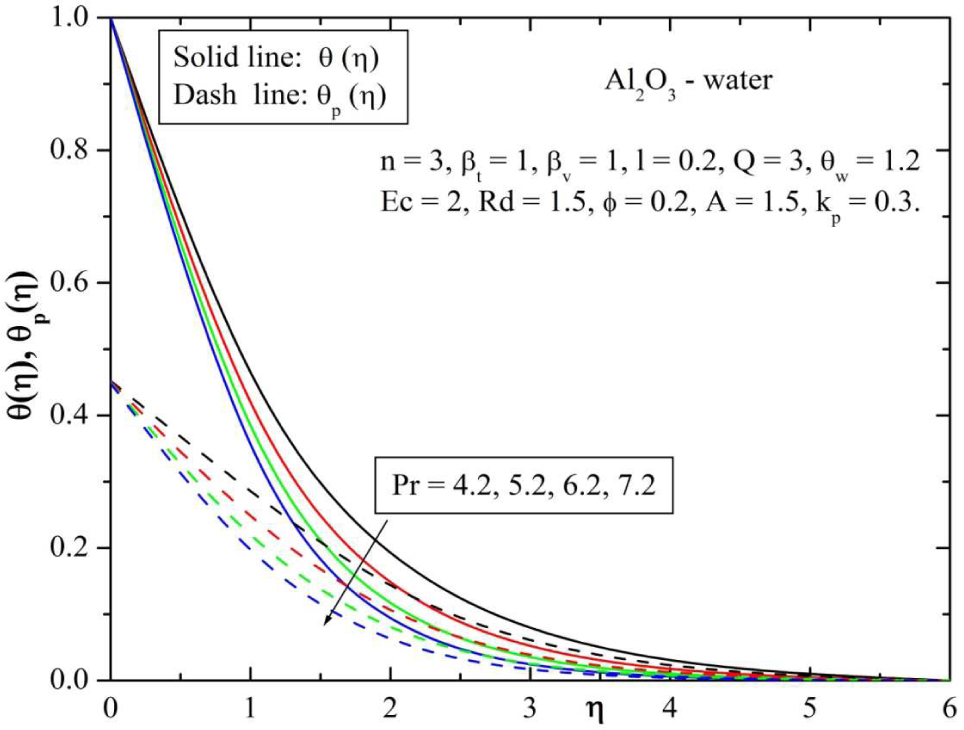
Behavior of temperature for varying values of Prandtl number (Pr).
Table 1 shows the values of skin friction coefficient of magnetic parameter (Q) for linear and nonlinear stretching surfaces for different cases. From this table we observed that compared to other fluids dusty nanofluids have high skin friction coefficient. Table 2 shows the values of skin friction coefficient for different types of parameters with two different types of nanoparticles. The values of Nusselt number for linear and nonlinear stretching cases for various values of pertinent parameters considered with two different types of nanoparticles was shown in Table 3 and 4. In this table we observed that the Copper nanoparticle has high heat transfer rate compared to other nanoparticle.
Values of skin friction coefficient for different types of fluids when n = 1 and n = 3.
| Ordinary fluid: | Dusty fluid: | Nano fluid: | Dusty nano fluid: | |||||
|---|---|---|---|---|---|---|---|---|
| l = βv = ϕ = 0 | l = 0.2, βv = 1, ϕ = 0 | l = βv = 0, ϕ = 0.2 | l = 0.2, βv = 1, ϕ = 0.2 | |||||
| Q | n = 1 | n = 3 | n = 1 | n = 3 | n = 1 | n = 3 | n = 1 | n = 3 |
| 0 | 0.41308 | 0.58418 | 0.4164 | 0.58978 | 0.71417 | 1.01 | 0.71782 | 1.01613 |
| 0.5 | 0.4366 | 0.61744 | 0.4389 | 0.62136 | 0.74071 | 1.04753 | 0.74361 | 1.05243 |
| 1 | 0.4545 | 0.64276 | 0.45619 | 0.64565 | 0.76298 | 1.07901 | 0.76533 | 1.08301 |
| 2 | 0.48027 | 0.67921 | 0.48129 | 0.68096 | 0.79843 | 1.12915 | 0.80007 | 1.13196 |
| 5 | 0.52218 | 0.73848 | 0.52255 | 0.73912 | 0.86516 | 1.22352 | 0.86589 | 1.22479 |
Values of skin friction coefficient for different values of the pertinent parameters when n = 3(nonlinear stretching sheet) and n = 1(Linear stretching sheet).
| Nonlinear stretching sheet: n = 3 | Linear strtching sheet: n = 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| βv | Q | ϕ | l | A | kp | Al2O3 | Cu | Al2O3 | Cu |
| 0 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16761 | −1.18808 | −0.82563 | −0.8401 |
| 0.3 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16908 | −1.18927 | −0.82656 | −0.84086 |
| 0.6 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16946 | −1.18958 | −0.82674 | −0.841 |
| 1 | 0 | 0.2 | 0.2 | 1.5 | 0.3 | −1.01613 | −1.0712 | −0.71782 | −0.75698 |
| 1 | 0.5 | 0.2 | 0.2 | 1.5 | 0.3 | −1.05243 | −1.09733 | −0.74361 | −0.77552 |
| 1 | 1 | 0.2 | 0.2 | 1.5 | 0.3 | −1.08301 | −1.12025 | −0.76533 | −0.79179 |
| 1 | 3 | 0 | 0.2 | 1.5 | 0.3 | −0.70578 | −0.70578 | −0.48129 | −0.49891 |
| 1 | 3 | 0.1 | 0.2 | 1.5 | 0.3 | −0.89662 | −0.90435 | −0.61236 | −0.63929 |
| 1 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16969 | −1.18976 | −0.80007 | −0.84107 |
| 1 | 3 | 0.2 | 0 | 1.5 | 0.3 | −1.16761 | −1.18808 | −0.79843 | −0.8401 |
| 1 | 3 | 0.2 | 0.5 | 1.5 | 0.3 | −1.17273 | −1.19222 | −0.80247 | −0.8425 |
| 1 | 3 | 0.2 | 1 | 1.5 | 0.3 | −1.1776 | −1.1962 | −0.8063 | −0.84483 |
| 1 | 3 | 0.2 | 0.2 | 0.5 | 0.3 | −2.33173 | −2.44098 | −1.56971 | −1.72523 |
| 1 | 3 | 0.2 | 0.2 | 1 | 0.3 | −1.55157 | −1.59204 | −1.05489 | −1.12537 |
| 1 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16969 | −1.18976 | −0.80007 | −0.84107 |
| 1 | 3 | 0.2 | 0.2 | 1.5 | 0 | −1.15104 | −1.17424 | −0.78309 | −0.83007 |
| 1 | 3 | 0.2 | 0.2 | 1.5 | 0.3 | −1.16969 | −1.18976 | −0.80007 | −0.84107 |
| 1 | 3 | 0.2 | 0.2 | 1.5 | 0.6 | −1.1863 | −1.20382 | −0.81489 | −0.85104 |
Values of Nusselt number for different values of the pertinent parameters when n = 3 (nonlinear stretching sheet).
| Nonlinear stretching sheet: n = 3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| βv | βt | Q | ϕ | l | Ec | Rd | Pr | A | θw | kp | Al2O3 | Cu |
| 0 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.269591 | 7.119287 |
| 0.3 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.752997 | 9.188412 |
| 0.6 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.980862 | 9.496683 |
| 1 | 0 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 2.843238 | 2.663868 |
| 1 | 0.5 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.04586 | 8.001809 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 0 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 9.161375 | 11.39672 |
| 1 | 1 | 0.5 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 8.726411 | 11.05532 |
| 1 | 1 | 1 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 8.339138 | 10.74004 |
| 1 | 1 | 3 | 0 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.513187 | 9.065777 |
| 1 | 1 | 3 | 0.1 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.925948 | 9.532146 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 2.880343 | 2.704961 |
| 1 | 1 | 3 | 0.2 | 0.5 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 11.33806 | 15.80813 |
| 1 | 1 | 3 | 0.2 | 1 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 16.34382 | 22.90732 |
| 1 | 1 | 3 | 0.2 | 0.2 | 0 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 8.349951 | 10.7694 |
| 1 | 1 | 3 | 0.2 | 0.2 | 1 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.724645 | 10.21332 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 2 | 6.2 | 1.5 | 1.2 | 0.3 | 7.692951 | 10.50114 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 3 | 6.2 | 1.5 | 1.2 | 0.3 | 8.665469 | 11.86541 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 2.2 | 1.5 | 1.2 | 0.3 | 3.737972 | 5.06474 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 4.2 | 1.5 | 1.2 | 0.3 | 5.580596 | 7.632391 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 0.5 | 1.2 | 0.3 | 6.192272 | 8.949947 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1 | 1.2 | 0.3 | 7.146878 | 9.809276 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1 | 0.3 | 6.372628 | 8.645918 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.4 | 0.3 | 7.870593 | 10.75431 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0 | 7.38668 | 9.918742 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 7.098943 | 9.656928 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.6 | 6.831997 | 9.407612 |
Values of Nusselt number for different values of the pertinent parameters when n = 1 (Linear stretching sheet).
| Linear stretchingsheet: n = 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| βv | βt | Q | ϕ | l | Ec | Rd | Pr | A | θw | kp | Al2O3 | Cu |
| 0 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 3.726164 | 5.034096 |
| 0.3 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 4.81774 | 6.561781 |
| 0.6 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 4.975291 | 6.772953 |
| 1 | 0 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 2.015815 | 1.890689 |
| 1 | 0.5 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 4.293938 | 5.685536 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.051793 | 6.874963 |
| 1 | 1 | 0 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.519396 | 8.11285 |
| 1 | 1 | 0.5 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.20975 | 7.870014 |
| 1 | 1 | 1 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.934152 | 7.645717 |
| 1 | 1 | 3 | 0 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.03789 | 6.450257 |
| 1 | 1 | 3 | 0.1 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.341128 | 6.783954 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 2.364272 | 1.912696 |
| 1 | 1 | 3 | 0.2 | 0.5 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 8.480547 | 11.25834 |
| 1 | 1 | 3 | 0.2 | 1 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 12.06466 | 16.31374 |
| 1 | 1 | 3 | 0.2 | 0.2 | 0 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 6.33239 | 7.655413 |
| 1 | 1 | 3 | 0.2 | 0.2 | 1 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.894844 | 7.265296 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 2 | 6.2 | 1.5 | 1.2 | 0.3 | 5.940582 | 7.476468 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 3 | 6.2 | 1.5 | 1.2 | 0.3 | 6.732852 | 8.448398 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 2.2 | 1.5 | 1.2 | 0.3 | 2.912236 | 3.605851 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 4.2 | 1.5 | 1.2 | 0.3 | 4.325001 | 5.434226 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 0.5 | 1.2 | 0.3 | 4.868439 | 6.404144 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1 | 1.2 | 0.3 | 5.48333 | 6.990926 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1 | 0.3 | 4.877866 | 6.154435 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.4 | 0.3 | 6.083426 | 7.657097 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0 | 5.696421 | 7.061297 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.3 | 5.456977 | 6.874963 |
| 1 | 1 | 3 | 0.2 | 0.2 | 2 | 1.5 | 6.2 | 1.5 | 1.2 | 0.6 | 1.457971 | 1.864563 |
5 Conclusion
The problem of two-phase slip flow of a dusty fluid with nano particles over a nonlinear stretching sheet embedded in a porous medium in the presence of nonlinear thermal radiation has been is studied. By using the appropriate transformation for the velocity and temperature, the basic equations governing the flow and heat transfer were reduced to a set of ordinary differential equations. These equations are solved numerically using the fourth-fifth-order Runge–Kutta-Fehlberg method. Some conclusions obtained from this investigation are summarized as follows:
The effect of transverse magnetic field is to suppress the velocity field, which in turn causes the enhancement of the temperature field.
Velocity of fluid and dust phases decrease with increases in slip parameter and permeability parameter.
Fluid phase temperature is higher than the dust phase temperature.
Velocity of nanofluid and dust phases decrease while the temperature of fluid and dust phases increase as solid volume fraction of nanoparticle (ϕ) increases.
It is found that the dusty fluid with Copper (Cu) nanoparticle have the appreciable cooling performance.
Temperature profile increases for Eckert number, radiation parameter, temperature ratio parameter, permeability parameter and decreases for Prandtl number and mass concentration particle parameter.
The Nusselt number increases for nonlinear stretching case when compared to linear stretching case.
Acknowledgement
The authors (B.C.Prasannakumara and Shashikumar, N.S) are thankful to the University Grants Commission, New Delhi, INDIA for financial support to pursue this work under a Major research project Scheme. [F.No-43-419/2014(SR)]. We would like to express our sincere thanks to the very competent Reviewers for the invaluable comments and suggestions, which led to further improvement of the paper.
References
[1] L. J. Crane, Flow past a stretching plate. Z. Angew Math Phys., 21, pp. 645–647, (1970).10.1007/BF01587695Suche in Google Scholar
[2] C. H. Chen, Laminar mixed convection adjacent to vertical continuously stretching sheets, Heat and Mass Transfer, 33(5), pp. 471–476, (1998).10.1007/s002310050217Suche in Google Scholar
[3] W. A. Khan and I. Pop, Boundary-layer flow of a nanofluid past a stretching sheet, Int. J. of Heat and Mass Transfer, 53(11–12), pp. 2477–2483, (2010).10.1016/j.ijheatmasstransfer.2010.01.032Suche in Google Scholar
[4] O. D. Makinde and A. Aziz, Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition, Int. J. of Thermal Sci., 50, pp. 1326–1332, (2011).10.1016/j.ijthermalsci.2011.02.019Suche in Google Scholar
[5] M. M. Khader and Ahmed M. Megahed, Approximate Solutions for the Flow and Heat Transfer due to a Stretching Sheet Embedded in a Porous Medium with Variable Thickness, Variable Thermal Conductivity and Thermal Radiation using Laguerre Collocation Method, Applications and Applied Mathematics: An Int. J., 10(2), pp. 817–834, (2015).Suche in Google Scholar
[6] M. M. Khader, Shifted Legendre collocation method for the flow and heat transfer due to a stretching sheet embedded in a porous medium with variable thickness, variable thermal conductivity and thermal radiation, Mediterranean J. of Mathematics, 13(4), pp. 2319–2336, (2015).10.1007/s00009-015-0594-3Suche in Google Scholar
[7] G. K. Ramesh, B. C. Prasannakumara, B. J. Gireeshaand M. M. Rashidi, Casson Fluid Flow near the Stagnation Point over a Stretching Sheet with Variable Thickness and Radiation, J. of Appl. Fluid Mech. 9, pp. 1115–1122, (2016).10.18869/acadpub.jafm.68.228.24584Suche in Google Scholar
[8] M. G. Reddy, P. Padma and R. S. R. Gorla, Influence of Double Stratification on MHD Three Dimensional Casson Nanofluid Flow Over a Stretching Sheet: A Numerical Study, J. of Nanofluids, 6, pp. 71–79(9), (2016).Suche in Google Scholar
[9] M. M. Khader and Ahmed M. Megahed, Numerical treatment for flow and heat transfer of Powell–Eyring fluid over an exponential stretching sheet with variable thermal conductivity, Meccanica, 51: 1763. (2016), 10.1007/s11012-015-0336-4Suche in Google Scholar
[10] C. Sulochana, G.P. Ashwinkumar and N. Sandeep, Similarity solution of 3D Casson nanofluid flow over a stretching sheet with convective boundary conditions, J. of the Nigerian Mathematical Society, 35(1), pp. 128–141, (2016).10.1016/j.jnnms.2016.01.001Suche in Google Scholar
[11] B. J. Gireesha, P. Venkatesh, N. S. Shashikumar, and B. C. Prasannakumara, Boundary layer flow of dusty fluid over a permeable radiating stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source. Nonlinear Engineering, (2017) 10.1515/nleng-2016-0058.Suche in Google Scholar
[12] Z. Abbas and T. Hayat, Stagnation Slip Flow and Heat Transfer over a Nonlinear Stretching Sheet, Numerical Methods Partial Diff. Eqs. 27, 302 (2011)10.1002/num.20523Suche in Google Scholar
[13] M. S. Abel, K. A. Kumar, and R. Ravikumara, MHD Flow and Heat Transfer with Effects of Buoyancy, Viscous and Joules Dissipation over a Nonlinear Vertical Stretching Porous Sheet with Partial Slip, Engineering, 3, pp. 285–291, (2011).10.4236/eng.2011.33033Suche in Google Scholar
[14] P. Rana and R. Bhargava, Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study, Communications in Nonlinear Science and Numerical Simulation 17(1), pp. 212–226, (2012).10.1016/j.cnsns.2011.05.009Suche in Google Scholar
[15] I. C. Mandal and S. Mukhopadhyay, Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium, Ain Shams Engineering J., 4, pp. 103–110, (2013).10.1016/j.asej.2012.06.004Suche in Google Scholar
[16] M. Khan, R. Malik, A. Munir and W. A. Khan, Flow and Heat Transfer to Sisko Nanofluid over a Nonlinear Stretching Sheet, PLoS ONE, 10(5): e0125683. (2015), http://dx.doi.org/10.1371/journal.pone.0125683.10.1371/journal.pone.0125683Suche in Google Scholar PubMed PubMed Central
[17] M. Khan and Hashim, Boundary layer flow and heat transfer to Carreau fluid over a nonlinear stretching sheet, AIP Advances, 5(10), (2015), 10.1063/1.4932627.Suche in Google Scholar
[18] M. R. Krishnamurthy, B. J. Gireesha, B. C. Prasannakumara and R. S. R. Gorla, Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, Nonlinear Engineering, (2016), 10.1515/nleng-2016-0013.Suche in Google Scholar
[19] T. Hayat, M. Imtiaz and A. Alsaed, Boundary layer flow of Oldroyd-B fluid by exponentially stretching sheet, Appl. Math. Mech. -Engl. Ed., 37(5), pp. 573–582, (2016).10.1007/s10483-016-2072-8Suche in Google Scholar
[20] J. Buongiorno, Convective transport in nanofluids, ASME J. Heat. Transfer, 128, pp. 240–250, (2006).10.1115/1.2150834Suche in Google Scholar
[21] W. A. Khan and I. Pop, Boundary-layer flow of a nanofluid past a stretching sheet, Int. J. Heat Mass Transfer, 53, pp. 2477–2483, (2010).10.1016/j.ijheatmasstransfer.2010.01.032Suche in Google Scholar
[22] O. D. Makinde, and A. Aziz, Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition, Int. J. of Thermal Sci., 50, pp. 1326–1332, (2011).10.1016/j.ijthermalsci.2011.02.019Suche in Google Scholar
[23] W. Ibrahim, B. Shankar, M. M. Nandeppanavar, MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet, Int. J. of Heat and Mass Transfer, 56(1–2), pp. 1–9, (2013).10.1016/j.ijheatmasstransfer.2012.08.034Suche in Google Scholar
[24] M. M. Rashidi, N. Freidoonimehr, A. Hosseini, O. A. Begand T. K. Hung, Homotopy simulation of nanofluid dynamics from a non-linearly stretching isothermal permeable sheet with transpiration, Meccanica, 49, pp. 469–482, (2014).10.1007/s11012-013-9805-9Suche in Google Scholar
[25] T. Hayat, M. Waqas, S. A. Shehzad and A. Alsaedi, Stretched flow of Carreau nanofluid with convective boundary condition, Pramana 86, pp. 3–17, (2016).10.1007/s12043-015-1137-ySuche in Google Scholar
[26] B. C. Prasannakumara, B. J. Gireesha, R. S. R. Gorla and M. R. Krishnamurthy, Effects of Chemical Reaction and Nonlinear Thermal Radiation on Williamson Nanofluid Slip Flow over a Stretching Sheet Embedded in a Porous Medium, J. of Aerospace Engineering, 29(5), (2016), DOI: http://dx.doi.org/10.1061/(ASCE)AS.1943-5525.0000578.10.1061/(ASCE)AS.1943-5525.0000578Suche in Google Scholar
[27] M. M. Nandeppanavar, Mixed Convection of MHD Boundary Layer Flow of Nanofluid Due to a Vertically Stretching Sheet with Partial Slip, J. of Nanofluids, 5(3), pp. 416–422(7), (2016).10.1166/jon.2016.1225Suche in Google Scholar
[28] H. I. Anderson, Slip flow past a stretching surface, Acta Mech., 158, pp. 121–125, (2002).10.1007/BF01463174Suche in Google Scholar
[29] T. Fang and J. Z. Shanshan Yao, Slip MHD viscous flow over a stretching sheet – An exact solution, Communications in Nonlinear Science and Numerical Simulation, 14(11), pp. 3731–3737, (2009).10.1016/j.cnsns.2009.02.012Suche in Google Scholar
[30] W. Ibrahim and O. D. Makinde, Magnetohydrodynamic Stagnation Point Flow and Heat Transfer of Casson Nanofluid Past a Stretching Sheet with Slip and Convective Boundary Condition, J. of Aerospace Engineering, 29(2), (2015), 10.1061/(ASCE)AS.1943-5525.0000529.Suche in Google Scholar
[31] M. M. Khader and Ahmed M. Megahed, Boundary layer flow due to a stretching sheet with a variable thickness and slip velocity, J. of Applied Mechanics and Technical Physics, 56(2), pp. 241–247, (2015).10.1134/S0021894415020091Suche in Google Scholar
[32] S. P. Anjali Devi and M. Prakash, Slip Flow Effects over Hydromagnetic Forced Convective Flow over a Slendering Stretching Sheet, J. of Applied Fluid Mechanics, 9(2), pp.683-692, (2016).10.18869/acadpub.jafm.68.225.24064Suche in Google Scholar
[33] T. Hayat, A. Shafiq, A. Alsaedi and S. A. Shahzad, Unsteady MHD flow over exponentially stretching sheet with slip conditions, Applied Mathematics and Mechanics, 37(2), pp. 193–208, (2016).10.1007/s10483-016-2024-8Suche in Google Scholar
[34] S. Shaw, P. K. Kameswaran and P. Sibanda, Effects of slip on nonlinear convection in nanofluid flow on stretching surfaces, Boundary Value Problems, (2016), 2016:2 10.1186/s13661-015-0506-2.Suche in Google Scholar
[35] P. G. Saffman, On the stability of laminar flow of a dusty gas, J. Fluid. Mech., 13, pp. 120–128, (1962).10.1017/S0022112062000555Suche in Google Scholar
[36] G. Palani and P. Ganesan, Heat transfer effects on dusty gas flow past a semiinfinite inclined plate, Forsch Ingenieurwes, 71, pp.223–230, (2007).10.1007/s10010-007-0061-9Suche in Google Scholar
[37] P. T. Manjunatha, B. J. Gireesha and B. C. Prasannakumara, Thermal analysis of conducting dusty fluid flow in a porous medium over a stretching cylinder in the presence of non-uniform source/sink, Int. J. of Mechanical and Materials Engineering (2014), 1:13 10.1186/s40712-014-0013-8.Suche in Google Scholar
[38] N. Sandeep, C. Sulochana and B. R. Kumar, Unsteady MHD radiative flow and heat transfer of a dusty nanofluid over an exponentially stretching surface, Engineering Science and Technology, an International Journal, 19, pp.227–240, (2016).10.1016/j.jestch.2015.06.004Suche in Google Scholar
[39] Mustafa Turkyilmazoglu, Magnetohydrodynamic two-phase dusty fluid flow and heat model over deforming isothermal surfaces, Physics of Fluids 29, 013302 (2017)10.1063/1.4965926Suche in Google Scholar
[40] S. A. Shehzad, T. Hayat, A. Alsaedi and M. A. Obid, Nonlinear thermal radiation in three-dimensional flow of Jeffrey nanofluid: A model for solar energy, Appl. Math. Comput., 248, pp.273–286, (2014).10.1016/j.amc.2014.09.091Suche in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Velocity and thermal slip effects on MHD third order blood flow in an irregular channel though a porous medium with homogeneous/ heterogeneous reactions
- Boundary Layer Flow and Heat Transfer of fluid particle suspension with nanoparticles over a nonlinear stretching sheet embedded in a porous medium
- Thermal Analysis of porous fin with uniform magnetic field using Adomian decomposition Sumudu transform method
- Two dimensional kinematic surfaces with constant scalar curvature in Lorentz-Minkowski 7-space
- Influence of nonlinear thermal radiation and viscous dissipation on three-dimensional flow of Jeffrey nano fluid over a stretching sheet in the presence of Joule heating
- A second order numerical method for a class of parameterized singular perturbation problems on adaptive grid
- The generalized fractional order of the Chebyshev functions on nonlinear boundary value problems in the semi-infinite domain
- Nonlinear Dynamics Analysis for the Taut Inclined Cable Excited by Deck Vibration
Artikel in diesem Heft
- Frontmatter
- Velocity and thermal slip effects on MHD third order blood flow in an irregular channel though a porous medium with homogeneous/ heterogeneous reactions
- Boundary Layer Flow and Heat Transfer of fluid particle suspension with nanoparticles over a nonlinear stretching sheet embedded in a porous medium
- Thermal Analysis of porous fin with uniform magnetic field using Adomian decomposition Sumudu transform method
- Two dimensional kinematic surfaces with constant scalar curvature in Lorentz-Minkowski 7-space
- Influence of nonlinear thermal radiation and viscous dissipation on three-dimensional flow of Jeffrey nano fluid over a stretching sheet in the presence of Joule heating
- A second order numerical method for a class of parameterized singular perturbation problems on adaptive grid
- The generalized fractional order of the Chebyshev functions on nonlinear boundary value problems in the semi-infinite domain
- Nonlinear Dynamics Analysis for the Taut Inclined Cable Excited by Deck Vibration


