Abstract
Numerical investigation for the effect of thermal stratification on MHD flow and heat transfer of dusty fluid over a vertical stretching sheet embedded in a thermally stratified porous medium in the presence of uniform heat source and thermal radiation. The governing equations for the problem were reduced in to dimensionless ordinary differential equations using suitable similarity transformations. The transformed nonlinear ordinary differential equations are numerically solved by applying efficient RungeKutta Fehlberg-45 Method with shooting technique. The effects of various flow controlling parameters such as Prandtl number, heat source/sink parameter, fluid particle interaction parameter, heat source parameter, radiation parameter on velocity and temperature distributions of both fluid and dust phases are depicted graphically. Finally, the numerical results are compared and found to be in good agreement with previously published results under special cases. The results indicate that the fluid phase velocity is always greater than that of the particle phase and thermal stratification significantly affects the surface shear stress as well as the surface heat transfer.
1 Introduction
Free convection in electrically conducting fluids through an external magnetic field has numerous and wide range of applications in the fields such as nuclear reactors, geothermal engineering, liquid metals and plasma flows, petroleum industries, the boundary layer control in aerodynamics, crystal growth, industrial and agricultural water distribution, oil recovery processes, thermal insulation engineering, pollutant dispersion in aquifers, the dispersion of chemical contaminants in various processes in the chemical industry and in the environment, soil pollution, fibrous insulation etc. Thermal radiation was identified as the important heat transfer mechanism in the indirect heating method in heat treatment furnaces. At high operating temperature, radiation effect is quite significant. Many processes in engineering areas occur at high temperature and knowledge of radiation heat transfer becomes very important for the design of the pertinent equipment. Nuclear power plants, gas turbines and the various propulsion devices for aircraft, missiles, satellites and space vehicles are examples of such engineering areas. Hossain and Takhar [1] studied the effect of thermal radiation using the Rosseland diffusion approximation on mixed convection along a vertical plate with uniform free stream velocity and surface temperature. Nandeppanavar et al. [2-5] have studied the effects of viscous dissipation and thermal radiation on heat transfer of second-grade fluid and viscoelastic fluid flow over a stretching plate. Krishnamurthy et al. [6] have studied the effects of thermal radiation and chemical reaction on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet. The work by Manjunatha et al. [7] includes the boundary-layer flow of a dusty fluid over a stretching cylinder embedded in a porous medium in presence of heat source and thermal radiation.
Stratification of fluid arises due to temperature variations, concentration differences or the presence of different fluids and it is a characteristic of all fluid bodies surrounded by differentially heated side walls. Several investigations have explored the importance of convective heat and mass transfer in thermally stratified environment. The concept of stratification is vital in still water such as lakes, ponds, etc. Also, the analysis of thermal stratification is important for solar engineers because higher energy efficiency can be achieved with a better stratification. Boundary layer flow in a stable stratified viscous fluid has been investigated theoretically and experimentally by several authors. The flow due to a heated surface immersed in a stable temperature stratified medium has been investigated experimentally and analytically in several studies such as Yang et al. [8], Jaluria and Gebhart [9], Chen and Eichhorn [10]. Saha et al. [11] have obtained the numerical solutions of natural convection flow from an isothermal vertical plate with uniform heat source embedded in a stratified medium. Srinivasacharya et al. [12,13] analyzed the free convection heat and mass transfer along a vertical plate embedded in a stable doubly stratified micropolar fluids. Using Lie group theory, Samuel and Zachary [14] studied the free convective flow along a heated vertical wall immersed in a thermally stratified environment. Numerical solutions for steady mixed convection boundary layer flow over a vertical surface embedded in a thermally stratified porous medium saturated by a nanofluid was presented by Yasin et al. [15] and Ibrahim and Makinde [16]. Swati et al. [17-19] discussed the effects of thermal stratification on flow and heat transfer past a porous vertical stretching surface and exponentially stretching sheet embedded in a thermally stratified medium.
Effect of Joule heating and viscous dissipation with thermal stratification, chemical reaction and Hall current has been analyzed by Zaib and Shafi [20]. Rashad et al. [21] have investigated the effect of chemical reaction on coupled heat and mass transfer by mixed convection boundary layer flow of a micropolar fluid over a continuously moving isothermal vertical surface immersed in a thermally and solutally stratified medium. Gnaneswara [22–24] studied the effects of thermal radiation, viscous dissipation, chemical reaction and Hall current on the hydromagnetic convection flow and MHD peristaltic flow of electrically conducting viscous fluid over a stretching flat plate. Loganthan and Vimala [25] have conducted a numerical procedure to investigate the influence of the combined effects of MHD, suction and radiation on the forced convection boundary layer flow of a nanofluid over an exponentially stretching sheet, embedded in a thermally stratified medium. Hayat et al. [26] investigated the stratified phenomenon through vertical stretching cylinder in the region of stagnation point point flow of Casson fluid with slip conditions. Further, Hayat et al. [27] studied the effects of thermal radiation, viscous dissipation and stratification process due to temperature and concentration on MHD unsteady flow of viscous nanofluid over an inclined stretching sheet.
Two-phase particulate suspension flows containing discrete particle phase and the continuous fluid phase have several engineering applications. Flow fields of this kind are of interest in connection with applications involving dust collection equipment’s, gas masks, turbine blade erosion and aircraft icing. Saffman [28] has formulated the basic equations for the flow of dusty fluid. Since then many researchers have discussed the problem of dusty fluid flow between parallel plate and over a stretching surfaces under different thermal conditions. Vajravelu and Nayfeh [29] investigated hydromagnetic flow of a dusty fluid over a porous stretching sheet. The flow of a electrically conducting dusty fluid in the presence of transverse magnetic field is encountered a variety of applications such as magneto hydrodynamic generators, pumps, accelerators and flow meters. There have been many articles dealing with theoretical modeling and experimental measurements of the fluid and particle-phase viscosity in a dusty fluid. Laminar flow of a two-phase particulate suspension induced by a suddenly accelerated infinite vertical permeable surface in the presence of fluid buoyancy, magnetic field, heat generation or absorption, and surface suction or blowing effects was presented by Chamkha [30]. Ganesan and Palani [31] studied free convection flow of a dusty fluid past a semi-infinite inclined plate with constant heat flux using an implicit finite difference method. Gireesha et al. [32] have analyzed the boundary layer flow and heat transfer of a dusty fluid over a stretching sheet with the effect of non-uniform heat source/sink.
Makinde and Chinyoka [33] studied MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. The effects of time dependent surface temperature on the flow and heat transfer of a viscous, incompressible and electrically conducting dusty fluid has been studied by Nandkeolyar et al. [34], by assuming fluid particles are heat absorbing and the temperature at the surface of the sheet is a result of convective heating. Nandkeolyar and Sibanda [35] investigated the steady two dimensional boundary layer flow of a viscous, incompressible and electrically conducting dusty fluid past a vertical permeable stretching sheet under the influence of a transverse magnetic field with the viscous and Joule dissipations. Gireesha et al. [36] obtained the interesting and new results on dusty fluid flow due to linear and exponential stretching of a porous and non porous plate with various effects like heat source/sink, radiation, viscous dissipation etc. Manjunatha et al. [37] have studied the heat transfer analysis of steady two dimensional flow of conducting dusty fluid over a stretching cylinder immersed in a porous media under the influence of non-uniform source/sink. Recently, Prasannakumara et al. [38] analyzed melting phenomenon in MHD stagnation point flow of dusty fluid over a stretching sheet in the presence of thermal radiation and non-uniform heat source/sink. Although the flow of dusty fluid over a stretching plate has been considered extensively in the literature, no work has been reported on the problem of effect of thermal stratification on flow and heat transfer of two-phase flow over stretching sheet.
As mentioned earlier, the present work deals with the effect of thermal stratification on MHD stretched flow and heat transfer of a dusty fluid over a vertical stretching sheet embedded in a saturated porous medium in the presence of uniform heat source and thermal radiation. The formulated mathematical equations for the problem were reduced to dimensionless ordinary differential equations using suitable similarity transformations. The effects of various flow controlling parameters like magnetic parameter, Prandtl number, heat source/sink parameter, fluid particle interaction parameter, heat source parameter, radiation parameter, Grashof number, as well as the local skin friction coefficient on velocity and temperature distributions of both fluid and dust phases are depicted graphically and in tabulated form.
2 Mathematical Analysis
Consider a steady two dimensional laminar boundary layer flow of an incompressible viscous electrically conducting dusty fluid over a vertical stretching flat plate. Let the temperature at the wall is Tw (x) and the plate is embedded in a thermally stratified porous medium of variable ambient temperature T∞(x), where Tw(x) > T∞(x) (heated plate). The positive x coordinate is measured along the stretching vertical surface and the positive y coordinate is measured normal to the sheet in the outward direction toward the fluid. The schematic illustration of the physical model and coordinate system is shown in figure 1. The porous medium is assumed to be transparent and is in thermal equilibrium with the fluid. Further the two phases to be considered here are a continuous fluid phase interspersed with a discrete solid particulate phase. The particles are taken to be small enough and of sufficient number and are treated as a continuum which allow concepts such as density and velocity to have physical meaning. A uniform magnetic field Bo is applied in the transverse direction y normal to the plate. The magnetic Reynolds number is assumed to be small so that the induced magnetic field is neglected in comparison with the applied magnetic field. Also, applied electric field, the Hall current and the Joule heating are neglected. The dust particles are assumed to be spherical in shape, uniform in size and mass, and are undeformable. Here both phases behave as viscous fluids and the volume fraction of suspended particles is finite and constant.
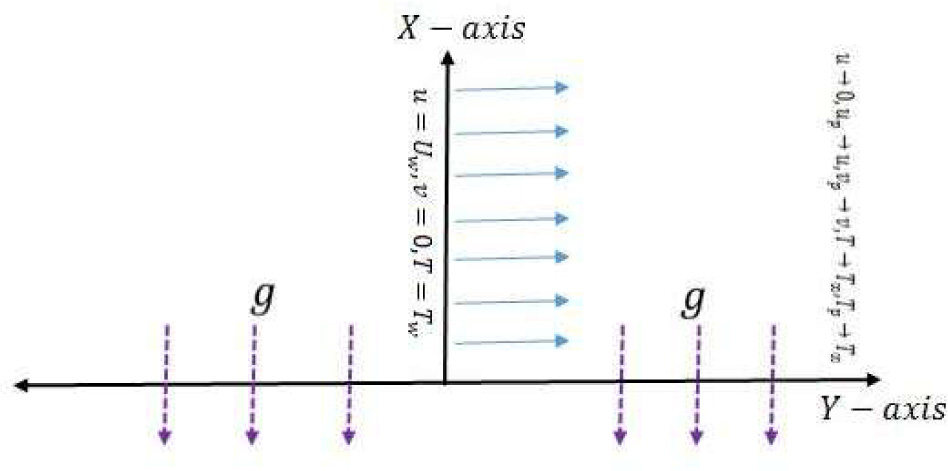
Physical model
Under these assumptions, along with the usual boundary layer approximations, the governing equations for the flow are,
Where (u, v) and (up, vp) are the velocity components of the fluid and dust particle phases along x and y directions respectively. µ, ρ and N are the co-efficient of viscosity of the fluid, density of the fluid, number density of the particle phase respectively, B0 is the strength of applied magnetic field, K is the Stokes’ resistance (drag co-efficient), m is the mass of the dust particle. T and Tp is the temperature of the fluid and temperature of the dust particle respectively, cp and cm are the specific heat of fluid and dust particles, τT is the thermal equilibrium time i.e., the time required by the dust cloud to adjust its temperature to the fluid, τv is the relaxation time of the of dust particle i.e., the time required by a dust particle to adjust its velocity relative to the fluid, β is the coefficient of thermal expansion, g is the acceleration due to gravity, Q0 is the heat source coefficient, kp is the permeability of the porous medium, k is the fluid thermal conductivity, σ is electric conductivity and υ is the kinematic viscosity. It is also assumed that the external electric field is zero and the electric field due to polarization of charges is negligible. In deriving these equations, the drag force is considered for the interaction between the fluid and particle phases.
Using the Rosseland approximation for radiation, radiation heat flux is given
Where σ* and k* are the Stefan-Boltzman constant and the mean absorption co-efficient respectively. Assuming that the temperature differences within the flow such that the term T4 may be expressed as a linear function of the temperature, and expand T4 in a Taylor series about T∞ and neglecting the higher order terms beyond the first degree in (T - T∞), then we get
Substitute equations (7) and (8) in (5) to get
The appropriate boundary conditions for the flow problem are given by Nadeem et.al. [39]
Where a, b and c are positive constants and c is known as stretching rate, T0 is the ambient temperature at the leading edge. T is the fluid temperature,
To convert the governing equations into a set of similarity equations, we have introduced now the following transformation
which are identically satisfies equations 1 and 3 and by substituting (11) into (2, 4, 6, 9) one can obtain the following non-linear ordinary differential equations:
where a prime denotes differentiation with respect to η and
The dimensionless boundary conditions defined as in (10) will becomes,
3 Numerical Solutions
In the first step, a set of non-linear ordinary differential equations (12) – (15) with boundary conditions (16) are discretized to a system of simultaneous differential equations of first order by introducing new dependent variables. Missed initial conditions are obtained with the help of shooting technique. Afterward, a finite value for η∞ is chosen in such a way that all the far field boundary conditions are satisfied asymptotically. Our bulk computations are considered with the value at η∞ =5, which is sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters considered.
After fixing finite value for η∞, integration is carried out with the help of Runge-Kutta-Fehlberg-45 order method. At each step, two different approximations for the solution are made and compared. If the two answers are in close agreement, the approximation is accepted otherwise, the step size is reduced until to get the required accuracy. For the present problem, we took the step size ∆η = 0.001, η∞ = 5 and accuracy to the fifth decimal places. To validate the accuracy of the numerical procedure used, first test computations for θ’(0) are carried out for viscous fluid for various values of Pr and compared with the available published results of Goyal and Grubka and Bobba [40], Abel and Mhaesha [41] and chen [42] in table 1 and they are found to be in excellent agreement.
Comparison of present values of -θ′(0) with values obtained by Grubka and Bobba and Abel and Mahesha and Chen for different values of stretching parameter Pr with βT = βυ = λ = R =Q = S = St = Ec = ∆ = 0.
| Pr | Grubka | Abel | Chen | Present |
|---|---|---|---|---|
| and Bobba [40] | and Mahesha [41] | [42] | (RKF45 Method) | |
| 0.72 | 1.0885 | 1.0885 | 1.0885 | 1.08854 |
| 1 | 1.3333 | 1.3333 | 1.3333 | 1.33333 |
| 10 | 4.7969 | 4.7969 | 4.7969 | 4.79693 |
4 Result and Discussions
The velocity and temperature profiles or obtained by solving equations (12–15) when subjected to the boundary conditions (16) by assigning numerical values to the parameter encounter in the problem. The velocity filed and the temperature profile for both fluid and dust phases are plotted to investigate the influence of various flow controlling parameters such as uniform heat source/sink parameter (∆), mixed convection or buoyancy parameter (λ), fluid particle interaction parameter for temperature (βv), magnetic parameter (Q) Prandtl number (Pr), fluid interaction parameter for velocity (βv), Eckert number (Ec), radiation parameter (R), stratification parameter (St) and permeable parameter (S).
Figures 2 and 3 shows the variations in velocity and temperature profile of fluid and dust phase in response to a change in the values of thermal stratification parameter. Here, we have consider both negative and positive stratification parameter. It is seen that as St increases, both velocity and temperature profile decreases. This is due to the fact that an increase in St means increase in free-stream temperature or decrease in surface temperature. Thermal boundary layer thickness is therefore also decreased with an increase in St values.
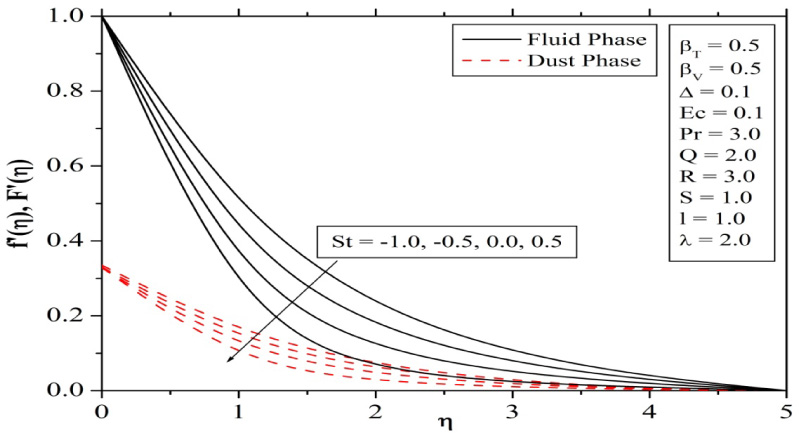
Variation in velocity profiles for different values of stratification parameter St
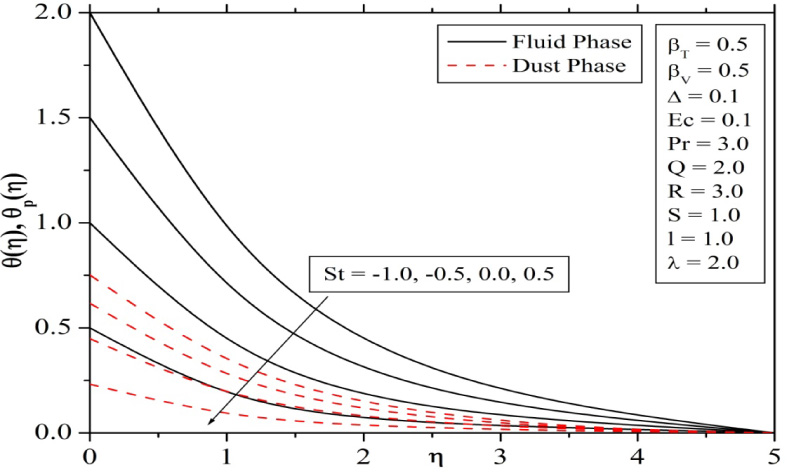
Variation in temperature profiles for different values of stratification parameter St
Figure 4 present the effects of variation of uniform heat source (∆ > 0) or sink (∆ < 0) parameter on temperature profiles of fluid and dust phases. It is observed that the dimensionless temperature profiles increases with increase in the heat source parameter and decreases for increasing strength of heat sink parameter. This is due to the fact that (∆ > 0) generates the additional energy, and this causes the increase in thickness of thermal boundary layers. Figure 5 depicts the effect of Prandtl number on temperature distributions for a fixed value of St (St = 0.5). In the presence of stratification, an increase in Prandtl number decreases the temperature of both fluid and dust phases. Figures 6 and 7 explains the effect of βv and βT on velocity and temperature profiles. Increase in βv will decrease fluid phase velocity and increases dust phase velocity. This is because, increase in βv is a result of decrease of τv and it is obvious that the time required by a dust particle to adjust its velocity relative to that of fluid also decreases with decrease of τv. From Figure 7 we can observe that the dust phase temperature increases while fluid phase temperature decreases with increase in βT.
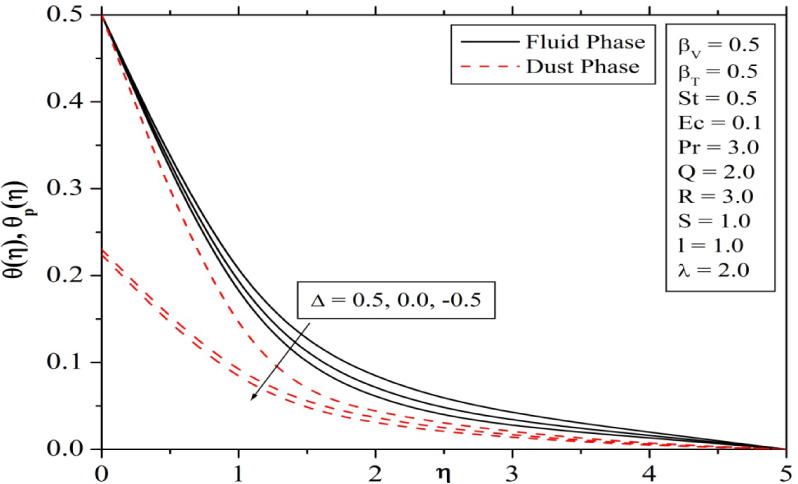
Influence of uniform heat source/sink parameter on temperature profiles
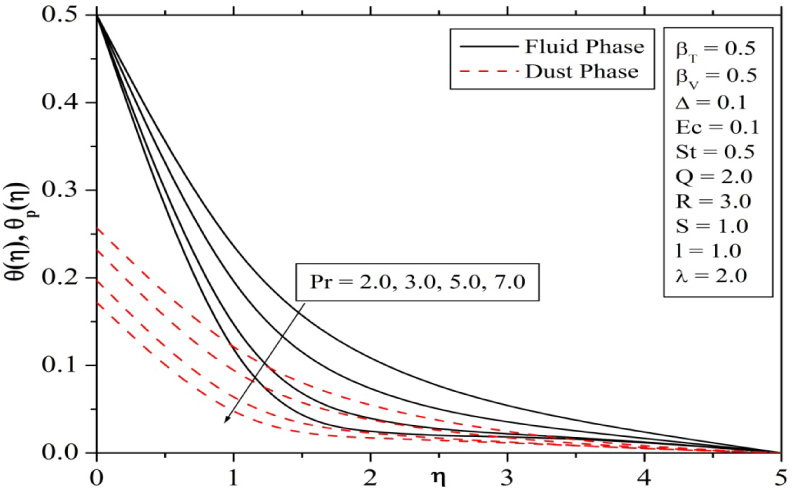
Influence of Prandtl number on temperature profiles
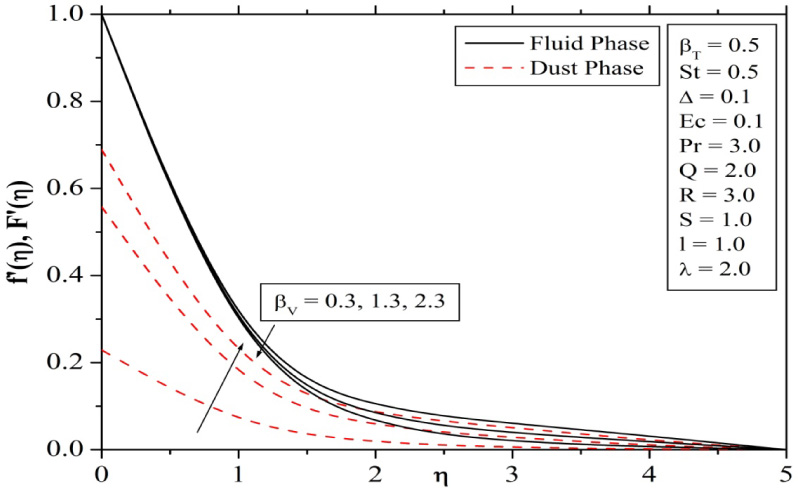
Influence of fluid interaction parameter for velocity on velocity profiles.
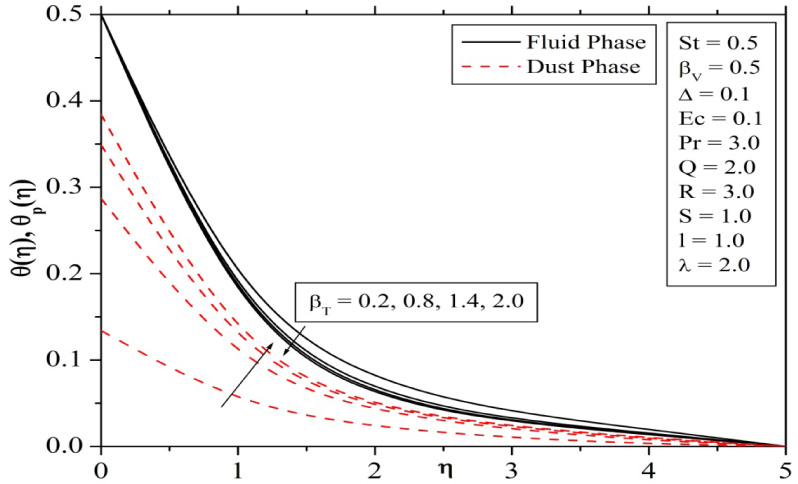
Influence of fluid interaction parameter for temperature on temperature profiles
Figure 8 depicts the effect of the magnetic parameter on dimensionless temperature distributions. The presence of magnetic field in an electrically conducting fluid induces a force called Lorentz force, which opposes the flow. This resistive force tends to slow down the flow and hence increases in its temperature. Figures 9 and 10 reveals that both temperature and velocity profiles of fluid and dust phases increases with increase in the Eckert number, which causes to increase the thermal boundary layer thickness also.
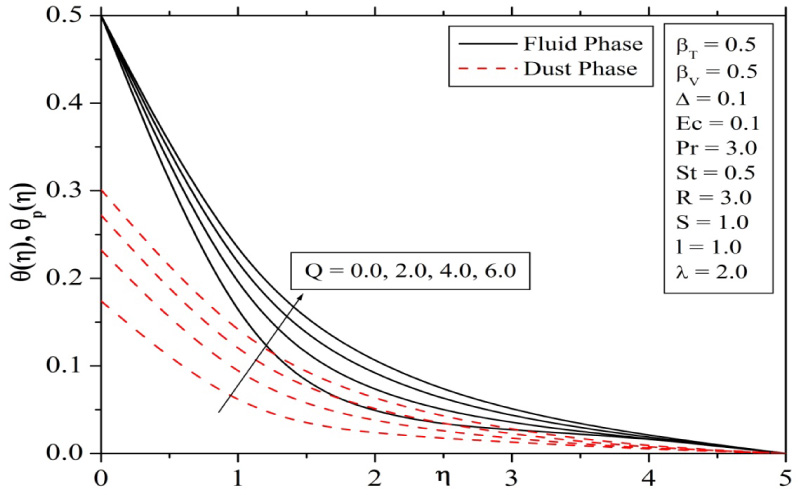
Variation in temperature profiles for Magnetic parameter
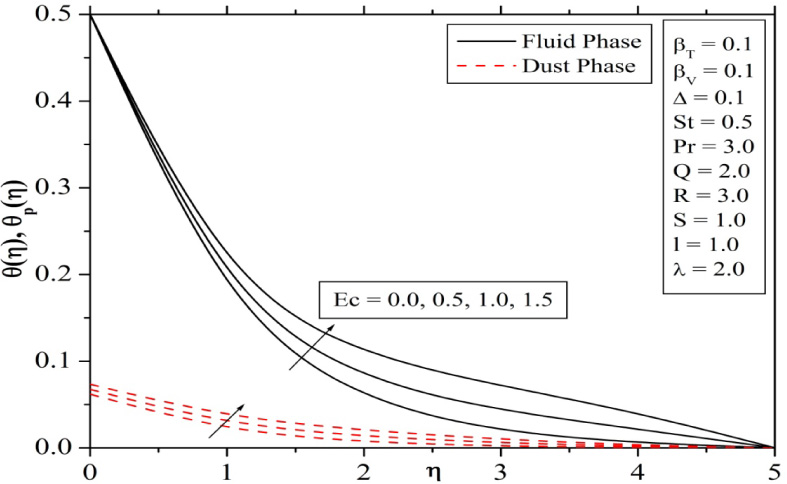
Effect of Eckert number on temperature profiles.
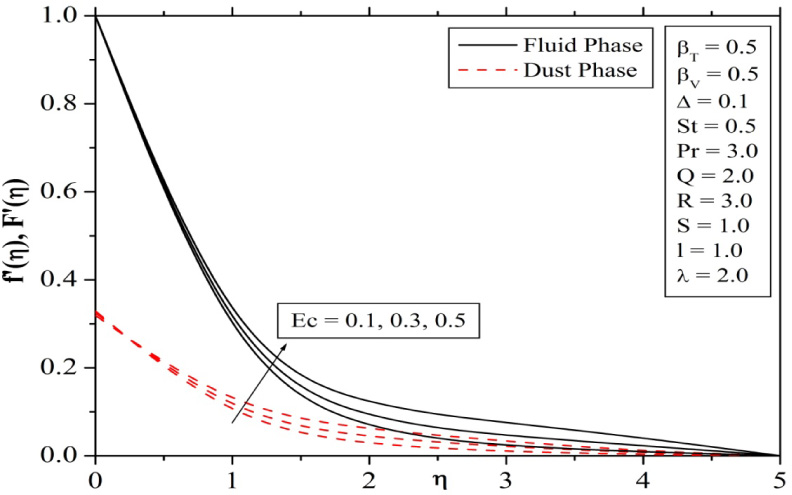
Effect of Eckert number on velocity profiles.
Figure 11 explains the effect of Radiation parameter on temperature profiles. It is observed that, the temperature profile increases for increasing values of R. This is because, an increase in radiation parameter provides more heat to the fluid that causes an enhancement in the temperature and thermal boundary layer thickness. Figure 12 and 13 demonstrate the effects of permeability parameter on velocity and temperature profiles. It is obvious that the presence of a porous medium causes higher restriction to the fluid flow which, in turn, slows its motion. Therefore, with increasing permeability parameter, the resistance to the fluid motion also increases and hence velocity decreases whereas the temperature increases with increasing values of S.
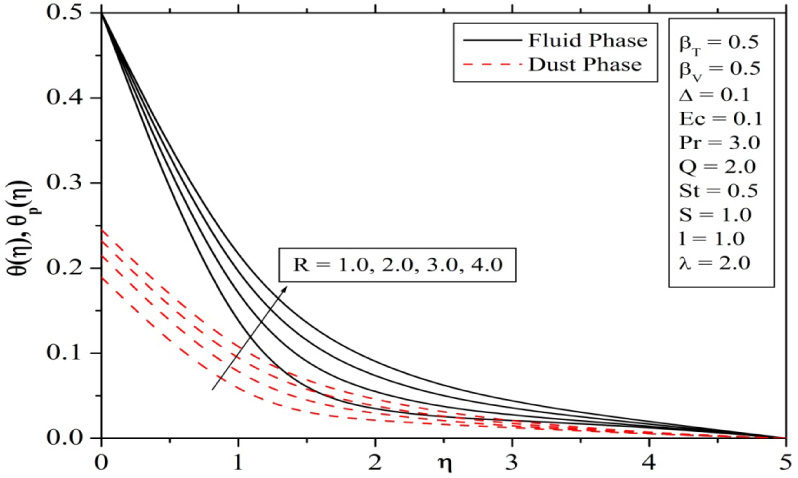
Variation in temperature profiles for radiation parameter
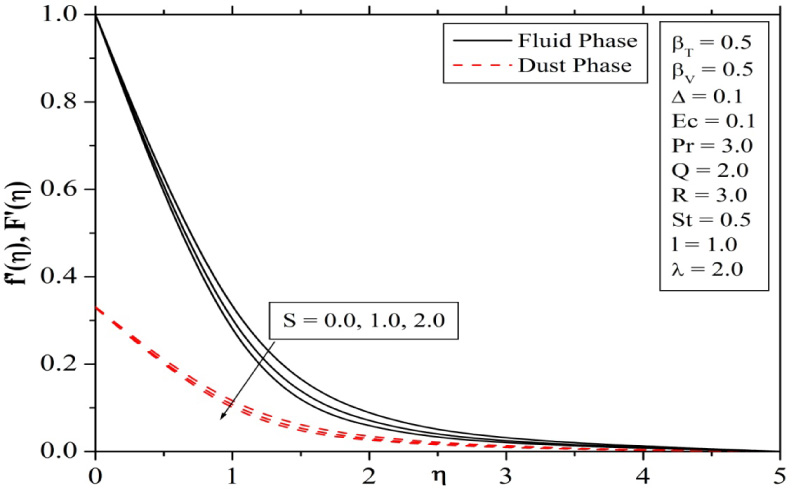
Influence of Permeability parameter on velocity profiles.
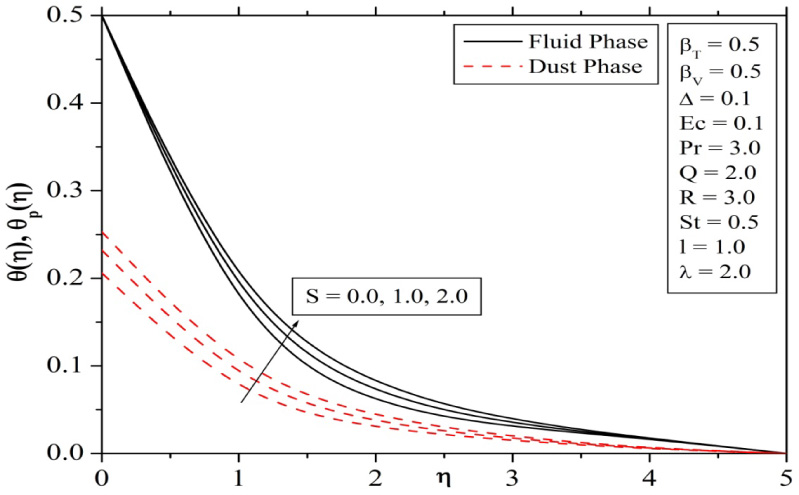
Influence of Permeability parameter on temperature profiles.
Figure 14 and 15 are plotted to show the variations of the velocities and temperature profiles of fluid and dust phase for different values of mixed convective parameter λ. The velocity and its momentum boundary layer thicknesses are increases with increasing the values of convection parameter. This is due to fact that larger values of λ correspond to stronger buoyancy forces and this buoyancy force leads to an accelerated fluid flow. Further, we can see that temperature profiles of both fluid and dust phases decreases with increasing values of mixed convective parameter.
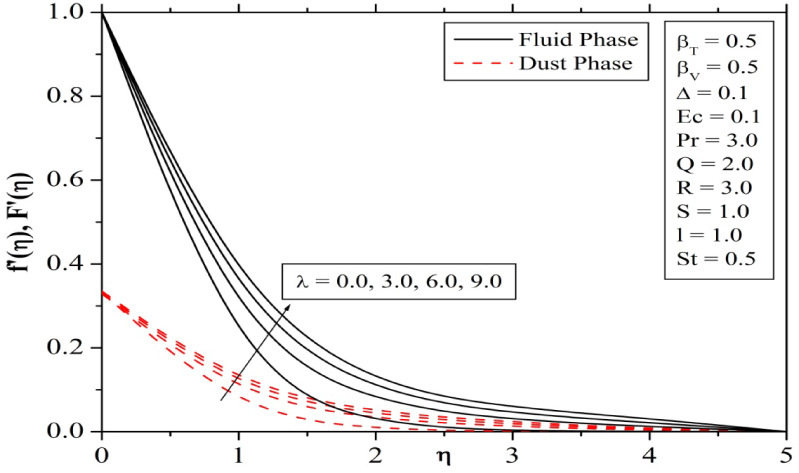
(λ) for velocity profiles.
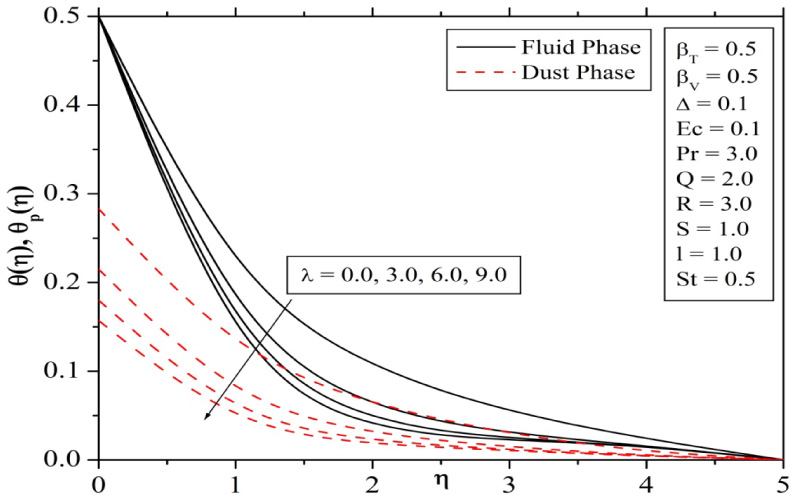
Variation of (λ) for temperature profiles.
We have numerically studied the effects of radiation parameter, and Prandtl number on skin friction coefficient and the local Nusselt number, which represents the heat transfer rate at the surface and are recored in the table 1. From this table it is clear that magnitude of both skin friction coefficient and local nusslet number are increasing functions of Pr and βT and decreasing function of λ. Also magnitude of skin friction coefficient increases with increase in Q, S and St and decreases with ∆ and λ. Further it is observed that, Increase in the values of Ec, λ, enhances the magnitude of local nusslet number. The skin friction coefficient increases with Pr and in consequence increases the heat transfer rate at the surface. This is due to the fact that the higher Prandtl number reduces the thermal boundary layer thickness and increases the surface heat transfer rate. Also, high Prandtl number implies more viscous fluid which tends to retard the motion.
5 Conclusions
A numerical analysis has been developed to investigate the effect of thermal stratification on boundary layer flow of a dusty fluid over a permeable stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source, transverse magnetic field and thermal radiation. The governing boundary-layer equations for the problem are reduced to dimensionless ordinary differential equations by a suitable similarity transformation. Numerical computations for the effects of controlling parameters on velocity and temperature fields have been carried out. A comparison between the present numerical solutions and previously published results have been included, and the results are found to be in excellent agreement. The effects of various parameters on the flow and heat transfer are observed from the graphs, and are summarized as follows:
Velocity and temperature profiles approach the ambient fluid conditions asymptotically and do not intersect the line which represents the boundary conditions.
Fluid phase velocity is always greater than that of the particle phase.
Both temperature and velocity profiles decrease with increase in thermal stratification parameter.
Increase of βv will decrease fluid phase velocity and increases dust phase velocity.
Both temperature and velocity profiles of fluid and dust phases increases with the increase of the Eckert number.
Temperature profile increases for increasing values of radiation parameter.
Magnitude of both skin friction coefficient and local Nusslet number are increasing functions of Pr and βT and decreasing function of λ.
Increase in the values of Ec, λ enhances the magnitude of local nusslet number.
Values of skin friction coefficient) and Nusselt number with Ec = ∆ = 0.1.
| BT | Bv | delta | Pr | Q | R | S | λ | St | –f “(O) | –θ’(0) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 1 | 3 | 2 | 3 | 1 | 2 | 1 | -1.55089 | -0.17162 |
| 0.3 | -1.59075 | -0.27058 | ||||||||
| 0.5 | -1.60955 | -0.31757 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 2 | 3 | 1 | 2 | -1.55089 | -0.17162 | |
| 0.3 | -1.5609 | -0.10409 | ||||||||
| 0.4 | -1.56274 | -7.33E-02 | ||||||||
| 0.1 | 0.1 | -0.5 | 3 | 2 | 3 | 1 | 2 | -1.73472 | -0.7518 | |
| 0 | -1.71149 | -0.64671 | ||||||||
| 0.5 | -1.6693 | -0.49662 | ||||||||
| 0.1 | 0.1 | 1 | 2 | 2 | 3 | 1 | 2 | -1.55173 | -0.14461 | |
| 4 | -1.55439 | -0.20721 | ||||||||
| 6 | -1.5706 | -0.30006 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 0 | 3 | 1 | 2 | -1.01299 | -0.47338 | |
| 2 | -1.55089 | -0.17162 | ||||||||
| 4 | -1.98609 | 0.145292 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 3 | 0 | 1 | 2 | -1.6119 | -0.51222 | |
| 2 | -1.55386 | -0.20327 | ||||||||
| 4 | -1.55082 | -0.15545 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 2 | 3 | 0 | 2 | -1.2996 | -0.32591 | |
| 0.5 | -1.32608 | -0.31071 | ||||||||
| 1 | -1.55089 | -0.17162 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 2 | 3 | 1 | 1 | -1.68564 | 0.273005 | |
| 5 | -1.14493 | -0.4514 | ||||||||
| 9 | -0.62863 | -0.56302 | ||||||||
| 0.1 | 0.1 | 1 | 3 | 2 | 3 | 1 | 1 | -0.16467 | 0.116526 | |
| -1.05592 | -2.79E-02 | |||||||||
| -1.55089 | -0.17162 |
Acknowledgement
One of the authors B. C. Prasannakumara and N.S.Shashikumar are pleased to acknowledge financial support from the University Grants Commission, New Delhi, INDIA under the Major research project Scheme. [F.No-43-419/2014(SR)].
Nomenclature
| c | Stretching ratio |
| cm | Specific heat of dust fluid |
| cp | Specific heat of fluid |
| m | Mass of the dust phase |
| g | Acceleration due to gravity |
| B0 | Strength of applied magnetic field |
| Q0 | Heat source coefficient |
| K | Stokes resistance |
| k | Thermal conductivity |
| kp | Permeability of the porous medium |
| l | Characteristic length |
| N | Number density of the dust phase |
| R | Radiation parameter |
| T | Temperature of the fluid phase |
| Tp | Temperature of the dust phase |
| Tw | Temperature at the wall |
| T∞ | Temperature at large distance from the wall |
| T0 | Ambient temperature at the leading edge |
| u, v | Velocity component of the fluid along x and y direction |
| up, vp | Velocity component of the dust fluid along x and y direction |
| a, b, and c | Positive constants |
Greek symbols
| µ | Coefficient of the velocity of the fluid |
| ρ | Density of the fluid |
| σ | Electric conductivity |
| ν | Kinematic viscosity |
| β | Coefficient of thermal expansion |
| τT | Thermal equilibrium time |
| τv | Relaxation time of the dust phase |
| θ | Fluid phase temperature |
| θp | Dust phase temperature |
| η | Dimensionless space variable |
Subscripts
| ω | Properties at the plate |
| ∞ | Free stream condition |
References
[1] M. A. Hossain and H. S. Takhar, Radiation Effects on Mixed Convection along a Vertical Plate with Uniform Surface Temperature, Heat Mass Transfer, 31, pp. 243-248,1996.10.1007/BF02328616Search in Google Scholar
[2] M. Subhas Abel and M. M. Nandeppanavar, Effects of thermal radiation and non-uniform heat source on MHD flow of viscoelastic fluid and heat transfer over a stretching sheet, International Journal of Applied Mechanics and Engineering, 12, 4, pp. 903-918, 2007.Search in Google Scholar
[3] Mahantesh M. Nandeppanavar a, M. Subhas Abel and K. Vajravelu, Flow and heat transfer characteristics of a viscoelastic fluid in a porous medium over an impermeable stretching sheet with viscous dissipation, International Journal of Heat and Mass Transfer, 53, 21, pp. 4707-4713, 2010.10.1016/j.ijheatmasstransfer.2010.06.021Search in Google Scholar
[4] M.M. Nandeppanavar and M.N. Siddalingappa, Effect of viscous dissipation and thermal radiation on heat transfer over a non-linearly stretching sheet through porous medium, International journal of applied mechanics and engineering, 18, 2, pp.461-474, 2013.10.2478/ijame-2013-0027Search in Google Scholar
[5] Mahantesh M. Nandeppanavar, M. Subhas Abel and M. N. Siddalingappa, Heat transfer through a porous medium over a stretching sheet with effect of viscous dissipation, Chemical Engineering Communications, 200,11, pp.1513-1529, 2013.10.1080/00986445.2012.749247Search in Google Scholar
[6] M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara and Rama Subba Reddy Gorla, Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, Nonlinear Engineering, 10.1515/nleng-2016-0013, 2016Search in Google Scholar
[7] P. T. Manjunatha, B. J. Gireesha and B. C. Prasannakumara, Effect of Radiation on Flow and Heat Transfer of MHD Dusty Fluid Over a Stretching Cylinder Embedded in a Porous Medium in Presence of Heat Source, Int. J. Appl. Comput. Math, 10.1007/s40819-015-0107-x.1-18,2015.Search in Google Scholar
[8] K. T. Yang, J. L. Novotny and Y. S. Cheng, Laminar Free Convection from a Non-isothermal Plate Immersed in a Temperature Stratified Medium, Int. J. Heat Mass Transfer, 15, pp. 1097-1109,1972.10.1016/0017-9310(72)90242-6Search in Google Scholar
[9] Y. JaluriaandB. Gebhart, Stability and Transition of Buoyancy-Induced Flows in a Stratified Medium, J. Fluid Mech., 66, pp. 593-612,1974.10.1017/S0022112074000383Search in Google Scholar
[10] C. C. Chen and R. Eichhorn, Natural Convection from Simple Bodies Immersed in Thermally Stratified Fluids, J. Heat Transfer, 98, pp. 446-451,1976.10.1115/1.3450574Search in Google Scholar
[11] Suvash C. Saha, Yuan Tong Gu, Md. M. Molla, Sadia Siddiqa and Md. Anwar Hossain, Natural Convection from a Vertical Plate Embedded in a Stratified Medium with Uniform Heat Source, Desalination and Water Treatment, 44, pp. 7-14, 2012.10.1080/19443994.2012.691696Search in Google Scholar
[12] D. Srinivasacharya and Mendu Upendar, Effect of Bouble Stratification on MHD free Convection in a Micropolar Fluid, Journal of the Egyptian Mathematical Society, 21, pp. 370-378, 2013.10.1016/j.joems.2013.02.006Search in Google Scholar
[13] D. Srinivasacharya and C. Ram Reddy, Natural Convection Heat and Mass Transfer in a Micropolar Fluid with Thermal and Mass Stratification, International Journal for Computational Methods in Engineering Science and Mechanics, 14, pp. 401-413, 2013.10.1080/15502287.2013.784378Search in Google Scholar
[14] Samuel Paolucci and Zachary J. Zikoski, Free Convective Flow from a Heated Vertical Wall Immersed in a Thermally Stratified Environment, International Journal of Heat and Mass Transfer, 67, pp. 1062-1071, 2013.10.1016/j.ijheatmasstransfer.2013.08.076Search in Google Scholar
[15] MohdHafizi Mat Yasin, Norihan Md. Arifin, Roslinda Nazar, Fudziah Ismail and Ioan Pop, Mixed Convection Boundary Layer Flow Embedded in a Thermally Stratified Porous Medium Saturated by a Nanofluid, Advances in Mechanical Engineering vol. 2013, Article ID 121943,10.1155/2013/121943Search in Google Scholar
[16] Wubshet Ibrahim and O.D. Makinde, The Effect of Double Stratification on Boundary-Layer Flow and Heat Transfer of Nanofluid over a Vertical Plate, Computers & Fluids, 86, pp. 433-441, 201310.1016/j.compfluid.2013.07.029Search in Google Scholar
[17] Swati Mukhopadhyay, Iswar Chandra Mondal and Rama Subba Reddy Gorla, Effects of Thermal Stratification on Flow and Heat Transfer Past a Porous Vertical Stretching Surface, Heat Mass Transfer, 48, pp. 915-921, 2012.10.1007/s00231-011-0930-5Search in Google Scholar
[18] Swati Mukhopadhyay, MHD Boundary Layer Flow and Heat Transfer over an Exponentially Stretching Sheet Embedded in a Thermally Stratified Medium, Alexandria Engineering Journal, 52, pp. 259-265, 2013.10.1016/j.aej.2013.02.003Search in Google Scholar
[19] Swati Mukhopadhyay, Krishnendu Bhattacharyya and G. C. Layek, MassTransfer over an Exponentially Stretching Porous Sheet Embedded in a Stratified Medium, Chem. Eng. Comm., 201, pp. 272-286, 2014.10.1080/00986445.2013.768236Search in Google Scholar
[20] Aurang Zaib and Sharidan Shafi, Thermal Diffusion and Diffusion Thermo Effects on Unsteady MHD Free Convection Flow over a Stretching Surface Considering Joule Heating and Viscous Dissipation with Thermal Stratification, Chemical Reaction and Hall Current, Journal of the Franklin Institute, 351, pp. 1268-1287, 201410.1016/j.jfranklin.2013.10.011Search in Google Scholar
[21] A.M. Rashad, S. Abbasbandy and Ali J. Chamkha, Mixed Convection Flow of a Micropolar Fluid over a Continuously Moving Vertical Surface Immersed in a Thermally and Solutally Stratified Medium with Chemical Reaction, Journal of the Taiwan Institute of Chemical Engineers, 45, pp. 2163-2169, 2014.10.1016/j.jtice.2014.07.002Search in Google Scholar
[22] Machireddy Gnaneswara Reddy, Influence of thermal radiation, viscous dissipation and hall current on MHD convection flow over a stretched vertical flat plate, Ain Shams Engineering Journal 5,1, pp.169-175, 2014.10.1016/j.asej.2013.08.003Search in Google Scholar
[23] Machireddy Gnaneswara Reddy, Thermal radiation and chemical reaction effects on MHD mixed convective boundary layer slip flow in a porous medium with heat source and Ohmic heating, Eur. Phys. J. Plus, 129: 41, 2014.10.1140/epjp/i2014-14041-3Search in Google Scholar
[24] M. Gnaneswara Reddy, Heat and mass transfer on magnetohydrodynamic peristaltic flow in a porous medium with partial slip, Alexandria Engineering Journal, 55, 2, pp.1225-1234, 2016.10.1016/j.aej.2016.04.009Search in Google Scholar
[25] P. Loganthan and C. Vimala MHD Flow of Nanofluids over an Exponentially Stretching Sheet Embedded in a Stratified Medium with Suction and Radiation Effects, Journal of Applied Fluid Mechanics, vol. 8, issue 1, pp. 85-93, 2015.10.36884/jafm.8.01.22556Search in Google Scholar
[26] Tasawar Hayat, MariaImtiaz and Ahmed Alsaedi, Unsteady Flow of Nanofluid with Double Stratification and Magnetohydrodynamics, International Journal of Heat and Mass Transfer, vol. 92, pp. 100-109, 2016.10.1016/j.ijheatmasstransfer.2015.08.013Search in Google Scholar
[27] Tasawar Hayat, Muhammad Farooq and A. Alsaedi, Thermally Stratified Stagnation Point Flow of Casson Fluid with Slip Conditions, International Journal of Numerical Methods for Heat & Fluid Flow, vol. 25, issue 4, pp. 724 – 748, 2015.10.1108/HFF-05-2014-0145Search in Google Scholar
[28] P.G.Saffman, On the stability of laminar flow of a dusty gas, J. of Fluid Mechanics, 13, pp. 120-128,1962.10.1017/S0022112062000555Search in Google Scholar
[29] K.Vajravelu and J.Nayfeh, Hydromagnetic Flow of a Dusty Fluid over a Stretching Sheet, Int. J. of Nonlinear Mechanics, 27, pp. 937-945,1992.10.1016/0020-7462(92)90046-ASearch in Google Scholar
[30] Ali J.Chamkha, The Stokes Problem for a Dusty Fluid in the Presence of Magnetic Field, Heat Generation and Wall Suction Effects, International Journal of Numerical Methods for Heat and Fluid Flow, 10(1), pp. 116-133, 2000.10.1108/09615530010297958Search in Google Scholar
[31] G.Palani and P.Ganesan, Heat Transfer Effects on Dusty Gas Flow Past a Semi-Infinite Inclined Plate, ForschIngenieurwes, 71, 223-230, 2007.10.1007/s10010-007-0061-9Search in Google Scholar
[32] B.J. Gireeshaa, G.K. Ramesha, M. Subhas Abelb and C.S. Bagewadia, Boundary layer flow and heat transfer of a dusty fluid flow over a stretching sheet with non-uniform heat source/sink, International Journal of Multiphase Flow, 37, 8, pp.977-982, 2011.10.1016/j.ijmultiphaseflow.2011.03.014Search in Google Scholar
[33] O.D.Makinde and T.Chinyoka, MHD Transient Flows and Heat Transfer of Dusty Fluid in a Channel with Variable Physical Properties and Navier Slip Condition, Comp. Math. Appl., 60, 660-669, 2010.10.1016/j.camwa.2010.05.014Search in Google Scholar
[34] R.Nandkeolyar, G.S.Seth, O.D.Makinde, P.Sibanda and M.S.Ansari, Unsteady Hydromagnetic Natural Convection Flow of a Dusty Fluid Past an Impulsively Moving Vertical Plate with Ramped Temperature in the Presence of Thermal Radiation, ASME J. Appl. Mech., 80(6), pp. 061003, 2013.10.1115/1.4023959Search in Google Scholar
[35] R.Nandkeolyar and Precious Sibanda, On Convective Dusty Flow Past a Vertical Stretching Sheet with Internal Heat Absorption, Journal of Applied Mathematics, vol. 2013, Article ID 806724, 9 pages, http://dx.doi.org/10.1155/2013/806724, 2013.10.1155/2013/806724Search in Google Scholar
[36] G.K.Ramesh, B.J.Gireesha and C.S.Bagewadi, MHD Flow of a Dusty Fluid near the Stagnation Point over a Permeable Stretching Sheet with Non-Uniform Source/Sink, International Journal of Heat and Mass Transfer, 55, pp. 4900-4907, 2012.10.1016/j.ijheatmasstransfer.2012.05.003Search in Google Scholar
[37] P.T.Manjunatha, B.J. Gireesha and B.C.Prasannakumara, Thermal Analysis of Conducting Dusty Fluid Flow in a Porous Medium over a Stretching Cylinder in the Presence of Non-Uniform Source/Sink, International Journal of Mechanical and Materials Engineering, 1:13, http://www.springer.com/40712/content/1/1/13, 2014.10.1186/s40712-014-0013-8Search in Google Scholar
[38] B.C. Prasannakumara, B.J. Gireesha and P.T. Manjunatha, Melting Phenomenon in MHD Stagnation Point Flow of Dusty Fluid over a Stretching Sheet in the Presence of Thermal Radiation and Non-Uniform Heat Source/Sink, International Journal for Computational Methods in Engineering Science and Mechanics (Taylor and Francis), 10.1080/15502287.2015.1047056, 2015.Search in Google Scholar
[39] S. Nadeem and Noor Muhammad, Impact of stratification and Cattaneo-Christov heat flux in the flow saturated with porous medium, Journal of Molecular Liquids, 224, pp.423-430, 2016.10.1016/j.molliq.2016.10.006Search in Google Scholar
[40] L.j. Grubka, K.M. Bobba, Heat transfer characteristics of a continuous stretching surface with variable temperature, J. Heat Transfer 107 (1985) 248-250.10.1115/1.3247387Search in Google Scholar
[41] M.S. Abel, N. Mahesha, Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uiniform heat source and radiation, Appl. Math. Model.32 (2008) 1965-1983.10.1016/j.apm.2007.06.038Search in Google Scholar
[42] C.H. Chen, Laminar mixed convection adjacent to vertical, continuously stretching sheet, Heat Mass Transfer 33 (1998) 471-476.10.1007/s002310050217Search in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Nonlinear Responses and Stability of an Elastic Suspended Cable System Subjected to Parametrical External Excitations
- Modelling of imbibition phenomena in two-phase fluid flow through fractured porous media
- Application of Kudryashov and functional variable methods to the strain wave equation in microstructured solids
- Boundary layer flow of dusty fluid over a radiating stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source
- Entropy Generation with nonlinear heat and Mass transfer on MHD Boundary Layer over a Moving Surface using SLM
- Images Encryption Method using Steganographic LSB Method, AES and RSA algorithm
- Numerical simulation of Burgers’ equation using cubic B-splines
Articles in the same Issue
- Frontmatter
- Nonlinear Responses and Stability of an Elastic Suspended Cable System Subjected to Parametrical External Excitations
- Modelling of imbibition phenomena in two-phase fluid flow through fractured porous media
- Application of Kudryashov and functional variable methods to the strain wave equation in microstructured solids
- Boundary layer flow of dusty fluid over a radiating stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source
- Entropy Generation with nonlinear heat and Mass transfer on MHD Boundary Layer over a Moving Surface using SLM
- Images Encryption Method using Steganographic LSB Method, AES and RSA algorithm
- Numerical simulation of Burgers’ equation using cubic B-splines


