Abstract
The aim of the present paper is to study the influence of Hall current and Joule heating on flow, heat and mass transfer over an exponentially stretching sheet in a viscous fluid. Using similarity transformations the governing nonlinear coupled equations are converted into ordinary differential equations. These equations are linearized using the successive linearization method and then solved using the Chebyshev pseudo spectral method. The influence of magnetic parameter, Hall parameter, suction/injection parameter and slip parameter on the physical quantities are presented graphically. The obtained results are compared with the previously published results for special cases.
1 Introduction
The analysis of flow, heat and mass transfer along a stretching surface is of considerable importance in view of its applications to polymer technology and metallurgy. These applications include wire and fibre coating, extrusion process, foodstuff processing, polymer processing, crystal growing, glass blowing, chemical processing equipment, continuous casting and design of various heat exchangers. The study of convective transport with the interaction of the magnetic field has gained attention of many scientists due to its comprehensive applications in engineering. Several processes in metallurgical contain the cooling of continuous strips or filaments such as strengthening and thinning of copper wires, which are sometimes stretched during the process. The proportion of cooling of these strips can be controlled by exposing them to magnetic fields. Similarly, the molten metals can be purified from non-metallic inclusions by utilizing a magnetic field. Several researchers analyzed the MHD flow, heat and mass transfer over a stretching surface in Newtonian and non-Newtonian fluids with various effects. Kameswaran et al. [1] analyzed the effect of radiation on MHD Newtonian fluid over an exponentially stretching sheet. Mandal and Mukhopadhyay [2] studied the flow and heat transfer along a surface stretching exponentially and embedded in porous media with variable surface heat flux. Singh and Agarwal [3] considered the influence of non-uniform heat source/sink and variable thermal conductivity on the MHD flow and heat transfer over an exponentially stretching sheet in a porous medium saturated with Maxwell fluid. Khidir and Sibanda [4] investigated the MHD mixed convective flow, heat and mass transfer along exponentially stretching surface in a porous medium with variable viscosity and Soret and Dufour effects. Gorla et al. [5] discussed the influence of non-uniform heat sink or source and viscous dissipation on MHD flow and heat transfer over an exponentially stretching sheet in a dusty nanofluid saturated porous medium in the presence of suction/injection. Hayat et al. [6] analyzed the unsteady three-dimensional flow by an exponential stretching sheet with effects of thermal and velocity slip conditions. Eid [7] studied the heat generation/absorption and chemical reaction effects on the MHD mixed convective flow of a nanofluid over a surface stretching exponentially in a porous medium.
In most of the MHD flows reported in the literature, the Hall current term in the Ohm’s law was ignored as it has no significant influence for smaller values of the applied magnetic field. However, when the strong magnetic field is applied the effect of Hall current is very important. Hence, the study of Hall current effects on magnetohydrodynamic flows has gained much importance due to its broad range of applications such as in Hall accelerators, refrigeration coils, power generators and pumps, electric transformers, etc. Megahed et al. [8] studied the heat and mass transport along a vertical flat plate by considering the effects of buoyancy force and Hall currents. Abo-Eldahab et al. [9] analyzed the impact of Hall current and internal heat generation/absorption on mixed convective heat transfer over an inclined stretching surface. El-Aziz [10] analyzed the Hall current effect on the flow and heat transfer over an unsteady stretching surface. Motsa and Shateyi [11] considered the MHD boundary layer flow over an unsteady stretching surface in the presence of Hall currents. El-Aziz and Tamer [12] investigated the MHD mixed convection flow past a sheet which is exponentially stretching under the influence of Hall current. Pal [13] investigated the Hall currents effect with radiation over an unsteady stretching surface. Zaib and Shafie [14] studied the effect of Hall currents with soret and dufour effects over an unsteady stretching surface. Zaman et al. [15] reported the influence of Hall current and suction on the MHD flow over an exponentially stretching sheet in a second grade fluid.
Although there are some investigations concerning the heat and mass transfer along an exponentially stretching surface, the combined effects of slip and Hall currents has received no attention so far. Hence, the present article deals with the mixed convection slip flow, heat and mass transfer over porous exponentially stretching sheet subjected to suction or injection with the inclusion of Hall currents.
2 Mathematical formulation
Consider a steady electrically conducting flow of incompressible viscous fluid past a stretching sheet with temperature Tw(x) and concentration Cw(x). The positive x-axis is taken along the sheet in the direction of flow, y-axis is perpendicular to the sheet in the outward direction of the flow and z-axis coincide with the leading edge of the sheet. The sheet velocity varies as an exponential function of the distance x from the slit. The temperature and concentration of ambient medium are assumed to be T∞ and C∞, respectively. A strong magnetic field of strength B(x) is applied in y-direction and the influence of Hall current is not neglected. Assuming the magnetic Reynolds number as very small leads to neglect of the induced magnetic field. The flow is three dimensional in view of the cross flow in the z-direction induced by the presence of Hall current. The velocity vector is (u, v, w) and the temperature and concentration of the plate are T and C, respectively.
With the above assumptions together with the Boussinesq and the boundary layer approximations, the equations governing the present flow problem in the presence of Joule heating are given by
where ρ, cp, g, ν, α, D and βh are the fluid density, specific heat at the constant pressure, acceleration due to gravity, kinematic viscosity of the fluid, thermal diffusivity, mass diffusivity of the medium and Hall parameter, respectively,
The associated conditions on the surface are
Here
Introducing the following Similarity variables
where the prime denotes deivative with respect to
The corresponding boundary conditions reduce to
Results of practical interest are the wall shear stress in x and z- directions, heat and mass transfer rates, respectively, acting on the stretching surface and are given by
The local skin friction in x-direction
where
3 Method of Solution
The successive linearisation method (SLM) ([16-18]) is implemented to linearize the system of differential equations (8)–(11). The Chebyshev pseudo spectral method is used to solve the resulting linearised system of equations.
In SLM, the functions f (η), g(η), θ(η) and ϕ(η) are assumed to be taken as
where fn(η), gn(η), θn(η) and ϕn(η) (n=1,2,3,...) are functions to be determined and fi(η), gi(η), θi(η) and ϕi(η) (i ≥ 1) are approximations and are obtained by solving recursively the linear part of the system of equations that results from substituting Eq. (15) in the governing equations (8) to (11).
We choose the initial approximation f0(η), g0(η), θ0(η) and ϕ0(η) so that they satisfy boundary conditions (12).
The succeeding solutions for fn(η), gn(η), θn(η) and ϕn(η)(n ≥ 1) are brought by recursively solving the below linearized system of ordinary differential equations
where the coefficients αk,n-1 (k = 1, 2,3), βk,n-1, δk,n-1 (k = 1, 2, 3, 4), γk,n-1 (k = 1, 2,3,4, 5) and ℰk,i-1(k = 1,2,3,4) are the coefficients in terms of known functions fi(η), gi (η), θi (η) and ϕi(η), i = 1, 2, 3,..., n-1 and
The associated boundary conditions are
Hence, f(η), g(η), θ(η) and ϕ(η) are obtained as
where the order of SLM approximation is M.
Chebyshev spectral collocation method [19] is used to solve the linearized equations (16) to (19).
The problem is solved for [0,L] instead of [0, ∞), where the parameter L is used to recover the conditions at infinity. To apply this method the domain under consideration [0,L] is transformed to [-1,1] by the transformation
Approximating the functions fn, gn, θn and ϕn and their derivatives in terms of Chebyshev interpolating polynomials at N + 1 Gauss-Lobatto collocation points
where
Here
The boundary condition reduce to
Incorporating boundary conditions (24) in (22) and solving the resulting matrix system, we get the solution.
4 Results and Discussions
To authenticate the correctness of the technique used, results for S = 0, λ = 0, ζ = 0 and Ha = 0 are compared with the results of Magyari and Keller [20]. Table 1 provides the comparative analysis between the results obtained for local skin-friction coefficient -f "(0) and f(∞) by using the present method and the results obtained by Magyari and Keller [20] and found to be in good agreement.
Comparison analysis for-f″(0) and f(∞) calculated by the present method for S = 0, λ = 0, ζ = 0 and Ha = 0.
| Magyari and Keller [20] | Present | |
|---|---|---|
| −f″(0) | 1.281808 | 1.28180856 |
| f(∞) | 0.905639 | 0.90564383 |
In order to analyze the effect of pertinent parameters, the values of other parameters are fixed as Pr = 0.71, Sc = 0.22, ζ =1.0, 𝔹 = 0.5, S = 0.5, λ = 1.0, βh = 2.0, Ha = 1.0, Ec = 0.5, N = 150 and L = 30 unless otherwise mentioned.
Figures 1a-1d indicates the effect of suction/injection parameter S on both the velocity components f′(η) and g(η), temperature θ(η) and concentration ϕ(η). From these figures it is noticed that all the physical quantities are decreasing with an enhancement in S. It is known that applying the wall suction have the propensity to lessen both the momentum and thermal boundary layer thickness. This reason decreases in both the velocity and temperature components.
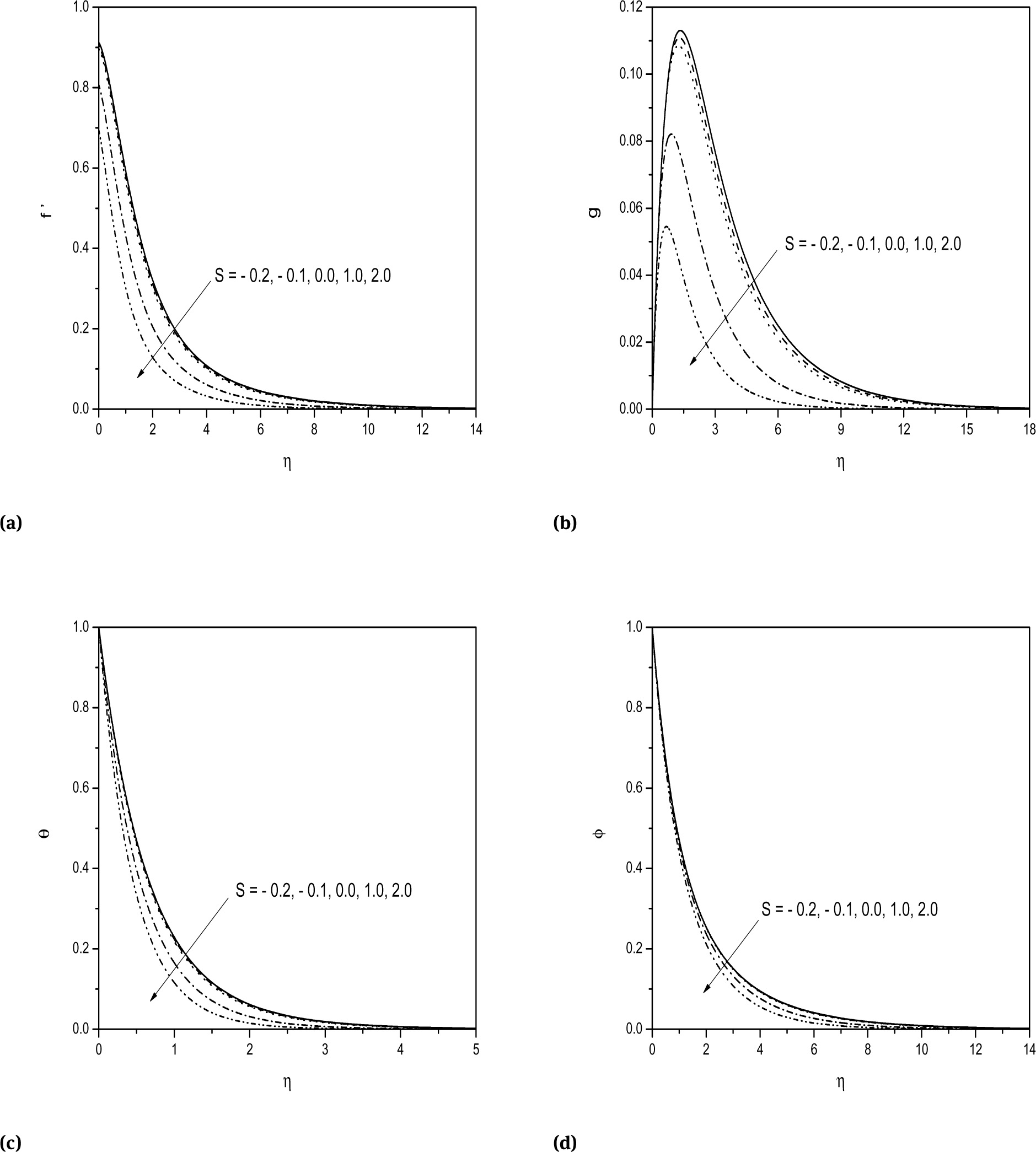
Effect of Son a) tangential velocity b) cross flow velocity c) temperature and d) concentration profiles.
The impact of mixed convection parameter ζ on f′ (η), g(η), θ(η) and ϕ(η) are depicted in Figs. 2a-2d. From the Fig. 2a, it is seen that the tangential velocity increases with an increase in the values of ζ. This is because, the positive values of ζ induces a favorable pressure gradient which, in turn, increases the fluid flow in the boundary layer. The same effect is observed for the cross flow velocity component as shown in Fig. 2b. From the Figs. 2c-2d, it is noticed that both the temperature and concentration are decreasing with increasing the values of ζ. This is due to the fact that positive values of ζ accelerates the fluid and which results in decreasing both the thermal and concentration boundary layers.
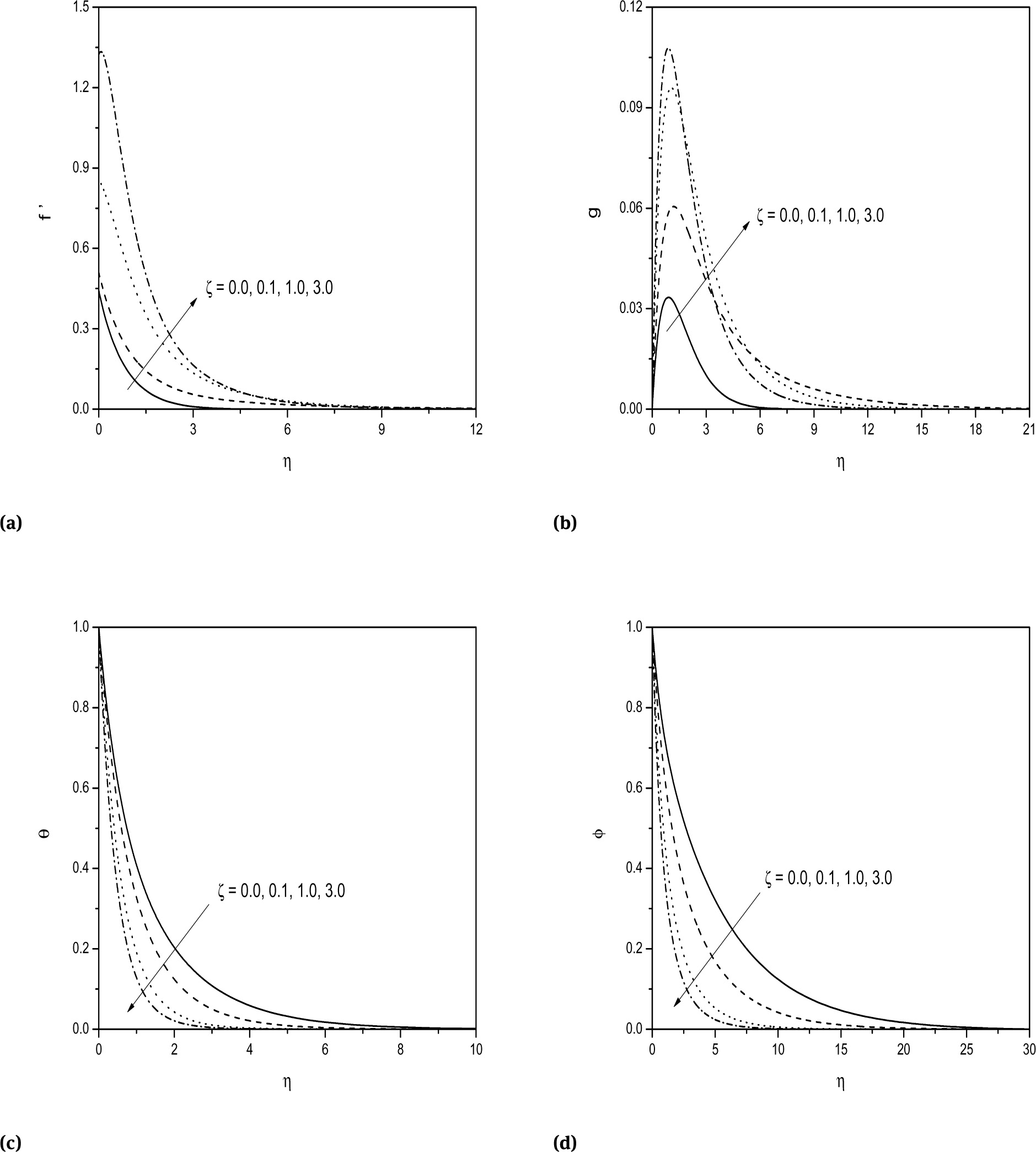
Effect of ζ on a) tangential velocity b) cross flow velocity c) temperature and d) concentration profiles.
Figures 3a-3d exhibit the influence of magnetic parameter Ha on both the velocities, the temperature and concentration. It is seen from Fig. 3a that the tangential velocity is decreasing with an increase in the value of magnetic parameter Ha. Applying the uniform magnetic field normal to flow direction gives rise to Lorentz force. This force has the tendency to slow down the velocity of the fluid in the boundary layer. Hence, the velocity diminishes with enhancement in Ha. From Fig. 3b, it is seen that there is no cross flow velocity in the absence of the magnetic field (Ha = 0) and it increases gradually with increase in Ha . Hence, for large values of Ha, a cross flow is generated due to the Hall effect. This is clearly depicted in the Fig. 3b. From Figs. 3c-3d, it is evident that the temperature and concentration are increasing with increasing values of Ha.
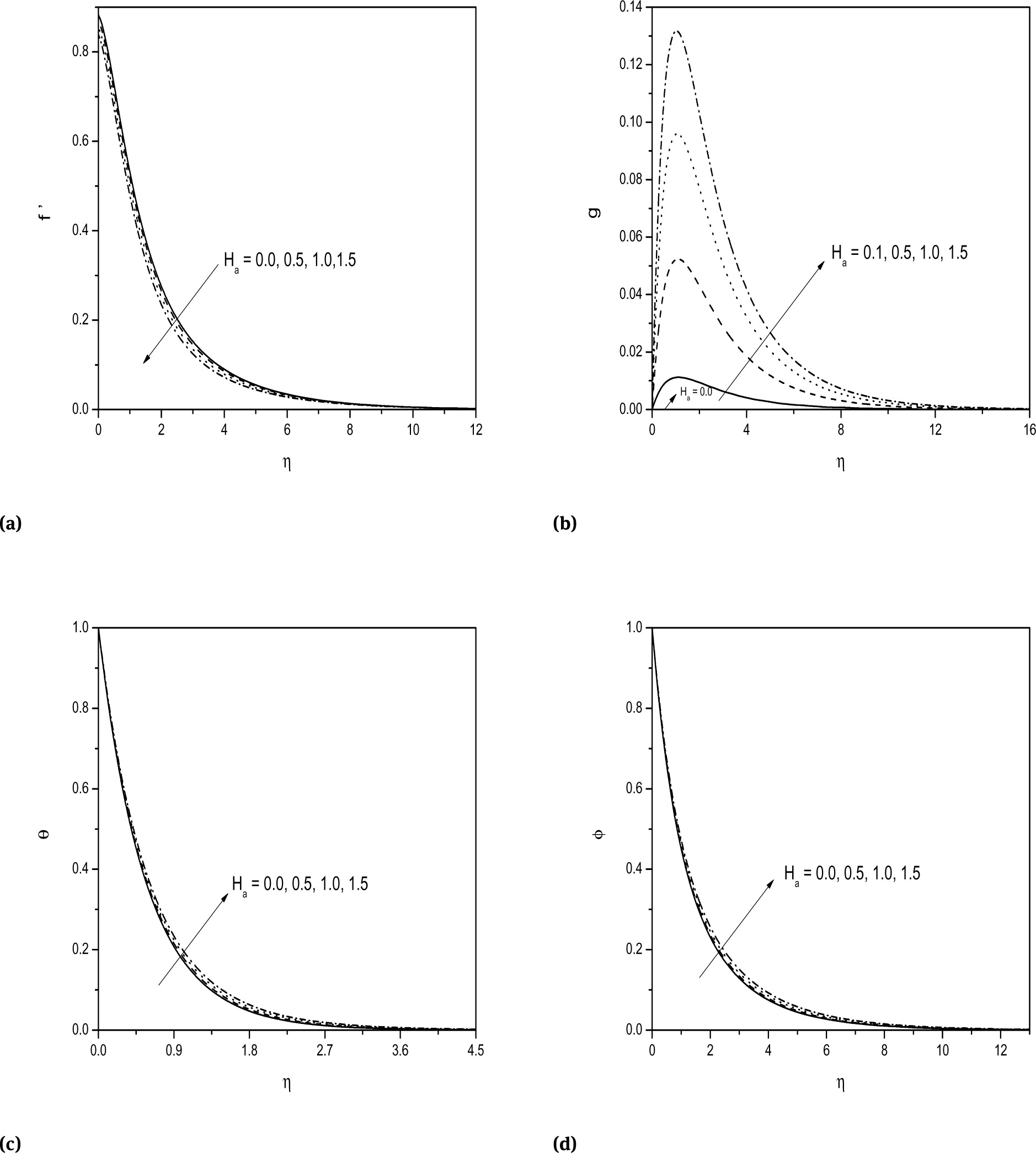
Effect of Ha on a) tangential velocity b) cross flow velocity c) temperature and d) concentration profiles.
The influence of Hall parameter on both the velocities, temperature and concentration is depicted in Fig. 4a-4d. From Fig. 4a it is observed that the tangential velocity increases with the increasing value of the Hall parameter βh. Fig. 4c reveals that the temperature decrease with increasing value of βh. As the Hall parameter βh increases, the effective conductivity reduces which in turn reduces the magnetic damping force on the tangential velocity. Hence the tangential velocity increases and temperature decreases with an increase in the Hall parameter. Fig. 4b shows that the cross flow velocity increases with an increase in the value of βh. Further, it is observed that the cross flow velocity first increases gradually with βh, attaining an extreme value and then drops to zero. From Fig. 4d, it is noticed that the concentration decrease with increasing value of βh.
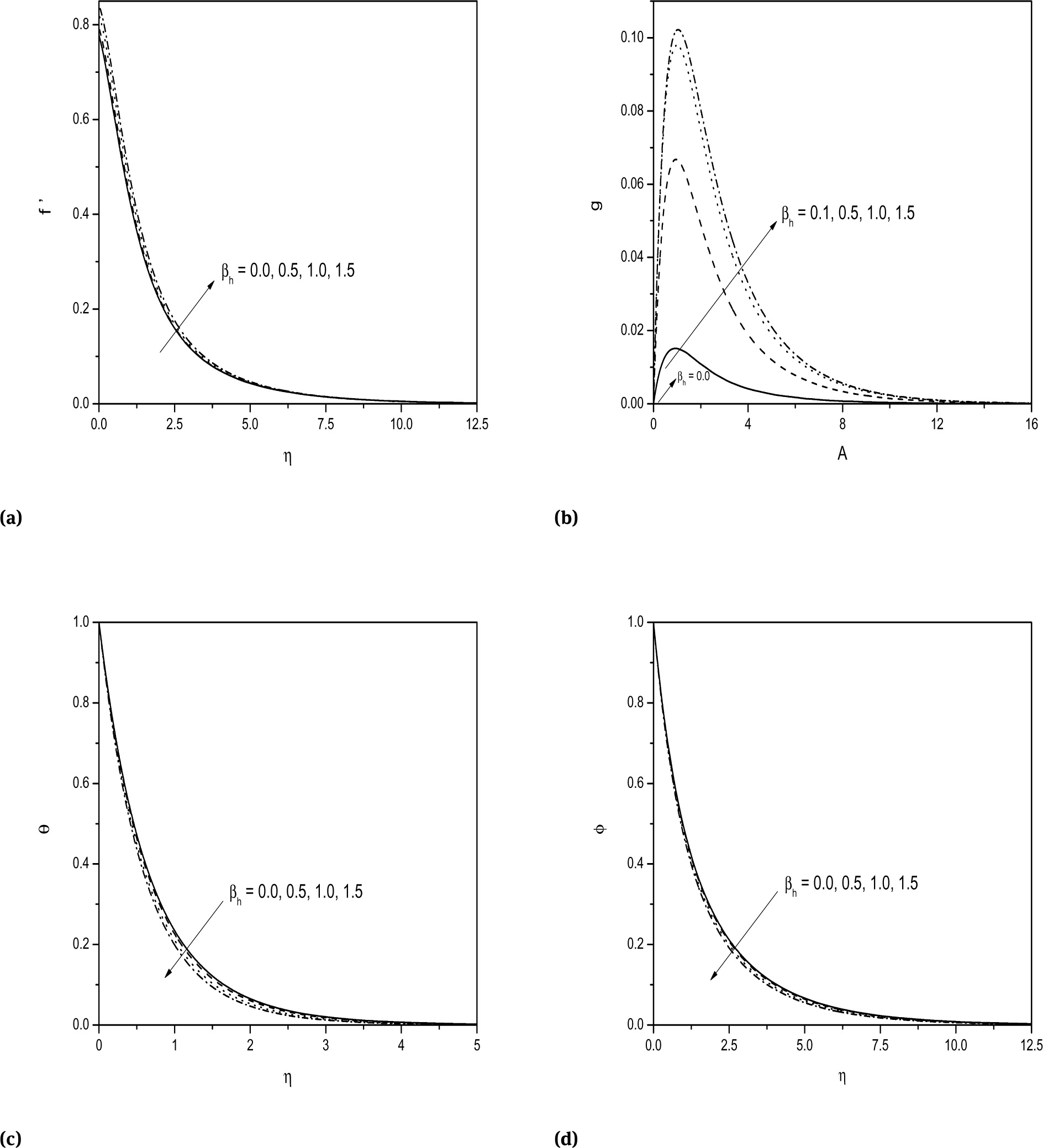
Effect of βh, on a) tangential velocity b) cross flow velocity c) temperature and d) concentration profiles.
The variation of heat transfer coefficient (-θ′(0)) against Pr and mass transfer coefficient (-ϕ′ (0)) against Sc for different values of suction/injection parameter S is presented in the Figs. 5a and 5b. It is seen from these figures that both the heat and mass transfer coefficients are increasing with the increase in the suction/injection parameter. Further, it is understood from the figures that heat and mass transfer rates are increasing with Pr and Sc, respectively. The effect of mixed convection parameter ζ on both the heat and mass transfer coefficients is shown in the Figs. 6a and 6b. These figures indicate that, heat and mass transfer rates are rising for increasing values of the ζ. The influence of slip parameter λ on the heat and mass transfer rates is demonstrated in the Figs. 7a and 7b. It is observed from these figures that, both the heat and mass transfer rates are reduced with increase in the values of slip parameter.
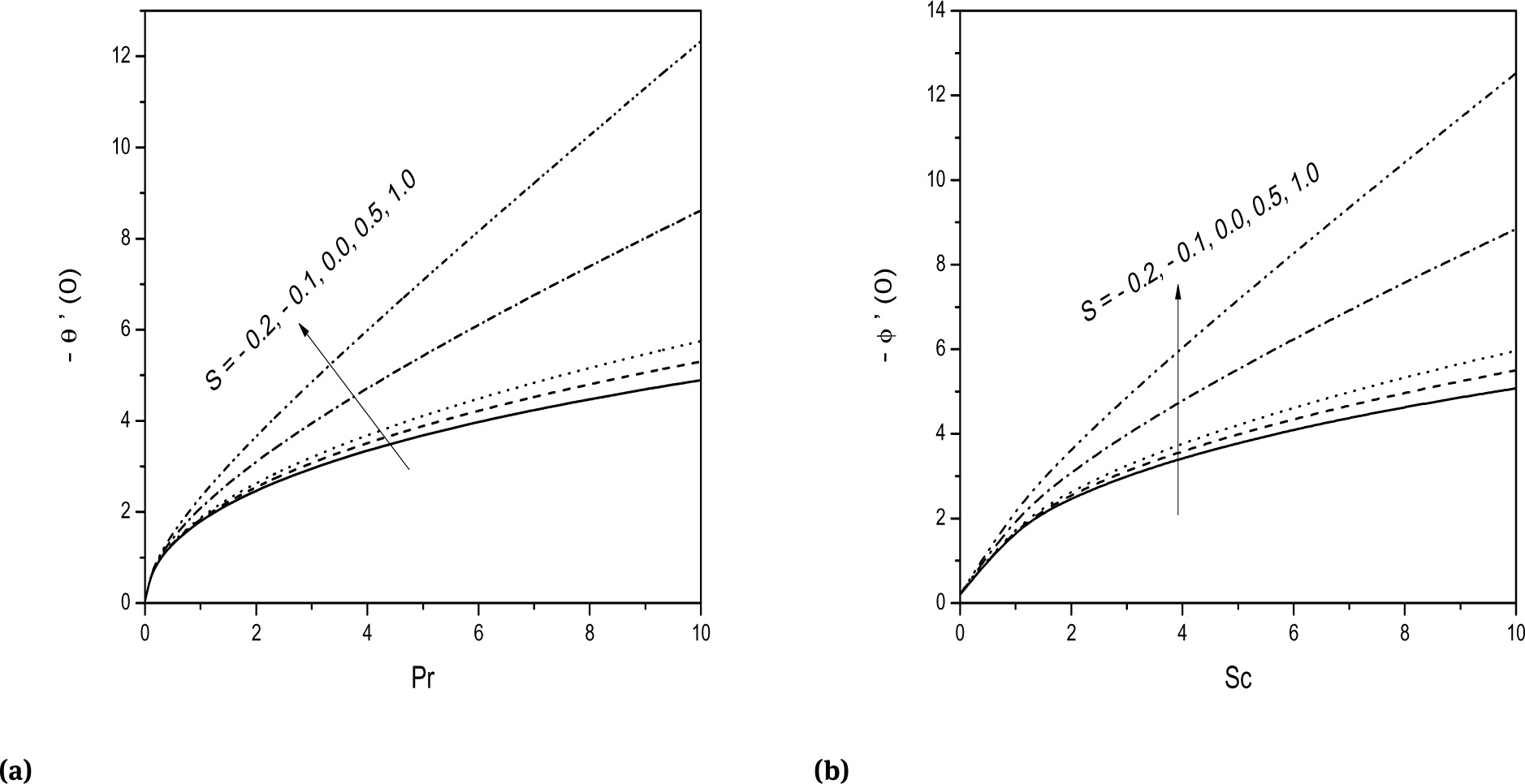
Effect of S on (a) -θ′(0) and (b) -ϕ′(0).
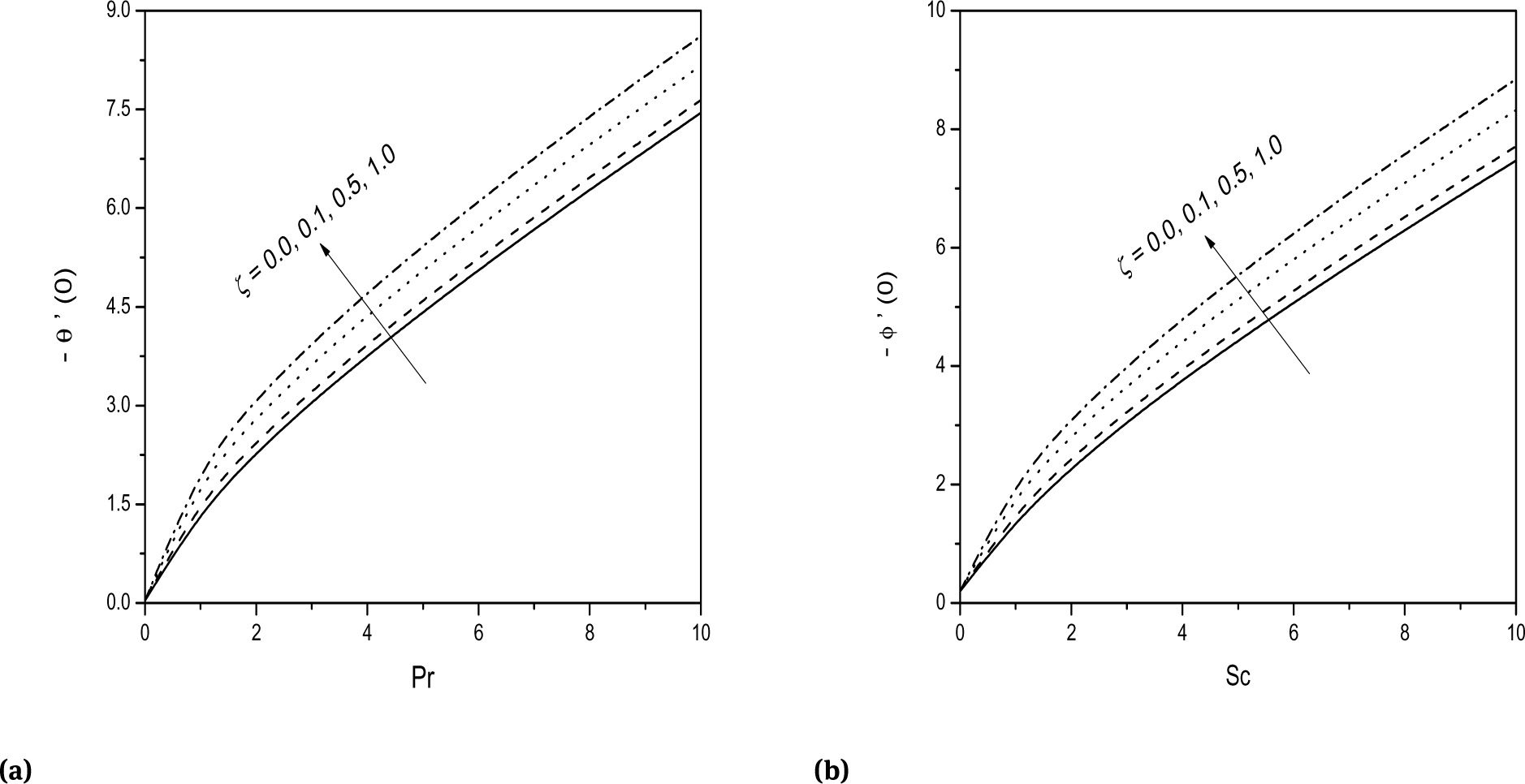
Effect of ζ on (a) -θ′(0) and (b) -ϕ′(0).
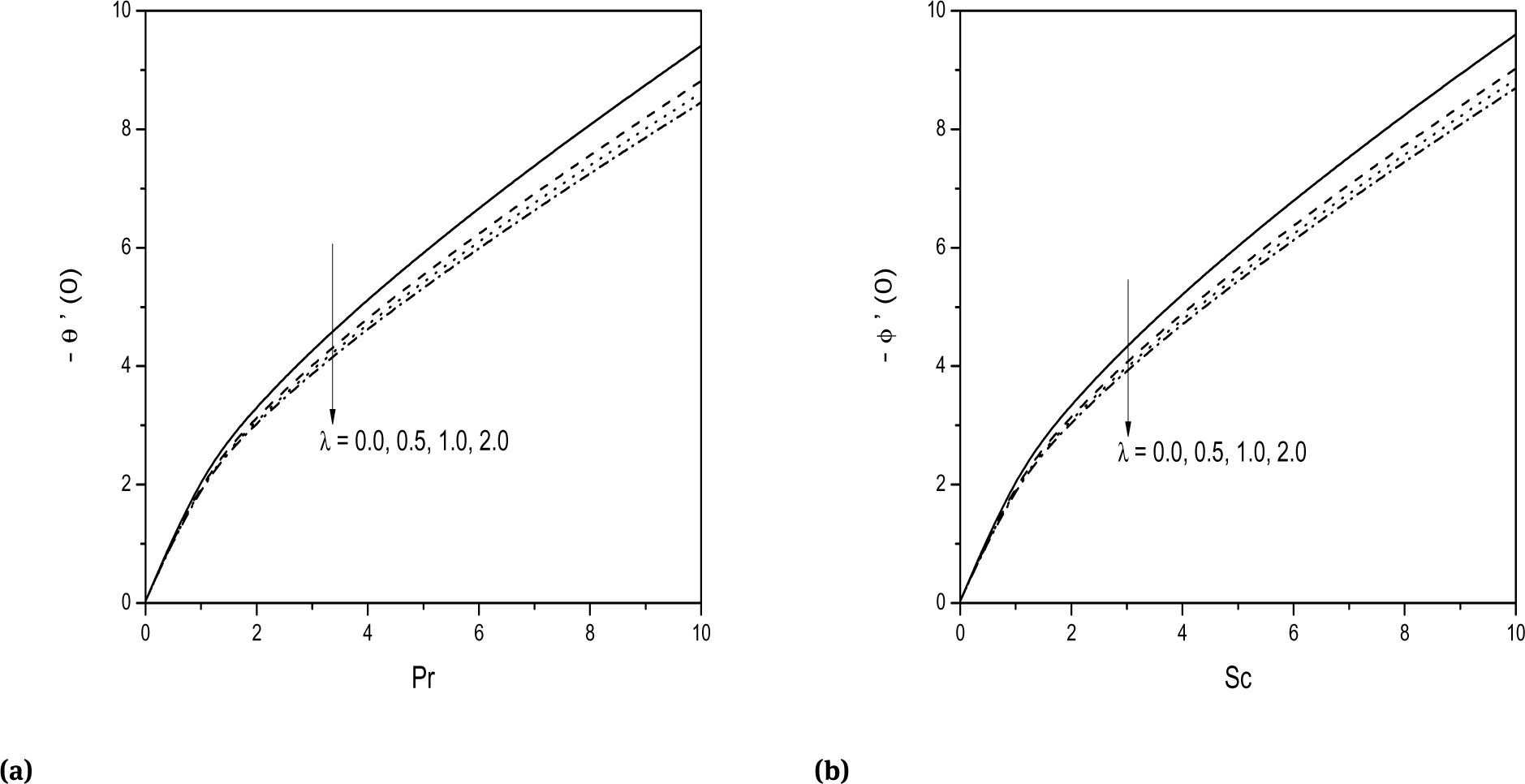
Effect of λ on (a) -θ′(0) and (b) -ϕ′(0).
The variation of heat and mass transfer rates with magnetic parameter Ha is presented in the Figs. 8a and 8b. These figures describe that the heat transfer rate is reduced with increasing values of Ha . The same trend is observed in the mass transfer rate also. The decrease in the mass transfer rate is low when compared to that heat transfer rate as shown in the Fig. 8b. Figures 9a and 9b depict the variation of heat and mass transfer rates for various values of βh. It is noticed from the figures that, the heat and mass transfers are slightly increasing with an increase in βh. Figures 10a and 10b represents the variation of heat and mass transfer rates for different values of Eckert number Ec. It is evident from the figures that the heat transfer rate is decreased and the mass transfer rate slightly increases with an increase in the values of Eckert number Ec.
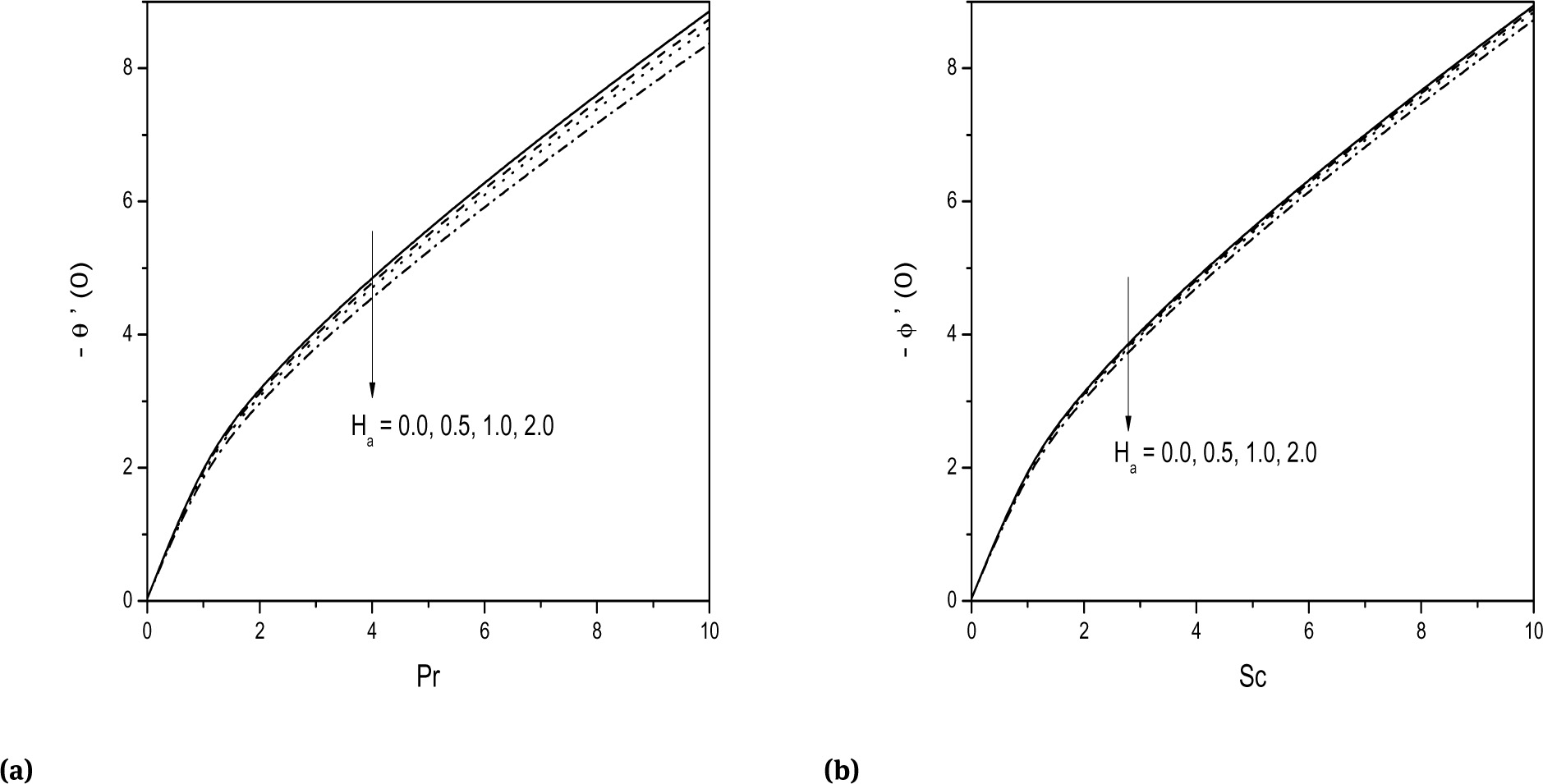
Effect of Ha on (a) -θ′(0) and (b) -ϕ′(0).
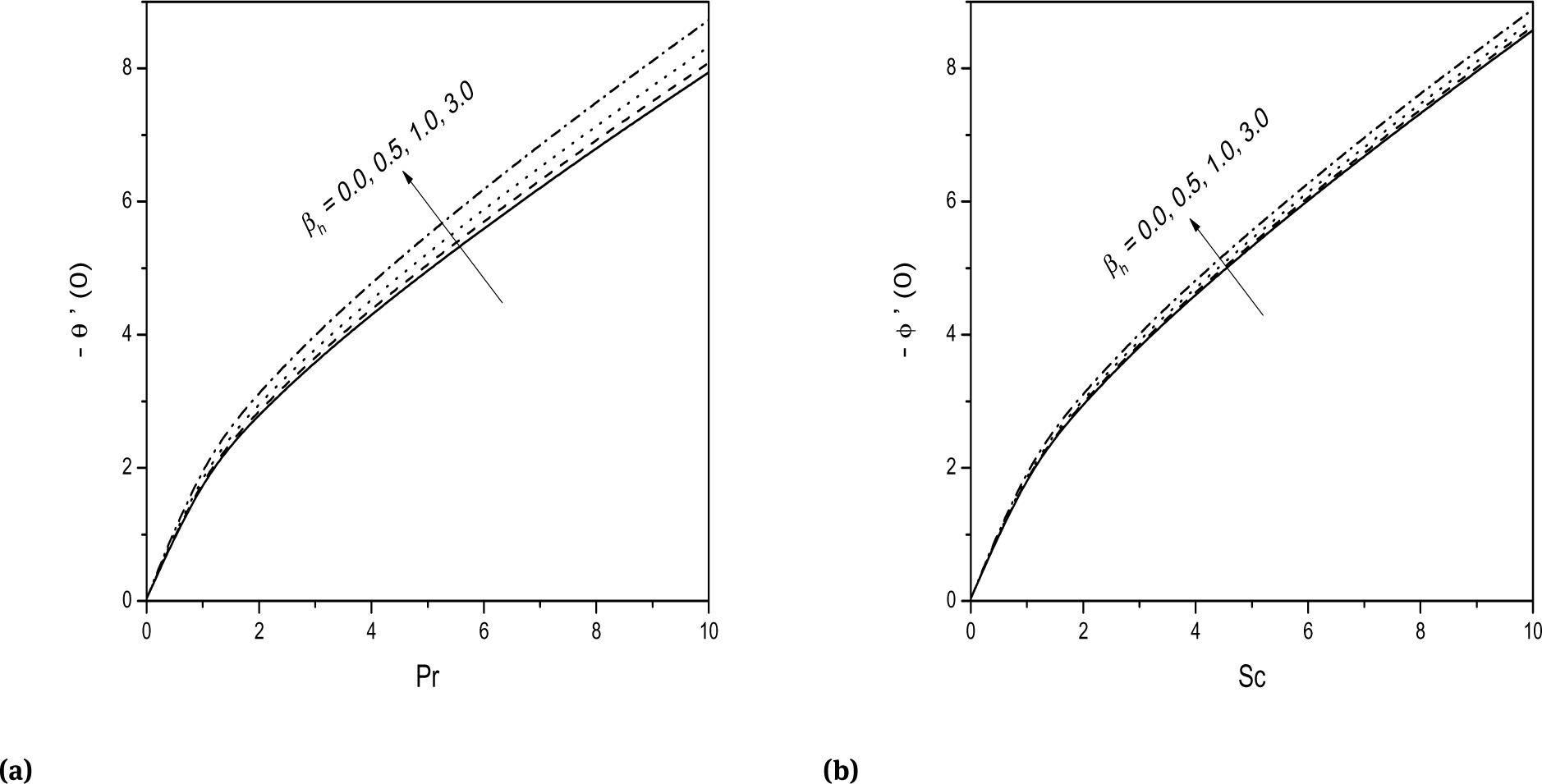
Effect of βh on (a) -θ′(0) and (b) -ϕ′(0).
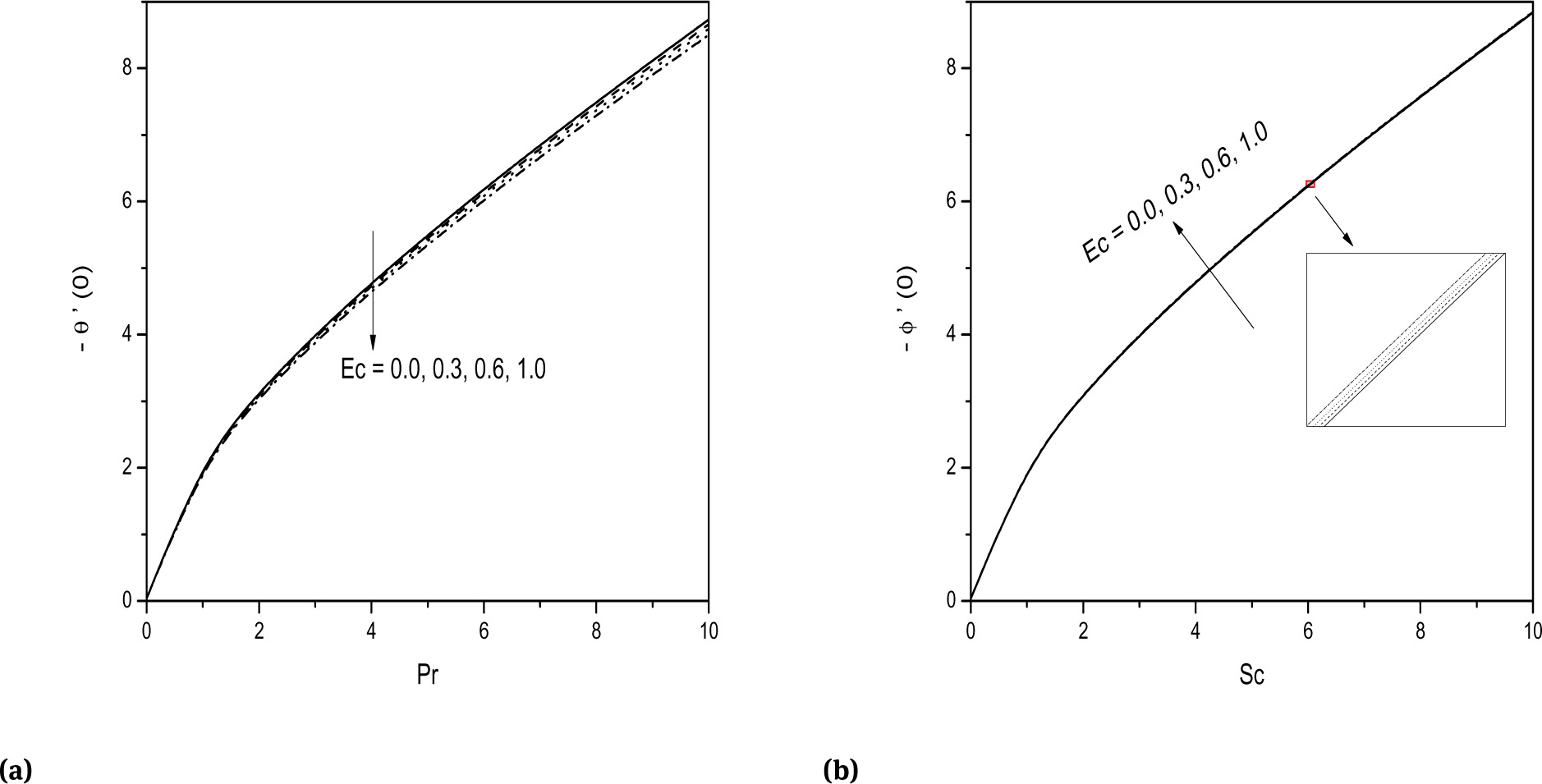
Effect of Ec on (a) -θ′(0) and (b) -ϕ′(0).
The values of local skin-friction coefficients in x-direction (f″(0)) and z′-direction (g′(0)) are presented in Table 2 for various values of S, λ, βh, Ha, ζ and Ec. Table 2 depicts that the skin-friction in x-direction is decreasing and in z-direction is increasing with increase in the values of suction/injection parameter S. While, f″(0) is increasing and g′(0) reducing with an increase in the values of the slip parameter λ. It is seen from the table that, both the skin-frictions are increasing with Hall parameter βh. Further, it is observed that there is no transverse velocity and hence no skin-friction in z-direction in the absence of Hall parameter. The skin-friction in x-direction reduces and in z-direction enhances as Ha increase. In the absence of magnetic field, there is no cross flow velocity and in turn, there is no skin-friction in z-direction. Further, It is noticed that both the skin-frictions are increasing as the values of the mixed convection parameter ζ and Eckert number Ec are increasing.
Values of the local skin-friction coefficients f″(0) and g′(0) for various values of the existing parameters.
| S | λ | βh | Ha | ζ | Ec | f″(0) | g′(0) |
|---|---|---|---|---|---|---|---|
| -0.2 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.08861064 | 0.22777178 |
| -0.1 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.09595488 | 0.23165002 |
| 0.0 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.10356520 | 0.23530727 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 1.0 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.19406497 | 0.25379633 |
| 0.5 | 0.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.49913209 | 0.26108622 |
| 0.5 | 0.5 | 2.0 | 1.0 | 1.0 | 0.5 | -0.22482289 | 0.25199037 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 0.5 | 2.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.08551156 | 0.24713579 |
| 0.5 | 1.0 | 0.0 | 1.0 | 1.0 | 0.5 | -0.22210688 | 0.00000000 |
| 0.5 | 1.0 | 0.1 | 1.0 | 1.0 | 0.5 | -0.22135817 | 0.04545125 |
| 0.5 | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | -0.20625815 | 0.19507657 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 0.5 | 1.0 | 2.0 | 0.0 | 1.0 | 0.5 | -0.11772203 | 0.00000000 |
| 0.5 | 1.0 | 2.0 | 0.1 | 1.0 | 0.5 | -0.12014634 | 0.02762108 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 0.5 | 1.0 | 2.0 | 3.0 | 1.0 | 0.5 | -0.21182255 | 0.59347177 |
| 0.5 | 1.0 | 2.0 | 1.0 | -0.1 | 0.5 | -0.65427230 | 0.00141668 |
| 0.5 | 1.0 | 2.0 | 1.0 | -0.05 | 0.5 | -0.59923787 | 0.06304113 |
| 0.5 | 1.0 | 2.0 | 1.0 | 0.0 | 0.5 | -0.55832267 | 0.10101136 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 0.5 | 1.0 | 2.0 | 1.0 | 2.0 | 0.5 | 0.11281021 | 0.29658203 |
| 0.5 | 1.0 | 2.0 | 1.0 | 3.0 | 0.5 | 0.32405756 | 0.32877845 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.0 | -0.14747427 | 0.24859705 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.2 | -0.14673011 | 0.24885803 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -0.14560661 | 0.24925067 |
| 0.5 | 1.0 | 2.0 | 1.0 | 1.0 | 1.0 | -0.14371460 | 0.24990813 |
5 Conclusions
In this paper Hall effect on viscous incompressible fluid flow over an exponentially stretching sheet has been studied. Suction/injection, velocity slip and Joule heating effects are taken into account. Similarity transformations are used to reduce the governing boundary layer equations to ordinary differential equations and then linearized using the successive linearization method. The resulting equations are solved using Chebyshev spectal collocation method. The main findings are as follows.
As the magnetic parameter increases, the tangential velocity and heat and mass transfer rate decrease but the cross flow velocity, temperature and concentration increase.
The tangential velocity, cross flow velocity, heat and mass transfer rates are increasing, but the temperature and concentration are decreasing with an increase in the values of Hall parameter.
Both the tangential and cross flow velocities, temperature and concentration decrease and the rate of heat and mass transfer increase with an increase in suction/injection parameter.
References
[1] P. K. Kameswaran, M. Narayana, P. Sibanda and G. Makanda, On radiation effects on hydromagnetic Newtonian liquid flow due to an exponential stretching sheet, Boundary Value Problems, Vol 2012, No. 105, pp. 1–16, 2012.10.1186/1687-2770-2012-105Suche in Google Scholar
[2] I.C. Mandal and S. Mukhopadhyay, Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium. Ain Shams Engineering Journal, Vol. 4, pp. 103–110, 2013.10.1016/j.asej.2012.06.004Suche in Google Scholar
[3] V. Singh, and S. Agarwal, MHD Flow and Heat Transfer for Maxwell Fluid over an exponentially stretching sheet with variable thermal conductivity in porous medium, Thermal Science, Vol. 18(2), pp. S599-S615, 201410.2298/TSCI120530120SSuche in Google Scholar
[4] A.A. Khidir and P. Sibanda, Effect of temperature-dependent viscosity on mhd mixed convective flow from an exponentially stretching surface in porous media with cross-diffusion, Special Topics & Reviews in Porous Media: An International Journal, Vol.5(2), pp. 157–170, 2014.10.1615/SpecialTopicsRevPorousMedia.v5.i2.60Suche in Google Scholar
[5] R.S.R. Gorla B. J. Gireesha, and Bhulinder Singh, MHD flow and heat transfer of dusty nanofluid embedded in porous medium over an exponentially stretching sheet, J. Nanofluids, Vol. 4, pp. 449–460, 2015.10.1166/jon.2015.1175Suche in Google Scholar
[6] T. Hayat, A. Shafiq, A. Alsaedi, and S. A. Shahzad, Unsteady MHD flow over exponentially stretching sheet with slip conditions, Appl. Math. Mech., Vol. 37(2), pp. 193–208, 201610.1007/s10483-016-2024-8Suche in Google Scholar
[7] M. R. Eid, Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation, Journal of Molecular Liquids Vol. 220, pp. 718–725, 201610.1016/j.molliq.2016.05.005Suche in Google Scholar
[8] A. Megahed, S. R. Komy and A. Afify, Similarity analysis in magnetohydrodynamics: Hall effects on free convection flow and mass transfer past a semi-infinite vertical flat plate, International Journal of Non-Linear Mechanics, Vol 38, pp. 513–520, 2003.10.1016/S0020-7462(01)00077-4Suche in Google Scholar
[9] E. M. Abo-Eldahad, M. A. El-Aziz, A. M. Salem and K. K. Jaber, Hall current effect on MHD mixed convection flow from an inclined continuously stretching surface with blowing/suction and internal heat generation/absorption, Applied Mathematical Modelling, Vol 31, pp. 1829–1846, 2007.10.1016/j.apm.2006.06.017Suche in Google Scholar
[10] M. A. El-Aziz, Flow and heat transfer over an unsteady stretching surface with Hall effect, Meccanica, Vol 45, pp. 97–109, 2010.10.1007/s11012-009-9227-xSuche in Google Scholar
[11] S. Shateyi and S. S. Motsa, Boundary layer flow and double diffusion over an unsteady stretching surface with hall effect, Chemical Engineering Communications, Vol 198, pp. 1545–1565, 2011.10.1080/00986445.2011.555488Suche in Google Scholar
[12] M. A. El-Aziz and T. Nabil, Homotopy analysis solution of hydromagnetic mixed convection flow past an exponentially stretching sheet with hall current, Mathematical Problems in Engineering, 2012.10.1155/2012/454023Suche in Google Scholar
[13] D. Pal, Hall current and MHD effects on heat transfer over an unsteady stretching permeable surface with thermal radiation, Computers and Mathematics with Applications, Vol. 66(7), pp. 1161–1180, 201310.1016/j.camwa.2013.07.010Suche in Google Scholar
[14] A. Zaib and S. Sharie, Thermal diffusion and diffusi on thermo effects on unsteady MHD free convection flow over a stretching surface considering Joule heating and viscous dissipation with thermal stratification, chemical reaction and Hall current, Journal of the Franklin Institute, Vol 351, pp. 1268–1287, 2014.10.1016/j.jfranklin.2013.10.011Suche in Google Scholar
[15] H. Zaman, A. Sohail, A. Ali and T. Abbas, Effects of hall current on flow of unsteady MHD axisymmetric second-grade fluid with suction and blowing over an exponentially stretching sheet, Open Journal of Modelling and Simulation, Vol 2, pp. 23–33, 2014.10.4236/ojmsi.2014.22005Suche in Google Scholar
[16] S. S. Motsa and S. Shateyi, Successive Linearisation Solution of Free Convection Non-Darcy Flow with Heat and Mass Transfer, Advanced topics in mass transfer, Vol. 19, pp. 425–438, 2006.10.5772/14519Suche in Google Scholar
[17] Z. G. Makukula, P. Sibanda and S. S. Motsa, A novel numerical technique for two dimensional laminar flow between two moving porous walls, Mathematical problems in Engineering, Vol. 2010, pp. 1–15, 2010.10.1155/2010/528956Suche in Google Scholar
[18] F. G. Awad, P. Sibanda, S. S. Motsa and O. D. Makinde, Convection from an inverted cone in a porous medium with cross-diffusion effects, Computers and Mathematics with Applications. Vol. 61, pp. 1431–1441, 2011.10.1016/j.camwa.2011.01.015Suche in Google Scholar
[19] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, Spectral Methods-Fundamentals in Single Domains, Journal od Applied Mathematics and Mechanics, Volume 87, No.1, 2007.10.1007/978-3-540-30726-6Suche in Google Scholar
[20] E. Magyari and B. Keller, Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface, Journal of Physics D: Applied Physics Vol 32, pp. 577–585, 1999.10.1088/0022-3727/32/5/012Suche in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Chaos Suppression in Fractional order Permanent Magnet Synchronous Generator in Wind Turbine Systems
- Solution of Fifth-order Korteweg and de Vries Equation by Homotopy perturbation Transform Method using He’s Polynomial
- A study on validating KinectV2 in comparison of Vicon system as a motion capture system for using in Health Engineering in industry
- MHD Flow with Hall current and Joule Heating Effects over an Exponentially Stretching Sheet
- Solitons and other solutions to the coupled nonlinear Schrödinger type equations
- Nonlinear Dynamic Characteristics of the Railway Vehicle
- Quadratic Convective Flow of a Micropolar Fluid along an Inclined Plate in a Non-Darcy Porous Medium with Convective Boundary Condition
- Viscous Dissipation and Thermal Radiation effects in MHD flow of Jeffrey Nanofluid through Impermeable Surface with Heat Generation/Absorption
Artikel in diesem Heft
- Frontmatter
- Chaos Suppression in Fractional order Permanent Magnet Synchronous Generator in Wind Turbine Systems
- Solution of Fifth-order Korteweg and de Vries Equation by Homotopy perturbation Transform Method using He’s Polynomial
- A study on validating KinectV2 in comparison of Vicon system as a motion capture system for using in Health Engineering in industry
- MHD Flow with Hall current and Joule Heating Effects over an Exponentially Stretching Sheet
- Solitons and other solutions to the coupled nonlinear Schrödinger type equations
- Nonlinear Dynamic Characteristics of the Railway Vehicle
- Quadratic Convective Flow of a Micropolar Fluid along an Inclined Plate in a Non-Darcy Porous Medium with Convective Boundary Condition
- Viscous Dissipation and Thermal Radiation effects in MHD flow of Jeffrey Nanofluid through Impermeable Surface with Heat Generation/Absorption

