Viscous Dissipation and Thermal Radiation effects in MHD flow of Jeffrey Nanofluid through Impermeable Surface with Heat Generation/Absorption

1 Introduction

Nanotechnology plays an important role in many electronic devices, vehicles, space craft, defense, biomedical science, solar water heating and cooling applications, etc. Choi [1] was the first who employed that if nanometer sized particles are suspended in base-fluid enhanced the heat transfer rate. It was expected that the nanofluids have a better thermal conductivity efficiency than the base fluid like water, ethylene glycol mixture etc. The feature study of nanofluid was originated in the book by Das et al. [2]. Wang and Majumdar [3], Yang et al. [4] and Jahani et al. [5] have done the first theoretical and experimental study on nanofluids with application in science and engineering. Recently Cai et al. [6] developed fractal based approaches to nanofluid and nanoparticle migration. Sheikholeslami and Shehzad [7] studied the convective MHD flow of nanofluid enclosed by heat flux boundary conditions in a porous medium. Hayat et al. [8] investigated the MHD flow of nanofluid due to rotating disk with slip effect. They also studied the heat generation/absorption effects in Oldroyd-B nanofluid induced by a stretching sheet [9]. Hashmi et al. [10] discussed the effects of magnetic field in mixed convective Oldroyd-B nanofluid induced by two infinite isothermal stretching disks. Anwar et al. [11] showed the MHD stagnation point flow of Micropolar nanofluid towards a stretching sheet. There is one important non-Newtonian fluids known as Jeffrey fluid [12– 17] which has been fascinated much by the researchers because of its simplicity. This fluid model is capable of describing the characteristics of relaxation and retardation times.

The investigation of flow of a viscous incompressible fluid over a stretching sheet has been taken up by many researchers because of various industrial applications, such as in the manufacturing of polymer sheets, filaments, and wires. During the manufacturing process, the moving sheet is assumed to stretch on its own plane, and the stretched surface interacts with the ambient fluid both mechanically and thermally. Stretching and shrinking can occur in a variety of materials. Two dimensional flows over a stretching sheet was first studied by Crane [18]. Sakiadas [19] studied the behavior of boundary layer flow due to a moving flat surface immersed in an otherwise quiescent fluid. Bataller [20] studied the effects of thermal radiation on the laminar boundary layer about a flat plate. A variety of aspects of flow and heat transfer of viscous fluid over a flat surface were investigated by many researchers [21–31].

The purpose of this paper is to discuss the analytical solution of the two dimensional MHD flow of viscoelastic Jeffrey fluid through impermeable surface in presence of thermal radiation and viscous dissipation with heat generation / absorption. Similarity transformation has been used to simplify the governing equations, and the reduced boundary value problems are solved analytically by homotopy analysis method (HAM). The HAM has been successfully applied to solve many nonlinear problems in science and engineering [32– 46] because this technique does not depend upon the auxiliary parameter and converges very rapidly the approximate solution into exact one. The main advantage is that HAM is independent of any small/large physical parameters. Unlike all other analytic techniques, the HAM provides us a convenient way to guarantee the convergence of solution series so that it is valid for highly nonlinear problems. The HAM can be applied to solve many nonlinear problems in science, finance and engineering, especially those without small/large physical parameters. So it is conclude that it can be applied directly to nonlinear differential equations without requiring linearization, discretization and therefore, it is not affected by errors associated to discretization. Same as the HAM, the Differential Transform Method (DTM) can overcome the forgoing restriction, assumptions and limitations of traditional perturbation method [47–50]. Recently many researchers and scientists applied the HAM to various fluid flow problems with different geometries. In the last obtained results are compared with those results which are presented by Khan and Pop [51], Wang [52], Gorla and Sidawi [53] and Ramesh et al. [54].

2 Mathematical formulation

Consider a two dimensional flow of an incompressible, electrically conducting viscoelastic Jeffrey fluid model persist the nanoparticle having uniform shape and size over an stretching impermeable sheet. The sheet is coinciding with the plane y = 0 and origin is located at y = 0, by which the sheet is stretching. A constant magnetic field of strength B₀ is applied in a direction normal to the plane at y = 0 as shown in the Figure 1. The simplified two dimensional boundary layer equations governing the flow, heat transfer and nano-particle concentration are given by

Fig. 1

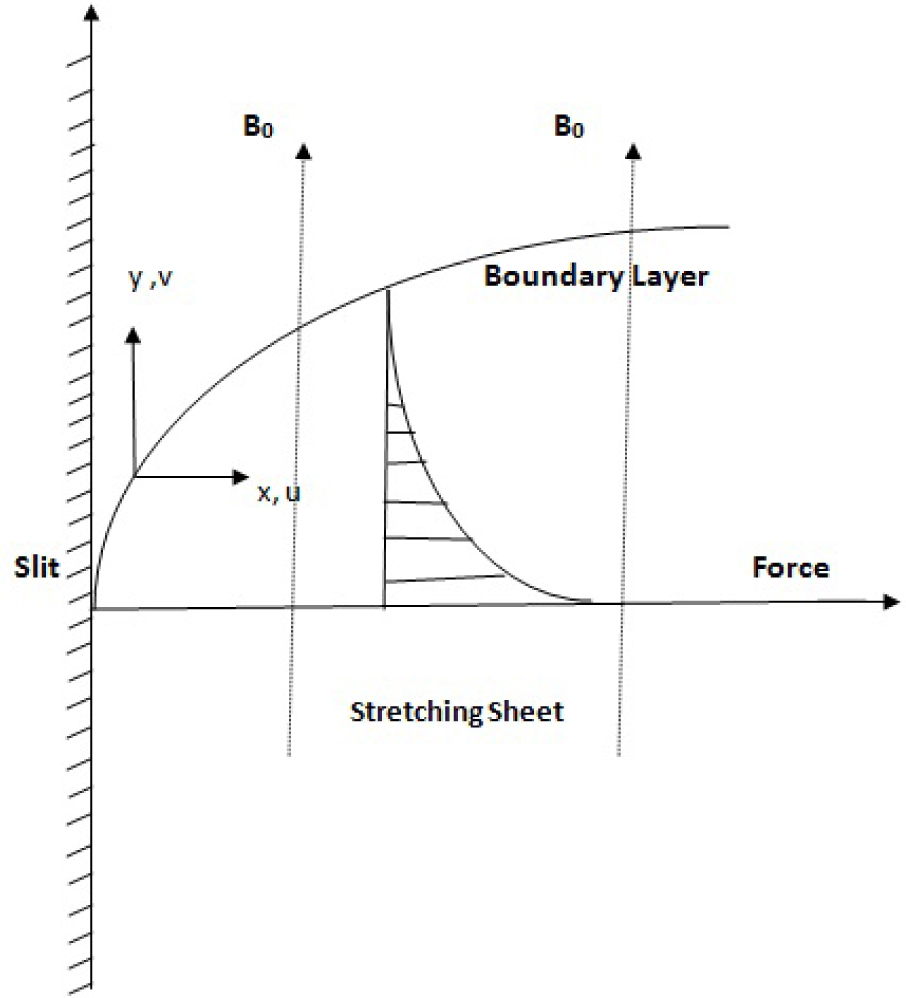
Schematic Diagram of Flow.

The associated boundary conditions are

where u and v are the velocity components in x and y direction, respectively. a > 0 is known as stretching rate, ν is the kinematic viscosity, λ is the ratio of relaxation to retardation times, λ₁ is the relaxation time, ρ_f is the density of base fluid, α is the thermal diffusivity, σ is the electrical conductivity, ρ_p is the density of the nanoparticles and T is the ambient fluid temperature, τ=ρpcpρfcf is the ratio of nanoparticle heat capacity and base fluid heat capacity, Q₀ is the internal heat generation/absorption coefficient, D_B is the Brownian diffusion coefficient, D_T is the thermophoresis diffusion coefficient and c_p is the specific heat at constant pressure. Here C is the nanoparticles volume fraction, T_w and T_∞ are the temperature of the fluid at the wall and ambient temperature when y → ∞, C_w and C_∞ are the nanoparticles volume fraction of the fluid at the wall and ambient nanoparticles volume fractions when y → ∞.

Using Rosseland approximation for radiation, we have

where σ is the Stefan-Boltzman constant, and k* is the mean absorption coefficient. Expanding T⁴ in terms of Taylor series about T_∞ and neglecting higher order terms, we have

Using (7), in (6) we get

By employing the Rosseland approximation of Eq. (8), Eq. (3) takes the form

Introducing the following similarity transformation

where the stream function ψ is defined as

Using equations (10) and (11) in equations (1) to (3), the equations of linear momentum, energy and concentration with their corresponding boundary conditions are reduced as follows

subject to the boundary conditions are as follows

where M=σcρfB0 is the dimensionless magnetic parameter, β = aλ is the Deborah number, Nb={τDB(Cw−C∞)}ν is the Brownian motion parameter, Nt={τDT(Tw−T∞)}νT∞ is the thermophoresis parameter, Le=νDB is the Lewis number, Pr=να is the Prandtl number, A=Q0aρfcp is the heat source for A > 0 and A < 0 for heat sink parameter, Ec = u02cpT0uwu04−A2 is the Eckert number, and Rd=16T∞3σ3kk∗ is the radiation parameter.

The skin friction coefficient, the local Nusselt number and Sherwood number are defined as

where τ_w is the shear stress along the stretching surface, q_w is the surface heat flux and q_m is the mass flux, are given by

respectively.

Using the non-dimensional variables in equation (16), we get

where Rex=xuw(x)ν is the local Reynolds’s number

3 Homotopy analysis method

The homotopy analysis method was derived from the fundamental concept of topology known as homotopy. The basic ideas of the homotopy analysis method (HAM) are here presented by considering the following nonlinear differential equation

where A is a nonlinear differential operator, u(η) is the unknown solution of the equation (19) and η is an independent variable. For simplicity, we ignore all boundary or initial conditions, which can be treated in a similar way. Applying the HAM to solve equation (19), one can construct the so called zeroth order deformation equation, as follows

Where p ∊ [0, 1] is an embedding parameter, ℏ ≠ 0 is an auxiliary parameter, L is a properly selected auxiliary linear operator satisfying L(f) = 0 when f = 0.H(η) ≠ 0 is an auxiliary function and u₀ (η) is an initial guess of u(η). Further, it is assumed that at p = 0, the function û(η; p) has derivatives up to infinity. Thus the variation of p from 0 to 1 is the continuous variation of û(η; p) from initial guess u₀ (η) to the unknown function u(η) of equation (19). In topology, this type of variation is called deformation, where u₀ (η) and u(η) are called homotopic.

Expanding û(η; p) in Taylor series with respect to embedding parameter p, we obtain

where

The convergence of the series (20) depends upon the auxiliary parameter ℏ. If it is convergent at p = 1, one has

which one of the solutions of the original nonlinear equation, as proven by Liao [32–34]. Define the vectors

Differentiating the zeroth-order deformation equation (20)m-times with respect to p and then dividing them by m! and finally setting p = 0, we get the following m^th-order deformation equation:

where

and

It should be highlighted that u_m (x, t) form ≥ 1 is governed by the linear equation (26) with linear boundary conditions that comes from the original problem, which can be easily solved by the symbolic computation software such as Maple, Mathematica and Matlab.

4 Solution of the problem by the homotopy analysis method

Now for solving the present boundary value problems given by the equations (12) to (14) subject to the corresponding boundary conditions (15) by the homotopy analysis method (HAM) by the rule of solution expression, we express the following initial guess f₀, θ₀, and φ₀ of f(η), θ (η) and φ (η) as follows

and with the auxiliary linear operator as

with the property that

and

where C_i(i = 1..7) are arbitrary constants and are determined by the boundary conditions.

Higher order deformation problem

The m^th order deformation equations are as follows:

Lf[fm(η)−χmfm−1(η)]=ℏfHf(η)Rmf(η),(40)

Lθ[θm(η)−χmθm−1(η)]=ℏθHθ(η)Rmθ(η),(41)

Lφ[φm(η)−χmφm−1(η)]=ℏφHφ(η)Rmφ(η),(42)

where

χm=1,m>10,m≤1(43)

with the boundary conditions

fm0=fm′0=fm′∞=fm″∞=0,θm(0)=θm(∞)=0,φm(0)=φm(∞)=0.(44)

where

Rmf(η)=fm−1‴+β∑k=0m−1fk″fm−1−k″−fm−1−kfkiv+(1+λ)∑k=0m−1fk″fm−1−k−fm−1−k′fk′−Mfm−1′,(45)

Rmθ(η)=1+4Rd3θm−1″+Pr∑k=0m−1fkθm−1−k′−Nbθm−1−kφk′+Nbθm−1−k′θk′+Aθm−1+PrEc∑k=0m−1fm−1−k″fk″,(46)

Rmφ(η)=φm−1″+LePr∑k=0m−1fm−1−kφk′+NtNbθm−1″.(47)

For p = 0 and p = 1,w have

f^(η;0)=f0(η),f^(η;1)=f(η),θ^(η;0)=θ0(η),θ^(η;1)=θ(η),φ^(η;0)=φ0(η),φ^(η;1)=φ(η).(48)

And when p varies from 0 to 1, f^(η;p),θ^(η;p)andφ^(η;p) vary from the initial guess f₀ (η), θ₀ (η), and φ₀ (η) to the final solution f(η), θ (η) and φ (η), respectively.

By means of Taylor’s series, we have

f^(η;p)=f0(η)+∑m=1∞fm(η)pm,(49)

θ^(η;p)=θ0(η)+∑m=1∞θm(η)pm,(50)

φ^(η;p)=φ0(η)+∑m=1∞φm(η)pm.(51)

where

fm(η)=1m!∂mf^(η;p)∂ηmp=0,(52)

θm(η)=1m!∂mθ^(η;p)∂ηmp=0,(53)

φm(η)=1m!∂mφ^(η;p)∂ηmp=0.(54)

The auxiliary parameters are so properly chosen that series (40)–(41) converges when p = 1 and thus

f(η)=f0(η)+∑m=1∞fm(η),(55)

θ(η)=θ0(η)+∑m=1∞θm(η),(56)

φ(η)=φ0(η)+∑m=1∞φm(η).(57)

The general solutions of Eqs. (36)–(37) can be written as

fm(η)=fm∗(η)+C1+C2exp⁡(−η)+C3exp⁡(η),(58)

θm(η)=θm∗(η)+C4exp⁡(−η)+C5exp⁡(η),(59)

φm(η)=φm∗(η)+C6exp⁡(−η)+C7exp⁡(η).(60)

In which fm∗(η),θm∗(η)andφm∗(η) are the particular solutions of the equations (40) to (42). Solving these equations in MATHEMATICA 10.0 one after the other in the order m = 1, 2, 3, …

The first order components of velocity, temperature and nanoparticle concentration profiles are given by as follows:

f1(η)=112e−3ηe3η(24+ℏ(−2+4M−2β))−2eηℏ(M+β−λ)−ℏ(1+λ)−e2η(24+ℏ(−3+M(2+6η)−4β+λ))),(61)

θ1(η)=18(3+4Rd)e−3η(3ℏ(1+Ec−Nb+Nt)Pr+8eηℏ(1+(−1+A)Pr)−2e2η(−6+3ℏ(2+(−1+2A+Ec−Nb+Nt)Pr)−8Rd)−ℏ2(1+λ)2+ℏ(1+λ),(62)

φ1(η)=124Nbe−3η3ℏLePrNb+8eηℏ(Nb+Nt−LeNbPr)+e2η(−8ℏNt+Nb(24−8ℏ+5ℏLePr))).⋮(63)

and so on.

It can be noticed that the series solutions (61)–(63) contain the non-zero auxiliary parameters ℏ_f,ℏ_θ and ℏ_φ we can adjust and control the convergence of the HAM solutions with the help of these auxiliary parameters. Hence to compute the range of admissible values of ℏ_f,ℏ_θ and ℏ_φ, we display the ℏ-curve of the functions f″(0), θ′(0) and φ′(0) of 20^th-order of approximations. Fig.2, 3 and 4 depicts that the range of admissible values of ℏ_f,ℏ_θ and ℏ_φ are −1.5 ≤ ℏ_f ≤ −0.5,−0.8≤ ℏ_θ ≤ −0.38. and −1.45≤ ℏ_θ ≤ −0.55. The series solution (61)–(63) converge in the whole region of η when ℏ_f = −0.8, ℏ_θ = −0.55 and ℏ_φ = −0.7.

Fig. 2

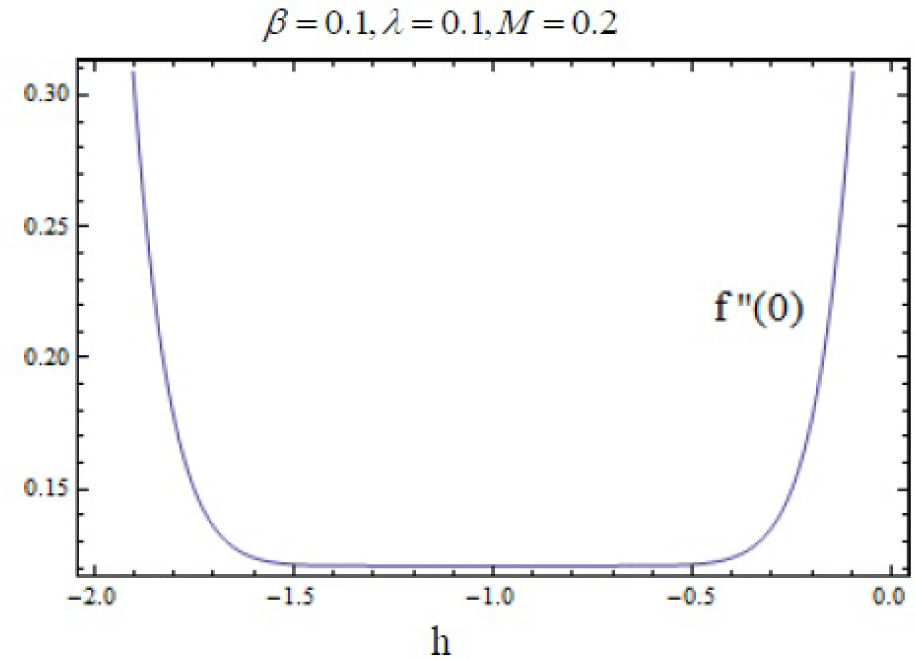
h_f curve for functions f for 20^th-order of HAM approximations.

Fig. 3

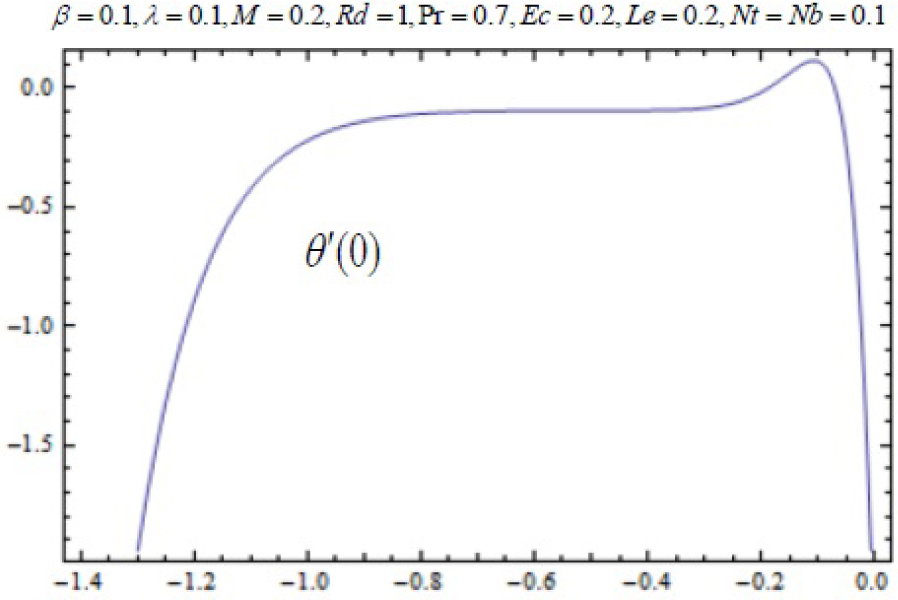
h_θ curve for functions θ for 20^th-order of HAM approximations.

Fig. 4

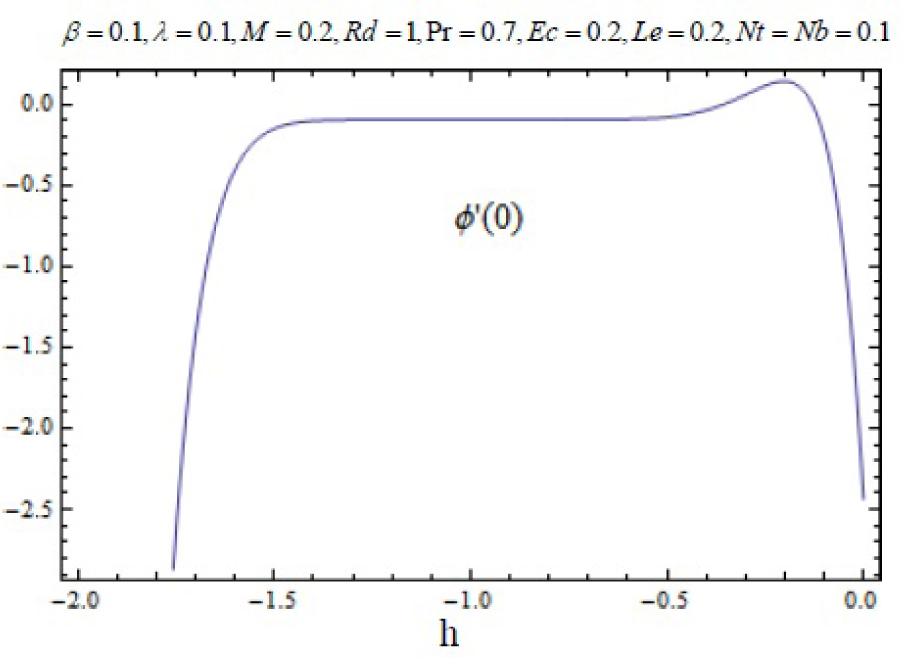
h_ϕ curve for functions ϕ for 20^th-order of HAM approximations.

Table 1

Convergence of series solution for different order of approximations β = 0.1, λ = 0.2, M = 0.2, Pr = 7, Le = 1.2, N_t = N_b = 0.1, Ec = 0.1, R_d = 0.1, ħ_f = −0.8, ħ_θ = −0.55 and ħ_φ = −0.7

Order of Approximation	−f″(0)	−θ′(0)	−φ′(0)
1	2.57333	0.888235	2.03667
3	2.53480	0.888136	2.04223
5	2.53266	0.887391	2.04361
10	2.53252	0.887262	2.04386
15	2.53252	0.887184	2.04402
20	2.53252	0.887102	2.04022
23	2.53252	0.887102	2.04022
25	2.53252	0.887102	2.04022
30	2.53252	0.887102	2.04022

Table 2

Numerical values of the skin friction coefficient-f″(0) for various values of β, λ and M.

λ	β	M	−f″(0)
0	0.2	0.2	1.33216
0.1			1.26613
0.2			1.18392
0.1	0.4	0.2	1.01326
	0.6		1.12364
	0.8		1.24142
0.1	1	0.1	0.93624
		0.3	1.10245
		0.5	1.15243

5 Results and Discussions

In this work, we employed the similarity transformation to convert the governing two-dimensional partial differential equations of velocity, temperature and nanoparticles concentration to ordinary differential equations for radiative electrically conducting fluid with viscous dissipation in an impermeable surface. The HAM has been successfully applied to compute the semi-numerical solution under appropriate boundary conditions. Numerical computations of results are demonstrated in Figures 5–22 for velocity, temperature and nanoparticles concentration for various values of Magnetic parameter M, Prandtl number Pr, heat source/sink parameter A, Eckert number Ec, Deborah number β, ratio of relaxation to retardation time parameter λ, radiation parameter R_d, Brownian motion parameter N_b, thermophoresis parameter N_t and Lewis number Le. Fig.5 exhibits the variation in velocity f′(η) for different values of magnetic parameter M. It has been shown that the increase in magnetic field parameter M reduces the velocity. As M increases, a resistive force like a drag force is produced, which is called a Lorentz force. The Lorentz force retards the force on the velocity which slows down its motion. Therefore the velocity decreases with the increase of magnetic field parameter M. In Figure 6, a similar behavior on the velocity profile for different values of λ can be noticed. Since for the larger value of λ the boundary layer thickness is decreases which affect the motion of the fluid within the boundary layer region. Thus increases of λ, the velocity decreases. Similarly in Fig. 7 for various values of Deborah number β, the velocity profile f′ is observed. Since Deborah number β is proportional to λ, therefore with increases of β, velocity decreases. In Fig. 8, effects of Thermophoresis parameter Nt with temperature profile is observed. It has been seen that with an increase of Nt, the temperature is also increases. This is due to the fact that the larger values of thermophoresis parameter Nt, produces the enhancement in the thermophoresis force which tends to move the nanoparticles from hot surface to cold one. Therefore the heat transfer is increases in boundary layer region for nanoparticles. In Fig. 9, effects of Brownian motion parameter Nb with temperature profile is analyzed. It has been noticed that as Brownian motion parameter Nb increases, the mass diffusivity increases which leads to the increases of the temperature profile in the boundary layer region. In Fig. 10, it is analyzed that the temperature is decreases with increase the Lewis number Le. This is due to the fact that Le number contains the Brownian diffusivity coefficient D_B which associates with the Brownian motion parameter Nb. Since the enhancement in Lewis number, decreases the thermal diffusivity of the boundary layer thickness causes to slow down the velocity in the boundary layer region. Fig. 11 represents the effects of Prandtl number Pr to temperature. It has been seen that the increases of Pr decreases the thermal boundary layer thickness, which lower the temperature within the boundary layer region. In Fig. 12, it is observed that the temperature profile is increases with increases of radiation parameter Rd. This is due to the fact that the larger value of radiation parameter Rd provided more heat to working fluid within the boundary layer region and is related to boundary layer thickness. Fig. 13 shows the variation in temperature for different values of magnetic parameter M. It has been concluded that the temperature increases with increases of M. This is due to the fact that magnetic parameter involves Lorentz force, higher magnetic field parameter involves the stronger Lorentz force leads to an enhancement in the temperature. In Figs (14) and (15), the variation of temperature θ (η) with respect to heat source/ sink parameter has been plotted. It shows that the temperature is increase with heat source parameter (A > 0) and decreases with heat sink parameter (A < 0) because the thermal boundary layer generates the energy and this causes the temperature in the thermal boundary layer increases with increases in A (for heat source) and decreases with decreases in A (for heat sink). Fig. 16 shows the effect of Eckert number on temperature. It has been observed that the temperature increases with increase of Ec. Larger value of Ec enhanced the heat in fluid flow within the boundary layer region. Fig. 17 represents the φ(η) for various value of Nb. It has been noticed that the concentration of boundary layer thickness decreases with increase of Nb. In Fig. 18 effects of nanoparticles concentration with thermophoresis parameter Nt is plotted. It has been visualized that the concentration profile increases with increase of Nt. This is due to fact that the larger value of Nt increases the thermophoresis force in the boundary layer region which leads to the higher nanoparticles concentration. In Fig. 19 the effects of Lewis number with nanoparticles concentration profile has been plotted. It shows that the larger values of Lewis number Le causes a reduction in the nanoparticles concentration. Therefore the nanoparticles concentration profile is decreases with increases of Le. The similar effect was found in Fig. 20 with Prandtl number Pr. In Fig. 21 we analyzed that the nanoparticles concentration profile is decreases with increase in heat source parameter. This is due to the fact that an increasing the heat source in the thermal boundary layers generates the energy in the boundary layer thickness and decrease the nanoparticles concentration. Fig. 22 shows the effect of Eckert number in nanoparticles concentration profile. It has been observed that the nanoparticles concentration profile is increases with increase of Ec, as larger value of Ec enhanced the heat in fluid flow within the boundary layer region. Also a comparative study has been made in Table 3 with HAM (present results) with previously published results.

Fig. 5

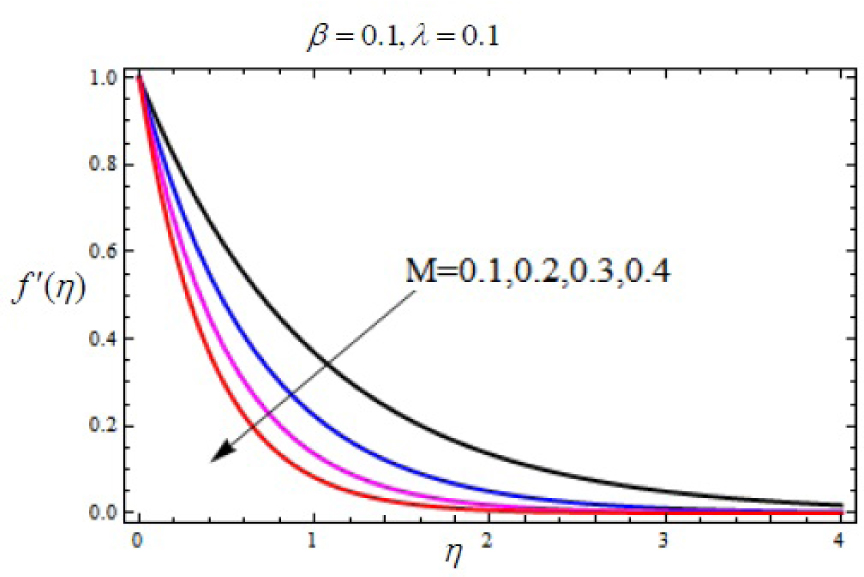
Variation of velocity f′(η) with η for several values of Magnetic parameter M.

Fig. 6

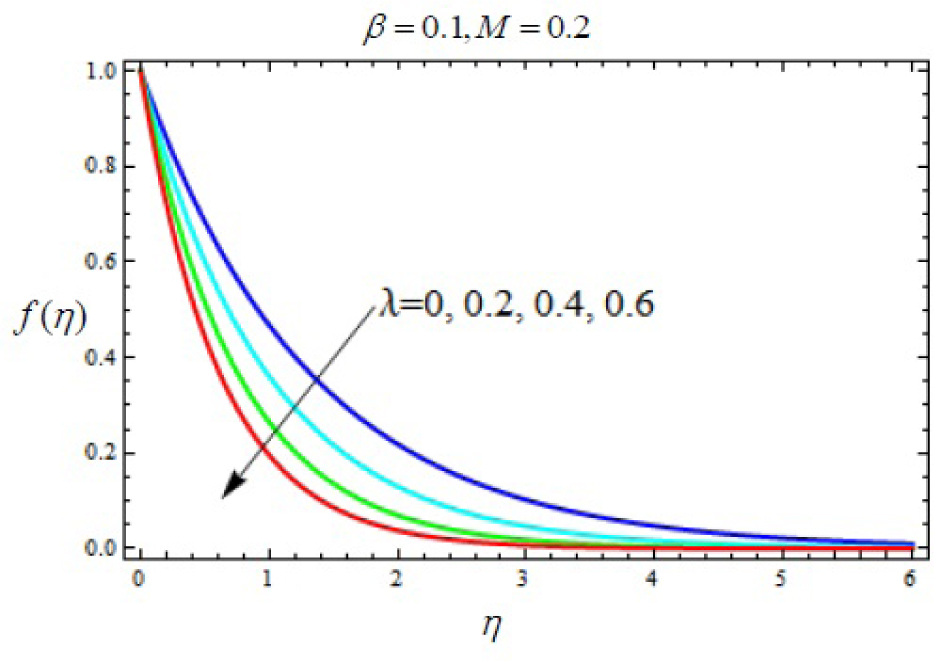
Variation of velocity f′(η) with η for several values of relaxation ratio parameter λ

Fig. 7

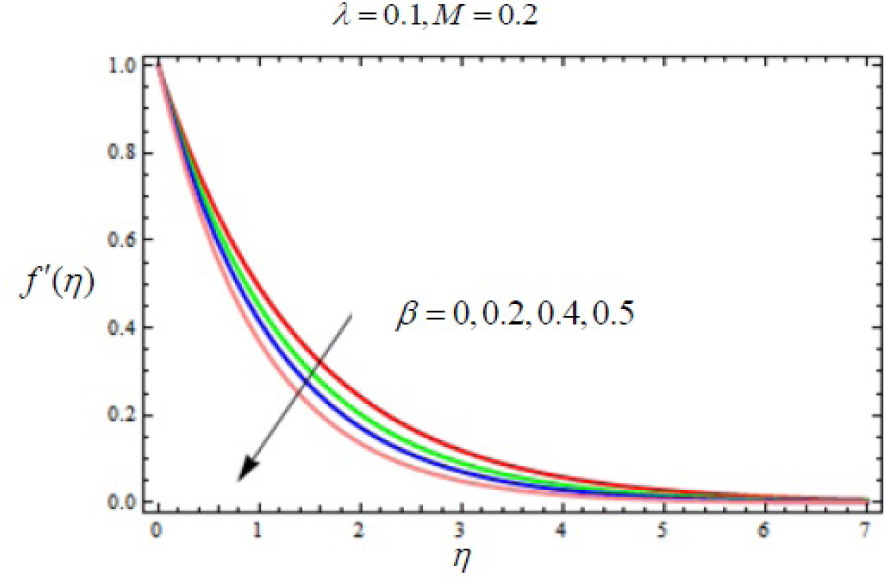
Variation of velocity f′(η) with η for several values of Deborah number λ.

Fig. 8

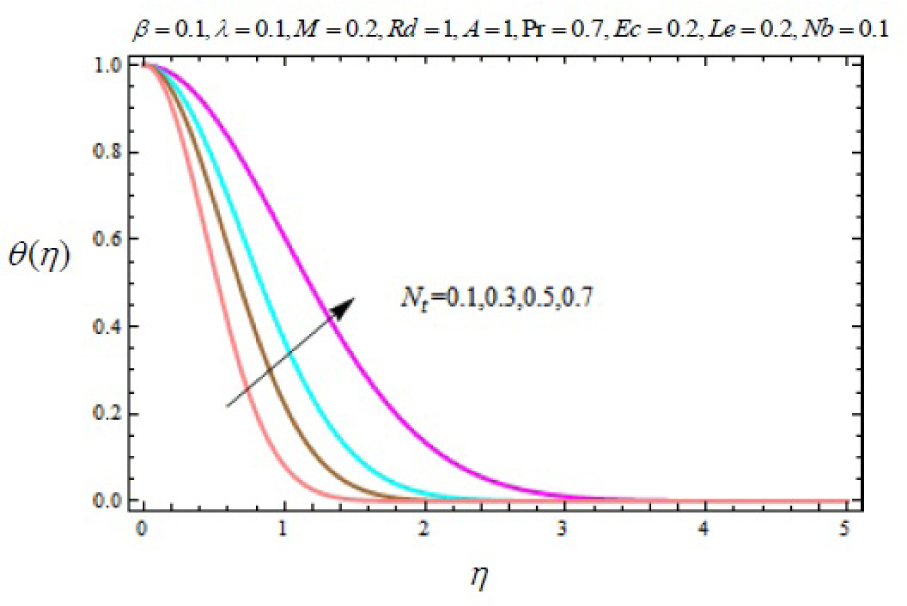
Variation of temperature profile θ (η) with η for several values of thermophoresis parameter N_t.

Fig. 9

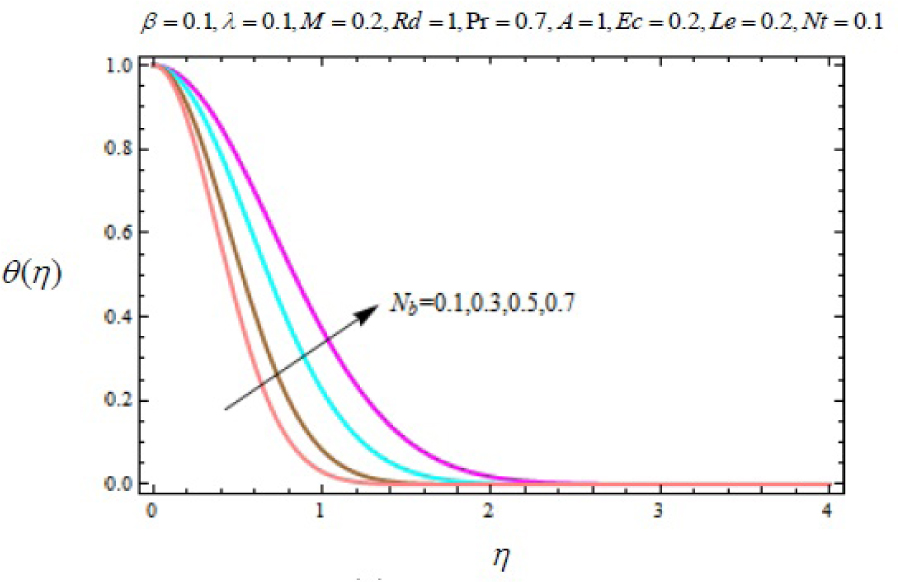
Variation of temperature profile θ (η) with η for several values of Brownian motion parameter N_b.

Fig. 10

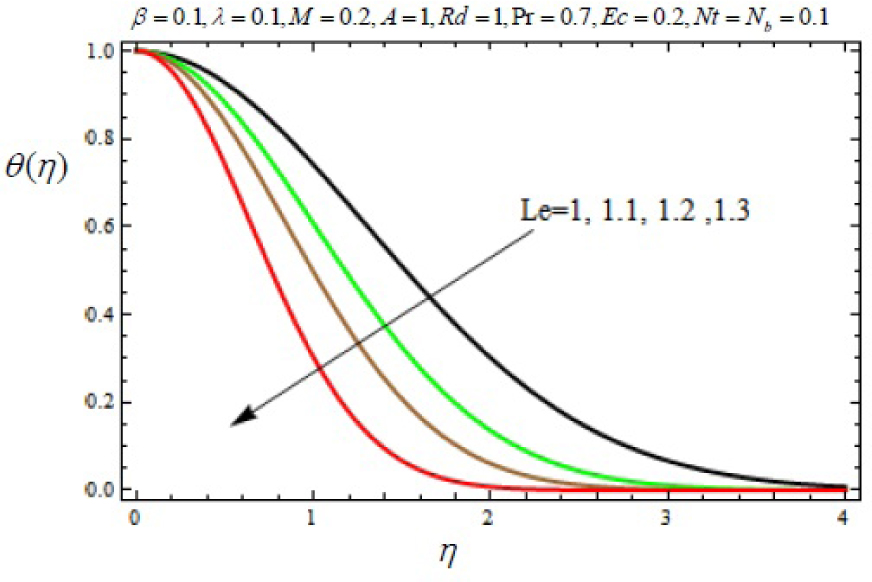
Variation of temperature profile θ (η) with η for several values of Lewis number Le.

Fig. 11

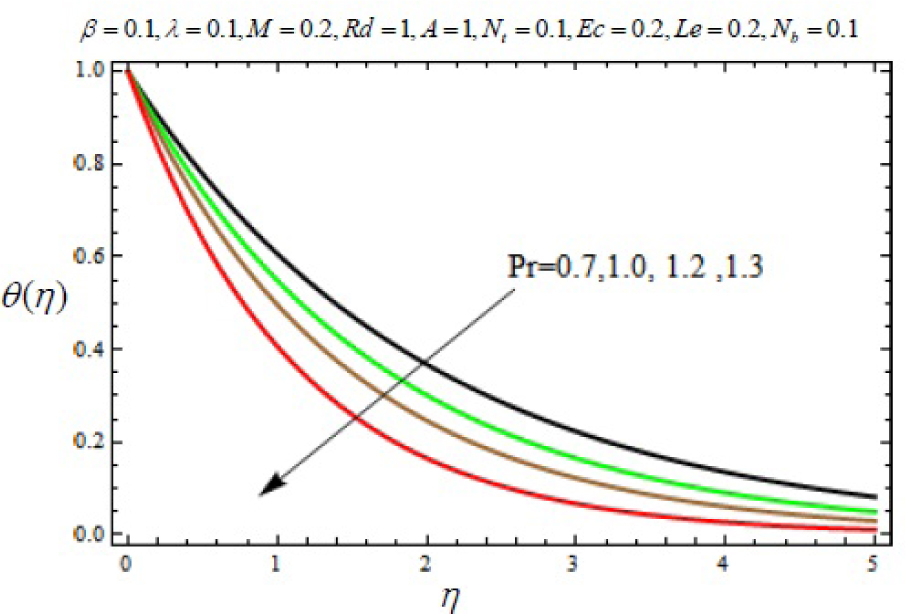
Variation of temperature profile θ (η) with η for several values of Prandtl number parameter Pr.

Fig. 12

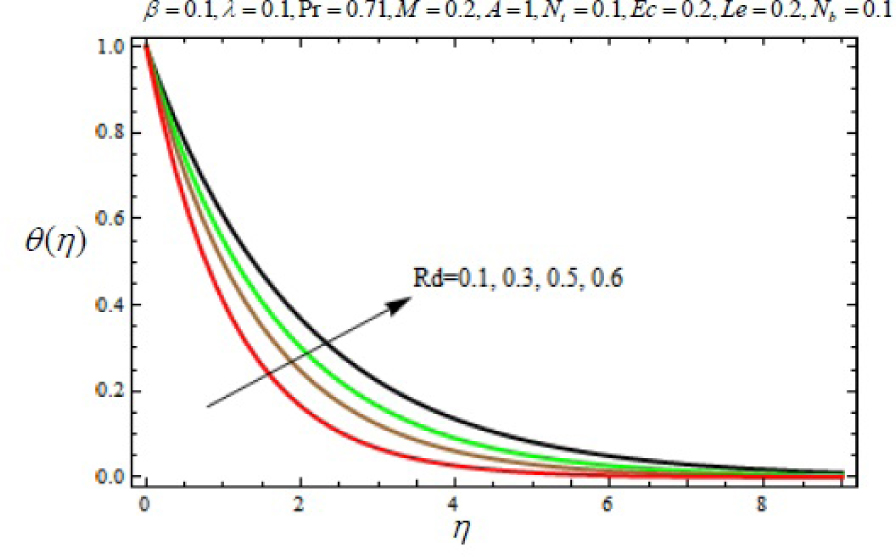
Variation of temperature profile θ (η) with η for several values of radiation parameter R_d.

Fig. 13

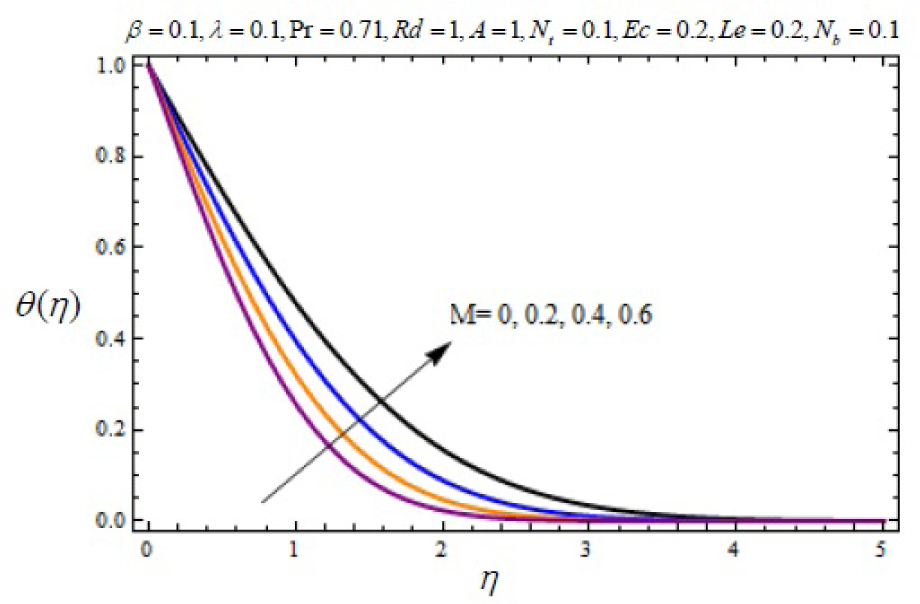
Variation of temperature profile θ (η) with η for several values of magnetic parameter M.

Fig. 14

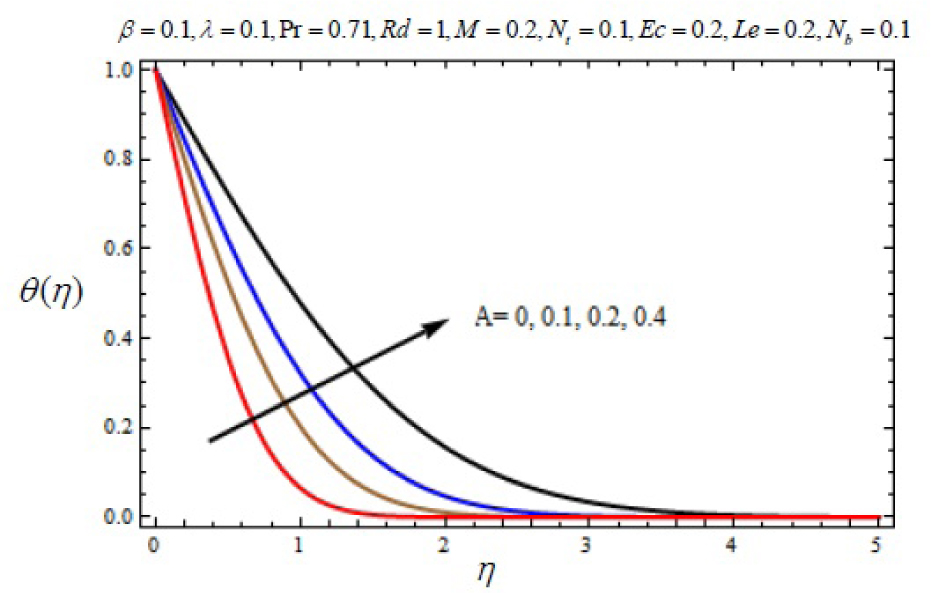
Variation of temperature profile θ (η) with η for several values of heat source parameter A > 0.

Fig. 15

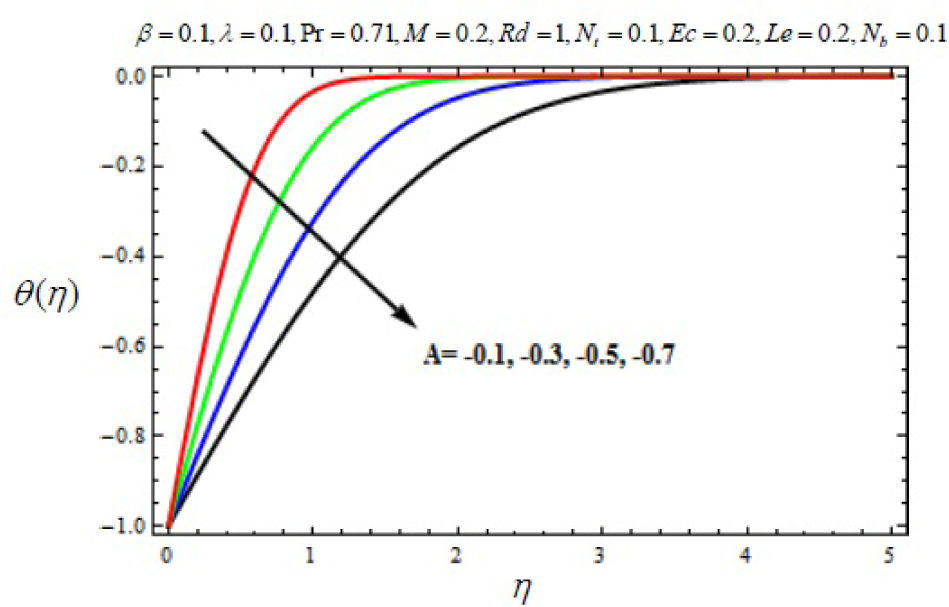
Variation of temperature profile θ (η) with η for several values of heat sink parameter A < 0.

Fig. 16

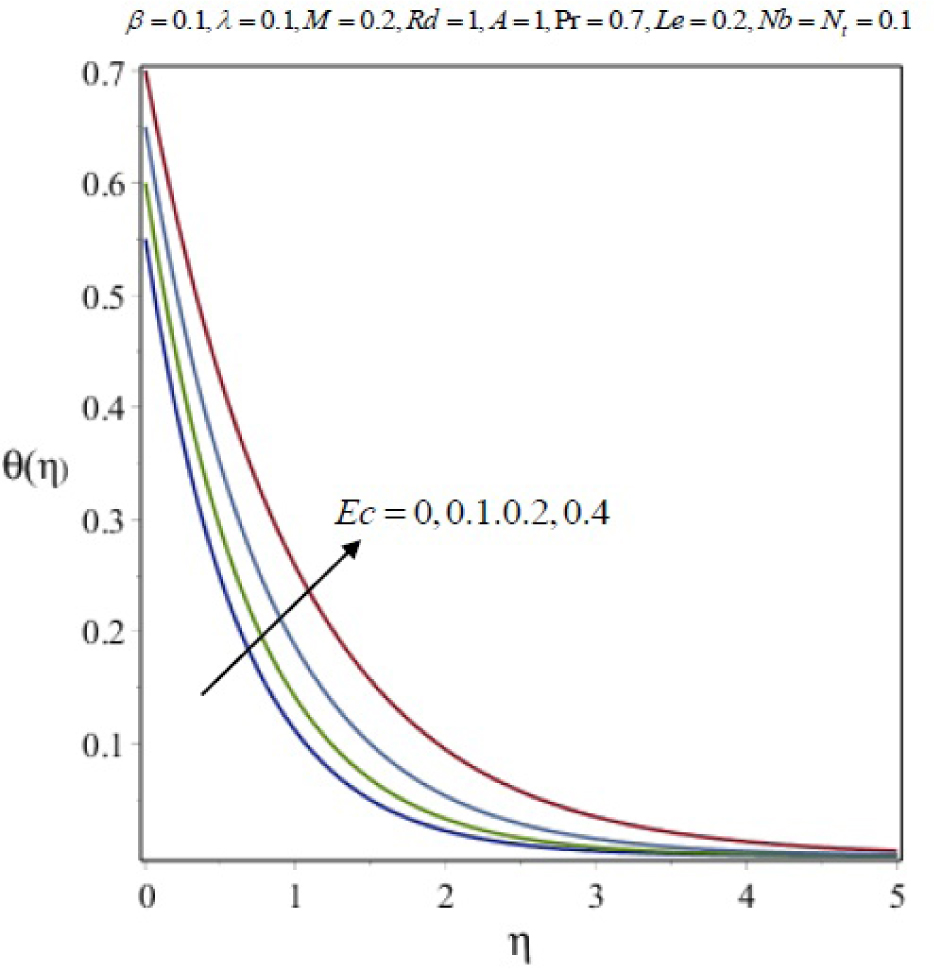
Variation of temperature profile θ (η) with η for several values of Eckert number Ec.

Fig. 17

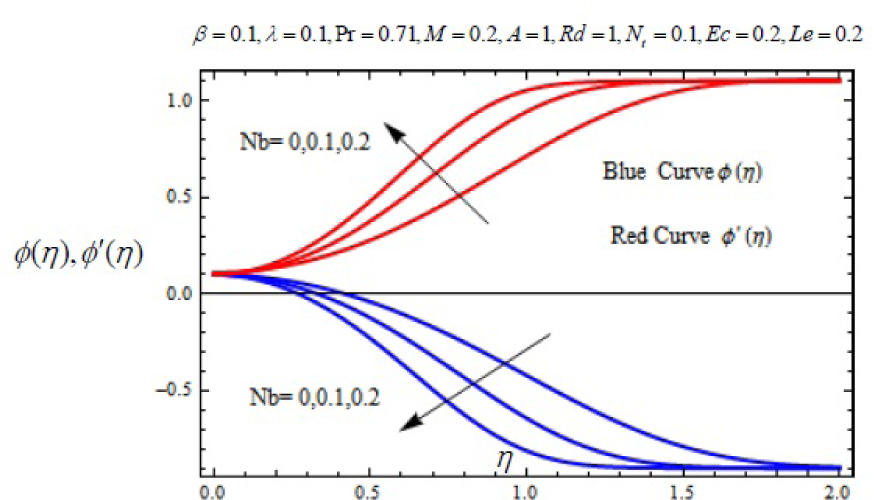
Variation ϕ(η) ϕ′ (η) with η for several values of Brownian motion parameter N_b.

Fig. 18

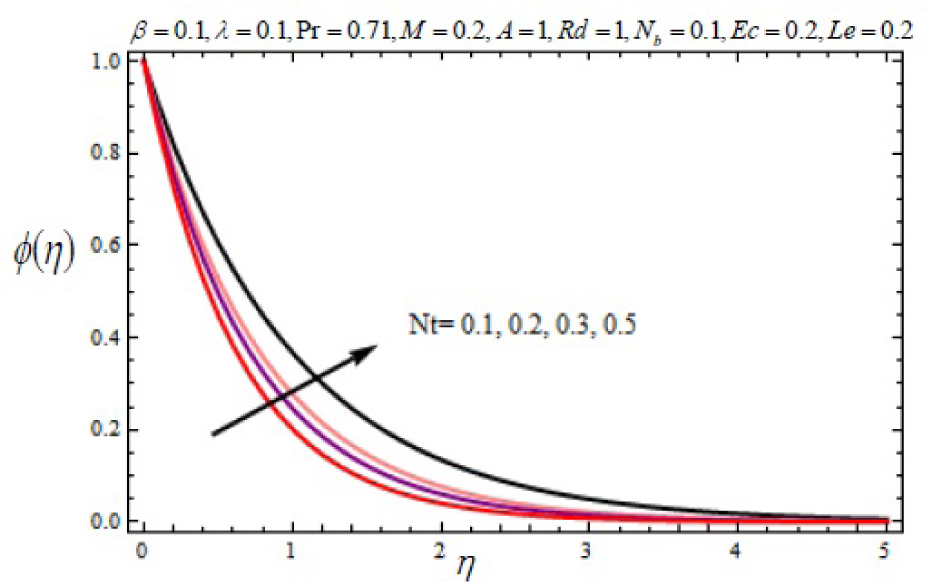
Variation of nanoparticle concentration with η for several values of thermophoresis parameter N_t.

Fig. 19

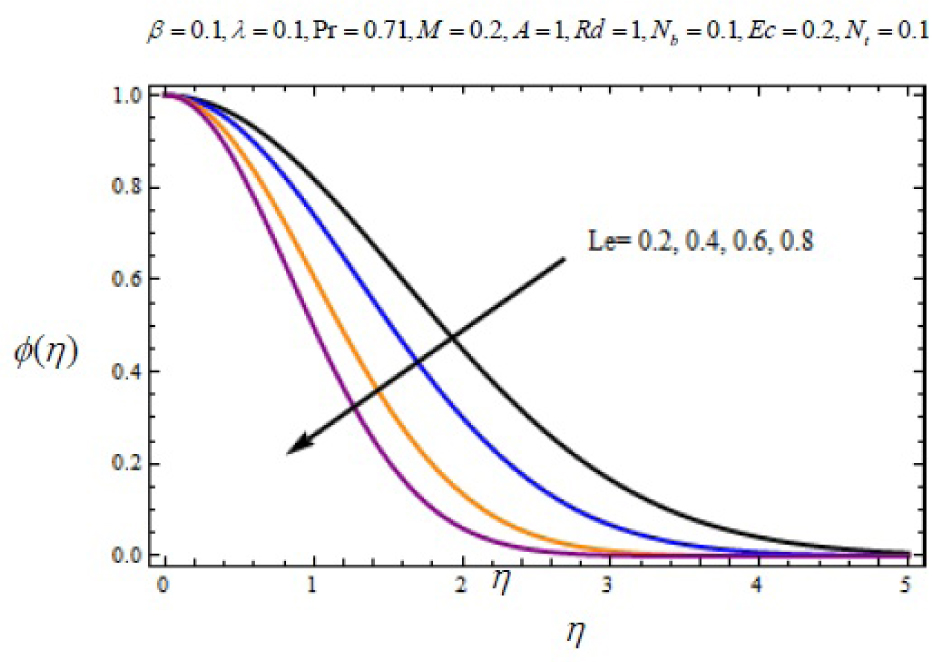
Variation of nanoparticle concentration with η for several values of Lewis number Le.

Fig. 20

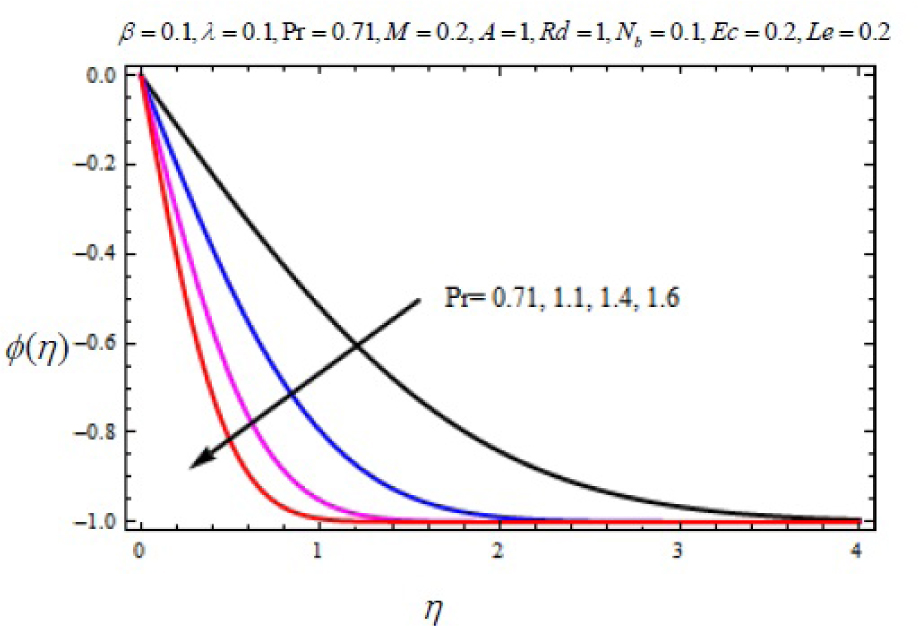
Variation of nanoparticle concentration with η for several values of Prandtl number Pr.

Fig. 21

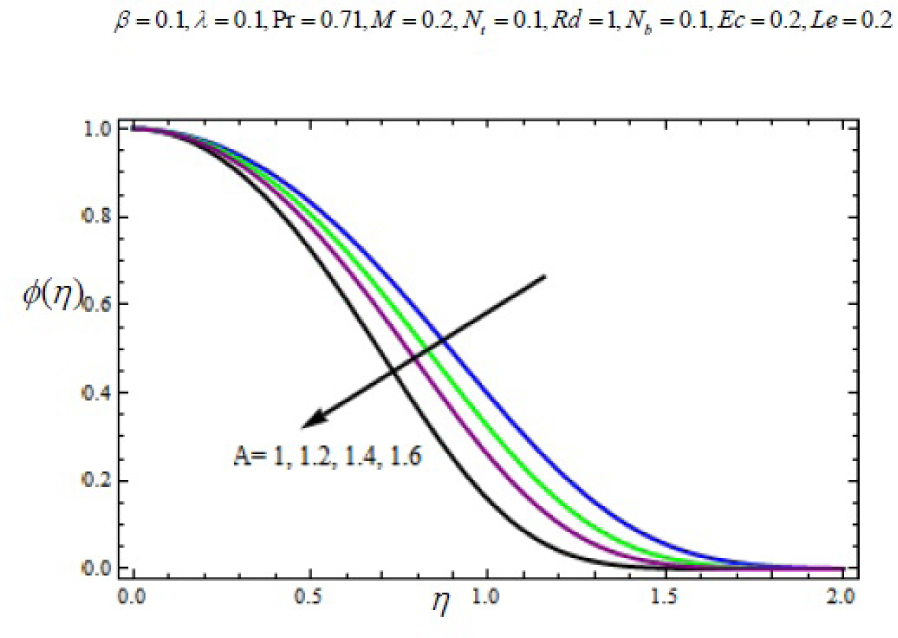
Variation of nanoparticle concentration with η for several values of Heat parameter A.

Fig. 22

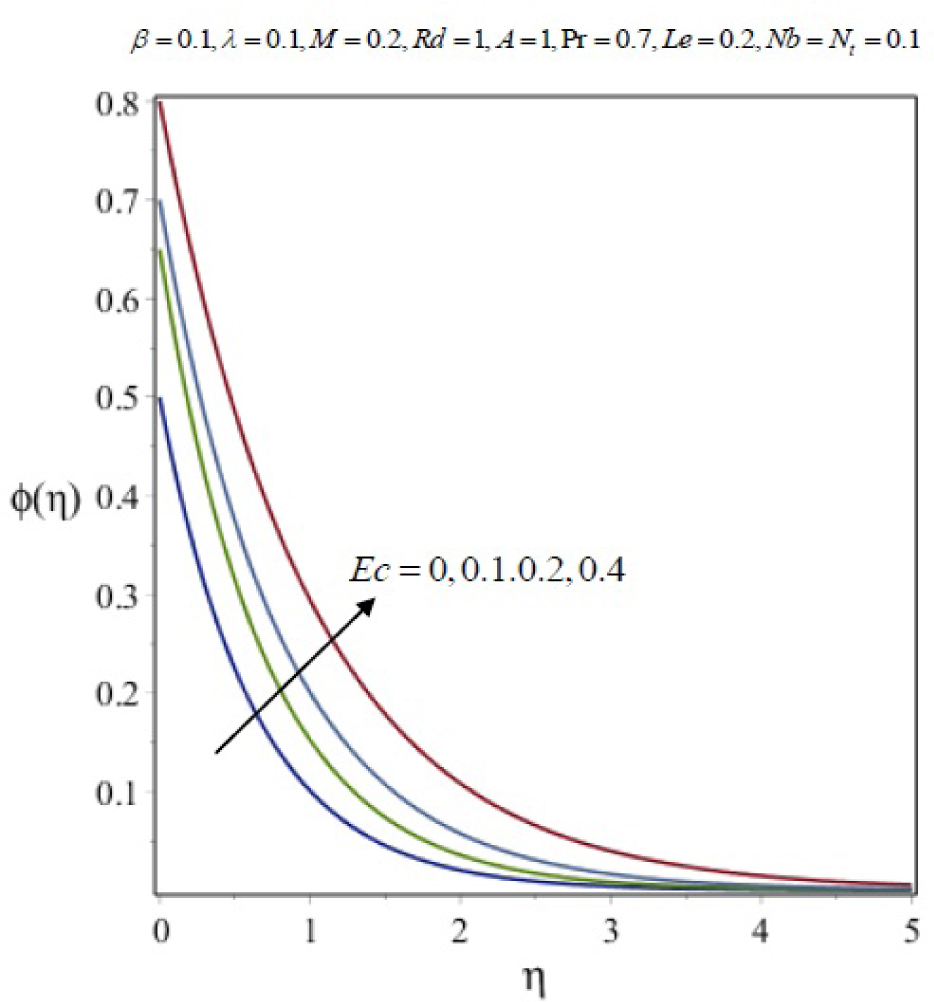
Variation of nanoparticle concentration with η for several values of Eckert Number Ec.

6 Concluding Remarks

In this study, the homotopy analysis method (HAM) has been successfully applied to evaluate the effects of magnetic parameter, Prandtl number, Eckert number, Brownian motion parameter, thermophoresis parameter, Lewis number and radiation parameter on the flow of an incompressible Jeffrey nanofluid over an impermeable stretching sheet. The effects of these physical parameters on the velocity, temperature and nanoparticles concentration are shown by graphs. Also a comparative study between the present analytical technique and known results is being presented in tabular form. It has been analyzed that the HAM contains an auxiliary parameter ℏ which can adjust and control the convergence region of the solution to a great extent and freely to choose any base function (exponential, algebraic, polynomials, logarithmic, trigonometrically etc.) are fully agreements with HAM. On the basis of present analyses the main outlines are listed below:

1. Flow velocity decreases with increase of β, M and λ.

2. Temperature increases with increase of N_b and N_t but decreases with the effects of Le and Pr.

3. For larger values of R_d and M leads to an enhancement in the temperature.

4. Temperature increases with heat source parameterA > 0 and decreases with heat sink parameter A < 0.

5. Nanoparticles concentration decreases with increases of N_b while it increases with increase of N_t.

6. Nanoparticles concentration profile is decrease with effects of Le,Pr and A..

7. Temperature and nanoparticles concentration is increases with increase of Eckert number Ec.