The influence of shot noise on the performance of phase singularity-based refractometric sensors

2.1 Basic principles of phase singularity-based sensors

We begin by outlining of the basic principles underlying the topological phase singularity-based sensing. Essentially, the refractometric sensor is represented by a linear reflecting structure covered with an optically thick water solution of the sensing medium (analyte), Figure 1a. A change in the concentration of the sensing medium induces a variation of the analyte refractive index, which in turn causes a change of the reflection intensity that can be detected. The idea of the ellipsometry-assisted sensing, in contrast to the common surface plasmon–polariton schemes, is to monitor the changes in the ratio of reflected s- and p-polarized waves ρ = r _p /r _s , which can be routinely assessed with spectroscopic ellipsometry [41], [45], [46].

Figure 1:

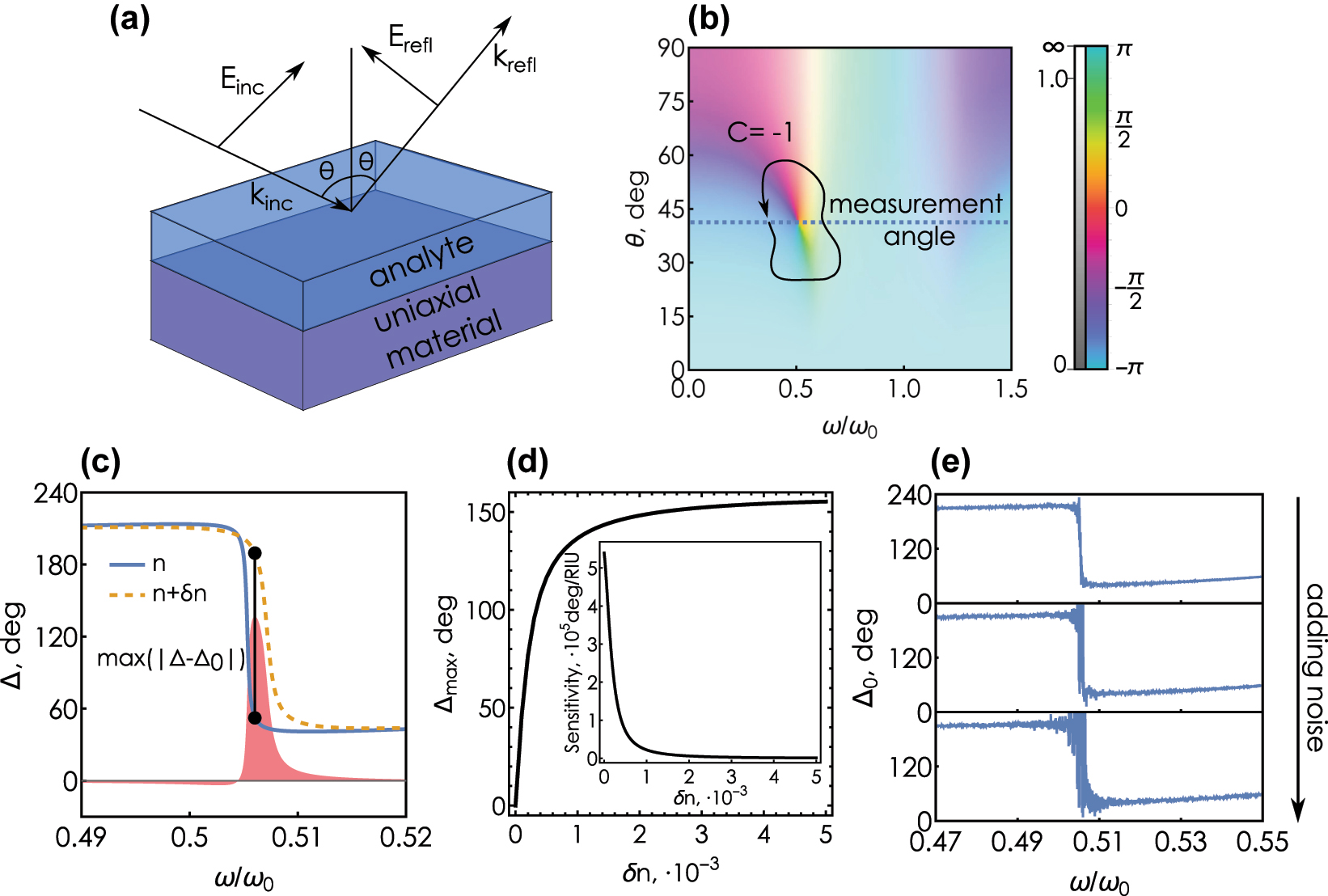
Basic picture of of phase singularity sensing. (a) Sketch of the refractometric sensor under study: a uniaxial absorbing material covered with an optically thick layer of analyte. The system is illuminated with a combination of s- and p-polarized waves; the amplitude and the phase of the reflected wave is read out using spectroscopic ellipsometry. (b) Plot of the complex-valued ellipsometric response function ρ = r _p /r _s for the system in (a) calculated for water reference solution, n = 1.33, and the uniaxial material is characterized by ɛ _∞ = 1, f = 0.5, γ = 0.1, ɛ _‖ = 1.5 + 0.1i. The color saturation encodes the magnitude of the ellipsometric response, the hue encodes the argument (see the colorbar on the right). (c) Frequency dependence of the ellipsometric phase of the reference solution (n = 1.33), and the analyte refractive index n = 1.33 + δn, δn = 0.001, calculated at an incidence angle slightly away from the phase singularity θ = θ _PS + δθ, δθ = −0.05°. The shaded area shows the difference Δ − Δ₀; the black line corresponds to the maximal difference of |Δ − Δ₀|. (d) Maximum shift of the ellipsometric phase Δ_max as a function of the analyte refractive index shift δn. Inset: sensitivity S = ∂Δ_max/∂δn as a function of δn. (e) The influence of noise on the optical phase near the PS according to the model, Eq. (7).

In our study we examine a system consisting of an anisotropic absorbing substrate and an optically thick water solution of the sensing medium with refractive index n, placed on it, Figure 1a. Optical anisotropy of the substrate will play the crucial role in the behavior of the ellipsometric response ρ. As a model of the anisotropic substrate we consider a uniaxial absorbing crystal with the optical axis perpendicular to the interface. The in-plane permittivity ɛ _xx = ɛ _yy ≡ɛ _⊥ is described by the Lorentz model:

where ɛ _∞ is the high-frequency permittivity, f is the oscillator strength of the resonant transition of the medium, ω ₀ is its resonant frequency, and γ describes its non-radiative decay rate. The permittivity along the optical axis is a complex-valued constant, ɛ _zz ≡ɛ _‖ = const.

The substrate–analyte interface is illuminated by a linearly polarized plane wave incident at an angle θ, Figure 1a. Since in real experiments the thickness of the analyte substantially exceeds the coherence length of optical radiation, reflection from the analyte–substrate interface can be considered as reflection at the interface of two semi-infinite media and described by Fresnel formulas for s- and p-polarized wave:

where k z = ω / c n 2 − sin 2 ⁡ θ is the z-component of the wave vector in the analyte, k z ( o ) = ω / c ε ⊥ ( ω ) − sin 2 ⁡ θ and k z ( e ) = ω / c ε ⊥ ( ω ) / ε ‖ ε ‖ − sin 2 ⁡ θ are the z-components of the wave vectors of the s- and p-polarized (ordinary, (o), and extraordinary, (e)) transmitted waves in the uniaxial medium. Reflection of the incident wave at the air-analyte interface slightly reduces the intensity of the transmitted wave, but barely affects the ellipsometry measurements, as demonstrated in a previous work [46].

As shown previously, a semi-infinite absorbing uniaxial crystal may exhibit points of zero reflection for p-polarized excitation [43], [57] (see Supplementary Material, Figure S1). Owing to the point of zero reflection, the ellipsometric response ρ exhibits a phase singularity at a point {ω _PS , θ _PS } of the frequency-incidence angle space {ω, θ}, where the ellipsometric phase Δ = arg  ρ becomes undetermined, Figure 1b. Furthermore, the non-zero roundtrip of the argument around the singularity, Figure 1b, gives it a conserved integer winding number:

where the integration contour encloses the singularity. This winding number renders the singularity topologically protected against small perturbations of the system [46]. By the same token, the very presence of this topological point guarantees that the response function of interest (such as the ellipsometric phase ρ) does necessarily reach either zero (r _p = 0) or a pole (r _s = 0) at some point of the parameter space inside the loop encircling the singularity.

At a fixed incidence angle close to θ _PS the argument of complex-valued ρ demonstrates a rapid variation in a narrow frequency range in the vicinity of the singularity. This implies that a weak change of the optical environment (e.g., the analyte index) may lead to a substantial change of the response function argument, Figure 1c. The core idea of the topological singularity-based sensor is thus to take advantage of this rapid variation of the ellipsometric phase near the point of zero reflection of p-polarized wave.

In order to detect a change of the analyte refractive index, one (i) measures the ellipsometric phase Δ(ω) near the phase jump, and (ii) calculates the difference between the measured values and the initial calibration curve Δ₀(ω) corresponding to the analyte refractive index, Figure 1c. Next, we create the correspondence between the known refractive index shift of the analyte δn and the maximum absolute deviation of the ellipsometric phase max(|Δ(ω) − Δ₀(ω)|) over a range of frequencies:

where the range ω _min to ω _max is determined by the experimental limitations. For this study we chose ω _min = 0.49 ω ₀ and ω _max = 0.52 ω ₀ (ω _PS ≈ 0.505 ω ₀). This correspondence allows us to determine δn given an experimentally measured value of Δ_max, as Figure 1d demonstrates. Tangent of the curve locally determines the sensitivity S of the system to the changes of the analyte index:

One could naively incorporate noises in this model by adding a randomly distributed noise term to the real and imaginary parts of s- and p-polarized reflection amplitudes:

where δ _i is a randomly distributed noise-induced quantity added to the real and imaginary parts of the corresponding amplitude. Close to zero of r _p the numerator of (6) behaves as δ ₁ + iδ ₂; as long as r _s does not approach zero, the denominator behaves as r _s in the limit of weak noise. Thus, the whole expression can be approximated as:

As expected, the argument of the remaining noise term produces a highly distorted magnitude of Δ close to the phase singularity, Figure 1e. In reality, however, incorporating noise sources into the ellipsometric scheme is a more non-trivial problem compared to the naive approach. In the following sections, we describe in more details the process of acquisition of phase information in ellipsometry and develop a theoretical model that accurately accounts for the presence of shot noise in a realistic measurement.

2.2 Phase measurement in ellipsometry

To offer a more accurate picture of the noise mechanism arising in a sensing experiment, we first briefly discuss the key steps of ellipsometric spectroscopy, schematically illustrated in Figure 2a. The end goal of ellipsometry is obtaining ρ = r _p /r _s ≡ tan Ψ exp(iΔ), where.

is the parameterization of the response function magnitude, and

is the ellipsometric phase. These quantities are assessed in the following fashion. An unpolarized light from a lamp source passes through a monochromator and next through a polarizer set at an angle θ _P , thus becoming linearly polarized and acquiring both s and p components with respect to the substrate. In the following calculations we set θ _P to π/4, such that transmitted light has equally weighted s and p-polarized components. After reflection from the substrate, the wave passes through an analyzer with a rotating axis characterized by the angle θ _A . Power of the signal reaching the detector reads:

where P ₀ is the power of the lamp source, and α and β are expressed via the desired ellipsometric parameters:

Figure 2:

Ellipsometry basics. (a) The principal scheme of spectroscopic ellipsometry measurement process. An unpolarized quasi-monochromatic light from the source passes through a polarizer, reflects off of the interrogated substrate, passes through an analyzer and gets recorded at the detector. (b) Recorded power P _D at the phase singularity frequency ω = ω _PS for different incidence angles: θ = θ _PS and θ = θ _PS + δθ, where δθ is set to be δθ = −2°. (c) The ellipsometric phase behavior near ω = ω _PS for the same incidence angles as in (b).

The detector records the signal for different analyzer angles. Figure 2b shows an example of detected signal as a function of the analyzer angle. Applying the Fourier transform to this data allows one to determine the coefficients α and β in Eq. (6), which in turns allows us to calculate the desired ellipsometric magnitude and phase:

The choice of the incidence angle profoundly affects the initial calibration curve Δ₀(ω). As can be seen from Figure 2b and c, a deviation of the incidence angle from the exact phase singularity θ _PS only slightly alters the power P _D , but that leads to a noticeable change of the calibration curve. Indeed, the signal power at each analyzer position characterizes the amplitude of the complex response function, which is a continuous value in the vicinity of the singularity and changes weakly with a small change in parameters such as the incidence angle. On the contrary, the phase is determined by a set of measurements for all analyzer positions and its change becomes noticeable near the topological point, upon approaching which the phase change becomes very rapid. As we will see in the following, the choice of the calibration curve profoundly affects the trade-off between the sensitivity and the resolution of the ellipsometry-assisted refractometric sensor.

2.3 Noise model

Next we develop an analytical model of noise that can be adopted for modeling the refractometric sensing process, illustrated in Figure 3a. Assume the detector is subject to an incoming photon stream reflected from the substrate with constant power P _D given by Eq. (10). Since photoelectron excitation is a probabilistic process, the number of recorded counts varies. This variation of the detected photon counts is the manifestation of shot noise [51]. The process of counting photoelectrons is described by the probability density p(n, τ) that describes the probability of recording n photoelectrons during the measurement time interval τ.

Figure 3:

Shot noise model. (a) Probabilistic registration of photoelectrons: incoming photon flux in each time interval δτ can excite a photoelectron with probability p ₀, which results in n detected photoelectrons during the entire measurement interval. (b) Probability density of recording n photoelectrons over a finite period time τ having a Poisson distribution for different expected values ⟨N ₁⟩ < ⟨N ₂⟩ < ⟨N ₃⟩. (c) Signal recorded by the detector near the singularity as a function of the analyzer angle θ _A in the presence of shot noise (blue dots). Red curve in the inset shows the signal behavior of the ideal noise-free model.

To determine the probability density p(n, τ), following [58] we divide the measurement interval τ into M infinitesimal intervals δt = τ/M, such that in each interval it is possible to register at most one photoelectron with elementary probability p ₀ = ηP _D δt/(ℏω) where ℏω is the photon energy and η is the detector quantum efficiency. Probability of recording n photoelectrons during the whole measurement interval τ is determined by the statistics of M independent events and is described by the binomial distribution:

In the limit δt → 0, M → ∞ this approaches the Poisson distribution (Figure 3b):

where the expected number ⟨N⟩ of registered photon counts reads:

The probabilistic distribution of detected photoelectrons leads to the variation of the signal recorded by the detector as a function of the analyzer angle, Figure 3c. The relative uncertainty of these variations is particularly noticeable around θ _A = πn, where the analyzer passes only (vanishingly small due to phase singularity) p-polarized component of the reflected field. This large relative uncertainty ∝ 1 / ⟨ N ⟩ is a natural property of a Poisson-distributed variable with low expected value. However, this uncertainty rapidly vanishes as the incidence angle gets detuned from the angle of phase singularity.

This noise in the number of detected photoelectrons leads to uncertainties in determining the Fourier coefficients α and β, Eq. (11), which in turn determine the magnitude tan Ψ and the sought for ellipsometric phase Δ. However, as we will see in the following, it is performing the ensemble of measurements for different analyzer angles that enables stable evaluation of the analyte index despite the seeming issue of absent photon flux at the phase singularity.

2.4 The effect of noise in the experiment simulation

To render the combined numerical-theoretical simulations more realistic and to grasp the scale of the physical parameters where the influence of noise becomes significant, we will set the numerical values of the quantities characterizing the actual experiment. A lamp with a monochromator is used as a quasi-monochromatic light source. In simulations, we consider the typical range of spectral power densities P ranging from 1 μW/nm to 100 μW/nm at the wavelength of the phase singularity λ _PS = 600 nm. The monochromator filters out a narrow wavelength band from the entire spectrum of bandwidth Δλ = 5 nm centered at a given wavelength.

Now we are in a position to analyze the influence of the spectral power and the incidence angle on the performance of the ellipsometry-based refractometric sensing close to the phase singularity point. To that end we run a set of numerical “experiments” characterized by different spectral powers and incidence angles and fixed measurement interval τ = 0.2 s, Figure 4. For each combination of incident power and incidence angle we run the simulation repeatedly many times (in our calculations, the number of repetitions is 500). For each δn, we obtain a set of values of the maximum ellipsometric phase shift Δ_max, for which we can calculate the mean ⟨Δ_max⟩ and standard deviation σ _Δ (see Supplementary Material, Figures S2 and S3). Notably, the mean measured value ⟨Δ_max⟩ deviates substantially from the etalon phase shift Δ m a x ( 0 ) obtained in the noise-free model, ⟨ Δ m a x ⟩ ≠ Δ m a x ( 0 ) , see Supplementary Material, Figure S2.

Figure 4:

The effect of shot noise on refractometric sensing. Behavior of noisy sensitivity with increasing spectral power P (from left to right) and increasing deviation |δθ| of the incidence angle θ = θ _PS + δθ from the angle of phase singularity θ _PS (from top to bottom). Each dot represents the result of a single simulated experiment. The gray area represents the corridor of values into which each point falls with a probability of 95 %. The red curve shows the ideal phase shift Δ_max obtained in the noise-free model. Inset: example of distribution of Δ_max for δn = 4 ⋅ 10⁻⁴ (vertical gray line) obtained from a numerical simulation of the experiment for P = 1 μW/nm and |δθ| = 0.05° in comparison with the normal distribution (red curve).

As we find from our numerical simulations, the probability distribution of Δ_max for each δn follows the normal distribution with a reasonable accuracy (see Supplementary Material, Figures S4–S9). The mean values and standard deviations can be approximated by smooth curves that are functions of the analyte medium refractive index shift δn and characterize the impact of shot noise on the measurement. This approximation allows us to visualize for each δn an interval ⟨ Δ m a x ⟩ ± σ ̃ Δ , where a simulated “measurement” falls with a probability of 95 % (shaded regions in Figure 4) with σ ̃ Δ = 2 σ Δ erf − 1 ( 0.95 ) and erf⁻¹(x) being the inverse of the error function. Figure 4 clearly demonstrates that this distribution interval characterizing the influence of shot noise can be reduced either by increasing the source spectral density P, which is limited in the experiment, or by shifting the incidence angle away from the phase singularity value θ _PS .

Interestingly, the authors of the pioneering work on phase singularity-assisted sensing [36] also detuned the incidence angle from the zero reflection point to ensure sufficient light intensity reaching the detector at the resonant minimum. However, the effect of angular detuning was not analyzed in details.

This observation allows one to use a phase singularity-based sensor even with a low-power optical source. However, deviating the incidence angle away from the singularity to achieve the required accuracy comes at the cost of reduced sensitivity. Figure 5b shows the behavior of the sensitivity S (see Eq. (4)) on δn for a few different values of the incidence angles close to the phase singularity. Deviating the incidence angle away from θ _PS results in a smoother sensitivity behavior. At the same time, in the region of weak variation of the analyte refractive index (δn < 3 ⋅ 10⁻⁴), the sensitivity drops from 2 ⋅ 10⁵ deg/RIU to 0.5 ⋅ 10⁵ deg/RIU upon a slight 0.5° deviation of the incidence angle.

Figure 5:

The trade-off of sensitivity and resolution in the ellipsometry-based sensor. (a) Incidence angles θ = θ _PS + δθ characterized by different deviations |δθ| from the angle θ _PS and defining calibration curves. The color saturation encodes the magnitude of the ellipsometric response, the hue encodes the argument. (b) The sensitivity of the sensor as a function of δn for deviation angles corresponding to the incidence angles shown in (a). (c) Graphic definition of the noise-induced resolution res(δn)_shot. (d) The resolution of δn for the incidence angles shown in (a) for a source spectral power P = 1 μW/nm. (e) Same as (d) for P = 10 μW/nm (f) (e) Same as (d) for P = 100 μW/nm.

Next, we study the effect of the incidence angle and the source power on the resolution of the refractometric sensor. We define the shot noise-limited resolution res(δn)_shot for a given measured value ⟨Δ_max⟩ as the width of the region bounded by the curves ⟨Δ_max⟩± σ _Δ, Figure 5c. Figure 5d–f show the behavior of the noise-limited resolution at different incidence angles and source spectral powers. Expectedly, increasing the source power improves the noise-limited resolution for any incidence angle. Increasing the deviation angle for a fixed power improves the resolution from ∼ 2 ⋅ 1 0 − 4 to ∼ 5 ⋅ 1 0 − 5 even at extremely low source powers of P = 1 μW/nm. In addition, improving the resolution by increasing |δθ| (and not the power) can be more effective, as shown by the curves corresponding to |δθ| = 0.05°; with an increase in power by two orders of magnitude, the resolution remains relatively crude ( ∼ 1 0 − 4 ) . As a result, one can substantially increase the sensor robustness by a slight change of the incidence angle without upgrading the light source to high-power version.

As a final step of our analysis, we note that sensitivity imposes another potential constraint on the resolution of our system even in the absence of shot noises. As a rule of thumb, an ellipsometer can reliably detect an ellipsometric phase shift Δ_max ≳ 1° [46]. This imposes another constraint on the resolution that can be easily estimated as

with S being the sensitivity of the setup, Eq. (5). As shown above, while increasing |δθ| improves the noise-limited resolution res(δn)_shot, it at the same time reduces the sensitivity. This causes the sensitivity, not the shot noise, to be the decisive factor determining the resolution at relatively large |δθ|. For our model system an increase of |δθ| up to 0.5° significantly reduces the sensitivity and becomes the decisive resolution factor at source powers exceeding P = 10 μW/nm (see Supplementary Material, Figure S10). Nevertheless, even then the sensitivity is sufficient to detect a refractive index variation of ≈ 1 0 − 4 accompanied by the ellipsometric phase shift Δ_max of more than 5°.

Figure 6 illustrates the resulting trade-off between the noise-limited and the sensitivity-limited resolution of our system as a function of the incidence angle for various source powers and analyte index shift. The pair of noise- and sensitivity-limited curves combined exhibit the characteristic “valley” behavior: detuning the incidence angle from the phase singularity improves the noise-limited resolution, until it equalizes with the sensitivity-limited one at the point of optimal resolution. Indeed, as can be observed, a further deviation from the topological point leads to a degradation in resolution due to a decrease in sensor sensitivity. Thus, at the angle at which both contributions become equal, the system exhibits the best resolution and reaches the optimal regime.

Figure 6:

The trade-off of noise- and sensitivity-limited resolutions in the ellipsometry-based sensor. (a) Behavior of the sensor’s noise-limited (solid lines) and sensitivity-limited (dashed line) resolution with the analyte refractive index shift δn = 0.0002 for different source powers. The asterisks indicate the optimal incidence angle at which the sensor exhibits the optimal resolution. (b) Same as (a) for δn = 0.0005. (c) Same as (a) for δn = 0.001.