Capillary-assisted flat-field formation: a platform for advancing nanoparticle tracking analysis in an integrated on-chip optofluidic environment

2.1 Operational principle

The concept of flat-field capillary-assisted NTA (CaNTA) combines the idea of confining NP diffusion to a cylindrical channel with defined external illumination (Figure 1(a)): the idea is that the NPs diffuse inside a capillary and are illuminated by a defined Gaussian beam with a mode field diameter much larger than the diameter of the capillary hole. If the RI of the liquid inside the channel n _mc is matched to that of the material of the cladding n _clad, no modes are formed inside the channel and the NPs experience an almost constant transverse intensity due to the very large extension of the illumination beam (Figure 1(b)).

Figure 1:

Flat-field capillary-assisted nanoparticle tracking analysis (CaNTA). (a) Illustration of the concept. The fluidic channel with gold nanoparticles is filled with a water-DMSO mixture that has a RI matching the cladding of the capillary. The inset shows the spatial distribution of the intensity of the Gaussian beam at the beginning of the capillary, showing an almost flat intensity distribution (the difference between the center and the edge is less than 1 %). (b) Sketch (top view) of the arrangement including the main elements and parameters.

2.2 Simulations

Key to the concept is the use of a defined, freely diffracting Gaussian beam inside a homogenous RI. In the arrangement discussed, this beam is generated by the mode at the end of an optical fiber. In case the RI contrast between core and cladding is sufficiently small, it can be shown that the behavior of the diffracting radiation can be approximated by a Gaussian beam (details in Supplementary Material Eq. (1)). To demonstrate the feasibility of the concept, the intensity distribution along the radial and longitudinal directions is simulated in the following, considering the experimental circumstances (details in Supplementary Material Figures S2 and S3).

The intensity distribution of a Gaussian beam (propagating inside a medium with a RI n _mc = 1.46 (close to the index of silica at visible wavelength), beam waist ω ₀ = 4.2 µm) is almost homogeneous along the radial direction (xy-plane) over the extent of the microchannel diameter considered (D _mc = 4 µm) if the distance between the delivery fiber and the NTA measurement area (z _a = 1 mm) is sufficiently large, as the intensity difference between center and edge of the channel is very small (<2 %, Figure 2).

Figure 2:

Properties of a diffracting Gaussian beam at a distance of 1 mm away from the beam waist. (a) Intensity distribution along a selected line along the radial direction for two distances from the fiber surface (cyan: z _a = 1 mm, magenta: z _b = 1.02 mm). The difference between the distances roughly refers to the diffusion length of a typical NP Δz = z _b − z _a ≈ L _dif (details in main text). The gray area bounded by vertical dashed lines corresponds to the diameter of the microchannel used in the experiments (D _mc = 4 µm). (b) Close-up of the region close to the fluidic channel of the capillary. The cyan circles indicate the intensity in the center and at the side of the fluidic channel, while the magenta circle indicates the intensity in the center of the hole at z _b. All simulation parameters are given in the main text.

The experimentally relevant intensity change along the longitudinal direction (z-axis) can be estimated from the diffusion length L _dif of a typical NP and the measurement time (τ _m = 65 s): for a single NP of diameter d = 50 nm diffusing in a liquid medium (viscosity η = 3 mPa·s), the Stokes–Einstein relation yields a diffusion coefficient of D _dif = 2.86 μm²/s, which corresponds to a diffusion length of L dif = 2 D dif τ m ≈ 19  µm. The longitudinal intensity decrease over such a length at the distance z _a is small ΔI(L _dif) ≈ 4 % and can practically be neglected in NTA experiments. It should be noted that I can be further reduced by increasing the distance between delivery and capillary fiber.

The working principle of the concept relies on using a liquid medium whose RI n _l must match that of the cladding n _clad at the operation wavelength to avoid mode formation, which would lead to an uneven field inside the microchannel. This leads to the flat-field condition Δn = n _mc − n _clad = 0 with the RI-mismatch Δn. To reveal the impact of a possible RI mismatch on the propagation of light inside the microfluidic channel and the cladding, finite-element simulations (COMSOL Multiphysics 5.2) were performed on a configuration that is comparable to the experiments performed (cladding material: silica with RI n _silica(λ ₀ = 0.532 µm) = 1.4607). In the simulation, a plane wave with a k-vector along the z-direction was defined as the excitation field at the input of the simulation area, and the scattered fields from the liquid-filled capillary with different Δn were studied (more details in the Supplementary Material).

In the following, the intensity distribution in the spatial domain Δz = 50 μm at a distance z _a is investigated for relatively small RI mismatches, which may be relevant due to practical limitations. Two cases can be distinguished:

1. For Δn > 0 total internal reflection is present and gives rise to guided modes in the microchannel (Figure 3(a)), which show a pronounced intensity variation both axially and transversely.

2. The complementary case (Δn < 0) leads to the formation of so-called leaky modes, which dissipate power transversely during light propagation (Figure 3(b)). In the ray picture, this behavior can be explained by a zigzagging beam inside the microchannel with less-than-unity reflection at the liquid/silica interface.

Figure 3:

FEM-simulation of the intensity distribution inside a selected section of the capillary (z _a  < z < z _a  + Δz) for three RI scenarios (characterized by n). (a) Δn = 0.004, (b) Δn = −0.004, (c) Δn = 0. (d) Corresponding radial intensity distributions at z = z _a  + Δz. All distributions shown in the figure are normalized to the value of the RI-matched case.

For both scenarios, intensity variations occur even at relatively small RI mismatches (Δn = ±0.004). In contrast, there is no visible intensity change in the case of matched RIs (Figure 3(c)). To further illustrate the impact of the RI mismatch, Figure 3(d) shows the radial intensity distributions at the end of the simulation volume at z = z _a + Δz along a selected line. For Δn = 0.004, the intensity in the center of the capillary is about 2.5 times greater than at the liquid/wall interface. In the complementary case (Δn = −0.004), the intensity in the center of the system is significantly lower than at the corresponding interface. This discussion clearly reveals that the RI of the liquid used in the experiments must be controlled precisely to minimize intensity variations.

2.3 Experiments

Gold nanospheres (average diameter 50 nm, concentration 8·10⁸ NPs/ml, [nanoComposix]) were used as NPs to confirm flat-field formation in the experiments. Based on the results of a previous study [13], a mixture of water and Dimethyl sulfoxide (DMSO) was used as the host liquid, allowing the RI to be precisely adjusted by changing the mixing ratio (details in the Methods section). In the current experiments, a mixing ratio (in weights) of 16.9 % water and 83.1 % DMSO mixture was chosen, giving an RI of n _mc ≈ 1.4607, which corresponds to the value for silica [19]. Note that the use of DMSO for biological specimen requires extra caution due to possible cytotoxicity [20].

The experimental setup consists of a low-NA delivery fiber (NA = 0.05) and a capillary (D _mc = 4 µm), both aligned in an etched V-groove on a silicon chip and exposed to the liquid environment mentioned above (more details in Methods section). The distance between the fiber and the capillary was set to z _a = 1 mm, considering the properties of the delivery fiber. The arrangement is exposed to the NP solution, which is filled into the central hole of the capillary (hole diameter: D _mc = 4 µm, outer diameter 125 µm) by the capillary effect [21]. Typical filling times are of the order of a few minutes (more details can be found in the Supplementary Information of Ref. [13]). Note that the experimental assembly was subjected to a plasma treatment before loading the sample solution to improve surface wettability and eliminate the risk of bubble formation. The diffusion of the NPs along the longitudinal direction (z-direction), confined by the microchannel, is measured using a microscope that detects the laterally scattered light using a fast camera (frame rate ν = 1 kHz). A tracking area close to the entrance of the capillary was selected to avoid the disturbing by the reflected beams from the outer surface of the capillary fiber.

Two selected images of frames before and after the liquid exposure are shown in Supplementary Material Figure S5. The quality of the imaging system is illustrated by the image shown in Figure 4(a and b). Here, the Airy pattern is clearly visible, indicating that the imaging system is diffraction limited (c.f. [14]). Note that the influence of the plasmonic properties of the NP used on the optical detection is minimal, since the variation of the scattering cross-section σ _scat within the spectral range of interest (the visible spectral domain, 500 nm < λ 0 < 700 nm) is less than one order of magnitude. The variation of the scattered intensity is therefore small when the operating wavelength is changed. The potential influences of photon pressure and induced pressure have been quantified by calculating critical intensities and comparing them to the system described in this study (Section 11 of the Supplementary Material). This analysis indicates that these factors are insignificant in the context of the experiments described herein.

Figure 4:

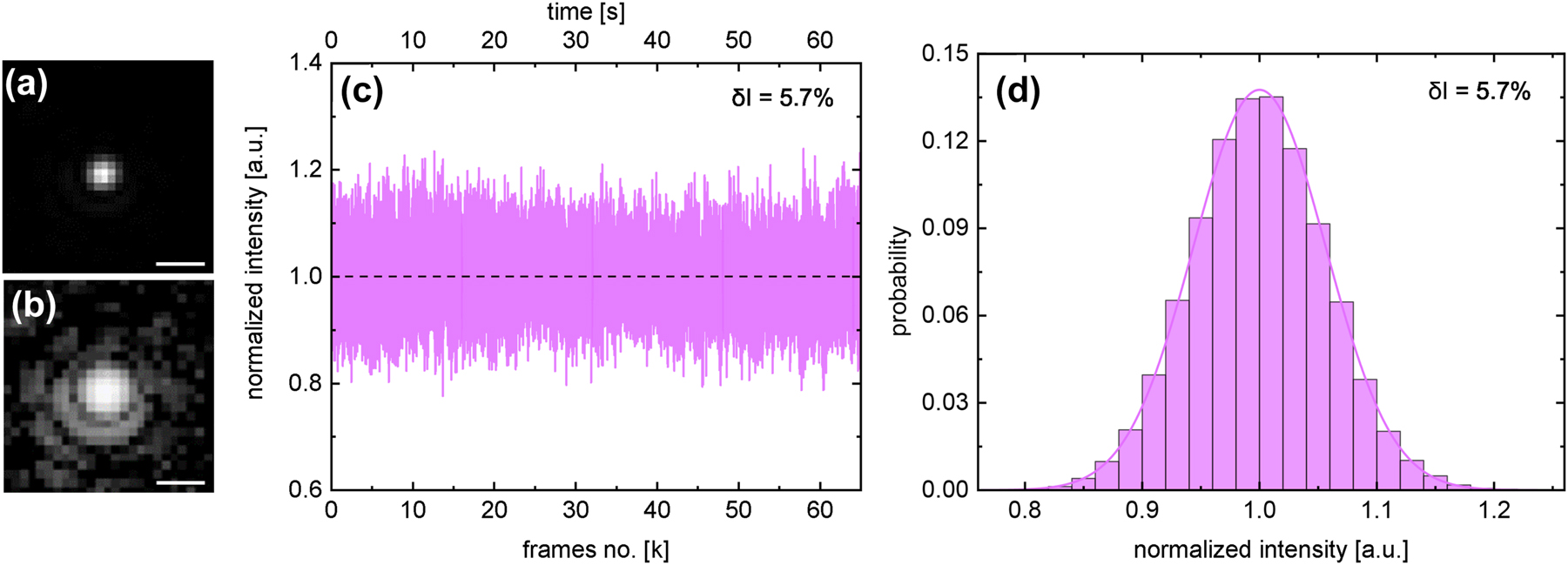
Statistical analysis of time-varying scattering intensity of a nanoparticle diffusing inside the illuminated capillary. (a and b) Close-up views of a NP in one selected frame using the mentioned imaging system ((a) linear scale, (b) logarithmic scale). The Airy rings are clearly visible, revealing that the imaging is diffraction-limited. The scale bar is 2 µm. (c) Measured temporal variation of the scattering intensity of the NP (d = 50 nm) diffusing inside the microchannel. (d) Histogram of I _s with a Gaussian fitting. Note that the intensities in (c) and (d) have been normalized to the value of the average intensity.

2.4 Data analysis

To get information on the field profile inside the microchannel, the scattering intensity of the diffusing NPs has been evaluated in selected regions of the microchannel (details can be found in the Method section and Ref. [17]). Specifically, the domain of the fluidic channel was transversely divided into a central bin (CB) and two intensity side bins (SBs, Figure 5(a)). Then the measured intensity values are binned within these spatial domains and the corresponding occurrence probabilities are plotted in histograms. To extract the key parameters of the individual distribution, Gaussian distributions have been fitted to the histograms. The diameter of the NPs of interest was determined using mean-square-displacement (MSD) analysis, i.e. a statistical analysis of the trajectory of the NPs resulting from Brownian motion (Figure 4). Details of MSD analysis, which is well-established in the context of FaNTA, can be found in several of our previous publications [12].

Figure 5:

Verification of the flat-field concept by statistical analysis of the time-varying scattering intensity in selected spatial domains of the microchannel. (a) Cross-section of the capillary with the areas in which the scattering intensity is binned and statistically analyzed (purple: central bin [CB], dark green: side bins [SBs]). The numbers are given in µm. (b) Histograms of the intensity distributions in the CB and the SBs. The colored lines indicate the corresponding continuous curves from a Gaussian fitting. The number of data points used for the histograms is N _CB = 17,632 and N _SB = 14,821 for the CB and SBs, respectively.

3.1 Experimental demonstration: analysis of the entire trajectory

To verify the flat-field concept, the trajectory of a single NP was recorded and the temporal variation of I was statistically analyzed (Figure 4(c)). As mentioned above, high statistical significance requires the recording of trajectories with a very large number of frames N, which can be achieved by restricting the diffusion to a defined spatial region. In the context of the FaNTA, this condition is enforced by the microchannel environment [11], [12]. In the present experiment, the characteristic feature led to a long measurement time (τ _m  = 65 s) at a high frame rate (ν = 1 kHz), resulting in a trajectory consisting of a very large number of frames (N = 65,000).

Analyzing the distribution of the time-varying scattering intensities results in an overall symmetrical Gaussian distribution (Figure 4(d)), which indicates a constant intensity distribution and thus flat fields within the microchannel. This can also be seen in the visual inspection of the analyzed movies, which show hardly any temporal variation of the scattered intensity (an example of a 1-min trajectory is uploaded as Visualization 1). It should be noted that due to intrinsic fluctuations, a Gaussian distribution can theoretically be expected even for a constant illumination [17]. Another indication of flat fields is the symmetry of the distribution in relation to the mean value of the scattering intensity I ̄ . In principle, a deviation of the intensity distribution in the microchannel from a flat field (e.g., evanescent decay) would lead to an asymmetric distribution, which was not observed in the present experiments. A further indication of the presence of flat fields results from the low value of the relative standard deviation of δ I = σ I / I ̄ = 5.7  % (σ _I : measured standard deviation). It can be assumed that this value essentially results from statistical fluctuations of the measurement approach and not from a variation in the intensity distribution in the microchannel.

3.2 Experimental demonstration: analysis in the two selected spatial domains

The next step in the analysis relies on comparing the occurrence probabilities of the scattered intensities in the two spatially separated regions named CB and SBs (I _i with i = CB, SB, Figure 5(a and b)). All intensities shown in the following are normalized to the maximum of the intensity of the Gaussian fit in the CB, i.e., I i → I i / I CB max,G . Several important characteristics can be extracted from this comparison that support the observation of flat-field formation (all numbers discussed here are summaries in Table 1): first, the probability distributions are symmetric regarding the corresponding average probability, which according to the discussion of the previous section indicates a constant intensity within the respective bin. This point is supported by the fact that the FWHM extents of the distributions are comparable Δ I CB FWHM ≈ Δ I SB FWHM . An even stronger argument for flat-fields is that the peak intensities of the Gaussian fits of both distributions have approximately the same peak intensity I SB max ≈ I CB max , as indicated by the red dashed line in Figure 5(b)). This point can be qualified by inspecting the difference between the peak intensities of the CB and SB I i max defined as δ I max = I CB max − I SB max / I CB max , which is δI _max = −0.23 % for the experiments reported here.

3.3 Mean-square-displacement analysis

The advantage of flat-field illumination and the resulting long trajectory length was used here to determine the hydrodynamic diameter d _h of the investigated NP by MSD analysis of the Brownian motion (Figure 6). A detailed description of this data processing method in relation to FaNTA can be found here [12]. The diffusion coefficient of the nanosphere was determined by fitting the MSD values of the first two lag times, (D _dif = 2.23 μm²/s) and the hydrodynamic diameter was calculated using the Stokes-Einstein relation d _h = k _b T/(3πη(T)D _dif). Note that in MSD analysis, a single lag time does not correspond to a single time, but refers to a statistical average of the position differences over the entire trajectory. For example, the shortest lag time Δt results from averaging over N − 1 values and thus leads to a high statistical significance. The significance decreases with longer lag times due to the smaller number of values considered. As detailed in one of our previous works [12], when the localization error in tracking experiments is negligible – as in the present study – the first two lag times generally achieve the greatest statistical significance and provide the most accurate determination of the diffusion coefficient through linear fitting the two experimental data points (c.f. [22]). Note that including more lag time typically reduces the accuracy of statistics, especially in situations where diffusion is spatially restricted. Considering the ambient temperature (T = 293.15 K), the viscosity of the DMSO/water mixture is approximately η = 3.3 × 10⁻³ Pa·s [23], yielding a hydrodynamic diameter of d _h = 58.4 ± 0.6 nm. The measured d _h is consistent with the expected value of the used NPs which have a mean hydrodynamic diameter of 59 nm.

Figure 6:

Application of the flat-field concept to determine the hydrodynamic diameter of the investigated NP using MSD analysis. MSD as a function of lag time (points: measured values). The dashed dark green line refers to a linear fit of the first two data points (magenta dots).

It should be noted that the influence of the confinement of the microchannel on diffusion can be neglected in this work, since the first four lag times show a clear linear dependence. Furthermore, the hindrance factor, which describes the influence of the confinement on the diffusion coefficient, was determined for the present geometry, yielding R _ave = 1.066 (a detailed analysis of confined diffusion in the context of FaNTA can be found here [24]). As this factor is in the range of 1, the value of d _h remains almost unchanged, i.e., free diffusion can be assumed (further details on this argumentation can be found in the Supplementary Information of Ref. [15] in Sections 15 and 16). Note that the work of Nitsche and Balgi [25] shows that the confinement of NP diffusion can be neglected when the ratio of NP to microchannel diameter is very small. Since the experiments show no average drift of the NPs along the fiber, an influence of the thermophoretic effect can be excluded.

6.1 Nanoparticle solution preparation

Gold nanopsheres (ultrauniform 50 nm, nanoComposix) dispersed in a mixture of water and DSMO were used as NPs in this study. By varying the mixing ratio, the RI of the binary liquid was precisely adjusted here to achieve the flat-field condition n _mc = n _clad = n _silica. The applicability of this liquid for NTA experiments was confirmed in one of our previous studies [13], showing that DMSO-water mixtures have no detrimental impact on diffusing gold NPs and NTA experiments, as long as the correct viscosity (η = 3.3 × 10⁻³ Pa·s @ T = 293.15 K) is considered in the Stokes-Einstein equation.

6.2 Experiments

The experimental setup is shown in Figure S1 in the Supplementary Material. Delivery (in-house made single-mode fiber with the cut-off wavelength of 457 nm, NA = 0.05) and capillary fibers (D _mc = 4 µm, made from silica [F300, Heraeus]) were aligned inside a V-groove etched into a silicon chip (both have an outer diameter of 125 µm), with the delivery fiber fixed by using UV curing epoxy (Vitralit^®1605). The distance between the fiber and the capillary surface was set to z _a = 1 mm, which can be adjusted by a 3D-stage during the experiment, according to the estimation discussed above. To prevent bubble formation, a plasma treatment of 100 W for 1 min was performed prior to liquid exposure. The area between the fibers was immersed in the prepared NP solution and covered with a glass slide to improve the image quality. For the tracking experiments, green laser light (Coherent Verdi G, λ = 532 nm) was coupled into the delivery fiber, yielding a power of P _out = 17 mW at the output of the delivery fiber. The NPs were imaged using a 10× objective (Olympus Plan Achromat, numerical aperture 0.25, depth of field 10 µm) and recorded by a CMOS camera (Basler acA4096-40 um) with a field-of-view of the captured frames of (30 × 600) pixel. In the tracking experiment, the frame rate and exposure time were ν = 1 kHz and τ _e = 0.2 ms, respectively. In this study, the trajectory of a single NP was recorded (number of frames: N = 65,000, total measurement time: τ _m = 65 s).

6.3 Data analysis

The trajectories of the NPs were extracted from the recorded images using the Python-based package Trackpy. The fluidic channel was divided into the center and side bins (CB and SBs) according to the x-positions (Figure 5(a)). To analyze the mode distribution in the channel, the scattered intensities in the CB and SBs were plotted as histograms and fitted by Gaussian distributions. The diameter of the NP of interest was calculated using mean-square-displacement (MSD) analysis by statistically analyzing the trajectory of the NPs, i.e., the Brownian motion (Figure 6). Details of MSD analysis in the context of FaNTA can be found in several of our previous works [12], [13].