Atomistic polarization model for Raman scattering simulations of large metal tips with atomic-scale protrusions at the tip apex

2.1 Atomistic discrete dipole approximation model

In the atomistic DDA model, each atom in a nanocluster is characterized as a point dipole with an isotropic polarizability, and these atoms interact with each other through the dipole-dipole interactions [39]. The atomic dipole moment of each atom is determined by the atomic polarizability and the electric field from both the incident light and the dipolar contributions of other atoms, resulting in the induced dipole moment p _i of the atom i expressed as

where the first term is ascribed to the response to the incident electric field E i inc at the ith atom’s position, and the second term is ascribed to the response to the other atomic dipole moments. Here α _i represents the atomic polarizability tensors of atom i and T _ij is the dipole–dipole interaction tensor between atomic dipoles i and j. The above equation can be simplified as a linear set of equations for each atom as

where N is the total number of metal atoms to compose the tip, and the matrix A _ij is defined as

Here the isotropic atomic polarizability tensor only contains diagonal elements from the Clausius–Mossotti relationship α _i,ll = (3V/4π)(ɛ − 1)/(ɛ + 2), where V is the volume of the atom obtained from the lattice constant (e.g., V = 17.05 ų for Ag atom with face-centered cubic structures) and ε is the dielectric constant from the experiments [42]. Note that the modified atomic polarizabilities by comparing with the quantum simulations would provide more accurate results [12, 43–45], which would be implemented in our further model. The full expression of the dipole–dipole interaction tensor can be written as

where k is the wavevector of dipole oscillation in free space, r _ij is the distance between atom i and j, and r ̂ i j is the unit vector for describing these two atoms’ direction. Once the size of the nanoparticles is smaller than ∼1/10 of the wavelength of the incident light, the retardation effect can be neglected and the dipole–dipole interaction tensor can be simplified as T i j = 3 r ̂ i j r ̂ i j − I / r i j 3 . In our simulation, the induced atomic dipole moments p _j can be obtained by numerically solving Equation (2) with the precise linear solver from the “linalg” module in Scipy [46] for smaller systems (<20,000 atoms). For the large-size tips with about one million atoms, the sparse matrix is introduced and the GMRES solver [47] is used.

2.2 Plasmonic response of a metal tip

After obtaining the values of atomic dipole moments (p _i ), the far-field and near-field properties of the metal tip can be directly obtained as a sum of the contributions from each atom. In particular, the far-field absorption cross section can be expressed as

where ω is the frequency of the incident field, and c is the speed of light. The near-field spatial distribution can be also evaluated from the sum of the atomic contributions as

where the near-field Green function G ↔ r , r i between the dipole source position r _i and the local field position r can be written as

2.3 Simulation of the Raman scattering from the tip apex

For a given structure of the metal tip, its polarizability can be evaluated from the induced dipole moments of the tip according to the polarized electric field along x, y and z directions as

where P E x Tip = ∑ i = 1 N p i is the total dipole moment of the tip induced by the x-polarized incident electric field E _x . Since the Raman intensity is directly related to the polarizability derivatives, the values of the derivatives with respect to each atomic displacement are calculated by the finite difference method [40] through the repetitive DDA simulations with the coordinate displacement Δ ξ = 0.01 Å. Here the index ξ represents the x, y or z coordinates of the equilibrium structure. Hence, one can express the polarizability derivative corresponding to the nth atomic coordinate as

where α ξ ± Δ ξ n Tip is the polarizability tensor of the tip with the deformed structure ξ ± Δξ _n . The Raman polarizability can be expressed through a coordinate transformation from the normal coordinates Q _k to the atomic coordinates ξ _n as

where μ _k and ω _k denote the reduced mass and frequency of the kth vibrational mode, ϕ k n denotes the vibrational eigenvector corresponding to the kth vibrational mode. The total number of the atomic coordinate is M = 3 × N. After applying an incident electric field E ^inc, the induce Raman dipole moment for the kth vibrational mode can be obtained as p k Raman  = α k Raman E inc  . As a result, the differential Raman scattering cross section of the tip can be calculated from

where the radiation frequency of Raman dipole moment for the kth vibrational mode can be expressed as ω _R = ω _inc − ω _k , and ω _inc is the frequency of incident light.

In our simulations, only the perturbed displacements of the atoms at the tip apex are considered during the calculations of the polarizability derivatives ∂α ^Tip/∂ξ _n . The values of polarizability derivatives can be also directly evaluated from the entire deformation of the tip apex following the corresponding vibrational eigenvectors without the coordinate transformation shown in Equation (10), which would result in the same derivative values if the incident light is plane wave [48]. The vibrational analysis of the tip including the vibrational eigenvector ϕ k n , vibrational frequency ω _k , and the reduced mass μ _k can be calculated by using the quantum chemistry [49] or molecular dynamics packages [50]. Here, we use the Gaussian16 package with the hybrid functional PBE0 and the def2-SVP basis set for the vibrational analysis simulations [41].

3.1 Influence of atomistic changes in tip apex

As shown in Figure 2(a), a silver cluster with a parabolic shape and a height of 15.2 nm is built up as the model system of the tip by stacking 16,512 atoms with a crystal lattice constant of 4.0897 Å [51], and three types of atomistic changes in tip apexes, namely, the sharp tip (intact Ag₁₆₅₁₂ cluster), the blunt tip (Ag₁₆₅₁₁ cluster by removing the apex atom from the sharp tip), and the flat tip (Ag₁₆₅₀₈ cluster built up by removing two layers of apex atoms from the sharp tip) are considered to study the influence of apex morphologies. Figure 2(b) shows far-field absorption spectra for these tips when the electric field of the incident planewave is polarized along the z-axis, showing similar spectral features with a main peak located at ∼2.5 eV. This resonant peak can be assigned to the dipolar plasmon (DP) mode according to the surface charge distribution around the tip (see Supplementary Figure 1). Two additional resonant peaks with higher energies at ∼3.1 eV are also observed, which are associated with quadrupolar plasmons (QP), which split into two peaks for the sharp tip with the atomic protrusion at the apex. The DP and QP peaks can also be identified in the near-field spectra of the local field enhancement under the tip apex (as shown in Figure 2(c)), showing stronger intensities of the near fields for the sharp tip. Such results imply that the near-field response of the tip would be very sensitive to the atomistic changes at the tip apex. Moreover, the spatial distributions of the local plasmonic field can directly reflect the outlines of atomic stacking patterns at the tip apex. Figure 2(d)–(f) show the corresponding local electric field distributions for the xy-plane with a distance of 0.2 nm from the surface of the apex atom in resonant condition with the DP mode (ω = 2.51 eV) for different tips. The local electric fields are generally confined at the atomic scale near the tip apex, exhibiting great field enhancement under the tip. For the sharp tip with only one atom at the tip apex, the local electric field distribution shows a circular shape, while for the blunt and flat tips, triangular shapes appear because of the truncated pyramid structures at the tip apexes. Such feature will be lost at longer distances (typically larger than 4–6 Å, see Supplementary Figure 2), showing a blurred round shape without any atomistic details [52, 53].

Figure 2:

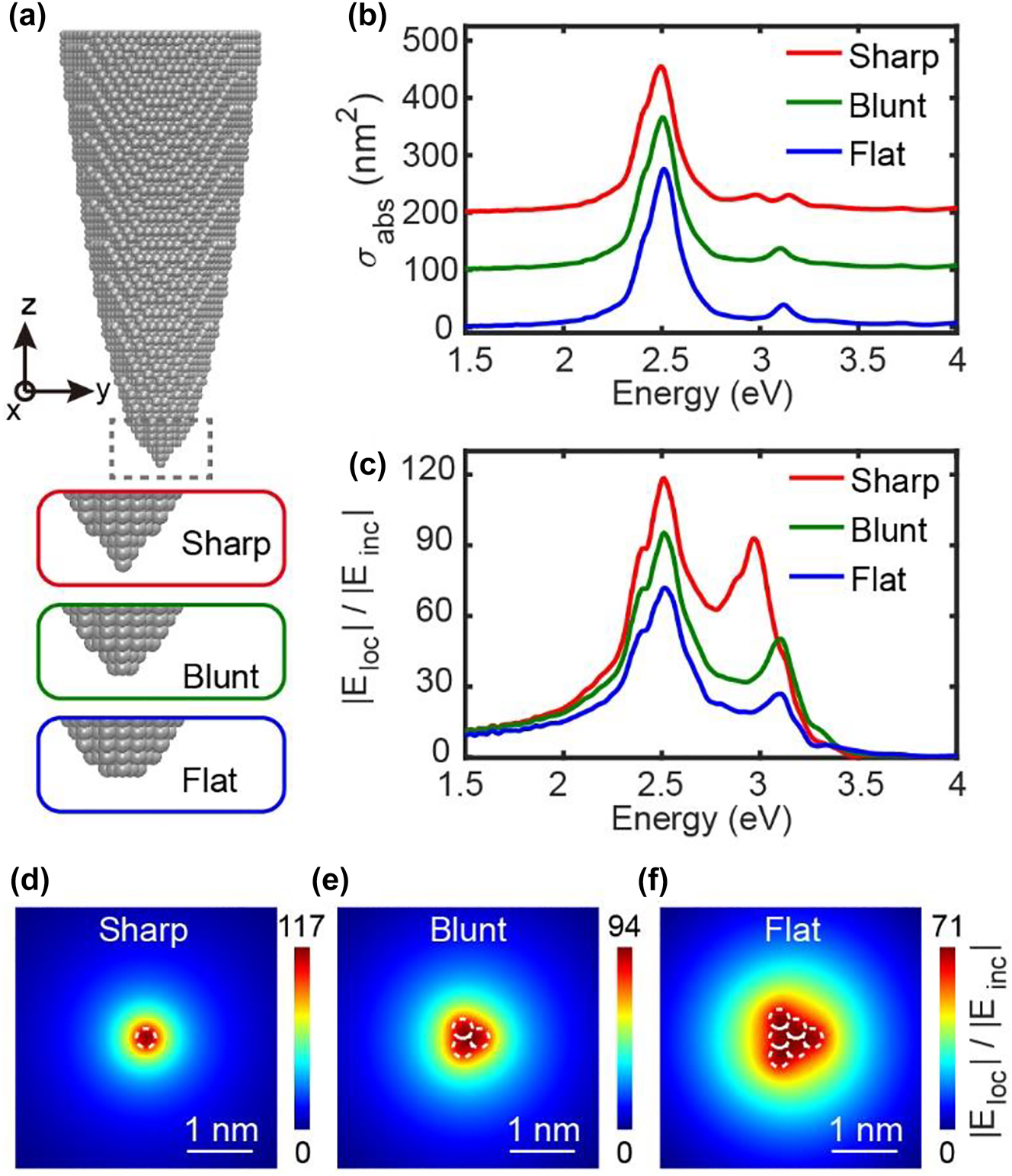
Plasmonic response properties of Ag tips. (a) Atomistic structures of Ag tips with three different atomic-scale apexes. (b–c) Absorption and near-field enhancement spectra of the three tips for an incident planewave with the electric field polarized along the z-axis. (d–f) Induced local electric field enhancement distribution in the xy-plane at a distance of 0.2 nm from the apex surface for an incident optical planewave with the energy of 2.5 eV. The white dotted circles with a radius of 0.144 nm represent the outlines of atoms at the tip apexes.

3.2 Vibrational modes of Ag tip apex

Since the incident light has been strongly confined to the tip apex region, the Raman scattering signals would be mainly contributed by the vibrations of the apex atoms rather than the rest part of the tip. Therefore, we first performed vibration analysis of a Ag₂₀ cluster to mimic the tip apex through the DFT calculations with Gaussian 16 package [41]. Based on the experiences in previous reports [27, 54, 55], three layers containing ten silver atoms at the tip apex are relaxed for optimization and the other atoms are fixed during the calculations to save the computing time. There are thirty vibrational modes in total, and all the vibrational frequencies are below 200 cm⁻¹. Figure 3 presents eight dominant vibrational modes, with the schematics of the displacement of the atoms for each mode demonstrated by the red arrows. The vibrational mode with the energy of 55 cm⁻¹ corresponds to the collectively out-of-plane vibrations of all atoms at the tip apex. The vibrational mode with the energy of 78 cm⁻¹ corresponds to the relative vibration of the apex atom and its nearest neighbor atom along the tip axis while other atoms exhibit approximate in-plane vibrations. The vibrational mode with the energy of 140 cm⁻¹ corresponding to v ₂₇ mode represents the so-called breathing mode, which involves collective vibration of the four atoms at the tip apex. The complete and detailed identification of the vibrational modes of the tip apex is shown in Supplementary Video 1.

Figure 3:

Atomic motions for eight dominant vibrational modes of the tip apex (a Ag₂₀ cluster). The red arrows highlight the directions and amplitudes corresponding to the characteristic atomic displacements.

3.3 Influence of tip shapes on the Raman scattering from tip apex

In the above vibrational analysis, the Raman scattering process can also be discussed once the polarizability derivatives are also calculated in DFT simulations. However, such simulation can only be carried out for the small clusters with hundreds of metal atoms. On the other hand, the polarization behavior of the metal tip involves the contributions in its entirety, and it would be far from the truth if only the polarizabilities from the apex atoms are considered. Moreover, the plasmonic response of the tip would be also strongly dependent on the shapes and sizes, requiring to take the whole part of the tip into account. Figure 4 shows the size-dependent plasmon response and Raman scattering of different Ag tips with the same apex radius (R = 0.8 nm) but different heights (from ∼3.4 nm with 725 atoms to ∼15.2 nm with 16,512 atoms). The shaft of the tip is built through the Ag crystal structure (with the z-axis along the [111] direction) and the optimized Ag₂₀ structure as mentioned in Figure 3 is epitaxially attached to the shaft as the tip apex. The incident electric field is a planewave with a wavelength of 532 nm and is polarized along the z-axis. As shown in Figure 4(a), the plasmonic resonance frequencies are generally red shifted as the tip height increases. For example, the DP mode located at 2.8 eV for the short tip with the height of 3.4 nm is shifted to 2.5 eV once the tip height increases to 15.2 nm, which is similar to the red-shift trend of the longitudinal dipolar mode of the nanorod with increasing length [44, 56]. The absolute intensities of absorption cross sections are increased with the increasing size of the tip, and the QD as well as other higher-order modes are also red shifted in general.

Figure 4:

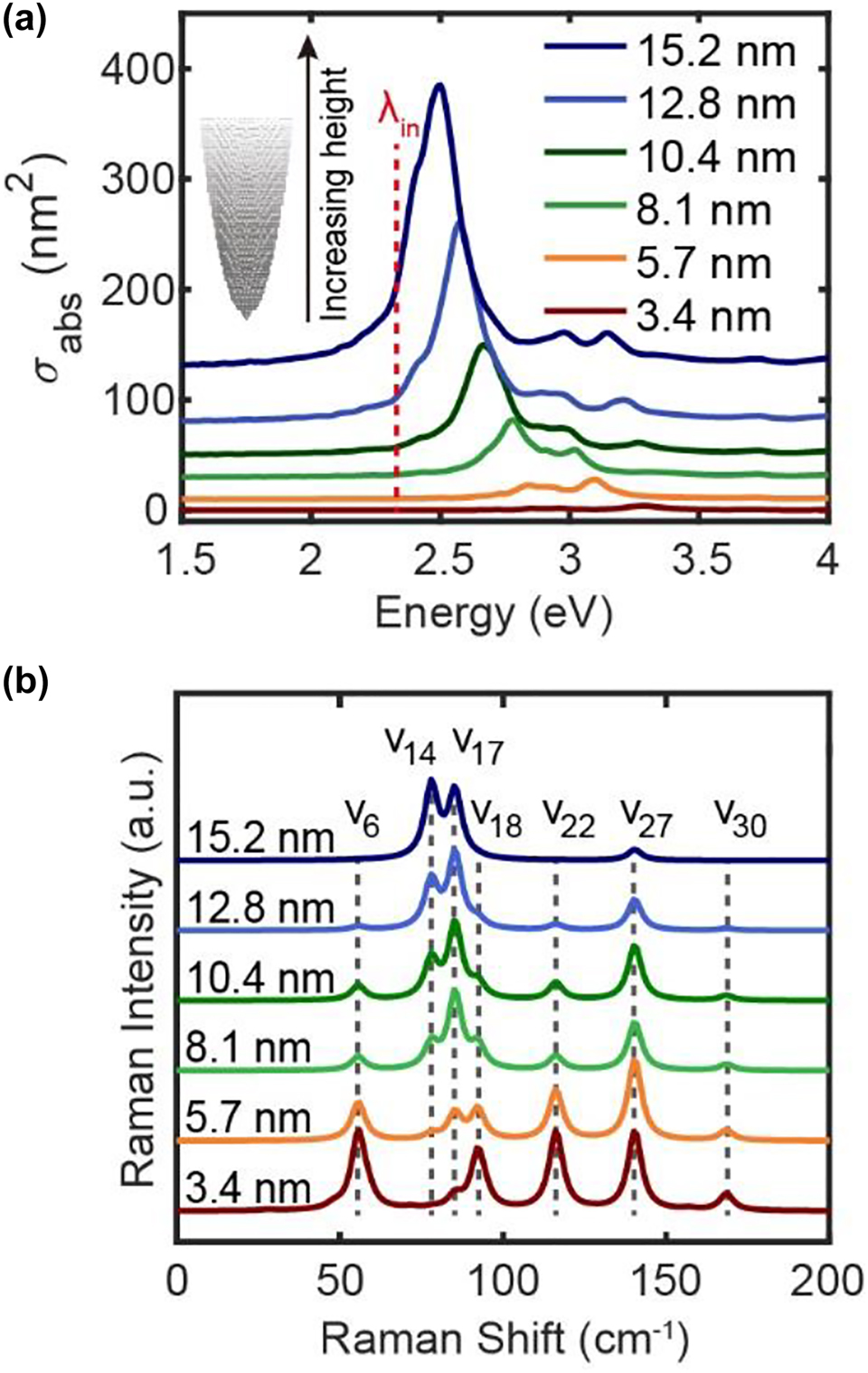
Absorption and Raman spectra of the tips with different heights. (a) Absorption spectra and (b) normalized Raman spectra of the tips with the shape of a paraboloid and the different heights from 3.4 nm to 15.2 nm. The stacking structure of the tip apex is similar to that shown in Figure 3. The red dashed line in (a) represents the frequency of the incident electric field at 2.33 eV for Raman scattering simulations in (b).

The simulated Raman spectra of tips with different heights are shown in Figure 4(b), which are normalized to show the differences in relative intensities between different vibrational modes. It should be noted that although only the vibrations from the last three layers of apex atoms are considered, the polarizability of the entire tip as well as its derivatives corresponding to these vibrational modes always take all the atoms into account. The influence of apex atom numbers on the vibrational modes is detailly discussed in Supplementary Section 4. Seven dominant Raman peaks appear in the spectra, showing different relative intensities for different tip sizes. As the height of the tip increases from 3.4 nm to 15.2 nm, the relative intensities of v ₁₄ and v ₁₇ peaks increase, while those of v ₆, v ₁₈, v ₂₂, v ₂₇ and v ₃₀ modes decrease gradually. There might be two reasons that account for the changes in spectral features for different tips: One is the red-shift of the DP mode, resulting in different enhancement factors for different vibrational modes; the other is the differences in the total polarizabilities of the tip, resulting in the differences in the equivalent polarizability as well as its derivatives of each atom. As a result, only v ₁₄, v ₁₇ and v ₂₇ modes are obvious and dominant in the Raman spectrum of longer tips.

Similar results can be also observed for the absorption and Raman scattering spectra of the tips with the same height (∼11.6 nm) but different tip radii (from 0.4 nm to 1.5 nm as shown in Figure 5(a)). Once the tip radius is changed, the stacking structures and the vibrational modes of apex atoms would be also influenced, which are detailed analyzed in Supplementary Figure 4 and Video 2. As shown in Figure 5(b), in contrast to the tip height changes, the main DP peaks of different tips in the far-field absorption spectra are blue-shifted as the apex radius increases. A split of the DP peak at ω = 2.20 eV can be observed for the slim tip with the radius R = 0.4 nm, since the atomistic roughness is more prevalent in such a tip structure to make the assignment of the plasmonic modes more difficult (see Supplementary Figure 5 for details). Figure 5(c) shows the Raman spectra corresponding to these tips, from which it can be seen that as the radius of the tip increases, the feature of Raman spectrum changes from individual narrow peaks to complex wide envelopes, and the relative intensities of the Raman peaks also vary significantly. Different from the situation in changing the tip heights where the apex structures are always the same, the atomic stacking structures at the apex of the tips with different radii would be quite different. Usually, the blunter tip would contain more atoms at the apex (assuming that only the first three atomic layers of the apex are considered in all tips), resulting in more vibrational modes with similar frequencies as well as the overlapping in Raman spectra. On the contrary, the Raman spectrum of the sharper tip is contributed by the vibrations of fewer atoms at the apex, resulting in the discrete Raman peaks with fewer overlaps. In this sense, it is difficult to assign the same vibrational modes for these tips with different radii, and we could only identify very few modes that always exist in all tips. For example, the Raman peak at ∼170 cm⁻¹ related to the vibrational mode v ₃₀ of the apex atoms is always visible for both the sharp or blunt tips. Moreover, if the tip radius is much larger (e.g., >10 nm), there always exist atomistic protrusions or local structures at the surface or very apex of the tip [13, 26], thus the final spectra would be mainly determined by the vibrations of such atomic details or roughness rather than the whole large tip.

Figure 5:

Absorption and Raman spectra of the tips with different radii. (a) The tip structures with the different curvature radii from 0.4 nm to 1.5 nm. (b) Absorption spectra and (c) normalized Raman spectra corresponding to different tip structures in (a). The detailed stacking structures of tip apexes are shown in Supplementary Figure 4. The red dashed line in (b) represents the energy of the incident electric field at 2.33 eV for Raman scattering simulations in (c).

3.4 Influence of apex-atom substitution on the Raman scattering from tip apex

In the above discussions, we have found that both the far-field absorption spectra and the near-field Raman spectra of the tip apexes are very sensitive to the atomistic changes of the tip structures. This raises an interesting question that whether it is possible to characterize the single-atom changes of the tip (e.g., with only one noble metal atom is substituted at the apex). Here we first simulate the plasmon response and Raman spectra for tips with different substitutions of noble metal atoms (e.g., a Au, Cu or Pt atom at the apex). The optimized geometries of the apex clusters corresponding to these tips are shown in Figure 6(a). No observable changes can be observed in the far-field absorption spectra in Figure 6(b) by only replacing one single atom of the apex. However, the simulated Raman spectra corresponding to these tips do exhibit some differences. For example, the Raman spectrum of the Ag tip with a single Au atom substitution exhibits two obvious peaks related to v ₂₂ and v ₃₀ modes, which are generally very weak for the pure Ag tip. For the Cu-adsorbed Ag tip, the v ₃₀ mode is also visible in the simulated spectrum but greatly blue-shifted to ∼193 cm⁻¹, while the intensity of v ₁₇ peak becomes very weak. For the Pt-adsorbed Ag tip, there is only one dominant peak corresponding to v ₁₇ mode, as well as a very weak v ₂₇ peak to be observed. Considering the similarities in all vibrational eigenvectors for the tips with different substitution atoms (Supplementary Video 3), the differences in the spectral features can be attributed to interactions between the apex atom and its neighboring atoms because of the changes in atomic polarizabilities. Therefore, it would be very convenient to judge the type of atom adsorbed at the tip apex directly from the distinguishable fingerprints in the Raman spectral features.

Figure 6:

Absorption and Raman spectra of the tips with different apex-atom substitutions. (a) The tip structures with the different noble mental atoms adsorbed at the tip apex. (b) Absorption spectra and (c) normalized Raman spectra corresponding to those tips in (a). The red dashed line in (b) represents the energy of the incident electric field at 2.33 eV for Raman scattering simulations in (c).

3.5 Raman spectra of the tip with sub-wavelength size

The sizes of the tips discussed above are generally much smaller than the wavelength of the incident light, although there are already >10,000 atoms involved. In order to verify whether our method can be applied to the tip with a sub-wavelength size, we construct a parabolic tip composed of 1,002,729 atoms with the height of ∼116.8 nm and the tip radius of 0.8 nm (see Figure 7(a)). For such a large-scale tip, a full description of the interaction matrix is inefficient and unnecessary. Considering that the interaction between atomic dipoles decays very fast following the r ⁻³ law, the sparse matrix for T is adopted with variable cut-off values for atoms far from the tip apex adapted for the matrix elements following the function T c = 1 0 − 6 × 1 0 ( L − 3 ) / L r Å⁻³, where L represents the layer index where the atom is located and increases for atoms from the tip apex (L = 1) to the tip shaft, and L _r represents the rate parameter to tune the cut-off values and is set to be 30 in our simulations (see the detailed discussion in Supplementary Section 6). The minimum and maximum values of T _c are set as 10⁻⁶ Å⁻³ and 10⁻⁴ Å⁻³ for the atoms very near or very far from the tip apex, respectively. The retardation effect [19, 57] is considered during the calculation of the interaction matrix, and the GMRES solver [47] is adopted to solve a set of linear response equations self-consistently because of its support for the sparse matrix. The induced local electric field distribution under an incident planewave with a wavelength of 532 nm and the polarized direction along the tip axis is shown in Figure 7(a). Although the maximum local electric field distribution is still in the proximity of the tip apex, the propagating plasmon along the sides of the tip can be clearly observed, resulting in the joint contributions in the polarization process from both the localized and propagation plasmons (see Supplementary Section 7 for the comparison with the simulated results using the continuum method). Figure 7(b) shows the normalized Raman spectra of tips with three different apex morphologies (same as Figure 2(a)) corresponding to two different heights of 15.2 nm and 116.8 nm, respectively. Both the small and large tips show similar spectral features, further confirming that the Raman spectral features are mainly determined by the tip apex and the influence of the tip shaft would be similar as long as the tip size is large enough. Especially, for the sharp tip, the Raman spectra are dominated by v ₁₄, v ₁₇ and v ₂₇ modes, which are consistent with the Raman spectra shown in Figure 4(b). For the blunt tip, the Raman spectra are dominated by v _b1 mode at 78 cm⁻¹ and v _b3 mode at 153 cm⁻¹, which are similar to v ₁₄ and v ₃₀ modes of the sharp tip. For the flat tip, the Raman spectra are dominated by v _f1, v _f2 and v _f3 modes at 82 cm⁻¹, 106 cm⁻¹, and 152 cm⁻¹, respectively. The detailed assignment and the schematics of atomic displacements for the dominant vibrational modes are shown in Supplementary Video 4. Therefore, for the simulation of Raman spectra of the tip, it is generally sufficient by modeling a short tip with the height of tens of nanometers to mimic the real tip systems.

Figure 7:

Local electric field distribution and Raman spectra of the tip with sub-wavelength size. (a) Induced local electric field distribution of a large-size tip composed of 1,002,729 atoms and with a height of ∼116.8 nm. (b) Normalized Raman spectra of the tips with a height of ∼116.8 nm (top) and ∼15.2 nm (bottom), respectively with three different apex morphologies (same as Figure 2(a)). The stacking structures and the dominant vibrational modes of the tip apexes are shown in Supplementary Video 4.