3D nanopolymerization and damage threshold dependence on laser wavelength and pulse duration

2.1 Experimental setup

The experiment was carried out using a broadly wavelength-tunable laser source with automated pulse GDD control (CRONUS-3P, Light Conversion). An autocorrelator capable of working under a high-NA objective (CARPE, APE Angewandte Physik and Elektronik) was used to measure pulse duration at the sample. A home-built microscope with a Zeiss Plan-Apochromat 100 × 1.4 NA oil-immersion objective was used to focus the excitation light on the sample. An automated 3-lens telescope integrated into the CRONUS-3P laser system was calibrated to maintain constant beam size and collimation while tuning the wavelength. Objective lens overfill was set so that beam size at 1/e ² was equal to objective entrance pupil. The sample was placed with the prepolymer side facing down. Sample translation was provided by a combined stage containing XY piezo-stages (P-563 PIMars, Physik Instrumente) and a motorized XY scanning stage (8MTF-75LS05, Standa). Another motorized translation stage (8MT167-100, Standa) was employed for objective positioning. Average power P _ave was controlled using an automated variable neutral density filter (VNDF) and measured before the objective using a power meter: PD300 (Ophir) for λ ≤ 1100 nm and 3A (Ophir) for λ > 1100 nm. Power loss at objective entry pupil was considered to be constant at 13.5%. During the experiment, the repetition rate was set to 1 MHz and the pulse duration after the objective was set to 100, 200 and 300 fs for each λ. Additional measurements were taken for several λ ≥ 1050 nm, where the GDD tuning range was sufficient for achieving 500 fs pulse duration. The layout of the experimental setup is depicted in Figure 1.

Figure 1:

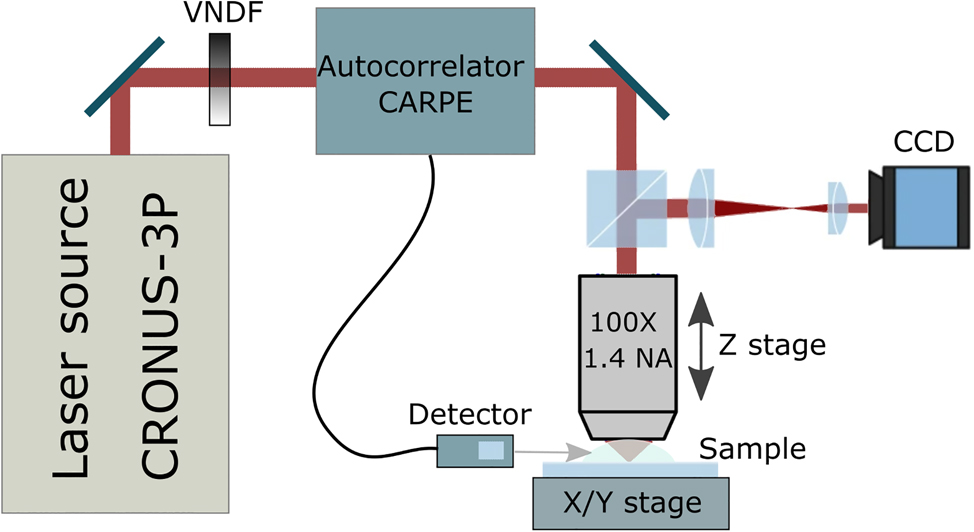
Layout of the experimental setup: wavelength-tunable laser system with pulse GDD control (CRONUS-3P), τ measurement (CARPE) and beam attenuation control (VNDF), custom-made microscope setup: piezo-stage stack for X and Y movement, Z-axis stage, focusing objective, CCD camera.

2.2 Laser system

The laser source used in this study is a combination of an amplified Yb:KGW laser and an optical parametric amplifier (OPA) followed by automated pulse GDD and beam size control. The standard system was extended for operation in the VIS range for this study. The laser provides µJ-level pulses down to 50 fs at repetition rates of up to 2 MHz and is tunable in the range from 400 nm to 1800 nm. Figure 2(a) shows the output power of the laser system, measured with a thermopile sensor (3A, Ophir). Output above 1050 nm is an idler beam (IDL), 650–1010 nm is a signal beam (SIG), 530–650 nm is the second harmonic (SH) of the idler beam (SH-IDL), and 400–500 nm is the SH of the signal beam (SH-SIG). Minimum pulse duration at laser output was measured using a scanning autocorrelator (GECO, Light Conversion) and is presented in Figure 2(b). Autocorrelator measurements were limited to 500–2000 nm wavelength range. Therefore, Fourier-transform-limited (FTL) pulse duration is provided for the 400–480 nm range. FTL values were estimated from the OPA spectral bandwidth measurements recorded using visible-range (AvaSpec-3648, Avantes) and near-infrared (NIRQuest-512, Ocean Optics) spectrometers.

Figure 2:

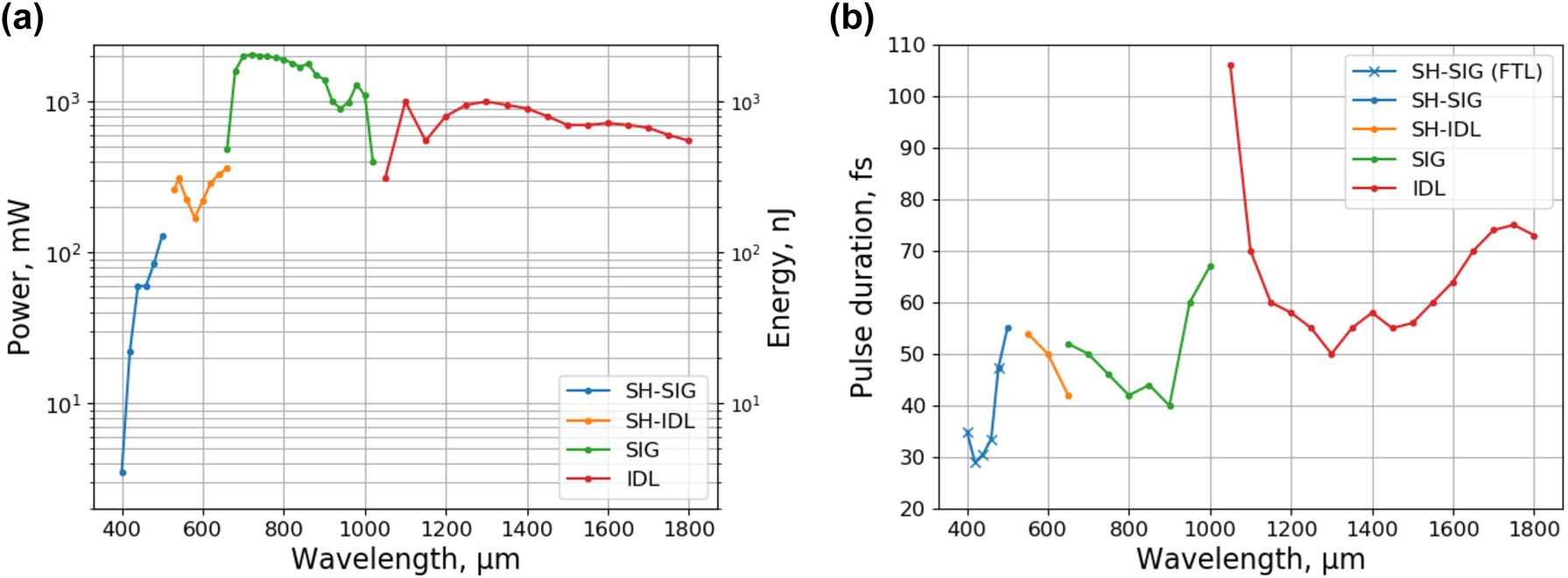
OPA parameters at system output, (a) – average power and pulse energy, and (b) – minimum pulse duration. Fourier-transform-limited values are given in the 400–480 nm range.

Automated beam and pulse conditioning is essential to the investigation of wavelength and pulse duration effects as they allow to study non-linear processes in MPP as function of a single parameter, while maintaining all other laser parameters constant. The compressor unit is capable of automated pulse GDD control over the entire 400–1800 nm OPA tuning range. In order to provide positive and negative GDD compensation capability with a single set of prisms, a design utilizing a prism compressor with a set of glass plates was chosen. Figure 3(a) shows the principal diagram of the compressor. Negative chirp is induced by tuning tip-to-tip prism spacing and the amount each prism is inserted into the beam, while positive chirp is created in discrete amounts by inserting or removing of glass plates. Such a combination expands GDD pre-compensation in the NIR range where many optical glasses exhibit anomalous dispersion. Similar folded prism compressor designs have been employed before [27, 28]. However, the presented design ensures that the optical path length through the compressor and, therefore, the pulse delay changes are minimized. Over the entire wavelength range, the pulse delay varies only by a few ps when GDD is tuned by changing the prism spacing. Insertion of glass plates adds from 16 to 93 ps delay for pulses in the NIR range when a positive chirp is needed. Such small delays can be compensated using a compact delay line suitable for most microscopy setups. This aspect is important in applications employing more than one laser pulse, for example, CARS, SRS and SFG, where temporal overlap between interacting pulses must be maintained [29].

Figure 3:

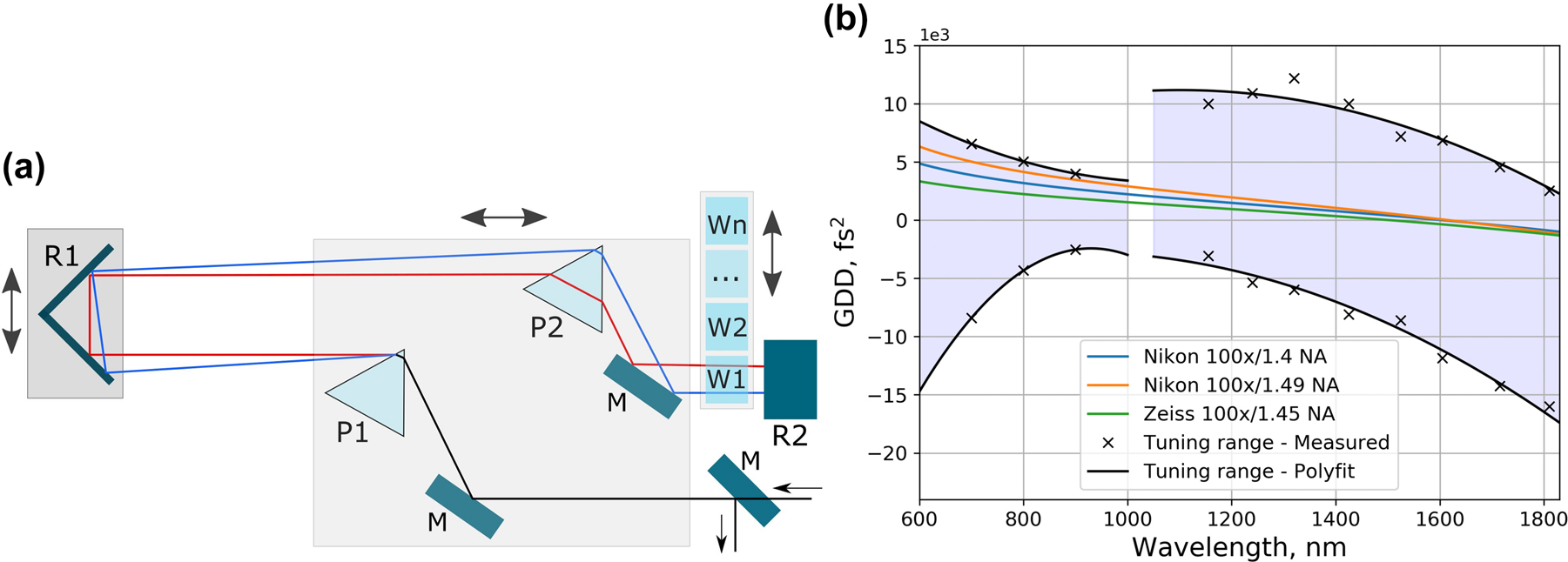
Group delay dispersion control: (a) – Principal diagram of the compressor. M – mirror, P – prism, R – retroreflector, W – glass plate. Double arrows represent compressor tuning by translating the components in the greyed-out areas. (b) – Compressor GDD tuning range compared to the dispersion of several high-NA immersive objectives.

Figure 3(b) shows the measured GDD compensation range of the compressor, as well as the theoretical dispersion values required for the compensation of several high-NA objectives typical in MPP applications. The objective GDD values were estimated from the optical prescription information provided in patents for 100 × 1.4 NA [30] and 100 × 1.49 NA [31] objectives patented by Nikon, and 100 × 1.45 NA objective patented by Zeiss [32]. The objective is usually the main source of dispersion in microscopy and nanopolymerization setups, and the presented compressor design is able to compensate the objective GDD over a broad range with a margin for other optical components in the setup.

2.3 Polymerization threshold and voxel size measurements

The intensity threshold values for polymerization were determined using the resolution bridge (RB) technique [33]. This technique is based on the manufacturing of thin lines of polymer suspended between large support columns. The experimental procedure and an example of a scanning electron microscopy (SEM) image of an RB object is shown in Figure 4. Each line had a length of 75 µm and was polymerized at a fixed intensity (I) in a single stage movement at a typical velocity of 100 μm/s. The intensity level was increased for each adjacent line from the pre-threshold value until the onset of damage. An offset of 8 µm from the monomer-substrate interface was used. To determine the voxel size, the width and height of the polymerized lines were measured from the SEM images obtained from perpendicular and 45°-tilted views. A region-of-interest (ROI) of 1000 × 200 pixels was defined at the center of each polymerized line. It included the center ∼25 µm of the line for analysis. Then, each pixel column in the defined ROI was evaluated to determine the top and bottom boundaries of the line. The difference between the top and bottom boundaries was used to calculate the mean size value and its variation across the ROI for each polymerized line.

Figure 4:

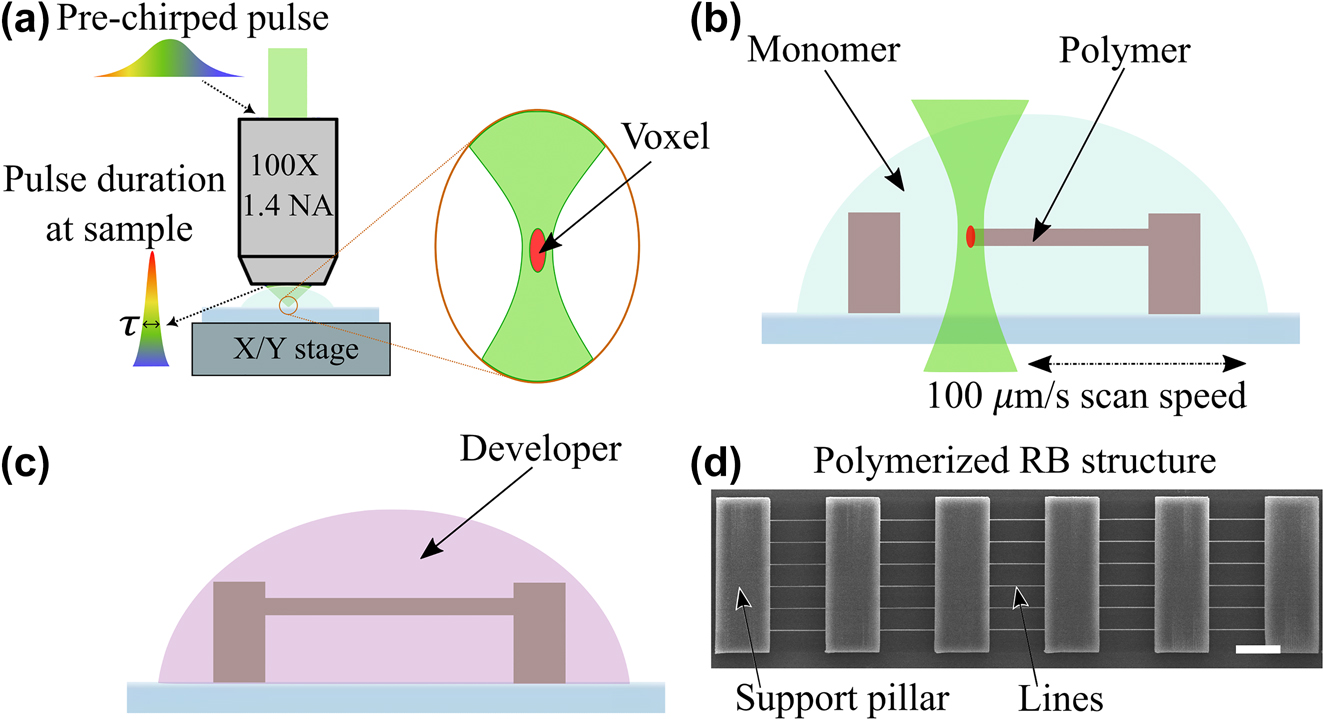
Experimental procedure: (a) – focusing of the pre-chirped pulse into the sample; (b) – multi-photon polymerization of RB structure; (c) – development of the sample; (d) – SEM image of an entire RB object with lines and support pillars. Scale bar is 20 µm.

2.4 Prepolymer material

Experiments were conducted using the SZ2080^TM prepolymer (Foundation for Research and Technology – Hellas (FORTH)), and photoinitiator 2-benzyl-2-dimethylamino-1-(4-morpholinophenyl)-butanone-1 (IRG369, Sigma Aldrich). The photosensitized mixture was prepared by adding PI (1% w/w of prepolymer) and stirring with a magnetic stirrer until the PI dissolved. Before the experiment, both pure and photosensitized SZ2080^TM were kept at 4 °C temperature. Absorbance spectra of the SZ2080^TM prepolymer and the IRG369 photoinitiator are shown in Figure 5.

Figure 5:

Absorbance spectra of the prepolymer and the photoinitiator. Blue lines represent measured 1P absorbance spectra (solid line) [34] and the corresponding expected 2P (dashed line) and 3P (dotted line) absorbance spectra of the SZ2080^TM prepolymer, marked as calc. in the legend. Red lines represent measured 1P absorbance spectra of the IRG369 photoinitiator (solid line), the same spectra shifted to the 2PA maximum measured using the Z-scan technique (dashed line) [35], and the corresponding expected 3PA spectra (dotted line). Vertical lines mark typical wavelengths used in MPP.

2.5 Sample preparation and analysis

Microscope coverslips (REF VBS638, Biosigma, Cona VE, Italy) were cleaned in an ultrasonic bath (EMAG Technologies, Mörfelden-Walldorf, Germany) in isopropanol for 20 min. To strengthen the adhesion between the polymerized objects and the coverslips, they were immersed in a mixture of isopropanol and 3-(trimethoxysilyl)propylmethacrylate (MAPTMS) (40:1 v/v). Afterwards, the coverslips were cleaned with acetone and pure or photosensitized prepolymer was drop-casted onto them. Prepared samples were dried on a hot plate (PZ 28-3T) controlled by programmer (PR 5-3T, Harry Gestigkeit GmbH, Düsseldorf, Germany). When the polymerization experiment was finished, the uncured prepolymer was developed with 4-methyl-2-pentanone. The samples were dried using a critical point dryer (CPD) (K850, Quorum Technologies, East Sussex, UK) and were sputtered with a 10 nm silver layer employing a rotary pumped coater (150R S, Quorum Technologies, East Sussex, UK). A SEM microscope (Prisma E, Thermo Fischer Scientific, Eindhoven, The Netherlands) was used to record images of the obtained suspended lines and determine the polymerization and damage thresholds.

3.1 Processing window: from threshold to breakdown

Despite MPP being a thresholded process, it was difficult to identify the polymerization threshold optically due to the nanoscale voxel size and a limited photo-induced refractive index change which is also intensity-dependent [36]. In contrast, the threshold was unambiguous in SEM images, where the first polymerized RB was already structurally strong enough to withstand the development in solvent and CPD. It is noted that the surviving lines were observed using SEM at distinctively lower I values in comparison to the optical microscope before the development. The MPP reaction has presumably started at an even lower intensity level; however, the polymerized lines were either discontinuous or structurally weak and collapsed during post-processing. Therefore, it must be taken into consideration that polymerization thresholds determined from SEM images are affected by geometry-related structural strength requirements. Theoretically, the threshold would be lower for shorter RBs or other self-supporting structures. Damage threshold estimates were also different for optical and SEM images. The formation of bubbles was optically seen at a lower intensity level, especially at shorter wavelengths where 2PA was expected (see Figure 7(a)). However, after the development in solvent and CPD, SEM images of the same RB series indicated optical damage threshold at a higher intensity level. This disparity could be explained by solvent post-processing, where the bubbles that were visible optically are washed off the RB surface or partially dissolve due to the large surface area of the bubble. Since post-processing in the solvent is an inseparable part of the MPP process, damage thresholds obtained from SEM images were used in further analysis.

Figure 7:

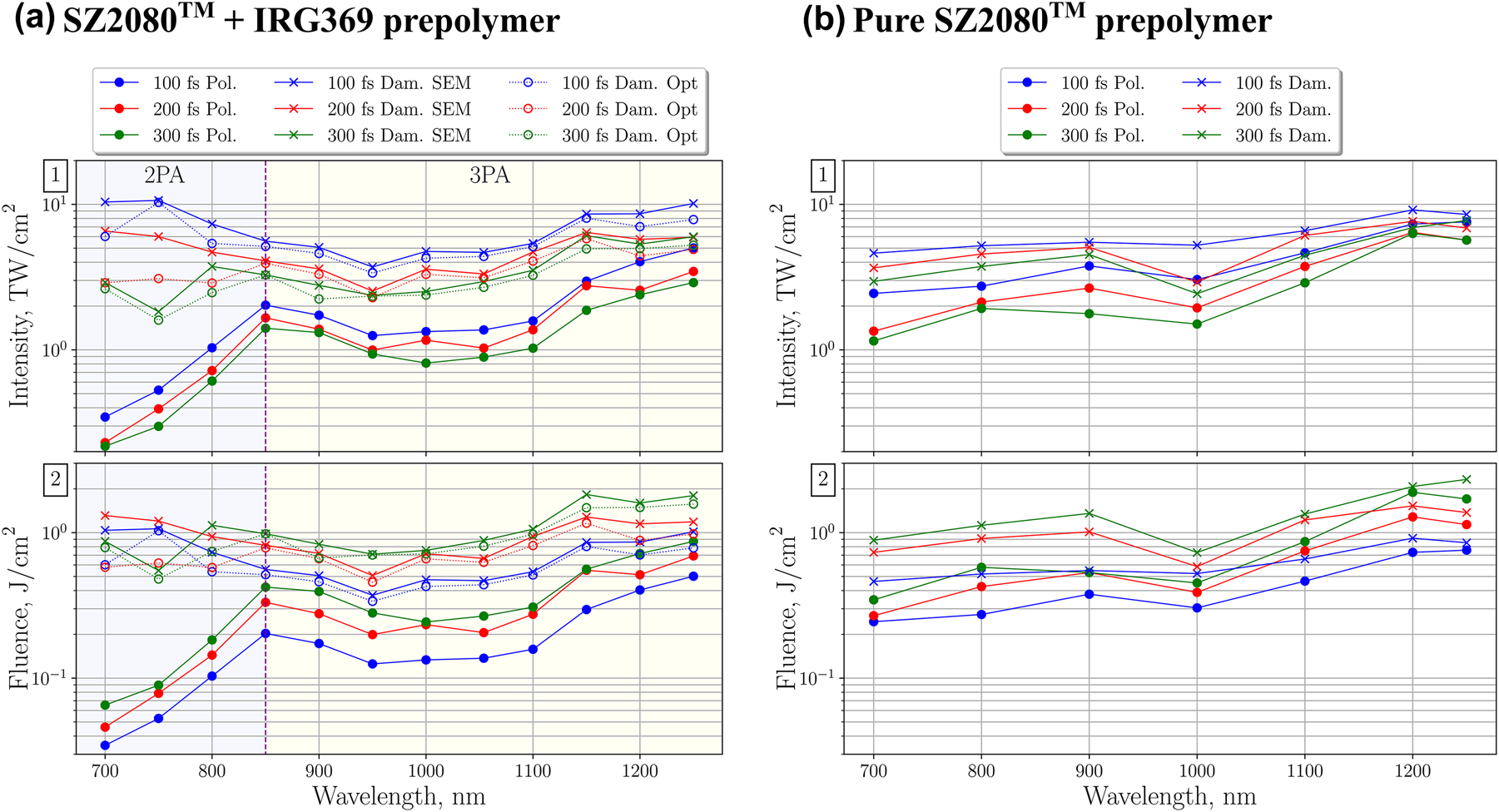
From the top: (1) polymerization threshold (solid lines with solid dot markers) and optical damage threshold (solid lines with cross markers) dependence on λ, when τ = 100, 200 and 300 fs. SZ2080^TM + IRG369 prepolymer includes damage thresholds recorded optically during the MPP process (dashed lines with empty circle markers); (2) fluence level at the same thresholds.

The dependence of the polymerization and optical damage thresholds on the wavelength and pulse duration for both SZ2080^TM + IRG369 and pure SZ2080^TM prepolymers are summarized in Figure 7. In both prepolymers, MPP was achieved at all wavelengths within the 400–1300 nm range. However, threshold values could not be reliably determined after the objective for sub-700 nm wavelengths due to limited autocorrelator range, thus the data was omitted from the analysis.

The polymerization threshold trend in SZ2080^TM + IRG369 prepolymer correlates with the expected multi-photon absorbance spectra (see Figure 5). The lowest polymerization threshold was recorded at 700 nm, which corresponds to the reported 2P absorbance peak in the photoinitiator, centered on 670 nm. This wavelength also corresponds to a considerable level of expected 3PA in SZ2080^TM. 2PA in the photo-initiator was dominant at the polymerization threshold since the probability for 2P transitions is higher than that for 3P transitions. However, 3PA in SZ2080^TM molecules may come into play at higher intensities when most of the photo-initiator molecules have already been transitioned to an excited state. Under such a condition, concentration of the photo-initiator can contribute toward the damage threshold level as will be discussed later. The second polymerization threshold dip was observed at ∼1050 nm, which corresponds to the expected 3P absorbance peak depicted in Figure 5. The transition from 2P to 3P excitation regime was centered on ∼850 nm, while the expected transition in the photoinitiator absorbance spectra is centered on ∼800 nm. The transitional absorption gap was found to be narrower than what the expected absorbance spectra suggests. One possible explanation for this is that prepolymer molecules have complex energy level structure and can store photon excitation energy in a variety of ways including: translational energy, rotational energy, vibrational energy and electronic energy. The combination of these different states leads to a broadening of the spectral absorption lines and can even result in shifted multi-photon absorption peaks.

No clear transition between non-linear absorption regimes could be observed for the optical damage threshold. This is due to optical damage being caused by avalanche ionization rather than just the multi-photon absorption. Optical breakdown thresholds presented in row 1 of Figure 7 show that in 1000–1200 nm range the damage thresholds in SZ2080^TM + IRG369 and pure SZ2080^TM are nearly identical, with the largest difference of just 20% observed at 1100 nm. This suggests that at the concentrations of photoinitiator used it does not contribute substantially to the damage process. This matches with findings reported by Fischer et al. with several different photoinitiators [37]. In contrast, at shorter wavelengths where 2PA starts to dominate, the addition of IRG369 photoinitiator resulted in up to 2.2× higher optical damage threshold than in pure SZ2080^TM prepolymer.

3.2 Pulse duration and wavelength dependence of polymerization

The pulse duration was found to affect both polymerization and damage thresholds. As the pulse shortens, the threshold intensity level increases. However, at the same time, the threshold fluence level is reduced, as shown in row 2 of Figure 7. MPP with shorter pulse duration required less optical energy, thus, a reduction in optically-induced thermal effects can also be expected. Cross-linking and radical diffusion are both temperature-dependent processes [38, 39]. In some prepolymers, thermal effects can limit the polymerization resulting in unwanted voxel spread [40], while in others; temperature-accelerated termination helps to achieve smaller voxel size [41]. As shown by the results, tunable τ can be used as a variable to control the fluence level, which in turn could provide control over the degree of thermal effects. In general, experimental results show nearly constant inverse τ-dependence for the polymerization and damage thresholds in both prepolymers. However, τ was found to have a stronger non-linear influence on the damage threshold within the 2PA region in the photosensitized prepolymer. For example, compressing the 700 nm pulse from 300 fs to 100 fs increased the optical damage threshold from 2.9 to 10.3 TW/cm² in the SZ2080^TM + IRG369 prepolymer, while a change from 2.9 to 4.6 TW/cm² was observed in pure SZ2080^TM. This, in turn, contributed toward 2PA region having the widest and τ-dependent dynamic fabrication window, which is defined as:

Here I _pol and I _dam are intensity values of the polymerization and damage threshold, respectively.

The DFW in SZ2080^TM + IRG369 prepolymer is shown in Figure 8 and the values are provided in Table 1. Here we see the transition between 2P and 3P polymerization regimes, which correlates with the expected photoinitiator absorbance spectra from Figure 5 shifted by ∼50 nm. As previously discussed, multi-photon absorbance lines seem to be wider than expected from Figure 5. DFW λ-dependence is linked to the fact that the 3P process at longer wavelength requires I ^3/2 higher intensity level than the 2P process, while the optical breakdown threshold increases with wavelength but does not scale directly with the order of the absorption non-linearity. As a result, the 2P polymerization region has higher DFW values than the 3P polymerization region. The highest DFW value of 29 was achieved for 100 fs, 700 nm irradiance. Although 800 nm is a standard wavelength used for MPP, decreasing it by just 100 nm results in the increase of DFW by the factors of 2.4 or even 4.8 for 300 fs and 100 fs pulses, respectively. These findings emphasize the importance of both λ and τ optimization for maximizing the DFW in 2P polymerization. Regarding 3P polymerization regime, the highest DFW value was recorded at the 1050–1100 nm 3PA peak. Interestingly, the DFW was found to also be τ-insensitive in this region.

Figure 8:

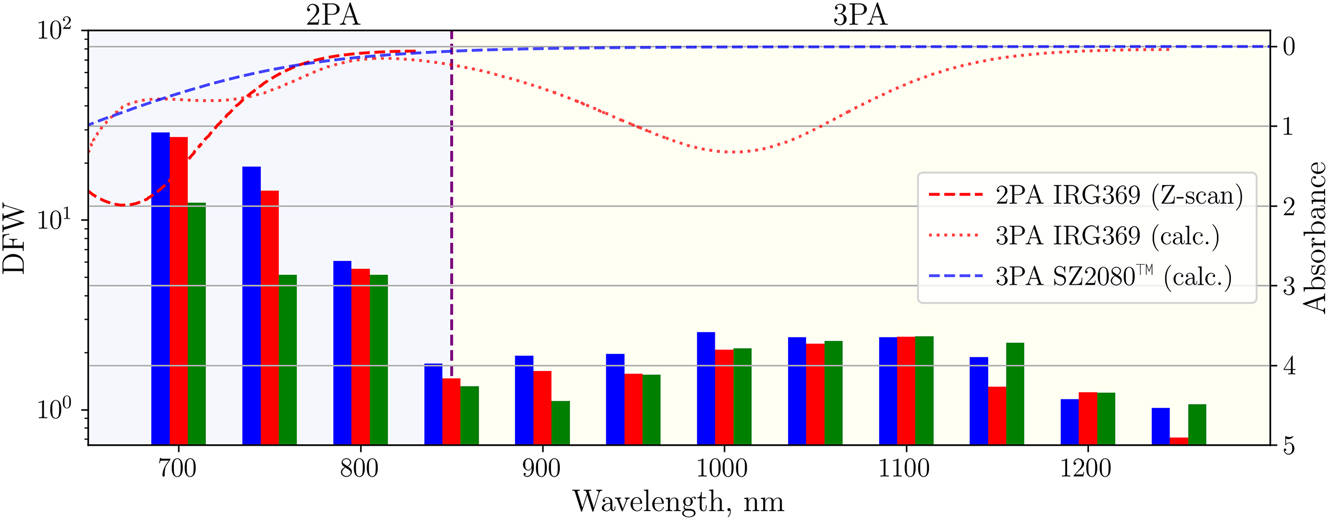
DFW dependence on λ and τ in SZ2080^TM + IRG369 prepolymer. Measured and expected (marked as calc. in the legend) multi-photon absorbance spectra of SZ2080^TM and IRG369 are presented on an inverted secondary Y axis on the right.

Figure 9 shows the voxel size limits and growth dynamics for the SZ2080^TM + IRG369 prepolymer case. The thinnest polymerized lines were obtained at 2PA and 3PA peaks – 0.21 µm and 0.18 µm, respectively, while at other wavelengths, the minimum lateral voxel size was larger. Somewhat surprisingly, thinner lines were obtained at longer wavelengths, despite the concomitant increase in diffraction limit. One explanation for this is higher-order non-linear absorption at longer wavelengths. The maximum obtainable lateral voxel size was found to be strongly λ-dependent and generally followed the DFW trend. The widest voxel of 4.5 µm was obtained at 700 nm irradiance. This value dropped to sub-µm levels at wavelengths exceeding that of the 3PA peak. The dependence of the longitudinal voxel size closely correlates with the lateral voxel size. However, longitudinal voxel size was generally significantly greater than the lateral dimension due to beam propagation along this axis. The average aspect ratio obtained at the polymerization threshold varied from 2.9 to 3.7 in 2P polymerization region and from 3.6 to 4 in 3P polymerization region for different pulse duration.

Figure 9:

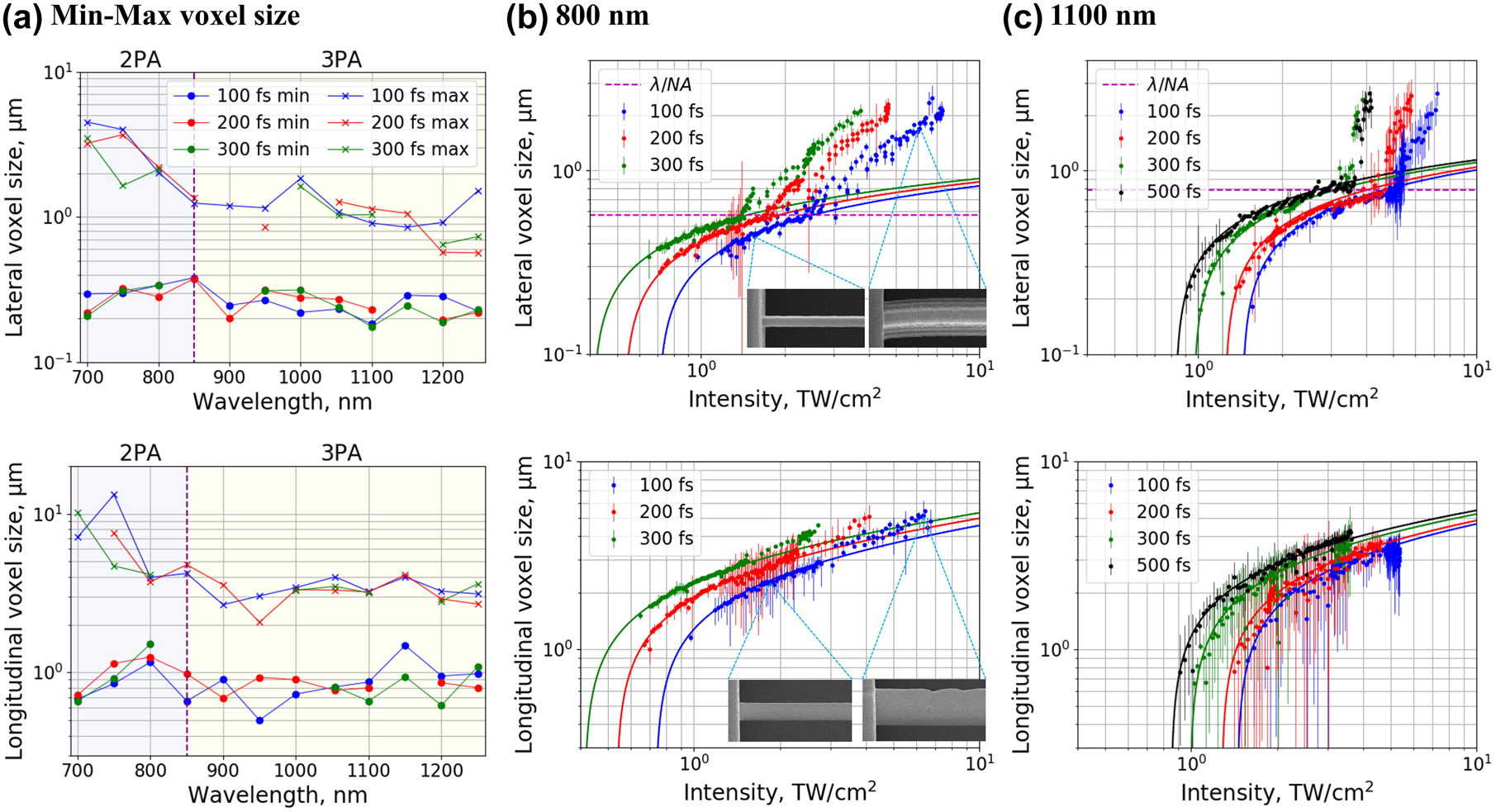
Experimental results of voxel growth. (a) Minimum and maximum voxel size dependence on λ and τ; (b) and (c) lateral and longitudinal voxel size dependence on the applied intensity with different τ for 800 nm and 1100 nm wavelengths respectively in SZ2080^TM + IRG369 prepolymer. Solid lines represent voxel growth model curves. Dashed horizontal line marks the diffraction limit. Polarization of the writing beam was set to linear. Sample SEM images of lines polymerized at 1.6 TW/cm² and 6.1 TW/cm² intensity levels are provided for the 800 nm, 100 fs case.

Figure 9(b) and (c) represent the voxel growth dynamics with increasing intensity at several τ values when λ was set to 800 nm and 1100 nm, respectively. The latter dataset includes additional results obtained with 500 fs pulse duration, which conform to the observed trends. The voxel growth can be approximated using Eqs. (2) and (3) for lateral (d _r ) and longitudinal (l _z ) growth, respectively [42].

Here, r ₀ and z _r were fixed parameters for each λ, while the order of absorption N was variable for each λ and the polymerization threshold I _th was set as a variable with initial experimental value for each λ and τ combination.

Interestingly, lateral voxel growth was found to depart from the model curve after reaching the size close to the diffraction limit of ∼λ/NA. Pulse duration and intensity level had no observable effect on the transition point. After reaching the transitional voxel size, further lateral growth switched to nearly linear I-dependence with a slope of γ = 1 in the 2PA region and γ = 2 in the 3PA region. Similarly, a departure from the expected trend was also observed for longitudinal voxel growth. The transition happened after reaching the longitudinal voxel size of ∼ 2 z r . It must be noted that lateral and longitudinal transition points were correlated and, in the 2PA region, occurred well below the damage threshold. For example, at 800 nm the transitional lateral and longitudinal voxel sizes for a given pulse duration were reached at the same intensity level, equal to ∼1/3 of the damage threshold. However, in the 3PA region, lateral and longitudinal transitions were observed at intensity levels equal to 70–100% of the damage threshold, with the closest equivalence observed at the 3PA peak. At 1100 nm, voxel growth did not diverge from Eq. (3) until the optical breakdown threshold. However, at adjacent wavelengths step-wise transition was observed before optical damage occurred.

The deviation from the expected voxel growth rate could have been caused by the overfilling of the back aperture of the objective. Under such a condition it would behave as a hard aperture causing rings of diffraction orders to form around the diffraction-limited focal point. Once the intensity level for a given pulse duration reached the polymerization threshold in the entire diffraction-limited volume, the outer diffraction rings might have started contributing toward the MPP process, resulting in the step-like change in the power law of polymerization.

3.3 Mechanism: step-wise change in power law of polymerization

To obtain further insights into the polymerization mechanisms reflected in the step-like changes of γ-slope in the power dependence of the lateral and axial voxel sizes (Figure 9), the energy deposition into the focal volume is considered next. Absorbed energy density per volume [J/m³] is driving physical and chemical modifications along the pulse propagation, especially since J/m³ ≡ N/m² ≡ Pa. i.e., pressure. This is suggested by the irregular patterns at high-intensity I _p ≥ 7 TW/cm² in Figure 6. The sole parameter describing the light–matter interaction at the focal region is the instantaneous refractive index ε ≡ n ̃ = ( n + i κ ) , where ɛ is the permittivity. The starting photo-polymer is a dielectric-like medium with negligible absorption (1.5 + i0) in the visible and NIR spectral range. The axial length of the polymerized focal region is up to a few micrometers and is much smaller than the pulse length (100 fs corresponds to 30 µm length). It can be thus considered that the entire focal region is exposed to the laser pulse. Upon optical excitation and free carrier generation, the real part of n is reduced while the imaginary κ is increased; the dielectric breakdown by definition is Re(ɛ) = 0 (hence n → 0). Both n and κ contribute to scattering (reflection is a type of back-scattering) and absorption. As revealed by the experiment, the diffraction limit is important for the onset of different polymerization power laws. A logical conjecture is to expect this change to be related to the change in light scattering from the sub-diffraction limited polymerized region since polymerization as densification and crosslinking is usually linked to an increase in n. There is a change of phase by π at the interface for the transmitted/reflected beam when the refractive index transitions from low to high and the lower n value is expected on the optical axis. When the index n contrast along the propagation is reversed from high to low, no phase change occurs. A lower reflectance R contributes to a stronger absorbance since A = 1 − R−T, where T is transmittance. Such redistribution of the pulse energy can enhance local energy deposition and the observed lateral spread of polymerization merging with the Airy disk as discussed earlier.

A stronger absorption due to augmented κ via increased free carrier density facilitates a positive feedback loop towards runaway breakdown. However, for short sub-1 ps pulses, this process is clearly controlled in the photo-polymer. Free-carrier absorption, which scales as ∝λ ² is a likely contributor to the step-like onset of the lateral voxel increase. This conjecture is probable due to observed stronger presence at longer wavelengths.

Competition between the decrease of n and increase in κ along the optical axis in a sub-diffraction limited volume can have one counter-intuitive contribution manifested in nanoscale deposition of energy and direct write nanolithography [43]. Namely, the normal component of the E-field (E _⊥) should satisfy the continuity of displacement ɛE _⊥ between the optically excited region on the optical axis and the surrounding pristine resist. Even a small difference in refractive index n low n high translates in intensity enhancement in the depressed index on-axis by a factor of I high = n high n low 4 I low , since I ∝ E ² and ɛ ∝ n ². For example, for n _high = 1.5 (resist) and 10% index decrease due to photo-excitation and ionization on the optical axis, the intensity is increased by 52%. Larger intensity increase exactly on the optical axis is expected when the material enters the epsilon-near-zero (ENZ) state ɛ = (n ²−κ ²) + i2nκ with n ≈ κ. With a laser pulse having ct _p ∼ 100 μm and a focal region of only 1–4 μm, the efficient energy deposition into the optically excited region is expected to take place during the very same pulse. As a result of the near-field on-axis enhancement of the field with a simultaneous increase of absorption (κ is augmented due to free carriers), longer axial polymerized features are expected and observed experimentally. The described qualitative picture applies to nanoscale laser writing [43] but not for features that are larger than the diffraction limit. The very same is observed in this experiment in the nanoscale (sub-diffraction) region of polymerization.

There are other factors that can further enhance energy absorption along the optical axis. Due to the tight focusing employed, there is a significant longitudinal E-field component E _‖ ∝ sin α, where α is the half-angle of the focusing cone. The E _‖ field is not reflected and contributes to a larger energy deposition. This type of energy deposition is referred to as resonant absorption and it has a strong contribution at tight focusing conditions [44]. At increasingly higher irradiance per pulse, close to the dielectric breakdown at ∼20 TW/cm²/pulse, the ionized focal volume acts as a metallic nanosphere and E-field enhancements change from the poles to the equator, causing a lateral increase of the E-field strength [45]. This drives a redistribution of the light intensity in the focal volume. Finally, an optomechanical action of high-power pulses E _p/t _p [W] could take place since Force = Power/c and can be accumulated due to a direct absorption (deposition of linear momentum) and reflection (doubled action per photon due to momentum reversal). A 10 nJ pulse of t _p = 230 fs exerts a force of F = 0.15 mN ( I p = E p / ( t p × ( π 0.61 λ / NA ) ) 2 ≈ 9.3 TW/cm² for λ = 500 nm and NA = 1.4). Energy deposition depth is the skin depth at the conditions of exposure l _abs = c/(2ωκ) (for intensity E ²) and can be sub-wavelength at high (pre-breakdown) irradiance.