Photon-pair generation in a lossy waveguide

2.1 Theoretical modeling

The split-step method was adopted to analyze the photon pair generation process in a lossy waveguide [17]. This method makes it easy to model the SFWM generation and propagation loss simultaneously, which is difficult to handle the propagation loss of single photons in a lump sum. A waveguide of length (L) is split into (M) segments of length (z = L/M). In each segment, the SFWM process occurs, and the loss process follows. These processes are repeated M times while the pump light passes through a waveguide. The SFWM and optical loss operators of the mth segment are as follows [18–21]:

where a x † and a _x are the photon creation and annihilation operators in a waveguide, respectively, and the subscripts x = {P, s, i} represent the pump, signal, and idler, respectively. γ and P _m are the Kerr coefficients of the waveguide and the pump power at the mth segment, respectively. The pump power at the mth segment is P _m+1 = P _m e^−αz , and P ₀ is the initial pump power in the waveguide. The wavevector mismatch Δk is Δk = 2k _P − k _s − k _i − 2γP _m , where k _x is the wavenumber. In our calculation, the influence of Kerr effect (2γP _m ), two-photon absorption, and free carrier absorption is sufficiently small below 2% under our experimental conditions. Therefore, we neglect the nonlinear loss and phase shift but consider the linear absorption loss α and Δk = 2k _P − k _s − k _i , to derive relatively simple equations for easy understanding and practical application. In addition, we ignored multiphoton pair events by assuming a low pump power. Eq. (2) is suitable for only one photon pair, and 1 − e − α z is approximated as α z , due to a small length z of the segment. In Eq. (2), the optical loss in a segment of length z can be described as a beam splitter with two input ports (one for input photons and the other for vacuum) and two output ports (transmission and reflection). A photon in the reflection port can be represented by the creation operator b m † , meaning that one photon of the photon pair is lost in the mth segment. The loss process for each segment is nonparametric and incoherent.

The operators function as follows for each Fock state:

The amplitude of the 11 state is much smaller than the 00 state as the pump power is small enough for ignoring multipair events. Therefore, the amount of transition from the 11 state to the 00 state is negligible compared to the existing 00 state. Therefore, the 00 terms were omitted in Eqs. (4) and (5).

Using the split-step method, the state of the photons passing through the mth segment is as follows:

According to Eq. (6), the amplitude of a Fock state 11 through the waveguide length L is given by

Therefore, the coincidence-count rate of photon pairs through a lossy waveguide of length L, considering the filter’s spectral bandwidth (Δν) and the channel efficiencies of the signal (η _s ) and idler (η _i ) photons, is as follows:

Assume that an idler photon is annihilated in the qth segment and the correlated signal photon passes through the remaining segments. This process can occur somewhere between the beginning of the waveguide (q = 1) and its end (q = M). Therefore, the total probability of the idler’s extinction and the signal’s survival is given as follows:

Finally, the single-count rate through a lossy waveguide of length L, considering the filter’s bandwidth and channel efficiency, is given as follows

Here, the multipair generation events and other nonlinear effects, including two-photon absorption, are neglected, assuming low pump power. The single-count rate for the idler photons is similar to that in Eq. (10), except when using the idler photon’s channel efficiency (η _i ). N _CC is a value related to only the two-photon states, but N _SC contains not only the two-photon states but also the one-photon states, which is the lost state of one photon in a photon pair, yielding a slight difference between the single-photon and two-photon brightness. The theoretical equations of N _CC and N _SC are consistent with the existing theory [22–24], and we show the difference between them experimentally.

2.2 Performance evaluation parameters

3.1 Fabrication

We fabricated several silicon photonic waveguides of various lengths to investigate the effects of propagation loss on photon-pair generation. In this study, we used a silicon-on-insulator platform. However, the investigation results were applicable to all material platforms using SFWM. The waveguides were patterned on a silicon-on-insulator chip with a silicon top layer of 260 nm and a buried oxide layer of 3 μm using KrF stepper photolithography. An inductively coupled plasma etcher with a mixture of C₄F₈ and SF₆ was used to transfer the waveguide patterns to silicon. The etching depth was set as 130 nm. Then, a SiO₂ layer was deposited on the chip as a top cladding by 1.4 μm. A cross-sectional scanning electron microscope image of the fabricated waveguide is shown in Figure 1(a). The waveguide width is 1 μm, and the waveguide lengths are 0.8 cm, 1.4 cm, 2.0 cm, 3.2 cm, 4.4 cm, and 5.6 cm. The measured absorption coefficient α is about 0.51 cm⁻¹ ( ≈ 2.22 dB/cm). Grating couplers are used to couple light in and out of a waveguide to a single-mode fiber.

Figure 1:

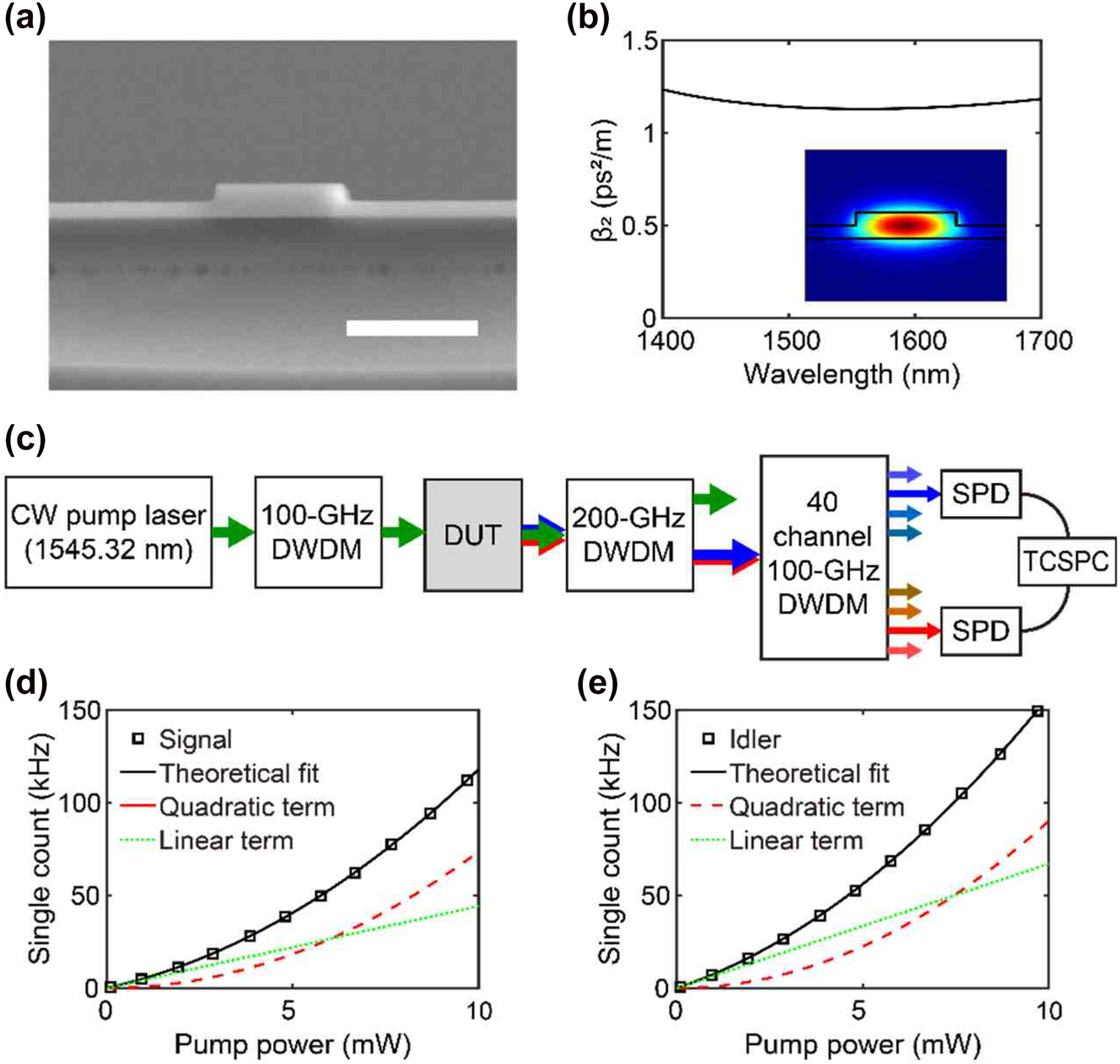
(a) Cross-sectional scanning electron microscope image of a fabricated waveguide. The scale bar is 1 μm. (b) Group velocity dispersion of the fabricated waveguide against wavelength. The lower right inset is the computed electric field profile of the optical transverse-electric-like mode. (c) Schematic diagram of the apparatus used to measure the properties of generated photon pairs. Components of the apparatus are labeled as follows: CW, continuous wave; DWDM, dense wavelength division multiplexing; DUT, device under test; SPD, single-photon detector; TCSPC, time-correlated single-photon counting circuits. (d) Measured single counts of signal photons against pump power. (e) Measured single counts of idler photons against pump power. The black squares in (d) and (e) are the experimental data, and the solid black lines are quadratic fittings of measured data. The dashed red and dotted green lines represent the quadratic and linear contributions of the fitting functions, respectively.

3.2 Simulation

COMSOL Multiphysics software was used to estimate the wavevector mismatch (Δk) using the mode-eigenvalue solver based on the finite element method. Figure 1(b) shows the group velocity dispersion (β ₂) extracted from the numerical calculations. β ₂ is 1.13 ps²/m and is almost constant over the C-band. Note that a zero-GVD wavelength does not exist in the telecom band, as shown in Figure 1(b). It is known that photon-pair generation with a small detuned frequency from the pump frequency occurs near the zero GVD wavelength. However, our recent results show that if the phase-mismatch parameter ΔkL is less than 1 [31], photon pairs can be created in an optical fiber, regardless of the zero GVD wavelength. If we apply this concept to silicon photonic waveguides, photon pairs can be generated even in a waveguide at a frequency far from the zero GVD wavelength. Therefore, a rib-type waveguide can be a photon-pair source as long as the waveguide length is sufficiently short, even if it has no zero GVD wavelength. Because a rib-type waveguide typically has less scattering loss than a ridge-type waveguide, the use of rib-type optical waveguides is advantageous in quantum optics experiments.

Using the second-order Taylor approximation [24], the wavevector mismatch is approximately

where df is the detuned frequency relative to the pump frequency ( d f = f P − f s = f P − f i ) and f _x is the frequency of pump, signal, or idler photons. Assuming that the detuned frequency of the signal and idler photons from the pump frequency is df = 300 GHz, the calculated wavevector mismatch is Δk = 4.01 m⁻¹. Then, photon pairs can be generated in the fabricated silicon waveguides with a length of dozens of centimeters. The inset of Figure 1(b) shows the fundamental transverse electric-like mode in a waveguide with the same waveguide geometry as shown in Figure 1(a).

3.3 Experiment

A schematic of the experimental setup is shown in Figure 1(c). The pump light source was a continuous-wave laser operating at 1545.32 nm, and a series of 100-GHz dense wavelength division multiplexing (DWDM) filters suppressed the sideband noise photons of the pump. The pump light passes through the device under test, and then a series of notch filters (200 GHz DWDM filters) filters out the pump from the generated photon pairs. Then, the signal photons are spectrally separated from the idler photons using a 40-channel 100-GHz DWDM module. The bandwidth Δν of the DWDM module was 0.6 nm. Photons were detected using superconducting nanowire single-photon detectors (Scontel). The estimated channel efficiencies of the signal and idler photons were approximately −15.5 and −14.7 dB, respectively. A time-correlated single-photon counting (TCSPC) module was used for the coincidence count measurements.

In addition to the generated signal and idler photons, single-photon detectors detect noise photons, including Raman-scattered photons, pump leakages, and dark counts. The single-count rate of each detector can be described as a quadratic function of pump power [30]. The quadratic term for the pump power is related to the generated signal or idler photons, whereas the noise photons contribute to the linear term. The dark counts of the detectors did not correlate with the pump power. The square markers in Figure 1(d) and (e) are the measured signal and idler single-count rates against the pump power, respectively. The theoretical fits were obtained using the quadratic function of the pump power and are shown as solid black curves superimposed on the data. The quadratic and linear contributions of the fitting functions corresponding to pair generation and noise photons are shown as dashed red and dotted green curves, respectively. The dark count rates were approximately 100 Hz and were negligible. Using the quadratic contributions of the fitting functions, we can estimate the contribution of the generated signal or idler photons to single-count rates, removing the contributions of noise photons and dark counts in the raw single-photon counts. However, CAR is affected by the contributions of noise photons according to Eq. (15).

4.1 Length dependence

The experimental results for brightness, heralding efficiency, and coincidence-to-accidental ratio are shown in Figure 2. From the simulation results for β ₂ and Eq. (16), the calculated wavevector mismatch is Δk = 4.01 m⁻¹ with df = 300 GHz, and the phase mismatch parameter can be neglected (ΔkL ∼ 0) by assuming a short waveguide L ≪ 1 m. From the measured absorption coefficient α = 0.51 cm⁻¹, the waveguide length for the maximum coincidence-count brightness is L _max = 1.96 cm and as shown by the magenta dashed lines in Figure 2. The red square markers in Figure 2(a) are the measured coincidence-count brightness (B _CC), and the B _CC value has a maximum value of 82 kHz/mW²/nm at a 2.0-cm ( ∼ 1 / α ) long waveguide. Kerr coefficient γ ≈ 114 W⁻¹ m⁻¹ is obtained from the γ value where the experimental data of B _CC, B _SC,s , and B _SC,i fit well to Eq. (11) and (12). The green circle and blue triangle markers in Figure 2(a) represent the measured single-count brightness of the signal (B _SC,s ) and idler (B _SC,i ) photons, respectively. From Eq. (12), the expected single-count brightness (B _SC) is shown as a dashed black curve in Figure 2(a) and has a maximum value of 126 kHz/mW²/nm at a 2.5-cm ( ∼ 1.26 / α ) long waveguide.

Figure 2:

Measured brightness and CAR with a 300-GHz detuned frequency. (a) Brightness against the waveguide length. The red squares (B _CC), green circles (B _SC,s ), and blue triangles (B _SC,i ) are the experimental data. The theoretical fit using Eqs. (11) and (12) are shown as solid red and dashed black lines, respectively, atop the experimental data. (b) The intrinsic heralding efficiency against the waveguide length. The green circles (HE _int,s ) and blue triangles (HE _int,i ) are the experimental data. The theoretical fit using Eq. (13) is shown as solid red atop the experimental data, and the dashed black curve is the linear approximation of HE _int ≈ 1 − 0.3αL for L ≤ 1/α. (c) The CAR against the measured coincidence counts for various waveguide lengths [0.8 cm, 3.2 cm, 4.4 cm, and 5.6 cm]. The symbols are the experimental data for various waveguide lengths. The theoretical fit using Eq. (15) is shown as solid black, dashed red, dotted green, and dashed-dotted blue atop the experimental data. The vertical dashed cyan line shows where N _CC = 1 kHz. (d) Standard CAR against the waveguide length. The black square represents experimental data. The theoretical fit (solid red) is obtained using Eq. (15) with g = 3972 HZ^1/2 and the extracted CAR value at N _CC = 1 kHz in (c). The dashed magenta lines in (a), (b), and (d) show where L = 1/α ≈ 1.96 cm.

According to Eq. (13), the heralding efficiency HE _int decreases as αL increases, as shown by the solid red curve in Figure 2(b). At L = 1/α, where B _CC has the maximum value, the expected HE _int ≈ 0.7. The measured intrinsic heralding efficiencies are 0.53 and 0.64 at a 2.0-cm long waveguide for signal and idler photons, respectively. The measured values differ from the theoretical expectation owing to fabrication and measurement errors, but the overall data trend follows the theory. When L ≤ 1/α, the intrinsic heralding efficiency can be approximated by a simple equation as HE _int ≈ 1 − 0.3αL, as shown by the dashed black curve in Figure 2(b).

Figure 2(c) shows that CAR generally decreases as N _CC and waveguide length increase. According to Eq. (15), CAR strongly depends on N _CC, and a high CAR value can be obtained at a low N _CC. Because such a low N _CC is not practical for quantum experiments, we define the CAR value at N _CC = 1 kHz, which is widely used in this study, as the standard CAR (vertical dashed cyan line) in Figure 2(c). In Eq. (15), the CAR is also affected by HE _int and g. The g value was extracted from the fitting results and was approximately 3972 Hz^{1 /2}. Figure 2(d) shows the experimental data of the standard CAR against the waveguide length owing to the influence of HE _int, which matches well with the theoretical value. This result shows that the waveguide length affects not only HE _int but also the standard CAR.

4.2 Frequency dependence

Figure 3 shows the brightness and HE _int against the detuned frequency for various waveguide lengths. According to Eqs. (11) and (12), B _CC and B _SC vary slowly when ΔkL < 1, and the B _CC value at ΔkL = 1 can be obtained with over 92% of the maximum B _CC, as shown in Figure 3(a). The slightly varying B _CC when ΔkL < 1 is similar for all waveguide lengths, as shown in Figure 3(b) and (c). The detuned frequency df for ΔkL < 1 is indicated by the gray region in Figure 3. As the waveguide length increases, the spectral bandwidth for ΔkL < 1 decreases. This result is consistent with our recent results for optical fibers [31].

Figure 3:

Brightness against the detuned frequency for the waveguide lengths of (a) 0.8 cm, (b) 2.0 cm, and (c) 4.4 cm. The red squares (B _CC), green circles (B _SC,s ), and blue triangles (B _SC,i ) are the experimental data. The theoretical fit using Eqs. (11) and (12) are shown as solid red and dashed black lines, respectively, atop the experimental data. The vertical dashed cyan line in (c) shows where ΔkL = 2π for L = 4.4 cm, and the grey regions represent where the detuned frequency for ΔkL < 1. (d) Intrinsic heralding efficiency of idler photons versus the detuned frequency for various waveguide lengths. The black, red, and green triangles (HE _int,i ) are the experimental data for L = 0.8 cm, 2.0 cm, and 4.4 cm, respectively. The theoretical fits for various lengths are shown atop the experimental data.

In Figure 3(c), the coincidence count brightness B _CC is zero when df ≈ 1.79 THz, where ΔkL = 2π. However, the single-count brightness B _SC is not zero because this phenomenon is related to the two-photon and one-photon states. The generation of two-photon states by SFWM is a parametric process that requires conservation of energy and momentum (phase-matching) conservation. From the phase-matching conditions, the probability of having two photons is zero when ΔkL = 2π. On the other hand, the one-photon states are caused by generating a pair of photons and losing one photon out of them, and the photon loss process is a nonparametric process that is not affected by the phase. Therefore, B _SC does not become zero when ΔkL = 2π.

Figure 3(d) shows that the spectral bandwidth of the signal photon HE _int,i decreased as the waveguide length increased. The spectrum of HE _int,s is similar to that of HE _int,i . The reduction in HE _int,i is negligible when ΔkL < 1, where B _CC is efficient.