Exfoliated Bi₂Te₃ nanoparticle suspensions and films: morphological and nonlinear optical characterization

1 Introduction

After the discovery of the thermoelectric properties of bismuth telluride (Bi₂Te₃) [1, 2] for a long time it was considered exclusively as a material for thermoelectric coolers. Meanwhile, Bi₂Te₃ also demonstrates the properties of topological insulators [3], [4], [5]. Currently, the use of topological insulators, and in particular bismuth telluride, is actively developing for applications in various areas of electronics [6]. In the last few years, various studies have been published that demonstrated the possibility of using the Bi₂Te₃-based photosensors in a wide range of wavelengths. In most of those studies, Bi₂Te₃ was used as a photosensitive component in the form of epitaxial layers [7] or individual nanoparticles (NPs): nanowires [8, 9] or nanoplates [10, 11]. This has led to a growing interest in the nanostructures of this material.

Previously, bulk bismuth telluride (energy bandgap E _g  = 0.13 eV, [12]) allowed the improvement of the characteristics of infrared (IR) radiation detectors [13]. The Bi₂Te₃ based materials grown by vacuum evaporation showed weak sensitivity in the case of mid-IR radiation (3–5 μm) at elevated temperature (195 K). At the same time, it was assumed that Bi₂Te₃ is generally similar to lead sulfide and has a maximum sensitivity in the range of 1–1.5 μm, and at the same time, a weak sensitivity is observed in the mid-IR only when the registrar becomes cooled. At room temperature, these nanostructured materials showed no sensitivity in the mid- and far-IR. Meanwhile, apart from the photosensitivity properties of Bi₂Te₃ nanostructures, this material may possess attractive nonlinear optical features. Bi₂Te₃ nanostructures found widespread applications not only in photodetectors and field-effect transistors but also as saturable absorbers in the mode-locked lasers or Q-switched lasers in different spectral regions.

Topological insulators are demonstrating saturable absorption (SA) in a broad spectral range. Additionally, topological insulators, such as bismuth selenide, demonstrate large nonlinear refraction, which is six orders of magnitude larger than that of bulk dielectrics. Recently, several papers have been published on the nonlinear optical properties of bismuth telluride [14], [15], [16], [17]. The effect of strong two-photon absorption (TPA) was demonstrated [14], while the mechanism of carrier transport leading to an increase of optical nonlinearity was also investigated [15]. The prospects of heterostructures based on bismuth telluride and reduced graphene oxide (rGO) for various optoelectronic devices are shown [16]. Broadband nonlinear optical properties of Bi₂Te₃ nanosheets have been investigated by both open-aperture (OA) and closed-aperture (CA) z-scan techniques using picosecond and femtosecond pulses [18]. The wavelength-dependent third-order nonlinear optical response of Bi₂Te₃ was experimentally reported and the third-order nonlinear refractive index was measured with a peak value of 2 × 10⁻⁸ cm² W⁻¹ at a wavelength of 1.93 μm. Those experimental results verified that Bi₂Te₃ nanosheet is not only a broadband nonlinear absorption material but also a medium possessing broadband Kerr-related features. All those nonlinear optical studies were carried out using short (pico- and femtosecond) laser pulses. Moreover, most of them were concentrated on the nonlinear optical absorption studies, while the fast Kerr-related mechanism of nonlinear refraction was considered only in Ref. [18]. In the meantime, the analysis of nonlinear refraction, SA, reverse mechanism of saturable absorption (RSA), and two-photon absorptionTPA using long (nanosecond) pulses can reveal the additional peculiarities of those processes, which could not be demonstrated using short laser pulses.

In this paper, we demonstrate the synthesis of exfoliated bismuth telluride NPs and analyze their nonlinear optical properties using 10 ns pulses at two wavelengths of laser radiation (1064 and 532 nm). We show that these structures possess the self-focusing properties and combination of SA and RSA (in the case of 532 nm probe pulses), as well as TPA (in the case of 1064 nm probe pulses). We compare the nonlinear refraction and nonlinear absorption of colloids and thin films of bismuth telluride nanostructures and show a significant growth of the nonlinear refractive index (γ) and nonlinear absorption coefficient (β) in the latter case.

2 Experimental arrangements, synthesis, and characterization of samples

Bi₂Te₃ nanostructures can be synthesized by different means. Micromechanical exfoliation method similar to the pioneer method for producing graphene is described in [19]. Rather complex hydro- and solvothermal methods [20, 21] and long-term (more than 15 h) high-temperature (more than 800 °C) gas-phase method [22] are described as well. In liquid exfoliation, the use of substituted pyrrolidones as a medium for dispersing mixtures is described in [14]. Exfoliation in a solution of lithium hydroxide in ethylene glycol over 70 h in an autoclave or in 1-buty-3-methylimidazole chloride at a temperature up to 150 °C was considered as an alternative method for the synthesis of nanostructures based on Bi₂Te₃ [23].

All the above-mentioned methods require the use of high temperatures or expensive equipment, as well as expensive and toxic dispersing media. At the same time, the analysis of the layered structure of bismuth telluride shows that, unlike graphite, it consists of repeated quintuple layers (QL) comprising five atomic layers in the sequence Te⁽¹⁾ – Bi – Te⁽²⁾ – Bi – Te⁽¹⁾ (Figure 1(a)), and the Van der Waals bounding between the QL [24]. In addition, the Bi–Te⁽¹⁾ bond is stronger than Bi–Te⁽²⁾, and it turns out that the Bi–Te⁽²⁾ bond, despite its covalent nature, has an energy not much higher than the Te⁽¹⁾–Te⁽¹⁾ bonds of neighboring QL [25]. Given that the thickness of each QL bound by the Van der Waals forces in Bi₂Te₃ is five atomic layers, which approximately corresponds to the dimension of 1 nm, it is fundamentally possible to delaminate the bulk bismuth telluride to the maximum thickness of 1–1.5 nm. Such weak bonds make it possible to obtain thin layers of Bi₂Te₃ using simple exfoliation methods without additional surfactants.

Figure 1:

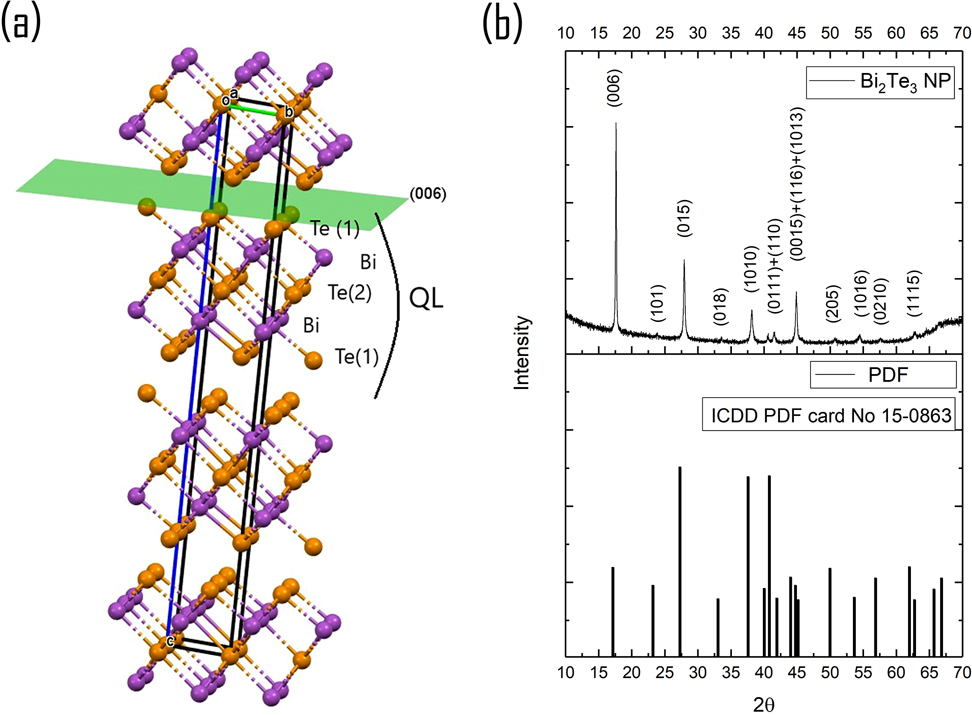
(a) Crystal structure of Bi₂Te₃ trigonal R-3m; (b) XRD of Bi₂Te₃ film drop-casted on Si wafer in comparison with ICDD PDF-card no. 15–0863, trigonal R-3m.

Previously, we have shown that it is possible to obtain stable dispersions of bismuth telluride NPs in alcohols using a simple laboratory ultrasonic bath [26]. Below we describe the procedure of samples preparation and characterization.

Preparation of Bi ₂ Te ₃ suspension. Suspension of two-dimensional (2D) Bi₂Te₃ NPs 0.01 M was made by liquid-phase exfoliation (LPE) of Bi₂Te₃ powder in butanol-1 with sonication bath (650 W) for 8 h at 30–45°С.

Preparation of Bi ₂ Te ₃ coatings. Bi₂Te₃ suspension was used for coating glass substrates by dip-coating method with different withdrawal speed (1.3 and 4.7 mm/h) immediately after LPE.

XRD. Bruker D8 Advance was used for the X-ray diffraction study of the Bi₂Te₃ suspension, which was drop-casted on Si substrate.

UV-Vis-NIR. These spectra were registered with the JACSO-770 spectrometer in the range of 310–2600 nm.

FTIR. Fourier transform infrared (FTIR) spectroscopy was made with Perkin Elmer Spectrum 100 FTIR in the range of 1.3–5.5 µm in transmission mode. Bi₂Te₃ suspension was drop-casted on a Si wafer.

ATR-FTIR. Multiple Attenuated Total Reflectance FTIR (or Internal Reflection Spectroscopy) was made with Perkin Elmer Spectrum 100 FTIR with HATR Accessory in the range of 1.3–16.6 µm. Bi₂Te₃ suspension was drop-casted on ZnSe ATR trough-plate (45°) in the same way as we prepared sample for transmission FTIR.

AFM. Atomic force microscopy of Bi₂Te₃ dip-coated glass substrates was made with Solver ProM (NT-MDT) in semicontacting mode. The coating was scratched to see the thickness of the films.

TEM. JEOL JEM-2100 was used for transmission electron microscopy of the fresh exfoliated Bi₂Te₃ suspension.

XRD of Bi₂Te₃ film drop-casted on Si wafer shows good matching of reflection position with PDF-card no. 15–0863 (trigonal Bi₂Te₃, R-3m) without any secondary phases or impurities (Figure 1(b)). The analysis of the mutual intensity of peaks in comparison with the PDF card 15–0863 showed very intense reflection from the plane (006) in the Bi₂Te₃ sample and an almost complete absence of reflection from the plane (101).

As it was recently shown in Bauer et al. [27], drop-casting of Bi₂Te₃ nanosheets dispersions in alcohol on substrate results in a preferred nanosheets orientation along the (001) plane that changes the relative intensities of the peaks and finally results in very intense reflex (006) (Figure 1(b)).

TEM images confirm the crystalline structure of obtained thin-layered Bi₂Te₃ particles, which also corroborates with XRD results. Each particle is an aggregate of several smaller thin 2D-crystallites with an average size of about 10 nm (Figure 2(a)). The aggregates had sizes of either 75–150 nm (Figure 2(c)), 200–300 nm (Figure 2(b) and (c)), or 600–1000 nm (Figure 2(c)). Atomic ratio Bi:Te was 2:3 according to EDS analysis. One can conclude that we obtained the Bi₂Te₃ NPs, which have a structure of the thin 2D sheets arranged in a stack along a (006) plane. In the perpendicular direction, the sheets apparently do not preserve the orientation of the lattice of the bulk material.

Figure 2:

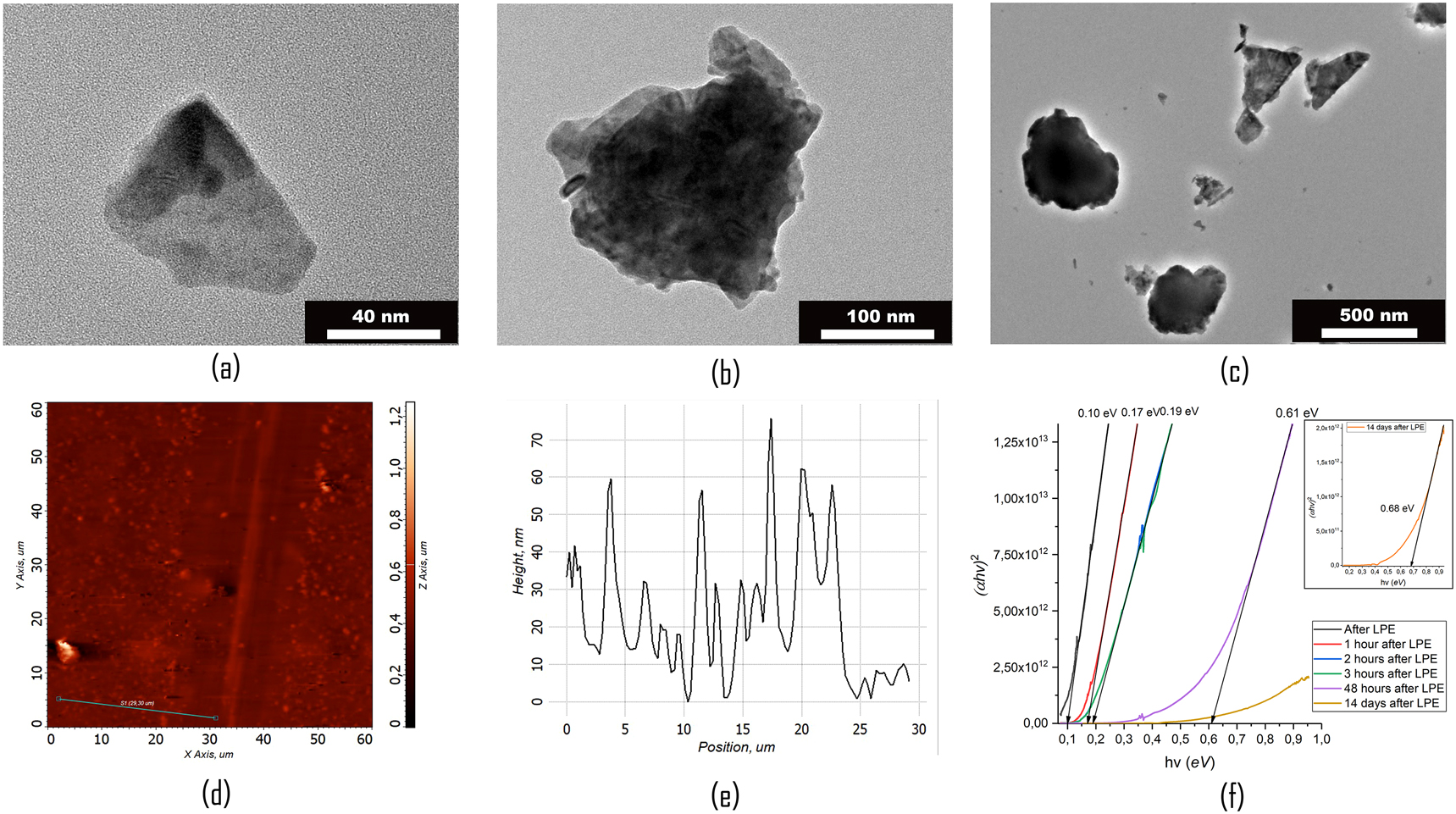
(a–c) TEM images of different Bi₂Te₃ particles in prepared suspension. AFM of surface (d) and cross-section of scratched Bi₂Te₃ coating (e) on the glass substrates (withdrawal speed 1.3 mm/h). (f) Calculation of bandgap using ATR FTIR spectrum.

Two thin films of different thicknesses were obtained by dip-coating from the same Bi₂Te₃ suspension at two withdrawal speeds (1.3 and 4.7 mm/h, respectively). AFM analysis provided 60–100 nm thickness for the sample prepared by the slower speed of dip-coating and 40–50 nm for faster withdrawal speed. Both layers have island-type structures, i.e. consist of large individual particle aggregates separated from each other (Figure 2(d) and (e)).

The absorption spectra of two coatings corresponding to different thicknesses are shown in Figure 3(a). According to Figure 3(a) and (b) bismuth telluride absorbs the light in a wide range from UV to mid-IR. The absorption spectra of Bi₂Te₃ NPs coatings have the same shape as those reported in [18]. However, the local maximum in our work is shifted to the shorter wavelength range (550–650 nm (Figure 3(a)), versus 700–800 nm in the [18]).

Figure 3:

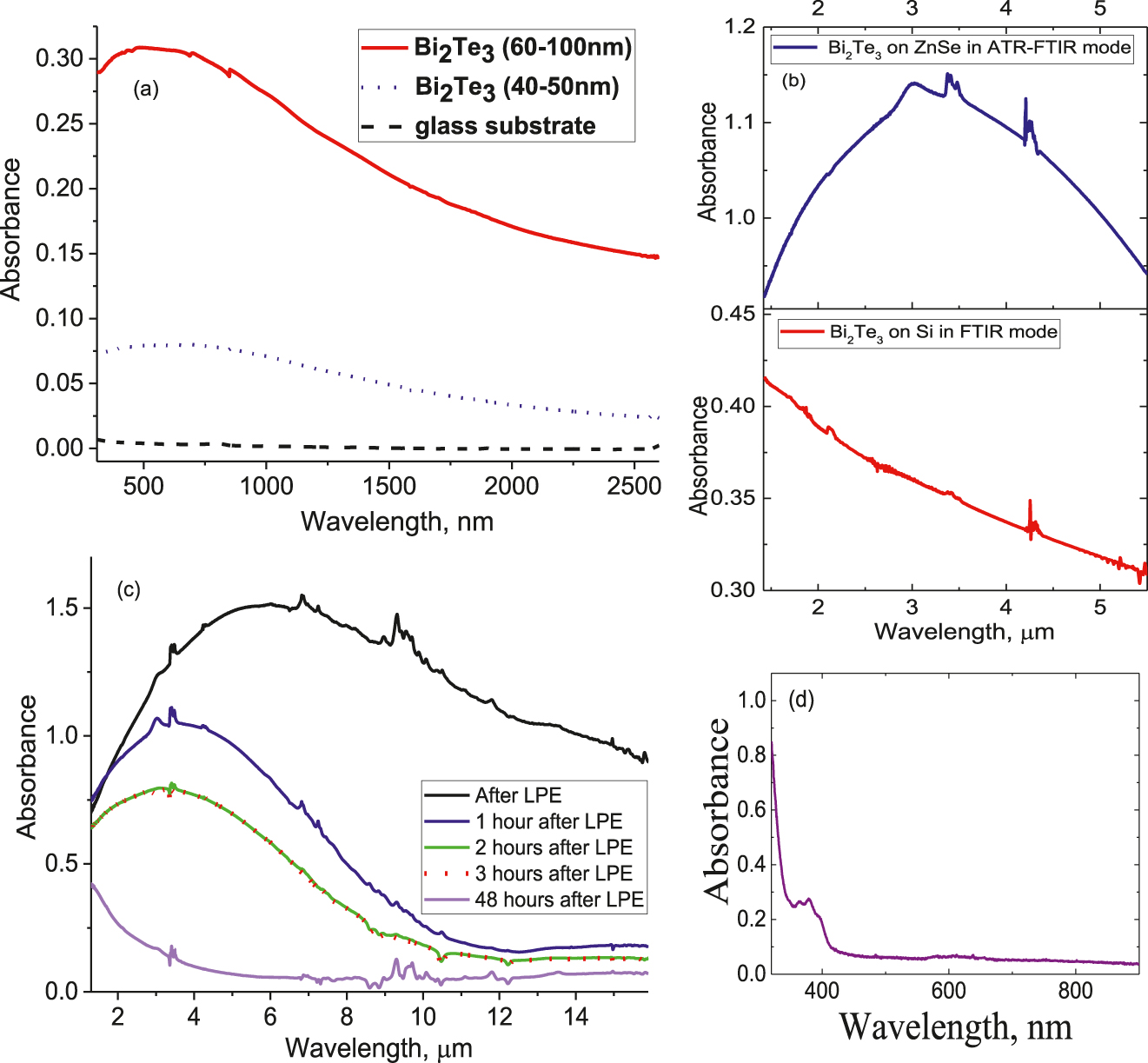
(a) Absorbance of Bi₂Te₃ coatings on glass substrates in UV-Vis-NIR with thickness 60–100 nm (withdrawal speed 1.3 mm/h) and 40–50 nm (withdrawal speed 4.7 mm/h) (b) Absorbance of Bi₂Te₃ film drop-casted on ZnSe by ATR-FTIR (top) and on Si wafer in FTIR mode, Si background excluded (bottom) (c) Absorbance of Bi₂Te₃ film drop-casted on ZnSe by ATR-FTIR using suspension after LPE (d) Absorbance of Bi₂Te₃ NPs suspension in UV-Vis-NIR.

A significant difference was observed in FTIR and ATR-FTIR spectra (Figure 3(b)). The ATR method is intended for the characterization of thin films and surface layers since it has a small penetration depth into the material (∼0.1–5 µm) and higher sensitivity than FTIR due to multiple reflections [28]. The peak observed in the ATR spectrum cannot be a consequence of Mie scattering, since, as was shown in [29], this method is insensitive to scattering. In ATR Spectroscopy evanescent wave due to its nature is bounded to the surface and not scattered in the powdered sample [30]. The dramatic difference in transmittance and multiple ATR spectra may be caused by the nature of the bismuth telluride as a topological insulator.

The width of the peak, as well as its shift to the short-wavelength part of the spectrum in time, can be explained by the presence of the larger particles in suspension. In the first moment after LPE, the suspension contains particles of different sizes (wide peak). Over time the smaller NPs become predominate in suspension due to sedimentation of large NPs (Figure 3(c)). The suspension completely precipitates not earlier than 20 days after exfoliation. However, the short treatment in the ultrasonic bath allows achieving completely the same ATR spectrum of the particles in the suspension as the one measured immediately after the liquid-phase exfoliation. The ATR spectrum for particles of suspension on day 14 after LPE has a maximum of 1.3 μm. The absorbance of Bi₂Te₃ NPs suspension in UV-Vis-NIR is shown in Figure 3(d).

The bandgap was estimated by Tauc equation [31]:

where α is the absorption coefficient, hν is the energy of the photon, A is the optical transition dependent constant of the material, E _g is the bandgap energy of the material and n is equal to 2 for indirect bandgap, and 0.5 for direct bandgap (for Bi₂Te₃ as an indirect bandgap semiconductor we took n = 2, which is also true for atomic layers in accordance with [32]).

The band gaps of studied NPs using ATR FTIR spectra (Figure 3(c)) were equal to 0.10, 0.17, 0.19, 0.61, and 0.68 eV (two weeks from suspension preparation) depending on the time after LPE (Figure 2(f)). According to APRES measurements [32], the change of the thickness from 1 to 5 QL leads to the change of the bandgap from 0.5 to 0.17 eV. On the other side, for thin films of Bi₂Te₃ NPs with a thickness of 12.5 nm, the band gap was reported to be up to 1.62 eV [33].

3 Measurements of the nonlinear optical properties of studied samples

Studies of the nonlinear optical properties of our samples were performed using the standard z-scan technique [34]. The second harmonic (λ = 532 nm) or the fundamental radiation (1064 nm) of the Nd:YAG laser (pulse duration 10 ns, pulse repetition rate 1 Hz) was focused using a 300 mm focal length spherical lens (FL, inset in Figure 4(a)). The 1-mm-thick fused silica cell containing bismuth telluride NPs, or the 1-mm-thick glass plate with a thin layer of Bi₂Te₃ NPs, was moved along the z-axis through the focal point using a translating stage (TS) controlled by a computer. The energies of the initial and propagated laser pulses were measured using the calibrated photodiodes (PD1 and PD2). The CA and OA schemes allowed the determination of the nonlinear refraction and nonlinear absorption of studied samples, respectively. We also measured the nonlinear scattering in our samples using photodiode PD3.

Figure 4:

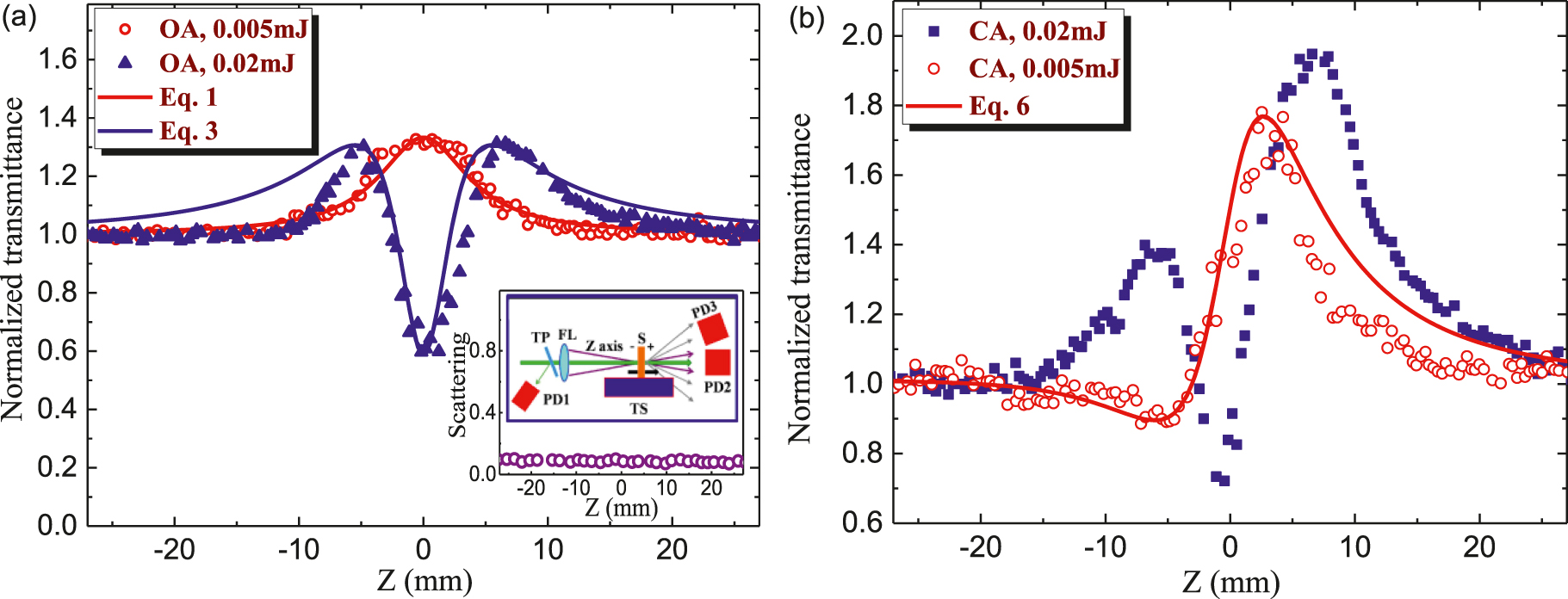
Z-scans of Bi₂Te₃ NPs using 532 nm radiation.

(a) Open-aperture (OA) z-scans using 0.005 mJ (red empty circles) and 0.02 mJ (blues filled triangles) and the corresponding fittings. Inset: Scattering of 532 nm radiation measured by the third photodiode (see text). Z-scan scheme comprising glass thin plate (TP), focusing lens (FL), translating stage (TS), sample (S), and photodiodes (PD1, PD2, and PD3). (b) Closed-aperture (CA) z-scans using 0.005 mJ (red empty circles) and 0.02 mJ (blue filled squares). The best fitting (red solid curve) is shown for the scan measured using 0.005 mJ pulses.

3.1 Nonlinear absorption and nonlinear refraction of Bi₂Te₃ NPs suspension

The negative nonlinear absorption attributed to SA was a dominant mechanism during our z-scan studies of this colloidal suspension using weak probe pulses. The following formula was used to fit our z-scan. The OA curve shown in Figure 3(a) (red empty circles) is obtained using 532 nm, 0.005 mJ pulses. These results can be fitted using the normalized transmittance

(2) T ( z ) = [ 1 + I 0 / I sat × ( 1 + z 2 / z 0 2 ) ] 0.5 .

Here, I ₀ and I _sat are the laser radiation intensity in the focal plane and saturation intensity, respectively, z ₀ is the Rayleigh length of the focused radiation, z ₀ = π(w ₀)²/λ, w ₀ is the beam waist radius (28 and 48 µm in the case of 532 and 1064 nm radiation, respectively), and λ is the wavelength of the probe radiation. This fitting (red solid curve) allowed determining the ratio of the maximum intensity of probe pulse and saturated intensity (I ₀/I _sat = 0.3). From this relation and assuming the maximal intensity of 532 nm pulse in the focal plane (2 × 10⁸ W cm⁻²) one can determine I _sat to be ∼7 × 10⁸ W cm⁻².

The increase of pulse energy from 0.005 to 0.02 mJ allowed observation of the valley in OA z-scan (Figure 4(a), blue empty triangles). Either TPA or RSA are the commonly reported mechanisms of the nonlinear absorption of NPs. In most cases, SA follows by RSA. However, taking into account the absorption band centered at around λ ≈ 370 nm (see the absorption curve shown in Figure 3(d)) one can assume that TPA of 532 nm pulses can be considered as an alternative to the RSA mechanism of positive nonlinear absorption. The latter process can be fitted by the following relation

(3) T ( z ) = q ( z ) − 1 ln [ 1 + q ( z ) ] .

where q(z) = β I(z) L _eff/[1 + ( z 0 2 /z ²)], L _eff = [1 − exp (−α ₀ L)]/α ₀ is the effective length of the sample, α ₀ is the linear absorption coefficient, and L is the thickness of the studied sample (L = 1 mm).

The joint influence of SA and positive nonlinear absorption can be considered as the multiplication of the transmittances attributed to these processes:

(4) T ( z ) = [ 1 + I 0 / I s a t × ( 1 + z 2 / z 0 2 ) ] 0.5 × q ( z ) − 1 × ln   [ 1 + q ( z ) ] .

The corresponding fitting of Eq. (4) and experimental data at E = 0.02 mJ (blue solid curve) allows determining the nonlinear absorption coefficient (β = 1 × 10⁻⁸ cm W⁻¹) attributed to the influence of either TPA or RSA.

The possibility of the dynamic scattering of the probe pulses by Bi₂Te₃ NPs was analyzed using 0.02 mJ pulses. We did not observe the nonlinear scattering in the case of 532 nm probe pulses (see the inset graph in Figure 4(a) showing a weak scattering measured by the additional photodiode (PD3) placed out of the optical axis of the radiation propagated through the cell contained Bi₂Te₃ NPs). These measurements showed the pattern of unchanged scattering of 532 nm radiation along with the whole range of used intensities of probe pulses. Thus the nonlinear scattering cannot be considered as the mechanism of the decrease of normalized transmittance at the used intensity of probe emission at this wavelength (532 nm) and pulse duration (10 ns).

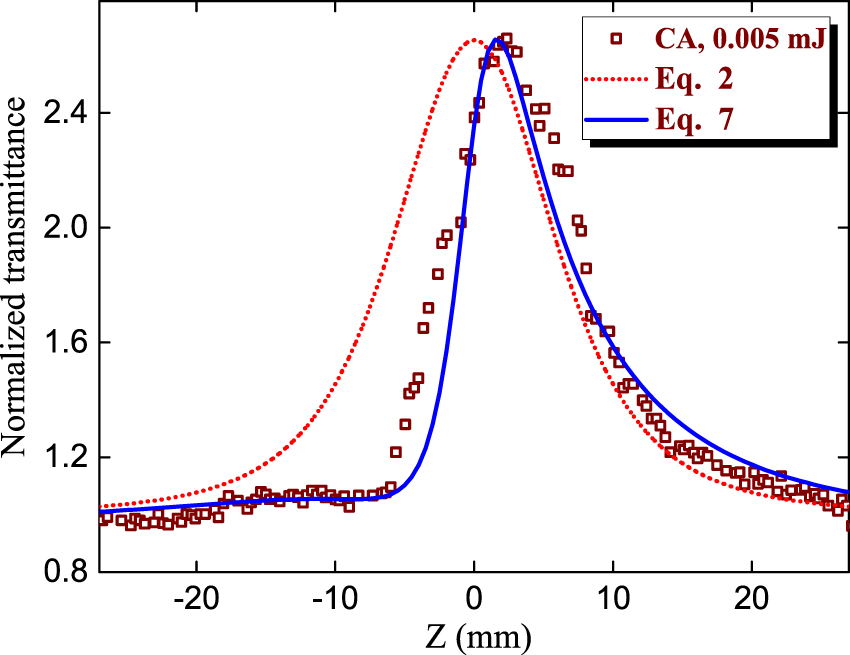
The definition of the nonlinear refractive index of this suspension is a rather difficult procedure taking into account the necessity in the fitting of the curve affected by three nonlinear optical processes in the case of relatively strong probe pulses: nonlinear refraction, RSA or TPA, and SA. The first and third processes can be manifested in the case of weak pulses (0.005 mJ, 532 nm, 10 ns; Figure 4(b), red empty circles), while all three processes are inevitably presented in the CA z-scan shown in Figure 4(b) (blue filled squares) using four times stronger probe pulses (0.02 mJ).

In the case of E = 0.005 mJ when apart from relatively strong SA only the positive nonlinear refraction plays an important role (Figure 4(b), red empty circles) one can exclude the positive nonlinear absorption from consideration. This asymmetric pattern with a larger peak with respect to the smaller valley points out the growing influence of the negative nonlinear absorption. The valley preceding peak indicates the positive sign of nonlinear refraction. In the case of any sign of nonlinear absorption and positive nonlinear refraction, the CA z-scan can be analyzed by fitting the following theoretical curve for the transmittance T with experimental dependencies [35]:

(5) T = 1 + 2 ( − ρ x 2 + 2 x − 3 ρ ) ( x 2 + 9 ) ( x 2 + 1 ) Δ Φ 0  .

Here, x = z/z ₀, ρ = β/2kγ, ΔΦ₀ = kγI ₀ L _eff, and k = 2π/λ. Since at small intensity (or energy) of probe pulses the parameter ρ can be taken close to zero, the Eq. (5) simplifies to

(6) T ≈ 1 + 4 x Δ Φ 0 / ( x 2 + 9 ) ( x 2 + 1 ) .

To take into account SA one has to multiply the transmittance describing this process (Eq. (2)) and Eq. (6):

(7) T ( z ) = [ 1 + I 0 / I s a t × ( 1 + z 2 / z 0 2 ) ] 0.5 × [ 1 + 4 x Δ Φ 0 / ( x 2 + 9 ) ( x 2 + 1 ) ] .

The fitting shown in Figure 4(b) (red solid curve) allowed determining the nonlinear refractive index (γ = 9 × 10⁻¹² cm² W⁻¹) and negative nonlinear absorption coefficient attributed to SA (β _SA = −7×10⁻⁸ cm W⁻¹) of colloidal bismuth telluride NPs in the case of 0.005 mJ, 10 ns, 532 nm probe pulses.

The influence of positive nonlinear refraction on the CA z-scan at the higher energy of probe pulses (0.02 mJ) makes this curve (Figure 4(b), blue filled squares) hardly analyzed using the fitting procedure. The fitting equation at that case includes RSA alongside the SA and nonlinear refraction:

(8) T ( z ) = [ 1 + I 0 / I s a t × ( 1 + z 2 / z 0 2 ) ] 0.5 × { 1 + [ ( − 2 ρ x 2 + 4 x − 6 ρ ) Δ Φ 0 ] / ( x 2 + 9 ) ( x 2 + 1 ) } .

This is a rather sophisticated formula to properly fit with the z-scan data. Our attempts to simultaneously determining three parameters (β _SA, β, and γ) failed to get the values similar to those defined from less sophisticated Equations (2), (4), and (7). Thus the uncertainty in fitting Eq. (8) with the data presented in Figure 3(b) (blue filled squares) did not allow us the accurate determination of the above nonlinear optical parameters.

The application of 1064 nm, 10 ns pulses also showed the prevailing influence of negative nonlinear absorption over positive nonlinear refraction (Figure 5, CA z-scan, brown empty squares). Notice stronger nonlinear optical SA of studied suspension in the case of 1064 nm pulses compared with 532 nm pulses at similar energies of probe radiation (0.005 mJ; compare with Figure 3(b)) The fitting of this asymmetric CA z-scan using Eq. (7) (blue solid curve) allowed determining the nonlinear refractive index and the nonlinear absorption coefficient, as well as saturated intensity at the used wavelength (γ = 5 × 10⁻¹² cm² W⁻¹ , β _SA = −1.2 × 10⁻⁷ cm W⁻¹, I _sat = 2 × 10⁸ W cm⁻²). Here we also show the anticipated dependence (red dotted curve) corresponding to the SA without the influence of nonlinear refraction. The observed decrease of saturated intensity for longer wavelength radiation corroborated with earlier reported data [14] for 1060 nm (I _sat = 1.6 × 10⁵ W cm⁻²) and 1562 nm (I _sat = 1.2 × 10⁵ W cm⁻²) picosecond pulses.

Figure 5:

CA z-scan of Bi₂Te₃ NPs using 1064 nm, 0.005 mJ probe pulses.

The red dotted curve corresponds to Eq. (2). The blue solid curve is the best fit using Eq. (7).

To confirm that the nonlinear optical properties are purely related to Bi₂Te₃ NPs, the main solvent (butanol) was analyzed at two wavelengths (532 and 1064 nm) of probe radiation using the similar procedure of z-scan. No nonlinear optical response was observed during this test study, which indicated that the observed processes were entirely attributed to Bi₂Te₃ NPs.

One can see that there is some discrepancy between the fitting curves and the experimental data (Figure 4). The exact coincidence of fitting curve and z-scan data is a rare case when one uses the ideal Gaussian beam, which in most cases is unrealistic once we consider the difficulty in obtaining such shape of the intensity distribution along the radial axis. To some extent, the Gaussian shape can be obtained once one applies the spatial filtering of the probe beam. However, in most cases, the experimenters use the laser beams containing the deviations from the Gaussian distribution due to the diffraction along the optical path and the heterogeneous amplification along different directions of the radial distribution. Correspondingly, the theoretical formulas of the z-scan technique based on the consideration of propagation of the Gaussian beam cannot precisely match with the experimental data. In addition, the participation of additional nonlinear optical processes, such as RSA, along with SA and nonlinear refraction, makes it difficult to simultaneously account for their influence on the OA and especially CA z-scans. The addition of those processes in the z-scan formulas makes them difficult to handle due to the complexity in the simultaneous determination of different fitting parameters. That is why the researchers use rather simplified approaches to determine β and γ by matching the peaks and valleys of the used fitting curves with those measured during the experiment. In each case, the discrepancy can be explained by the above-mentioned factors. Below we describe a few such examples that occurred during the fitting with of our experimental results.

The discrepancy between the fitting curve in Figure 4(b) and the CA data is attributed to the difficulty in the application of Eq. (8) taking into account the involvement of the third nonlinear optical effect (RSA) appearing even at small energy of probe pulses (0.02 mJ) alongside the nonlinear refraction and SA. That is why we used the simplified formula (Eq. (7)), which does not contain the component describing RSA.

The discrepancy between the fitting OA curve in Figure 4(a) (blue curve) and the experimental data in the case of the relatively strong pulse energy is probably attributed to the asymmetric shape of the used beam (see the discrepancy in the case of the negative values of z). Additional deviations of the experimental results from the theoretical model can also be attributed to the experimental errors, such as the determination of beam waist, and the doping of Bi₂Te₃ NPs suspension with some impurities.

3.2 Nonlinear absorption and nonlinear refraction of Bi₂Te₃ NPs films

In previous studies, the nanocrystalline Bi₂Te₃ thin films were grown by different chemical methods. Their saturable and nonlinear absorption properties were determined via OA z-scans using femtosecond and picosecond laser sources [14], [15], [16]. In our case, the CA and OA z-scans of 60 nm thick films using 532 nm, 10 ns pulses (Figure 6(a) and (b)) showed similar properties compared with the suspension of these NPs (Figure 4). The nonlinear refraction of films in the case of 532 nm probe pulses maintained the same positive sign as for the liquid suspension, which points out the prevailing influence of Kerr-related self-focusing. The nonlinear absorption was entirely determined by SA.

Figure 6:

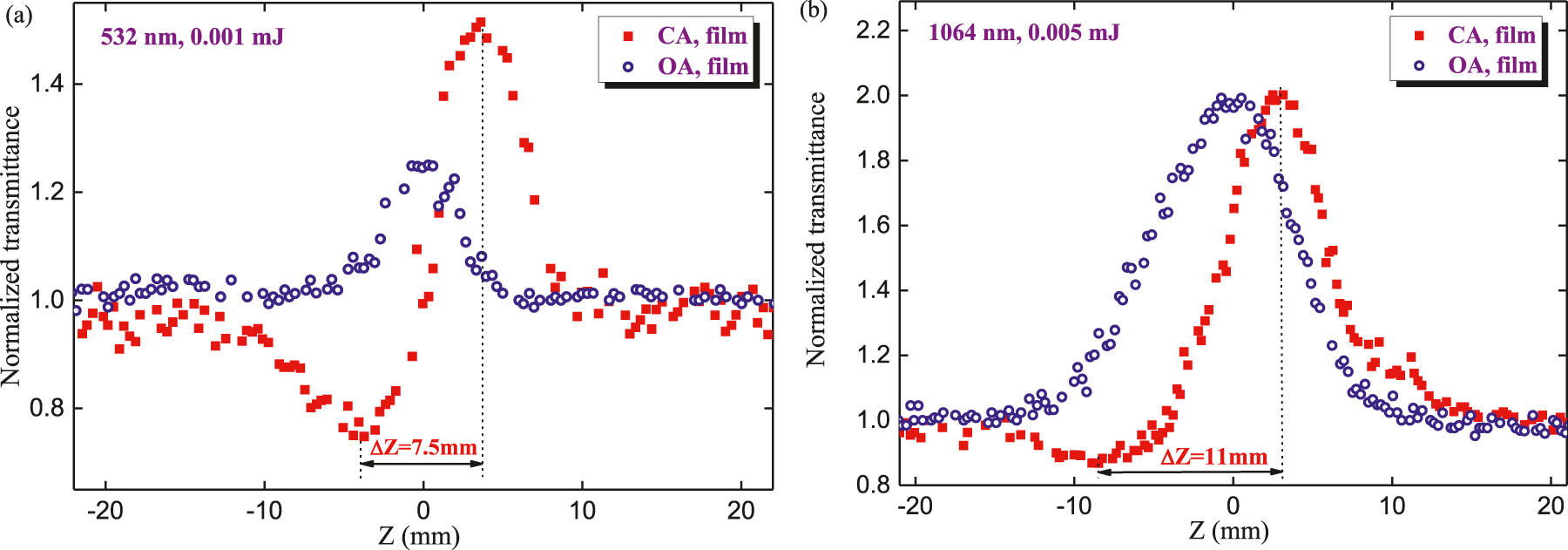
Z-scans of 60-nm thick film containing Bi₂Te₃ NPs.

(a) OA (blue empty circles) and CA (red filled squares) z-scans using 532 nm, 0.001 mJ pulses. (b) OA (blue empty circles) and CA (red filled squares) z-scans using 1064 nm, 0.005 mJ pulses.

We varied the methods of films deposition, as well as their thickness (between 30 and 300 nm), and all these samples revealed the negative nonlinear absorbance and positive nonlinear refraction. The microscopic analysis of films after z-scans did not show the appearance of holes, which is proved with the use of weak intensities of the 532 nm pulses. The used intensities during these studies (4 × 10⁷–1 × 10⁸ W cm⁻²) were far less than the breakdown threshold of these films (∼4 × 10⁹ W cm⁻²), thus pointing out the involvement of SA in the bleaching of the studied films. The γ of the studied film was calculated from the fitting of the CA z-scan (Figure 6(a), red filled squares) to be 5 × 10⁻⁷ cm² W⁻¹ in the case of 532 nm, 10 ns probe pulses.

The OA z-scan of 60 nm thick films using 0.001 mJ, 532 nm probe pulses (Figure 6(a), blue empty circles) clearly show the bleaching of the films in the vicinity of the focal area of the focusing lens. We observed the steady growth of the peak of normalized transmittance up to the normalized transmittance of T ≈ 1.25. The corresponding negative nonlinear absorption coefficient and saturated intensity measured using this film at λ = 532 nm were as follows: β _SA = −1.2 × 10⁻⁴ cm W⁻¹, I _sat = 6 × 10⁸ W cm⁻². One can see a notable growth of γ and β _SA of studied film compared with NPs suspension. The application of notably stronger pulses (0.05 mJ) led to the appearance of visible damage on the surface of the film.

The application of 1064 nm, 10 ns pulses as the probe radiation (Figure 6(b), OA z-scan, blue empty circles) showed that similar SA can be achieved only using a few times larger energy of pulses (0.005 mJ) compared with 532 nm radiation (0.001 mJ, Figure 6(a)). The corresponding nonlinear optical parameters at this wavelength were as follows: I _sat = 4 × 10⁸ W cm⁻² and β _SA = −5×10⁻⁵ cm W⁻¹. The CA z-scan (Figure 6(b), red-filled squares) showed the self-focusing manifested by the small valley and large peak (with the distance between the valley and peak ΔZ = 11 mm). The strong asymmetry in the valley and peak values is attributed to the strong influence of SA compared with nonlinear refraction. The Rayleigh length of the focused 1064 nm radiation was measured to be z ₀ = 6.5 mm. Thus the relation ΔZ ≈ 1.7z ₀ was maintained in the case of these experiments, which points out the prevailing influence of the Kerr-related nonlinearity leading to the self-focusing of 1064 nm pulses in the studied film. The γ calculated from this z-scan was equal to 6 × 10⁻⁸ cm² W⁻¹.

One can exclude the nonlinear absorption from the CA experimental results via the CA/OA operation. We considered such a possibility in retrieving the purely nonlinear refractive effect. However, in our case, the pattern of a complex nonlinear optical response of these nanostructures becomes less clearly observed. Moreover, the CA/OA procedure in some cases leads to inadequate results since our measurements of OA and CA z-scans were carried out separately. Correspondingly, in the present studies, the experimental OA and CA data were taken at different positions of the sample with regard to the focal plane. Thus the division of CA/OA led to larger fluctuations of the purely CA z-scan. Notice that the CA/OA operation is a useful tool once one determines those scans in a single set of measurements.

4 Discussion

Below we address the results of CA studies showing the self-focusing of 532 nm pulses in both liquid and film samples containing bismuth telluride. As was mentioned, if one considers the prevailing role of Kerr-related fast processes then the distance between valley and peak along Z-axis should correspond to the following rule: ΔZ ≈ 1.7z ₀ [32]. In our experiments, the Rayleigh length in the case of 532 nm radiation was measured to be 4.5 mm, while ΔZ in the case of Bi₂Te₃ NPs suspension was equal to 7.6 mm (see Figure 7, blue filled balls). Correspondingly, the relation between z ₀ and Rayleigh length was equal to ΔZ = 1.69z ₀. Similar characteristics of the CA z-scan were observed in the case of thin film (ΔZ = 7.5 mm, Figure 6(a)). Correspondingly, the self-focusing in Bi₂Te₃ NPs suspension and film was attributed to the Kerr effect. Thus, in present studies, the role of thermal lens leading to self-defocusing and commonly playing a decisive role during application of long (nanosecond) probe pulses was insignificant.

Figure 7:

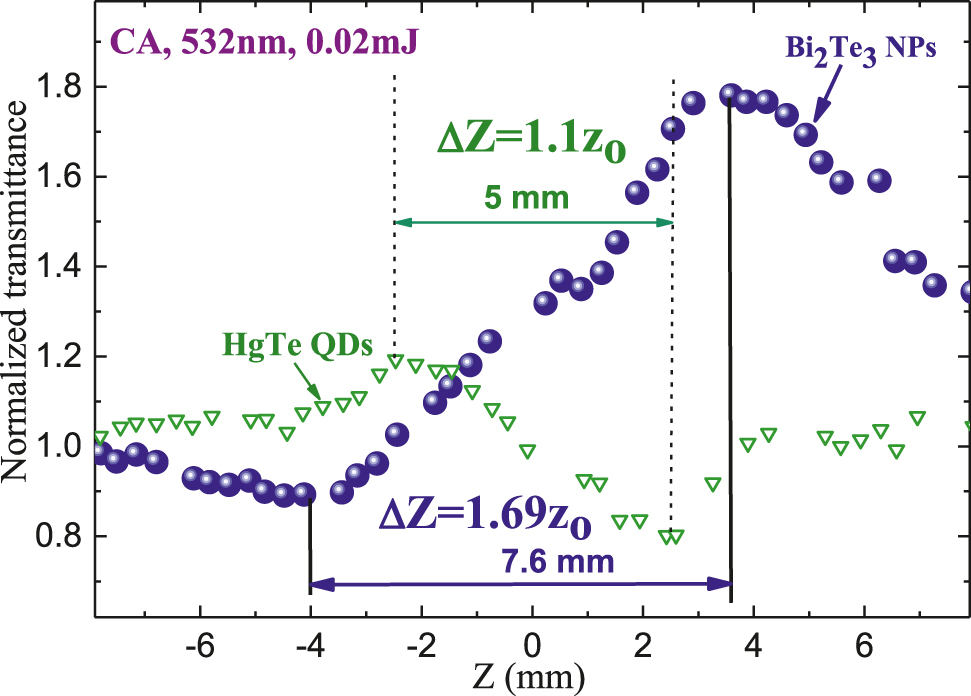
Variation of ∣ΔZ∣ in the case of CA z-scans of Bi₂Te₃ nanoparticles (NPs) suspension (blue filled balls) and HgTe quantum dots (QDs) suspension.

This parameter was equal to 7.6 and 5 mm for the former and latter samples. CA measurements were carried out at similar conditions of the experiment (z ₀ = 4.5 mm, 532 nm, and 0.02 mJ probe pulses).

To demonstrate a difference between Kerr- and thermal-related processes leading to the nonlinear refraction we compared present studies with the measurements of HgTe quantum dot suspension at similar conditions of the experiment. CA z-scan of the latter species is shown in Figure 7 (green empty triangles). In that case, we observed a self-defocusing manifested by the peak preceding the valley, with the distance between them equal to 5 mm. This peak-to-valley distance in CA z-scan becomes narrower compared with the conventional third-order nonlinear optical process, with a separation corresponding to the relation ΔZ ≈ 1.1z ₀, which can be attributed to the thermal lens induced self-defocusing in the case of different mechanisms of absorption and especially in the case of strong positive nonlinear absorption [36, 37]. The absence of thermal-related nonlinear refraction in the case of bismuth telluride species can be attributed to lesser absorption, both linear and nonlinear, of 532 and 1064 nm pulses in the studied suspension and film.

Below we discuss the wavelength- and geometry-dependent nonlinear refraction of the Bi₂Te₃ NPs suspensions. The consideration of fast, Kerr-related, processes in semiconductors is analyzed in [38] using Kramers-Kronig relations. The nonlinear refraction changes sign at ħω/E _g = 0.69 (ħ is the Planck’s constant, ω is the frequency of laser radiation, and E _g is the bandgap energy of semiconductor). Particularly, once this parameter becomes larger than 0.69 the medium starts showing the self-defocusing properties. In this connection, the sign of nonlinear refraction can be changed once one considers bulk material and NPs of the same elemental consistency. Smaller NPs may demonstrate a large blue shift in the absorption edge that leads to variations in the effective bandgap. At these conditions the parameter ħω/E _g becomes less than 0.69 and the smaller NPs start demonstrating self-focusing properties since their bandgap became notably increased. This reversion of optical nonlinearities can be understood in terms of the quantum size effect resulting from the confinement of an electron-hole pair in a small volume.

Similarly, the Kramers-Kronig model provides some clues in the definition of the transformation from self-focusing to self-defocusing and vice versa once one uses different wavelengths of probe pulses. Again, the crucial parameter in this model is the relation between the photon energy and the bandgap of semiconductors. Once the radius of semiconductor NPs decreases their bandgap can be increased.

There are different approaches in the application of the absorption spectra in the determination of E _g . The maximal value of the bandgap in the case of the bismuth telluride NPs presented in suspensions was estimated by the application of the Tauc equation for ATR-FTIR spectra to be 0.68 eV (see inset in Figure 3(f)). The corresponding ħω/E _g value for Bi₂Te₃ NPs at the used wavelengths of probe pulses (532 and 1064 nm) was calculated to be notably larger than 0.69 (3.44 and 1.72 in the case of 532 and 1064 nm, respectively). Thus, we can expect a negative sign of γ in these NP-containing suspensions and films, once considering the determination of E _g using ATR-FTIR spectra. Meanwhile, our studies showed that the sign of nonlinear refraction in the case of the colloidal suspensions and films containing bismuth telluride NPs was positive at two wavelengths of the probe pulses. The separate studies of the main solvent (butanol) did not show the nonlinear refraction at similar conditions of experiments. Thus the positive sign of γ was entirely attributed to the influence of Bi₂Te₃ NPs.

As for the application of the Kramers-Kronig relation, the following should be noted. Its application is usually considered for a two-level system. Meanwhile, the energy structure of the NPs studied by us is much more complex. Accordingly, the sign of refraction can be any since it is not fully described by these relations. It all depends on the energy properties of the studied nanostructure. In addition, it should be taken in mind both the presence and the impact of defects, which, as far as we know, no one has considered in the case of Bi₂Te₃. Thus, the application of the Kramers-Kronig relation can be justified if we know a set of highly probable transitions in a nanocrystal that occur under the action of laser radiation. A similar problem arises when considering various quantum dots, for example, Ag₂S, where it is also difficult to determine the sign of nonlinear refraction by the formula reflecting the effect of filling states obtained from the above relation.

The analyzed species in our case seems to be quite complex if we consider it from the point of view of the absorption characteristics (Figure 3). Therefore, below we offer another consideration of the problem of determining the sign of nonlinear refraction based on the presented absorption spectra, which also proceeds from the evaluation of this process following the Kramers-Kronig relation, but takes into account another, ultraviolet, absorption region. Note that this is only a hypothesis but at the moment we have no other assumptions about the nature of self-focusing in bismuth telluride NPs.

The use of the Tauc equation for the interpretation of dimensional effects has limitations due to the absence of direct and indirect transitions in quantum-dimensional particles. Therefore, below we estimate the role of the absorption zone in the ultraviolet range and provide an approximate estimate of the bandgap.

The contradiction between the experimental CA data showing positive signs of γ and the Kerr-related consideration predicting negative nonlinear refraction while applying the bandgap value taken from the Tauc equation points out that there could be another explanation related to strong transitions and bands in the spectrum of studied samples. Particularly, once one considers the role of the absorption band appeared in the UV-visible range and centered at ∼368 nm (Figure 3(d)), the “bandgap” associated with this wavelength (see Figure 8 of Ref. [17]) can provide some clues in explanation of above contradiction.

During the last 30 years, a large number of artificial low-dimensional semiconductor systems have been fabricated and studied. They are characterized by enhanced excitonic binding energy, enhanced excitonic oscillator strength, and consequently enhanced optical nonlinearity, in comparison to the corresponding three-dimensional (3D) systems. The fabrication of very small semiconductor structures like those studied in present experiments and comprising few-atomic-layers particles makes it possible to observe the effects of spatial restrictions on the wave functions of electrons, holes, or Wannier excitons—i.e., electron-hole pairs bound by a screened Coulomb interaction. The consequence of these effects is a dramatic change in the energetic spectrum of quantum states. Consequently, the optical properties of these artificial materials, mostly governed by the physics of excitons, are very different from those of bulk 3D semiconductors, which they are made of. The low-dimensional semiconductors show strong excitonic optical absorption bands mostly in the UV spectral region.

The corresponding bandgap associated with the observed absorption region can be estimated as 3.52 eV. In that case, the ħω/E _g values for Bi₂Te₃ NPs at the used wavelengths of probe pulses were calculated to be smaller than 0.69 (0.66 and 0.33 in the case of 532 and 1064 nm, respectively). Correspondingly, the signs of the nonlinear refractive index should be positive in the case of two used wavelengths of the probe pulses, which corroborates with the measured CA z-scan data. Notice that a positive value of nonlinear refractive index (γ = 0.97 × 10⁻¹⁰ cm² W⁻¹) of the 20 nm thick film comprising Bi₂Te₃ NPs was also reported in Ref. [18]. In the case of the correctness of our assumption of the decisive role of the observed excitonic band enhancing the optical nonlinearity of the whole ensemble of small-sized particles, one can conclude that the influence of excitons prevails over the basic consideration of studied particles that assumes the low bandgap and negative nonlinear refraction.

The wavelength- and geometry-dependent mechanisms of the nonlinear absorption in the Bi₂Te₃ NPs are quite sophisticated as well. This problem has been analyzed in [14], [15], [16], [17], [18]. Those studies offer different scenarios in explanation of the observed peculiarities of nonlinear absorption in these species. Even shortened description of all mechanisms suggested in the above-mentioned research will significantly increase the volume of our paper. We rather refer to those studies, while discussing below some peculiar features of the nonlinear absorption in the studied bismuth telluride NPs allowing their practical applications.

Strong TPA in a layered Bi₂Te₃, which can be considered as a topological insulator, was reported under excitation with a femtosecond laser pulse at a wavelength of 1056 nm [15]. The large TPA effect in the Bi₂Te₃ layered film was attributed to the existence of high-lying bulk states located above the first bulk state. Authors of [15] also used this assumption to explain the discontinuity of the optical nonlinear transmittance between the low and high excitation energy regions. Due to its similar band structure to graphene, such 2D Bi₂Te₃ structures have been applied as saturated absorbers for the mode-locking of fiber lasers or Q-switching of solid-state lasers in different ranges of spectra [16, 18, 39], [40], [41], [42]. Those studies have demonstrated two ranges of saturation intensities with several orders of magnitude difference while measuring this parameter in the case of mode-locked and Q-switched lasers, which yet find the explanation.

The studies of Bi₂Te₃/rGO composites using the Nd:YAG laser at the laser wavelength of 532 and 1064 nm with a repetition frequency of 10 Hz, pulse width of 4 ns were recently reported in [17]. They analyzed the normalized transmittance curves of Bi₂Te₃ presenting SA at two studied wavelengths in the case of the lowest incident energy (8.5 μJ). The reason for SA was attributed to the fact that the energy band gap of Bi₂Te₃ is smaller than the incident light energy of 2.33 eV (532 nm) and 1.164 eV (1064 nm) pulses, which allow the upper energy levels of Bi₂Te₃ nanosheets to be excited and saturated at those wavelengths. Stronger excitation of samples allowed them to observe a valley in SA curves representing either RSA or TPA. The appearance of the valley was attributed to the influence of the hybridized carbon atoms of sp ³ matrix in graphene oxide (GO), converted into sp ² domain by removing the oxygen of GO and named as rGO. To explain the difference between pristine bismuth telluride and Bi₂Te₃/rGO the charge transfer process model based on the donor-acceptor structure in the latter composite was introduced. Meanwhile, they did not found the nonlinear refraction effect for all samples studied, while our studies using similar probe pulses clearly reveal this effect. This difference can be attributed to the influence of the graphene oxide used in [17], which can suppress the Kerr-related nonlinear refractive properties in this compound.

Different approaches in NPs formation in liquids [43], thin films, and bulk media [44], [45], [46], [47], as well as during pulsed laser ablation [48] have proved to be the efficient methods for the application of small-sized structures in optical limiters and mode-lockers. The chemical methods also showed their applicability for the synthesis and use of NPs in various devices. Below we address the applicability of the nonlinear optical properties of studies NPs.

Initially, Bi₂Te₃ NPs were used for the creation of various thermoelectric devices [49], [50], [51], [52]. Meanwhile, the nonlinear optical properties of synthesized exfoliated Bi₂Te₃ NP suspensions and films can find various applications in optoelectronics and nanophotonics as well. The optical and optoelectronic properties of topological insulators, like Bi₂Te₃ NPs layers, are extremely attractive since, while possessing the unique energy band, they demonstrate wideband nonlinear SA. Besides, bismuth selenide, a similar topological insulator, has been demonstrated to exhibit a large nonlinear refractive index at 800 nm wavelength, which is on the order of 10⁻¹⁰ cm² W⁻¹, which is almost six orders of magnitude larger than that of bulk dielectrics [53]. Our studies of Bi₂Te₃ NPs showed an even larger (6 × 10⁻⁸ cm² W⁻¹) nonlinear refractive index at 532 nm wavelength. These properties allow the application of such topological insulators for various nonlinear devices, like optical Q-switchers, mode-lockers, and wavelength converters [54], [55], [56], [57], [58]. One can anticipate the application of the SA properties of Bi₂Te₃ NP suspensions and films demonstrated in the present study for the mode-locking of free-running lasers, similarly to Pt NP suspensions showing the same SA properties, which create conditions for the formation of picosecond pulses [59]. Thus the potential in using synthesized Bi₂Te₃ NPs suspensions and thin layers is broad enough to continue the studies of their properties and applications.

As it was mentioned, bismuth telluride NPs may play an important role as the photosensitive layers in broadband (i.e. between visible and mid-infrared ranges) photodetectors due to their absorption properties. The optical and nonlinear optical characteristics of these NPs are governed by quantum mechanical effects. Particularly, size dependence of absorption in near-infrared and mid-infrared regions is directly related to the structural changes of Bi₂Te₃ NPs, which allows for creating cheap and sensitive photosensors with improved photoresponse in low energy range, which is important for telecommunication optoelectronics, self-driving car night vision, and food sorting [60]. In addition, obtained stable suspension enables direct photodetector arrays printing on flexible substrates. Moreover, combining synthesized Bi₂Te₃ NPs with graphene layers will result in heterostructures formation with both broadband and high gain photoresponse [61]. Thus the optical and nonlinear optical properties of these materials can find practical application in manufacturing optoelectronic and photonic devices. At low (far-infrared or terahertz) frequencies, they can be used as optical frequency converters, modulators, and switchers.

Additionally, the peculiar features of bismuth telluride NPs can find the application in such fundamental research as high-order harmonics generation of ultrashort pulses, which can lead to the creation of efficient sources of coherent extreme ultraviolet radiation. The dimensional dependence of the transition energy in absorption opens up possibilities for achieving resonances, the use of which can reduce the threshold for optical nonlinearities [62]. The potential application of this effect is an efficient generation of high-order harmonics in the laser-induced plasmas containing such small-sized species [63, 64].

5 Conclusions

The general goal of this manuscript was to analyze the nonlinear optical characteristics of exfoliated Bi₂Te₃ NPs. Various properties of synthesized NPs were presented for the morphological clarification of this subject prior to the nonlinear optical studies.

We have described the synthesis and characterization of Bi₂Te₃ colloidal NPs and films and analyzed their low-order nonlinear optical properties using 1064 and 532 nm, 10 ns pulses. The Bi₂Te₃ colloidal NPs have shown the SA and positive nonlinear refraction, while at stronger excitation by 532 nm, 10 ns pulses the RSAdominated over other nonlinear optical processes. We have demonstrated significant growth of the nonlinear optical parameters (γ = 5 × 10⁻⁷ cm² W⁻¹, β _SA = −1.2 × 10⁻⁴ cm W⁻¹ and γ = 6 × 10⁻⁸ cm² W⁻¹, β _SA = −5×10⁻⁵ cm W⁻¹ in the case of 532 and 1064 nm probe pulses, respectively) of thin films compared with Bi₂Te₃ colloidal NPs and discussed the observed peculiarities of the nonlinear response of Bi₂Te₃ nanostructures. We have also shown that, at the used experimental conditions (nanosecond probe pulses), the thermal process does play important role in the determination of the nonlinear refraction of studied species. Our studies have shown that Bi₂Te₃ NPs cause significant bleaching, which can be used for the mode-locking and Q-switching of lasers. Finally, we have discussed the applicability of the nonlinear optical properties of these NPs for optoelectronic and photonic devices.