Few picosecond dynamics of intraband transitions in THz HgTe nanocrystals

1 Introduction

Mercury telluride (HgTe) nanocrystals [1] (NCs) appear as a promising active material for low-cost infrared sensors [2]. In its bulk form, HgTe is a zero-band gap semiconductor, which means that the bandgap of HgTe NCs can potentially be reduced to zero eV [3], unlike infrared NCs such as lead chalcogenides that have their tunability limited by the bulk bandgap (≈0.4 eV for PbS) [4]. Over the past decade, rapid progress has been realized on the colloidal growth of HgTe NCs. Rogach et al. were the first to report the growth of such narrow bandgap II–VI NCs and obtained very small particles with a bandgap corresponding to 1300 nm [5]. The addition of a ripening step allowed Kovalenko et al. to push the absorption beyond the telecom range and reach 3 µm [6]. Later Keuleyan et al. reported absorption edges up to 5 µm [7], which can be extended up to 12 µm by the addition of a regrowth step [8]. Recently, Goubet et al. developed a high-temperature procedure for HgTe NCs in order to push the absorption of NCs to 200 µm (i.e. 1.5 THz) [9]. Such long-wavelength absorption is enabled by the growth of large NCs (up to 1 µm) with sizes above the HgTe Bohr radius (40 nm) [10]. While intensive efforts have been dedicated to the synthesis and device integration of short-wave [11, 12] and mid-wave [7, 13, 14] infrared NCs, very little work has to date been focused on the investigation of the electronic structure, charge transport, and optical properties of mercury chalcogenide THz NCs [10, 15].

In such large nanoparticles, the absorption spectrum presents interband absorption at high energy and a peak at low energy that is the signature of self-doping [16–19]. This doping mechanism is specific to narrow bandgap NCs and corresponds to a reduction of the NCs by the environment as the low confinement brings the Fermi level above the ground state of the conduction band (1 Se state). In this case, the carrier density is not driven by the introduction of extrinsic impurities but rather by the confinement, which tunes the relative position of the conduction band and the Fermi level [20]. As the cut-off is pushed toward higher wavelengths, the material becomes less confined, making the density of state denser and high carrier densities, up to several carriers per nanoparticle, can be observed [20, 21]. It thus raises a question about the physical origin of the low energy absorption resonance: is it the result of intraband absorption described by a 1 electron Hamiltonian or do collective plasmonic effects already occur? [22]. This question is of utmost importance for the realization of optoelectronic devices based on THz NCs. As the number of involved electrons rises, a stronger absorption can be achieved but the carrier lifetime is expected to drop quickly. In strongly doped NCs of tin-doped indium oxide, the decay of the photocarriers associated with the plasmonic absorption is as fast as 50 fs, which makes the material incompatible with the emission scheme and photodetection [23]. Here, we combine THz time-domain spectroscopy (THz-TDS) with Fourier transform infrared spectroscopy (FTIR) measurements to fully probe the absorption of self-doped large HgTe NCs in the THz spectral range. We develop a microscopic model including both quantum confinement and thermal carrier distribution effects to interpret this broad THz absorbance and unveil the dominant contribution of intraband excitations of individual carriers over collective excitations. Furthermore, using optical pump-THz probe measurements, we probe the dynamics of nonequilibrium carriers at low energies in these large HgTe NCs and report on carrier dynamics as long as few picoseconds attributed to resonant and nonresonant nonradiative carrier recombination processes.

2 Results and discussion

We start by growing HgTe NCs using the procedure developed by Goubet et al. [9]. Briefly, mercury chloride and trioctylphosphine telluride are simultaneously injected in hot (300 °C) oleylamine, used as coordinating solvent. After reaction quenching, the particles are cleaned and capped with 1-dodecanethiol ligands. The obtained NCs have large sizes according to electronic microscopy (see Figure 1A and S1 in Supplementary material) and X-ray diffraction (XRD) (see Figure S2 in Supplementary material). The Scherrer size extracted from the XRD pattern is L ≈ 90 nm, which is consistent with the small particles observed by electronic microscopy and suggests that the largest NCs are polycrystalline.

Figure 1:

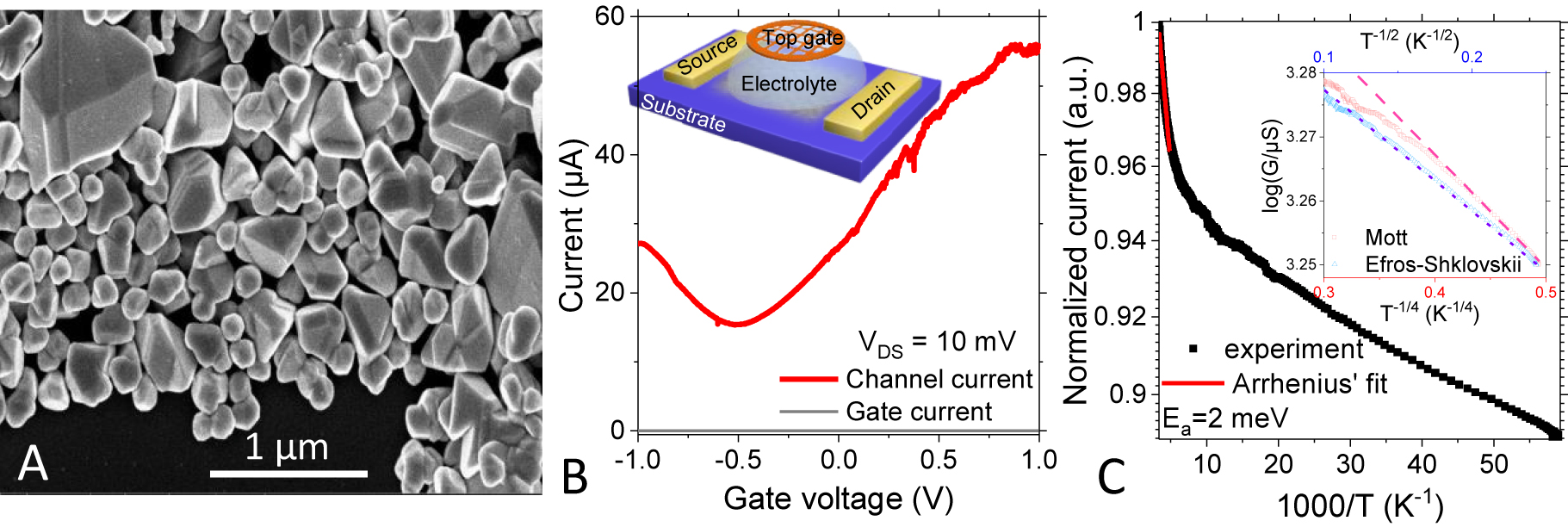
(A) Scanning electron microscopy image of large HgTe NCs. (B) Transfer curve (drain and gate current as a function of the applied gate bias) for a thin film made of large HgTe NCs used as the channel of an electrolytic transistor. Inset is a scheme of the field-effect transistor. (C) Current in logarithmic scale as a function of the temperature for a thin film made of large HgTe NCs. Arrhenius’ fit of the curve in the vicinity of room temperature leads to an activation energy of 2 meV. The inset is a plot of the log of the current as a function of T ^−1/2 and T ^−1/4.

We initially investigate the charge transport in the THz NCs. To make the material conductive we prepare a conductive ink [11, 24] in which the NCs end being capped with sulfide ions. Using this procedure, the obtained films are conductive and present an ohmic I–V curve, (see Figure S4 in Supplementary material). Upon cooling the conductance of the film slowly drops, see Figure 1C. The activation energy of the current, obtained by fitting the I–T curve close to room temperature is estimated to be 2 meV. For such quasi-metallic nanoparticles, the activation energy is mostly determined by the nanoparticle charging energy. Such low value (<k _b T) for the charging energy indicates that charges in an array of large HgTe NCs behave almost as free charges. In this disordered array of NCs, the low-temperature transport is driven by variable range hopping [25, 26], whose temperature dependence gives insight into the charge delocalization [27] and bottleneck of transport. In particular, a Mott scaling (log(G) ∝ T ^−1/4, where G is the conductance) is expected when the density of state (availability of arrival state) is the transport bottleneck. On the other hand, when the carrier density is higher, only the Coulomb gap [26] drives the dot-to-dot transport and an Efros–Shklovskii scaling (log(G) ∝ T ^−1/2) is expected. Such behavior is typically the one observed in arrays of metallic nanoparticles [28]. From the inset of Figure 1C, we clearly see that the latter scaling fits better than the Mott case, confirming this quasi-metallic nature. Thus, these self-doped THz NCs contain high carrier densities up to several carriers per nanoparticle. To determine the nature of the carriers, we use a field-effect transistor configuration. As we anticipate a large carrier density in this very narrow bandgap semiconductor, we design an electrolytic transistor whose gate capacitance (≈1 μF cm⁻²) allows both a large tunability of the carrier density of the NCs and air operation [29]. A scheme of the device is shown in the inset of Figure 1B. We obtain an ambipolar conductance with both hole and electron conduction. The on/off ratio is low (<4) which is consistent with the expected large thermally activated carrier density, but similar to what can be obtained in graphene using electrolyte gating [30, 31].

To study the optical properties of large HgTe NCs at low frequencies, we probe the transmittance of composite films, composed by the NCs, and their surrounding environment made of dodecanethiol ligands and air, using THz TDS. We probe HgTe composite films deposited on a high-resistivity silicon substrate and use a bare high-resistivity silicon substrate as a reference sample. The THz pulse transmitted through a HgTe sample (red line) shows a temporal shift and a decrease of the electric field relative to the pulse transmitted through a reference sample (black line), as reported in Figure 2A. Applying a Fourier transform on the two recorded time-resolved electric fields, we obtain the amplitude spectra (see insert Figure 2A) and the transmittance of the composite film in the frequency domain, t 0 ˜ ( ω ) = E ˜ sample ( ω ) / E ˜ ref ( ω ) . The calculation of the THz electric field propagation across the two samples links the amplitude transmittance t 0 ˜ ( ω ) to the complex refractive index n ˜ eff ( ω ) of the composite film (see details in Supplementary material). Figure 2B reports the real and imaginary parts of n ˜ eff ( ω ) extracted from our analysis. We observe that Re [ n ˜ eff ( ω ) ] slowly decreases with increasing frequency. It remains close to the HgTe bulk value (n _HgTe ≈ 3–4) [32] but higher than the values of films composed of 10 nm-size HgTe NCs (n ≈ 2.3) [33]. A clear rise of Im [ n ˜ eff ( ω ) ] is observed as the frequency increases, reaching a plateau above 3.5 THz. To extend the investigated spectral range up to 40 THz (i.e. 1335 cm⁻¹), we use an FTIR spectrometer in an attenuated total reflection configuration. The association of TDS and FTIR measurements provides the absorbance spectrum over a very broad frequency band ranging from 1330 cm⁻¹ to 10 cm⁻¹ (i.e. 40 THz to 0.35 THz), see Figure 2C. The low-frequency absorbance A is calculated from THz TDS experiments using A ≈ 4 π Im [ n eff ] d / λ , where d = 13.2 µm is the thickness of the composite film. Note that as measurements were performed independently, the absorbance spectra are reported in relative values: the FTIR data are arbitrarily matched to the TDS one in their overlapping spectral region. From the full (enlarge) absorbance spectrum of the composite film, two distinct regimes clearly emerge. At high energy (>1000 cm⁻¹), a broad absorption is observed from interband transitions in the HgTe NCs. Below 400 cm⁻¹ (50 meV or 12 THz or 25 µm), there is a large absorption resonance centered at ≈4.5 THz, unveiling the doped nature of the NCs [4, 5]. We attribute the absorption feature observed at 120 cm⁻¹ to the additional transverse optical (TO) phonon absorption according to the Raman spectrum (see Figure S3 in Supplementary material). From the characterization of several composite films of various thicknesses, we find that the thicker the composite film, the more intense the THz absorption resonance.

Figure 2:

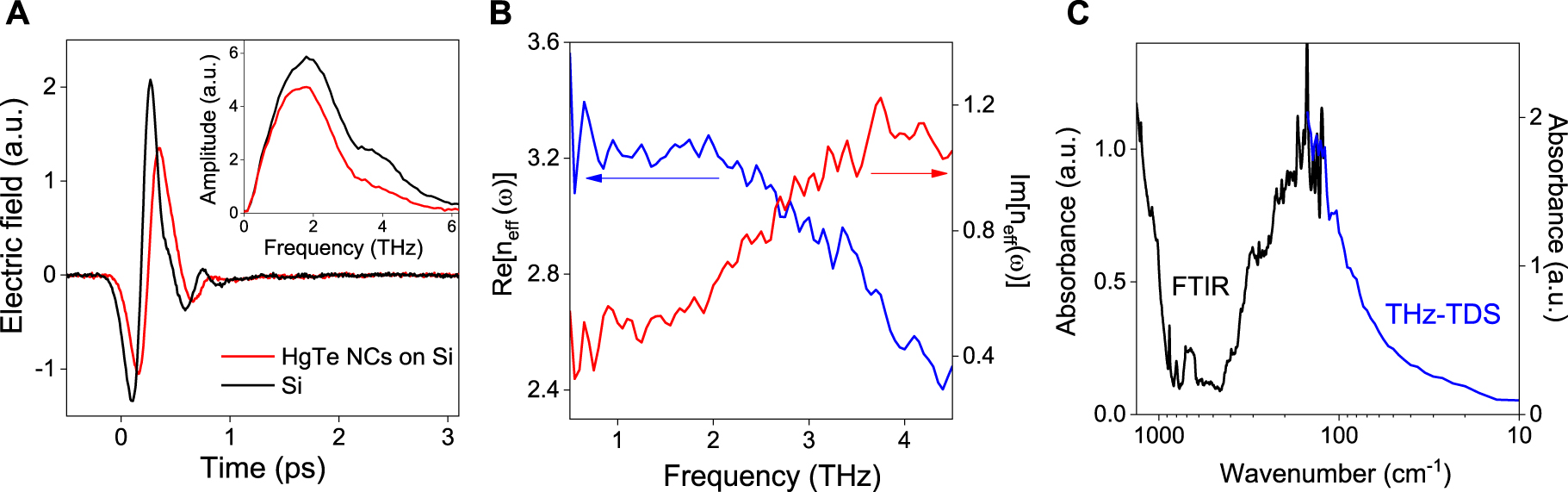
(A) The electric fields of the THz pulses transmitted through the HgTe composite film sample (red line) and through the Si substrate reference sample (black). Inset: corresponding amplitude spectra obtained by fast Fourier transform of the temporal traces. (B) The real and imaginary part of the effective index n ˜ eff ( ω ) of the composite film composed by the NCs and their surrounding environment is made of dodecanethiol ligands and air. (C) Absorbance spectra from 1330 cm⁻¹ to 10 cm⁻¹ of the HgTe sample obtained by THz TDS (blue line) and FTIR (black line) measurements. The FTIR data are arbitrarily matched to the TDS one in their overlapping spectral region, as measurements were performed independently.

To gain insight into the physical origin of the THz absorption resonance, we model a HgTe NC as a cubic (size L) hard-box and assume a parabolic effective mass description (m _e * = 0.03m₀). The one-electron wave functions of this model, labeled by the positive integers (n, k, l), are ψ k , l , n ( x , y , z ) = ϕ k ( x ) ϕ l ( y ) ϕ n ( z ) = 8 / L 3  sin ( k π x / L ) sin ( l π y / L )  sin ( n π z / L ) . The electronic state energies are: E k , l , n = E k + E l + E n = ℏ 2 π 2 ( k 2 + l 2 + n 2 ) / ( 2 m e ∗ L 2 ) . At room temperature, the conduction band is populated with electrons both thermally excited from the near heavy valence states and potentially transferred from the nearby environment. These electrons are assumed to be at thermal equilibrium with a Fermi–Dirac distribution given by F n , k , l = 1 / { exp [ ( E n , k , l − μ ) / k B T ] + 1 } with µ the chemical potential. The number of electrons in the conduction band of the NC is N e = 2 ∑ n , k , l F n , k , l . In previous works, the effect of thermal carrier distribution among the NC states was disregarded, as small NCs of typically <10 nm sizes were investigated with characteristic level spacings largely surpassing k _B T [34]. Here, on the contrary, population effects are of paramount importance, as the largest NCs have a denser energy spectrum and host a smaller density of conduction band electrons (in the order of 10¹⁷ cm⁻³, as discussed below). Our quantum model distinctively accounts for this thermal carrier distribution effect. We evaluate the induced intraband polarization P intra for an exciting light with the electric field E z = E z ω e − i ω t polarized along the z-axis: P intra = − e 〈 z 〉 / L 3 , where − e 〈 z 〉 represents the thermal average of the electron dipole along the field direction. In the linear response model, considering the dipolar coupling V dip = e E z z as the perturbation, one obtains:

where factor 2 accounts for the spin degeneracy, and we have used the fact that the electric field in the Oz direction only couple states with the same (k, l) quantum numbers. The intraband linear susceptibility of an NC, χ intra , is then evaluated after its definition: P intra ≡ ϵ 0 χ intra ( ω ) E z . One obtains

which is the standard form of the linear susceptibility, as composed of an ensemble of Lorentzian terms weighted by the population factors F n , k , l − F m , k , l and by the dipole matrix elements | − e ( z n , m ) | 2 (see Supplementary material). The matrix elements | − e ( z n , m ) | 2 introduce selection rules that allow only transitions between electronic states of different parities. The permittivity writes ϵ ( ω ) = 1 + χ inter ( ω ) + χ intra ( ω ) . As the interband resonance (>30 THz) is far away from the low-energy spectral range (0.35 to 10 THz), the interband contribution to the susceptibility is described as a constant offset ϵ ∞  − 1. We thus have ϵ ( ω ) = ϵ ∞ + χ intra ( ω ) . To link the calculated permittivity of the NCs to the experimental absorption of the HgTe composite film, we calculate the absorption cross-section C abs ( ω ) . Indeed, for a HgTe NC of size much smaller than the wavelength in the medium, the optical extinction is dominated by absorption of light. In the quasi-static approximation, one has (see e.g. [35]):

where ε _M is the relative dielectric constant of the environment of the particles and k M = ω ϵ M / c is the light wavevector in the host medium and b a shape-dependent parameter accounting for the local-field effect. We neglect interference effects from different NCs in the composite sample. In the calculation, we take ϵ ∞  = 16, ε _M = 2 (dodecanethiol ligands and air) and assume energy-independent damping constant γ . For a cubic NC, the value of b is not analytical; we use b = 1/3 (value for a spherical particle) in the calculations, which is not expected to change the physical meaning of the results [34].

To include in the calculation the inhomogeneous distribution of sizes of the ensemble of NCs forming the composite film, we introduce the average absorption cross-section: C abs ( ω ) = ∑ n P n   C abs ( ω ; L n ) where P n = N n / N NC is the normalized inhomogeneous distribution of sizes with N _n the number of NCs of size L _n and N_NC the total number of NCs in the composite film. It is important to stress that all the NCs share the same chemical potential µ regardless of their size since they are embedded in the same environment. Thus, it is the number of electrons in the NCs that evolves with the NC size, such that larger NCs host a larger number of electrons. For independent NCs and neglecting scattering effects [35], the absorbance A(ω) of the composite medium is expressed as A ( ω ) ≈ ∑ n N n C abs ( ω ; L n ) / S , where S is the surface of the THz beam.

Figure 3A shows the result of calculations based on the full quantum-mechanical model of the normalized absorbance of the composite film, A ( ω ) (red line), for a chemical potential μ = 8 meV, a broadening of γ  = 10 meV and inhomogeneous size distribution of the NCs (see Supplementary material), with an average size of 90 nm. The values of μ and γ were adjusted to allow the best fit of the overall spectral shape of the experimental data (blue line). The calculations capture all the key experimental features, including the peak frequency and the asymmetric broadening of the absorbance resonance. From the extracted parameters μ, we obtain an electron density N e / V NC ≈ 10 17   cm − 3 for the largest NCs, which slightly decreases with L. From this analysis, we can obtain the absorption cross-section per unit volume of individual NCs, C abs ( ω ; L ) / V NC , for different NC sizes, assuming μ = 8 meV and γ = 10 meV, as shown in Figure 3B. As the size of the NC is decreased from 1000 to 50 nm, the resonant-like profile of the absorption cross-section shows a blue shift as expected for a quantum-confinement effect. More quantitatively, the peak frequency of C abs ( ω ; L ) increases linearly as 1/L ² for decreasing L, reflecting more quantum confinement of carriers as NCs become smaller (see insert Figure 3B in semi-log scale). For large NCs of L = 1000 nm, the frequency of the absorption peak is slightly higher than the screened plasma frequency ( ν P = ν ‾ P / ϵ ∞ = N e   e 2 / ( 4 π 2 m e ∗ ϵ 0 ϵ ∞ V NC )  = 4.5 THz).

Figure 3:

(A) Calculations based on the full quantum-mechanical model of the normalized absorbance of the composite film, A(ω) (red line), for a chemical potential μ = 8 meV, a broadening of γ = 10 meV, a size distribution reported in Figure S4 and experimental data obtained from THz-TDS and FTIR measurements (blue dots). (B) The absorption cross-section per unit volume of individual NCs, C abs ( ω ; L ) / V NC , for NC sizes ranging from L = 1000 nm to L = 50 nm, assuming μ = 8 meV and γ = 10 meV. Inset: Peak frequency of C abs ( ω ; L ) as a function of 1/L ² in semi-log scale reflecting more quantum confinement of carriers as NCs become smaller. (C) Real, Re [ ϵ ( ω ) ] , and imaginary parts, Im [ ϵ ( ω ) ] , of the intraband permittivity as a function of the photon frequency, for a HgTe NC of size L = 92 nm, µ = 8 meV and γ  = 10 meV. For comparison, dashed curves are the real and imaginary parts of the permittivity based on classical Drude model.

To evaluate the interplay between the quantum mechanical transitions and collective excitations, we calculate the real part, Re [ ϵ ( ω ) ] and the imaginary parts, Im [ ϵ ( ω ) ] , of the permittivity of a HgTe NC of size L = 90 nm, for μ = 8 meV and γ  = 10 meV (see Figure 3C). We observe that Im [ ϵ ( ω ) ] displays a resonant profile and vanishes at ω  = 0, while Re [ ϵ ( ω ) ] has a positive value at ω  = 0 and displays a damped dispersive profile up to a frequency close to the maximum one for Im [ ϵ ( ω ) ] . Importantly, the real part of the permittivity remains positive for all frequencies. This feature indicates that the plasma contribution is not enough at these low doping values to modify the permittivity such that its real part decreases down to − 2 ϵ M . Consequently, the absorption does not have a pole preventing the existence of localized plasmon resonance. The broad resonant profile for Im [ ϵ ( ω ) ] and the dispersive profile for Re [ ϵ ( ω ) ] predicted by our model for a relatively weak damping rate is peculiar to large NCs. Indeed, for a HgTe NC of size L = 90 nm, E 1,1,1 ≈ 4.4  meV < μ ≪ k B T , which leads to a large number of states partially populated and thus available for the dipolar transitions. In striking contrast with nanometer-scale NCs for which broad resonance at low frequency is a signature of a large damping rate [36], the broadening of the absorbance for large NCs hosting a small number of conduction electrons (around 10 17 cm − 3 in Figure 3A) investigated in this work is governed by thermal carrier redistribution effect. Our model includes both quantum confinement [37] and thermal effects [38] that are essential to interpret the experimental THz absorption features of large and weakly (self) doped NCs. We conclude from this analysis that the broad THz absorption resonance is fully described by multiple intraband transitions of single carriers between quantized states and that the contribution of collective effects is unimportant at such low doping values. Also, we compare the calculated permittivity based on our quantum model with a classical Drude profile [37] (dashed curves) with ϵ Drude ( ω ) = ϵ ∞ + χ Drude ( ω ) , where χ Drude ( ω ) = − ω ‾ P 2 / [ ω ( ω + i / τ ) ] . ω ‾ P = 2 π ν ‾ P is the unscreened plasma pulsation and 1 / τ = 2 γ / ℏ . We observe that at frequencies of interest in this work, the permittivity significantly differs from the Drude model, showing the contribution of quantum confinement even for such large NCs with γ  = 10 meV. Indeed, as discussed in previous works [39], such marked deviations of ϵ ( ω ) − ϵ ∞ from the Drude model predictions can be traced back to the intraband transitions among the confined NC energy levels.

The photoresponse of NCs at THz frequencies under optical excitation at 800 nm wavelength is now presented. For this purpose, the HgTe NC film is deposited in a z-cut quartz substrate. The silicon substrate is replaced by a quartz substrate to avoid any absorption of the optical pump light by the substrate. The incident pump fluence is 6 μJ cm⁻² corresponding to a photoexcited carrier density in the range of 10¹⁶ cm⁻³. This difference of the THz electric field transmitted through the NCs with and without optical pumping, expressed as |ΔE(t)| = |E _ON(t) − E _OFF(t)|, is reported in Figure 4A, for a delay after the optical pump excitation of 2 ps. We observe that |ΔE(t)| shows a faster transient than the THz electric field pulse transmitted without illumination with a derivative-like temporal shape. The photoexcitation changes the electron density of the NCs and leads to a heating of the carrier distribution. Indeed, after photoexcitation at high energy (1.55 eV), the electron/hole populations are both redistributed by ultrafast intraband scattering to low energy states that are not Pauli blocked as μ ≪ k B T . This hot photoexcited carrier distribution directly affects the transmission of the THz pulse by modifying occupied and unoccupied states around the chemical potential. Thus, |ΔE(t)| results from a modification of the involved intraband transitions of single carriers between quantized states. As ΔE(ω)/E _OFF(ω) = Δt(ω)/t ₀(ω), the amplitude spectrum of the pump-induced change in transmission Δt(ω)/t ₀(ω), reported in Figure 4B, is determined from the entire THz waveforms ΔE(t) and E _OFF(t). Δt(ω)/t ₀(ω) is negative, meaning that the absorption is increased as a result of photoexcitation. It shows a monotonic decrease indicating a photoinduced increase of the absorption with the frequency from 0.4 to 3 THz and a plateau above 3 THz, which is fully consistent with the derivative-like shape observed in the temporal domain. Also, we observe in Figure 4C that Δt/t ₀ at the peak of the THz pulse follows a square root law with the incident fluence (red line), indicating that the intensity transmittance ΔT/T ₀ scales linearly with the pump excitation fluence and consequently with the photoexcited carrier density.

Figure 4:

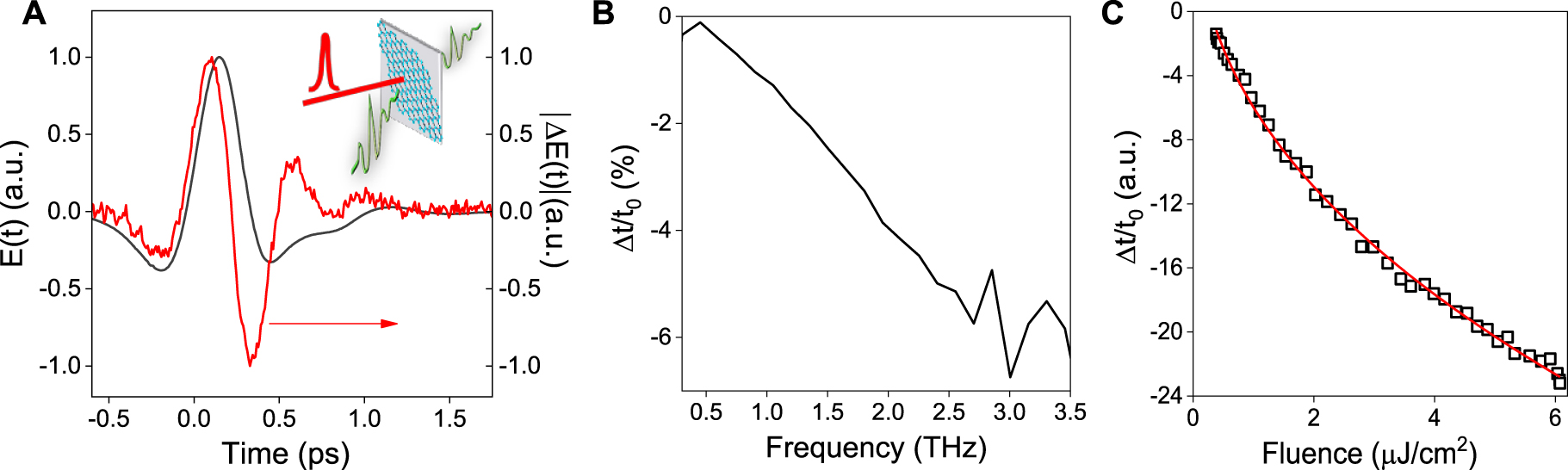
(A) The pulse transmitted through the composite HgTe film E(t) (left) and the difference of the THz electric field transmitted through the NCs with and without optical pumping, expressed as |ΔE(t)| = |E _ON(t) − E _OFF(t)| (right). (B) Amplitude spectrum of the pump-induced change in transmission, Δt(ω)/t ₀(ω) for a delay after the optical pump excitation of 2 ps and an incident pump fluence of 6 μJ cm⁻². Δt(ω) is the difference of the transmission with and without photoexcitation, Δt(ω) = t _ON(ω) − t _OFF(ω). (C) The peak amplitude of Δt/t ₀ as a function of the incident optical pump fluence from 0.4 μJ cm⁻² to 6 μJ cm⁻². The red line is a fit by a square root law.

Finally, we investigate the dynamics of the observed photoinduced change in THz transmission in the HgTe NCs. Figure 5A reports −Δt/t ₀ at the peak of the THz pulse as a function of the pump–probe delay time τ for a pump fluence of 6 μJ cm⁻². The temporal evolution of −Δt/t ₀ first rises with a characteristic time of ≈2 ps, reaches a maximum, and then decays over the next few tens of picoseconds. These observations can be explained as follows. The photocarriers are generated by the optical pump at high energies (within 100 fs). At first, the THz absorption does not change. The THz absorption only increases after the photoexcited carrier distribution cooled down to low energy states, within 1–2 ps. The photoexcited carriers are then trapped and recombine within 6 ps, where the THz absorption decreases back to its original value. The initial rise time of 2 ps is consistent with the intraband carrier–carrier and electron–optical phonon scattering in large NCs. Indeed, the weak confinement energies and high density of states in large NCs (≈100 nm diameters) lead to the efficient carrier–carrier scattering between the photoexcited carriers and the carriers in the Fermi sea, and to efficient electron–phonon coupling as even the lowest electronic states are separated by only one or two optical-phonon energies. Note that other intraband relaxation mechanisms relying on near-field energy transfer to electronic states mediated by the surface states or to molecular vibrations of the surface ligands, previously reported in strongly confined NCs of smaller sizes, are less dominant in these large NCs [40]. The decay time of −Δt/t ₀ is well described by a mono-exponential decay function (red line) with a value as long as τ = 6 ps. By varying the optical pump pulse fluences from 0.08 to 0.57 μJ cm⁻², the dynamics of −Δt/t ₀ are still well-described by an approximatively constant relaxation time of ≈2 ps followed by a mono-exponential recombination time. Figure 5B shows that the recombination times extracted from the dynamics of −Δt/t ₀ rise linearly with increasing pump fluence. We observe that the frequency dependence of Δt/t ₀ is constant for all-optical pump fluences. As shown in Figure 5C, the frequency-resolved photoinduced change in transmission at different times after excitation with the pump pulse reveals that the photoinduced transmission change is progressively suppressed over the entire bandwidth of the THz probe. Importantly, the carrier recombination time of few picoseconds supports our conclusion that collective excitations are negligible since sub-picosecond decays are expected for photocarriers associated with the plasmonic absorption [23].

Figure 5:

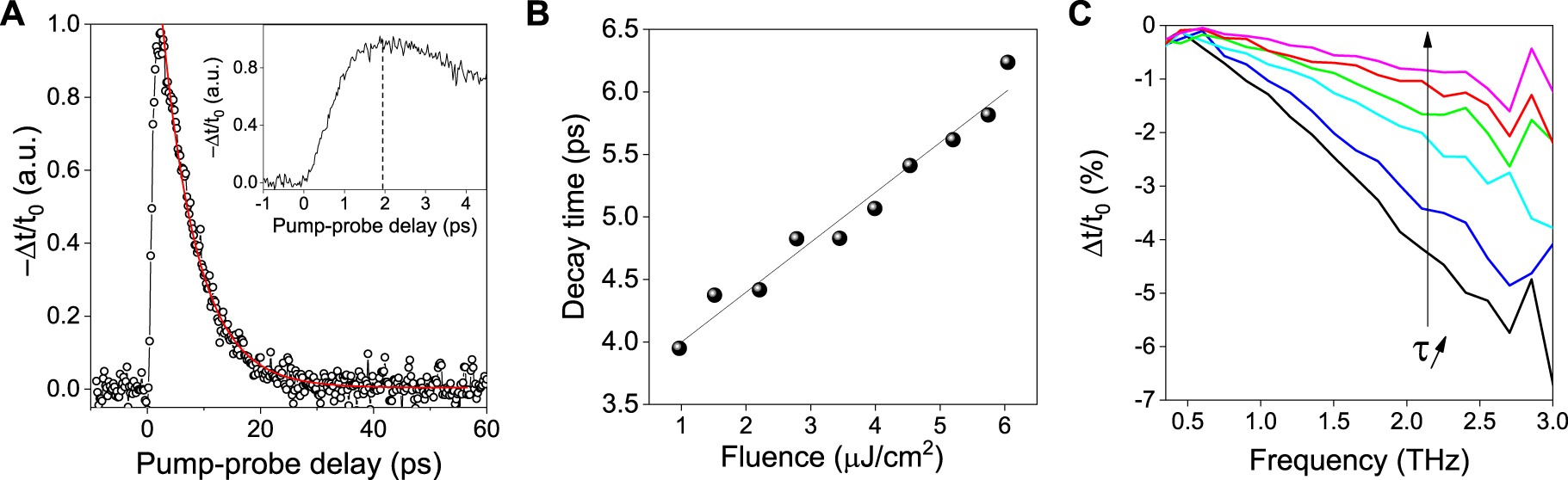
(A) The dynamics of the change of the transmission −Δt/t ₀ as a function of the pump–probe delay time. (B) Decay time of  −Δt/t ₀  as a function of the incident optical pump fluence, showing a slow-down of the decay as the incident fluence is increased. (C) Frequency-dependent differential transmittance spectra Δt(ω)/t ₀(ω) measured at different pump–probe delay times from 2 ps to 9 ps.

This raises the question of the physical mechanism responsible for these few picoseconds recombination times. Recombination pathways for hot carriers can involve Auger recombination, scattering with the optical phonon of HgTe NCs, radiative recombination, the emission of vibration modes in ligands, and trap-assisted recombination. Auger recombination processes lead to faster decay at larger incident fluence [41], which is inconsistent with our experimental observations. Moreover, interband Auger relaxation time τ Auger in HgTe NCs is expected on a notably longer timescale as the Auger coefficient C _A scales as C A = γ r 3 , with γ = 1.2 × 10⁻⁹ cm³/s, giving for an NC of 100 nm radius, τ Auger = V 2 / 8 C A in the microsecond range [42, 43]. Considering the relatively large interband energy gap of the HgTe NCs (>1000 cm⁻¹), direct nonradiative recombination via emission of a large number of phonons of only 120 cm⁻¹ is improbable. Interband radiative recombination time falls in the nanosecond range [44, 45] and thus cannot be responsible for the few picoseconds decay dynamics measured here. As the electronic states close to the bandgap (≈1000–1500 cm⁻¹) overlap the broad low-frequency ligand vibrational band (≈1350 cm⁻¹) of n-dodecanethiol [45], efficient hot carriers cooling through the direct energy transfer from the electronic transition to the ligand vibrational modes is expected [46, 47]. Also, previous works on smaller size NCs have observed that this resonant recombination process based on direct energy transfer occurs on typically few tens of picosecond timescales [45, 48]. Alternatively, owing to the existence of traps localized on the surface of the HgTe NCs, nonresonant nonradiative carrier recombination assisted by surface traps can play a significant role. This nonresonant recombination process, detailed in Ref. [49], relies on the coupling of a shallow surface trap state with low-energy electron and hole states in the NCs. This is mediated by optical phonons with nonzero angular momenta, and the subsequent recombination of electron–hole pairs assisted by other deeper states of the surface trap, coupled by vibrational modes of the NC environment. Therefore, we attribute these both resonant and nonresonant recombination channels as the main mechanisms involved in the recombination process of hot carriers in THz HgTe NCs. The nonresonant recombination process is consistent with the relaxation slow down observed when increasing the pump fluence as more phonons are needed for carriers of higher energy to be trapped by shallow surface states.

3 Conclusion

In conclusion, the optical properties of large self-doped HgTe NCs in the full THz spectral range were studied and showed a broad THz resonant absorption centered at ≈4.5 THz. Combining experiments with microscopic calculations, we showed that the THz absorption results from multiple intraband transitions of single carriers between quantized states and that collective excitations are negligible in self-doped THz HgTe NCs. Also, we probe the dynamics of the photo-induced transmission changes at THz frequencies and report on a relaxation time of a few picoseconds. We highlight that Auger recombination is not the main relaxation mechanism at play in this system. We attribute the main carrier recombination pathways to a resonant energy transfer from the electronic transition to the ligand vibrational modes and nonresonant nonradiative recombination channels assisted by surface traps. Our analysis of these NCs will permit to exploit large HgTe NCs for quantum engineering at THz frequencies and for the development of THz photodetectors and emitters. Further investigation will be performed to enhance the doping in large HgTe NCs to induce plasmonic effects.

4 Methods