Transition to strong coupling regime in hybrid plasmonic systems: exciton-induced transparency and Fano interference

1 Introduction

Strong coupling between surface plasmons in metal–dielectric structures and excitons in semiconductors or dye molecules has recently attracted intense interest driven to a large extent by possible applications in ultrafast reversible switching [1–3], quantum computing [4, 5], and light harvesting [6]. In the strong coupling regime, the coherent energy exchange between excitons and plasmons [7] leads to the emergence of mixed polaritonic states with energy bands separated by the anticrossing gap (Rabi splitting) [8]. For excitons coupled to cavity modes in microcavities, the Rabi splitting magnitudes are relatively small on the scale of several meV [9–11]. However, in hybrid plasmonic systems, where surface plasmons are coupled to excitons in J-aggregates [12–22], in various dye molecules [23–27], or in semiconductor nanostructures [28–31], the Rabi splittings can be much greater even reaching hundreds meV. For single excitons, however, achieving a strong exciton–plasmon coupling is a challenging task as it requires extremely small plasmon mode volumes, which can mainly be achieved in nanogaps [32–34].

At the same time, the scattering spectra of hybrid plasmonic systems, such as excitons in J-aggregates or colloidal QDs coupled to gap plasmons in nanoparticle-on-metal systems [35–38] or those in two-dimensional atomic crystals conjugated with Ag or Au nanostructures [39–44], exhibit a narrow minimum even before reaching the strong coupling transition point. The emergence of such a minimum in the weak coupling regime is referred to as exciton-induced transparency (ExIT) [45–47], in analogy to electromagnetically induced transparency (EIT) in pumped three-level atomic systems that is attributed to the Fano interference between different excitation pathways. Recently, we have shown that, in the linear regime (i.e. in the absence of pump), the emergence of this minimum is due to the imbalance of energy exchange between the emitter and plasmon in a narrow frequency interval [48]. Typically, the plasmon optical dipole moment significantly (by ∼10⁴) exceeds that of an exciton in a semiconductor quantum dot and so the emitter’s direct interaction with the radiation field is relatively weak [49]. In this case, the ExIT minimum in scattering spectra is described, with reasonably good accuracy, by the dressed plasmon model or by its classical analog – the coupled oscillators model, in which only the plasmon interacts with the radiation field, so that the scattering spectra show a narrow ExIT minimum on top of a broad plasmon band, while the overall spectral weight is tilted toward the higher frequency range [38, 47, 48].

On the other hand, in hybrid plasmonic systems, the optical interference between an exciton and a plasmon can arise from the indirect coupling of the exciton to the radiation field. Namely, if the incident light frequency is tuned to the plasmon resonance, the exciton dipole moment induced by the plasmon near field is not necessarily small, so that the exciton can substantially contribute, albeit indirectly, to the system optical transition. This gives rise to Fano interference between the plasmon and plasmon-induced exciton dipoles which can significantly affect the overall shape of optical spectra. As we show in this paper, such Fano interference effects can lead to inversion of spectral asymmetry, characterized by spectral weight shift toward lower frequency range, which was observed for excitons coupled to localized plasmon modes [22, 39, 40].

In this paper, we present a microscopic model for the linear optical response of a single exciton resonantly coupled to a surface plasmon mode in a metal–dielectric structure which accounts for both ExIT and Fano interference effects as the system transitions to a strong coupling regime. Starting with the canonical Hamiltonian with microscopic coupling parameters [50], we set up the system of Maxwell–Bloch equations for induced dipole moments which determine the scattering spectrum of the hybrid plasmonic system. We further show that while the ExIT minimum results from the energy exchange imbalance in a narrow frequency interval, the overall spectral shape of scattering spectra is strongly affected by the Fano interference between radiating plasmon and plasmon-induced exciton dipoles. Specifically, we demonstrate that the Fano interference can lead to an inversion of spectral asymmetry, consistent with the experiment [22, 39, 40].

2 The system Hamiltonian and microscopic coupling parameters

We consider a quantum emitter (QE) with dipole moment μ _e and excitation frequency ω _e situated at a position r _e near a metal–dielectric structure characterized by complex dielectric function ɛ(ω, r ) = ɛ′(ω, r ) + iɛ″(ω, r ) supporting localized plasmon modes with frequencies ω _m interacting with external electromagnetic (EM) field E (t). For monochromatic EM field of frequency ω, in the rotating wave approximation (RWA), the system dynamics is described by the Hamiltonian

where a ̂ m † and a ̂ m are the plasmon creation and annihilation operators, σ ̂ † and σ ̂ are the raising and lowering operators for the QE, while the parameters g and μ _m characterize, respectively, plasmon’s coupling to the QE and EM field.

For plasmonic nanostructures with characteristic size smaller than the radiation wavelength, the coupling parameters can be obtained microscopically by relating them to system geometry and local field [50]. For such systems, the plasmon modes are determined by the quasistatic Gauss equation [51] ∇ ⋅ ε ′ ( ω m , r ) ∇ Φ m ( r ) = 0 , where Φ_m( r ) is the mode potential that defines the mode field E _m( r ) = −∇Φ_m( r ), which we choose to be real. To determine the plasmon dipole moment for optical transitions, we recast the Gauss’s law as ∇ ⋅ E m ( r ) + 4 π P m ( r ) = 0 , where P _m( r ) = χ′(ω _m, r ) E _m( r ) is the electric polarization vector and χ = (ɛ − 1)/4π is the plasmonic system susceptibility. The plasmon dipole moment has the form

The Gauss’s equation does not determine the overall field normalization [51], but the later can be found by matching the plasmon radiative decay rate and that of a localized dipole with excitation energy ℏω _m. The plasmon radiative decay rate has the form [52] γ m r = W m r / U m , where

is the plasmon mode energy [53, 54] and

is the radiated power (c is the speed of light) [8]. The normalized modes E ̃ m ( r ) are thus determined by setting

where μ _m is the mode optical transition matrix element. We then find the normalization relation as

where the scaling factor ℏ ω m / U m converts the plasmon energy U _m to ℏω _m in order to match the EM field energy (the factor 1/2 reflects positive-frequency contribution). Accordingly, the plasmon optical transition matrix element in the Hamiltonian (1) takes the form [compare to Eq. (2)]

In a similar way, the plasmon nonradiative decay rate is γ m n r = W m n r / U m , where W m r = 1 8 π ∫ d V ε ″ ( ω m , r ) E m 2 ( r ) is the power dissipated in the plasmonic structure due to Ohmic losses. In terms of normalized fields, the nonradiative rate takes the form

and so the plasmon full decay rate is γ m = γ m n r + γ m r . Note that in structures with a single metallic component, the standard expression [51] for γ m n r is recovered: γ m n r = 2 ε ″ ( ω m ) / [ ∂ ε ′ ( ω m ) / ∂ ω m ] . The optical polarizability tensor of a plasmonic structure describing its response to the external field E e^−iωt has the form

where we kept only the resonance term [52].

The QE–plasmon coupling in the Hamiltonian (1) is expressed via normalized plasmon mode fields as [50]

To present the coupling in a cavity-like form, we use the original plasmon mode fields (6) to obtain [7]

where V is projected plasmon mode volume characterizing plasmon field confinement at the QE position r _e along its dipole orientation n _e [52, 54, 55]. The plasmon mode volume defines the Purcell factor characterizing radiation enhancement of a QE near a plasmonic structure:

where Q _m = ω _m/γ _m is the plasmon quality factor, γ e r = 4 μ e 2 ω m 3 / 3 ℏ c 3 is the emitter’s radiative decay rate (at plasmon resonance frequency) and γ _e→m is the rate of energy transfer (ET) from QE to plasmon, given by

Comparing Eqs. (11) and (13), we obtain a relation between the QE–plasmon coupling and decay rates:

Thus, all coupling parameters in the Hamiltonian characterizing plasmon interactions with the QE and EM fields are expressed via system parameters and related to plasmon and QE decay rates. Below, we employ these microscopic expressions to elucidate the role of ExIT and Fano interference in scattering spectra of hybrid plasmonic systems.

3 Optical dipole moment of a hybrid plasmonic system

We are interested in the linear response of hybrid plasmonic system to the external EM field. We assume that there is only a single excitation in the system and disregard any nonlinear effects. In this case, we can approximate the QE by bosonic operators to setup Maxwell–Bloch equations for nondiagonal elements of density matrix (polarizations) ρ _e(t) and ρ _m(t) related to QE and plasmon induced dipoles as p _e(t) = μ _e ρ _e(t) and p _m(t) = μ _m ρ _m(t), respectively. Using the Hamiltonian (1), in the linear approximation, the Maxwell–Bloch equations for ρ _m(t) and ρ _e(t) are obtained in a standard manner as

where dot stands for the time-derivative and γ _e is the QE spectral linewidth assumed much smaller than γ _m.

In the steady-state case, substituting ρ _m(t) = ρ _me^−iωt and ρ _e(t) = ρ _ee^−iωt , we find

and

The system’s induced dipole moment is p _s = p _m + p _e = μ _m ρ _m + μ _e ρ _e. To elucidate the processes contributing to p _s, we define QE polarizability tensor (in RWA) as

and introduce plasmon-induced QE dipole moment as

Then, the hybrid system dipole moment can be decomposed into three contributions:

The main contribution comes from the dressed plasmon characterized by induced dipole moment

where

is the plasmon’s self-energy due to its interactions with the QE. Specifically, the imaginary part of the self-energy determines the ET rate from the plasmon to QE as

which represents a Lorentzian centered at QE frequency ω _e and maximum value γ _m→e ≡ γ _m→e(ω _e) = 4g ²/γ _e.

The QE–plasmon interference term has the form

and describes indirect, i.e. mediated by plasmon, interactions of QE with the EM field. The last term represents dressed QE contribution,

where

is the QE self-energy, whose imaginary part now determines the ET rate from the QE to plasmon as

which represents a Lorentzian centered at plasmon frequency ω _m and maximum value γ _e→m ≡ γ _e→m(ω _m) = 4g ²/γ _m, matching Eq. (14). Importantly, in a narrow frequency interval |ω − ω _e| ≲ γ _e, the reverse plasmon–QE ET rate γ _m→e exceeds the direct QE–plasmon ET rate γ _e→m:

While the overall ET balance over the entire frequency range is preserved, the ET imbalance in the frequency interval ∼γ _e leads to the emergence of the ExIT minimum in the dressed plasmon spectra [48]. For a typical case μ _e/μ _m ≪ 1, the dressed emitter’s dipole moment (25) is negligibly small relative to dressed plasmon’s dipole moment (21) and can be omitted. While the position and magnitude of the ExIT minimum are accurately described by this energy exchange mechanism within dressed plasmon approximation, i.e. p _s ≈ p _dp, it does not include QE interactions with the EM field. The latter is included indirectly in the interference term (24) via plasmon-induced QE dipole moment q _e, which as we show below, gives rise to Fano interference that strongly affects the overall shape of scattering spectra as the system transitions to a strong coupling regime.

4 Exciton-induced transparency vs. Fano interference

The scattering cross-section σ s s c ( ω ) of a hybrid plasmonic system is obtained by normalizing the radiated power W _s = (ω ⁴/3c ³)| p _s(ω)|² with the incident flux S = (c/8π)E ² [8]. In the following, we disregard the relatively small direct QE coupling with the EM field but include the indirect coupling via plasmon-induced dipole moment, so that the induced system dipole includes the interference term: p _s ≈ p _dp + p _int. The resulting expression for σ s s c ( ω ) is quite cumbersome as it depends sensitively on mutual polarizations of the incident light E , the plasmon dipole moment μ _m and the QE dipole moment μ _e. Here, to simplify the analysis, we consider the case when all dipole moments are parallel to the incident field, i.e. μ _e∥ μ _m∥ E , so that the coupling between the system components and to the EM field is strongest. In this case, the two terms in the numerator in Eq. (24) are equal, and using Eqs. (19) and (22), we obtain

where ω _F = −2gμ _e/μ _m is QE frequency shift due to Fano interference between the plasmon and plasmon-induced QE dipole moments as the system interacts with the EM field. In fact, this shift is the only difference between the current model and dressed plasmon model (with p s ≈ p ̃ m ), which does not include the interference effects [48]. To highlight the role of Fano interference, we relate the scattering cross-section (29) to dressed plasmon scattering cross-section σ d p s c ( ω ) , which is obtained from (29) by setting ω _F = 0, as

where F(ω) is the Fano function,

Here, δ = 2(ω − ω _e)/γ _e is frequency detuning in units of linewidth and q is the Fano parameter:

The Fano function has asymmetric shape that depends on the sign of parameter q. Using Eq. (14), the magnitude of q can be expressed via the Purcell factor as

where η m = γ m r / γ m is the plasmon radiation efficiency. Although the ratio γ e r / γ e is typically very small (∼10⁻⁵) due to the broadening of spectral linewidth γ _e by phonons or vibrons, for small nanostructures we have F _p ≫ 1 and η _m ≪ 1, implying that in a plasmonic hot spot, the actual value of q can be appreciable.

To elucidate the interplay between Fano interference and ExIT, we recall that in the scattering spectra, the ExIT minimum emerges in the weak coupling regime as a narrow dip on the top of a wide plasmon band. The plasmon scattering cross-section is obtained by setting g = 0 in Eq. (29) and, for μ _m∥ E , has the form

To trace the emergence of ExIT minimum, we recast the dressed plasmon scattering cross-section as σ d p s c ( ω ) = σ m s c ( ω ) R ( ω ) , where the function

modulates the plasmon band, and so the system scattering cross-section is factorized as

In the frequency interval |ω _m − ω|/γ _m ≪ 1, using the relation (14), the function R(ω) simplifies to

where the parameter

characterizes the ExIT minimum depth. The ExIT function (37) describes the emergence of spectral minimum due to excessively large plasmon–QE ET in the frequency interval ∼γ _e. Specifically, in the weak coupling regime, the dressed plasmon decay rate has the form γ _dp(ω) = γ _m + γ _m→e(ω). Using Eq. (23) and the relation (14), we obtain

implying linewidth increase by factor (1 + p) in the frequency interval |ω − ω _e| ∼ γ _e which, in turn, leads to the ExIT minimum in the dressed plasmon spectrum.

Thus, in the weak coupling regime, the ExIT and Fano interference effects are distinct and described by different factors in the scattering cross-section (36). While the ExIT factor R(ω) leads to a narrow minimum at the QE frequency position, the Fano factor F(ω) is an asymmetric function of ω that affects the overall shape of the scattering spectra. Remarkably, as we show in numerical calculations below, the Fano interference effect is most visible for intermediate and strong QE–plasmon coupling as it shifts the spectral weight between polaritonic bands resulting in the inversion of spectral asymmetry.

5 Numerical results and discussion

In this section, we present the results of numerical calculations for a QE situated at a distance d from the tip of an Au nanorod in water with excitation frequency in resonance with the surface plasmon frequency, ω _e = ω_m . The nanorod was modeled by a prolate spheroid with semi-major and semi-minor axes a and b, respectively, the QE’s dipole orientation was chosen along the nanorod symmetry axis, the Au experimental dielectric function was used in all calculations [56], and the dielectric constant of water was taken as ɛ _s = 1.77. We used the standard spherical harmonics for calculations of the local fields near the prolate spheroid to obtain the plasmon parameters μ _m, γ _m, η _m, the QE–plasmon coupling g, and the Purcell factor F _p, which determine the ExIT parameter p and Fano parameter q. The QE spectral linewidth γ _e was chosen much smaller than the plasmon decay rate, γ _e/γ _m = 0.1, and its radiative decay time was chosen τ e r = 10 ns, which are typical values for excitons in quantum dots. Note that the QE radiative decay rate γ e r is much smaller than its spectral linewidth: for our system we have γ e r / γ e ∼ 1 0 − 5 .

In Figure 1, we plot the calculated ExIT parameter p, given by Eq. (38), and the Fano parameter q, given by Eq. (32), against the distance to nanorod tip d normalized by a. Figure 1(a) shows the ExIT parameter p = F p γ e r / γ e for three different values of nanorod aspect ratio: a/b = 1.0 (sphere), 2.0 and 3.0. Note that the Purcell factor near the tip of the elongated particle (a/b = 3.0) is much greater than that for a nanosphere (a/b = 1) so that p > 1 in the former case while being negligibly small in the latter case. In Figure 1(b), we show distance dependence of the Fano parameter q for fixed nanorod aspect ratio a/b = 3.0 and different lengths 2a = 40, 20, and 10 nm. The Fano parameter is largest for the smallest nanorod with 2a = 10 nm and is significantly reduced for larger nanorods with 2a = 20 and 40 nm. Both p and q sharply decrease as the QE moves away from the hot spot near the nanorod tip.

Figure 1:

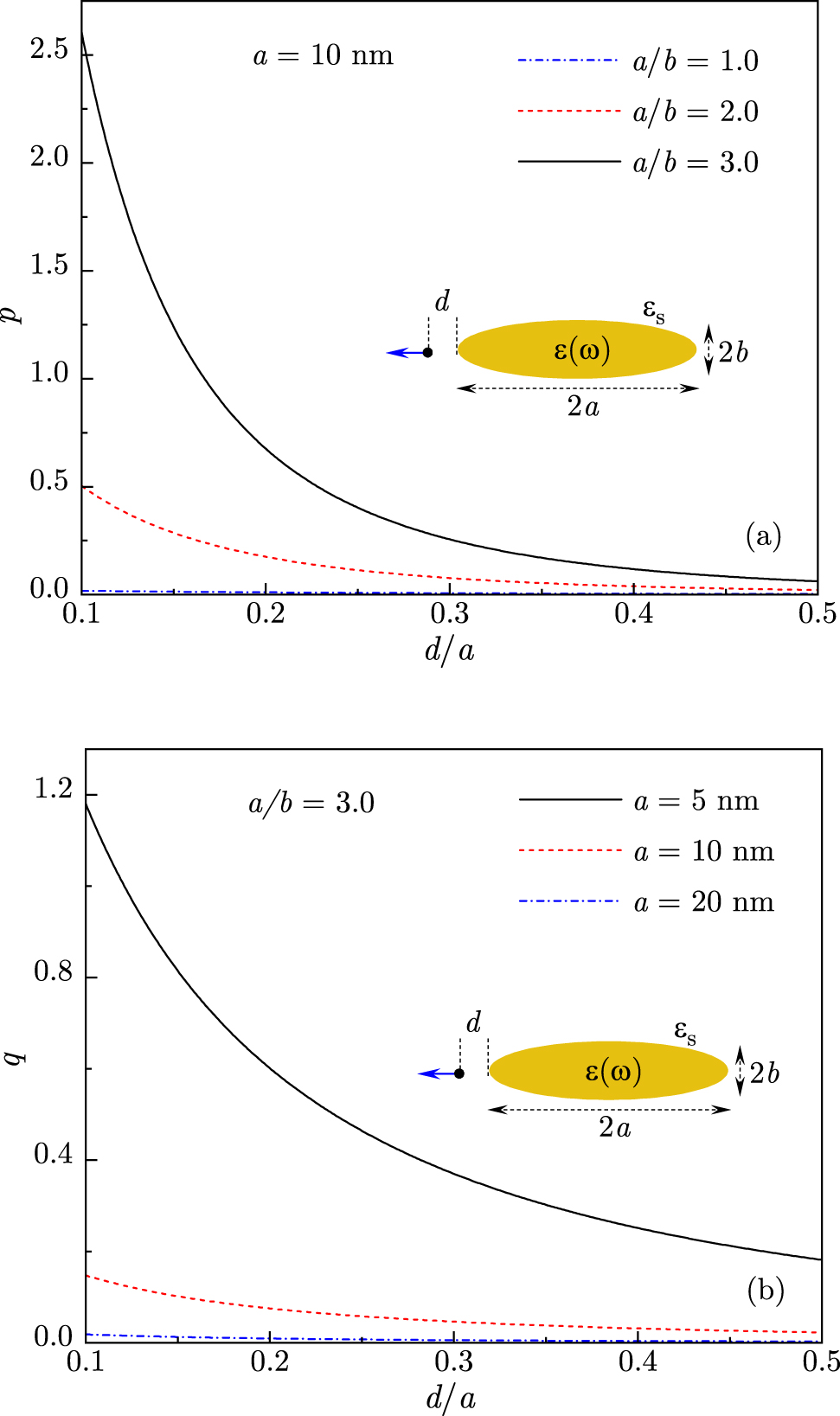
(a) The ExIT parameter p is plotted against the QE distance d to the tip of Au nanorod of length 2a = 20 nm placed for different values of aspect ratio a/b = 1.0, 2.0, and 3.0. (b) The Fano parameter q is plotted against the distance d at nanorod aspect ratio a/b = 3.0 for different values of nanorod length 2a = 40, 20, and 10 nm. Inset: schematics of a QE situated at a distance d from the tip of Au nanorod in water for QE dipole moment oriented along the nanorod axis.

In Figure 2, in order to illustrate the emergence of ExIT, we show the evolution of function R(ω), given by Eq. (35), and of dressed plasmon’s scattering cross-section σ d p sc ( ω ) = σ m sc ( ω ) R ( ω ) (i.e. without Fano interference effect) with decreasing QE–nanorod distance for 2a = 20 nm and a/b = 3.0. With decreasing d, the function R(ω) develops a minimum, as shown in Figure 2(a), which modulates the plasmon scattering spectrum, as shown in Figure 2(b). As discussed in the previous section, the double-peak structure of σ dp sc ( ω ) is caused by ET imbalance between the QE and plasmon in a narrow frequency interval. In order to highlight the role of ExIT parameter p, we plot in Figure 2(a) the asymptotic expression for R(ω), given by Eq. (37), for each value of QE–nanorod distance d (dotted lines). Clearly, in the weak coupling regime (small p), the ExIT function Eq. (37) accurately describes the spectral minimum (blue curves), while for larger p (i.e. closer to the tip) the spectrum develops “wings” outside the minimum region as the system undergoes strong coupling transition. The onset of strong coupling transition can be seen in Figure 2(b) as well, as for d/a = 0.5 and 0.3, the scattering spectrum develops a narrow ExIT minimum at QE frequency on top of unchanged plasmon band, while for d/a = 0.2, the overall spectral width slightly increases signaling the emergence of Rabi splitting. We note that the ExIT function Eq. (37) accurately reproduces the central part of ExIT minimum for any distance d.

Figure 2:

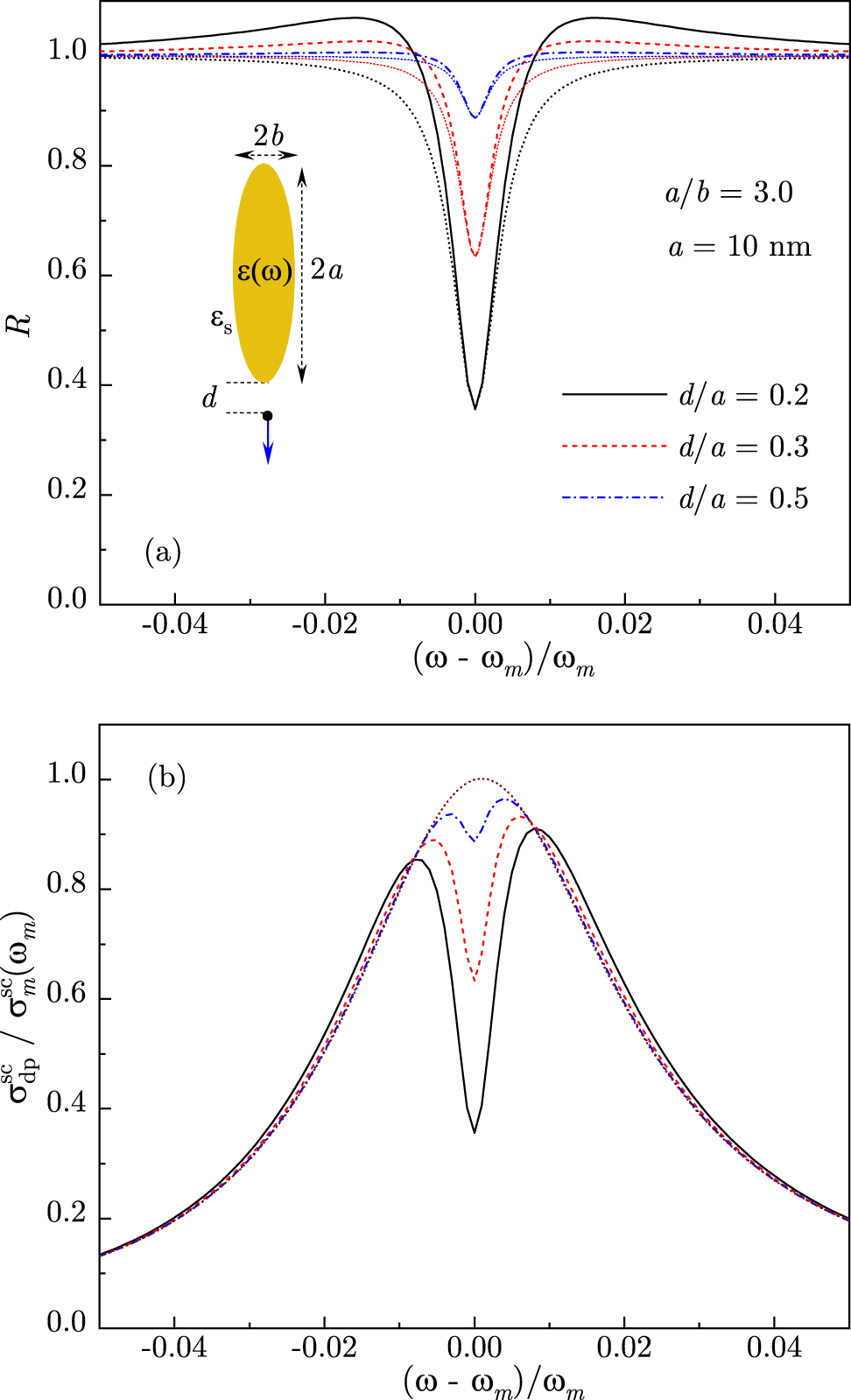
(a) The ExIT function R(ω), given by Eq. (35), and its asymptotic expression (dotted lines), given by Eq. (37), are shown for a QE near the tip of Au nanorod with aspect ratio a/b = 3.0 and length 2a = 20 nm at distances d/a = 0.5, 0.3, and 0.2. (b) Normalized scattering cross-section in the dressed plasmon approximation is shown for the same system parameters. The dotted line is the plasmon band. All curves are calculated for ω _e = ω _m. Inset: schematics of a QE situated at a distance d from the tip of Au nanorod in water for QE dipole moment oriented along the nanorod axis.

While the dressed plasmon model describes the position and depth of ExIT minimum relatively well, it predicts a sustained asymmetry as the higher frequency region of scattering spectrum carries a larger spectral weight [see Figure 2(b)]. In the absence of QE coupling to the EM field, emission takes place from the plasmonic antenna, whose power spectrum is ∝ω ⁴ due to a larger radiation rate at higher frequencies. Therefore, in the presence of double-peak structure due to either ExIT minimum or Rabi splitting centered at resonance frequency ω = ω _m = ω _e, the higher frequency peak is enhanced. Note that similar scattering spectra are predicted by the classical model of coupled oscillators which disregards optical interference effects [38, 47]. Below we demonstrate that extending the dressed plasmon model to include Fano interference between the plasmon antenna and plasmon-induced QE dipole, as described in Eq. (36), can strongly affect the overall shape of scattering spectra.

In Figure 3, we plot the Fano function and scattering spectra for a QE situated at several distances from the tip of Au nanorod with aspect ratio a/b = 3.0 and overall length 2a = 20 nm. As indicated above, we consider the case of QE’s dipole moment oriented along the normal to tip surface (see inset in Figure 3), so that the Fano parameter q is positive. For nanorod of this length, q is relatively small [see Figure 1(b)] and so the Fano function’s variation ranges from about 2% for d = 4 nm to 15% for d = 1 nm, as the QE–plasmon coupling g increases close to the tip [see Figure 3(a)]. Importantly, for q > 0, the spectral shape of the Fano function, which enters in the scattering cross-section (36), leads to the suppression of higher frequency region and enhancement of lower frequency region. As a result, the aforementioned asymmetry of dressed plasmon scattering spectra in Figure 2(b) is largely compensated, and so the full scattering spectra are now close to symmetric [see Figure 3(b)].

Figure 3:

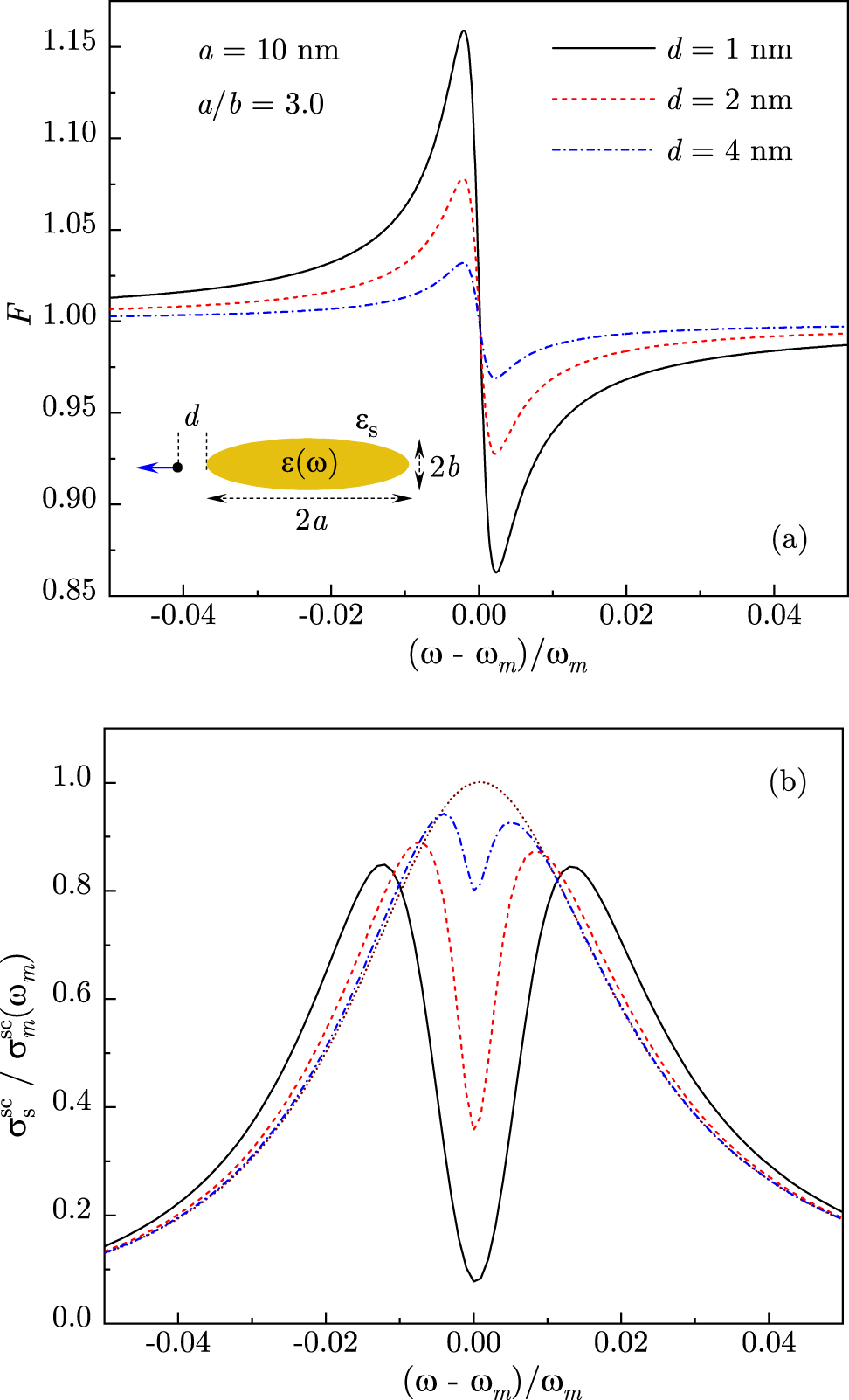
(a) The Fano function F(ω), given by Eq. (31), is shown for a QE near the tip of Au nanorod with aspect ratio a/b = 3.0 and length 2a = 20 nm at distances d= 4, 2, and 1 nm. (b) Normalized scattering cross-section, given by Eq. (36), is shown for the same system parameters. The dotted line is the plasmon band. All curves are calculated for ω _e = ω _m. Inset: schematics of a QE situated at a distance d from the tip of Au nanorod in water for QE dipole moment oriented along the nanorod axis.

In Figure 4, we show the Fano function and scattering spectra for a small nanorod of length 10 nm. With decreasing nanostructure size and, hence, the reduction of plasmon mode volume, the QE–plasmon coupling increases and so does the Fano parameter q, which now reaches values q ∼ 1 [see Figure 1(b)]. In this case, the Fano function variation is larger as well, reaching about 80% close to the nanorod tip [see Figure 4(a)]. As a result, the scattering spectra, shown in Figure 4(b), exhibit inversion of spectral asymmetry relative to the dressed plasmon spectra [see Figure 2(b)], with the lower frequency peak now substantially higher than the higher frequency peak. Note that for the smallest d, the system has clearly transitioned to a strong coupling regime since the double-peak structure is well beyond the plasmon spectral envelope. We stress that although the mechanisms of ExIT and Fano interference are distinct, as discussed in the previous section, the two effects are intimately related as Fano interference manifests itself via redistribution of spectral weight across the ExiT minimum in the scattering spectra.

Figure 4:

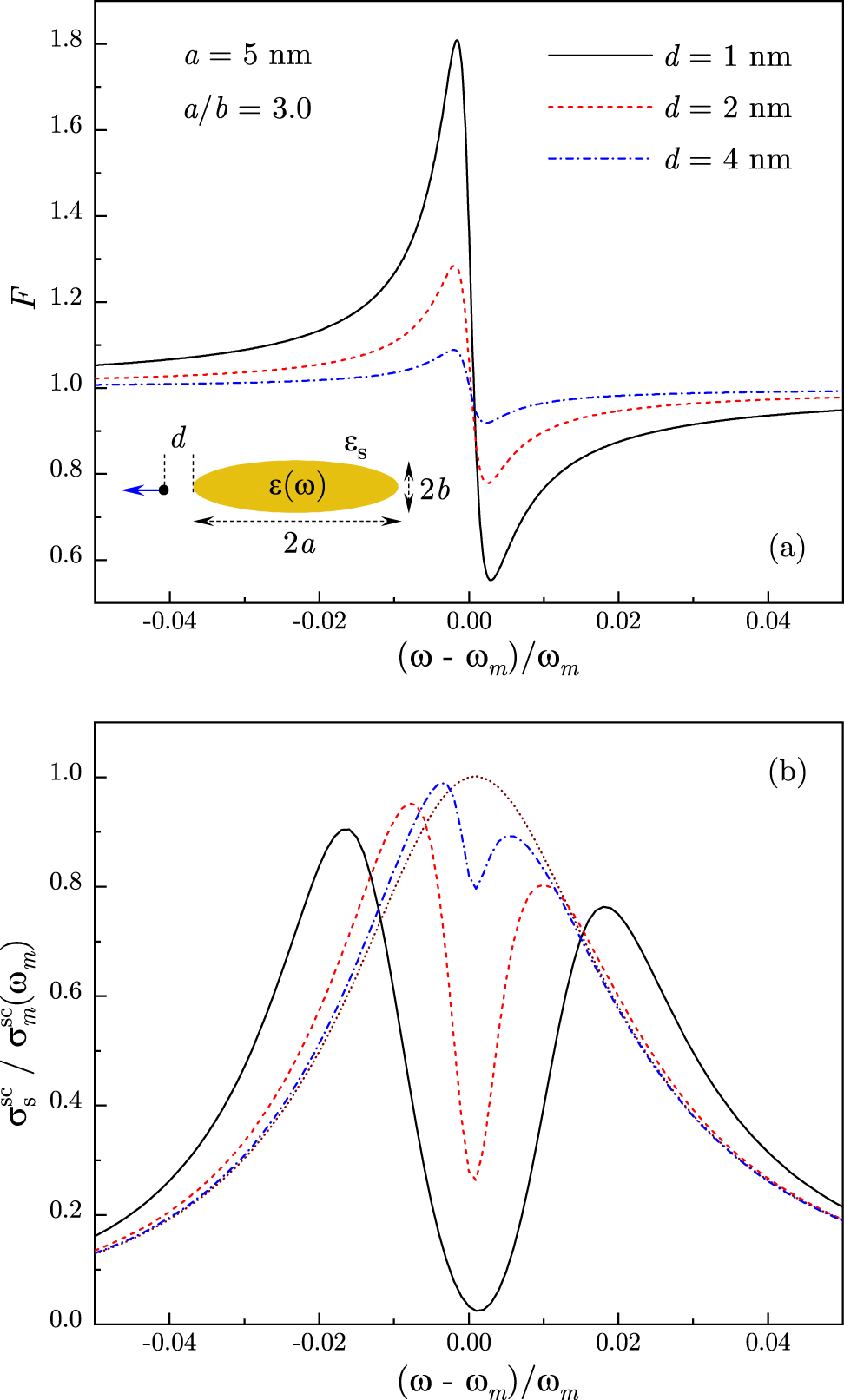
(a) The Fano function F(ω), given by Eq. (31), is shown for a QE near the tip of Au nanorod with aspect ratio a/b = 3.0 and length 2a = 10 nm at distances d = 4, 2, and 1 nm. (b) Normalized scattering cross-section, given by Eq. (36), is shown for the same system parameters. The dotted line is the plasmon band. All curves are calculated for ω _e = ω _m. Inset: schematics of a QE situated at a distance d from the tip of Au nanorod in water for QE dipole moment oriented along the nanorod axis.

6 Conclusions

In this paper, we developed a model for ExIT and Fano interference in hybrid plasmonic systems comprised a single emitter resonantly coupled to a surface plasmon in a metal–dielectric structure. We have shown that the shape of scattering spectra is determined by two distinct mechanisms. First is near-field coupling between the emitter and plasmon that defines the energy spectrum of the hybrid system. This mechanism relies upon energy exchange between the system components and gives rise to the ExIT minimum in scattering spectra and, in the strong coupling regime, to the Rabi splitting of polaritonic bands. The second mechanism is the Fano interference between the plasmon and the plasmon-induced emitter’s dipoles as the system interacts with the radiation field. Although the Fano interference does not significantly affect the position or magnitude of ExIT minimum, it determines the overall shape of scattering spectra. Specifically, the Fano interference leads to the inversion of spectral asymmetry that was recently reported in the experiment [22, 39, 40].