Harmonic generation with multi-layer dielectric metasurfaces

1 Introduction

Photonics at the micro- and nano-scale has experienced a spectacular development in the last two decades, thanks to technological progress and capability of manipulating near and far fields of radiating nanoparticles. Plasmonic and high-contrast dielectric meta-atoms arranged in an ordered array, in two or three dimensions, have shown their potential for shaping nonlinear optical effects at the nanoscale [1], [2], [3], [4], [5], [6], [7], [8].

Harmonic generation and wavefront shaping can occur in all-dielectric open Mie resonators, depending on their nonlinear and scattering properties, as light at the fundamental frequency (FF) is coupled to their displacement currents. To this end, the resonator should have a characteristic size L and a refractive index n such that L ≈ λ / n , with λ the FF wavelength which is also referred to as Mie wavelength λ _Mie.

Historically, the first nonlinear nanoresonator of this type was made of silicon and resulted in third-harmonic generation (THG) with two-order-of-magnitude higher efficiency than in bulk silicon [5]. To increase such efficiency, nanoresonators with multi-mode interference in the form of Fano resonances [9], [10], nonradiative anapole [11] or bound states in the continuum [12], [13] have been proposed. Moreover, a feedback mechanism provided by a gold mirror has been used to boost THG pumped at the anapole condition [14]. However, bulk silicon only exhibits relatively weak cubic nonlinearity and is affected by two-photon absorption at telecom wavelength, which limits the maximum FF power. Higher conversion efficiencies have been achieved with quadratic nonlinearity in noncentrosymmetric III-V semiconductors such as GaP [6], GaAs [15], and AlGaAs [7], [8], where resonators with low-quality factor (Q) have enabled second harmonic generation (SHG) efficiency η SHG = 10 − 6   W − 1 [7], whereas η SHG = 10 − 2   W − 1 has been predicted for high-Q resonators [16]. Remarkably, semiconductor alloys such as Al x Ga 1 − x As also lend themselves to TPA-free operation in the near-infrared, via an energy-gap increase depending on molar fraction x.

The special case of nonlinear metasurfaces and 2D nonlinear metamaterials, where the electromagnetic features are further engineered by the ordered structure of nonlinear meta-atoms, have attracted a great interest in the scientific community in the quest for molding the properties of light beyond what was previously possible [1, 17–20]. Their planar profiles make them particularly appealing, because of a simpler fabrication process than 3D metasurfaces and metamaterials and the long-sought promise for integration with on-chip nanophotonic devices [21], [22].

Different metasurfaces have already been demonstrated for several optical operations (lenses, imaging, harmonic generation, just to mention a few) [23], [24], and the natural question of how to design and engineer layered systems with stacked metasurfaces has been raised only recently [25], [26], [27], [28]. The research field is promising and potentially huge, with the long-term vision of multi-layer systems able to perform complex optical transformations by combining linear, nonlinear, passive, and active metasurfaces into a single device. However, this problem is very challenging, not only from the fabrication viewpoint but also for modeling, as full-wave simulations become easily too cumbersome for device engineering [29]. Apart from simple cases where the metasurface is placed in front of a reflector, to date, the issue has only been addressed in the linear regime [25], [26], [27], [28].

Recently, we demonstrated that a periodic structure of Mie resonators can achieve the independent control of the second harmonic (SH) radiation diagram and polarization [30], [31]. In those works, we defined an effective metasurface polarizability accounting for the perturbation of resonances from the isolated constituents, because of in-plane Bragg scattering. By engineering this polarizability, we were able to excite higher-Q resonances, whereas both preserving the polarization properties of single Mie-resonators and achieving SHG in the zero-diffracted order. Here, for the first time to our knowledge, we demonstrate a multi-layer semiconductor metasurface to perform SHG. Our specific answer to the problem of low conversion efficiency, which is currently at the forefront of research in nonlinear nanophotonics, is a three-layer stack (i.e., an optical triplet) in the AlGaAs platform, as illustrated in Figure 1. In such a system, the combination of three metasurfaces is experimentally demonstrated to increase SH frequency bandwidth and power conversion efficiencies. The multi-functional behavior of our triplet by means of beam shaping is also confirmed by the zero-order diffraction measured at the SH, resulting from the combination of the meta-atoms radiation and a 3D nonuniform array factor.

Figure 1:

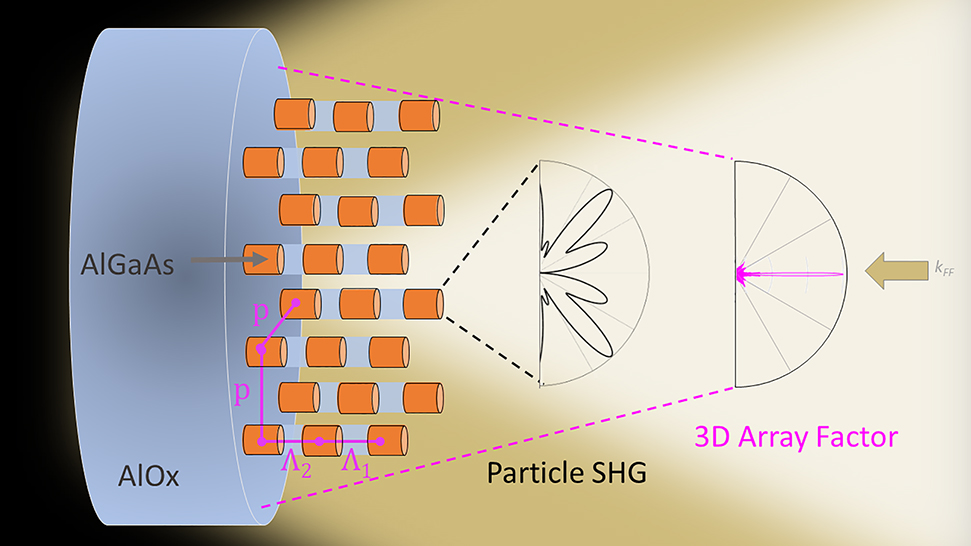
Schematic of a three-layer metasurface (Λ₁ and Λ₂ apart from each other) with SH emission pattern decomposed in SHG from the single nanoresonator (dark line) and array factor radiation from the 3D array with in-plane periodicity p (pink line).

Our results demonstrate properties which are very promising for a variety of applications, including nonlinear spectroscopy [32], [33], high lateral resolution imaging [34], photodynamic therapy [35], and photocatalysis [36].

The rest of this Letter is organized as follows: Sections 2 and 3 describe the design and fabrication of the three-layer nonlinear metasurface, respectively; in Section 4, measurements of SH frequency bandwidth and power efficiency of our triplet are reported and compared with 3D theoretical simulations.

2 Design

To achieve a feedback mechanism at the FF in the vertical direction, we piled up three layers of the nonlinear AlGaAs metasurface reported in [30], separated by layers of a low-index material, whose thickness is designed so as to maximize the FF internal energy in each meta-atom. The internal energy, E _int, is calculated as E int = 1 2 ∭ V ε | E | 2 d V where V represents the volume of AlGaAs nanoresonators. The numerical study is performed via Finite Element Method simulations with Comsol Multiphysics. As shown in Figure 2a, the unitary cell includes five nanodisks with fixed radius r = 200 nm made of AlGaAs and AlOx alternatively stacked. As it will be discussed later, the fabricated structure includes an additional cylinder of 500 nm of SiO₂ and one of 50 nm of nickel on top of the unitary cell and another cylinder of 500 nm of AlOx at the bottom. The calculations made in Figure 2 consider these additional layers, even though their contribution to the FF electric field and thus to SHG is negligible, as reported in Section S1 of the Supplementary Material. The height of each AlGaAs nanodisk is chosen to be 400 nm to excite a magnetic dipolar resonance [30], whose field distribution is reported in Figure 2b. The in-plane period p of the metasurface is, instead, chosen to be 1 μm. The excitation is assumed to be a plane wave polarized along the (100) crystallographic direction with 1  GW / cm 2 intensity. Firstly, we vary the incident wavelength and the thickness of the two intermediate AlOx layers, i.e., the vertical spacing Λ₁ (see Figure 2c). This allows us to find the exact value of Λ₁ that maximizes the internal energy inside the AlGaAs cylinders at a fundamental wavelength of 1550 nm (see Figure 2d). Note that depending on the application the two spacings can be different, see Λ₁ and Λ₂ in Figure 1, however, here we chose them to be both equal to Λ ₁ . Figure 2d shows that the internal energy is maximized for Λ₁ equal to 900 nm. Interestingly, the resulting thickness of AlOx (500 nm) corresponds to an effective distance almost equal to λ AIOx / 2 , where λ AlOx is the wavelength inside the AlOx layer, consequently, constructive reflections between consecutive layers occur. This FF internal energy enhancement is expected to produce a square root boost of the SHG intensity. Thus, we simulate the nonlinear harmonic generation, following the same procedure of Ref. [30], but considering the three AlGaAs nanodisks of the unitary cell as the source of the nonlinear signal. The AlGaAs crystalline axes are all considered to be aligned with the laboratory reference system.

Figure 2:

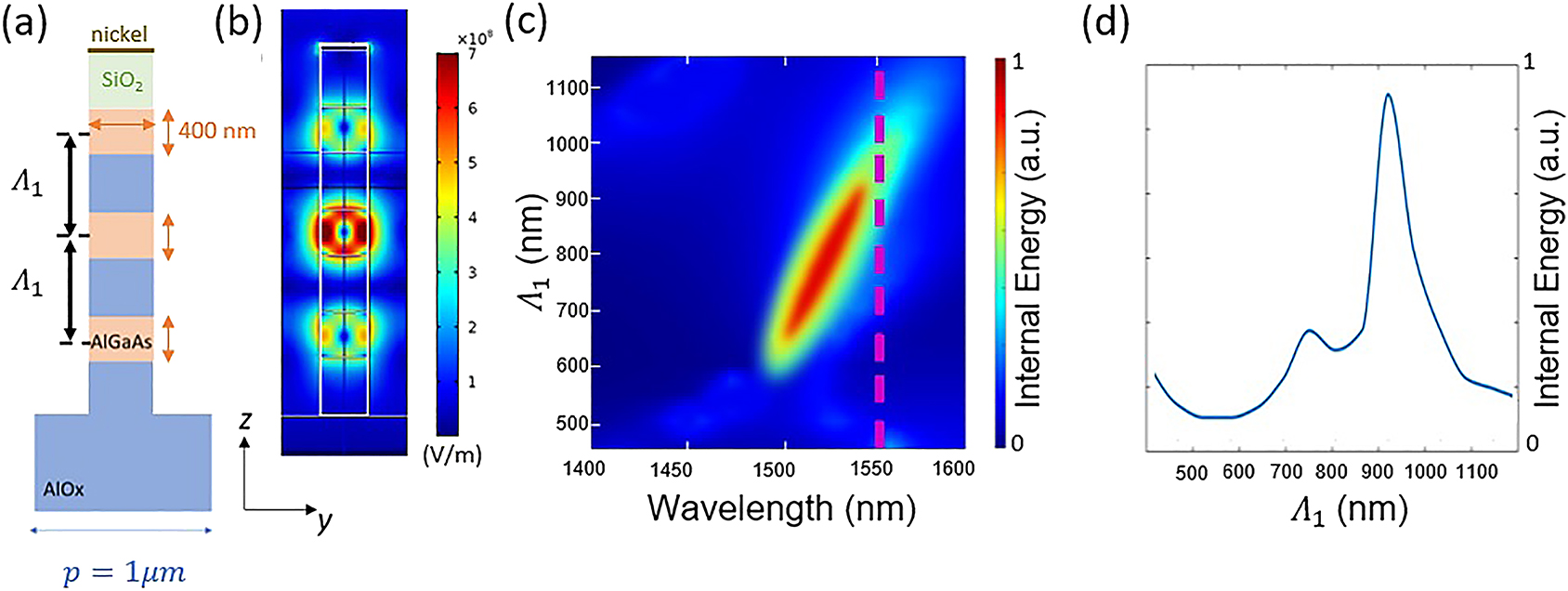
(a) Sketch of the proposed unitary cell with vertical spacing Λ₁ = 900 nm and in-plane period p = 1 μm. Note that for the sake of coherence with the fabricated structure, the simulation includes additional cylinders of SiO₂ and nickel on the top and of AlOx at the bottom, even though they are optically inactive (see Section S1 of the Supplementary Material) (b) Electric-field distribution for the triplet metasurfaces in (a). The pump is a y-polarized plane wave with 1 GW/cm² intensity. (c) Internal energy inside the AlGaAs nanodisks vs. incident FF wavelength. (d) Internal energy vs. Λ₁, for a pump wavelength λ = 1550 nm.

3 Fabrication

The metasurface triplet (see Figure 3) consists of three Al_0.18Ga_0.82As layers (orange regions in Figures 2a and 3a) separated by a low-index oxide spacer (AlOx, n = 1.6), with the whole stack lying on an optical substrate of AlOx (blue layers in Figures 2a and 3a). Following the technique that was established for single-layer metasurfaces [22], the epitaxial structure is grown by MOCVD on a (100)-GaAs wafer. It includes three Al_0.98Ga_0.02As layers to be selectively oxidized at a later stage (bottom layer of 1 µm and two upper layers of 500 nm), alternated with three Al_0.18Ga_0.82As layers to provide optical confinement. At each Al 0.98   Ga 0.02  As / Al 0.18 Ga 0.82 As interface, a GaAs capping interlayer of 5 nm is also grown. However, the major fabrication challenge of the three-layer metasurfaces consists in patterning a deep structure, more than 1.8 μm thicker than the single-layer metasurface. For such deep etching, traditional fabrication techniques cannot be used, if one wants to preserve the shape of the active layers. Consequently, different resists such as CSAR, Ti-prime, and Electra92 and the deposition of a metallic layer, respectively, before and after lithography, are necessary. The main fabrication steps can be summarized as follows: 1) Plasma Enhanced Chemical Vapor Deposition (PECVD) of a SiO₂ layer serving as hard mask for the etching process; 2) spin coating of CSAR + Ti-prime + Electra92; 3) 20 kV electron-beam lithography (EBL) and development; 4) Electron Beam Physical Vapor Deposition (EBPVD) of a 50 nm-thick layer of nickel, 5) CSAR lift-off; 6) Inductively Coupled Plasma Reactive Ion Etching (ICP-RIE); 7) selective oxidation of Al_0.98Ga_0.02As at 390    °C [37], [38]. We fabricated square-lattice stacked metasurfaces with Bravais lattice vectors parallel to (100) and (010) crystallographic axes, resulting in 3D periodic arrays with a square footprint of 70 µm side, as shown in Figure 3b. Two series of samples were produced: 1) with period p ∈ [ 900  nm − 3  μm  ] and pillar radius r = 200    nm ; and 2) with p = 1.1 µm and r ∈ [ 180  nm − 240  nm ] .

Figure 3:

(a) Scanning Electron Microscope (SEM) image of three lines of a three-layer metasurface with Λ 1 = 900    nm and p = 3    μm (b) SEM image of an entire three-layer metasurface.

4 Results and discussions

The SHG from the three-layer metasurface is measured via a customized nonlinear microscope pumped with a 160 fs pulse, 1 MHz repetition rate, and I F W ≈ 0.1    GW / cm 2 peak intensity. The pulsed beam is provided by Amplitude optical parametric amplifier (Mango) pumped by a mode-locked ytterbium-doped fiber laser (Satsuma). To get the incident polarization parallel to the [100] AlGaAs crystallographic axis, a λ / 2 plate is used. A 10× microscope objective (NA = 0.2), preceded by a 400 mm lens which focuses the pump on its back focal plane, generates a w ∼ 100 μm beam waist incident onto the sample and collects the SH in reflection geometry. Then, the image, filtered with an 850 nm low-pass and a 700 nm long-pass filters, is detected by a high-QE CCD camera (Starlight Xpress Trius SX825). The measured SHG efficiency normalized for the incident power is defined as: η norm = P cyl S H / P cyl F W 2 ( W − 1 ) , where P cyl S H = P tot S H / m   ( W ) is the collected SHG power, m = π w 2 / Λ 2 is the number of pillars lying within the incident beam waist, w, whereas P cyl F W = I F W π r 2 = ( P F W / π w 2 ) π r 2   ( W ) is the pump power, where r is the pillar radius.

Figure 4a shows both numerical and measured SHG from the three-layer metasurface as a function of the pillar radius, for a fixed in-plane period p = 1.1 μm. Our numerical predictions are made for two different configurations: 1) three-layer metasurfaces made of identical pillars with nominal radius r (solid blue line); 2) three-layer metasurfaces made of pillars with distributed radii (dashed blue line), according to fabrication constraints (from top to bottom radii are: r + 10 nm, r − 10 nm, r − 30 nm, see Figure S3 in Supplementary Material). We numerically estimate an SHG efficiency almost equal to 7 × 10 − 4     W − 1 , which leads to a factor-100 enhancement with respect to the single-layer metasurface with the same pillar radius and periodicity [30]. Although our numerical simulations of the identical radii three-layer metasurfaces predict a peak at a radius of r = 200 nm, in good agreement with the measured η _norm from the sample (orange solid line in Figure 4a), its width is about 15 nm thinner. An improved accord with the measured width of the nonlinear resonance can only be found with numerical predictions from the distributed radii three-layer metasurfaces which paves the way to intentionally designed broad SH frequency bandwidth multi-layer metasurfaces similar to what has been demonstrated in the linear regime [39].

Figure 4:

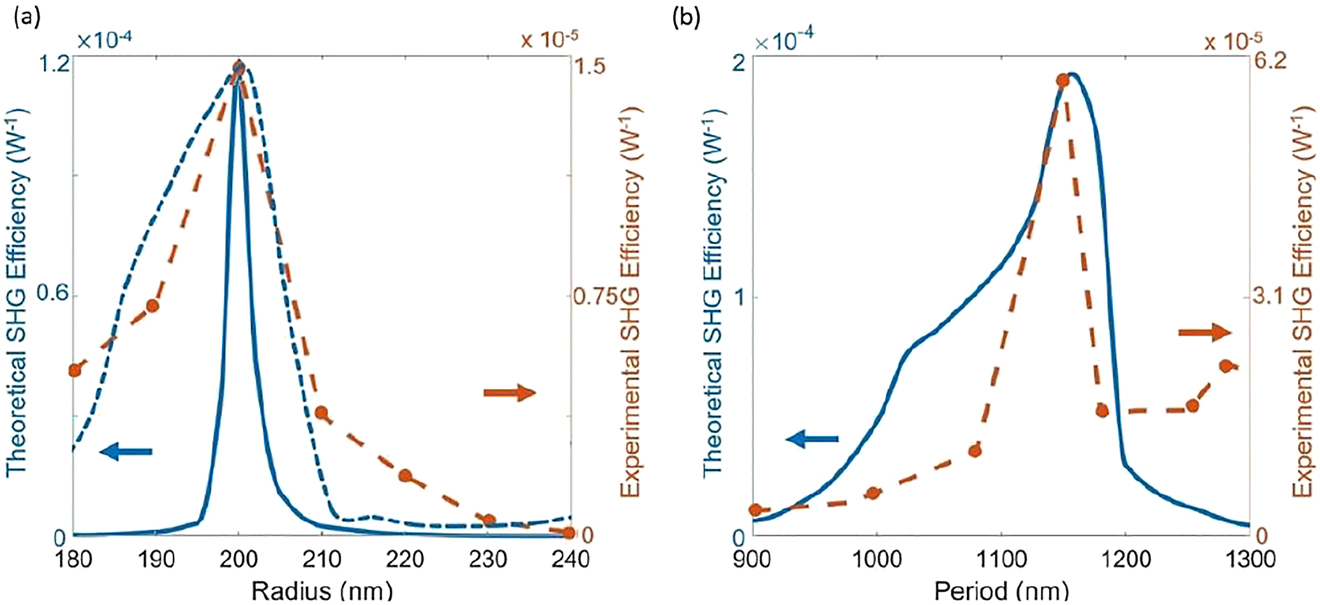
(a) Calculated three-layer metasurfaces with identical pillar radii r (blue solid curve), three-layer metasurfaces with distributed pillar radii r + 10 nm, r − 10 nm, r − 30 nm (blue dashed curve), and experimental (orange line) SHG efficiency vs. nanodisks radius, for p = 1100 nm, (b) Calculated (blue curve) and experimental (orange line) SHG efficiency vs. p for a pillar radius r = 200 nm. A negative shift of about 80 nm in the experimental period is added in the figure.

Figure 4b reports the SHG efficiency as a function of the metasurface period, for a fixed radius of 200 nm. Again, the maximum numerical estimation (blue line) of SHG efficiency is of the order of 1.2 × 10 − 4  W − 1 , whereas the maximum value of measured η norm (orange line) is 6 × 10 − 5   W − 1 being 15 times (15×) higher than the one-layer metasurface [30]. The two maxima have a rigid shift of about 80 nm, which has been compensated in the Figure. This may be attributed to nonuniform walls of the stack of meta-atoms induced by proximity effects near the substrate during dry-etching, resulting in a radius reduction in the proximity of the substrate, which in turn results in maxima for higher values of the period.

Moreover, we have investigated the SHG radiation pattern of the three-layer metasurfaces. The peculiar spatial frequency selectivity, reported in Figure S3 of the Supplementary Material, recalls the zero-order diffraction already demonstrated for the single metasurface [30]. However, at variance with the latter, here the far-field SHG results from the contribution of the single-particle SH radiation and the 3D array factor, giving rise to more than one order of magnitude (15×) enhanced emission power, as aforementioned. Further design of these two parameters, out of the scope of this work, could result in fine beam shaping and improve the multi-functional behavior of the three-layer metasurfaces.

Finally, to disentangle the contribution of the vertical confinement from the in-plane Bragg scattering we have also investigated isolated three-layer nanoresonators, whose fabricated structure is imaged in Figure 3a. Experimentally, a diffraction-limited spot with a 2.4 µm waist was applied via a high-NA (=0.8) objective in the aforementioned microscopy working in reflection geometry. Figure 5a shows the typical two lobes expected from the isolated structure [40] with a maximum peak at around 45° from the normal, confirming that Mie-resonances involved in the SHG process are not affected by the vertical confinement. More importantly, looking at the normalized SHG efficiency as a function of the radius reported in Figure 5b (orange dashed line), the maximum value of 6 × 10 − 6   W − 1 for a radius of 185 nm results to be about six times (6×) higher than in a single isolated structure without feedback [7]. These results are in good agreement with numerical calculations (solid blue line in Figure 5b). The reduced relative enhancement because of vertical confinement of the three-layer nanoresonators (6×) with respect to the relative enhancement of the three-layer metasurfaces (15×) can be attributed to stronger proximity effects near the substrate during dry-etching, resulting in a stronger radius reduction for pillars close to the substrate (see Figure 3a), and in a relative decrease of SH efficiency.

Figure 5:

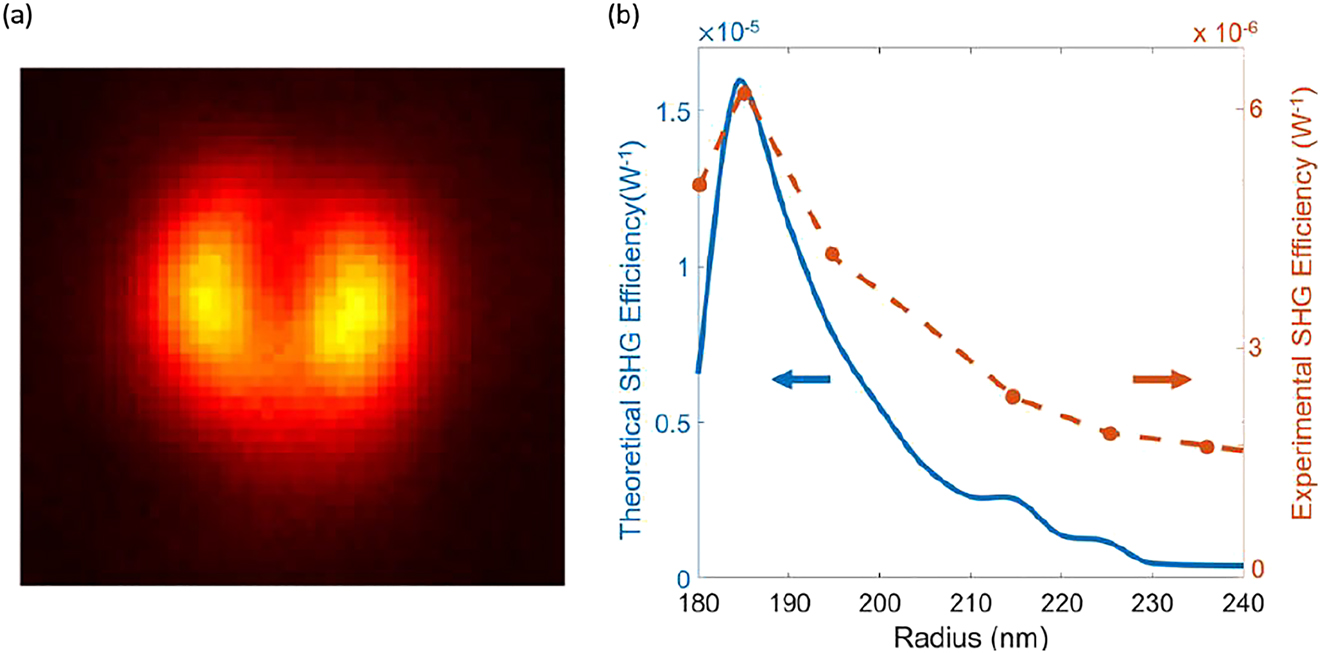
(a) Microscope image of SHG from in-plane isolated nano-resonator in the multilayer structure with radius equal to 185 nm. (b) Measured (orange curve) and calculated (blue curve) SHG efficiency from (a) as a function of radius.

5 Conclusion

We have designed, fabricated, and characterized a three-layer metasurface in AlGaAs platforms, proving the feasibility of enhanced SH generation. With respect to one-layer metasurface, we predict and measure more than one-order-of-magnitude (15×) enhanced SHG efficiencies. Beyond harmonic efficiency, the multi-functional behavior of the three-layer metasurfaces is proved by maintaining a high SH signal for different triplet radii. Our results pave the way to a multifunctional nonlinear platform via multi-layer all-dielectric metasurfaces.