Three-dimensional plasmonic nano-router via optical antennas

Yi Xu; Baowei Gao; Axin He; Tongzhou Zhang; Jiasen Zhang

doi:10.1515/nanoph-2021-0094

Article Open Access

Three-dimensional plasmonic nano-router via optical antennas

Yi Xu , Baowei Gao , Axin He , Tongzhou Zhang and Jiasen Zhang

Published/Copyright: May 27, 2021

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nanophotonics Volume 10 Issue 7

Abstract

A three-dimensional (3D) nanoscale optical router is a much-desired component in 3D stacked optical integrated circuits. However, existing 3D routers based on dielectric configurations suffer from large footprints and nanoscale routers based on plasmonic antennas only work in a 2D in-plane scene. Here, we propose and experimentally demonstrate cross-layered all-optical 3D routers with nanoscale footprints. Optical slot antenna pairs are used to realize the routing of plasmonic signals between different layers for arbitrary direction in a broadband wavelength range. The routers are also integrated with waveguide directly for exploring further applications. Based on these router elements, a 3D network of optical butterfly interconnection is demonstrated for multi-directional all-optical data communication. The proposed configuration paves the way for optical cross-layer routing on the nanoscale and advances the research and applications for 3D plasmonic circuits with high integration density in the future.

Keywords: integrated optics; optical slot antenna pairs; plasmonic circuit; plasmonics; router

1 Introduction

With the explosive growth of information technology, three-dimensional (3D) photonic integrated circuit architecture needs to be developed owing to its capacity to improve integration density and processing speed [1], [2]. This complex system is composed of vertically stacked layers integrated with functional components such as lasers [3], [4], [5], detectors [6], [7], [8], and switching [9], [10], [11], [12]. The involvement of multi-stack layer configurations can increase the number of on-chip devices and simultaneously decrease the cross-talk between adjacent devices on the same layer. To realize these integrated photonic circuits, chip-integrated and ultra-compact 3D routers are needed for signal exchange among the vertical layers. Conventionally, optical dielectric waveguides are widely utilized for 3D layer-to-layer signal routing [13], [14], [15], [16], [17], [18]. However, all of these suffer from large footprints and complicated configurations, which cannot satisfy the practical requirements of dense integration. Alternatively, surface plasmon polaritons (SPPs) with strong subwavelength spatially confined characteristics allow for miniaturization of on-chip photonic devices in nanoscale regions [19], [20], [21], [22], [23], [24]. Intensive efforts have been devoted to explore on-chip plasmonic nano-routers based on plasmonic nanoantennas [25], [26], [27], [28] or waveguide [29], [30], [31], [32], [33], [34] configurations. However, all these devices are only focused on the routing signal in a 2D plane scene. The height of the plasmonic nanoantennas in these devices is optically thin. Thus, they are forced to behave as planer configurations owing to strong cross-layer interaction. Ultra-compact 3D interlayer plasmonic routers for multi-layer circuits are challenging and in strong demand for multi-layer plasmonic circuits.

An optically thick metal film has intrinsic 3D characteristics because the SPPs propagating on the upper and lower surfaces of the metal film are not coupled with each other and they can realize different functions on demand. The signals of the two surfaces need to be connected by 3D routers. It is possible to implement 3D routing by controlling the launching and propagation direction of cross-layer SPPs. Benefiting from the strong field confinement of SPPs, the routers can be minimized to the nanoscale.

In this study, we propose an ultra-compact 3D plasmonic router based on optical antenna pairs etched on a 200 nm Au film. The SPP input signal is incident into the antenna pairs, and the output signal is launched at the adjacent surface. An L-shaped or rectangular antenna pair is used to obtain the requisite propagation direction of the output signal based on the control of the phase and intensity of the SPPs launched by the antennas. Direct coupling between the router and the plasmonic waveguide is demonstrated, which benefits from the nanoscale size of the router. Moreover, an optical 3D butterfly interconnection network is constructed by integrating two routers. The proposed method provides an appealing way to control the flow of SPPs between different stacked layers and demonstrate the feasibility of multi-level plasmonic networks for 3D photonic nanoscale integration.

2 Results and discussion

2.1 Schematic of the proposed 3D plasmonic nano-router

The schematic of the proposed 3D optical router is depicted in Figure 1(a), which is fabricated in an Au film on a silica substrate. The router connects SPP signals propagating at the air–Au, and silica–Au interfaces. The input SPP signal propagates at the air–Au film interface and is incident into the router. SPPs propagating along a fixed direction at the silica–Au film interface is launched. The angle α between the propagating directions of the input and output SPPs can be tuned in the range from 0° to 360°. Depending on the value of α, different optical slot antennas are used to implement routing.

Figure 1:

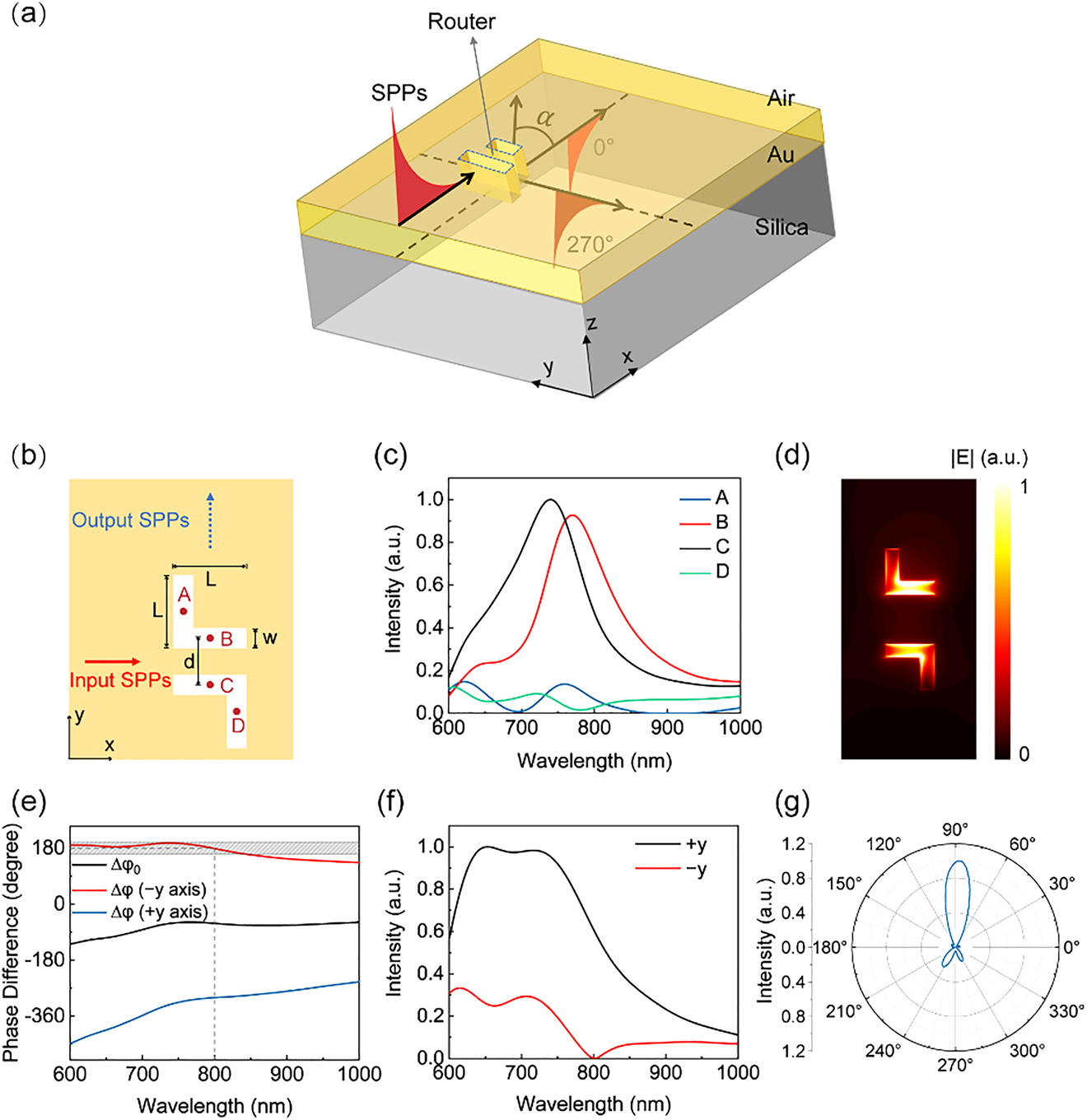
Calculation results of the router. (a) Schematic of the three-dimensional (3D) plasmonic nano-router. (b) Schematic of the 90° router. The solid red arrow indicates the direction of the input surface plasmon polaritons (SPPs) propagating at the air–Au film interface and the blue dashed arrow indicates the direction of the output SPPs propagating at the silica–Au film interface. (c) Near-field electric field intensities at points A, B, C, and D in (b) versus the wavelength. (d) Near-field electric field amplitude in the xy plane for λ = 800 nm. (e) Calculated initial phase difference and total phase difference versus the wavelength. (f) Calculated intensities of the SPPs propagating along the ±y-axes versus the wavelength. (g) Calculated angular radiation distributions in the xy plane for λ = 800 nm.

2.2 Theory and design of 3D routing via optical antenna pairs

First, we designed a router with α = 90°, which is schematically shown in Figure 1(b). The router is composed of two L-shaped slot antennas with the same geometry and different orientations. The amplitudes and phases of the antennas are controlled by changing the geometry dimensions. Here, the designed length (L ₁) and width (w) of the antenna arms are 250 and 70 nm, respectively. The depth of the antenna is 200 nm, which is the same as the thickness of the Au film. The nanoscale size of the device contributes to dense integration through short-distance data communication. The origin of the Cartesian coordinate is located at the center point between the two antennas at the silica–Au film interface. The input SPPs propagate along the +x-axis at the air–Au film interface and the launched SPPs propagate along the +y-axis at the silica–Au film interface.

Here, we used a finite-difference time-domain method to numerically analyze the mode profiles of the antennas. When the input SPPs were incident into the antenna pair along the +x-axis, the calculated intensity of the electric field at the center of the four arms in the xy plane [marked as A, B, C, and D in Figure 1(b)] is shown in Figure 1(c). Resonant wavelengths of 770 and 740 nm with 130-nm full width at half maximum (FWHM) appear at points B and C, respectively. In the FWHM, the field intensity of the SPPs in the x-arms of the two antennas is much larger than that in the y-arms. The corresponding near-field electric field amplitude |E| distribution on the bottom surface (z = 0 plane) of the Au film at 800 nm is shown in Figure 1(d). The electric field is strongly localized in the x-arms of the two antennas, which can be considered as two SPP point sources at the silica–Au film interface and launched SPPs propagating along the ±y directions (see Supplementary material). We calculated the initial phase difference Δφ ₀ = φ _yB − φ _yC between the SPPs at points B and C and show the result as the black line in Figure 1(e). Considering the phase retardation induced by the spatial separation d, the total phase difference for the SPPs propagating along the ±y-axes is Δφ = k _SPP d ∓ Δφ ₀, where k _SPP is the wave vector of SPPs on the bottom layer. The intensity of the SPPs can be controlled by varying d. For d = 344 nm, the calculated Δφ for the ±y directions is plotted in Figure 1(e). At the wavelength range of 600–850 nm, the total phase difference Δφ along the −y-axis is in the range of 180° ± 20°, which is denoted by the shadowed region in Figure 1(e). The intensity of SPPs propagating along the −y-axis should be very small due to the destructive interference. On the contrary, the phase difference Δφ of the SPPs propagating along the +y-axis in the above wavelength range is in the range of −360° ± 60°, which results in constructive interference. As a result, the launched SPPs at the silica–Au interface has a propagation direction of α = 90°. Then, we calculated the intensities of the SPPs launched by the two antennas along the ±y-axes, and the normalized intensities of the SPPs propagating along the ±y-axes with respect to the wavelength are shown in Figure 1(f). The black line indicates the intensity of SPPs propagating along the +y-axis, which is much larger than that in the −y-axis (red line) in a broadband range from 600 to 850 nm. At λ = 800 nm, a minimum value of the intensity in the −y direction is obtained, denoted by a dip in the red line. The calculated angular radiation distributions in polar coordinates of the SPPs at the silica–Au film interface for λ = 800 nm is shown in Figure 1(g) (see Supplementary material). Highly unidirectional SPP propagation is observed along the +y direction with a half-power beamwidth of 30°. SPPs propagating along the ±x-axes and −y-axis are fairly weak, which results in a 90° routing with a high signal-to-noise ratio. The high directivity of the device can meet the demand for complex connectivity. The working spectral range depends on the resonance properties of the antennas and the distance d between them. The large FWHMs of the resonant antennas enable a broadband operation wavelength. The distance d, which modifies the interfere of the SPPs launched by the two antennas, affects the optimal routing wavelength.

2.3 Fabrication and experiment

To demonstrate the designed 3D router experimentally, optical slot antennas and gratings were fabricated, and the fabrication process is illustrated in Figure 2. A 20-nm-thick Au film was deposited on a silica substrate using electron beam evaporation [Figure 2(a)]. Then, grooves with a depth of ∼90 nm were fabricated in the Au film and the silica substrate using focused ion beam (FIB) milling [Figure 2(b)], which were used to fabricate SPP scattering gratings. After another Au film with 180 nm thickness was deposited on the 20 nm Au film and filled the grooves [Figure 2(c)], an antenna pair with the same geometry as the design and a launching grating with a depth of ∼70 nm were fabricated in the Au film using FIB milling [Figure 2(d)]. The depth of the launching grating is small, which can only excite SPPs propagating at the air–Au film interface (see Supplementary material).

Figure 2:

Fabrication process of the routers and gratings for the launching and measurement of surface plasmon polaritons (SPPs). (a) A 20-nm-thick Au film is deposited on a silica substrate. (b) Fabrication of the scattering grating. (c) Deposition of a 180-nm-thick Au film. (d) Fabrication of the antenna pair and the launching grating at the air–Au interface.

The scanning electron microscopy (SEM) image of the router and gratings is shown in Figure 3(a). The arc grating with a period of 784 nm is the launching grating fabricated at the air–Au film interface, which was used to launch and focus the input SPPs. At the silica–Au film interface, two rectangular scattering gratings with a period of 526 nm were fabricated to measure the intensity of the output signals.

Figure 3:

Experimental results of the 90° router.

(a) Scanning electron microscopy (SEM) image of the experimental sample. Inset: Magnified SEM image of the antenna pair. (b) Charge-coupled device (CCD) images of the sample for different incident wavelengths. The two white dotted frames represent the positions of the scattering gratings. The yellow one represents the position of the launching grating. (c) Experimental extinction ratio R versus the wavelength. The red dashed line indicates R = 5. The blue line is a guide for the eyes. (d) SEM image of the sample integrated with waveguides. Inset: Magnified SEM image of the antenna pair. (e) CCD image of the scattering gratings for λ = 802 nm. The two white dotted frames represent the positions of the scattering gratings. (f) Experimental extinction ratio R versus the wavelength for the router integrated with waveguides. The blue line is a guide for the eyes.

A continuous laser beam from a tunable Ti:sapphire laser was normally incident upon the launching grating along the −z-axis to launched SPPs at the air–Au film interface. The SPPs were focused at the antenna pair and routed to propagate at the silica–Au film interface along the ±y-axes, which were scattered by the scattering gratings. An objective was used to image the scattering gratings on a charge-coupled device (CCD) to measure the intensities of the SPPs (see Supplementary material).

The CCD images of the scattering gratings for different incident wavelengths are shown in Figure 3(b), in which the image of the launching grating is also included in the left image at λ = 810 nm. The images of the router and a part of the launching grating were blocked by a spatial filter to reduce noise. Due to the destructive interference of the SPPs propagating along the −y-axis, the upper scattering grating is much brighter than the lower one. The intensity of the SPPs propagating along the −y-axis depends strongly on the wavelength and reaches the minimum at λ = 827 nm. We defined the extinction ratio R as the intensity ratio between the SPPs propagating along the design direction and the opposite direction. The experimental result of the extinction ratio R with respect to the wavelength is shown in Figure 3(c), in which a maximum value of 211 is obtained at λ = 827 nm. Half of the data are larger than five, and the antenna pair can serve as a 90° router with a sufficient signal-to-noise ratio for plasmonic integration. Compared with the calculated result of the destructive interference wavelength along the −y-axis, the experimental result redshifts 27 nm.

Waveguide is the basic component in functional photonics circuits, therefore the effective integration between the router and a waveguide offers an important connection to other functional optical components. Owing to the nanoscale size of the proposed router, it can integrate with the plasmonic waveguide directly, which is vital for enhancing the integration density. We fabricated two groove-shaped plasmonic waveguides coupled with the router, and the SEM image is shown in Figure 3(d). The waveguides have a width of 1 µm and a depth of 70 nm (see Supplementary material). The width of the waveguide, which is limited by the cutoff width of the fundamental mode, can be narrowed to 270 nm for λ = 800 nm (see Supplementary material). The output SPPs of the router are coupled into the waveguides directly. Two scattering gratings were also fabricated at the output ends of the waveguides to measure the intensities of the SPPs propagating in the waveguides. Figure 3(e) illustrates the image of the gratings at λ = 802 nm, in which the intensity of the SPPs scattered at the upper grating is much larger than that at the lower one and an extinction ratio of 56 was obtained. The extinction ratio with respect to the wavelength is shown in Figure 3(f). In the wavelength range of 775–833 nm, the extinction ratio is larger than five, which means that the router has a larger working wavelength range. The result in Figure 3(f) is different from that in Figure 3(c), which may originate from the scattering of the SPPs at the ends of the waveguides. This result indicates the device can integrate with waveguide directly. Considering the diverse configuration of the waveguide, this 3D router can be utilized for more complex route arrangements.

2.4 Arbitrary routing angle on demand: 180° and −45°

Using a similar method, we designed a router with α = 180°, which is composed of two rectangular slot antennas and schematically depicted in Figure 4(a). The antennas have the same width (w = 70 nm) and different length (L ₂ = 300 nm and L ₃ = 210 nm) (see Supplementary material). The distance d between the antennas is 320 nm. The input SPPs propagating along the +x-axis at the air–Au film interface is incident into the antennas. The SPPs are launched at the silica–Au film interface, which acts as two SPP point sources and propagates along the ±x-axes. The numerical calculation shows that this design allows for a total phase difference of the two SPP waves propagating along the +x-axis of −180 ± 20° and destructively interfering in the wavelength range of 753–853 nm (see Supplementary material). On the contrary, the SPPs propagating along the −x-axis constructively interfere, and a 180° router is obtained.

Figure 4:

Experimental results of the 180° and −45° routers.

(a) Schematic of the 180° router. The solid red arrow indicates the direction of the input surface plasmon polaritons (SPPs) propagating at the air–Au film interface and the blue dashed arrow indicates the direction of the output SPPs propagating at the silica–Au film interface. (b) and (c) Scanning electron microscopy (SEM) images of the experimental samples with different positions of scattering gratings. Inset: Magnified SEM image of the antenna pair. (d) and (e) Charge-coupled device (CCD) images of the scattering gratings in (b) and (c), respectively, for different incident wavelengths. The white dotted frames represent the positions of the scattering gratings. (f) Extinction ratio R versus the wavelength. The red dashed line indicates R = 5. The blue line is a guide for the eyes. (g) Schematic of the −45° router. (h) SEM image of the sample of the −45° router. Inset: Magnified SEM image of the antenna pair. (i) CCD image of the scattering gratings at λ = 837 nm. The white dotted frames represent the positions of the scattering gratings. (j) Experimental extinction ratio R of the −45° router versus the wavelength. The blue line is a guide for the eyes.

Two SEM images of the experimental samples are shown in Figures 4(b) and (c) to measure the intensities of the SPPs propagating along the ±x-axes at the silica–Au film interface, respectively. The insets show the close-up view of the antenna pairs with the same geometry as the design. To avoid noises in the measurements of the SPP intensity, two arc-shaped gratings at the air–Au film interface with a period of 784 nm on each sample were fabricated to launch and focus SPPs on the routers. Two rectangular scattering gratings at the silica–Au film interface with a period of 526 nm on the two samples with different locations were fabricated to measure the intensities of the output SPPs. We fabricated the two scattering gratings separately on two samples to reduce the noise originating from the reflection of the SPPs on the gratings.

Figures 4(d) and (e) show the CCD images of the scattering gratings in Figures 4(b) and (c), respectively, for the same incident light with wavelengths of 764, 787, and 801 nm. The transmitted light from the antennas was blocked using a spatial filter. The scattering lights from the grating in Figure 4(e) are much stronger than those in Figure 4(d) for the three incident wavelengths, which indicate that the launched SPPs propagate along the −x-axis and a 180° router is implemented. The extinction ratio R with respect to the wavelength is shown in Figure 4(f). In the wavelength range of 760–860 nm, the value of R is larger than five, which shows a broadband working wavelength range. The maximum value of R reaches 97 at 787 nm.

We have demonstrated 3D routers with routing angles of an integer multiple of 90°. To design routers with an arbitrary routing angle, the antenna pairs used above should rotate an angle. Here, we demonstrate a router with α = −45°, the schematic of which is shown in Figure 4(g). The input SPPs propagate along the +x-axis at the air–Au film interface and the output SPPs launched by the router propagates along the −45° direction at the silica–Au film interface. The router is composed of two slot antennas, whose short axes have a −45° angle with respect to the +x-axis. The geometries of the antenna pair are L ₄ = 200 nm, L ₅ = 400 nm, w = 70 nm, and d = 400 nm. The SEM image of the designed router is shown in Figure 4(h). The arc grating at the air–Au film interface launches and focuses SPPs on the router, and the output SPPs propagate along the −45° direction. Two rectangular scattering gratings were used to measure the intensity of the output SPPs. Figure 4(i) shows the CCD image of the scattering gratings at λ = 837 nm. The intensity of the image of the lower grating is much larger than that of the upper one, and an extinction ratio of 17 is obtained. The extinction ratio with respect to the wavelength is shown in Figure 4(j). The extinction ratio R is larger than five in the wavelength ranges of 811–823 and 830–851 nm.

2.5 2 × 2 butterfly plasmonic interconnection

Using the proposed routers, a 3D plasmonic interconnection can be implemented. A butterfly network connects n input ports with the same number of output ports with crossing-enabled interconnections [35]. Here, we demonstrate a 2 × 2 butterfly network, which has two inputs and two outputs ports [Figure 5(a)]. Two input SPP signals propagating along the +x-axis (input port I₁) and −y-axis (input port I₂) at the air–Au film interface are incident into the interconnection device, which is composed of four rectangular antennas. The corresponding output SPP signals propagate along the +x-axis (output port O₁) and −y-axis (output port O₂) at the silica–Au film interface. The device is composed of two rectangular antenna pairs with the same geometry and different orientations, and the geometry parameters are L ₆ = 210 nm, L ₇ = 300 nm, w = 70 nm, and d = 380 nm. The distance D, which is the distance between the center of the two antenna pairs in the x and y directions, is 500 nm.

Figure 5:

Schematic and experimental results of the three-dimensional (3D) butterfly plasmonic interconnection.

(a) Schematic of the 2 × 2 butterfly network. The solid blue and red arrows indicate the directions of the input SPPs propagating at the air–Au film interface, and the blue and red dashed arrows indicate the directions of the output surface plasmon polaritons (SPPs) propagating at the silica–Au film interface. (b) Scanning electron microscopy (SEM) image of the 3D butterfly plasmonic interconnection network. Inset: Magnified SEM image of the antenna pair. (c) and (d) Charge-coupled device (CCD) images of the sample for different incident directions at λ = 800 nm.

Figure 5(b) illustrates the SEM image of the sample. Two arc gratings with the same parameter as mentioned above were utilized to launch and focus SPPs propagating at the air–Au film interface into the routers. Two rectangular scattering gratings were used to measure the intensities of the output signals propagating at the silica–Au film interface. When SPPs were launched and incident into input port I₁, the CCD image of the scattering gratings for λ = 800 nm is shown in Figure 5(c). The scattering light from the grating located at the O₁ port is much brighter than that at the O₂ port. A similar result was obtained when the SPPs were incident into input port I₂ [Figure 5(d)]. The results show that the 3D butterfly interconnection was implemented at the nanoscale with low crosstalk.

3 Discussion

The resonant modes of the L-shaped and rectangular slot antennas are different, which can be used for signal routing with different angles. For an L-shaped antenna with two perpendicularly placed arms, two modes of the antenna can be excited effectively when the propagation direction of the input SPPs is parallel to one arm of the antenna. Based on the superposition of these two modes, the antenna can launch SPPs propagating perpendicularly to the input SPPs (Figure 1d). Thus, L-shaped antennas can be used to implement routers with angles in the ranges of 45° ≤ α ≤ 135° and 225° ≤ α ≤ 315°. For a rectangular antenna with dipole resonance, the polarization is parallel to its short axis (Figure S8b in the Supplementary material). As a result, the rectangular antenna launches SPPs propagating along its short axis. For the same reason, the launching efficiency of the dipole mode of the rectangular antenna is the maximum when the propagation direction of the input SPPs is parallel to the short axis. And it decreases to zero when the propagation direction of the input SPPs is perpendicular to the short axis. Therefore, rectangular antennas can be used to implement routers with angles in the ranges of −45° ≤ α ≤ 45° and 135° ≤ α ≤ 225°.

The calculated maximum routing efficiency is 12.4% for the 180° router and 5.1% for the 90° router (see Supplementary material). The imperfect efficiencies indicate that the SPPs also propagate along with the original layer. While benefiting from the optically thick Au film, the SPPs propagating along the upper surface are isolated and cannot affect the signal on the lower surface. The efficiencies are limited by the nanoscale dimensions of the routers, which can be improved by increasing the number of antenna pairs.

Due to the nanoscale footprint size and the capability of integration with waveguides, the 3D routers can act as exchange nodes for cross-layer routing in highly integrated photonic circuits [36], [37], [38]. The 3D routers can be applied in the two broad categories of optical interconnects including index-guided type and free-space type. The ultra-small size of the 3D routers can address the feature-size incompatibility between photonic and electronic circuits, and these routers can be applied in the parallel interconnection between memory and processing elements in the 3D integration of plasmonics and electronics [39], [40].

4 Conclusion

In summary, we have demonstrated cross-layer 3D optical routers with ultra-compact footprints. Optical slot antennas were used to connect SPPs propagating at the superstrate– and substrate–Au film interfaces. The direction of the output SPPs was controlled by controlling the phases and propagation directions of the SPPs launched by the antennas. The “wired” connection between the router and plasmonic waveguides was demonstrated due to the nanoscale size of the router. We also showed the application of the routers in 3D butterfly plasmonic interconnection. Benefiting from their ultra-compact size, high directivity, and the effective connection with waveguides, these plasmonic nano-devices can be used as promising signal routers for vertical connectivity in dense, complex, and integrated plasmonic or hybrid circuits, which are critical for next-generation 3D integrated technology. As the metal sustains both plasmonic and electrical signal transfer, these 3D routers also offer an ideal solution to the interface connection between the optical layer and the electrical layer, paving the way to the hybrid integration of electronics and photonics in the signal processing field.

Corresponding author: Jiasen Zhang, State Key Laboratory for Artificial Microstructures and Mesoscopic Physics, School of Physics, Peking University, Beijing, 100871, China; and Peking University Yangtze Delta Institute of Optoelectronics, Nantong, 226010, Jiangsu, China, E-mail: jszhang@pku.edu.cn

Funding source: National Natural Science Foundation of China

Award Identifier / Grant number: 91850104

Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: The authors are grateful for support by the National Natural Science Foundation of China (NSFC) (Grant No. 91850104).
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.

References

[1] Y. Liu, J. Zhang, and L.-M. Peng, “Three-dimensional integration of plasmonics and nanoelectronics,” Nat. Electron., vol. 1, pp. 644–651, 2018, https://doi.org/10.1038/s41928-018-0176-z.Search in Google Scholar

[2] T. Tajiri, S. Takahashi, Y. Ota, K. Watanabe, S. Iwamoto, and Y. Arakawa, “Three-dimensional photonic crystal simultaneously integrating a nanocavity laser and waveguides,” Optica, vol. 6, pp. 296–299, 2019, https://doi.org/10.1364/optica.6.000296.Search in Google Scholar

[3] R.-M. Ma and R. F. Oulton, “Applications of nanolasers,” Nat. Nanotechnol., vol. 14, pp. 12–22, 2019. https://doi.org/10.1038/s41565-018-0320-y.Search in Google Scholar PubMed

[4] X. Liu, Q. Zhang, J. N. Yip, Q. Xiong, and T. C. Sum, “Wavelength tunable single nanowire lasers based on surface plasmon polariton enhanced Burstein–Moss effect,” Nano Lett., vol. 13, pp. 5336–5343, 2013, https://doi.org/10.1021/nl402836x.Search in Google Scholar PubMed

[5] S. I. Azzam, A. V. Kildishev, R.-M. Ma, et al.., “Ten years of spasers and plasmonic nanolasers,” Light Sci. Appl., vol. 9, p. 90, 2020, https://doi.org/10.1038/s41377-020-0319-7.Search in Google Scholar PubMed PubMed Central

[6] A. L. Falk, F. H. L. Koppens, C. L. Yu, et al.., “Near-field electrical detection of optical plasmons and single-plasmon sources,” Nat. Phys., vol. 5, pp. 475–479, 2009, https://doi.org/10.1038/nphys1284.Search in Google Scholar

[7] P. Neutens, P. Van Dorpe, I. De Vlaminck, L. Lagae, and G. Borghs, “Electrical detection of confined gap plasmons in metal–insulator–metal waveguides,” Nat. Photonics, vol. 3, pp. 283–286, 2009, https://doi.org/10.1038/nphoton.2009.47.Search in Google Scholar

[8] I. Goykhman, B. Desiatov, J. Khurgin, J. Shappir, and U. Levy, “Locally oxidized silicon surface-plasmon Schottky detector for telecom regime,” Nano Lett., vol. 11, pp. 2219–2224, 2011, https://doi.org/10.1021/nl200187v.Search in Google Scholar PubMed

[9] O. Melchert, C. Brée, A. Tajalli, et al.., “All-optical supercontinuum switching,” Commun. Phys., vol. 3, p. 146, 2020, https://doi.org/10.1038/s42005-020-00414-1.Search in Google Scholar

[10] N. Large, M. Abb, J. Aizpurua, and O. L. Muskens, “Photoconductively loaded plasmonic nanoantenna as building block for ultracompact optical switches,” Nano Lett., vol. 10, pp. 1741–1746, 2010, https://doi.org/10.1021/nl1001636.Search in Google Scholar PubMed

[11] M. R. Shcherbakov, S. Liu, V. V. Zubyuk, et al.., “Ultrafast all-optical tuning of direct-gap semiconductor metasurfaces,” Nat. Commun., vol. 8, p. 17, 2017, https://doi.org/10.1038/s41467-017-00019-3.Search in Google Scholar PubMed PubMed Central

[12] J. D. Cox and F. J. García de Abajo, “Single-plasmon thermo-optical switching in graphene,” Nano Lett., vol. 19, pp. 3743–3750, 2019, https://doi.org/10.1021/acs.nanolett.9b00879.Search in Google Scholar PubMed

[13] S. M. Garner, L. Sang-Shin, V. Chuyanov, et al.., “Three-dimensional integrated optics using polymers,” IEEE J. Quant. Electron., vol. 35, pp. 1146–1155, 1999, https://doi.org/10.1109/3.777214.Search in Google Scholar

[14] J. Chiles, S. Buckley, N. Nader, S. W. Nam, R. P. Mirin, and J. M. Shainline, “Multi-planar amorphous silicon photonics with compact interplanar couplers, cross talk mitigation, and low crossing loss,” APL Photonics, vol. 2, p. 116101, 2017, https://doi.org/10.1063/1.5000384.Search in Google Scholar

[15] W. D. Sacher, J. C. Mikkelsen, P. Dumais, et al.., “Tri-layer silicon nitride-on-silicon photonic platform for ultra-low-loss crossings and interlayer transitions,” Opt. Express, vol. 25, pp. 30862–30875, 2017, https://doi.org/10.1364/oe.25.030862.Search in Google Scholar PubMed

[16] S. Zhu and G.-Q. Lo, “Vertically stacked multilayer photonics on bulk silicon toward three-dimensional integration,” J. Lightwave Technol., vol. 34, pp. 386–392, 2016, https://doi.org/10.1109/jlt.2015.2499761.Search in Google Scholar

[17] N. Nishiyama, J. Kang, Y. Kuno, et al.., “Si-Photonics-Based layer-to-layer coupler toward 3D optical interconnection,” IEICE Trans. Electron., vol. E101.C, pp. 501–508, 2018, https://doi.org/10.1587/transele.e101.c.501.Search in Google Scholar

[18] K. Shang, S. Pathak, B. Guan, G. Liu, and S. J. B. Yoo, “Low-loss compact multilayer silicon nitride platform for 3D photonic integrated circuits,” Opt. Express, vol. 23, pp. 21334–21342, 2015, https://doi.org/10.1364/oe.23.021334.Search in Google Scholar

[19] E. Ozbay, “Plasmonics: merging photonics and electronics at nanoscale dimensions,” Science, vol. 311, pp. 189–193, 2006, https://doi.org/10.1126/science.1114849.Search in Google Scholar PubMed

[20] W. L. Barnes, A. Dereux, and T. W. Ebbesen, “Surface plasmon subwavelength optics,” Nature, vol. 424, pp. 824–830, 2003, https://doi.org/10.1038/nature01937.Search in Google Scholar PubMed

[21] S. A. Maier, Plasmonics: Fundamentals and Applications, New York, NY, USA, Springer, 2007.10.1007/0-387-37825-1Search in Google Scholar

[22] D. K. Gramotnev and S. I. Bozhevolnyi, “Plasmonics beyond the diffraction limit,” Nat. Photonics, vol. 4, pp. 83–91, 2010, https://doi.org/10.1038/nphoton.2009.282.Search in Google Scholar

[23] J. A. Schuller, E. S. Barnard, W. Cai, Y. C. Jun, J. S. White, and M. L. Brongersma, “Plasmonics for extreme light concentration and manipulation,” Nat. Mater., vol. 9, pp. 193–204, 2010, https://doi.org/10.1038/nmat2630.Search in Google Scholar PubMed

[24] J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen, and D. R. Smith, “Extreme nanophotonics from ultrathin metallic gaps,” Nat. Mater., vol. 18, pp. 668–678, 2019, https://doi.org/10.1038/s41563-019-0290-y.Search in Google Scholar PubMed

[25] N. Li, Y. Lai, S. H. Lam, H. Bai, L. Shao, and J. Wang, “Directional control of light with nanoantennas,” Adv. Opt. Mater., vol. 9, p. 2001081, 2021, https://doi.org/10.1002/adom.202001081.Search in Google Scholar

[26] R. Guo, M. Decker, F. Setzpfandt, et al.., “High-bit rate ultra-compact light routing with mode-selective on-chip nanoantennas,” Sci. Adv., vol. 3, p. e1700007, 2017, https://doi.org/10.1126/sciadv.1700007.Search in Google Scholar PubMed PubMed Central

[27] M. Cohen, Y. Abulafia, D. Lev, A. Lewis, R. Shavit, and Z. Zalevsky, “Wireless communication with nanoplasmonic data carriers: macroscale propagation of nanophotonic plasmon polaritons probed by near-field nanoimaging,” Nano Lett., vol. 17, pp. 5181–5186, 2017, https://doi.org/10.1021/acs.nanolett.7b00266.Search in Google Scholar PubMed

[28] A. Alu and N. Engheta, “Wireless at the nanoscale: optical interconnects using matched nanoantennas,” Phys. Rev. Lett., vol. 104, p. 213902, 2010, https://doi.org/10.1103/physrevlett.104.213902.Search in Google Scholar PubMed

[29] Y. Fang and M. Sun, “Nanoplasmonic waveguides: towards applications in integrated nanophotonic circuits,” Light Sci. Appl., vol. 4, p. e294, 2015, https://doi.org/10.1038/lsa.2015.67.Search in Google Scholar

[30] H. S. Won, K. C. Kim, S. H. Song, et al.., “Vertical coupling of long-range surface plasmon polaritons,” Appl. Phys. Lett., vol. 88, p. 011110, 2006, https://doi.org/10.1063/1.2159558.Search in Google Scholar

[31] Y. Fang, Z. Li, Y. Huang, et al.., “Branched silver nanowires as controllable plasmon routers,” Nano Lett., vol. 10, pp. 1950–1954, 2010, https://doi.org/10.1021/nl101168u.Search in Google Scholar PubMed

[32] S. Kumar, N. I. Kristiansen, A. Huck, and U. L. Andersen, “Generation and controlled routing of single plasmons on a chip,” Nano Lett., vol. 14, pp. 663–669, 2014, https://doi.org/10.1021/nl403907w.Search in Google Scholar PubMed

[33] V. S. Volkov, S. I. Bozhevolnyi, E. Devaux, J.-Y. Laluet, and T. W. Ebbesen, “Wavelength selective nanophotonic components utilizing channel plasmon polaritons,” Nano Lett., vol. 7, pp. 880–884, 2007, https://doi.org/10.1021/nl070209b.Search in Google Scholar PubMed

[34] Z. Liu, Y. Zhang, G. Weixuan, Y.-C. Liu, X. Hu, and C. Lu, “Ultrasmall broadband wavelength and polarization router based on hybrid waveguide of monolithic-LiNbO3,” Opt. Lett., vol. 44, p. 5772, 2019, https://doi.org/10.1364/ol.44.005772.Search in Google Scholar PubMed

[35] K. M. Iftekharuddin and M. A. Karim, “Butterfly interconnection network: design of multiplier, flip-flop, and shift register,” Appl. Opt., vol. 33, pp. 1457–1462, 1994, https://doi.org/10.1364/ao.33.001457.Search in Google Scholar PubMed

[36] S. I. Bozhevolnyi, V. S. Volkov, E. Devaux, J.-Y. Laluet, and T. W. Ebbesen, “Channel plasmon subwavelength waveguide components including interferometers and ring resonators,” Nature, vol. 440, pp. 508–511, 2006, https://doi.org/10.1038/nature04594.Search in Google Scholar PubMed

[37] R. Zia, J. A. Schuller, A. Chandran, and M. L. Brongersma, “Plasmonics: the next chip-scale technology,” Mater. Today, vol. 9, pp. 20–27, 2006, https://doi.org/10.1016/s1369-7021(06)71572-3.Search in Google Scholar

[38] B. Schwarz, P. Reininger, D. Ristanić, et al.., “Monolithically integrated mid-infrared lab-on-a-chip using plasmonics and quantum cascade structures,” Nat. Commun., vol. 5, p. 4085, 2014, https://doi.org/10.1038/ncomms5085.Search in Google Scholar PubMed PubMed Central

[39] U. Koch, C. Uhl, H. Hettrich, et al.., “A monolithic bipolar CMOS electronic–plasmonic high-speed transmitter,” Nat. Electron., vol. 3, pp. 338–345, 2020, https://doi.org/10.1038/s41928-020-0417-9.Search in Google Scholar

[40] A. W. Elshaari, W. Pernice, K. Srinivasan, O. Benson, and V. Zwiller, “Hybrid integrated quantum photonic circuits,” Nat. Photonics, vol. 14, pp. 285–298, 2020, https://doi.org/10.1038/s41566-020-0609-x.Search in Google Scholar PubMed PubMed Central