Superlattice nonlinearities for Gigahertz-Terahertz generation in harmonic multipliers

1 Introduction

The inherent nonlinearities of electronic systems can be exploited for the development of novel compact sources in the terahertz (THz) region [1], [2], [3], [4], [5]. The very same nonlinearities and their underlying microscopic origin serve as sensitive means for controlling high harmonic generation (HHG) processes. A notable very recent example is the generation of THz harmonics in a single-layer graphene due to hot Dirac fermionic dynamics under low-electric field conditions [6]. In a parallel effort, advances in strong-field and attosecond physics have paved the way to HHG in bulk crystals operating in a highly nonperturbative regime [7], [8], [9], [10], [11]. The first experimental observation of non-perturbative HHG in a bulk crystal was explained on the basis of a simple two-step model in which the nonlinearity stemmed from the anharmonicity of electronic motion in the band combined with multiple Bragg reflections at the zone boundaries [12]. The high frequency (HF) nonlinearities which contribute to harmonic upconversion in bulk semiconductors have been associated to dynamical Bloch oscillations (BO) combined with coherent interband polarization processes [7], [13]. The aforementioned models allow the use of tight-binding dispersions [14] to describe the electronic band and therefore the radiation from a nonlinear intraband current. One of the systems that demonstrate a similar highly nonparabolic energy dispersion are man-made semiconductor superlattices (SSLs) [15], [16]. In fact, the possibility of spontaneous frequency multiplication due to the effect of nonparabolicity in a SSL miniband structure was first predicted in the early works of Esaki-Tsu [17] and Romanov [18]. Superlattices are created by alternating layers of two semiconductor materials with similar lattice constants resulting in the formation of a spatial periodic potential. Furthermore, SSLs host rich dynamics in the presence of a driving field, which include the formation of Stark ladders [19], the manifestation of Bragg reflections and Bloch oscillations [20]. From the viewpoint of applications, SSLs have attracted great interest because they allow the development of devices which operate at microwave [21] and far-infrared frequencies [5], [21] suitable for high precision spectroscopic studies and detection of submillimeter waves. In addition, a considerable number of studies have tackled the task of engineering parametric amplifiers [22], [23] and frequency multipliers [24], [25], [26] based on superlattice periodic structures. Note that although the first semiconductor superlattice frequency multipliers (SSLM) were developed for the generation of microwave radiation [27], significant progress has been achieved combining high-frequency operation (up to 8.1 THz, ∼ 50th harmonic) [5], [25] and high conversion efficiency [28] comparable to the performance of Schottky diodes [28], [29].

There are various mechanisms that contribute to the HF nonlinearities of SSL devices. Once this distinction has been clearly made, it is simple to connect the underlying physical mechanisms to the frequency multiplication effects. It was found that spontaneous multiplication takes place in a dc biased tight-binding SSL, when the Bloch-oscillating electron wave packet is driven by the input oscillating field [30], [31]. Moreover, the increase of optical response [30] was due to the frequency modulation of Bloch oscillations [32], [33] which arise in the negative differential conductivity (NDC) region of the current-voltage characteristic, i. e., the current decreases with increasing bias. On the other hand, if a SSL device is in a NDC state, the nonlinearities can be further enhanced by the onset of high-field domains [34], [35] and the related propagation phenomena [36] in a similar way as the electric-field domains in bulk semiconductors [37]. Thus, the ultrafast creation and annihilation of electric domains during the time-period of an oscillating field contributes to harmonic generation processes in SSLs [38]. This type of dynamics has been found to depend on plasma effects [39], [40] induced by the space-charge instabilities and the dielectric relaxation time processes which dictate the exact conditions for the NDC state [40]. The expected THz response from BO in a miniband SSL, under the influence of a THz electric field, might also deviate due to strong excitonic effects [41], [42], [43]. Harvesting the nonlinearities discussed above can potentially lead to more efficient SSLMs or other devices suitable for achieving extremely flexible frequency tuning.

Our approach is inspired by very recent theoretical and experimental investigations [26], [44], [45], [46] of SSLM behavior, which revealed the development of even harmonics due to imperfections in the superlattice structure. In general, when an adequately strong oscillating field couples energy into the SSLM in the absence of constant bias, only odd harmonics are emitted. However, Ref. [26] showed that symmetry breaking was induced by asymmetric current flow and scattering processes under forward and reverse bias. This approach combined nonequilibrium Green’s function calculations with an Ansatz solution of the Boltzmann equation in the relaxation rate approximation. Furthermore, the asymmetric scattering rates were attributed to the different elastic (interface roughness) scattering rates which have raised from the non-identical qualities of the SSL interfaces. In general, elastic scattering processes can have a significant effect on the electron transport in SSLs.The conventional method to study the role of elastic scattering on miniband transport and generation of high-frequency radiation [47], [48] are the one dimensional (1D) SSL Balance equations [47] which can be extended to address two-dimensional and three-dimensional [49], [50] SSL transport and optical properties. They cannot, however, include systematically the different scattering processes under forward and reverse bias. A handful of experiments have been devoted to examine the harmonics of current oscillations [35], transient THz response [51], dephasing mechanisms of Bloch oscillations [52] and the electron mobility [53] under the influence of isotropic-elastic-scattering time.

In this paper, we elucidate how the effects of asymmetric scattering processes could be used to control the implications of the SL potential on the response of miniband electrons to an oscillating electric field E(t)=Eaccos(2πνt). We solve the Boltzmann transport equation (BTE) by the method of characteristics [54], [55], which allows to address explicitily the asymmetric intraminiband relaxation processes in SSLs. Earlier in Refs. [56], [57] the relaxation rate was assumed to depend on the electron velocity allowed to estimate analytically the high-frequency conductivity of an asymmetric superlattice but with resorting to perturbative analysis of the Boltzmann equation. Before proceeding further it is worthwhile first to highlight the main points of this work:

1. We eliminate the numerical instabilities which originate from the Ansatz solution of Refs. [26], [57].

2. Our solution delivers a time-domain analysis of the mechanism responsible for the built up of high harmonic generation.

3. We theoretically demonstrate that the multiplication effects can be effectively controlled by special designs of superlattice interfaces (asymmetric elastic scattering).

The anisotropic effects [26] reflect that typically the interfaces of a host material (A) grown on a different host material (B) are found to be rougher than those of B on A (see Figure 1), indicating grading or intermixing of the constituent materials between SSL layers [58], [59].

Figure 1:

Schematic diagram of the origin of asymmetric current flow in a semiconductor superlattice due to differences in interface roughness depending on the sequence of layers. GaAs layers are depicted in blue (color online) and AlAs layers in gray (color online). The interface of GaAs over AlAs has lower quality than that of AlAs over GaAs. The different relaxation rates Γ⁺ (Γ⁻) depend on the direction of the time-dependent miniband velocity v(k_z(t_i), k_z(t₀)). Here t₀′ and t′0 designate just different starting times [see Eq. (3)]. The SSL sample is biased by an electric field, E = (0, 0, E_ac cos(2πvt)) parallel to the direction of the z–axis.

This paper is organized as follows. Section 2 provides an overview of a semiclassical theory describing the charge transport in SSLs in the presence of asymmetric scattering. In Section 3, we discuss the nonlinear optical response of miniband electrons in an asymmetric SL structure and we present results of exact numerical simulations describing the spontaneous HHG. Complementary insight is provided next with time-domain calculations. In Appendix A, we revisit in more detail the path-integral expressions implemented in this work. On the other hand, Appendix B entails analytical solutions for HHG based on an Ansatz that can lead to numerical instabilities to highlight our far more efficient solution.

2 Semiclassical formulation

Throughout this work we use the standard energy dispersion, ϵ(kz)=ϵa−2|T|cos(kzd), which describes the kinetic energy carried by an electron in the lowest SL miniband [15], [16]. Here ϵa is the center of the miniband, |T| is the miniband quarter-width, k_z is the projection of crystal momentum on the z–axis (axis parallel to the general grown direction) and d is the superlattice period. Note that in this transport model, the effects of inter-miniband tunneling are neglected. To simulate the temporal distribution function f(k, t) of the single electron, we employ a semiclassical approach based on the Boltzmann transport equation [16]

where F is the force (−e)E corresponding to a time dependent electric field in the z–direction of the SSL and k is the total momentum which can decomposed into k_z and the quasimomentum in the x–y plane k_∥=(k_x, k_y). The right-hand side term of Eq. (1) represents the collision integral. Instead of using a single relaxation rate approximation model equivalent to I{f}=−(f−f0)Γ/ℏ [60] with f₀(k) being the equilibrium fermi distribution, we will resort to two scattering rates Γ to adequately describe the asymmetric relaxation processes. The asymmetric elastic scattering would result to enhanced scattering processes into certain directions. Thus, the kinetic equation can be rewritten in the following form

where Ł±=1/ℏ(F∂/∂k+ℏ∂/∂t+Γ±) are integral operators corresponding to the different relaxation rates (Γ⁺ and Γ⁻). By using the inverse of the operator, Ł⁻¹, on the left of Eq. (2), we obtained the time-dependent current density

where k_z is integrated over the Brillouin zone, the integration limits of the in-plane components k_∥ are ±∞ and Δ(t, t₀) controls the level of current flow asymmetry. Equation (3) summarizes that an electron which passes through the point k at time t, follows different collisionless trajectories which takes it through the points k(t₀) at times t₀ < t. This compact solution requires the assumption of the following condition for the relaxation energy

Here v(t, t₀) represents the time-dependent miniband velocity which reveals the propagation direction of the electron along the sample and therefore indicates the interaction with the high-quality or low-quality interface (see Figure 1). For a further discussion of Eqs. (2)–(4) see Appendix A. The time dependence of the velocity v(t, t₀) is obtained from the set of the equations

where the parameter α=eEacd/(hν) critically affects the strength of the nonlinear optical response and consequently the harmonic-conversion properties of the SSLM.

The Fourier transform of the time-dependent current [Eq. (3)] can be used to obtain spectral peaks at multiples of the driving frequency. In particular, the intensity of the emitted radiation from the SSL structure is determined by the Poynting vector, which is proportional to the harmonic current term [26]

where the integration ⟨…⟩ signifies time-averaging over time interval of infinite time in the general case. Nevertheless, considering that the current response is induced merely by a monochromatic field (ν), it is sufficient to average only over the time-period Tν=1/ν. Both even and odd harmonics are present in a biased SSL due to symmetry breaking. However, in this paper we focus on symmetry breaking due structural effects leading to asymmetric current flow. Thus in all numerical results for harmonic generation, there is no static electric field, i. e., eE_dcd = 0 and the Bragg reflections from minizone boundaries are not assigned to BO with the conventional oscillation frequency v_B = eE_dcd/h. In contrast, the Bragg scattering is manifested as frequency modulation of electron oscillations during a cycle (T_v = 1/v) of the oscillating field. Oscillations of this type are known as BO in a harmonic field (BOHF) [33].Combining the Bloch acceleration theorem [Εq. (5a)] and the energy dispersion ϵ(k_zd), one can find the dependence of miniband energy on time

where ϵ₀ = ϵ^α − 2 | T | J₀(α) and J0(.), J2n(.) are bessel functions of the first kind. From Eq. (7) we see that the electron energy oscillates within the miniband with frequency ν∈2n at every even mupltiple of ν:ν∈2n=ln with l = 2, 4, 6, 8… On the contrary, the miniband velocity varies at every odd multiple of ν:νν2n+1=ln with l = 3, 5, 7, 9… stemming directly from the equation ν(t)=4|T|d/ℏ∑n=0∞J2n+1(α)sin{(2n+1)(2πνt)} which is derived, just as Eq. (7), from a real-valued expression of Jacobi–Anger expansion [61]. Due to the collisions the electron experiences damped BOHF and thus the latter equation can be used as an input for the solution of the BTE [see Eq. (3)]. Hereafter, it becomes clear that the Boltzmann-Bloch transport theory requires a self-consistent solution of the BTE and the semiclassical equations of motion obeyed by Bloch momentum k_z. In the quasistatic limit the electron performs high quality BOHF whenα>αc. Here α_c = U_c/(hν) with U_c = eE_acd = Γ designating the energy required from the ac-field in order to bring temporarily the SSL to an active state equivalent to the NDC region of the VI characteristic result to the formation of high electric field domains which act as additional linearities. We must underline that in this work the high-frequency field considered to be acting on the superlattice leads to a single-electron state and the electric field within the SSL remains uniform. As a result, the gain at some harmonics of the oscillating field is related only to the nonlinearity of the voltage-current characteristic and the BOHF oscillations.

The conditions [Eq. (4)] dictate the different relaxation times Γ(t)=Γ+orΓ−, reflecting on the coefficient Δ(t, t0)=1 or δ in Eq. (3). This asymmetry coefficient δ=Γ+/Γ− plays an important role in this work, since it indicates the differences between the interfaces leading to deviation from the perfectly anti-symmetric voltage of the Esaki and Tsu model [15]. See Figure 7 per se in Appendix B. An increase of δ can be interpreted as a structural variation of the initial SSL structure. In the present work we assume that δ ≥ 1 which implies that the flow from left to right will be favored over the flow from right to left. Furthermore, the asymmetry coefficient depends on the elastic and inelastic scattering rates, which are either determined from measured values [35], [62] or nonequilibrium Green’s functions calculations [26], [45]. It is important to notice that similar kinetic formulas to Eq. (3) have been used to treat the different different types of scattering processes in superlattices [63], [64]. However, none of these works have systematically included a tensor analyzing the different relaxation processes which correspond to an asymmetric SSL structure. In this paper the values of the SSL parameters in Eqs. (3)–(5) are taken from recent experiments and predictive simulations [26], [44]: d = 6.23 nm, |T| = 30 meV, Γ⁺ = 21 meV, j₀ = 2.14 × 10⁹ A/m² and the corresponding critical field is Ec+=3.4 kV/mm. For the integration of the equation of motions (5a), (5b) we implement the classical fourth-order Runge-Kutta method known for its stability [65].

Figure 2:

(Color online) Comparison of the nonlinear response |ℐl(ν)|2 characterizing the generation of second [panels (a) and (b)] and third [panels (c) and (d)] harmonics. The curves are calculated using either the path integral approach of Eq. (3) [(a) and (c)], or the ansatz of Eq. (19) [(b) and (d)] as a function of the parameter α=eEacd/(hν) and different values of the asymmetry coefficient δ=1.05, 1.2, 1.4. The dashed curve (c) indicates the usual third harmonic at δ = 1 whereas the vertical dashed lines [(a) and (c)] designates the critical field (a=ac) for which the SSL can operate in the NDC part of the VI characteristic. The inset zooms on numerical instabilities for |ℐ3(ν)|2 with small parameter α in the third harmonic. In all cases the frequency of the oscillating field is ν= 141 GHz.

Before moving forward with results, we should make a brief recap of a previous research. A NEGF approach, in which the different interfaces were described by using an interface roughness self-energy, gave good agreement with static current voltage, but could not be implemented for a GHz input. Thus, this predictive input was used in a hybrid NEGF-Boltzmann equation approach by employing an analyical Ansatz solution for the asymmetric current flow [26], [44], [45], [46]. However, the Ansatz leads in some cases to numerical instabilities and errors as shown in Figure 2. This is one of the main motivations of this paper, which delivers a clean numerical solution that does not need the Ansatz. For correctness the analytical Ansatz solution is described in Appendix B.

3 Results

In this section we will investigate the effects of asymmetric scattering on HHG by implementing the approach developed in the previous section and compare its predictions to those of the analytical Ansatz solution. The basic idea is to vary the asymmetry coefficient δ which in both approaches is defined as the ratio of the different relaxation rates (Γ±) and then examine the effects on even and odd order harmonics. Figure 2 depicts the second harmonic (left-handed panels) and third harmonic output (right-handed panels) as a function of α parameter for different values of the asymmetry coefficient δ. The dependencies |ℐl(ν)|2(α) were calculated using Eqs. (15)–(19) and Eqs. (3)–(6) in Figure 2(a) and Figure 2(b), respectively. Both approaches yield similar results for the second harmonic in a wide range of α. In particular, we highlight that asymmetric relaxation times are an unconventional mechanism for frequency doubling in SSLs. As δ increases, the frequency doubling effects become more pronounced and, eventually, give rise to stronger optical response almost up to 0.6%. We note that the Ansatz solution may, however, contribute to nonphysical numerical instabilities by revealing intense second harmonic generation even at small amplitudes of the oscillating field. Therefore, the numerical solution offers a reliable way to treat the scattering induced asymmetries in the current flow. Now we turn our attention to the third harmonic output in the presence of asymmetric current flow which is quite different from the behavior of the second harmonic output. Moreover, increasing δ suppresses it, implying a redistribution of spectral components in favor of even harmonics as shown in Figure 2(d). One can see that the maximum output of the third harmonic might be potentially reduced from 20 to 15%. In this case the different solutions appear to be more consistent with each other. However, as shown in the inset of Figure 2(d) the Ansatz solution can lead to numerical instabilities comparable with the maximum output of the second harmonic. Once we established that the novel approach developed in this work affords the significant variation of the asymmetry coefficient, we can have an in-depth look into the HHG processes.

Further insight on how asymmetric effects can result in a significant gain at some even harmonic frequencies and suppression at some other odd-order harmonics, is given by the color maps in Figure 3. It shows the calculated values |ℐl(ν)|2 as a function of α and δ. The black area indicates values (α, δ) for which ℐ1 exhibits small or negligible harmonic response. The colored areas unfold distinct islands of significant harmonic response. For example, Figure 3(a) reveals significant enhancement of I2 for 1.2≲δ≲1.4 and 10 ≲ α ≲ 70. On the other hand, in the same region Figure 3(d) demonstrates a weak third harmonic response of the irradiated superlattice. The corresponding island of enhanced I₃ is shifted to significantly larger α values. The magnitude of I3 increases approximately from δ=1.2 to δ = 1 and thus obtaining a maximum for a SSL structure with perfectly symmetric interfaces. The width of the islands changes significantly for the higher-order even harmonics as shown in Figure 3(b), (c). However, although the width of the colored islands is increased, the strength of the harmonic content is reduced, by an order of magnitude for I₆ (Figure 3(c)) in comparison with I₂ (Figure 3(a)). The colored areas of the higher-odd harmonics are notably suppressed in the regions where higher-even harmonics are being developed. Therefore, in order to achieve easily detectable odd harmonics the SSL should operate deep inside the NDC region. At this point it is important to highlight that the higher the harmonic order, the larger the input power must be. However, note that arbitrarily increasing the input power is not a solution for high nonlinear output, in contrast with materials described by conventional susceptibilities. There is a complex combination of asymmetry and power values leading to maximum HHG generation. For example, Figure 4 demonstrates the output of higher even-order harmonics (beyond the 2nd harmonic) which drastically drops when the input power is significantly larger. The SSL device after excitation by a strong GHz input signal can generate measurable 8th harmonic up to ∼ 0.02%. The magnitude of the emitted power in unit’s μW is related to harmonic term ℐl as Pl(ν)=Tℐl2(ν) where the coefficient T=Aμ0cL2/(8nr) obtained from the time-averaged Poynting vector by neglecting the waveguide effects. Here μ₀ is the permeability and c is the speed of light by considering both of them in free-space. For typical mesa area A = ((10 × 10) μm², effective path length through the crystal L = 121.4 nm and refractive index n_r = √13 (GaAs), one can obtain T≃77μW. Now it is straightforward to calculate the emitted power corresponding to Figures 2–4. As a consequence, for a value α≃34 close to but below the α_c the emitted power can reach the values P2=0.4 μW and P4=0.01 μW at room temperature for the second and fourth harmonic respectively. These magnitudes indicate that significant gain can appear at second and fourth-order harmonics in the absence of electric domains which might affect the HHG processes when α>αc.

Figure 3:

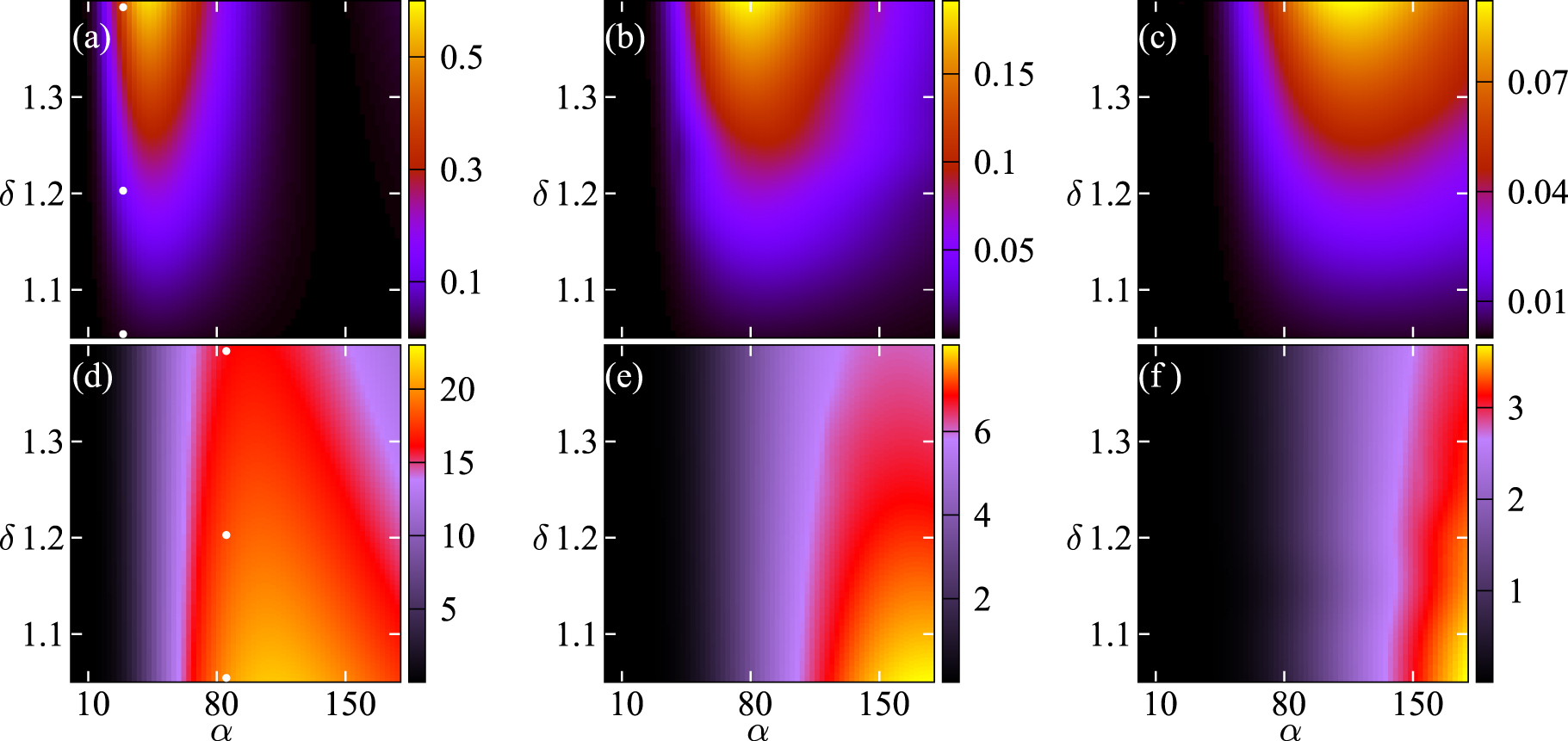
Color maps showing the dependence of the harmonic emission |ℐ(v) |² on the parameter α and asymmetry coefficient δ for (a) l = 2, (b) l = 4, (c) l = 6, (d) l = 3, (e) l = 5 and (f) l = 7 harmonics. The white dots in panels (a) and (d) correspond to the values of α and δ used in the time domain calculations depicted in Figure 6(c) and Figure 6(d) respectively. The color bar is normalized to the peak current j₀. The color maps were calculated using Eqs. (3)–(6).

Figure 4:

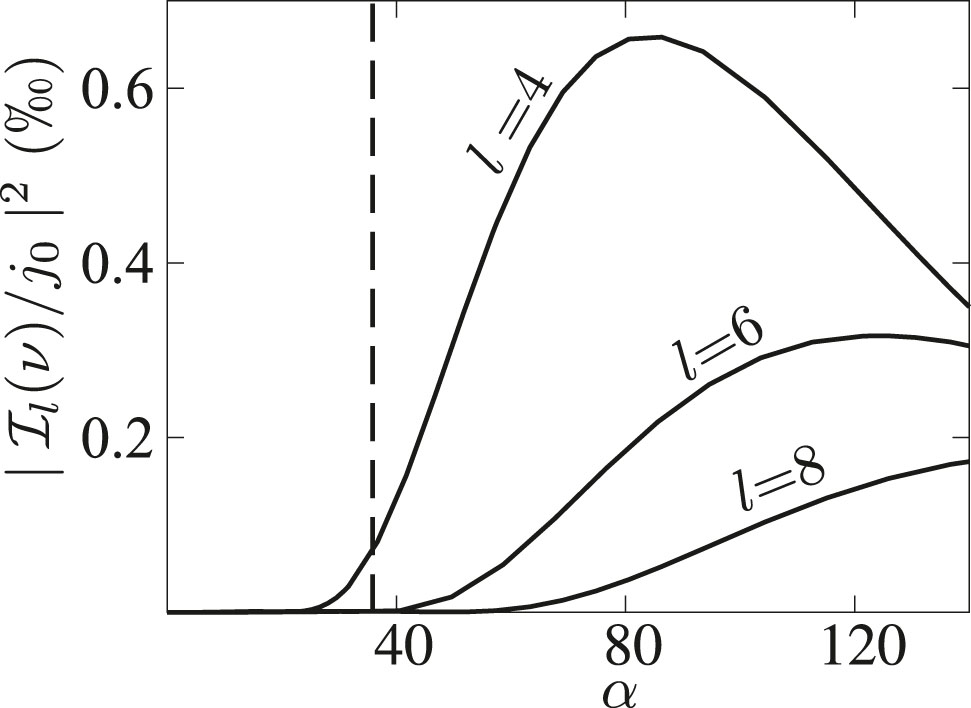
High-order even harmonics as a function of the parameter α. The asymmetry parameter is δ=1.2 and the frequency of the oscillating field is s v = 141 GHz. The dashed curve signifies the critical value α_c for which the SSL can operate in the NDC part of the VI characteristic.

Next, we complement the steady-state analysis with calculations of the time-dependent nonlinear response of the miniband electrons. Our time-dependent solution [see Eq. (3)] can provide further insight in the frequency-conversion of the input signal related to the asymmetric scattering processes. Figure 5 depicts the oscillating field, the nonlinear current oscillations, the second harmonic component and the third harmonic component which occur in the presence of asymmetric scattering rates. The oscillating field E(t) (see Figure 5(a)) causes a time-dependent electron drift with a time dependent current j(t) which contains different harmonic components due to the enhanced nonlinear response as shown in Figure 5(b).

Figure 5:

(Color online) Nolinear response of miniband electrons by considering asymmetric scattering processes. (a) The normalized electric field [E(t)/E_ac] which causes the time dependent drift. (b) The time-dependent current j(t) [see Eq. (3)] is depicted over two cycles of the input field E(t). (c) The second-harmonic j₂(t) and (d) the third-harmonic current oscillations j3(t) calculated for different values of the asymmetry parameter δ=1,1.05,1.2,1.4. The labels (1) and (2) denote relevant relative minimum and maximum points. In all cases, the value of the parameter α ≃ 27 corresponds to an electric field with amplitude E_c = 0.75 Ec and oscillating frequency ν=141 GHz. The arrow marks increasing asymmetry.

Figure 6:

(Color online) Nolinear response of miniband electrons by considering asymmetric scattering processes. (a) The normalized electric field [E(t)/E_ac] which causes the time dependent drift. (b) The time-dependent current j(t) [see Eq. (3)] is depicted over two cycles of the input field E(t). (c) The second-harmonic j₂(t) and (d) the third-harmonic current oscillations j3(t) calculated for different values of the asymmetry parameter δ=1, 1.05, 1.2, 1.4. The labels (1) and (2) denote relevant local minima and maxima. In all cases, the value of the parameter α ≃ 86 corresponds to an electric field with amplitude E_ac = 2.4 Ec and oscillating frequency v = 141 GHz. The arrow marks increasing asymmetry.

Figure 7:

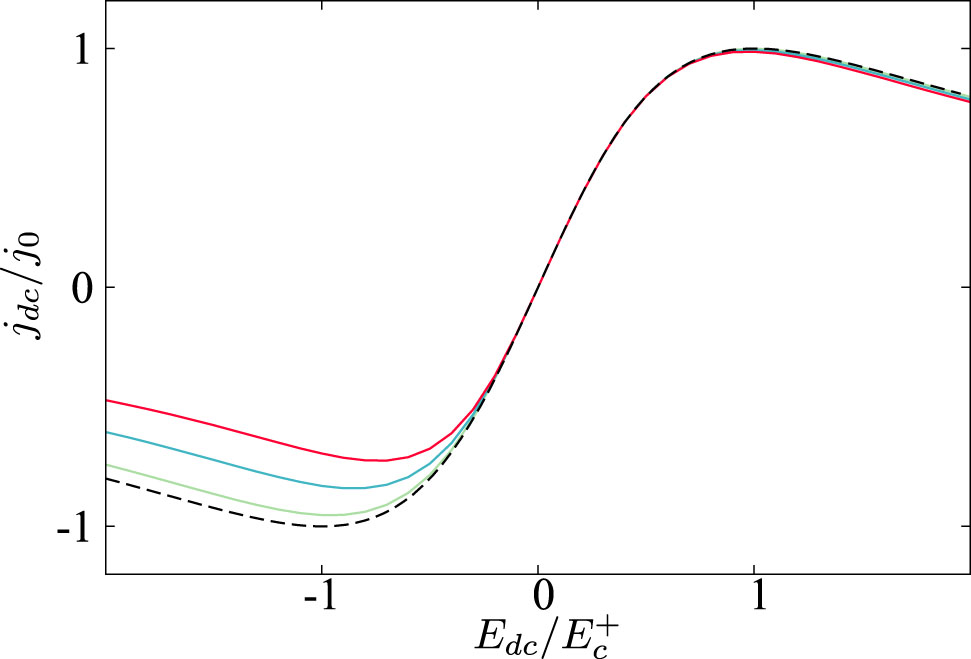
The current-voltage characteristics calculated for different values of the asymmetry parameter, from bottom (dashed) to top δ = 1,1.05,1.2, 1.4. The connection with the relaxation rates reads Γ+=eEc+d and Γ⁻ = Γ⁺/δ. The dashed curve represents the Esaki-Tsu characteristic without taking into account the time relaxation-induced asymmetries, or in other words, δ = 1.

In a perfectly symmetric structure, the irradiation of the superlattice with input radiation leads only to odd-order multiplication and therefore the second harmonic signal j2(t)=j(t)cos(4πνt) (dashed curve in Figure 5(c)) averaged over time is < j₂ >_t = 0. On the contrary, for a higher asymmetry parameter δ (arrowed), the time realization of j2(t) demonstrates oscillations whose amplitude is highly asymmetric. In this case, the the first peak (1) becomes sufficiently smaller than peak (2) resulting in < j₂ >_t different than zero as is evident from Figure 5(c). The third harmonic component in the current is due to the BOHF which stem from the anharmonic motion of the electron within the miniband. Every half-period (T_v/2), j3 contributes a phase of an opposite sign with respect to the temporal evolution of the electric field (see Figure 5(a), (d)). With increasing asymmetry coefficient δ, the amplitude of the arrowed peak is reduced, which leads to suppression of the third harmonic component < j₃ >_t.

For an electric field with sufficiently larger amplitude but with the same oscillating frequency, the current response becomes evidently more anharmonic (see Figure 6(b)). This has important implications for both second and third-order harmonics and serious consequences in the case of increasing the asymmetry parameter δ.

On the one hand, the increase of the asymmetry between the two relaxation rates results in more pronounced differences between the oscillations amplitudes (1), (2) of the second harmonic j₂(t) and their adjacent peaks (Figure 6(c)). Consequently, the second harmonic is suppressed for a larger Eac but still enhanced for a different δ. On the other hand, α parameter being larger than α_c would induce higher quality BOHF and therefore larger third harmonic components (Figure 6(d)). We note though that a larger asymmetry will reduce the emission of j₃ due to the strong suppression of the closely neighboring peaks to the main one.

Before summarizing the main results of this paper, it is noteworthy to highlight further immediate applications of our approach. Evidently the electron energy oscillates within the miniband with frequency at every even multiple of the frequency of the oscillating electric field [see Eq. (3)]. The behavior of effective electron mass, which explicitly depends on energy [66], varies significantly in the presence of highly asymmetric scattering and thus the generated harmonics could be linked to the concept of negative effective mass similar to [67]. Significant production of even harmonics has been previously predicted for an electrically excited SSL due to parametric amplification [68] or other parametric processes [60] which stem from the existence of an internal electric field in the structure. In this respect, it is interesting to study how the parametric processes can affect the harmonic generation [70] or the Bloch gain [69] profile in the presence of asymmetric current flow. Moreover, our approach has a great potential for analyzing the effects of asymmetric scattering processes on the intensity of harmonics by means of externally applied voltages and/or intense ultrafast optical pulses [51], [43]. Finally, the predictions in the present work highlight the prospects for the systematic study of asymmetric effects in different superlattice systems including coupled superlattices in a synchronous state [71] and, even more generally, in other multilayer structures such as high temperature superconductors [72].

4 Conclusions

In summary, the Boltzmann-Bloch approach is used to deliver general, non-perturbative solutions of HHG in SSLs. This method allows us to investigate details of the generation processes in both spectral and time domains. The non-approximative nature of our approach eliminates numerical errors which could cast doubt upon the origin of harmonic generation. Thus, our study conclusively demonstrates striking features of HHG when asymmetric relaxation processes are taken into account in superlattice structures. While these effects are relatively small on the odd harmonic generation, significant features appear at even harmonics leading to measurable effects in the GHz-THz range. Our algorithms have immediate potential to analyze the combination of asymmetric flow with parametric processes, externally applied voltages and ultrafast optical pulses.Future work should focus on investigating thoroughly the conditions for formation of destructive electric domains in SSLs in the case of harmonic generation due to asymmetric scattering processes.