Robust optical physical unclonable function using disordered photonic integrated circuits

1 Main Text

Disorder and entropy are pervasive characteristics of nature and can be harnessed by physical unclonable functions (PUFs) [1], [2], [3], [4], [5] or random number generators [6], [7], to achieve significantly higher levels of hardware and/or information security than conventional methods. Manufacturing process variations are among the most technologically relevant forms of such randomness and are the primary means by which PUFs extract their chip-unique signatures [1], [2], [3], [8], [9], [10]. Recently, classical time-varying PUFs have been applied in secure communications [11] and in schemes obtaining perfect secrecy cryptography [12]. In another highly demanded application, PUFs have emerged as promising security primitives for authentication and identification throughout the untrusted supply chain as illustrated in Figure 1.

Figure 1:

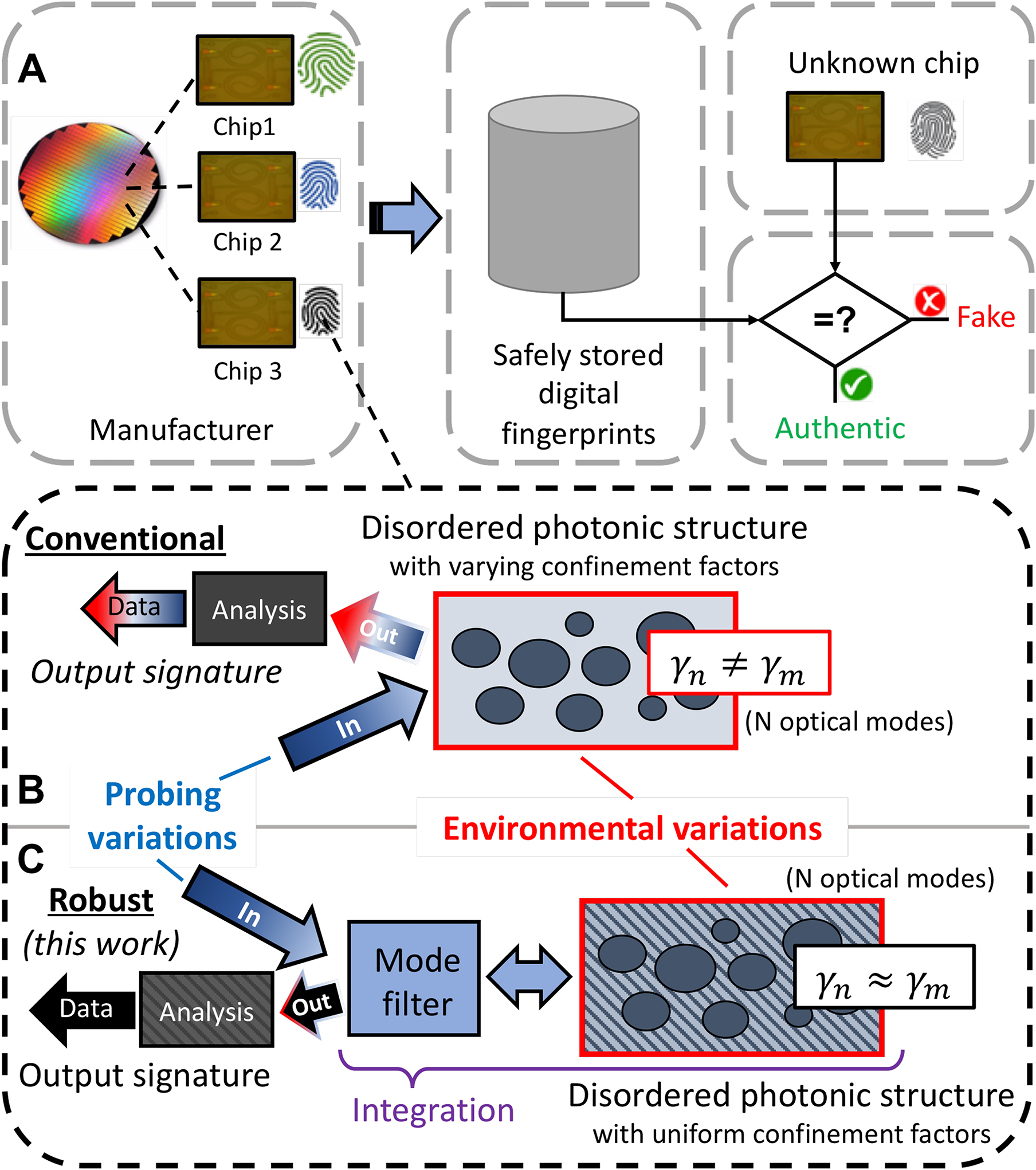
High level overview. (A) A typical PUF authentication scheme, and overview of: (B) a conventional optical PUF, and (C) a robust optical PUF (the type introduced and demonstrated in this work). Here robustness refers to achieving immunity against probing and environmental variations.

Much of the technological progress in PUFs over the last 15 plus years has come in complementary metal oxide semiconductor (CMOS) micro- and nanoelectronics [13], [14], [15], [16], [17]. However, interest in developing PUFs for hardware and information security applications has recently rapidly expanded to almost all areas of physical science including investigations based on chemical methods [18], quantum tunneling [19], disordered nanomaterials [20], [21], [22], magnetic media [23], and even biological species [24]. Attractively, the immense information capacity and rich physics of photonic systems offer the prospect of both passive and active security devices operating in classical and quantum regimes [1], [25], [26]. Moreover, highly complex and distributed multiple-scattering optical systems with high fabrication sensitivities can be very difficult to model or trim. Thus, the question remains open as to whether emerging technology could enable successful physical or machine learning attacks on emerging optical PUFs [27], as has been demonstrated in specific types of non-optical silicon PUFs [28], [29], [30].

In general, a PUF should be close to truly random in nature across different devices (so-called ‘inter-chip’ variation), while operating in a robust manner over a wide range of environmental conditions (so-called ‘intra-chip’ variation). In the optical domain, speckle patterns are famous for their high complexity and uniqueness which arise from underlying photonic disorder, making them well suited for generating strong ‘inter-chip’ variation. However, as illustrated in Figure 1B, speckle phenomena from conventionally disordered photonic devices are notoriously sensitive to probing and environmental variations. Thus optical PUFs realized from laser speckle patterns suffer from high ‘intra-chip’ variation and are generally not robust nor widely considered to be a scalable technology, as they require precisely controlled optical alignment, tilt, polarization, temperature, and stable 2D spatially resolved optical imaging to measure and verify [1], [3], [31]. To realize a robust and scalable PUF technology, it remains imperative to enhance ‘inter-chip’ variation while simultaneously minimizing ‘intra-chip’ variation. Hence, emphasis must be placed on obtaining signatures which are highly visible, easy to measure in scale, computationally efficient to analyze, and robust over a range of measurement and/or environmental conditions.

Confining light in a waveguide on the surface of a chip is an alternative method of probing spatial randomness, and could be performed in a highly integrated fashion without imaging or discrete sampling of arrayed devices, while storing an enormous amount of information in the frequency or impulse response. Along this vein, on-chip photonic PUFs have recently been investigated using chaotic optical micro-resonators [32], [33]. The optical chaos effect relies on extreme sensitivity to initial conditions, which dramatically alters the near field speckle patterns formed from a large number of spatial modes with varying Q/V. However, these modes also generally exhibit variable modal confinement factors γn (matter-light interaction) with the constituent optical media, where the confinement factor may be defined as (see Supplementary Information):

Hence, the various modes may be variably perturbed in frequency according to Δω_n/ω_n = −(Δn/n_g)γ_n, where Δn is the index perturbation and n_g is the group index of the medium subject to perturbation. This renders such devices inherently very sensitive to all conditions, including both fabrication and environmental fluctuations such as temperature variations or non-linear effects [32], [33], [34]. On the other hand, Rayleigh backscatter from single-mode fiber or single-mode waveguide roughness naturally provides very stable and reliable random signatures. By supporting only a single-transverse mode with uniform confinement factor γn, the random frequency response of such devices does not ‘evolve’ but rather is shifted deterministically in response to environmental stimuli such as temperature, strain, or aging [35], [36]. Such backscatter signatures are however inherently very weak (poor visibility), requiring time domain or frequency domain backscatter interferometry to detect, and cannot be applied in transmission. Addressing all of these issues is critical to unlocking the promise of PUF technology and advancing both classical and quantum hardware security. Moreover, as integrated photonics continues to scale and become more intimately intertwined with both CMOS [37] and high volume datacom applications [38], powerful new opportunities arise, such as the prospect for photonic security systems-on-a-chip or optical hardware enabled encryption of communication links.

Here we introduce and demonstrate a robust optical PUF constructed from silicon photonic circuitry which can readily be interrogated from industry standard wafer-scale fiber-optic probing and yields random, highly visible, and unclonable signatures with distinct features that are immune to probing and environmental variations. The robustness of our high level approach, illustrated in Figure 1C, is realized through the combination of several unique aspects. First, co-integration of a mode-filter and disordered photonic structure is employed to suppress the effect of probing variations. Secondly, we developed a photonic design which achieves very high sensitivity toward ‘weak’ perturbations (see Section 2); and in the photonic design all modes exhibit approximately the same confinement factor in silicon (γn≈γm). This preserves the PUF’s complex and non-deterministic signature in response to environmental thermo-optic variations as all spectral features shift together according to Δωn/ωn=−(Δn/ng)γn, where Δn is the thermo-optic index change and n_g is the group index of silicon (see Supplementary Information for additional detail). Lastly we demonstrate application of feature extraction using wavelet analysis [39], [40], to enable efficient and robust device authentication and identification. We also carry out conventional Hamming distance authentication of our PUFs in different settings and contrast our device with the random signatures of clonable (insecure) device designs manufactured in the same process.

2 Approach

Our integrated silicon photonic PUF is depicted in Figure 2. Unlike free-space or multimode waveguide/fiber optical PUFs [1], [3], [31], our PUFs interface with disorder in a stable fashion (i.e. Figure 1C) through a co-integrated mode filter consisting of TE polarization grating couplers [41] and single-mode waveguides [42]. This design guarantees robust modal selectivity [43] and immunizes the devices against variations in polarization and spatial/angular alignment. The rest of the design is motivated to amplify the device’s sensitivity to ‘weak’ disorder, while simultaneously suppressing the effect of environmental variations on device unique features. Here, we accomplish this through the introduction of a quasicrystal interferometer (QCI) with a weakly modulated index profile in a Michelson type configuration. Our QCI importantly breaks the translational symmetries exhibited in standard silicon photonic circuitry by using a 1D multi-periodic Moiré patterned grating with a slowly varying and non-uniform radius of curvature. This offers access to the unique physics and analyticity breaking offered by quasicrystals and 1D Aubry–André systems, including their distinct characteristics in response to disorder [44], [45], [46], [47], [48]. The weak index modulation meanwhile, ensures approximately constant or slowly varying confinement factor in silicon for all modes.

Figure 2:

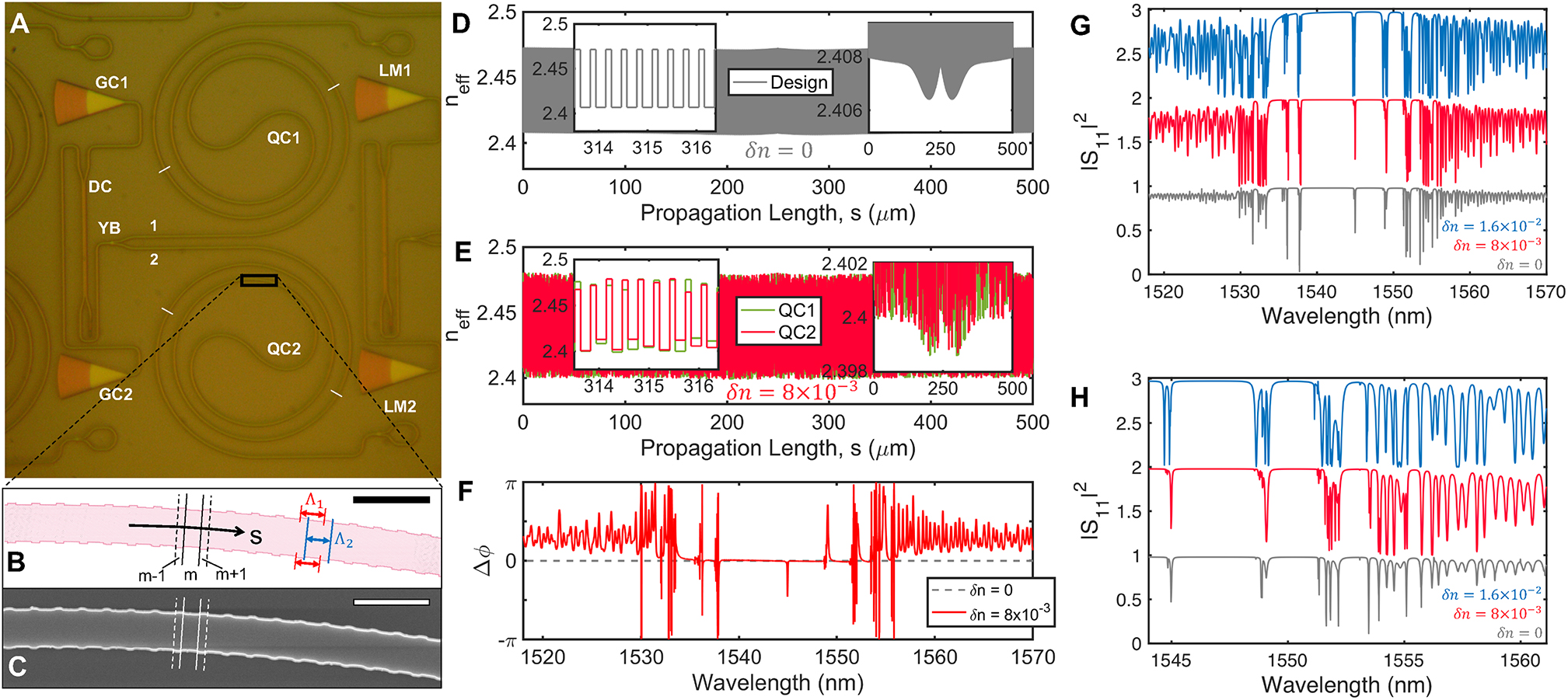
Overview of photonic circuitry and quasicrystal interferometry. (A) Optical microscope image of the integrated silicon photonic QCI PUF architecture. Input/output grating couplers (GC1/GC2), single mode waveguides, and a 50:50 directional coupler (DC) enable pure mode filtering and stable QCI device measurement in transmission. A compact y-branch (YB) splits light into two symmetric arms, (1) and (2), routed to the spiral quasicrystal (QC) arms and loop mirrors (LM1/LM2). (B) Zoomed view of design and (C) SEM image of the curved QC and illustration of the mth segment considered in device modelling (scale bar = 1 μm). (D) Nominal QC effective index profile @ 1550 nm. (E) Example effective index profiles with random errors introduced, and (F) corresponding phase differences between the two arms. (G) Simulated QCI spectra (YB port reflectance) for nominal and random QCIs with varying disorder parameters, and (H) zoomed view of the same.

In our devices, fabrication variations are assumed to primarily stem from local nanoscale variations in waveguide width and surface roughness. To capture the effect of these variations with high sensitivity and visibility, and to not allow them to average out into very few parameters (as in a simple interferometer) or manifest as an ultimately very weak signal (as in waveguide Rayleigh backscatter), it is desirable to create a structure which supports multiple-scattering through the use of many discrete waveguide segments. However, the arrangement of the segments should not have perfect translational symmetry as in a crystal or distributed Bragg reflector (DBR). The properties of a DBR are generally very robust against weak perturbations such as nanoscale disorder owing to destructive interference, with only two narrow windows of enhanced sensitivity near the band edges. The use of linear DBRs instead of our spiral QCs would effectively make the device function like a symmetric single etalon Michaelson Gires–Tournois interferometer (MGTI) [49]. Further, locally breaking the translational symmetry of a DBR in a limited number of locations would effectively yield photonic crystal cavities which only probe disorder in those discrete locations, thus severely limiting the device complexity. Thus, we observe that the use of a QC which entirely lacks translational symmetry (aside from allowed rotational symmetries), naturally arises as a powerful solution to sensitively probing spatially distributed fabrication variations while fostering enhanced complexity.

The arms our QCI PUF consist of width modulated (500 nm ± 20 nm) single mode Si waveguides with nominal device thickness 220 nm cladded by SiO₂. The QCs each utilize a slowly varying radius of curvature spiral (R ≈ 50–25 μm), containing 500 µm long multi-periodic Moiré patterned gratings formed by the superposition of gratings with periods Λ₁ = 316 nm and Λ₂ = 317 nm. Grating teeth (i.e. width equal to 520 nm) are placed at the intersection of Λ₁ and Λ₂ gratings by performing a Boolean AND function. When considered as a standalone component without disorder, the 1D QC forms longitudinal modes as a result of several effects, which are all related to breaking translational symmetry: (i) the low frequency band edge of the Λ₁ grating forms a defect region within the overlapped band gap of the Λ₂ grating, (ii) the high frequency band edge of the Λ₂ grating forms a defect region within the overlapped band gap of the Λ₁ grating, and (iii) additional defect modes are introduced owing to the weak gradual reduction of waveguide effective index with reducing radius of curvature [50]. The output of the QCs are routed to loop mirror (LM)s which offer broadband reflectivity and supports the formation of higher order resonances owing to multi-pass effects. The initial onset of disorder is expected to introduce unique extended states fostering slow-light and resonantly enhanced transmission through the QC in the vicinity of the overlapping fundamental band gaps, while increasing disorder strength should foster the introduction of random localized states and optical resonances exhibiting unique spatial and spectral characteristics. In principle, the exact device design that is used can be flexible, but should ideally provide the following traits: (i) offer high complexity and require numerical methods to model even qualitatively, (ii) support the presence and formation of many spectrally and spatially isolated resonances, (iii) support regions of slow-light effects or high dispersion, (iv) be realized in a regime where fabrication variations constitute a non-negligible fraction of the critical dimensions, and (v) be comprised entirely of weakly modulated single transverse mode waveguides with approximately uniform confinement factors.

The predicted characteristics for QCIs with varying disorder, δn≥0 are shown in Figure 2D–H. The designed width and radius of curvature modulation of the spiral quasicrystal arms yields a nominal effective index profile vs. propagation length (Figure 2D) which is then locally and randomly distorted owing to spatially distributed fabrication variations (i.e. Figure 2E). To model the potential effect of such fabrication variations (see Section 5 and Supplementary Information S2) we apply a uniformly distributed random error of no more than ±5 nm in waveguide width, corresponding to a maximum effective index error in any segment of δn=8×10−3. These random fabrication variations are usually interpreted as ‘weak’ perturbations in the context of waveguide or photonic crystal backscatter [51], and are indeed weak in the sense that they do not significantly perturb the transverse optical confinement factor in silicon. However, in our device where the effective index modulation is intentionally small, Δn≈6.5×10−2, and where there is a lack of perfect translational symmetry, these ‘weak’ perturbations contribute significant disorder (i.e. >10% the effective index modulation of the unperturbed grating), both randomly perturbing existing states and introducing random extended and localized states into the spiral quasicrystal. This yields a highly complex and spectrally randomized phase difference between the arms (Figure 2F) which can be converted into highly visible spectral fingerprints (Figure 2G,H) using the Michelson configuration.

In a balanced and lossless interferometer with no phase errors, the reflection spectrum detected from the y-branch should theoretically measure as 100% across the entire spectrum. In our devices however, the waveguides have a finite propagation loss (∼2.4 dB/cm) owing to sidewall roughness and bend loss, as well as passive insertion loss at the interfaces to/from the quasicrystals and loop-mirror y-branches. This loss is significantly enhanced in regions of optical resonance or band edges, becoming a form of coherent perfect loss when critically coupled to quasicrystal or higher order etalon modes [52], [53], and provides distinct features in the spectrum even for a perfectly symmetric and balanced QCI with no disorder, δn=0. In effect, our QCI exploits randomization in both the amplitude and phase degrees of freedom to generate its unique signatures, while our photonic circuitry specifically constrains the transverse spatial-mode and polarization degrees of freedom to foster robustness.

Regarding environmental stability, it should be emphasized that thermo-optic stimuli can easily perturb a mode frequency ωn by a magnitude |Δωn| much larger than its full-width half maximum and much larger than the nearest mode to mode frequency spacing – i.e. in general it is likely that in practice |Δωn|≫ωfwhm,n and |Δωn|≫|ωn±1−ωn|. If an optical device has many resonant modes contributing features to its spectrum, then the optical spectrum will ‘evolve’ or be reconfigured to generate a different spectral fingerprint if the modal confinement factor in the thermo-optic medium, γn is not a uniform or very slowly varying function of the mode frequency ωn. This can lead to extreme sensitivities to temperature, for example in certain multi-mode speckle devices where 50% decorrelation in the output speckle pattern has been observed in response to temperature variations of 0.16 °C [54]. Unlike chaotic microcavity PUFs [32], [33], multi-mode speckle devices [31], [54], or strongly disordered photonic systems considered in other applications [44], [55], [56], all of the modes in the QCI are engineered to exhibit nearly the exact same confinement factor in silicon via the single transverse mode that is supported and narrow ±20 nm waveguide width modulation that is utilized. This unique design ensures that thermo-optic effects fractionally perturb the frequency of all modes equally; thereby suppressing the effect of intra-chip variations and preserving the output device signature across temperature (see Supplementary Information S3/S5 for further detail).

3 Results/Discussion

To experimentally demonstrate our devices, both QCI PUFs and single etalon DBR integrated MGTI reference devices were fabricated in a standard 220 nm device layer SOI platform (see Section 5). Devices were then measured with a tunable laser under TE polarization using the fiber-to-chip grating couplers as illustrated in Figure 2A. The double pass insertion loss of the directional coupler used to probe the QCI sets the minimum on-chip insertion loss to ∼6 dB, rendering the devices easy to measure and align to in an automated testing environment, while the single mode waveguides and single polarization grating couplers render the devices immune to errors in spatial or angular alignment and polarization. To assess the impact of thermal/environmental variation, devices were measured at two temperature settings: setting 1) 23 °C, and setting 2) 30 °C (settings were measured ∼48 h apart from one another). The +7 °C temperature variation mimics the effect of a significant temperature drift which is expected to shift the wavelength for most of the PUF’s spectral features by significantly more than their 3 dB linewidth.

Figure 3A,C shows the measured spectra of three triplicated integrated QCI PUFs (e.g. Figure 2), fabricated in the same process and located next to each other on the same die. The designs of the triplicate structures are all exactly the same with no modifications. However, their optical spectra are entirely unique, effectively serving as a fingerprint for each device. The devices exhibit excellent visibility in grating-coupled transmission, with extinction ratios well in the ∼5–30 dB range.

Figure 3:

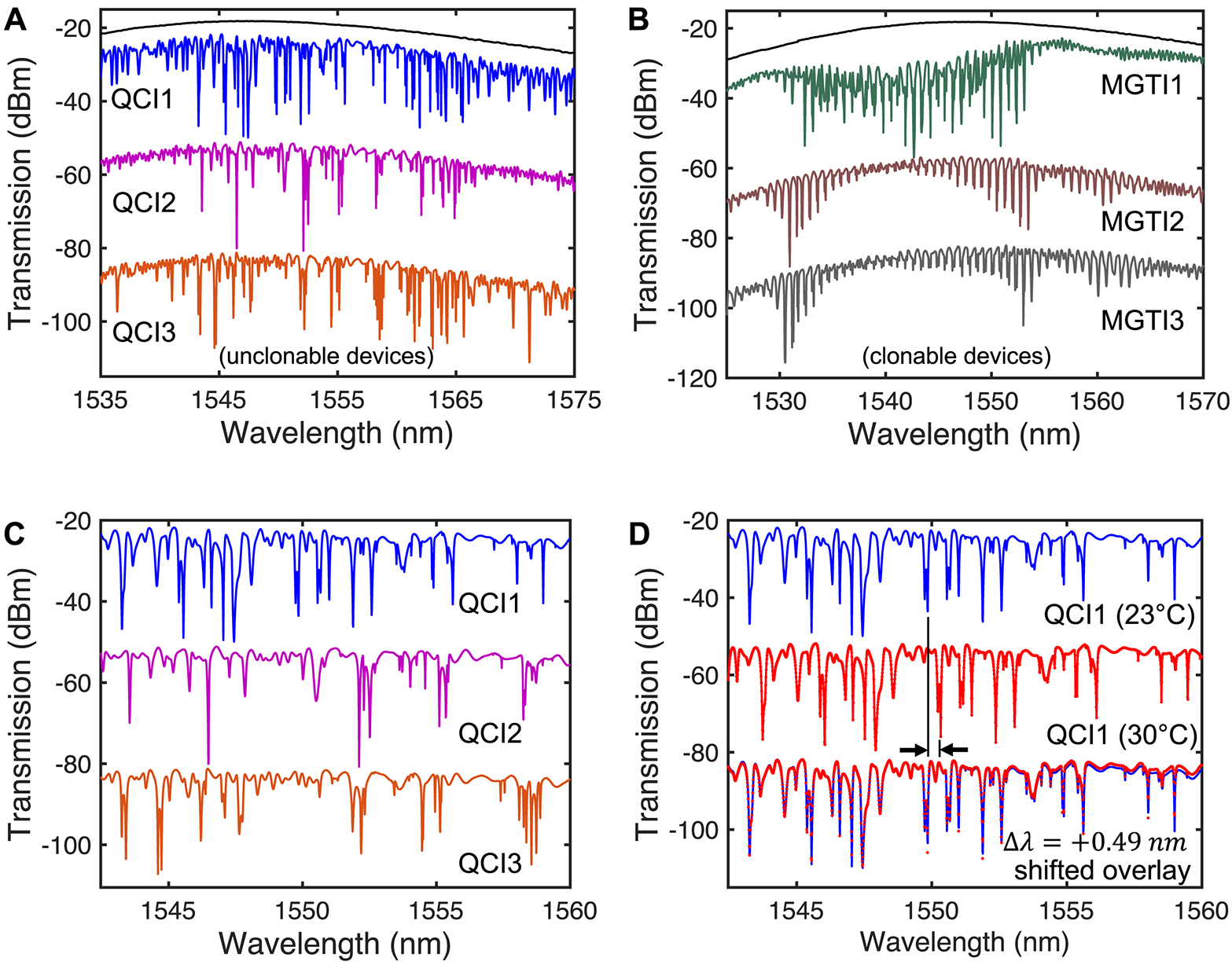
Experimental transmission spectra for triplicated silicon photonic (A) QCI PUFs, and (B) single etalon DBR integrated MGTIs. Black curve corresponds to single pass directional coupler (DC) transmission. Probing of QCIs and MGTIs adds ∼3 dB insertion loss owing to double pass loss through the DC. Device 2/3 spectra are shifted on the y-axis for clarity (C) Zoomed view of QCI PUF spectra showing device uniqueness. (D) Zoomed view of QCI1 spectra at both temperature settings, revealing a deterministic spectral shift.

In the same fabrication run, we also included triplicated single etalon MGTI designs wherein the spiral quasicrystals were replaced with a waveguide delay and simple DBR structure. The DBR length was ∼23 μm with a sidewall grating width modulation of 500 ± 80 nm. The waveguide path length from the y-branch (YB) to the DBR was ∼280 μm and from the DBR to the LM was ∼340 μm. Although the MGTI spectra are ‘randomized’ by fabrication induced phase errors, as visible by the difference in device-to-device spectrum variations from Figure 3B, the device spectra are not unclonable. In the single etalon MGTI devices, an analytical description and exact parameter fit of the device properties could be achieved since the distributed fabrication variations are simply averaged into very few device parameters (i.e. Two values of DBR kappa-L, and four values of optical path lengths, effective/group indices, and optical losses). Over many process runs or iterations, the likelihood of repeating the same MGTI device signature twice (i.e. cloning) becomes very significant despite the randomness imparted into each device. In the QCI PUF device however, the distributed fabrication variations are locally captured in each unique segment of the 1D multiple-scattering waveguide which exponentially increases the device complexity and exponentially suppresses the probability of cloning.

Assuming fabrication errors in a given segment could be simply discretized to five values (i.e. width deviation of ±5 nm in increments of 2.5 nm), the number of device permutations in an MGTI structure with four segments is only on the order of 54≈102.8, whereas our finite length QCI device has >6000 multiple-scattering segments resulting in more than 56000≈104193 possible unique physical device permutations. Hence, despite being qualitatively similar types of devices at an architectural level, the MGTI and QCI are exponentially different in terms of complexity.

Figure 3D shows the transmission spectrum for an integrated QCI PUF measured at both temperature settings. All features in the spectral fingerprint of the device near 1550 nm are shifted in wavelength by Δλ≈+0.49 nm, in excellent agreement with the predicted thermo-optic sensitivity of the single-transverse mode silicon waveguides. This provides an experimental measurement of the confinement factor in silicon, determined to be ∼0.884, and confirms that all modes of the QCI exhibit approximately the same confinement factor. Crucially, this provides evidence that the non-deterministic inter-chip characteristics are preserved and deterministically perturbed by temperature, as desired (also see Supplementary Information S3). Simulations suggest this deterministic spectral response to temperature can be sustained for even larger temperature variations ΔT=±30°C (Supplementary Information S5). However, if the modal confinement factors were not uniform, then randomized features corresponding to different modes would shift with different thermo-optic sensitivities and the spectrum would dynamically evolve in an unpredictable fashion, rather than simply shifting in response to temperature.

As shown in Figure 4, we first performed Hamming distance authentication analysis on the three QCI PUFs. In this computation, each raw spectrum is normalized to the directional coupler reference spectra and then converted to a binary sequence with >10,000 bits. A central subset of 8000 bits is then enrolled and computationally shifted relative to various test keys, at both temperature settings, to search for a match (i.e., Hamming distance <0.3), which is a strong indication of the authenticity. The results confirm the uniqueness of each PUF and validate authentication of each device at both temperature settings.

Figure 4:

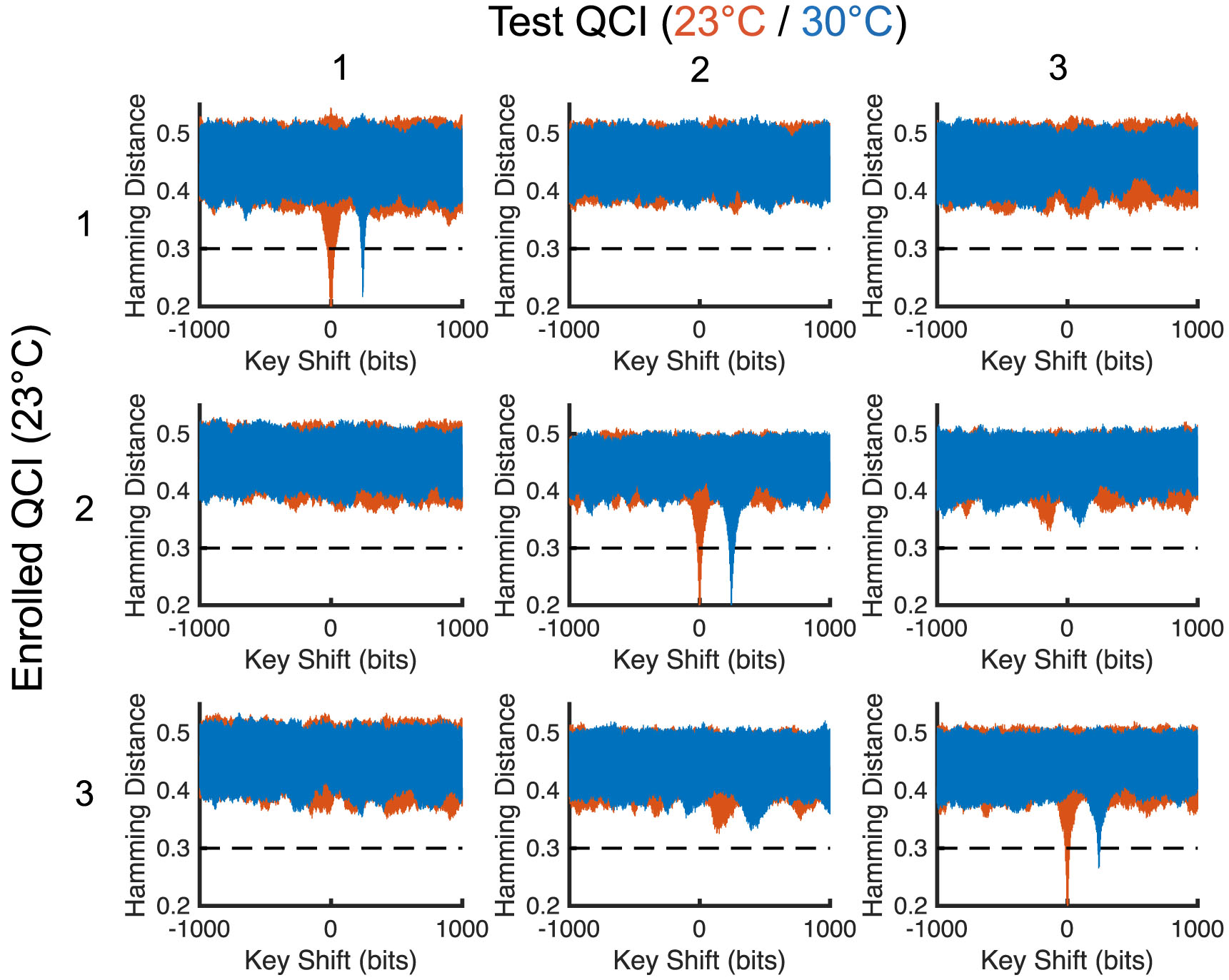
Hamming distance authentication analysis for each silicon photonic QSI PUF at two temperature settings.

In general, directly using the raw output signals of the PUFs for authentication or identification is neither efficient nor robust. To this end, an entropy-harvesting method that can extract chip-unique features will significantly improve the overall performance and functionality of the proposed PUFs and enable scalable identification with large device libraries. The entropy of the spectra of the PUFs generally comes from two sources: inter-chip and intra-chip variations. Inter-chip variations are the intrinsic variations introduced during the fabrication, while intra-chip variations are caused by environmental changes or device aging [9], [57], [58]. Thus, in order to enhance both the uniqueness and reliability of the PUF signature, an ideal entropy-harvesting method should be able to leverage manufacturing process variations, while mitigating intra-chip variations [9], [57], [58], [59], [60]. This includes mitigating any residual probing and/or environmental variations in the grating coupler’s low frequency spectral envelope (Figure 3A) or the PUF’s spectral fingerprint. In our experiments, we applied two types of techniques, i.e., feature extraction and correlation analysis, to illustrate the effectiveness of our integrated photonic PUFs.

For the feature extraction method, we use wavelets to decompose the signal. Figure 5 shows an example of the wavelet decomposition of the raw output signal, s, for QCI1 along with part of the first level of decomposition for all three devices. The best results are observed when we use five-level decompositions (e. g. d₅, d₄, d₃, d₂, d₁) with Fejer–Korovkin, Symlet, Reverse Biorthogonal wavelets [61] (see Supplementary Information S4). The standard deviation and variance of corresponding sub-bands are then chosen as features. It can be clearly seen from both Figure 5 and Table 1, which illustrates the Fejer–Korovkin derived features, that different devices yield distinct features. As indicated in Table 1, it is observed that the features of the QCI PUFs are stable, since the intra-chip variation is significantly less than the inter-chip variation.

Figure 5:

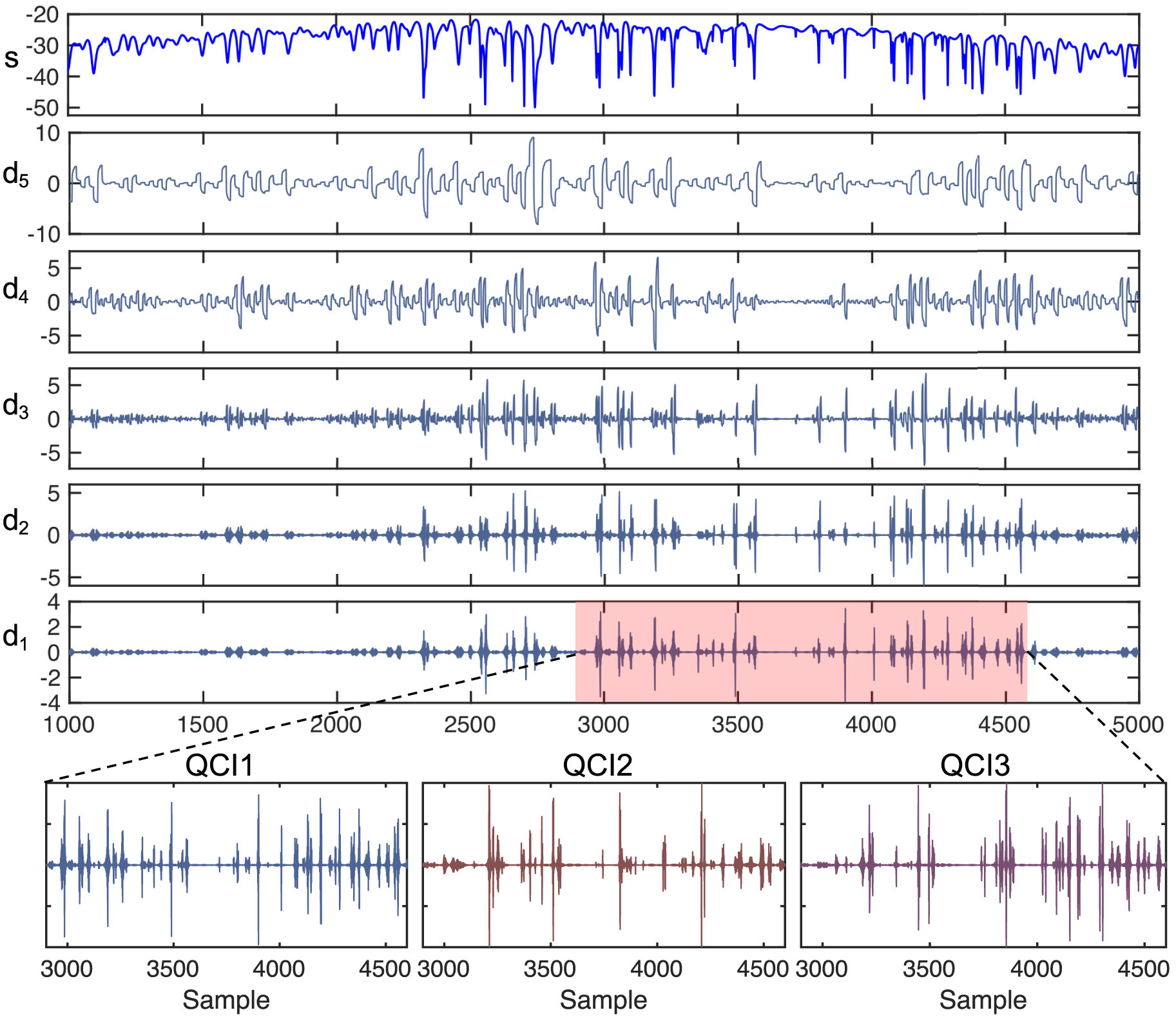
Five-level decomposition of an output signal analyzed by Fejer–Korovkin wavelets. After decomposition, the devices can be distinguished effectively.

Device identification can be performed by enrolling the device under test’s features and carrying out an error analysis to identify the device features which yield the lowest mean squared error. Identification can be further strengthened by verifying agreement across different decompositions or complementary techniques such as a power spectral density derived signal correlation. Results for device identification are displayed in Table 2. Correct identification of our QCI PUFs are achieved in all cases, regardless of temperature setting, allowing us to conclude that each PUF will be distinguishable across temperature. For the clonable MGTI devices however, the features are not sufficiently unique and hence different wavelet decompositions mis-identify the enrolled device.

4 Conclusion

In this work, we introduced and demonstrated photonic circuitry employing single mode TE polarization mode filtering alongside a weakly modulated QCI as a means for realizing a robust PUF. Similar to the original vision of the first optical scattering PUFs, our device probes spatially distributed randomness but realizes it in a highly integrated fashion which is designed to be inherently stable against probing and environmental variations. By comparing our QCI to less complex interferometers, we also experimentally highlighted how randomness is a necessary but not sufficient criterion to achieve unclonable device signatures. We further demonstrated feature extraction as a viable means for optical PUF identification. Since the main source of inter-chip variations are in waveguide width and surface roughness, by precisely analyzing each signal segment within a specific ‘frequency’ domain, and confined ‘time’ domain, it is ensured that these variations are captured during feature extraction and that the most unique features are chosen for the proposed PUFs. Unlike highly multi-mode devices based on chaos, which are extremely sensitive to all conditions, or single-mode optical backscatter which is environmentally stable but extremely weak, the signatures of our device are highly visible, random, and environmentally stable. As a result, our PUF architecture is fully compatible with automated Wafer-scale measurement techniques and fosters scalable implementation within silicon photonic transceivers or photonic systems on a chip as an optical hardware security layer. This work also unveils a new means for amplifying and harnessing the effects of ‘weak’ disorder in photonics – while simultaneously harnessing or constraining specific degrees of freedom – and highlights a viable technological application of quasicrystals and Anderson localized and extended states. Applying the principles of degree of freedom constraints, modal selectivity, and confinement factor control principles, could support the realization of a new generation of disordered photonic systems. In the future, we envision opportunities to further enhance and utilize the functionality of integrated photonic PUFs by leveraging active devices, reconfigurability, multiplexing, far-field signaling, or quantum optics to realize entirely new levels of hardware and information security.

5 Methods