Startseite Mathematik Novel weighted distribution: Properties, applications and web-tool
Artikel Open Access

Novel weighted distribution: Properties, applications and web-tool

  • Emrah Altun EMAIL logo und Christophe Chesneau
Veröffentlicht/Copyright: 12. Dezember 2025
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Informationen für Autor*innen Erkunden Sie dieses Fachgebiet
Mathematica Slovaca
Aus der Zeitschrift Mathematica Slovaca Band 75 Heft 6

Abstract

Weighted distributions play an important role in reliability and engineering. This research contributes to the topic by presenting a novel flexible two-parameter weighted distribution characterized by extensive statistical properties. Various parameter estimation methods are also thoroughly investigated. Their effectiveness is validated by complete simulation studies. Within the framework of generalized linear models, a regression model is established for positively defined response variables. Two data sets are examined to emphasize the importance of the proposed model. In addition, the WBreg tool is presented to facilitate its use by researchers. WBreg is available “free of charge” at https://beststat.shinyapps.io/WB2reg.

Keywords: Weighted distributions; different estimation methods; simulation; regression; software
MSC 2010: Primary 62E15

1 Introduction

Weighted distributions play an important role in several applied fields, including ecology, reliability and biology. In [20], weighted distributions to human populations and wildlife management were applied. In [17], the importance of weighted distributions in reliability and life testing was studied. In [19], the utility of weighted distributions in ecology, particularly in the context of resource selection probabilities, was demonstrated. The general definition of a weighted distribution is based on a probability density function (pdf) of the following form:

(1.1) fweighted(x)=Dw(x)f(x),

where D is the normalization constant, w(x) is the weighting function and f(x) is a given pdf, usually from a known baseline distribution. Note that when w (x) = x, the resulting distribution is called a length-biased distribution [15]. Several weighted distributions have been proposed using the mathematical equation in (1.1), such as the weighted Lomax distribution by [3], the weighted Lindley distribution by [15], the weighted gamma distribution by [18], the weighted Weibull distribution by [12], and the weighted xgamma distribution by [23].

For the purposes of this research, we need to introduce a remarkable distribution known as the Bilal (B) distribution. First proposed by [1], it has emerged as a direct competitor to the exponential and Lindley distributions. Since then, the B distribution has received a lot of attention from researchers. [7] introduced the log-Bilal distribution and developed its regression model for bounded response variables in the interval (0, 1). [8] obtained a new one-parameter discrete distribution derived from the B distribution. [6] introduced a new mixed Poisson distribution by using the B distribution as a mixture distribution. A generalization of the B distribution was proposed by [2]. [22] introduced the power B distribution and applied it to some COVID-19 data. This literature review shows that the B distribution has been extensively studied by researchers and remains of modern interest.

In this research, we introduce the weighted Bilal (WB) distribution following the results of [15]. A size-biased version of the B distribution has been studied by [5]. Their work introduces an order value, t, which is taken to be a fixed value. More precisely, [5] studied the special cases of the size-biased B distribution, such as the length-biased B distribution for t = 1 and the area-biased B distribution for t = 2. The resulting distributions thus have one parameter. However, we believe that significant flexibility can be gained by considering the parameter t as a variable. We therefore consider a one-parameter weighting function to obtain a more flexible distribution. The proposed WB distribution has a simple form and tractable properties. We study its mathematical properties in detail. The parameter estimation process is carried out using three approaches, and simulation studies are given for each approach. The WB regression model is defined using the generalized linear models approach. The parameter estimation process and residual analysis of the WB regression model are also discussed. The model is tested on life expectancy data and the results are interpreted. In addition, a cloud-based software called WBreg is developed in the R Shiny environment. The aim is to ensure widespread use of the model developed.

The research is organized as follows: The second section provides an in-depth examination of the statistical properties associated with the WB model. The third section outlines the various methods employed for parameter estimation. The fourth section compares these techniques with the results of a simulation study. Section five defines a new regression model based on the WB model, discussing both parameter estimation and residual analysis for this model. Section six presents two applications and introduces WBreg, the software developed for the WB model. The seventh section concludes by summarizing the main findings of the research.

2 Weighted Bilal distribution

2.1 Presentation

We start with the presentation of the WB distribution, which leads to a recall on the B distribution. The pdf and cumulative distribution function (cdf) of the B distribution are, respectively,

(2.1) f(x;θ)= 6θexp(−2xθ)(1−exp(−xθ)),
(2.2) F(x;θ)= 1−exp(−2xθ)(3−2exp(−xθ)),

where x > 0 and θ > 0. Using the idea of [15], we propose the WB distribution with one extra shape parameter. It is therefore defined as

(2.3) f(x;α,θ)=Cxα−1f0(x;θ),

where f0(x; θ) is the pdf of the B distribution in (2.1), C refers to the normalization constant, and α > 0. Using the definition in (2.3) and after computing C, the pdf of the WB distribution is

(2.4) f(x;α,θ)=6αθ−αxα−1exp−2xθ1−exp−xθ3α−2αΓα,

where x > 0, θ > 0, α > 0 and Γ (·) is the standard gamma function. After integrating this pdf, the cdf of the WB distribution is as follows:

(2.5) F(x;α,θ)=2αγα,3xθ−3αγα,2xθΓα2α−3α,

where γ⋅,⋅ is the standard incomplete gamma function. Note that, for α = 1, the WB distribution reduces to the B distribution. The pdf and cdf plots of the WB distribution are displayed in Figure 1. From this figure, it is clear that the WB distribution has right-skewed shapes.

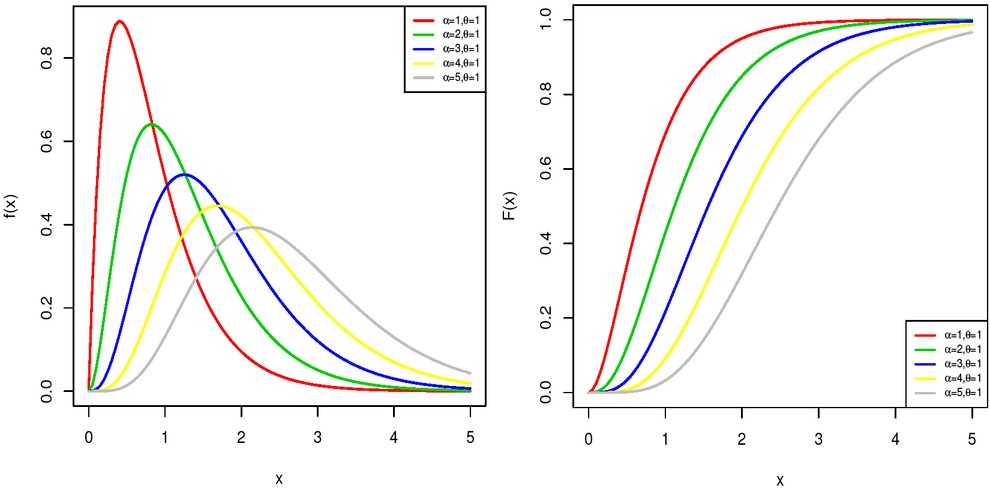
Figure 1 The pdf and cdf plots of the WB distribution.
Figure 1

The pdf and cdf plots of the WB distribution.

2.2 Properties

Some of the properties of the WB distribution can be derived from the work in [5]. In this subsection, we only highlight or develop those that are determinant or new.

Important functions are the survival and hazard rate functions of the WB distribution, given, respectively, by

(2.6) S(x;α,θ)=1−2αγα,3xθ−3αγα,2xθΓα2α−3α,
(2.7) h(x;α,θ)=6αθ−αxα−1exp−2xθexp−xθ−1Γα2α−3α−2αγα,3xθ+3αγα,2xθ.

The behaviour of the pdf at x = 0 and x → ∞ can be investigated. When x → ∞, by the decreasingness properties of the exponential function that dominate the power weighting function, we get f (x) → 0. When x → 0, since

1−exp−xθ∼xθ

and α > 0, we have f (x) → 0.

As a new structural remark, the pdf of the WB distribution can be re-defined as follows:

(2.8) f(x;α,θ)=6αθ−αxα−1exp−2xθ3α−2αΓα−6αθ−αxα−1exp−3xθ3α−2αΓα.

We recognize a mixture representation of two pdfs associated with the standard gamma distribution, that is

(2.9) f(x;α,θ)=wf1(x;α,θ)+1−wf2(x;α,θ),

where w = 3α/(3α – 2α), f1(x; α, θ) and f2(x; α, θ) are the pdfs associated with the distributions Gamma(shape = α, scale = θ/2) and Gamma (shape = α, scale = θ/3). Obviously, most of the statistical properties of the WB distribution can be obtained using the mixture representation.

The proposition below deals with the expression of the raw moments associated with the WB distribution.

Proposition 1

The rth raw moment of a random variable X with the WB distribution is

(2.10) EXr=θrΓα+r2α+r−3α+r6rΓα2α−3α.

For ease of reading, the proof of this proposition and the results to be obtained are postponed to the appendix.

Thanks to Proposition 1, the mean and variance associated with the WB distribution are

(2.11) E(X)=αθ2α+1−3α+132α+1−23α+1,
(2.12) Var(X)=αθ232α+2+22α+2−6α13+α362α−3α2.

In a sense, the proposition below completes Proposition 1; it determines the moment generating function associated with the WB distribution.

Proposition 2

The moment generating function associated with the WB distribution is

(2.13) Mt=3α3α−2α(1−θt2)−α−2α3α−2α(1−θt3)−α.

Similarly, the characteristic function associated with the WB distribution is given in the proposition below.

Proposition 3

The characteristic function associated with the WB distribution is

(2.14) φt=3α3α−2α1−θit2−α−2α3α−2α1−θit3−α.

To conclude this analysis, we present the mode of the WB distribution for the case α ≥ 1.

Proposition 4

For α ≥ 1, the mode of the WB distribution is given by

(2.15) mode=θα−13α+1−2α+163α−2α.

3 Estimation

We now develop the parametric estimation in the context of the WB distribution, namely, the maximum likelihood estimation (MLE), the least squares estimation (LSE) and the weighted LSE (WLSE).

3.1 Maximum likelihood

Assume that x1, x2, . . . , xn is a random sample from the WB distribution. In the setting of the MLE, based on the pdf in (2.4), the associated log-likelihood function is

ℓα,θ= nαlog6−nαlogθ−α−1∑i=1nlogxi−2nxˉθ+∑i=1nlog1−exp−xiθ−nlog3α−2α−nlogΓα,

where xˉ=1n∑i=1nxi. By calculating the partial derivatives of this function with respect to the parameters α and θ, we have

(3.1) ∂ℓ∂α=nlog6−nlogθ−∑i=1nlogxi−n3αlog3−2αlog23α−2α−nψα,
(3.2) ∂ℓ∂θ=−nαθ+2nxˉθ2+∑i=1nxiθ21−expxi/θ,

where ψ⋅ is the digamma function. The MLEs of the parameters can be obtained by solving these score vectors simultaneously. However, explicit estimates for α and θ cannot be derived due to the presence of non-linear functions within the score vectors. Consequently, the maximization of the log-likelihood function must be performed using software tools. In this context, we use the optim function in R. The observed information matrix (OIM) is

Iα,θ=−IααIαθIθαIθθαˆ,θˆ,

where

(3.3) Iαα=∂2ℓ∂α2=6αnlog(3/2)23α−2α2−nψ(1)(α),
(3.4) Iαθ=Iθα=∂2ℓ∂α∂θ=−nθ,
(3.5) Iθθ=∂2ℓ∂θ2=nαθ2−4nxˉθ3−∑i=1nxi2αθ+expxi/θxi−2θθ41−expxi/θ2,

where ψ1⋅ is the first derivative of the digamma function. The diagonal elements of I–1(α, θ), when squared, give the standard errors associated with αˆandθˆ. Thus, the confidence intervals for the estimated parameters are constructed from the asymptotic standard errors as follows:

αˆ±zp/2Var(αˆ),θˆ±zp/2Var(θˆ),

where zp/2 denotes the %p/2 quantile value derived from the standard normal distribution, N (0, 1). This quantile can be readily obtained using the quantile function associated with this normal distribution.

The study has two significant limitations. First, since the parameter estimates cannot be obtained in closed form, it takes a long time to compute large data sets. The second is that, when there are a large number of outliers in the data set, the parameter estimates can be biased and yield high standard errors. Therefore, robust parameter estimation methods need to be employed. This is planned for future work.

3.2 Other estimation methods

We now consider the order values of x1, x2, . . . , xn, denoted as x1:n, x2:n, . . . , xn:n. The derivation of LSEs and WLSEs is achieved through the minimization of the following functions:

(3.6) ∑i=1n2αγα,3xi:nθ−3αγα,2xi:nθΓα2α−3α−in+12,
(3.7) ∑i=1nn+12n+2in−i+12αγα,3xi:nθ−3αγα,2xi:nθΓα2α−3α−in+12.

4 Simulation study

In this section, the MLE, LSE and WLSE methods are compared through a simulation study. Two parameter vectors are used. These are α = 0.5, θ = 2 and α = 2, θ = 5. The simulation is repeated by 1000 times. Three sample sizes are used. These are n = 50, 100 and 500. The bias and mean squared error (MSE) are calculated using estimated parameter values and theirs true values. The results are summarized in Table 1. We have the following results:

Table 1

Comparison of estimation methods.

Parameters Sample sizes Metrics MLE
 LSE
 WLSE
α θ α θ α θ
α = 0:5 50 Bias 0.084 –0.029 0.044 0.105 0.049 0.064
MSE 0.108 0.192 0.154 0.333 0.133 0.263
100 Bias 0.046 –0.028 0.020 0.037 0.026 0.011
MSE 0.044 0.102 0.063 0.163 0.050 0.122
θ = 2 500 Bias 0.007 –0.004 –0.003 0.018 0.002 0.007
MSE 0.009 0.021 0.011 0.031 0.009 0.024
α = 2 50 Bias 0.182 –0.098 0.073 0.266 0.100 0.132
MSE 0.442 1.217 0.676 2.280 0.552 1.708
100 Bias 0.123 –0.107 0.043 0.105 0.070 0.014
MSE 0.191 0.558 0.255 0.898 0.207 0.670
θ = 5 500 Bias 0.017 –0.009 0.006 0.024 0.013 0.004
MSE 0.035 0.119 0.054 0.190 0.043 0.145

  1. As the sample size increases, bias and MSE converge towards zero for all estimation methods.

  2. All estimation methods give similar results for large sample sizes.

  3. For small sample sizes, the MSE values of the MLE are closer to zero than those of the LSE and WLSE methods.

  4. Although the estimation methods are slightly different for large sample sizes, we recommend using the MLE method for small sample sizes, such as less than 100.

5 WB regression model

5.1 Framework

This section is devoted to the construction of the WB regression model. To do this, we first need to describe the mean-parametrized WB distribution. We use the following transformation for the parameter θ:

(5.1) θ=62α−3αμ2α+1−3α+1α,

where μ is the mean associated with the WB distribution.

Inserting (5.1) in (2.4), we obtain the pdf of the mean-parametrized WB, given as

(5.2) fy;α,μ=6αωα,μ−αyα−1exp−2yωα,μ1−exp−yωα,μ3α−2αΓα,

where ω(α, μ) is defined in (5.1). Under this parametrization, the mean and variance of a random variable Y with the WB distribution is

(5.3) EY=μ,
VarY=32α+2+22α+2−6αα+13μ22α+1−3α+12α.

In (5.2), the parameter α is the dispersion parameter that defines the relationship between variance and mean, determining the level of randomness in the model. In the WB distribution, the variance is proportional to the square of the mean. The dispersion is inversely proportional to the parameter α. As α increases, the dispersion decreases. Therefore, the dispersion parameter can be expressed as ϕ = 1/α.

Let k be the number of the independent variables, β = (β0, β1, . . . , βk)T be the regression parameters, and, for any i=1,…,n,μi=expxxiTββ,yi be the response variable and xi = (1, xi1, xi2, . . . , xik)T be the values of the independent variables for ith observation. Based on the WB distribution defined with the pdf in (5.2), the log-likelihood function associated with the WB regression model is

(5.4) ℓα,ββ=nαlog6−α∑i=1nlogωα,μi+α−1∑i=1nlogyi +∑i=1n−2yiωα,μi+∑i=1nlog1−exp−yiωα,μi−nlog3α−2αΓα.

The parameter vector, represented as (α, β), is estimated via the MLE method. This estimation uses the Nelder-Mead algorithm. The asymptotic standard errors are obtained from the OIM. To check the accuracy of the model, a residual analysis is performed using the Cox-Snell (CS) residuals as developed by [11]. Based on the cdf of the WB distribution, the definition of the CS residuals is as follows:

(5.5) eˆi=−log1−Fyi;α,μi,i=1,2,…,n.

If the fitted model is an accurate representation of the data, the CS residuals will have an exponential distribution, Exp (λ = 1). The other residuals used to check the model accuracy is the randomized quantile residuals (RQR) [13] that are calculated by

(5.6) rˆi=Φ−1uˆi,

where Φ–1 (·) is the quantile function of N (0, 1) and uˆi=Fyi. If the WB model is suitably compiled with the data, the RQR follows N (0, 1).

5.2 Simulation of WB regression model

Parameter estimation of the WB regression model is performed using the MLE method. The performance evaluation of the ML estimates of the WB regression model is demonstrated with a simulation study. The settings below are considered.

  1. Set the simulation replication, as N = 1000.

  2. Set the regression parameters: β0 = –2, β1 = 2, β2 = 0.5.

  3. Set the dispersion parameter of the WB regression model, α = 2.

  4. Set the sample size as n = 100, 300, 500 and 1000.

The independent variables are generated using the standard uniform distribution, U (0, 1). Using each generated independent variable, we calculate the mean parameter of the WB distribution, as follows:

(5.7) μi=expβ0+β1xi1+β2xi2,i=1,2,…,n.

The dependent variable is then generated using the parameters μi and the predefined dispersion parameter α. Table 2 contains the results of the simulation. They are interpreted on the basis of the average of the estimates (AEs), the bias and the MSEs. We have the following results:

Table 2

Simulation results of the WB regression model.

Sample size Evaluation metrics β0 β1 β2 α
100 AE −2.0100 2.0042 0.5030 2.1547
Bias −0.0100 0.0042 0.0030 0.1547
MSE 0.0265 0.0458 0.0486 0.2230
300 AE −1.9986 2.0013 0.4909 2.0349
Bias 0.0014 0.0013 −0.0091 0.0349
MSE 0.0092 0.0153 0.0156 0.0594
500 AE −2.0005 1.9963 0.5039 2.0263
Bias −0.0005 −0.0037 0.0039 0.0263
MSE 0.0051 0.0081 0.0085 0.0368
1000 AE −1.9978 1.9990 0.4965 2.0169
Bias 0.0022 −0.0010 −0.0035 0.0169
MSE 0.0024 0.0042 0.0045 0.0198

  1. The MLE method works very well for small sample sizes, as the MSE and bias values are close to zero for small sample sizes.

  2. As expected, bias and MSE are the decreasing function of sample size n.

  3. For large sample sizes, the bias and MSE approach zero and the AEs approach the true parameter values.

  4. The results show that the ML estimates of the WB regression model are consistent and asymptotically unbiased.

6 Applications

6.1 Bladder cancer data

The WB distribution is compared with the gamma, log-normal and exponentiated-exponential (Exp-exp) [16] and Weibull distributions using the data set on remission times of bladder cancer patients. This data set was recently analyzed by [4]. The parameter estimation process is performed by the MLE approach for all distributions and the results are summarized in Table 3, which includes the standard errors of the estimated parameters, Kolmogorov-Smirnov (KS), Anderson-Darling (A), Cramér-von Mises (W) goodness of fit statistics, as well as Akaike information criterion (AIC) and Bayesian information criterion (BIC). The best model is deduced based on these metrics. If the model (or distribution) has the lowest values of these statistics, it is selected as the best model for the data. From this table, we can see that the WB distribution outperforms the competitor. We visualize this performance in Figure 2, which shows the histogram of the data with the fitted pdfs of the considered distributions superimposed, as well as the associated probability-probability (PP) plots for complementary analysis.

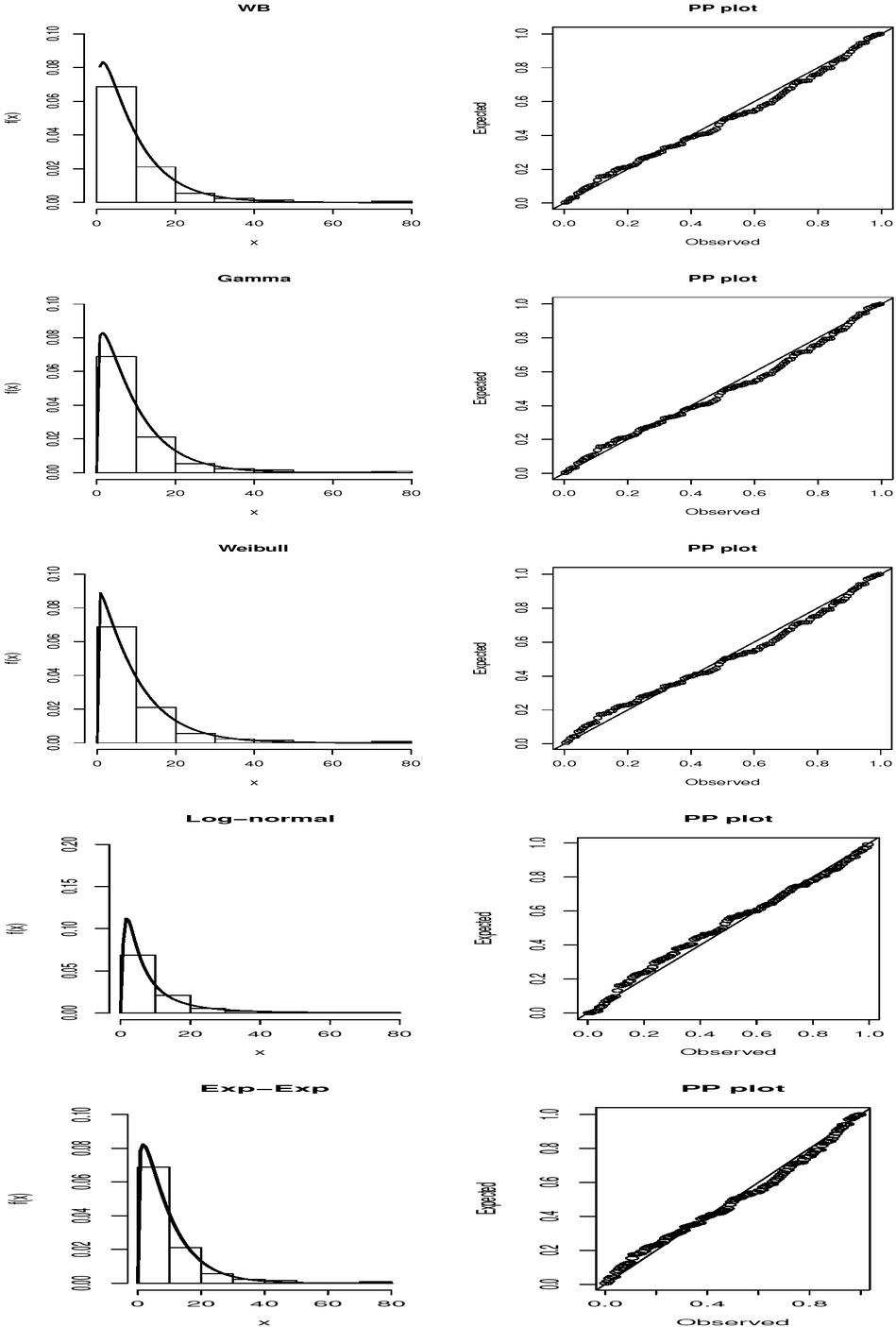
Figure 2 Fitted pdfs and PP plots.
Figure 2

Fitted pdfs and PP plots.

Table 3

Estimated parameters of the WB, gamma and Weibull distributions.

Distribution Parameters Estimates Std. Errors KS p-value A W AIC BIC
WB α 0.203 0.136 0.066 0.638 0.586 0.095 831.928 837.632
θ 18.938 2.701
Gamma α 1.178 0.131 0.069 0.575 0.641 0.105 832.747 838.451
θ 0.125 0.017
Weibull α 1.053 9.660 0.066 0.626 0.710 0.116 834.197 839.901
θ 0.068 0.857
Log-normal μ 1.764 0.095 0.065 0.643 0.870 0.131 837.295 842.999
σ 1.075 0.067
Exp-Exp α 1.223 0.149 0.068 0.586 0.597 0.097 832.181 837.885
θ 0.120 0.013

6.2 Application of the WB regression model and its web-tool

Here, we demonstrate the importance of the WB regression model by applying it to the data set on life expectancy of developed and developing countries. The data are taken from the Kaggle platform and are available at https://www.kaggle.com/datasets/kumarajarshi/life-expectancy-who. The variables are measured in the year of 2014 for 131 countries. The research question is Do body mass index (BMI) and country status have an effect on life expectancy? Here, the life expectancy is the dependent variable yi, BMI xi1 and country status (1: developed, 0:developing) xi2 are the independent variables.

The results of the WB regression model are shown in Table 4. All estimated parameters are found to be statistically significant. Life expectancy in developed countries is exp (0.1274) = 1.1359 times higher than in developing countries. Similarly, for every unit increase in BMI, life expectancy increases by exp (0.0021) = 1.0021 times. Alternatively, if BMI increases by one unit, life expectancy increases by (1.0021–1)×100 = 0.21%. So although BMI is statistically significant, its effect on life expectancy is quite negligible. Table 5 shows the AIC and BIC values for the WB regression model and Figure 3 shows the CS and RQR of the WB regression model. The KS test is also performed on both CS and RQR residuals and the results are reported in Table 6, indicating that both residuals confirm the fit of the WB model to the data.

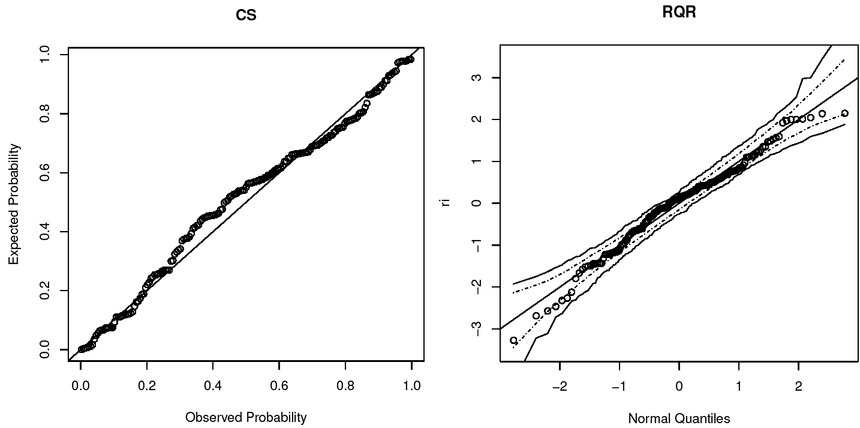
Figure 3 Estimated parameters of the fitted models.
Figure 3

Estimated parameters of the fitted models.

Table 4

Results of the WB regression model.

β0 β1 β2 α
Estimate S.E. p-value Estimate S.E. p-value Estimate S.E. p-value Estimate
4.1583 0.0155 < 0:001 0.0021 0.0003 < 0:001 0.1274 0.0192 < 0:001 108.1097
Table 5

AIC and BIC values of the WB regression model.

–ℓ AIC BIC
605.178 1218.356 1231.15
Table 6

KS test results for the CS and RQR residuals.

CS RQR
Test Statistics p-value Test Statistics p-value
0.078 0.217 0.078 0.217

Implementing the WB regression model requires advanced knowledge of R or Python. People who want to use this model should maximize the likelihood function using optimization algorithms.

In this study, a cloud-based application called WBreg is developed to enable the widespread use of this model by researchers. WBreg is built using the R Shiny package and available at https://beststat.shinyapps.io/WB2reg that can be easily used. The data set is uploaded to the following website https://github.com/emrahaltun/WBreg. The results can be reproduced by readers and practitioners using the WBreg web application by downloading the data set from the GitHub website.

WBreg application consists of three main panels. These are the home, data upload and analysis panels. The home panel is shown in Figure 4. It gives general information about the programme.

Figure 4 Welcome panel of WBreg.
Figure 4

Welcome panel of WBreg.

Figure 5 shows how to load data into the WBreg model. WBreg only accepts two file types. These are the CSV and xlsx file types. After the file has been uploaded, the screen opens where the dependent and independent variables are selected.

Figure 5 Data upload panel of the WBreg.
Figure 5

Data upload panel of the WBreg.

The analysis panel consists of three sub-panels. The first panel is given in Figure 6 and contains the parameter estimates of the WBreg model. In this panel, not only the parameter estimates are given, but also the standard errors and p-values.

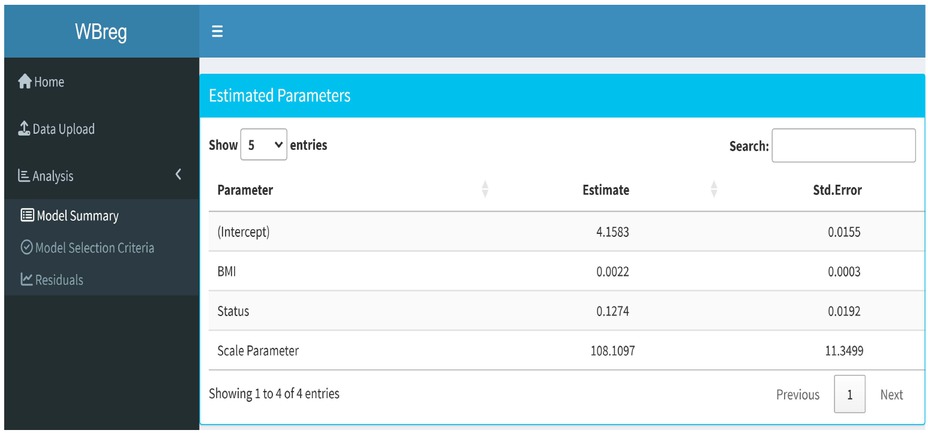
Figure 6 Model summary panel of the WBreg.
Figure 6

Model summary panel of the WBreg.

In the second sub-panel of the analysis panel, the information criteria are given and shown in Figure 7.

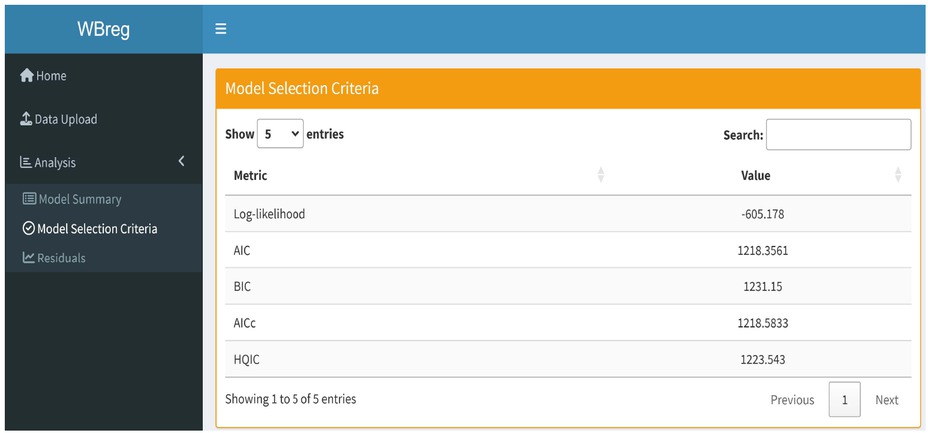
Figure 7 Model selection criteria panel of the WBreg.
Figure 7

Model selection criteria panel of the WBreg.

Finally, in the third sub-panel of the analysis panel, the results of the residual analysis obtained with CS and RQR are presented. The KS test results for these residuals are also included (see Figure 8).

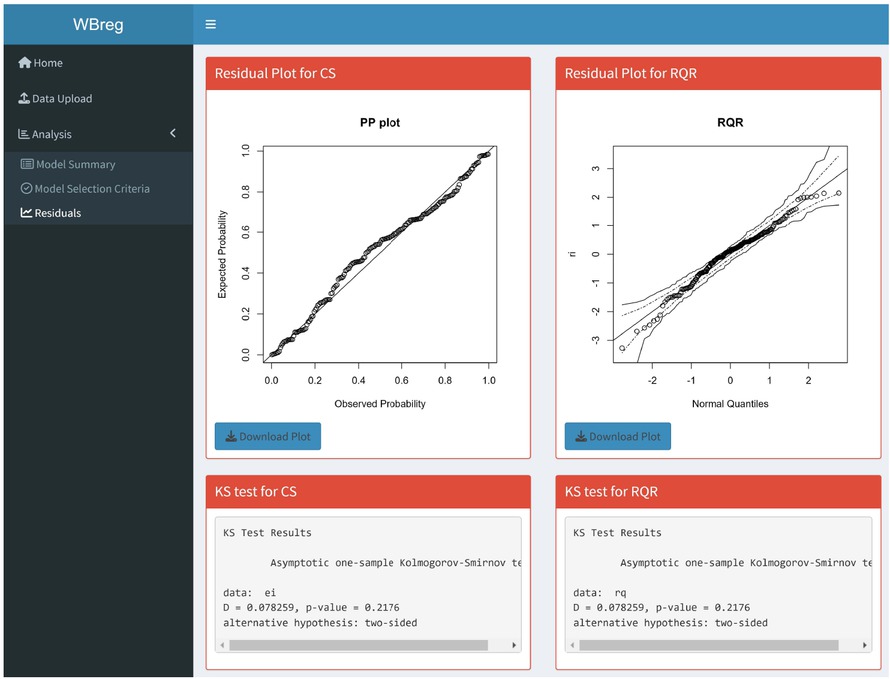
Figure 8 Residual analysis panel of the WBreg.
Figure 8

Residual analysis panel of the WBreg.

6.3 Development process of the WBreg

The WBreg user interface is designed using the shinydashboard package to provide a modular, navigable, and user-friendly layout. Several R packages are utilized in the development process.

  • User Interface and Interactivity: shinydashboard [10], and DT [25] are used to design the dynamic interface and to render interactive data tables.

  • Data Import and Preprocessing: The readxl [24] package allows users to upload both CSV and Excel files.

  • Statistical Computation: The log-likelihood function is defined for the WB model and optimized using the optim() [21] function. zipfR [14] is used for the computation of special distributional properties.

  • Visualization: Base R plotting functions are used for producing PP and QQ plots. The envelopes for QQ plots are constructed using the boot::envelope() [9] function.

The WBreg is deployed on a free public R Shiny Server via shinyapps.io, enabling cloud-based usage without the need for local R/ R Studio installation. The application is developed with reproducibility and simplicity. All calculations are executed within the Shiny server without external dependencies. All outputs such as tables and plots update automatically in response to user inputs.

7 Conclusion

This research introduces a novel weighted distribution called the WB distribution. We have highlighted its important mathematical properties. In addition, its statistical aspect has been extensively studied. Various estimation techniques have been used to determine the unknown parameters of the model. A generalized linear model framework has been constructed under the assumption that the response variable follows the WB distribution. In order to assess the effectiveness of the parameter estimation methods, simulation studies are carried out for both the WB model and the associated regression. In addition, the WBreg tool has been developed and made available to researchers at https://beststat.shinyapps.io/WB2reg. The WBreg tool serves as a powerful tool for implementing the WB regression model.

  1. (Communicated by Gejza Wimmer)

References

[1] Abd-Elrahman, A. M.: Utilizing ordered statistics in lifetime distributions production: a new lifetime distribution and applications, J. Probab. Stat. Sci. 11 (2013), 153–164.Suche in Google Scholar

[2] Abd-Elrahman, A. M.: A new two-parameter lifetime distribution with decreasing, increasing or upside-down bathtub-shaped failure rate, Comm. Statist. Theory Methods 46 (2017), 8865–8880.10.1080/03610926.2016.1193198Suche in Google Scholar

[3] Ahmad, A.—Ahmad, S. P.—Ahmed, A.: Length-biased weighted Lomax distribution: statistical properties and application, Pak. J. Stat. Oper. Res. XII (2016), 245–255.10.18187/pjsor.v12i2.1178Suche in Google Scholar

[4] Aldeni, M.—Lee, C.—Famoye, F.: Families of distributions arising from the quantile of generalized lambda distribution, J. Stat. Distrib. Appl. 4 (2017), 1–18.10.1186/s40488-017-0081-4Suche in Google Scholar

[5] Al-Omari, A. I.—Alsultan, R.—Alomani, G.: Asymmetric right-skewed size-biased Bilal distribution with mathematical properties, reliability analysis, inference and applications, Symmetry 15 (2023), Art. No. 1578.10.3390/sym15081578Suche in Google Scholar

[6] Altun, E.: A new one-parameter discrete distribution with associated regression and integer-valued autoregressive models, Math. Slovaca 70 (2020), 979–994.10.1515/ms-2017-0407Suche in Google Scholar

[7] Altun, E.—El-Morshedy, M.—Eliwa, M. S.: A new regression model for bounded response variable: An alternative to the beta and unit-Lindley regression models, Plos One 16 (2021), 1–15.10.1371/journal.pone.0245627Suche in Google Scholar PubMed PubMed Central

[8] Altun, E.—El-Morshedy, M.—Eliwa, M. S.: A study on discrete Bilal distribution with properties and applications on integer valued autoregressive process, REVSTAT 20 (2022), 501–528.Suche in Google Scholar

[9] Canty, A.—Ripley, B.: boot: Bootstrap R (S-Plus) Functions. R package version 1.3-31, https://CRAN.R-project.org/package=boot 2024.Suche in Google Scholar

[10] Chang, W.—Ribeiro, B. B.: shinydashboard: Create Dashboards with ’Shiny’. R package version 0.7.2, https://CRAN.R-project.org/package=shinydashboard 2021.Suche in Google Scholar

[11] Cox, D. R.—Snell, E. J.: A general definition of residuals, J. R. Stat. Soc. Ser. B. Stat. Methodol. Series B (Methodological) (1968), 248–275.10.1111/j.2517-6161.1968.tb00724.xSuche in Google Scholar

[12] Dey, S.—Dey, T.—Anis, M. Z.: Weighted Weibull distribution: properties and estimation, J. Stat. Theory Pract. 9 (2015), 250–265.10.1080/15598608.2013.875966Suche in Google Scholar

[13] Dunn, P. K.—Smyth, G. K.: Randomized quantile residuals, J. Comput. Graph. Statist. 5 (1996), 236–244.10.1080/10618600.1996.10474708Suche in Google Scholar

[14] Evert, S.—Baroni, M.: zipfR: Word frequency distributions in R. In: Proceedings of the 45th Annual Meeting of the Association for Computational Linguistics, Posters and Demonstrations Sessions, 2007, 29–32, Prague, Czech Republic.10.3115/1557769.1557780Suche in Google Scholar

[15] Ghitany, M. E.—Alqallaf, F.—Al-Mutairi, D. K.—Husain, H. A.: A two-parameter weighted Lindley distribution and its applications to survival data, Math. Comput. Simul. 81 (2011), 1190–1201.10.1016/j.matcom.2010.11.005Suche in Google Scholar

[16] Gupta, R. D.—Kundu, D.: Theory & methods: Generalized exponential distributions, Aust. N. Z. J. Stat. 41 (1999), 173–188.10.1111/1467-842X.00072Suche in Google Scholar

[17] Gupta, R. C.—Kirmani, S. N. U. A..: The role of weighted distributions in stochastic modeling, Comm. Statist. Theory Methods 19 (1990), 3147–3162.10.1080/03610929008830371Suche in Google Scholar

[18] Jain, K.—Singla, N.—Gupta, R.: A weighted version of gamma distribution, Discuss. Math. Probab. Stat. 34 (2014), 89–111.10.7151/dmps.1166Suche in Google Scholar

[19] Lele, S. R.—Keim, J. L.: Weighted distributions and estimation of resource selection probability functions, Ecology 87 (2006), 3021–3028.10.1890/0012-9658(2006)87[3021:WDAEOR]2.0.CO;2Suche in Google Scholar

[20] Patil, G. P.—Rao, C. R.: Weighted distributions and size-biased sampling with applications to wildlife populations and human families, Biometrics (1978), 179–189.10.2307/2530008Suche in Google Scholar

[21] R Core Team: R: A Language and Environment for Statistical Computing, Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.Suche in Google Scholar

[22] Riad, F. H.—Alruwaili, B.—Gemeay, A. M.—Hussam, E.: Statistical modeling for COVID-19 virus spread in Kingdom of Saudi Arabia and Netherlands, Alex. Eng. J. 61 (2022), 9849–9866.10.1016/j.aej.2022.03.015Suche in Google Scholar

[23] Sen, S.—Chandra, N.—Maiti, S. S.: The weighted xgamma distribution: properties and application, J. Reliab. Stat. Stud. 10 (2017), 43–58.Suche in Google Scholar

[24] Wickham, H.—Bryan, J.: readxl: Read Excel Files. R package version 1.4.3, https://CRAN.R-project.org/package=readxl.Suche in Google Scholar

[25] Xie, Y.—Cheng, J.—Tan, X.: DT: A Wrapper of the JavaScript Library ’DataTables’. R package version 0.33; https://CRAN.R-project.org/package=DT.Suche in Google Scholar

Appendix

Proof of Proposition 1. Based on the mixture representation in (2.8), we have

EXr=∫0∞xr6αθ−αxα−1exp−2xθ3α−2αΓα−6αθ−αxα−1exp−3xθ3α−2αΓαdx=∫0∞xr6αθ−αxα−1exp−2xθ3α−2αΓαdx−∫0∞xr6αθ−αxα−1exp−3xθ3α−2αΓαdx=6αθ−α3α−2αΓα∫0∞xr+α−1exp−2xθdx−6αθ−α3α−2αΓα∫0∞xr+α−1exp−3xθdx=6αθ−α3α−2αΓαΓα+rθ2α+r−6αθ−α3α−2αΓαΓα+rθ3α+r=θrΓα+r2α+r−3α+r6rΓα2α−3α.

This concludes the proof. □

Proof of Proposition 2. The moment generating function of the WB distribution is defined by M (t) = E (exp (tX)), where X is a random variable with the WB distribution. Based on this classical definition, we have

Mt=∫0∞exptx6αθ−αxα−1exp−2xθ3α−2αΓα−6αθ−αxα−1exp−3xθ3α−2αΓαdx=∫0∞exptx6αθ−αxα−1exp−2xθ3α−2αΓαdx−∫0∞exptx6αθ−αxα−1exp−3xθ3α−2αΓαdx=6αθ−α3α−2αΓα∫0∞xα−1exptx−2xθdx−6αθ−α3α−2αΓα∫0∞xα−1exptx−3xθdx=6αθ−α3α−2αΓαθαΓα2−tθα−6αθ−α3α−2αΓαθαΓα3−tθα=6α3α−2α12−tθα−6α3α−2α12−tθα=6α3α−2α121−tθ2α−6α3α−2α131−tθ2α=3α3α−2α11−tθ2α−2α3α−2α11−tθ3α=3α3α−2α1−tθ2−α−2α3α−2α1−tθ3−α.

This end the proof. □

Proof of Proposition 3. Using the following expression: φ (t) = M (it) and Proposition 2, we conclude directly. □

Proof of Proposition 4. The proof can be easily done using the mixture representation of the WB distribution. □
Received: 2025-01-27
Accepted: 2025-08-14
Published Online: 2025-12-12
Published in Print: 2025-12-17

© 2025 Mathematical Institute Slovak Academy of Sciences

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. A new categorical equivalence for stone algebras
  2. On special classes of prime filters in BL-algebras
  3. A note on characterized and statistically characterized subgroups of 𝕋 = ℝ/ℤ
  4. New Young-type integral inequalities using composition schemes
  5. The structure of pseudo-n-uninorms with continuous underlying functions
  6. Jensen-type inequalities for a second-order differential inequality condition
  7. A direct proof of the characterization of the convexity of the discrete Choquet integral
  8. Envelope of plurifinely plurisubharmonic functions and complex Monge-Ampère type equation
  9. Fekete-Szegö inequalities for Φ-parametric and β-spirllike mappings of complex order in ℂn
  10. Entire function sharing two values partially with its derivative and a conjecture of Li and Yang
  11. Oscillatory properties of third-order semi-canonical dynamic equations on time scales via canonical transformation
  12. Weighted B-summability and positive linear operators
  13. Some properties and applications of convolution algebras
  14. On measures of σ-noncompactess in F-spaces
  15. On the kolmogorov–feller–gut weak law of large numbers for triangular arrays of rowwise and pairwise negatively dependent random variables
  16. Intermediately trimmed sums of oppenheim expansions: A strong law
  17. Novel weighted distribution: Properties, applications and web-tool
  18. On the q-Gamma distribution: Properties and inference
  19. Finiteorthoatomistic effect algebras and regular algebraic E-test spaces
  20. Prof. RNDr. Anatolij Dvurečenskij, DrSc. 75th anniversary
https://doi.org/10.1515/ms-2025-0110
Schlagwörter für diesen Artikel
Weighted distributions; different estimation methods; simulation; regression; software
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. A new categorical equivalence for stone algebras
  2. On special classes of prime filters in BL-algebras
  3. A note on characterized and statistically characterized subgroups of 𝕋 = ℝ/ℤ
  4. New Young-type integral inequalities using composition schemes
  5. The structure of pseudo-n-uninorms with continuous underlying functions
  6. Jensen-type inequalities for a second-order differential inequality condition
  7. A direct proof of the characterization of the convexity of the discrete Choquet integral
  8. Envelope of plurifinely plurisubharmonic functions and complex Monge-Ampère type equation
  9. Fekete-Szegö inequalities for Φ-parametric and β-spirllike mappings of complex order in ℂn
  10. Entire function sharing two values partially with its derivative and a conjecture of Li and Yang
  11. Oscillatory properties of third-order semi-canonical dynamic equations on time scales via canonical transformation
  12. Weighted B-summability and positive linear operators
  13. Some properties and applications of convolution algebras
  14. On measures of σ-noncompactess in F-spaces
  15. On the kolmogorov–feller–gut weak law of large numbers for triangular arrays of rowwise and pairwise negatively dependent random variables
  16. Intermediately trimmed sums of oppenheim expansions: A strong law
  17. Novel weighted distribution: Properties, applications and web-tool
  18. On the q-Gamma distribution: Properties and inference
  19. Finiteorthoatomistic effect algebras and regular algebraic E-test spaces
  20. Prof. RNDr. Anatolij Dvurečenskij, DrSc. 75th anniversary
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2026 De Gruyter Brill
Heruntergeladen am 6.2.2026 von https://www.degruyterbrill.com/document/doi/10.1515/ms-2025-0110/html
Button zum nach oben scrollen