Utilizing collagen-coated hydrogels with defined stiffness as calibration standards for AFM experiments on soft biological materials: the case of lung cells and tissue
Abstract
Atomic Force Microscopy (AFM) is crucial in mechanobiology for high-resolution imaging and nanomechanical measurements of biological samples, providing insights into their mechanical properties. However, AFM faces challenges such as tip damage and cantilever selection errors, impacting measurement accuracy. This study proposes a methodology using collagen-coated hydrogels with predefined stiffness for calibrating AFM measurements on soft biological materials. By facilitating appropriate cantilever selection, assessing systematic errors, and evaluating tip damage, this approach ensures reliable Young’s modulus measurements. The proof of concept with human lung cells and tissue specimens demonstrates improved accuracy and reliability of AFM-based nanomechanical characterizations, essential for understanding cellular mechanics and disease progression.
1 Introduction
Atomic Force Microscopy (AFM) has become a cornerstone in mechanobiology due to its ability to provide high-resolution imaging and detailed nanomechanical measurements of biological samples [1]. This powerful technique enables researchers to probe the mechanical properties of cells and tissues at the nanoscale, offering insights into their stiffness, elasticity, and overall mechanical behaviour [2], [3]. Understanding these properties is crucial for elucidating cellular mechanics, disease progression, and the effectiveness of therapeutic interventions [4], [5]. AFM’s capacity to measure mechanical properties such as Young’s modulus provides a deeper understanding of how cells and tissues respond to mechanical forces, which is essential for applications ranging from drug development to tissue engineering [6].
Despite its widespread use and significance, AFM imaging and measurements are not without their challenges [7], [8], [9]. The technique is susceptible to various errors and artifacts that can significantly impact the accuracy and reliability of results [10]. One major concern is AFM-tip damage, which can profoundly affect measurements of mechanical properties by introducing inaccuracies in force measurements, systematic errors in stiffness assessment, and inconsistencies in data interpretation [11], [12], [13]. In addition to AFM-tip damage, calibration errors in the AFM lever system can introduce significant variability in stiffness measurements. Recent advances, such as the standardized nanomechanical AFM procedure (SNAP), have successfully reduces these uncertainties from nearly 30 % to less than 1 %, ensuring highly reliable measurements across different laboratories [12]. Also, errors can arise from the incorrect selection of cantilevers, particularly regarding the appropriate spring constant (N/m), which is crucial for accurate force measurements. Other factors contributing to measurement errors include the choice of tools and protocols, such as the applied force and the model used (e.g., Hertz model), which must be carefully selected to ensure they provide reliable results [14], [15]. Addressing these issues requires a comprehensive approach to calibration and methodology to enhance the precision and reproducibility of AFM-based measurements.
The primary objective of this paper is to propose a new methodology utilizing collagen-coated hydrogels with predefined stiffness as calibration standards for Atomic Force Microscopy (AFM) experiments on soft biological materials, such as cells and tissues. This methodology aims to facilitate the selection of appropriate cantilevers for experiments, assess potential systematic errors in measuring mechanical properties in terms of Young’s modulus, and evaluate errors caused by AFM-induced damage.
2 Materials and methods
2.1 Collagen hydrogels
For this study, commercially available collagen-coated hydrogels with predefined stiffness were utilized. Specifically, we used collagen-coated hydrogels with stiffness values of 0.5 kPa and 1.0 kPa, bound to 35 mm Petri dishes (Petrisoft™ 35 mm Dish Collagen, Cell Guidance Systems). More specifically, the hydrogels used in this study were commercially available polyacrylamide-based gels crosslinked with bisacrylamide and coated with type I collagen from bovine skin. These collagen-coated hydrogels were approximately 500 μm thick, bound to 35 mm polystyrene dishes. The collagen was applied at a surface density of 0.02 mg/ml across different stiffness values, as confirmed by chemiluminescence-based detection. This uniform surface collagen density enables cell attachment and growth, providing a more physiologically relevant environment for cellular mechanics studies. Importantly, the stiffness of the hydrogels can be tuned to reflect different biological environments, while the collagen coating offers an ECM-like surface for cells. Hence, the term “collagen-coated hydrogels” is used in the manuscript to accurately describe the experimental setup.
2.2 Cell culturing
Commercially available lung native human fibroblasts (FBs), specifically LL 24 (normal FBs), were cultured in F − 12 K Medium in an incubator set to 37 °C with 5 % CO2. For AFM experiment, the lung cells were cultured on 35 mm Petri dishes, which could be directly mounted onto the AFM system for nanoindentation measurements.
2.3 Human lung specimens
Patients were recruited at the Nicosia Lung Center by Dr. Zachariades. Those who consented provided tissue samples for research. The Cyprus National Bioethics Committee (licenses EEBK/EΠ/2022/04) approved all procedures and experimental protocols. Human tissue samples were obtained via routine bronchoscopy conducted for diagnostic or therapeutic reasons in newly diagnosed pulmonary fibrosis patients. Following the biopsy, a portion of the collected tissue was allocated to our research, while the rest was processed by the clinical pulmonologist and histopathologist for histopathological analysis.
2.4 Atomic Force Microscopy
Atomic Force Microscopy (AFM) experiments were carried out using a commercial AFM (5,500 Keysight Technologies, Santa Rosa, CA, USA) equipped with V-shaped soft silicon nitride probes (MLCT-Bio, cantilever C for cells and D for tissue, Bruker) and colloidal AFM probe, AFM cantilever with round AFM tip like a ball (CP-PNPL-BSA-A, SQube, acquired through NanoAndMore). Given the high-water content of the sample, a Poisson’s ratio of ν = 0.5 was assumed. The spring constant was calibrated using the thermal noise method, while the sensitivity calibration (measured as nanometers of cantilever deflection per volt signal from the laser detection system) was performed by obtaining force-versus-distance curves on a Petri dish, which provided a pristine, rigid surface [16], [17]. For the AFM nanoindentation technique a set point of 1 nN normal force for the cells and 1.8 nN for the tissue [18]. The Young’s modulus was assessed by acquiring 8 × 8 points of force curves in an area of 1 × 1 µm. For the cells’ this area was selected to be near the centre of the cells. For each specimen at least 3 different regions of interest (ROI) were selected, while for the cells ∼10 cells per condition were studied [19], [20]. MLCT tips were approximated as conical, and the data was fitted to Sneddon’s equation:
For experiments using spherical indenters, the data were processed using the Hertz equation below:
In equations (1) and (2) E is the Young’s modulus, θ is the cone’s half-opening angle and R is the indenter’s radius.
The force-distance curves were processed using the AtomicJ software [21], which was also used to identify the contact point for each curve. The procedure is as follows: each point on the curve is treated as a potential contact point. A polynomial is fitted to the pre-contact region, and the corresponding contact model is applied to the force-indentation data. The associated sums of squares are recorded, and the point that results in the lowest total sum of squares is selected as the contact point.
2.5 Proposed methodology
The primary objective of this study is to propose a novel methodology using collagen-coated hydrogels with predefined stiffness as calibration standards for AFM experiments on soft biological materials, such as cells and tissues. This approach aims to: (i) Facilitate the selection of appropriate cantilevers for AFM experiments, (ii) Assess potential systematic errors in measuring mechanical properties in terms of Young’s modulus and (iii) Evaluate errors caused by AFM-induced damage.
The proposed methodology is very simple and is based on the use of collagen-coated hydrogels with pre-defined stiffness. Such hydrogels are commercially available, like the ones presented previously in Section 2.1. However, similar hydrogels (polyacrylamide gels coated with collagen) or pure collagen gels with different concentration (and consequently different stiffness) can be easily formed at a lab using commercially available collagen. Relevant protocols can be found in previous publications [16], [22].
2.5.1 Selection of hydrogel standards and cantilevers with appropriate spring constant
The first step is to choose the appropriate collagen-coated hydrogels with stiffness close to the expected stiffness of the biological material under investigation. The known stiffness of the hydrogel is the Eknown. Then by measuring the Young’ modulus of the hydrogel will ensure that the selected cantilever has the appropriate spring constant for measuring the specific material.
2.5.2 Normalization factor and error assessment
By using the simple equation
we can compute a normalization factor that can be used to normalize the measured Young’s modulus values, ensuring consistency and reliability in the AFM measurements.
The next step includes the measurement of the stiffness of the selected collagen hydrogel (with known stiffness Eknown) using AFM before conducting experiments on the actual biological material. This will be the Emeasured.
Then we can calculate the measurement error using the equation:
2.5.3 Error measurement due to tip damage
In addition to their use as calibration standards, collagen-coated hydrogels can also be employed to assess errors that might arise from tip damage during repeated measurements. This assessment involves the following steps:
In addition to their use as calibration standards, collagen hydrogel can also be employed to assess errors that might arise from tip damage during repeated measurements. This assessment involves the following steps:
2.5.3.1 Initial stiffness measurement
Measurement of the stiffness of the collagen hydrogen before conducting experiments on the biological materials. This value is set as Ebefore.
2.5.3.2 Experimental measurements
Subsequently, the same AFM-tip is used to perform AFM measurements on the biological material under investigation, such as cells or tissues.
2.5.3.3 Post-experiment stiffness measurement
After completing the experiments on the biological material, the same tip is used to measure the stiffness of the same collagen hydrogel again. This value is set as Eafter.
2.5.3.4 Error estimation
By comparing the initial and post-experimental stiffness values of the hydrogel, researchers can quantify the extent of error introduced by any damage to the cantilever. This approach ensures the integrity and reliability of AFM measurements by identifying and accounting for errors that might otherwise compromise the experimental results. This can be performed by estimating the error (%) due to potential cantilever damage by modifying the previously described equation:
In the next sections we used the proposed methodology in relevant materials, lung cells and human lung specimens, as proof of concept.
3 Results and discussion
3.1 Selection of hydrogel standards and cantilevers with appropriate spring constant
The first step of our study was to investigate whether collagen-coated hydrogels with predetermined stiffness can be utilized for selecting appropriate cantilevers for a specific material. This approach aims to enhance the accuracy of Atomic Force Microscopy (AFM)-based nanomechanical measurements by ensuring that the cantilever’s spring constant is suitably matched to the stiffness of the sample material.
To achieve this, we employed MLCT-BIO cantilevers (Bruker), which are frequently used in AFM-based nanomechanical experiments, particularly for force spectroscopy on soft biological samples, such as cells and tissues [18], [23], [24]. The MLCT-BIO chip is equipped with six cantilevers of varying spring constants and geometries, providing a versatile tool for a range of stiffness measurements.
For our specific application, we selected two triangular cantilevers from the MLCT-Bio chip, each featuring a nominal tip radius of 20 nm. The cantilevers chosen were the MLCT-BIO-C and MLCT-BIO-D, which have spring constants of 0.01 N/m and 0.03 N/m, respectively. These cantilevers were chosen based on our extensive prior experience with their use in nanomechanical characterization of biological samples [18], [23], [24]. The MLCT-BIO-C cantilever has been previously utilized for measuring the mechanical properties of cells, while the MLCT-BIO-D cantilever has been employed in studies involving tissue samples.
In our current study, we used these cantilevers to measure the stiffness of collagen-coated hydrogels, provided with known Young’s modulus values of 0.5 kPa and 1.0 kPa by the manufacturer. By measuring these hydrogels, we aimed to validate the use of MLCT-Bio cantilevers in obtaining accurate nanomechanical characterizations. Specifically, the MLCT-BIO-C cantilever was used to measure the softer 0.5 kPa hydrogel, and the MLCT-BIO-D cantilever was used for the 1.0 kPa hydrogel. These measurements served to confirm that the cantilevers with different spring constants can effectively capture the stiffness variations in collagen-coated hydrogels, thereby assisting in the selection of appropriate cantilevers for materials with specific mechanical properties.
As expected, the selection of the cantilever’s spring constant is critical to accurately measure the properties of the studied material. Figure 1 illustrates the importance of this selection. When we used the MLCT-BIO-C cantilever to measure the 0.5 kPa collagen hydrogel, the measurements were quite accurate, yielding a Young’s modulus of 0.46 ± 0.02 kPa. However, when this same cantilever was used to measure the 1.0 kPa collagen hydrogel, the results were less accurate, with a measured Young’s modulus of 0.37 ± 0.02 kPa.
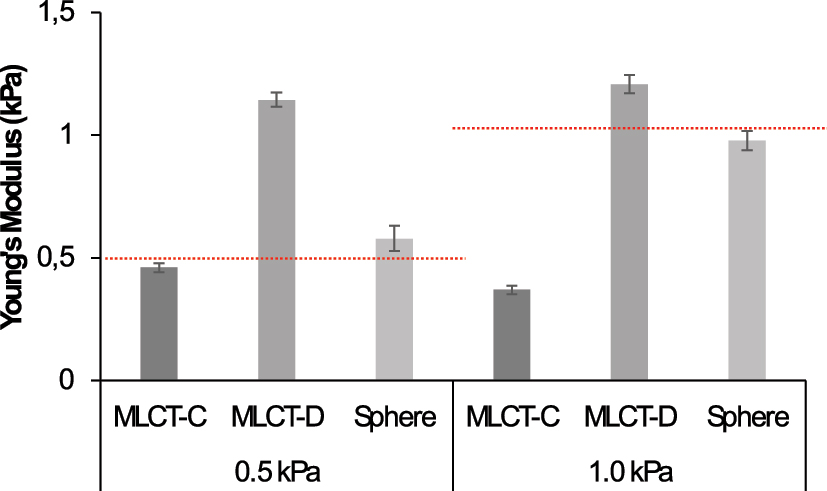
Young’s modulus measurements of collagen-coated hydrogels with predetermined stiffness using different AFM cantilevers and tips. The first column shows measurements with the MLCT-BIO-C cantilever (spring constant 0.01 N/m), which were accurate for the 0.5 kPa hydrogel (0.46 ± 0.02 kPa) but underestimated the stiffness of the 1.0 kPa hydrogel (0.37 ± 0.02 kPa). The second column presents measurements with the MLCT-BIO-D cantilever (spring constant 0.03 N/m), which overestimated the stiffness for both the 0.5 kPa hydrogel (1.14 ± 0.03 kPa) and the 1.0 kPa hydrogel (1.2 ± 0.04 kPa). The third column shows results using spherical tips with a 5 μm diameter (force constant 0.08 N/m), providing more accurate measurements for both the 0.5 kPa (0.58 ± 0.05 kPa) and the 1.0 kPa (0.98 ± 0.04 kPa) collagen-coated hydrogels.
Conversely, when using the MLCT-BIO-D cantilever, which has a higher spring constant, the results were more accurate for the stiffer 1.0 kPa hydrogel, yielding a measured Young’s modulus of 1.2 ± 0.04 kPa. However, the same cantilever overestimated the stiffness of the 0.5 kPa hydrogel, measuring it at 1.14 ± 0.03 kPa. This indicates that the MLCT-BIO-D cantilever is not suitable for softer hydrogels like the 0.5 kPa sample, and even the 1.0 kPa hydrogel might require a stiffer cantilever for accurate measurement.
To further investigate and improve our measurements, we utilized spherical tips with a 5 μm diameter (CP-PNPL-BSA-A, force constant 0.08 N/m). The results from these spherical tips are also shown in Figure 1, in the third column of each panel. The spherical tips provided more accurate measurements for both hydrogels: 0.58 ± 0.05 kPa for the 0.5 kPa hydrogel and 0.98 ± 0.04 kPa for the 1.0 kPa hydrogel. These results suggest that spherical tips might be more suitable for measuring the Young’s modulus of collagen-coated hydrogels, particularly at the micrometer scale, as the sphere’s size facilitates more accurate indentation over a larger contact area. In Figure S1, representative examples of force-displacement and force-indentation curves used in this paper are presented.
Our findings highlight the necessity of carefully selecting the cantilever’s spring constant to match the mechanical properties of the material being studied. The MLCT-BIO-C cantilever is appropriate for softer hydrogels, such as the 0.5 kPa collagen hydrogel, while the MLCT-BIO-D cantilever is better suited for stiffer hydrogels, though possibly requiring even stiffer samples for optimal performance. Additionally, spherical tips with a larger radius demonstrate potential for more accurate measurements across a range of stiffnesses, emphasizing their utility for micrometer-scale characterization.
3.2 Normalization factor
The next step in our investigation was to calculate the Normalization Factor (NF) based on Equation (3) for the measurements presented in the previous section. The NF serves as a crucial parameter for normalizing measurements across different cantilevers and materials, thereby enhancing the reliability and comparability of nanomechanical characterizations. Using Equation (3), we calculate the NF for each set of measurements discussed earlier. These calculations are summarized in Table 1.
Normalization factors and measurement errors for different cantilevers and collagen-coated hydrogels.
| Cantilever/tip | Hydrogel stiffness | Measured Young’s modulus | Normalization factor (NF) | Error (%) | ||
|---|---|---|---|---|---|---|
| (kPa) | (kPa) | SEM | SD | |||
| MLCT-BIO-C | 0.5 | 0.46 | 0.02 | 0.03 | 1.09 | 8 |
| MLCT-BIO-C | 1.0 | 0.37 | 0.02 | 0.06 | 2.70 | 63 |
| MLCT-BIO-D | 0.5 | 1.14 | 0.03 | 0.08 | 0.44 | −128 |
| MLCT-BIO-D | 1.0 | 1.2 | 0.04 | 0.04 | 0.83 | −20 |
| CP-PNPL | 0.5 | 0.58 | 0.05 | 0.08 | 0.86 | −16 |
| CP-PNPL | 1.0 | 0.98 | 0.04 | 0.05 | 1.02 | 2 |
From Table 1, it is evident that the Normalization Factor is close to 1 for the more accurate measurements. For example, the MLCT-BIO-C cantilever, which provided an accurate measurement of the 0.5 kPa hydrogel (0.46 ± 0.02 kPa), has an NF of 1.09. Similarly, the spherical tip measurements yielded NFs near 1, indicating high accuracy.
These NFs can be utilized for normalized measurements on unknown specimens, such as cells and tissues. By applying the NF, we can adjust for the discrepancies between measured and known values, thus ensuring that our nanomechanical characterizations are both precise and reliable across different experimental setups.
3.3 Error assessment
Using the provided technique, researchers can not only determine a Normalization Factor (NF) but also assess the percentage error in their measurements. This process involves measuring the stiffness of a selected collagen hydrogel with a known stiffness using AFM before conducting experiments on the actual biological material. The measured stiffness can then be compared to the known value to calculate the measurement error.
The measurement error can be calculated using the Equation (4).
This equation allows for a straightforward calculation of the percentage error, providing an indication of the accuracy of the AFM measurements.
To illustrate this, consider the measurements presented in the previous sections. For the MLCT-BIO-C cantilever measuring the 0.5 kPa collagen hydrogel, the known Young’s modulus is 0.5 kPa, and the measured Young’s modulus is 0.46 kPa. Using the equation, the error is calculated 8 %. Similarly, for the MLCT-BIO-D cantilever measuring the 1.0 kPa collagen hydrogel, where Eknown = 1.0 kPa and Emeasured = 1.2 kPa, the error is: −20 %. A negative error indicates an overestimation in the measured value compared to the known value.
From Table 1 (last column), it is apparent that the measurement errors vary significantly depending on the cantilever and the stiffness of the hydrogel being measured. For instance, the MLCT-BIO-C cantilever has a low error (8 %) for the 0.5 kPa hydrogel but a much higher error (63 %) for the 1.0 kPa hydrogel. The MLCT-BIO-D cantilever shows large negative errors, indicating an overestimation of stiffness. The spherical tips demonstrate relatively lower errors, highlighting their potential for more accurate measurements.
Assessing the percentage error in this manner allows researchers to identify and account for potential inaccuracies in their AFM measurements. By doing so, they can ensure greater precision and reliability in their nanomechanical characterizations of biological materials.
All the tested measurements have an indentation depth of approximately 1 μm (Figure S1). For conical indentations, we ensured that the maximum indentation depth is significantly larger than the tip apex radius (approximately 20 nm) to guarantee the applicability of Sneddon’s equation (Equation (1)). For spherical indentations, Hertz equation (equation (2)) is valid for hmax ≪ R [25]. However, a very small indentation depth can result in significant errors in contact point determination [26]. Indentation depths greater than 400 nm are required to avoid errors due to uncertain determination of the contact point [26]. In the case of the measurements presented in this paper, hmax/R ≈ 0.4 (since hmax ≈ 1 μm and R = 2.5 μm). According to previous studies [25], this ratio yields an approximately 4 % error in the calculation of Young’s modulus, which is considered small compared to other experimental uncertainties. It should also be noted that accurate expressions for deep spherical indentations are presented in [25].
3.4 Error measurement due to tip damage
A crucial parameter in AFM measurements is the AFM tip, and potential damage to the tip during use can significantly alter the measurements. As described in the Methodology section, collagen-coated hydrogels can be employed not only as calibration standards but also to assess errors that might arise from tip damage during repeated measurements. This assessment involves several steps, Initial Stiffness Measurement, Experimental Measurements, Post-Experiment Stiffness Measurement and Error Estimation as presented in the methodology section.
Using the MLCT-BIO-C cantilever on a 0.5 kPa collagen hydrogel and the MLCT-BIO-D cantilever on a 1.0 kPa collagen hydrogel, we conducted initial measurements as presented in Section 3.1. We then conducted experiments on lung cells (∼20 cells) with the MLCT-BIO-C cantilever and a human lung specimen (∼15 maps) with the MLCT-BIO-D cantilever. Subsequently, the same tips/cantilevers were used to measure the same hydrogels again.
The results presented in Figure 2 show a significant alteration in the Young’s modulus measurements, indicating potential tip damage. Table 2 summarizes the calculated errors based on Equation (5). By using the Normalization Factor (NF) to normalize the measurements (third column in the panels of Figure 2), we recalculated the error, demonstrating that the NF minimizes the error and enhances measurement accuracy.

Young’s modulus measurements before and after biological material experiments, demonstrating the effect of cantilever damage.
Error estimation due to tip damage.
| Cantilever/tip | Hydrogel stiffness (kPa) | Initial Ebefore (kPa) | Post-experiment Eafter (kPa) | Error (%) | Normalized post-experiment Eafter (kPa) | Error after normalization (%) |
|---|---|---|---|---|---|---|
| MLCT-BIO-C | 0.5 | 0.46 | 0.33 | 28.88 | 0.36 | 22.75 |
| MLCT-BIO-D | 1.0 | 1.21 | 1.30 | −7.73 | 1.08 | 10.80 |
The first column shows initial measurements of collagen-coated hydrogels (0.5 kPa and 1.0 kPa) using MLCT-BIO-C and MLCT-BIO-D cantilevers, respectively. The second column shows post-experiment measurements of the same hydrogels, indicating changes in measured Young’s modulus due to potential cantilever damage. The third column presents normalized measurements using the Normalization Factor (NF), highlighting improved accuracy.
By applying the NF, we can significantly reduce the measurement error attributed to cantilever damage, ensuring the integrity and reliability of AFM measurements in subsequent experiments. This approach enables more precise nanomechanical characterizations of biological materials, accounting for potential deviations due to repeated tip use.
3.5 Physical considerations and reasons behind the errors
In previous sections, it was demonstrated that the cantilever’s spring constant, the geometry of the AFM tip, and the excessive use of a tip significantly influence Young’s modulus calculations. The reasons behind these effects are presented in this section. More specifically, a major question that arises from the analysis presented above is why the choice of the spring constant so significantly affects the measurements of Young’s modulus. To accurately assess the mechanical properties of a biological system, it is essential to select cantilevers with spring constants that closely match the stiffness of the system [13]. If the cantilever is significantly stiffer than the sample, the resulting deflection will be minimal, rendering the measurement insensitive. In this case there is not ‘abrupt’ increase of force when the indenter comes into contact with the sample. Therefore, there is a major uncertainty regarding the contact point determination as presented in Figure 3. To provide a brief explanation, consider an experiment using a pyramidal tip, which can be approximated as a cone with the same projected contact area as the actual tip at the same indentation depth. For example, according to the manufacturer, the front, back, and side angles of the MLCT tips used in this paper are 35 ± 2°. To simplify the analysis, we can consider an equivalent cone with a half-angle of θ ≈ 29° according to the mathematical procedure described in [27], and use Sneddon’s equation (equation (1)) for conical indenters. The indentation depth is defined as h = z − δ, where z is the sample’s displacement towards the AFM tip (also known as “piezo-displacement” due to the piezoelectric material below the tested sample), and δ is the cantilever’s deflection (which equals the “piezo-displacement” when testing a hard material that is not deformed by the indenter, such as mica). If the contact point is at “point A,” then the maximum indentation depth would be hmax(A). If the contact point is at “point B,” the maximum indentation depth would be hmax(B), where hmax(A) > hmax(B).

When using cantilevers with large spring constants on soft samples, there is no abrupt increase in the applied force on the sample, making the determination of the contact point very difficult. The contact point in the F–z curve could be either ‘point A’ or ‘point B’ or any point in between.
The work done by the indenter (which is equal to the area under the force (F)-indentation (h) curve) can be easily calculated as follows:
Therefore, the Young’s modulus equals to:
Choosing “point A” or “point B” as the contact point in the Figure 3 will have minimal influence on the work done by the indenter due to the very small forces present at the initial stage of the experiment (as previously mentioned, the cantilever is only slightly deflected, which makes determining the contact point difficult). However, the maximum indentation depth is significantly affected. Thus, if hmax(A) > hmax(B) and WA
It is also important to note that a stiff cantilever may result in large indentation depths, leading to a substrate effect. In this case, Young’s modulus will be significantly overestimated (the maximum indentation depth should not exceed 10 % of the sample’s thickness) [13].
In addition, the average stiffness of the system when using a conical indenter can be calculated as follows:
while for a spherical indenter,
Equations (8) and (9) offer a straightforward explanation for why the micro-spherical tip with k = 0.08 N/m was more suitable for both samples (with E = 0.5 kPa and 1 kPa). The average stiffness when using a conical indenter is proportional to the indentation depth (equation (8)), so it can vary widely. In other words, depending on the indentation depth (or the maximum applied force on the sample), the average stiffness can be similar to or significantly different from the cantilever’s spring constant (an experiment with a maximum indentation depth of 1,000 nm results in an average stiffness that is an order of magnitude larger compared to an experiment with a maximum indentation depth of 100 nm). On the other hand, when using a spherical tip, the average stiffness is proportional to the square root of the maximum indentation depth, resulting in a much smaller variation in average stiffness when the indentation depth is changed. Therefore, a micrometer-sized spherical indenter with an appropriate spring constant can be effectively used across a wide range of materials with Young’s moduli of the same order of magnitude. Another reason for the suitability of spherical tips is related to the linear elastic behavior of the sample. In particular, the applied strains should not exceed 20 % [13]. The deformation of the sample when using a conical can be approximated to [18]:
Therefore, a conical indenter with θ ≈ 29° can cause significant deformation, making it difficult to describe the behavior using equations derived from linear elastic models. On the other hand, when using a spherical indenter [28],
Thus, using spherical tips with micrometer-sized diameters will result in low strain, ensuring that linear elastic models remain valid.
In addition, significant errors in determining Young’s modulus can arise from extensive use of the AFM tip. As shown in Table 2, tip damage can lead to either overestimation or underestimation of the calculated Young’s modulus. The overestimation can be easily explained by modelling the tip as a truncated cone (a simplified geometric representation of a blunt tip [29]. The results for this case can also be extended to more complex models, such as the sphero-conical model of the tip). As previously shown in [29] when using a truncated cone, the applied force on the sample equals to:
The first term on the right side of Equation (12) is Sneddon’s classic equation, while the second term is a correction factor accounting for tip damage. The magnitude htip represents the difference in indentation depth between using a perfect conical indenter and a truncated cone [29]. By comparing Equations (1) and (12) and considering that E is the actual Young’s modulus while E c is the Young’s modulus obtained using Equation (1) instead of Equation (12) for data processing, it is easy to derive the following equation [29]:
Depending on the extent of tip damage (i.e., the value of htip), the Young’s modulus can be significantly overestimated – by as much as 150 %, as shown in [29]. The possibility of underestimating Young’s modulus is also significant. Consider a scenario where contamination of the AFM tip substantially affects the attractive surface forces (such as adhesion) between the tip and the sample. In this case,
In Equation (14), FSn/Hetrz represents the classic Sneddon/Hertz equations (i.e., Equations (1) and (2)), while Fattr⋅ denotes the attractive forces from the surface. As shown, using Equation (12), which adds a term to the classic Sneddon equation, can lead to a significant overestimation of Young’s modulus if Equation (1) is used for data processing instead of Equation (12). Therefore, by subtracting the term Fattr⋅, we can conclude that there may be a significant underestimation of Young’s modulus when using Equation (1) if attractive forces have increased due to contamination (the case of the MLCT-BIO C tips in Table 2).
3.6 Proof of concept: human lung specimens
As a proof of concept for the proposed methodology, we used human lung fibroblasts (FBs) and human lung specimens from a patient with pulmonary fibrosis. To carry out the measurements, we employed the MLCT-C and MLCT-D cantilevers, respectively. In cases where there is a non-negligible influence from the substrate effect, equations (1) and (2) can be corrected by adding a correction function f(h, H), where h is the indentation depth and H is the sample’s thickness, as discussed in [26], [30], [31]. The only difference is that the force-indentation data should be fitted to these extended equations instead of fitting them to (1) and (2) [26], [30], [31], [32], [33]. At this point, it is important to note that the bottom effect correction for conical indenters was first studied by Gavara and Chadwick [26]. However, when applying this model, the force exerted by a conical tip on the sample does not converge as more terms are included in the force calculation. This issue was identified by Garcia and Garcia, who corrected the equation for conical indenters [32]. In Garcia and Garcia’s expression, the forces for the third and fourth orders are almost identical [32]. Finite element simulations have demonstrated the accuracy of the corrected equation [32].
3.6.1 Lung cells
For the cellular measurements, we employed the softer cantilever, MLCT-BIO-C, which has a lower spring constant suited for measuring softer biological materials. The initial measurements, without applying the Normalization Factor (NF), yielded an average Young’s modulus of 0.666 kPa (Figure 4A). Upon applying the normalization methodology, the average Young’s modulus was adjusted to 0.724 kPa. The percentage error associated with these measurements was calculated to be 8 %. This adjustment demonstrates the importance of normalization in correcting for systematic overestimation and ensuring the accuracy of AFM measurements.

Proof-of-concept application of the proposed methodology. (A) Human lung cells elasticity with and without normalization. For the cells we used the MLCT-BIO-C cantilever. (B) Elasticity spectrum of human lung specimens with pulmonary fibrosis. The solid line represents the average Young’s modulus (∼0.48 kPa) obtained from direct measurements using the MLCT-BIO-D cantilever. The dotted line represents the normalized average Young’s modulus (∼0.4 kPa) after applying the proposed normalization methodology. The normalization corrects for the systematic overestimation of stiffness, shifting the spectrum to lower values.
3.6.2 Human lung specimens
Initially, we calibrated our system by measuring on collagen hydrogel with a predefined stiffness of 1.0 kPa. This provided a baseline for comparison. Following the calibration, we measured the tissue specimens, systematically obtaining 15 maps across the length of the specimen. After these measurements, we recalibrated by measuring the collagen-coated hydrogels again to ensure consistency and accuracy in our readings (some of these data were presented in the previous subsections).
From the tissue measurements, we calculated the average Young’s modulus, which was approximately 0.48 kPa. This value was used to form the Elasticity spectrum in terms of Young’s modulus values, represented by the solid line in Figure 4. The measurements indicated variability in tissue stiffness, characteristic of the heterogeneous nature of pulmonary fibrosis.
Applying the proposed methodology, we proceeded to normalize the obtained data. This involved calculating the normalized factor (NF) and subsequently the normalized average Young’s modulus, which was approximately 0.4 kPa. The normalized elasticity spectrum is depicted by the dotted line in Figure 4. Errors were meticulously calculated to ensure the robustness of our results.
The comparison between the original and normalized elasticity spectrums reveals a clear shift to lower values post-normalization. This shift aligns with our previous findings that indicated an overestimation of stiffness with the MLCT-D cantilever. The normalization process effectively adjusts for this overestimation, providing a more accurate representation of the tissue’s mechanical properties.
Overall, this proof of concept demonstrates the efficacy of our proposed methodology in accurately characterizing the mechanical properties of human lung tissue specimens, particularly in the context of pulmonary fibrosis. The normalization process corrects for systematic overestimation, ensuring the reliability and accuracy of our measurements.
From the proof of concept section and the previous sections, it is evident that calibration with hydrogels is essential for obtaining more accurate estimations of Young’s modulus values. The use of collagen-coated hydrogels with predefined stiffness values allows for precise calibration of the AFM system, helping to account for potential measurement errors. Furthermore, the correction factors depend significantly on the type of cantilever used, highlighting the importance of selecting appropriate cantilevers for specific measurements. This approach ensures the reliability and accuracy of nanomechanical characterizations of biological materials, particularly when dealing with the complexities of soft tissues like those found in pulmonary fibrosis.
4 Discussion and conclusions
In this study, we demonstrated a novel methodology utilizing collagen-coated hydrogels with predefined stiffness as calibration standards for Atomic Force Microscopy (AFM) measurements of soft biological materials, particularly cells and tissues. This approach addresses common issues in AFM, such as the selection of appropriate cantilevers and the assessment of systematic errors, including those induced by AFM-tip damage. By employing collagen-coated hydrogels, we were able to calibrate our system accurately, calculate normalization factors, and assess measurement errors. The application of this methodology to human lung cells and tissue specimens from a patient with pulmonary fibrosis confirmed its effectiveness.
The use of hydrogels as calibration standards for AFM-based mechanical measurements is well-established, as evidenced by studies utilizing materials such as polyacrylamide, PDMS, and agarose. However, many of these gels, including those sold by manufacturers, are limited in their stiffness range. For example, commercially available PDMS gels typically have a stiffness around some MPa, which is not representative of most biological tissues. In contrast, the collagen-coated hydrogels used in our study offer a broad range of stiffness values (0.1–100 kPa), which are more aligned with the mechanical properties of biological environments such as the lung, where a stiffness of 1 kPa closely mimics its physiological condition.
While other studies, such as Guo et al. and Kain et al., have used agarose gels for AFM calibration, these gels require in-lab preparation and an additional characterization step, introducing variability between laboratories [34], [35]. Our approach, using commercially available collagen-coated hydrogels, minimizes this variability and provides a convenient, biologically relevant calibration standard. This is particularly important for our study, as collagen-coated hydrogels allow for both calibration and direct cell culture, thus providing a more physiologically accurate environment for nanoindentation measurements. Moreover, compared to complex methods like SNAP [12], which requires special equipment and software, our methodology offers a simpler and more accessible alternative for researchers in this field.
We selected collagen-coated hydrogels for this study due to their biological relevance and suitability for interrogating cellular mechanics. Collagen is the major component of the extracellular matrix (ECM) and is biocompatible, making it an ideal substrate for studying cellular behaviour in environments that closely mimic in vivo conditions. Unlike polyacrylamide hydrogels, which are commonly used as standard substrates for nanoindentation, collagen-coated hydrogels support direct cell culturing, providing a more accurate representation of cellular interactions with the ECM. This is particularly important in research involving the tumour microenvironment and diseases like pulmonary fibrosis, where collagen plays a pivotal role. Additionally, the commercially available collagen-coated hydrogels used in our methodology streamline the experimental setup by eliminating the need for gel preparation, while also allowing for seamless calibration and nanoindentation measurements directly on cultured cells.
One important consideration when using collagen-based hydrogels as calibration standards is the correlation between the macroscopic modulus, measured through techniques such as Hertzian indentation (which is used by the manufactured), and the modulus measured by AFM. While the manufacturer provides stiffness values based on macroscopic indentation, these values have been shown to correlate well with AFM-based measurements according to the manufacture. However, as discussed in the literature [36], the mechanical properties of soft materials like hydrogels can exhibit scale-dependent behaviour, leading to discrepancies between bulk and microscale measurements. This can arise due to factors such as surface roughness, local heterogeneity, or the influence of the thin collagen coating. In our study, we rely on the stiffness values provided by the manufacturer but acknowledge the potential for variations in the AFM-measured modulus due to these factors. Also, in our approach, the absolute value of the calibration standard is not always critical, as selecting the appropriate cantilever primarily requires an approximation of the material’s Young’s modulus, while assessing errors due to tip damage relies on comparing the values measured with the same setup before and after completing a set of measurements. Future studies could benefit from further validation of AFM-based stiffness measurements against macroscopic data, particularly when working with biologically relevant soft materials like hydrogels.
Our findings showed that normalization corrects the Young’s modulus values estimations, resulting in more accurate measurements of cell and tissue mechanical properties. This proof of concept highlights the potential of our methodology to enhance the precision and reliability of AFM-based nanomechanical characterizations, contributing to a better understanding of cellular mechanics and disease progression.
Concerning the used collagen-coated hydrogels our study showed that these hydrogels offer several advantages for AFM-based mechanical measurements, particularly in studies requiring biologically relevant environments. The collagen coating enables direct cell culture on a physiologically relevant substrate, mimicking the ECM, which is crucial for investigating cellular behaviour in conditions such as tumour microenvironments or pulmonary fibrosis. While synthetic hydrogels like polyacrylamide and agarose are more homogeneous and reproducible, they lack the biological relevance provided by collagen. The collagen-coated hydrogels used in this study combine the reproducibility of polyacrylamide with the biological significance of collagen, offering a reliable yet relevant calibration standard for AFM measurements. Additionally, using commercially available hydrogels reduces the variability and time-consuming preparation associated with manually produced collagen gels, ensuring greater consistency in mechanical properties across experiments.
In the future, this methodology could be expanded to include other soft biological materials, enabling its application in a broader range of studies, such as different disease models or cell mechanics investigations. Additionally, exploring the use of alternative hydrogels or biological specimens may further enhance the versatility of the method. Future research should also aim to refine this approach, addressing limitations such as tip damage and cantilever selection errors, to improve the precision and reliability of AFM-based nanomechanical characterizations. These advancements will be crucial for deepening our understanding of cellular mechanics and their role in disease progression.
Funding source: The project is implemented under the programme of social cohesion “THALIA 2021–2027” co-funded by the European Union, through Research and Innovation Foundation
Award Identifier / Grant number: “MechanoLung” (EXCELLENCE/0421/0263)
Acknowledgments
The authors would like to express their gratitude to Prof. M. Lekka (Department of Biophysical Microstructure, The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences) for providing the cell lines used in part of the experiments described in this paper.
-
Research ethics: Patients were recruited at the Nicosia Lung Center by Dr. Zachariades. Those who consented provided tissue samples for research. The Cyprus National Bioethics Committee (licenses EEBK/EΠ/2022/04) approved all procedures and experimental protocols.
-
Informed consent: Informed consent was obtained from all individuals included in this study, or their legal guardians or wards.
-
Author contributions: Conceptualization: AS, Methodology: AS, SVK, Software: AS, SVK, Formal analysis: AS, SVK,KP, Investigation: AS, Resources: AS, AZ, Writing Original Draft: AS, SVK, Writing Review & Editing: AS, SVK, Visualization: AS, SVK, Supervision: AS, Funding acquisition: AS.
-
Use of Large Language Models, AI and Machine Learning Tools: None declared.
-
Conflict of interest: The authors state no conflict of interest.
-
Research funding: This work was conducted under the project “MechanoLung” (EXCELLENCE/0421/0263). The project is implemented under the programme of social cohesion “THALIA 2021–2027” co-funded by the European Union, through Research and Innovation Foundation.
-
Data availability: The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
[1] V. J. Morris, A. R. Kirby, and A. P. Gunning, Atomic Force Microscopy for Biologists, London, Imperial College Press, 2008.10.1142/9781848164680Search in Google Scholar
[2] A. Magazzù and C. Marcuello, “Investigation of soft matter nanomechanics by atomic force microscopy and optical tweezers: a comprehensive review,” Nanomaterials, vol. 13, no. 963, p. 963, 2023. https://doi.org/10.3390/nano13060963.Search in Google Scholar PubMed PubMed Central
[3] M. Li, D. Dang, L. Liu, N. Xi, and Y. Wang, “Atomic force microscopy in characterizing cell mechanics for biomedical applications: a review,” IEEE Trans. NanoBiosci., vol. 16, no. 6, pp. 523–540, 2017. https://doi.org/10.1109/tnb.2017.2714462.Search in Google Scholar
[4] M. Eroles and F. Rico, “Advances in mechanical biomarkers,” J. Mol. Recognit., vol. 36, no. 8, 2023, Art. no. e3022. https://doi.org/10.1002/jmr.3022.Search in Google Scholar PubMed
[5] T. M. Kiio and S. Park, “Nano-scientific application of atomic force microscopy in pathology: from molecules to tissues,” Int. J. Med. Sci., vol. 17, no. 7, pp. 844–858, 2020. https://doi.org/10.7150/ijms.41805.Search in Google Scholar PubMed PubMed Central
[6] A. Stylianou, S. V. Kontomaris, E. Alexandratou, and C. Grant, “Atomic Force Microscopy on biological materials related to pathological conditions,” Scanning, vol. 2019, 2019, Art. no. 8452851. https://doi.org/10.1155/2019/8452851.Search in Google Scholar PubMed PubMed Central
[7] F. Gołek, P. Mazur, Z. Ryszka, and S. Zuber, “AFM image artifacts,” Appl. Surf. Sci., vol. 304, pp. 11–19, 2014. https://doi.org/10.1016/j.apsusc.2014.01.149.Search in Google Scholar
[8] B. Voigtländer, “Artifacts in AFM,” in Atomic Force Microscopy, B. Voigtländer, Ed., Cham, Springer International Publishing, 2019, pp. 137–147.10.1007/978-3-030-13654-3_8Search in Google Scholar
[9] S. Kim, Y. Lee, M. Lee, S. An, and S. J. Cho, “Quantitative visualization of the nanomechanical Young’s modulus of soft materials by atomic force microscopy,” Nanomaterials, vol. 11, no. 159, 2021. https://doi.org/10.3390/nano11061593.Search in Google Scholar PubMed PubMed Central
[10] D. Almasi, R. Sharifi, M. R. A. Kadir, G. Krishnamurithy, and T. Kamarul, “Study on the AFM force curve common errors and their effects on the calculated nanomechanical properties of materials,” J. Eng., vol. 2016, 2016, Art. no. 2456378. https://doi.org/10.1155/2016/2456378.Search in Google Scholar
[11] K.-H. Chung, Y.-H. Lee, and D.-E. Kim, “Characteristics of fracture during the approach process and wear mechanism of a silicon AFM tip,” Ultramicroscopy, vol. 102, no. 2, pp. 161–171, 2005. https://doi.org/10.1016/j.ultramic.2004.09.009.Search in Google Scholar PubMed
[12] H. Schillers, et al., “Standardized nanomechanical atomic force microscopy procedure (SNAP) for measuring soft and biological samples,” Sci. Rep., vol. 7, no. 1, p. 5117, 2017. https://doi.org/10.1038/s41598-017-05383-0.Search in Google Scholar PubMed PubMed Central
[13] M. Krieg, et al.., “Atomic force microscopy-based mechanobiology,” Nat. Rev. Phys., vol. 1, pp. 41–57, 2019. https://doi.org/10.1038/s42254-018-0001-7.Search in Google Scholar
[14] K. Haase and A. E. Pelling, “Investigating cell mechanics with atomic force microscopy,” J. R. Soc., Interface, vol. 12, 2015, Art. no. 20140970. https://doi.org/10.1098/rsif.2014.0970.Search in Google Scholar PubMed PubMed Central
[15] M. Lekka, “Discrimination between normal and cancerous cells using AFM,” BioNanoScience, vol. 6, pp. 65–80, 2016. https://doi.org/10.1007/s12668-016-0191-3.Search in Google Scholar PubMed PubMed Central
[16] A. Stylianou, V. Gkretsi, and T. Stylianopoulos, “Atomic force microscopy nano-characterization of 3D collagen gels with tunable stiffness,” MethodsX, vol. 5, pp. 503–513, 2018. https://doi.org/10.1016/j.mex.2018.05.009.Search in Google Scholar PubMed PubMed Central
[17] A. Stylianou, V. Gkretsi, C. S. Patrickios, and T. Stylianopoulos, “Exploring the nano-surface of collagenous and other fibrotic tissues with AFM,” in Fibrosis: Methods and Protocols, L. Rittié, Ed., New York, NY, Springer, 2017, pp. 453–489.10.1007/978-1-4939-7113-8_29Search in Google Scholar PubMed
[18] A. Stylianou, C. Voutouri, T. Stylianopoulos, and F. Mpekris, “Pancreatic cancer presents distinct nanomechanical properties during progression,” Ann. Biomed. Eng., vol. 51, no. 7, pp. 1602–1615, 2023. https://doi.org/10.1007/s10439-023-03168-3.Search in Google Scholar PubMed
[19] A. Stylianou, V. Gkretsi, M. Louca, L. Zacharia, and T. Stylianopoulos, “Collagen content and extracellular matrix stiffness remodels pancreatic fibroblasts cytoskeleton,” J. R. Soc., Interface, vol. 16, 2019, Art. no. 20190226. https://doi.org/10.1098/rsif.2019.0226.Search in Google Scholar PubMed PubMed Central
[20] A. Stylianou, V. Gkretsi, and T. Stylianopoulos, “Transforming growth factor-β modulates pancreatic cancer associated fibroblasts cell shape, stiffness and invasion,” Biochim. Biophys. Acta, vol. 1862, no. 7, pp. 1537–1546, 2018. https://doi.org/10.1016/j.bbagen.2018.02.009.Search in Google Scholar PubMed PubMed Central
[21] P. Hermanowicz, M. Sarna, K. Burda, and H. Gabryś, “AtomicJ: an open source software for analysis of force curves,” Rev. Sci. Instrum., vol. 85, 2014, Art. no. 063703. https://doi.org/10.1063/1.4881683.Search in Google Scholar PubMed
[22] V. Gkretsi, A. Stylianou, M. Louca, and T. Stylianopoulos, “Identification of Ras suppressor-1 (RSU-1) as a potential breast cancer metastasis biomarker using a three-dimensional in vitro approach,” Oncotarget, vol. 8, no. 16, pp. 27364–27379, 2017. https://doi.org/10.18632/oncotarget.16062.Search in Google Scholar PubMed PubMed Central
[23] K. Kapnisis, et al., “Multi-level assessment of stent-induced inflammation in the adjacent vascular tissue,” Acta Biomater. Sci. Eng., vol. 9, no. 8, pp. 4747–4760, 2023. https://doi.org/10.1021/acsbiomaterials.3c00540.Search in Google Scholar PubMed PubMed Central
[24] A. Stylianou, et al.., “Nanomechanical properties of solid tumors as treatment monitoring biomarkers,” Acta Biomater., vol. 154, pp. 324–334, 2022. https://doi.org/10.1016/j.actbio.2022.10.021.Search in Google Scholar PubMed
[25] S. V. Kontomaris and A. Malamou, “A novel approximate method to calculate the force applied on an elastic half space by a rigid sphere,” Eur. J. Phys., vol. 42, 2021, Art. no. 025010. https://doi.org/10.1088/1361-6404/abccfb.Search in Google Scholar
[26] N. Gavara and R. S. Chadwick, “Determination of the elastic moduli of thin samples and adherent cells using conical atomic force microscope tips,” Nat. Nanotechnol., vol. 7, no. 11, pp. 733–736, 2012. https://doi.org/10.1038/nnano.2012.163.Search in Google Scholar PubMed PubMed Central
[27] S. V. Kontomaris, A. Malamou, and A. Stylianou, “The Hertzian theory in AFM nanoindentation experiments regarding biological samples: overcoming limitations in data processing,” Micron, vol. 155, 2022, Art. no. 103228. https://doi.org/10.1016/j.micron.2022.103228.Search in Google Scholar PubMed
[28] V. L. Popov, Contact Mechanics and Friction: Physical Principles and Applications, Heidelberg, Springer Berlin, 2010.Search in Google Scholar
[29] S.-V. Kontomaris and A. Malamou, “The truncated cone effect in AFM nanoindentation on soft materials,” Micro Nanosyst., vol. 15, no. 2, pp. 153–158, 2023. https://doi.org/10.2174/1876402915666230209140024.Search in Google Scholar
[30] E. K. Dimitriadis, F. Horkay, J. Maresca, B. Kachar, and R. S. Chadwick, “Determination of elastic moduli of thin layers of soft material using the atomic force microscope,” Biophys. J., vol. 82, no. 5, pp. 2798–2810, 2002. https://doi.org/10.1016/s0006-3495(02)75620-8.Search in Google Scholar
[31] J. A. C. Santos, L. M. Rebêlo, A. C. Araujo, E. B. Barros, and J. S. de Sousa, “Thickness-corrected model for nanoindentation of thin films with conical indenters,” Soft Matter, vol. 8, pp. 4441–4448, 2012. https://doi.org/10.1039/c2sm07062f.Search in Google Scholar
[32] P. D. Garcia and R. Garcia, “Determination of the elastic moduli of a single cell cultured on a rigid support by force microscopy,” Biophys. J., vol. 114, no. 12, pp. 2923–2932, 2018. https://doi.org/10.1016/j.bpj.2018.05.012.Search in Google Scholar PubMed PubMed Central
[33] B. L. Doss, K. Rahmani Eliato, K.-H. Lin, and R. Ros, “Quantitative mechanical analysis of indentations on layered, soft elastic materials,” Soft Matter, vol. 15, pp. 1776–1784, 2019. https://doi.org/10.1039/c8sm02121j.Search in Google Scholar PubMed
[34] X. Guo, K. Bonin, K. Scarpinato, and M. Guthold, “The effect of neighboring cells on the stiffness of cancerous and non-cancerous human mammary epithelial cells,” New J. Phys., vol. 16, 2014, Art. no. 105002. https://doi.org/10.1088/1367-2630/16/10/105002.Search in Google Scholar
[35] L. Kain, et al.., “Calibration of colloidal probes with atomic force microscopy for micromechanical assessment,” J. Mech. Behav. Biomed. Mater., vol. 85, pp. 225–236, 2018. https://doi.org/10.1016/j.jmbbm.2018.05.026.Search in Google Scholar PubMed
[36] E. S. Krivega, S. L. Kotova, P. S. Timashev, and Y. M. Efremov, “Mechanical characterization of soft biomaterials: which time and spatial scale to choose?” Soft Matter, vol. 20, pp. 5095–5104, 2024. https://doi.org/10.1039/d4sm00530a.Search in Google Scholar PubMed
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/mim-2024-0014).
© 2024 the author(s), published by De Gruyter on behalf of Thoss Media
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Editorial
- What is open access and what is it good for?
- News
- Community news
- View
- Optical sectioning in fluorescence microscopies is essential for volumetric measurements
- Review Article
- Wrapped up: advancements in volume electron microscopy and application in myelin research
- Research Articles
- Reducing artifact generation when using perceptual loss for image deblurring of microscopy data for microstructure analysis
- Utilizing collagen-coated hydrogels with defined stiffness as calibration standards for AFM experiments on soft biological materials: the case of lung cells and tissue
- Phase characterisation in minerals and metals using an SEM-EDS based automated mineralogy system
- Corrigendum
- Corrigendum to: FAST-EM array tomography: a workflow for multibeam volume electron microscopy
Articles in the same Issue
- Frontmatter
- Editorial
- What is open access and what is it good for?
- News
- Community news
- View
- Optical sectioning in fluorescence microscopies is essential for volumetric measurements
- Review Article
- Wrapped up: advancements in volume electron microscopy and application in myelin research
- Research Articles
- Reducing artifact generation when using perceptual loss for image deblurring of microscopy data for microstructure analysis
- Utilizing collagen-coated hydrogels with defined stiffness as calibration standards for AFM experiments on soft biological materials: the case of lung cells and tissue
- Phase characterisation in minerals and metals using an SEM-EDS based automated mineralogy system
- Corrigendum
- Corrigendum to: FAST-EM array tomography: a workflow for multibeam volume electron microscopy


