Abstract
Cloud computing is an emerging technology in distributed computing, which facilitates pay per model as per user demand and requirement. Cloud consists of a collection of virtual machines (VMs), which includes both computational and storage facility. In this paper, a task scheduling scheme on diverse computing systems using a hybridization of genetic and group search optimization (GGSO) algorithm is proposed. The basic idea of our approach is to exploit the advantages of both genetic algorithm (GA) and group search optimization algorithms (GSO) while avoiding their drawbacks. In GGSO, each dimension of a solution symbolizes a task, and a solution, as a whole, signifies all task priorities. The important issue is how to assign user tasks to maximize the income of infrastructure as a service (Iaas) provider while promising quality of service (QoS). The generated solution is competent to assure user-level (QoS) and improve Iaas providers’ credibility and economic benefit. The GGSO method also designs the producer, scrounger ranger, crossover operator, and suitable fitness function of the corresponding task. According to the evolved results, it has been found that our algorithm always outperforms the traditional algorithms.
1 Introduction
Cloud computing has, as of late, developed as an appealing model of offering information technology (IT) foundation (i.e. registering, stockpiling, and system) to expansive and, in addition, little endeavors both in private and open areas [2], [6]. Cloud administration suppliers offer these administrations focused around altered service-level agreements (SLAs), which characterize the client’s obliged quality of service (QoS) parameters. Distributed computing decreases speculation in different assets like equipment, programming [10], and permit assets to be rented and discharged. It decreases beginning speculation, support cost, and working expenses. Cloud administrations are facilitated on administration supplier’s own particular framework or on outsider cloud foundation suppliers [27]. As a critical piece of distributed computing, infrastructure as a service (Iaas) gets to be exceptionally well known as the establishment for larger amount administrations [4]. Chiefly, three sorts of administrations are conveyed: platform as a service (Paas), infrastructure as a service (Iaas), and software as a service (Saas). Cloud clients utilize these administrations at whatever point required by interest utilizing pay-every-use model. Iaas suppliers, for example, Amazon EC2 and IBM Smart Cloud Enterprise [6], permit clients to lease assets as virtual machines (VMs). They can offer distinctive VM sorts that are described by machine arrangement, QoS, and estimating model. One average agent is Amazon EC2, which can give three sorts of evaluating models: on-interest, reticent, and spot [35].
Furthermore, clouds can be named public, private, and hybrid [26]. At the point when the cloud is made accessible for the general client on a pay-every-use premise, then, it is denoted as a public cloud. At the point when associations create their own particular applications and run them in the framework, then, it is referred to as a private cloud as access is restricted to clients within the association. Hybrid cloud is provided by the incorporation and combining of public and private clouds [38]. Furthermore, Millions of client offer cloud assets by submitting their registering task to the cloud framework. Scheduling these great many undertakings is a test to the distributed computing environment. Distinctive scheduling systems are proposed in Refs. [16], [21], [22], [23], [30], [31], [32], [37], [42]. These techniques consider assorted variables like expense network produced by employing credit of assignments to be appointed to a specific asset [31], QoS-based meta-scheduler, and backfill methodology-based light-weight VM scheduler for dispatching occupations [16], QoS prerequisites [31], [32], [42], heterogeneity of the cloud setting, and workloads [22].
Cloud computing can give full adaptability, dependability, superior and generally minimal effort arrangement as contrasted with devoted frameworks. The area of information stockpiling and application execution is a basic issue that needs to be tended to [31]. Furthermore, undertaking planning is a standout among the most issues in the cloud computing framework. The objective of an assignment scheduler is to relegate tasks to accessible processors such that priority necessities for these assignments are fulfilled, and in the meantime, the general performance length (i.e. makes compass) is minimized [43]. For the most part, the planning issue could be of the accompanying two sorts: static and dynamic. About the situation static scheduling, the qualities of a parallel program, for example, task preparing periods, correspondence, information conditions, and synchronization prerequisites, are known before execution [29]. As per the element planning, a couple of suppositions about the parallel system ought to be made before execution, and then, scheduling choices must be “tackled the fly” [39]. To understand the scheduling intricacy, a cloud assets assignment structure is recommended, as of late, to allow it to adventure outside mists to make an Iaas cloud, itself, versatile. In this structure, an Iaas cloud has its own particular individual cloud and is capable of outsourcing its undertakings to other cloud suppliers called external clouds when its neighborhood assets are not satisfactory [20]. Every obligation has an extreme due date to meet, so that the asset portion issue can be viewed as a due date-constrained task scheduling (DCTS) one. A number programming definition of the DCTS issue is propelled, with the motivation behind augmenting the preference of the individual cloud on the guideline of ensuring QoS. The major contribution is made in the research for task scheduling process as follows:
An approach, namely, GGSO is done for task scheduling, which has the advantages of easily realizing and quickly converging, so that this scheduling approach is able to get an optimal or suboptimal solution in a shorter computational time than individual genetic algorithm (GA) and group search optimization algorithm.
In GGSO, the hybridization uses the process of best solution replacement ahead of worst solution to improve the solution quality.
The basic organization of the paper is as follows: Section 2 presents the review of literature survey, and the system model is described in Section 3. Section 4 presents the problem definition of the approach, and the proposed algorithm design is discussed in Section 5. The result and discussion part is presented in Section 6, and the conclusion is given in Section 7.
2 Literature Survey
Assignment scheduling is vital to exploratory research processes, and task scheduling is important to test issues as well. This has been researched before in conventional conveyed figuring frameworks. Kosar et al. [18] were schedulers in the grid that ensure that assignment planning exercises were lined, planned, observed, and oversaw in an issue-tolerant way. Adapt et al. [7] clarified an undertaking planning methodology for pressing figuring situations to ensure the information’s vigor. Xie [40] have presented an energy-attentive technique for task planning in RAID organized capacity frameworks. Also, Rafique et al. [33] studied multicore computational hastening accelerators and the Map Reduce programming model for elite processing at scale in distributed computing. Another issue-tolerant scheduling strategy Maxre was clarified in Ref. [44]. This strategy consolidates the unwavering quality assessment into the dynamic replication pattern and endeavors an element number of facsimile for diverse tasks. Additionally, a conviction system-based task planning model was displayed by Wang and Zeng [36]. A trust relationship was constructed among figuring hubs, and the dependability of the hubs was assessed using the Bayesian cognitive system. A critical dynamic strategy for preemptable employment planning system is presented in Ref. [24]. A preemptable scheduling enhances the use of assets in mists and input strategy in the above strategy functions admirably in the circumstances where asset controversies are wild.
Omara and Arafa [28] clarified the GA for task scheduling issue. At this point, two GAs were utilized to take care of these planning issues. They perform GAs with some heuristic standards that have been added to enhance the execution. In Ref. [1], creators Abrishami and Naghibzadeh clarified the deadline-obliged work process planning in programming as an administration cloud. They utilized partial critical paths (PCP), which tries to minimize the expense of work process execution while meeting a client characterized due date. Furthermore, with a specific end goal to minimize the expense of the transformation, the creator Guo et al. [11] clarified the task scheduling employing the optimization strategy (PSO), which is focused around the little position quality principle. To strike the work process issue further presented the work process planning for the cloud setting focused around the artificial bee colony algorithm by Kumar and Anand [19]. Banharnsakun et al. [3] clarified the job shop scheduling with the best-so-far ABC. Now, their predisposition is the arrangement heading at the best-so-far arrangement rather than the neighboring arrangement as was proposed in the initial ABC system.
Moreover, Di and Wang [9] clarified the error-tolerant resource allocation and payment minimization to cloud system. At this juncture, they utilized (i) figure, a due date-driven asset assignment issue focused around the cloud environment encouraged by the VM asset confinement innovation, which furthermore presented a response with polynomial time, which could minimize the clients’ installment as far as their normal due dates. (ii) By dissecting the upper bound of the undertaking execution length focused around the conceivably mistaken workload expectation, they further proposed an error-tolerant strategy to ensure the task consummation inside its due date. (iii) They accepted its adequacy over a genuine VM-encouraged bunch environment under diverse levels of rivalry. In a similar manner, Khaldi et al. [17] clarified the parallelization system for logical processing focused around BDSC, a proficient programmed planning strategy for parallel projects in the vicinity of asset stipulations on the quantity of processors and their neighborhood memory size. BDSC augments Yang and Gerasoulis’ dominant sequence clustering (DSC) strategy; it uses complex expense models and locations both imparted and appropriated parallel memory architectures.
The overall mentioned works spotlighted on the neighborhood asset allotment in a solitary Iaas cloud and do not consider scheduling assignments among distinctive clouds. In addition, the priority was a vital issue of task scheduling in cloud situations. In these arrangements, Iaas suppliers reject assignment demands when their assets were not sufficient to finish those assignments; on the other hand, this has a negative effect on its guaranteed QoS and notoriety. As indicated by taking care of this issue, Zuo et al. [46] created a self-adaptive learning PSO-based deadline-constrained task scheduling for hybrid base as an administration (Iaas) Cloud. The key issue of planning was the way to apportion the clients’ assignments to augment the benefit of the Iaas supplier while ensuring QoS. This issue was planned as an integer programming (IP) demonstrate and unraveled by an adaptable toward self-adaptive learning particle swarm optimization (SLPSO)-based scheduling approach in Ref. [46]. Yet, their methodology is not suitable for high-issue example sorts because of the required execution of computational time. These analyses (especially in Zuo et al. [46]) roused to proceed with my assessment for task planning issue with the help of a hybrid optimization strategy.
3 System Model
The component-based resource allocation diagram in Figure 1 shows the software architecture used inside the deadline-constrained task scheduling project. In this part, we offer a brief overview of this architecture in order to add more to the context of the research offered in this document. The external channels present a public interface for creating and managing VM instances inside their proprietary infrastructure. ECs present a public interface for creating and managing VM instances inside their proprietary infrastructure. The private cloud and external cloud are the most important elements of the cloud computing.

Component View of a Hybrid Cloud Framework.
In the private cloud, a few of the significant components are applied, which are follows:
User interface: the user interface component is an interface through which users’ application requests (i.e. tasks) are obtained.
Request manager: user tasks are forwarded to the request manager, which gathers and manages all recognized users’ requests.
Resource monitor: the resource monitor component monitors the cloud resource pool, together with the CPU pool, memory pool, storage pool, and I/O bandwidth pool.
Cloud interface: the cloud interface gathers pricing models of ECs and sends tasks to ECs when needed.
Scheduler: the Scheduler component programs tasks to the private cloud or ECs to maximize profit. This scheduling problem is a limit-constrained task scheduling one. Initially, the scheduler component gathers scheduling data from the request manager, resource monitor, and cloud interface and then makes a decision to assign each task to either the private cloud or one of the ECs. If a task requires to be allocated to an EC, pricing models of ECs are sent to the scheduler through the cloud interface to assist in finding out a particular EC to outsource.
The aim of a task scheduler is to allocate tasks to accessible processors such that precedence requirements for these tasks are accepted, and simultaneously, the overall execution length (i.e. make span) is minimized.
4 Problem Definition
Our solution focuses on batch workload, more specially, a bag of independent tasks, each of which can be large-scale data processing, scientific simulation, or image/video rendering. This kind of bag-of-task is very familiar in enterprise applications such as customer behavior mining or sensor data study to calculate machine failure in IT infrastructure [25]. Workloads that are not wrapped by our model comprise strongly coupled tasks complex workflows and online transaction processing (OLTP). Each submitted application contains a number of embarrassingly parallel and autonomous tasks and has a firm deadline by all when all its consisting tasks must be terminated. Each task needs to be implemented in one VM instance type.
Presume that PCS={PCS1, PCS2, …, PCSn } is a set of cloud providers. Presume that this is the private cloud, and PCS2, …, PCSn are the external clouds.
Time is clearly symbolized in the IP model by bringing in time slots with a granularity of 1 h. Let T be the number of time slots; we contain S=maxi∈{1,2,…,m}(Di ). The aim is to assign the w applications to PCSk (k∈{1, 2, …, n}) to exploit the profit of PCS1.
Each task must be assigned to one PCSk (k∈{1, 2, …, n}). Once a task begins to be implemented, it can never be disrupted, so that its running slots are successive. In any time slot s(s∈{1, 2, …, S}), resources employed by all tasks performed in PCS1 can never go beyond the total resources of PCS1, and from the viewpoint of PCS1, all its ECs, have an infinite source.
The difficulty can be devised as the subsequent IP model.
Maximize
Subject to;
In eq. (1), the objective function of our research is specified. Consider the first term of eq. (1). It signifies the income of the source, and the second one means its cost. Constraint (2) assures that each task is allocated to exactly one cloud provider. Constraint (3) ensures that each task is concluded before its deadline. Constraints (4)–(6) promise that each task is non-preemptable, i.e. a task is performed without any disturbance. Constraints (7) and (8) are used to PCS1 to make certain it does not employ CPUs and memory away from its capacity, in each slot. Last, eqs. (9)–(11) provide definitions of the decision variables.
From the formulation, we can observe that the difficulty is a task allocation. Using a mathematical programming approach, working out such problems will obtain a huge amount of computational time for a big size problem. This nature forbids the use of mathematical programming in this scenario where tasks need to be planned in real time. In Figure 1, the overall diagram of our work is shown.
5 Algorithm Design
In this section, first we discuss the back ground of the group search optimization algorithm and GA. Then, the detail of the proposed algorithm GGSO will be presented.
5.1 Genetic Algorithm
A GA, introduced by Holland 1975 [15], is an iterative stochastic in which natural evaluation is used to model the search method. GAs may be used to solve the optimization problems by imitating the genetic process of a biological organism [34], [45]. As, a name suggests, GA emulates the evolutionary nature to solve the optimization problems. A simple GA includes three genetic operations: selection, crossover, and mutation. In selection, some solutions from the populations are selected as parents; in crossover, the parents are crossbred to produce an offspring; in mutation, the offspring may be ordered according to the mutation rules. In GA, solutions are called individual, and iterations of the algorithm called generation. Many GAs also employ elitism, which means that a number of the best individuals are copied to the next generation.
Unlike, other traditional search techniques, GAs use multiple search nodes simultaneously. Each of the search nodes corresponds to one of the current solutions and is represented by a sequence of symbol. Such a sequence is called chromosome, while the symbol composing the sequence are called genes. Each chromosome has an associated value called a fitness value, which is evaluated using the objective function (fitness function) value f(x). In a GA, only good chromosomes that have high fitness values survive and generate an offspring transmitting their biological heredity to new generations. By evolving the chromosome continuously, the solutions corresponding to the search nodes improve gradually. A set of chromosomes at a given stage of a GA is called a pop. The number of chromosomes (individuals) in a population is called the pop size. Elitism size is the number of fit individuals that are copied directly to the next generation. Algorithmically, the basic GA is outlined below:
Step 1: Initialize the random population of chromosomes that is a suitable solution for the problem.
Step 2: Evaluate the fitness f(x) of the chromosome in the population.
Step 3: Create a new population by replacing the following steps until the new population is complete.
Select two parent chromosomes from a population according to their fitness. The better the fitness, the bigger the chance to be selected as the parent.
With a crossover probability, cross over the parent to form new offspring, that is, children. If no crossover was performed, the offspring is the exact copy of the parent.
With a mutation probability, mutate the new offspring at each locus.
Place the new offspring in the new population.
Step 4: Use the new generated population for a further run of the algorithm.
Step 5: If the end condition is satisfied, stop and return the best solution in the current population.
Step 6: Go to step 2.
5.2 Group Search Optimization Algorithm
The GSO algorithm is first proposed by He et al. [12]. It is population-based optimization algorithm and employs the producer-scrounger (PS) model and animal scanning mechanism. The producer-scrounger model for designing optimum searching strategies was inspired by the animal searching behavior and group living theory. It has led to the adoption of two foraging strategies within groups: (1) producing, searching for food; and (2) scrounging, joining resources uncovered by others. In order not to be entrapped in local minima, GSO also employs “ranger” foraging strategies. The population of the GSO algorithm is called a group, and each individual in the population is called a member. There are three kinds of members in the group which are given below:
Producer: The producer performs producing strategies, searching for food sources, and also, at each iteration, the member who located the most promising resource is called the producer.
Scrounger: The scrounger performs scrounging strategies, joining resources uncovered by others, and also, a number of members except the producer in the group are selected as scroungers.
Ranger: The ranger employs random walk-searching strategies for randomly distributed resources, and also, in a group, aside from the producer and scroungers, the members are called rangers.
Recently, Couzin et al. [8] suggested that the larger the group, the smaller the portion of informed individuals needs to guide the group with better accuracy. Therefore, for accuracy and convenience of computation, we simplify the PS model by assuming that there is only one producer at each searching bout, and the remaining members are scroungers and rangers. It is also assumed that the producer, the scroungers, and the rangers do not differ in relevant phenotypic characteristics. Therefore, they can switch between the three roles.
5.3 GGSO Algorithm-based Task Scheduling
The objective of this research is to schedule the task based on the GGSO algorithm. Here, our hybrid optimization algorithm is designed between the GA [28] and the group search optimization algorithm [13]. Our approach is exploiting the advantages of the GA and group search optimization algorithm while avoiding their drawbacks. By hybridizing these two optimization algorithms, the disadvantages of the individual performance of the GSO and GA will be overcome, and it has the advantages of easily realizing and quickly converging, so that this scheduling approach is able to get an optimal or suboptimal solution in a shorter computational time. By our assumptions, the result section shows that the proposed optimization of the GGSO achieved better performance than the individual optimization. In our approach, at first, we apply the GSO algorithm to the application, which find out the optimal task scheduling to the corresponding application. Finally, the worst population is replaced by the crossover operator. The detailed process of the GGSO algorithm is explained below:
Step 1: Solution encoding
One of the most important matters in cloud computing is how to symbolize a solution for task scheduling. Each application encloses many tasks, such that all applications can be regarded as a set of tasks, i.e.
The ranked-order value (ROV) rule [41] is applied to work out a particle Yi =(yi1, yi2, …, yiD ) into a variation of tasks T={TK1, TK2, …, TKD } to assess this particle [20]. For instance, for a problem with five tasks (D=5), the ith particle is indicated by Yi =(6.14, 6.24, 5.47, 4.12, 4.25). The position yi2 has the greatest value, such that the task symbolized by yi2 is allocated a rank value, as illustrated in Table 1; next, yi2=6.14 is allocated a rank value two. Likewise, the rank values of 3, 4, and 5 are allocated to yi3, yi5, and yi4, correspondingly. Therefore, we can get a priority series of task,
The Parameters used in Problem Definition.
| Parameter | Variable description |
|---|---|
| N | Number of cloud provider |
| I | Number of VM type |
| M | Number of application |
| Mu | Price of the uth VM type in PCS1 |
| Cku | Cost of the uth VM type in PCSk |
| Di | Deadline of the ith application |
| Ri | Run time of each task in the ith application |
| hiu | If hiv =1, the ith application use VM type |
| CPUu | Number of CPUs for the uth VM type in PCS1 |
| uth | Size of memory for the uth VM type in PCS1 |
| total_CPU | Total number of CPUs in PCS1 |
| total_mem | Total size of memory in PCS1 |
| Xilk | Binary decision variable |
| stil | Integer decision variable |
| Vils | Binary decision variable |
Priority={2, 1, 3, 5, 4}.
The search solution is the observed task, which size is initialized by N×M
Solution Coding and Decoding.
| Dimension | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Position value | 6.16 | 6.64 | 5.57 | 4.20 | 4.38 |
| Priority | 2 | 1 | 3 | 5 | 4 |
where N means the number of the applications present in the work; M means the task.
Step 2: Evaluation of fitness function
An assessment function is required when applying the GGSO to optimize the task permutation to maximize the profit of PCS1, to work out the fitness value of each task in the application. Each task is assigned to one PCSk (k=1,2, …, n) according to its priority stated by the code of a member as shown in Table 2. We attempt to assign each task to PCS1 as the cost of PCS1 is the lowest among all clouds. If PCS1 has accessible resources to meet a task’s demand during its runtime, after that, the task is assigned to PCS1, or else, the task is assigned to an EC with minimal cost. After completing the allocation of all the tasks, the profit of PCS1 is treated as the fitness value of the particle. The fitness value of the calculation algorithm is given in Table 3.
Algorithm for Fitness Calculation.
| – Initialize, total_cost=0; avail_cpus=total_cpu, avail_mems=total_mem, s∈{1, 2, …, S}. |
| – calculate the total income using equation (13) |
| – after that we calculate the total cost of the system |
| Sort the task set T={TK1, TK2, …, TKD } in an ascending order according to the rank values represented by the code of a member. |
| Let the lth task be TKl and its start time be sTKl , l∈{1, 2, …, D}. |
| For (l=1 to D) |
| While (sTKl ≤DAP(l)+1) |
| IsPC=true |
| For each s∈{sTKl , …, sTKl +RAP(l)−1} |
| If |
| IsPC=false |
| Break for. |
| End if |
| End for |
| If (IsPC=true) |
| Calculate the cost for task TKl by |
| Update avail_cpus and avail_mems for each s∈{sTKl , …, sTKl +Rl −1} |
| Break while |
| End if |
| sTKl =sTKl +1 |
| End While |
| If IsPC=false |
| Select the EC with minimum cost using (14). |
| Calculate the cost TKl of task by |
| End if |
| total_cost=total_cost+costl |
| End for |
Step 3: Producer operation
At first, find the producer YP from the group member X based on the best fitness function. The producer is the best fitness value of Yi , and it is denoted by YP . Initially, the head angle of each individual is computed using eqs. (18)–(20).
The head angle of each individual is expressed by:
The search direction of the member based on the head angle is:
The search direction can be calculated from the head angle by using the polar and Cartesian coordinate transformation using eqs. (15)–(17).
In the GSO algorithm, at the kth iteration, the producer XP behaves as follows:
The producer will scan at 0° and then scan laterally by randomly sampling three points in the in the scanning field:
One point at 0°, the equation given in equation (21):
One point on the right-hand side in the hypercube scanning using eq. (22):
One point on the left-hand side in the hypercube scanning using eq. (23):
where r1∈R1 is a normally distributed random number with mean 0 and standard deviation 1, and r2∈Rn−1 is a uniformly distributed random sequence in the range (0, 1).
The maximum search angle θmax is given by:
The constant c is given by:
where n is the dimension of the search space
The maximum distance lmax is calculated from the following equation:
where lUi is the upper bound for the ith dimension, and lLi is the lower bound for the ith dimension. The best point with the best resource is finding, using eqs. (21)–(23), if the best point has a better resource than the present best position; then, it will switch to the new best point. Otherwise, it will remain in its position and turn the producer head to the randomly generated head angle direction, using the equation:
where αmax∈R1 is the maximum turning angle.
If the producer cannot find a better area after the α iteration, it will turn its head back to 0°:
where α→ is a constant.
Step 4: Scrounger operation
At each iteration, apart from the producer, there is a number of group members that are selected as scroungers. The common scrounging behavior in the GSO algorithm is the area copying behavior. In the kth iteration, the area copying behavior of the ith scrounger can be designed as a movement toward the producer using eq. (31).
where ∘ is the Hadamard product; it calculates the entrywise product of the two vectors and r3∈Rn−1 uniform random sequence in the range (0, 1). The ith scrounger keeps searching for the alternative opportunities to join. This behavior can be designed by turning the ith scrounger head to a new randomly generated angle (29).
Step 5: Ranger performances
The rest of the group members that are dispersed from their current position are named rangers. Rangers perform the searching strategies, which include random walks and systematic searching strategies to locate resources efficiently. Random walks are the most important searching method for randomly distributed resources. They create a random head angle using eq. (29), and also, they prefer random distance
and random walk to the new point
After completing all these procedures, calculate the fitness of the updated solution. This process is continuously followed at the li =kth iteration in order to find out the best solution. The output matrix obtained from the GSO algorithm is denoted as “A”. The pseudocode for the GSO algorithm is listed in Table 4.
Overall Process of GSO Algorithm.
| Set K=0 |
| Randomly initialize the position Yi and head angle ϕi of all members |
| Calculate the fitness value of the initial members: f(Yi ) |
| WHILE (the termination conditions are not met) |
| FOR (each members i in the group) |
| Choose producer: Find the producer Yp in the group; |
| Perform producing: |
| 1) the producer will scan at zero degree and then scan laterally by randomly sampling three points in the scanning field using (21) to (23) |
| 2) Find the best point with the best resource (fitness value). If the best point has a best resource than its current position, then it will fly to this point. Otherwise it will stay in its current position and turn its head to a new angle Using (29) |
| 3) If the producer cannot find to a better area α iteration, it will turn its head back to zero degree using (30) |
| Perform scrounging: Randomly select 80% from the rest members to perform scrounging. |
| Perform ranging: For the rest members they will be perform ranging: 1) generate a random |
| head angle using (29); and 2) choose a random distance li from the |
| Gaussian distribution using (32) and move to the new point using (33) |
| Check feasibility: Check weather each member of the group violates the constraints. If it |
| does, it will move back to the previous position to guarantee a feasible |
| solution. |
| END FOR |
| Set k=k+1; |
| END WHILE |
Step 6: Crossover operation
After completing the GSO operation, we will do the genetic operator to the worst of the GSO solution. In our work, the most dominant genetic operator is crossover, as it usually changes the solutions most. A crossover is a procedure of replacing some of the genes in one parent by the corresponding genes of the other. In the task scheduling problem, the crossover operator combines two valid parents, whose subtasks are ordered topologically to generate two offspring that will also be valid. Here, the crossover operator takes a pair of the worst chromosomes selected from the GSO operation. After that, it chooses a crossover point Cr at random for each chromosome and then exchanges portions of their genes based on the crossover point. In this paper, a single point crossover is applied. For example, there are eight subtasks, and a chromosome is coded as an integer list shown in Figure 2. Suppose that the first chromosome selected from the obtained worst population (obtained using GSO) is denoted as the father (i), and the second chromosome selected from the obtained worst population (obtained using GSO) is denoted as mother (j). When Cr =4, two parents swap some genes to generate two offspring by means of single-point crossover operator. The left segment of the son or daughter is inherited from the corresponding segment of the father (2, 4, 6, 8) or mother (1, 3, 5, 7), respectively. Here, we can delete the subtasks from the topological order, and it will still be a topological order (total order) without violating the precedence constraints. For, example, the left segment of the mother is still a topological order (5, 7, 13, 15), when we delete the subtasks that are in the left segment of father (1, 2, 3, 4). Similarly, the left segment of the father is still a topological order (4, 6, 10, 16), when we delete the subtasks that are in the left segment of the mother (1, 3, 5, 7). Finally the genes of the right segment of the son is copied from the mother (5, 7, 13, 15) or father (4, 6, 10, 16) by inserting them from right to left one by one in the order given by the mother (father, respectively) that do not appear in the left segment of the father (mother, respectively). A detailed description of the crossover operation is given in Table 5.

Single Point Crossover Operator.
Algorithm for Crossover Operator.
| Input: |
| Two parents from the current population |
| Output: |
| Two new offspring |
| 1. Choose randomly a suitable crossover point j |
| 2. Cut the father chromosome and the mother chromosome into left and right segments |
| 3. Generate new offspring, namely, son |
| 4. Inherit the left segment of the father chromosome to the left segment of the son chromosome |
| 5. Copy genes in mother chromosome that do not appear in the left segment of the father chromosome to the right segment of the son chromosome |
| 6. Generate a new chromosome, namely, daughter |
| 7. Inherit the left segment of the mother chromosome to the left segment of the daughter chromosome |
| 8. Copy genes in father chromosome that do not appear in the left segment of the mother chromosome to the right segment of the daughter chromosome |
| 9. Return the new two offspring |
Step 7: Termination criteria
The algorithm discontinues its execution only if maximum number of iterations is achieved, and the solution that is holding the best fitness value is selected, and it is specified as the best feature of task scheduling. Once the best fitness is attained by means of the GGSO algorithm, the selected task is allocated for cloud computing process. The GGSO-based task scheduling algorithm is presented in Table 6.
Algorithm for GGSO in Task Scheduling.
| Input |
| Parameter for the GGSO algorithm; |
| Parameter for the task scheduling; |
| Output |
| A task scheduled |
| 1. Call step 1 to create an initial solution |
| 2. Repeat |
| 3. Call algorithm 2 to evaluate the fitness function |
| 4. Copy the elitism directly to the next new solution |
| 5. Repeat |
| 6. Call step 3 to select a producer for the task |
| 7. Call step 4 to select the scrounger of the task |
| 8. Call step 5 to select the rangers |
| 7. Call algorithm 4 to replace a worst solution by crossover operator |
| 8. Until the new population is complete |
| 9. Replace the old population by the new population |
| 10. Until the termination condition is satisfied |
| 11. Return optimal scheduled task |
6 Results and Discussion
In this section, we discuss the result obtained from the proposed GGSO algorithm-based task scheduling technique. In implementing the proposed technique, we have used Mat lab version (7.12). This proposed technique is done with Windows having Intel Core i5 processor with speed 1.6 GHz and 4 GB RAM.
Experimental design
We employ it to numerous problem instances to authenticate the efficiency of our approach. VM instance types and the personal cloud and EC’s prices are placed based on our observation on public clouds and are specified in Tables 7–12 . Two kinds of resources, i.e. CPU and memory, are selected as they are the two most typical configurations in selecting a VM instance in cloud [5], [14].
VM Instance Types.
| Name | CPUs | Memory |
|---|---|---|
| Small | 1 | 1.7 |
| Large | 4 | 7.5 |
| X large | 8 | 15 |
Private Cloud’s Cost and Price.
| Cost | Price | |
|---|---|---|
| Small | 0.03 | 0.08 |
| Large | 0.12 | 0.32 |
| X large | 0.24 | 0.64 |
EC Price.
| ECs | Small | Large | X large |
|---|---|---|---|
| a | 0.085 | 0.34 | 0.68 |
| b | 0.070 | 0.30 | 0.70 |
| c | 0.100 | 0.40 | 0.72 |
Parameters of Problem Instance 1.
| Application | Cloud resources | ||
|---|---|---|---|
| Parameters | Values (integer) | Resources | Number |
| Number of tasks | ~Unit [1, 5] | CPU | 20 |
| VM instance type | ~Unit [1, 3] | Memory | 40 GB |
| Deadline (h) | ~Unit [1, 5] | ||
| Runtime (h) | ~Unit [1, deadline] | ||
Parameters of Problem Instances 2 and 3.
| Application | Cloud resources | ||
|---|---|---|---|
| Parameters | Values (integer) | Resources | Number |
| Number of tasks | ~Unit [1, 50] | CPU | 512 |
| VM instance type | ~Unit [1, 3] | Memory | 1024 GB |
| Deadline (h) | ~Unit [1, 168] | ||
| Runtime (h) | ~Unit [1, deadline] | ||
Parameters of GGSO Algorithm.
| Pop_size | maxSol | LL | UL | Head angle | Crossover rate |
|---|---|---|---|---|---|
| 8 | 20 | −5 | 5 | 0.5 |
Three problem examples are planned. Example 1 contains eight applications, and their parameters are demonstrated in Table 10. The VM instance type requested by each application is arbitrarily chosen from the above three VM types. The deadline of each application is a consistently distributed random integer between 1 h and 5 h in order to limit the search space. To make certain the deadline of each application is longer than its runtime, the runtime is selected as a consistently allocated integer between 1 h and its deadline. In order to reproduce the situation of the resource shortage, we placed the number of CPUs as 20 and the size of the memory as 40 GB. Instance 2 contains five applications and instance 3 contains 10. Their parameters are demonstrated in Table 11.
Problem instance 1: The suggested approach attained maximum profit in 24 assessments for this small size instance, which is high compared with other algorithms like GSO, GA, and SLPSO. The standard profit acquired in the 24 runs of the GGSO and SLPSO, GA and GSO, and their average runtime are specified in Table 13. In Table 13, we observe that the average profit attained by the GGSO is 6.7, which is better than the presented algorithms. Figure 3 illustrates the profit presentation for problem instance 1 with dissimilar assessments.
Problem instances 2 and 3: Problem instances 2 and 3 contain more tasks and devour more resources than instance 1. The suggested approach attained maximum profit in 24 evaluations for this large size instance, which is high compared with other algorithms like SLPSO, GSO, and GA. The average profit attained in the 24 runs of the GGSO and SLPSO, GSO and GA, and their average runtime are specified in Table 13. In Table 13, we observe that the standard profit acquired by the GGSO is 6893 for problem instance 2 and 5743.73 for problem instance 3, which is better than the presented algorithms. Figures 4 and 5 illustrate the profit presentation for problem instances 2 and 3.
Comparison of Profit and Avg. Time for Problem Instances 1, 2, and 3.
| Algorithms | Problem instance 1 | Problem instance 2 | Problem instance 3 | |||
|---|---|---|---|---|---|---|
| Maximum profit | Avg. run time (ms) | Maximum profit | Avg. run time (ms) | Maximum profit | Avg. run time (ms) | |
| GA | 2.18 | 14 | 3784 | 5485.4 | 2897.94 | 5435.54 |
| GSO | 4.5 | 15.5 | 4890 | 3945.56 | 4284.34 | 4734.85 |
| SLPSO | 4.9 | 29.55 | 3545 | 2934.37 | 2974.45 | 4300.28 |
| GGSO | 6.7 | 13,375 | 6893 | 2875.45 | 5743.73 | 3484.67 |

Performance of Profit Plot Proposed Against Existing Algorithm for Instance 1.

Performance of Profit Plot Proposed Against Existing Algorithm for instance 2.
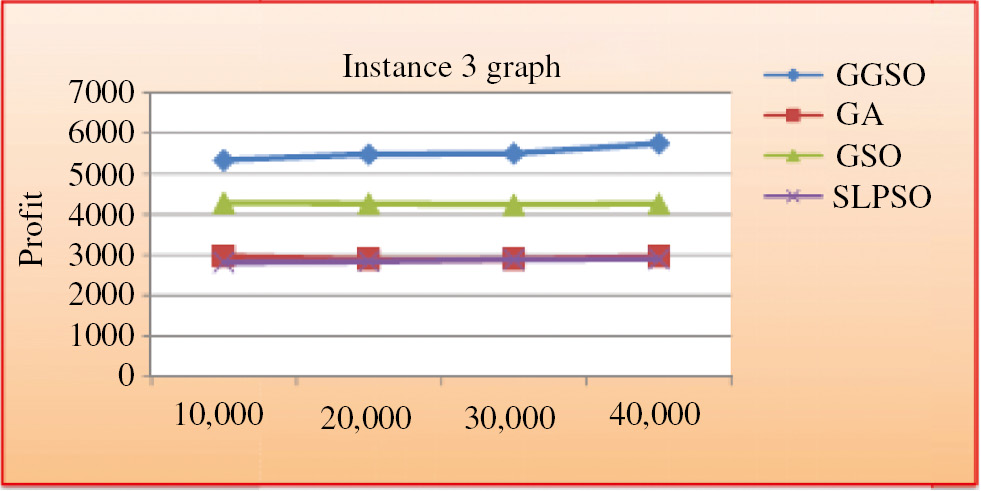
Performance of Profit Plot Proposed Against Existing Algorithm for Instance 3.
Both average profit and average run time for the GA, GSO, SLPSO, and GGSO are presented in Table 13. It can be observed that the GGSO can attain a higher resource utilization ratio. Tables 14 and 15 present both CPU and memory utilization rates for the GA, GSO, SLPSO, and GGSO. It can be observed that GGSO can attain a higher resource utilization ratio. In Table 12, the parameters used for our suggested algorithm are tabularized. Figures 6–8 explains the runtime of the approach.
Comparison for CPU Utilization Rate.
| Average CPU utilization rate | |||
|---|---|---|---|
| Algorithm | Instance 1 | Instance 2 | Instance 3 |
| GA | 0.445632 | 0.45335 | 0.46332 |
| GSO | 0.55621 | 0.54224 | 0.613325 |
| SLPSO | 0.71245 | 0.68441 | 0.72335 |
| GGSO | 0.953254 | 0.86775 | 0.797566 |
Comparison for Memory Utilization Rate.
| Average memory utilization rate | |||
|---|---|---|---|
| Algorithm | Instance 1 | Instance 2 | Instance 3 |
| GA | 0.41225 | 0.38665 | 0.574412 |
| GSO | 0.547784 | 0.532241 | 0.63225 |
| SLPSO | 0.68356 | 0.657741 | 0.732256 |
| GGSO | 0.853254 | 0.83224 | 0.8432 |

Runtime Performance of Instance 1.

Runtime Performance of Instance 2.

Runtime Performance of Instance 3.
7 Conclusion
In this paper, an integer programming model is established for the resources allocation problem of an IasS cloud in a hybrid cloud environment. The GGSO-based scheduling approach for this problem is proposed. In the GGSO, each dimension of a solution represents a task, and a solution, as a whole, represents all task priorities. The main matter is how to assign the users’ tasks to maximize the revenue of IaaS provider while guaranteeing QoS. By hybridizing two optimization algorithms like the GA and GSO, this approach is competent to attain a high-quality scheduling solution. The produced solution is competent to assure user-level (QoS) and enhances IaaS providers’ credibility and economic benefit. For the task scheduling problem, experimental effects demonstrated that the GGSO-based scheduling approach was well suited.
Bibliography
[1] S. Abrishami and M. Naghibzadeh, Deadline-constrained workflow scheduling in software as a service Cloud, Scientia Iranica19 (2012), 680–689.10.1016/j.scient.2011.11.047Search in Google Scholar
[2] M. Armbrust, M. Armbrust, A. Fox, R. Griffith, A. D. Joseph, R. Katz, A. Konwinski, G. Lee, D. Patterson, A. Rabkin, I. Stoica and M. Zaharia, A view of cloud computing, Commun. ACM53 (2010), 50–58.10.1145/1721654.1721672Search in Google Scholar
[3] A. Banharnsakun, B. Sirinaovakul and T. Achalakul, Job shop scheduling with the best-so-far ABC, Eng. Appl. Artif. Intell.25 (2012), 583–593.10.1016/j.engappai.2011.08.003Search in Google Scholar
[4] S. Bhardwaj, L. Jain and S. Jain, Cloud computing: a study of infrastructure as a service (IaaS), Int. J. Eng. Inf. Technol.2 (2010), 60–63.Search in Google Scholar
[5] R. V. Bossche, K. Vanmechelen and J. Broeckhove, Cost-optimal scheduling in hybrid IaaS clouds for deadline constrained workload, in: Proc. IEEE Int. Conf. Cloud Comput., pp. 228–235, Miami, FL, 2010.10.1109/CLOUD.2010.58Search in Google Scholar
[6] R. Buyya, C. S. Yeo, S. Venugopal, J. Broberg and I. Brandic, Cloud computing and emerging IT platforms: vision, hype, and reality for delivering computing as the 5th utility, Future Gener. Comput. Syst.25 (2009), 599–616.10.1016/j.future.2008.12.001Search in Google Scholar
[7] J. M. Cope, N. Trebon, H. M. Tufo and P. Beckman, Robust data placement in urgent computing environments, in: IEEE International Symposium on Parallel and Distributed Processing, IPDPS, pp. 1–13, 2009.10.1109/IPDPS.2009.5160914Search in Google Scholar
[8] I. D. Couzin, J. Krause, N. R. Franks and S. A. Levin, Effective leadership and decision-making in animal groups on the move, Nature434 (2005), 513–516.10.1038/nature03236Search in Google Scholar PubMed
[9] S. Di and C.-L. Wang, Error-tolerant resource allocation and payment minimization for cloud system, IEEE Trans. Parall. Distri. Sys.24 (2013), 1097–1106.10.1109/TPDS.2012.309Search in Google Scholar
[10] J. Geelan, “Twenty one experts define Cloud computing Virtualization”, Electronic magazine, [Online] Available at http://virtualization.sys.con.com/node/612375.Search in Google Scholar
[11] L. Guo, S. Zhao, S. Shen and C. Jiang, Task scheduling optimization in Cloud computing based on heuristic algorithm, J. Netw.7 (2012), 547–553.10.4304/jnw.7.3.547-553Search in Google Scholar
[12] S. He, Q. H. Wu and J. R. Saunders, A group search optimizer for neural network training, Lect. Notes Comput. Sci.3982 (2006), 934–943.10.1007/11751595_98Search in Google Scholar
[13] S. He, Q. H. Wu and J. R. Saunders, Group search optimizer: an optimization algorithm inspired by animal searching behavior, IEEE Trans. Evol/Comput.13 (2009), 973–990.10.1109/TEVC.2009.2011992Search in Google Scholar
[14] S. He, L. Guo and Y. Guo, Real time elastic cloud management for limited resources, in: Proc. IEEE Int. Conf. Cloud Comput., pp. 622–629, Washington, DC, 2011.10.1109/CLOUD.2011.47Search in Google Scholar
[15] J. Holland, Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, MI, 1975.Search in Google Scholar
[16] R. Jeyarani, R. Ram Vasanth, N. Nagaveni, Design and implementation of an efficient two-level scheduler for cloud computing environment, IEEE (2010), 884–886.10.1109/CCGRID.2010.94Search in Google Scholar
[17] D. Khaldi, P. Jouvelot and C. Ancourt, Parallelizing with BDSC, a resource-constrained scheduling algorithm for shared and distributed memory systems, Parallel Comput.41 (2015), 66–89.10.1016/j.parco.2014.11.004Search in Google Scholar
[18] T. Kosar and M. Livny, Stork: making data placement a first class citizen in the grid, in: Proceedings of 24thInternational Conference on Distributed Computing Systems, pp. 342–349, 2004.10.1109/ICDCS.2004.1281599Search in Google Scholar
[19] P. Kumar and S. Anand, An approach to optimize workflow scheduling for Cloud computing environment, J. Theor. Appl. Inf. Technol.57 (2013), 617–623.Search in Google Scholar
[20] Y. Kwok and I. Ahmad, Static scheduling algorithms for allocating directed task graphs to multiprocessors, ACM Comput. Surv.31 (1999), 406–471.10.1145/344588.344618Search in Google Scholar
[21] K.-R. Lee, M.-H. Fu and Y.-H. Kuo, A hierarchical scheduling strategy for the composition services architecture based on cloud computing, IEEE (2011), 163–169.Search in Google Scholar
[22] G. Lee and R. H. Katz. Heterogeneity-aware resource allocation and scheduling in the cloud, in: HotCloud, University of California, 2011.Search in Google Scholar
[23] H. Li and H. Li, A research of resource scheduling strategy for cloud computing based on Pareto optimality M×N production model, IEEE (2011), 1–5.10.1109/ICMSS.2011.5998998Search in Google Scholar
[24] J. Li, M. Qiu, J. Niu, W. Gao, Z. Zong and X. Qin, Feedback dynamic algorithms for preemptable job scheduling in cloud systems, IEEE1 (2010), 561–564.10.1109/WI-IAT.2010.30Search in Google Scholar
[25] H. Liu and D. Orban, GridBatch: Cloud computing for large-scale data-intensive batch applications, in: Proc. IEEE Int. Symp. Cluster Comput. Grid, pp. 295–305, 2008.10.1109/CCGRID.2008.30Search in Google Scholar
[26] J. C. Mace, A. V. Moorsel, P. Watson, The case for dynamic security solutions in public cloud workflow deployments, in: Proceeding of the IEEE/IFIP 41st International Conference on Dependable Systems and Networks Workshops, 2011.10.1109/DSNW.2011.5958795Search in Google Scholar
[27] L. Mei, W. K. Chan and T. H. Tse, A Tale of clouds: paradigm comparisons and some thoughts on research issues, in: IEEE Asia-Pacific Services Computing Conference (APSCC), pp. 464–469, 2008.10.1109/APSCC.2008.168Search in Google Scholar
[28] F. A. Omara and M. M. Arafa, Genetic algorithms for task scheduling problem, J. Parallel Distrib. Comput.70 (2010), 13–22.10.1016/j.jpdc.2009.09.009Search in Google Scholar
[29] M. A. Palis, J. C. Liou, S. Rajasekaran, S. Shende and S. S. L Wei, Online scheduling of dynamic trees, Parallel Process. Lett.5 (1995), 635–646.10.1142/S0129626495000564Search in Google Scholar
[30] M. Paul and G. Sanyal, Survey and analysis of optimal scheduling strategies in cloud environment, IEEE (2012), 789–792.10.1109/WICT.2011.6141347Search in Google Scholar
[31] M. L. M. Peixoto, M. J. Santana, J. C. Estrella, T. C. Tavares, B. T. Kuehne and R. H. C. Santana, A metascheduler architecture to provide QoS on the cloud computing, IEEE (2010), 650–657.10.1109/ICTEL.2010.5478877Search in Google Scholar
[32] H. Qi-yi and H. Ting-lei, An optimistic job scheduling strategy based on QoS for cloud computing, IEEE (2010), 673–675.10.1109/ICISS.2010.5655492Search in Google Scholar
[33] M. M. Rafique, A. R. Butt and D. S. Nikolopoulos, A capabilities-aware framework for using computational accelerators in data-intensive computing, J. Parallel Distrib. Comput.71 (2011), 185–197.10.1016/j.jpdc.2010.09.004Search in Google Scholar
[34] S. Song, K. Hwang and Y.-K. Kwok, Risk-resilient heuristics and genetic algorithms for security-assured grid job scheduling, IEEE Trans. Comput.55 (2006), 703–719.10.1109/TC.2006.89Search in Google Scholar
[35] A. N. Toosi, R. N. Calheiros, P. K. Thulasiram and R. Buyya, Resource provisioning policies to increase IaaS provider’s profit in a federated cloud environment, in: Proc. IEEE Int. Conf. High Perform. Comput. Commun., pp. 279–287, Banff, Canada, 2011.10.1109/HPCC.2011.44Search in Google Scholar
[36] W. Wang and G. Zeng, Trusted dynamic scheduling for large-scale parallel distributed systems, IEEE (2011), 884–886.10.1109/ICPPW.2011.8Search in Google Scholar
[37] S.-C. Wang, K.-Q. Yan, S.-S. Wang and C.-W. Chen, A three-phases scheduling in a hierarchical cloud computing network, IEEE (2011), 114–117.10.1109/CMC.2011.28Search in Google Scholar
[38] L. I. Wenhao, A community cloud oriented workflow system framework and its scheduling strategy, in: IEEE 2nd Symposium on Web Society (SWS), 2010.10.1109/SWS.2010.5607434Search in Google Scholar
[39] A. S. Wu, H. Yu, S. Jin, K.-C. Lin and G. Schiavone, An incremental genetic algorithm approach to multiprocessor scheduling, IEEE Trans. Parallel Distribution Sys15 (2004), 824–834.10.1109/TPDS.2004.38Search in Google Scholar
[40] T. Xie, SEA: a striping-based energy-aware strategy for data placement in RAID-structured storage systems, IEEE Trans. Comput.57 (2008), 748–761.10.1109/TC.2008.27Search in Google Scholar
[41] X. F. Xie, W. Zhang and Z. Yang, Hybrid particle swarm optimizer with mass extinction, in: Proc. Int. Conf. Commun., Circuits, Syst., pp. 629–634, Chengdu, China, 2002.Search in Google Scholar
[42] M. Xu, L. Cui, H. Wang and Y. Bi, A multiple QoS constrained scheduling strategy of multiple workflows for cloud computing, IEEE (2009).10.1109/ISPA.2009.95Search in Google Scholar
[43] W. Zhangjun, L. Xiao, N. Zhiwei, Y. Dong and Yun, A market-oriented hierarchical scheduling strategy in cloud workflow systems, J. Supercomput.63 (2011), 1–38.10.1007/s11227-011-0578-4Search in Google Scholar
[44] L. Zhao, Y. Ren, Y. Xiang and K. Sakurai, Fault-tolerant scheduling with dynamic number of replicas in heterogeneous systems, IEEE (2011), 434–441.10.1109/HPCC.2010.72Search in Google Scholar
[45] A. Zomaya, C. Ward and B. Macey, Genetic scheduling for parallel processor systems: comparative studies and performance issues, IEEE Trans. Parall. Distri. Sys.10 (1999), 795–812.10.1109/71.790598Search in Google Scholar
[46] X. Zuo, G. Zhang and W. Tan, Self-adaptive learning PSO-based deadline constrained task scheduling for hybrid IaaS Cloud, IEEE Trans. Automation Sci. Eng.11 (2014), 564–573.10.1109/TASE.2013.2272758Search in Google Scholar
©2019 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- An Effective Technique to Track Objects with the Aid of Rough Set Theory and Evolutionary Programming
- A Novel Word Clustering and Cluster Merging Technique for Named Entity Recognition
- Simulation-Based Analysis of Intelligent Maintenance Systems and Spare Parts Supply Chains Integration
- Retinal Fundus Image for Glaucoma Detection: A Review and Study
- Task Reallocating for Responding to Design Change in Complex Product Design
- Fuzzy Mutual Information-Based Intraslice Grouped Ray Casting
- An Efficient Compound Image Compression Using Optimal Discrete Wavelet Transform and Run Length Encoding Techniques
- A Fast Internal Wave Detection Method Based on PCANet for Ocean Monitoring
- A Wheelchair Control System Using Human-Machine Interaction: Single-Modal and Multimodal Approaches
- Design of Optimized Multiobjective Function for Bipedal Locomotion Based on Energy and Stability
- Hybridization of Genetic and Group Search Optimization Algorithm for Deadline-Constrained Task Scheduling Approach
- An Effective Optimization-Based Neural Network for Musical Note Recognition
Articles in the same Issue
- Frontmatter
- An Effective Technique to Track Objects with the Aid of Rough Set Theory and Evolutionary Programming
- A Novel Word Clustering and Cluster Merging Technique for Named Entity Recognition
- Simulation-Based Analysis of Intelligent Maintenance Systems and Spare Parts Supply Chains Integration
- Retinal Fundus Image for Glaucoma Detection: A Review and Study
- Task Reallocating for Responding to Design Change in Complex Product Design
- Fuzzy Mutual Information-Based Intraslice Grouped Ray Casting
- An Efficient Compound Image Compression Using Optimal Discrete Wavelet Transform and Run Length Encoding Techniques
- A Fast Internal Wave Detection Method Based on PCANet for Ocean Monitoring
- A Wheelchair Control System Using Human-Machine Interaction: Single-Modal and Multimodal Approaches
- Design of Optimized Multiobjective Function for Bipedal Locomotion Based on Energy and Stability
- Hybridization of Genetic and Group Search Optimization Algorithm for Deadline-Constrained Task Scheduling Approach
- An Effective Optimization-Based Neural Network for Musical Note Recognition

