Abstract
A methodology based on sound non-equilibrium thermodynamics principles is developed to estimate the extremum dissipation point for steady-state incompressible flow past a sphere at low Reynolds numbers. It is shown, that the extremum dissipation point appears at the point when both the shear stress and the pressure at the surface of the sphere are equal to zero. The Reynolds number and the position of the extremum dissipation flow past a sphere were further estimated with the aid of a mathematical model for pressure distribution on the sphere surface, accounting for both creeping and ideal flow. The parameters of the model were determined by comparison of the calculated pressure distribution at the surface with the available literature data. The conditions at which the separation angle and the extremum dissipation angle coincide were also investigated. It is believed that this work could be used to further elucidate the flow past a sphere.
1 Introduction
Flow past a sphere attained significant scientific interest since the 19th century due to its importance in many phenomena in science and technology. In particular, the flow past a sphere at a low Reynolds number (1–400) due to its wide applications in many industrial processes, such as chemical reactor engineering and process designing, was the subject of extensive investigation during the past years.
For example, Taneda (1956) used photographic techniques to experimentally investigate the wake behind a sphere moving in a water tank at Reynolds numbers from 5 to 300. Jenson (1959) utilized relaxation methods to study the viscous incompressible flow around a sphere at low Reynolds numbers (<40). Moreover, the pressure distribution results calculated at the surface of the sphere for Re = 5, 10, 20, and 40 were tabulated.
Chester, Breach, and Proudman (1969) considered the flow of an incompressible, viscous fluid past a sphere for small values of the Reynolds number. They also proposed a novel correlation for the drag force. Rimon and Cheng (1969) studied theoretically the transient uniform flow around a sphere by solving the complete Navier–Stokes equations. The considered fluid was incompressible and homogeneous, while the range of Reynolds number studied was from 1 to 1000.
Abraham (1970) proposed a correlation for the drag coefficient of a sphere in Newtonian incompressible flow valid for a wide range of Reynolds numbers: 0 ≤ Re ≲ 5000 by using simple but effective arguments. Lin and Lee (1973) studied the transient state solutions of the Navier–Stokes equations for incompressible flow around a sphere by solving a set of implicit finite difference equations. Seeley, Hummel, and Smith (1975) studied the velocity profiles in laminar flow around spheres experimentally using a non-disturbing flow visualization technique for uniform laminar flow around a sphere at Reynolds numbers 290, 750, 1300, and 3000.
Lee, Downie, and Bettess (1991) presented a procedure for calculating the starting flow around a sphere in a uniform stream. In particular, the flow field was simulated by a flow of ideal fluid with embedded vorticity. With the assumption that the flow remains symmetric, the vorticity field was approximated by a number of discrete circular line vortices. Later, Lee (2000) solved the discretized Navier–Stokes equations in three-dimensional space using Galerkin’s finite element method. Numerical simulations of uniform flow past a sphere were presented for Reynolds numbers from 100 to 500.
The flow of an incompressible viscous fluid past a sphere was investigated numerically and experimentally over flow regimes, including steady and unsteady laminar flow at Reynolds numbers of up to 300 by Johnson and Patel (2000). The unsteady three-dimensional flow around the sphere was also studied by Sadikin et al. (2014) by using numerical simulation computational fluid dynamics for moderate Reynolds number between 20 ≤ Re ≤ 500.
The three-dimensional structures of flow around a rigid sphere at moderate Reynolds number (Re) between 20 and 400 were also investigated by Li and Zhou (2021) by using the finite volume method with adaptive mesh refinement. For a recent detailed review of the published literature for flow past a single stationary sphere, the interested reader must resort to Tiwari et al. (2020a, b).
Strongly related to the flow problems are the dissipation energy (Ψ) and entropy production (σ). These fundamental quantities of non-equilibrium thermodynamics are related to each other as Ψ = σT. T stands for the absolute temperature. The entropy production inflows was the subject of intensive research during past years, as reviewed by Sadiki, Agrebi, and Ries (2022) and Hussien et al. (2021).
The recent advance in the area of complex fluid flow (Christov 2022), biofluids (Sanal Kumar et al. 2022), and microfluidics (Hafemann and Fröhlich 2023) lead to a re-examination of flows in terms of the entropy production rate (Gandhi et al. 2023; Mallikarjuna et al. 2022; Shahsavar et al. 2021). In our previous work (Verros 2020), we developed comprehensive criteria for the extrema in entropy production rate for heat transfer at the limit of the linear region of the extended thermodynamics framework.
This communication aims to investigate the flow past a sphere in terms of energy dissipation. In particular, in the following sections, a detailed methodology for estimating the extremum point of energy dissipation for flow past a sphere is proposed, and the results of this work are presented. Finally, conclusions are drawn, and ideas for future work are proposed.
2 Theoretical part
The starting point of this analysis is the definition of total dissipation energy Ψ in terms of drag force F k for flow past a sphere (Bird, Stewart, and Lightfoot 2002):
where V 0 is a constant velocity of a fluid approaching the sphere, τ is the shear stress tensor (see Figure 1). The rest symbols are explained in the notation section. Alternatively, the drag force acting on the interface between the fluid and a particle is defined as the component of the fluid force in the fluid direction. The fluid drag compromises skin friction drag and pressure drag. Therefore, the fluid drag force F k is defined as (Dey, Ali, and Padhi 2019):
where τ w is the wall shear stress, P is the pressure intensity, and S is the surface area of the particle (see Figure 1).
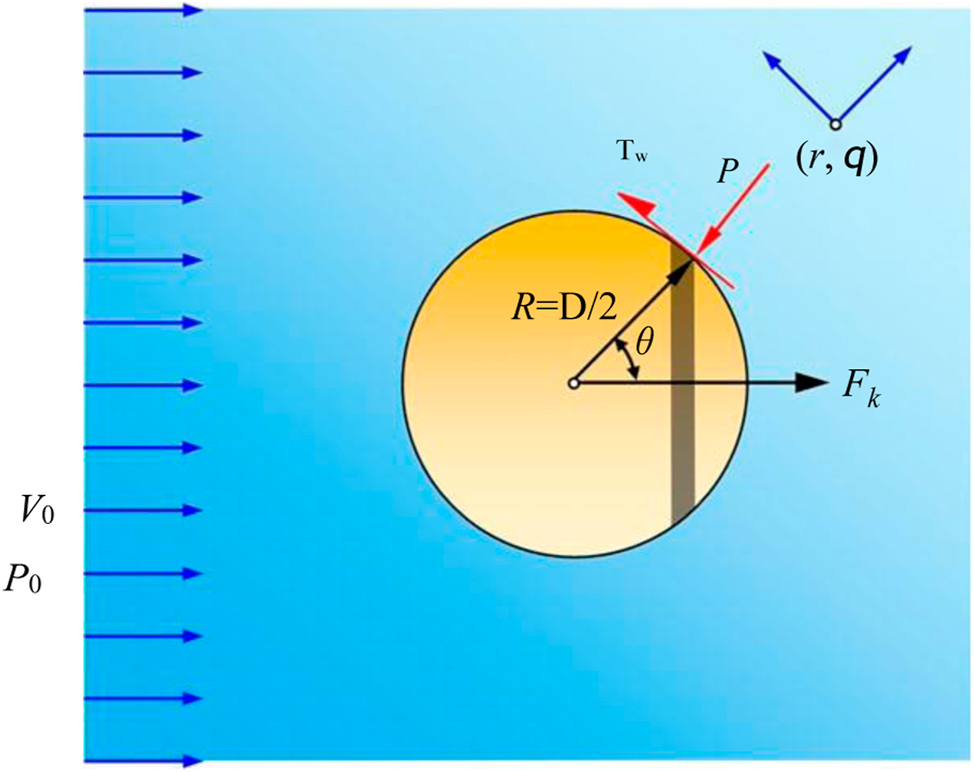
Schematic of fluid drag on a sphere.
Eq. (1) relates a fundamental quantity of non-equilibrium thermodynamics, such as the total dissipation energy Ψ with an important quantity of fluid mechanics, such as drag force F k . Eq. (2) is nothing else than a force balance at the surface of the sphere.
The following equation holds true for a sphere having a diameter equal to D by taking into account its symmetry (Dey, Ali, and Padhi 2019):
By further using Eqs. (1–3), the following equation holds true for the derivative of total dissipation energy with respect to angle θ:
Therefore, the extremum point for total dissipation energy appears when F (θ) = 0.
This extremum point is at a maximum if
To calculate the condition for P = 0 at the surface of the sphere, one has to resort to dimensional analysis. According to the dimensional analysis, the pressure P of a Newtonian fluid at the surface of the sphere could be written as:
where P 0 is the pressure of the fluid as approaching the sphere, μ is the viscosity, ρ stands for density, and D stands for sphere diameter. C (θ) is a function of angle θ.
Outside the boundary layer, the flow could be approximated as ideal flow; in other words, the flow is independent of viscosity (ξ = 0) (Landau and Lifshitz 1959). By setting ξ = 0 and transforming the area outside the boundary (R + δ) to the surface of the sphere, the pressure distribution at the surface of a sphere having radius R could be written as:
δ is the boundary layer thickness as proposed by Abraham (1970): δ/R = δ 0/Re0.5, δ 0 ≅ 9.06.
The above Eq. (6) is compatible with Eq. (5). This analysis for the transformation of ideal flow with the aid of the boundary layer theory is not a new idea; the origin of this idea could be found in the pioneering work of Abraham (1970) for the functional dependence of drag force of a sphere on Reynolds number. Besides its simplicity, this methodology has been proven very effective in developing correlations for the drag force valid over a wide range of Reynolds numbers: 0 ≤ Re ≲ 5000.
According to Bird, Stewart, and Lightfoot (2002), and Landau and Lifshitz (1959), the pressure distribution for ideal flow past a sphere is written as:
The pressure distribution at the surface of the sphere for creeping flow is written as (Dey, Ali, and Padhi 2019):
Finally, in this work, the function C(θ) was approached as follows:
c i are adjustable parameters estimated by fitting to Eq. (6) literature data for the k parameter. In this way, the limit of pure creeping flow is reached for Eq. (6) for Re ≈ 0, while for Re→, ∞ the limit of ideal flow is approximated.
3 Results & discussion
The first step is to estimate the ci parameters (see Eq. (9)) by fitting predictions obtained by using Eq. (6) to the data reported by Jenson (1959) for Reynolds numbers equal to 5 and 40, respectively. The resulting graph is illustrated in Figure 2.
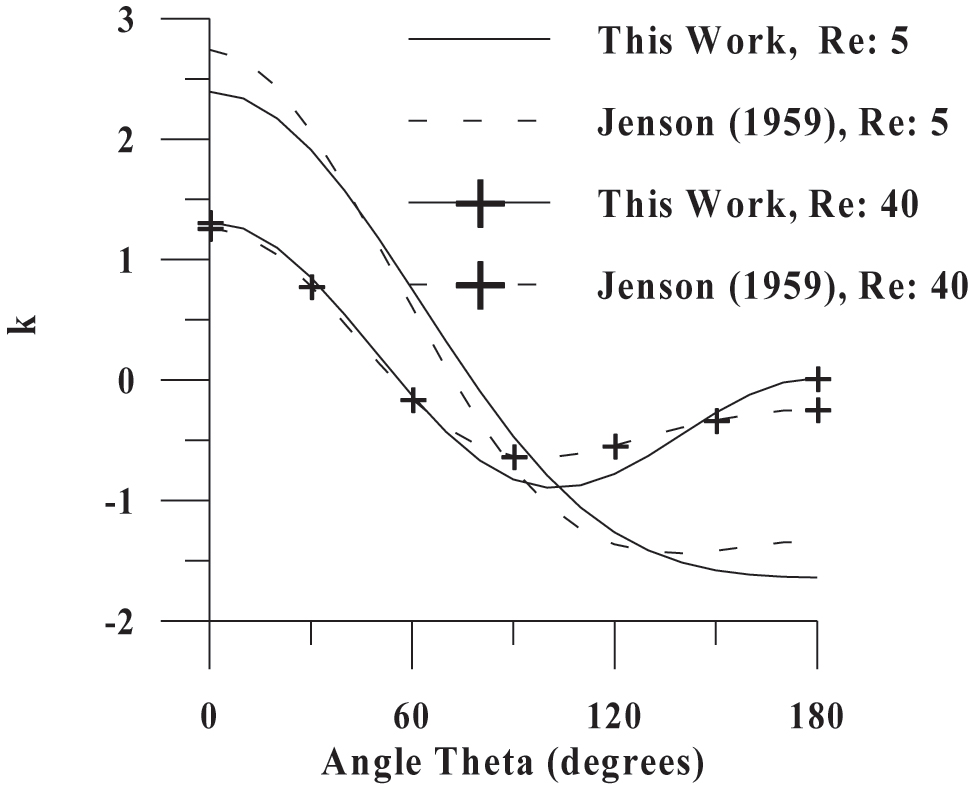
Comparison of calculated pressure distribution at the surface of the sphere with literature results (Jenson 1959).
The selected Reynolds numbers are the lower and upper limits of the tabulated data of Jenson (1959) for pressure distribution at the surface of the sphere. The estimated c i parameters have the values −0.4967, 6.3 × 10−3, and 2.97 × 10−3, respectively. For a detailed analysis of the results shown in Figure 2, the interested reader has to resort to the original work of Jenson (1959).
To further validate the developed model, the calculated pressure distribution by using Eq. (6) and Eq. (9) was compared with the limit of creeping flow (Re = 10−3) and the limit of ideal flow (Re = 105).
The excellent fitting depicted in Figures 3 and 4 could be attributed to the fact that Eq. (9) is reduced to the limit of creeping flow and ideal flow as the Reynolds number tends to zero and infinite, respectively.
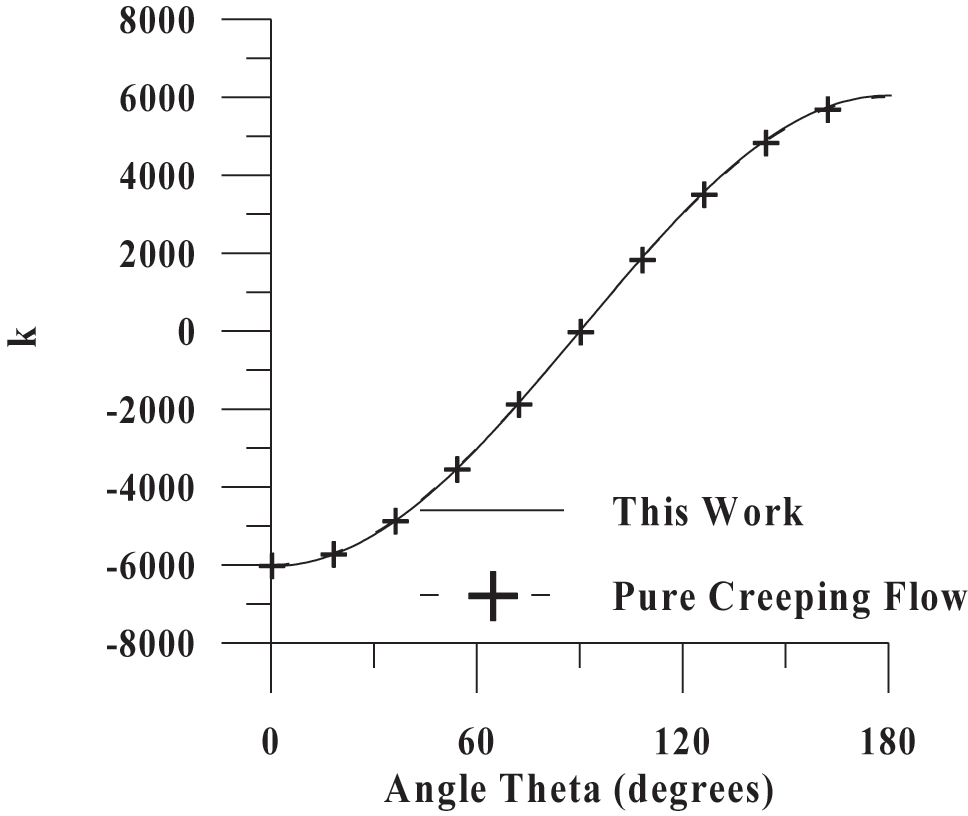
Comparison of calculated pressure distribution at the surface of the sphere at the limit of creeping flow (Dey, Ali, and Padhi 2019).
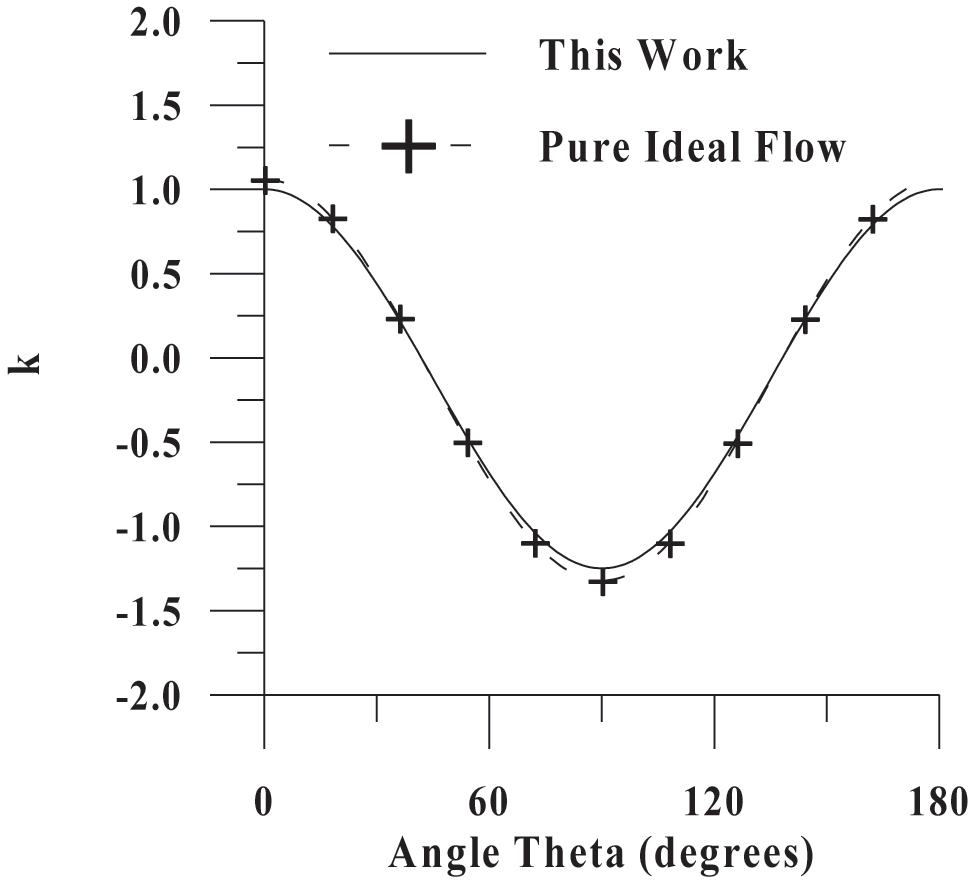
Comparison of calculated pressure distribution at the surface of the sphere at the limit of pure ideal flow (Bird, Stewart, and Lightfoot 2002; Landau and Lifshitz 1959).
The calculated extremum dissipation angles as a function of k parameters for various Reynolds numbers are depicted in Figure 5.
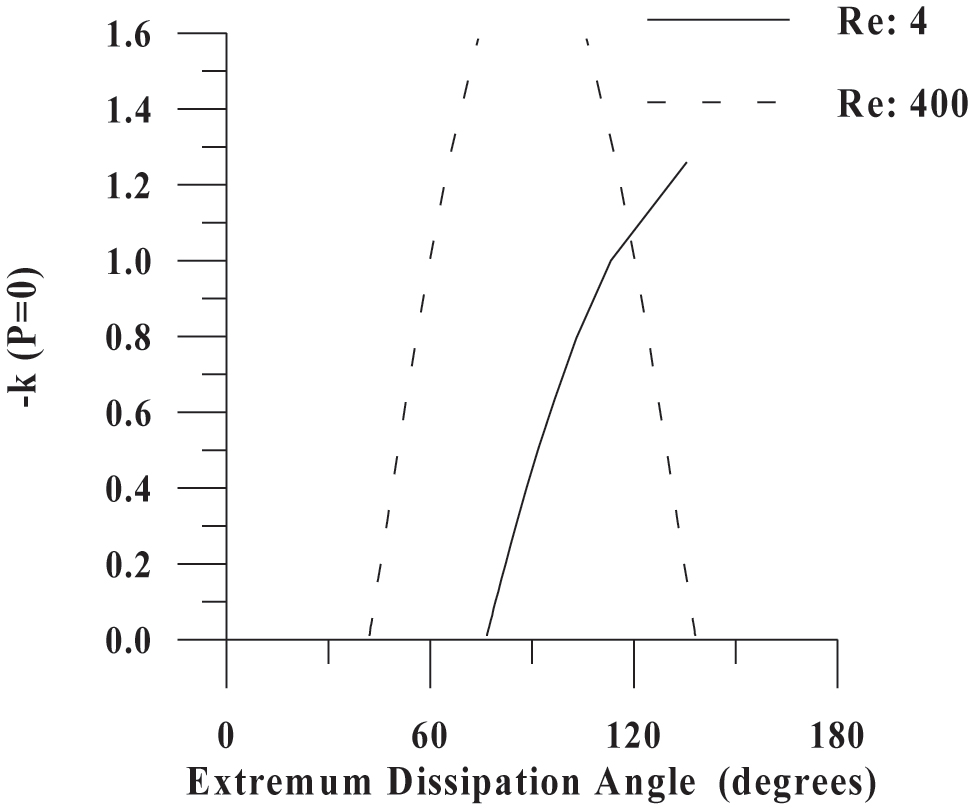
Parameter k versus extremum dissipation angle for various Reynolds Numbers.
The different shapes of curves shown in Figure 5 for Reynolds numbers equal to 4 and 400 could be attributed to the different flow phenomena observed at the above numbers. In particular, according to the experimental results of Taneda (1956), there is no flow separation or vortices formation at Reynolds number equal to 4. However, according to Li and Zhou (2021) vortices exist at Reynolds number equal to 400 while the separation phenomena are dominant above Reynolds 40.
A more profound question arises from the above analysis: What are the conditions under which the extremum dissipation value, as calculated in this work, coincides with the separation angle? In Table 1, the separation angles for various Reynolds numbers, as determined experimentally by Taneda (1956), are summarized with the k values as calculated in this work for the same angle.
Separation angle (Taneda 1956) and extremum dissipation angle as a function of parameter k.
| Reynolds number | Re: 40 | Re: 100 | Re: 200 | Re: 300 |
|---|---|---|---|---|
| Separation angle (Taneda 1956)-extremum dissipation angle | 34° | 53° | 63° | 67° |
| −k (P = 0) | – | 0.39 | 0.94 | 1.23 |
Strongly related to this work is the Prigogine theorem (Kondepudi and Prigogine 2015) that states, for systems in the linear regime (such as a Newtonian fluid), the total internal entropy production reaches a minimum value at non-equilibrium steady states. Therefore, one could anticipate that the described extremum of entropy production (σ) in an isothermal flow corresponds to a minimum of energy dissipation (Ψ = σΤ) if a non-equilibrium steady state was assumed. Regarding the results shown in Table 1, one could anticipate highly convective flows in the case that the separation angle coincides with the extremum dissipation angle and minimum energy dissipation for the system was assumed according to the Prigogine theorem (Kondepudi and Prigogine 2015).
4 Conclusions
In this work, it was shown using sound non-equilibrium principles that the extremum dissipation point appears at the point where both the shear stress and the pressure at the surface of the sphere are equal to zero. Furthermore, a novel mathematical model for pressure distribution on the sphere surface accounting for creeping and ideal flow was developed. The parameters of this model were determined by fitting literature data. The conditions at which the separation angle and the extremum dissipation angle coincide were also calculated to give values here. Moreover, the extremum dissipation point was related to a minimum point according to the Prigogine theorem if a non-equilibrium steady state was assumed. Limitations of this work include the empirical methodology involved in the model development for pressure distribution at the sphere surface that limits the application to a low Reynolds number. The authors are hopeful that this work will attract the interest of both experimentalists and theoreticians to investigate further fluid mechanics phenomena related to the extremum dissipation angle.
- Notation
- C(θ)
-
dimensionless auxiliary parameter
- c i
-
adjustable dimensionless parameter
- D
-
diameter of the sphere
- F k
-
drag force
- k
-
dimensionless pressure coefficient
- P
-
pressure function at the surface of the sphere
- P 0
-
static pressure in an undisturbed stream
- Re
-
Reynolds number
- R
-
radius of the sphere
- r
-
radial spherical polar co-ordinate
- S
-
surface of the particle
- V 0
-
undisturbed stream velocity
- v
-
velocity vector
- Greek letters
- δ 0
-
dimensionless parameter
- δ
-
boundary layer thickness
- θ
-
angular spherical polar co-ordinate
- μ
-
coefficient of viscosity
- ρ
-
density
- σ
-
entropy production rate
- τ
-
shear tensor
- τ w
-
shear stress at the surface of the sphere
- φ
-
angular spherical polar co-ordinate
- Ψ
-
energy dissipation
Acknowledgments
The authors are thankful to Ms. Sarada Paul Roy for her help regarding proofreading and language editing. The anonymous reviewers of this work are also acknowledged for their efforts to improve this work further.
-
Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: None declared.
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
Abraham, F. F. 1970. “The Functional Dependence of the Drag Coefficient of a Sphere on Reynolds Number.” The Physics of Fluids, 13: 2194–5. https://doi.org/10.1063/1.1693218.Suche in Google Scholar
Bird, R. B., W. E. Stewart, and E. N. Lightfoot. 2002. Transport Phenomena, 2nd ed. New York: Wiley.Suche in Google Scholar
Chester, W., D. R. Breach, and I. Proudman. 1969. “On the Flow Past a Sphere at Low Reynolds Number.” Journal of Fluid Mechanics 37: 751–60. https://doi.org/10.1017/S0022112069000851.Suche in Google Scholar
Christov, I. C. 2022. “Soft Hydraulics: From Newtonian to Complex Fluid Flows through Compliant Conduits.” Journal of Physics: Condensed Matter 34 (6): 063001. https://doi.org/10.1088/1361-648X/ac327d.Suche in Google Scholar PubMed
Dey, S., S. K. Ali, E. Padhi. 2019. “Terminal Fall Velocity: The Legacy of Stokes from the Perspective of Fluvial Hydraulics.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 475: 20190277. https://doi.org/10.1098/rspa.2019.0277.Suche in Google Scholar PubMed PubMed Central
Gandhi, R., B. K. Sharma, Q. M. Al-Mdallal, and H. V. R. Mittal. 2023. “Entropy Generation and Shape Effects Analysis of Hybrid Nanoparticles (Cu-Al2O3/blood) Mediated Blood Flow through a Time-Variant Multi-Stenotic Artery.” International Journal of Thermofluids 18: 100336. https://doi.org/10.1016/j.ijft.2023.100336.Suche in Google Scholar
Hafemann, T., and J. Fröhlich. 2023. “Simulation of Non-spherical Particles in Curved Microfluidic Channels.” Physics of Fluids 35 (3): 033328. https://doi.org/10.1063/5.0139105.Suche in Google Scholar
Hussien, A. A., W. Al-Kouz, M. E. Hassan, A. A. Janvekar, and A. J. Chamkha. 2021. “A Review of Flow and Heat Transfer in Cavities and Their Applications.” European Physical Journal Plus 136 (4): 353. https://doi.org/10.1140/epjp/s13360-021-01320-3.Suche in Google Scholar
Jenson, V. G. 1959. “Viscous Flow Around a Sphere at Low Reynolds Numbers (<40).” Proceedings of the Royal Society of London A 249: 346–66. https://doi.org/10.1098/rspa.1959.0029.Suche in Google Scholar
Johnson, T. A., and V. C. Patel. 2000. “Flow Past a Sphere up to a Reynolds Number of 300.” Journal of Fluid Mechanics 378: 19–70. https://doi.org/10.1017/S0022112098003206.Suche in Google Scholar
Kondepudi, D., and I. Prigogine. 2015. Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed. New Delhi: Wiley.10.1002/9781118698723Suche in Google Scholar
Landau, L. D., and E. M. Lifshitz. 1959. Fluid Dynamics. Oxford: Pergamon.Suche in Google Scholar
Lee, D. K., M. J. Downie, and P. Bettess. 1991. “An Axisymmetric Model of Separated Flow about a Sphere Using Discrete Vortices.” International Journal for Numerical Methods in Fluids 12: 809–23. https://doi.org/10.1002/fld.1650120902.Suche in Google Scholar
Lee, S. 2000. “A Numerical Study of the Unsteady Wake behind a Sphere in a Uniform Flow at Moderate Reynolds Numbers.” Computers & Fluids 29: 639–67. https://doi.org/10.1016/S0045-7930(99)00023-7.Suche in Google Scholar
Li, J., and B. Zhou. 2021. “The Symmetry and Stability of the Flow Separation Around a Sphere at Low and Moderate Reynolds Numbers.” Symmetry 13: 2286. https://doi.org/10.3390/sym13122286.Suche in Google Scholar
Lin, C. L., and S. C. Lee. 1973. “Transient State Analysis of Separated Flow Around a Sphere.” Computers & Fluids 1: 235–50. https://doi.org/10.1016/0045-7930(73)90009-1.Suche in Google Scholar
Mallikarjuna, B., J. Srinivas, G. G. Krishna, O. A. Bég, and A. Kadir. 2022. “Spectral Numerical Study of Entropy Generation in Magneto-Convective Viscoelastic Biofluid Flows through Poroelastic Media with Thermal Radiation and Buoyancy Effects.” Journal of Thermal Science and Engineering Applications 14 (1): 011008. https://doi.org/10.1115/1.4050935.Suche in Google Scholar
Rimon, Y., and S. I. Cheng. 1969. “Numerical Solution of a Uniform Flow over a Sphere at Intermediate Reynolds Numbers.” Physics of Fluids 12: 949–59. https://doi.org/10.1063/1.2163685.Suche in Google Scholar
Sadiki, A., S. Agrebi, and F. Ries. 2022. “Entropy Generation Analysis in Turbulent Reacting Flows and Near Wall: A Review.” Entropy 24 (8): 1099. https://doi.org/10.3390/e24081099.Suche in Google Scholar PubMed PubMed Central
Sadikin, A., N. A. Mohd Yunus, K. Abdullah, and A. N. Mohammed. 2014. “Numerical Study of Flow Past a Solid Sphere at Moderate Reynolds Number.” Applied Mechanics and Materials 660: 674–8. https://doi.org/10.4028/www.scientific.net/AMM.660.674.Suche in Google Scholar
Sanal Kumar, V. R., B. R. Sundararam, P. K. Radhakrishnan, N. Chandrasekaran, S. K. Choudhary, V. Sankar, A. Sukumaran, V. Rajendran, S. A. R. M. Rafic, D. Panchal, Y. Raj, S. Shrivastava, C. Oommen, A. Jayaraman, D. Rajamanickam, and B. Srinivasan. 2022. “In Vitro Prediction of the Lower/upper-Critical Biofluid Flow Choking Index and In Vivo Demonstration of Flow Choking in the Stenosis Artery of the Animal with Air Embolism.” Physics of Fluids 34 (10): 101302. https://doi.org/10.1063/5.0105407.Suche in Google Scholar
Seeley, L. E., R. L. Hummel, and J. W. Smith. 1975. “Experimental Velocity Profiles in Laminar Flow Around Spheres at Intermediate Reynolds Numbers.” Journal of Fluid Mechanics 68: 591–608. https://doi.org/10.1017/S002211207500184X.Suche in Google Scholar
Shahsavar, A., M. Jafari, P. Talebizadehsardari, and D. Toghraie. 2021. “Hydrothermal and Entropy Generation Specifications of a Hybrid Ferronanofluid in Microchannel Heat Sink Embedded in CPUs.” Chinese Journal of Chemical Engineering 32: 27–38. https://doi.org/10.1016/j.cjche.2020.08.053.Suche in Google Scholar
Taneda, S. 1956. “Experimental Investigation Wakes behind Sphere Low Reynolds Numbers.” Journal of the Physical Society of Japan 11: 1104–8. https://doi.org/10.1143/JPSJ.11.1104.Suche in Google Scholar
Tiwari, S. S., E. Pal, S. Bale, N. Minocha, A. W. Patwardhan, K. Nandakumar, and J. B. Joshi. 2020a. “Flow Past a Single Stationary Sphere, 1. Experimental and Numerical Techniques.” Powder Technology 365: 115–48. https://doi.org/10.1016/j.powtec.2019.01.037.Suche in Google Scholar
Tiwari, S. S., E. Pal, S. Bale, N. Minocha, A. W. Patwardhan, K. Nandakumar, and J. B. Joshi. 2020b. “Flow Past a Single Stationary Sphere, 2. Regime Mapping and Effect of External Disturbances.” Powder Technology 365: 215–43. https://doi.org/10.1016/j.powtec.2019.04.032.Suche in Google Scholar
Verros, G. D. 2020. “Comprehensive Criteria for the Extrema in Entropy Production Rate for Heat Transfer in the Linear Region of Extended Thermodynamics Framework.” Axioms 9 (4): 1–7. https://doi.org/10.3390/axioms9040113.Suche in Google Scholar
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Editorial
- Preface: special issue dedicated to the “International Conference on Energy Sustainability and Advanced Materials – 2022 (ICESAM-2022)” part of the Energy Summit-2022 UPES, Dehradun, India
- Special Issue Articles
- Biogas production from canteen waste
- Compositional numerical analysis of multiphase flow of crude oil in porous media under non-isothermal conditions
- Numerical investigations on sc-CO2 gas sequestration in layered heterogeneous deep saline aquifers
- Energy optimization and neural-based dynamic analysis of integrated multiple stage evaporator
- Modelling and experimental studies for the recovery of valuable chemical intermediates from mustard husk pyrolysis oil
- Effect of noble bacteria Ochrobactrum intermedium (Alhpa-22) on decolorization of methyl orange dye in a bioreactor
- Assessment of engine oil viscosity and vibration characteristics of CI engine fuelled with jatropha biodiesel blends
- Green and recyclable mesoporous silica supported WO3–ZrO2 solid acid catalyst for biodiesel production by transesterification of Ankol seed oil with methanol
- On the extremum dissipation for steady state incompressible flow past a sphere at low Reynolds number
- Determining and modeling of density and viscosity of biodiesel-diesel and biodiesel-diesel-butanol blends
Artikel in diesem Heft
- Frontmatter
- Editorial
- Preface: special issue dedicated to the “International Conference on Energy Sustainability and Advanced Materials – 2022 (ICESAM-2022)” part of the Energy Summit-2022 UPES, Dehradun, India
- Special Issue Articles
- Biogas production from canteen waste
- Compositional numerical analysis of multiphase flow of crude oil in porous media under non-isothermal conditions
- Numerical investigations on sc-CO2 gas sequestration in layered heterogeneous deep saline aquifers
- Energy optimization and neural-based dynamic analysis of integrated multiple stage evaporator
- Modelling and experimental studies for the recovery of valuable chemical intermediates from mustard husk pyrolysis oil
- Effect of noble bacteria Ochrobactrum intermedium (Alhpa-22) on decolorization of methyl orange dye in a bioreactor
- Assessment of engine oil viscosity and vibration characteristics of CI engine fuelled with jatropha biodiesel blends
- Green and recyclable mesoporous silica supported WO3–ZrO2 solid acid catalyst for biodiesel production by transesterification of Ankol seed oil with methanol
- On the extremum dissipation for steady state incompressible flow past a sphere at low Reynolds number
- Determining and modeling of density and viscosity of biodiesel-diesel and biodiesel-diesel-butanol blends

