Abstract
MD simulations have been accomplished to study the transport properties of molten CaO-SiO2-P2O5-FeO system. The self-diffusion coefficients of Ca, Si, P, Fe and O ions increase with increasing slag basicity and FeO content, while decrease with increasing P2O5 content. The diffusivities of these ions in the quaternary melts follow the sequence of Ca>Fe>O>P>Si. The calculated viscosities are in good agreement with the experimental ones. It is obvious that increasing the amount of network formers (e. g., Si and P ions) leads to larger viscosity and degree of slag polymerization, while adding network modifiers (e. g., Fe and Ca ions) causes viscosity and slag polymerization to decrease. Except for the calculation, the FT-IR analysis also confirmed the relationship between structural properties of the slag and composition. The viscosity of the slag increases linearly with increasing the parameter of Q(Si+P).
Introduction
The transport properties (including diffusion coefficient, viscosity, electrical, and thermal conductivity, etc.) of liquids or melts are important for most physical, chemical and biotechnological processes. In engineering practices, such properties must be gained through measurement, theoretical calculation, or even guessing.
It is well known that CaO-SiO2-P2O5 system is one of the most important melts in metallurgical, glass and ceramic industries [1, 2, 3, 4, 5]. The quaternary CaO-SiO2-P2O5-FeO melts have played a crucial role in the steel metallurgical process. The transport properties of CaO-SiO2-P2O5-FeO system are critical for understanding the chemical reactions at the interface between molten slag and liquid metal.
Among a large number of transport properties, the diffusion coefficient and viscosity are of the greatest practical and scientific importance and are associated with the transport of mass and momentum, respectively. The diffusion coefficient in molten slag refers to a specific ions rather than to the bulk melt. It describes the rate of chemical or isotopic transport due to thermally activated random walk of atomic species. In the absence of a chemical gradient, we call it self-diffusion coefficient. This parameter cannot be measured without introducing an isotopic gradient. However, in theoretical calculation, such as molecular dynamics (MD) simulations, an isotopic gradient is not required as the motion of individual particles can be traced [6].
Viscosity of molten slag describes the resistance of fluid against its deformation by a shear stress and can be measured by concentric cylinder viscometer. However, in some metallurgical process, the temperature is always well above the experimental conditions. In this case, viscosity of molten slag also can be computed from MD simulations using the Green-Kubo relation [7, 8].
In the present study, we performed a MD simulation and emphatic studied the effect of slag composition on the transport properties of molten CaO-SiO2-P2O5-FeO system. By tracing the mean square displacements of atoms in this melts, MD simulation in the present work not only obtained the self-diffusion coefficient values but also provide an intrinsically link between the viscosity and the structure of the molten system.
Computational approach
Classical molecular dynamics (CMD) simulations were employed to calculate the transport properties and structural information of the quaternary system. All calculations were performed with the parallel package Materials Explorer 5.0 using the Born-Mayer-Huggins (BMH) function [9, 10]:
where U(rij) is the interatomic potential; qi and qj are the charges of ion i and ion j; rij represents the distance between ion i and ion j; Aij, Bij and Cij are parameters for BMH potentials.
The charge of Ca, Si, P, Fe and O are 2, 4, 5, 2 and –2, respectively. The coulombic potential in eq. (1) (the first term) was calculated by using the Ewald summation. All the noncoulombic parts of the pair potentials were subjected to a short-range cutoff of 10 Å. Based on the data from Hirao and Kawamura [11], the interatomic potential parameters were optimized using Lammps program and shown in Table 1. The slag composition and total number of atoms are detailed in Table 2. In order to ensure the melts is a homogeneous molten slag, the compositions are designed based on the CaO-SiO2-P2O5-FeO phase diagram and all the slags are located in the liquid phase region at 1,673 K [12].
Potential parameters used in computation.
| i | j | Aij/ (gÅ/fs2) | Bij/ (1/Å) | Cij/ (gÅ8/fs2) |
|---|---|---|---|---|
| O | O | 2.40E-20 | 5.88E+00 | 2.78E-25 |
| Si | Si | 3.47E-23 | 6.25E+00 | 0 |
| Ca | Ca | 5.27E-21 | 6.25E+00 | 6.95E-26 |
| Fe | Fe | 4.70E-23 | 3.45E+00 | 0 |
| P | P | 4.56E-22 | 7.06E+00 | 0 |
| O | Si | 1.01E-21 | 6.06E+00 | 0 |
| O | Ca | 1.15E-20 | 6.06E+00 | 1.39E-25 |
| O | Fe | 6.41E-22 | 5.16E+00 | 0 |
| O | P | 3.04E-23 | 3.45E+00 | 0 |
| Si | Ca | 4.28E-22 | 6.25E+00 | 0 |
| Si | Fe | 9.22E-23 | 1.29E+01 | 0 |
| Si | P | 1.73E-23 | 1.25E+01 | 4.49E-25 |
| Ca | Fe | 3.53E-23 | 6.25E+00 | 0 |
| Ca | P | 2.64E-21 | 1.25E+01 | 0 |
| Fe | P | 2.05E-22 | 6.25E+00 | 0 |
Chemical compositions and number of atoms. Nos 1~4 slags concern the parameter series of slag basicity. No. 2 and Nos 5~8 slags concern the parameter series of P2O5 content. No. 2 and Nos 9~10 slags concern the parameter series of FeO content.
| Mass fraction/wt% | Atomic number | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. | CaO | SiO2 | P2O5 | FeO | R | Ca | Si | P | Fe | O |
| 1 | 36 | 24 | 10 | 30 | 1.5 | 675 | 420 | 148 | 437 | 2,320 |
| 2 | 32.8 | 27.2 | 10 | 30 | 1.2 | 606 | 471 | 146 | 432 | 2,345 |
| 3 | 28.4 | 31.6 | 10 | 30 | 0.9 | 517 | 537 | 144 | 425 | 2,377 |
| 4 | 22.5 | 37.5 | 10 | 30 | 0.6 | 401 | 624 | 141 | 416 | 2,418 |
| 5 | 35.5 | 29.5 | 5 | 30 | 1.2 | 663 | 515 | 74 | 435 | 2,313 |
| 6 | 33.8 | 28.2 | 8 | 30 | 1.2 | 628 | 489 | 117 | 434 | 2,332 |
| 7 | 31.6 | 26.4 | 12 | 30 | 1.2 | 583 | 454 | 175 | 430 | 2,358 |
| 8 | 30.5 | 25.5 | 14 | 30 | 1.2 | 561 | 437 | 203 | 429 | 2,370 |
| 9 | 30 | 25 | 10 | 35 | 1.2 | 565 | 440 | 149 | 514 | 2,332 |
| 10 | 27.3 | 22.7 | 10 | 40 | 1.2 | 524 | 408 | 152 | 598 | 2,318 |
In the calculation, the Newton motion equations were numerically integrated with a step of 1 fs. The initial temperature was set at 4,000 K for 15,000 steps to eliminate the effect of the initial distribution. Then, the temperature was decreased slowly to 2,000 K, 1,873 K and 1,673 K for 10,000 steps, respectively. The calculation was equilibrated at 1,673 K for another 25,000 steps. All simulations were performed in NVT (constant number of particles, volume and temperature) ensemble. The self-diffusion coefficients D of the ions in the molten system can be estimated from the mean squared displacements (MSD) by using following relation [13];
where ri(0) and ri(t) denote the position of the ion i at time t and time origin, respectively. N is the number of the ion i.
The shear viscosity η of the molten slag system can be calculated by Einstein-Stokes equation [14].
where kB is the Boltzmann constant. T is temperature in Kelvin. λ is the diffusion step, which is usually considered to be equal to the diameter of the ion.
Results and discussion
MSD and self-diffusion coefficients
Figure 1 shows the MSD of Ca, Si, P, Fe and O ions calculated as a function of time in the No. 2 slag system at 1,673 K. The self-diffusion coefficients of each ion can be obtained from the slope of the linear part of the MSD vs. time curve. The self-diffusion coefficients obtained at 1,673 K of Ca, Si, P, Fe and O ions are 0.056 Å2/ps, 0.023 Å2/ps, 0.032 Å2/ps, 0.053 Å2/ps and 0.045 Å2/ps, respectively. The results show that the Ca and Fe ions diffuse more rapidly than other ions in the CaO-SiO2-P2O5-FeO system. The O ion is somewhat less mobile, and the Si and P ions have the lowest mobility. As Table 3 shows, the diffusivity sequence of Ca>O>Si is also reported in molten CaO-SiO2, CaO-MgO-Al2O3-SiO2 and CaO-CaF2-SiO2 slag systems [15, 16, 17, 18]. This suggests the restricted diffusion of the Si ion within a SiO4 tetrahedron. To our knowledge, there are few experimental or computational diffusion studies for the CaO-SiO2-P2O5-FeO system. Although very limited data are available in the literatures, the Fe ion is more diffusive than O ion, but much less diffusive than Ca ion is confirmed [19, 20]. The self-diffusion coefficient of P is less than O, but larger than Si, which indicating its weaker bonding in tetrahedral coordination. The self-diffusion coefficients in present work are on the same order and magnitude as those reported molten oxide systems.
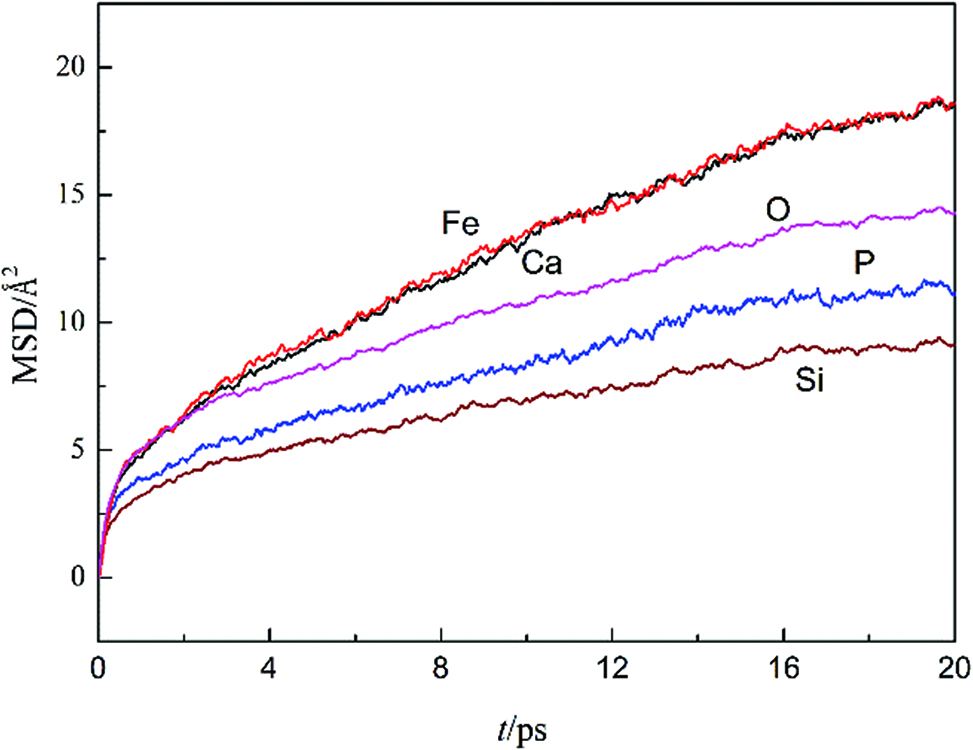
Mean squared displacements as a function of time of different ions in the CaO-SiO2-P2O5-FeO system at 1,673 K.
Diffusivity sequence of ions in different molten systems.
| References | System | T, K | Sequence |
|---|---|---|---|
| Matsumiya et al. [15] | CaO-SiO2 | 1,873 | Ca>O>Si |
| Seo and Tsukihashi [16] | CaO-SiO2 | 1,873 | Ca>O>Si |
| Shimoda and Saito [17] | CaO-MgO-Al2O3-SiO2 | 1,873 | Ca>Mg>Al>O>Si |
| Asada et al. [18] | CaO-CaF2-SiO2 | 1,773 | F>Ca>O>Si |
| Seo and Tsukihashi [19] | FeO-SiO2 | 1,600 | Fe>O>Si |
| Belashchenko and Ostrovskii [20] | CaO-FeO-SiO2 | 1,873 | Ca>Fe>O>Si |
| Belashchenko and Ostrovskii [21] | CaO-P2O5 | 2,000 | Ca>O>P |
| Present work | CaO-SiO2-P2O5-FeO | 1,673 | Ca>Fe>O>P>Si |
Table 4 shows all the self-diffusion coefficients of Ca, Si, P, Fe and O ions in Nos. 1~10 slags. It can be seen that with the slag basicity increases from 0.6 to 1.5, the self-diffusion coefficients of Ca, Si, P, Fe and O ions increase from 0.04 to 0.065 Å2/ps, 0.017 to 0.027 Å2/ps, 0.023 to 0.038 Å2/ps, 0.037 to 0.057 Å2/ps and 0.033 to 0.053 Å2/ps, respectively. The self-diffusion coefficients of all ions increase with increasing slag basicity. The results represent reasonably well the structural properties of molten CaO-SiO2 system, which were restricted to the diffusion of Si and O ions by the formation of silica network structure [16]. With the increase of P2O5 content from 5 to 14 %, the self-diffusion coefficients of Ca, Si, P, Fe and O ions decrease from 0.097 to 0.043 Å2/ps, 0.04 to 0.018Å2/ps, 0.057 to 0.025 Å2/ps, 0.092 to 0.042 Å2/ps and 0.08 to 0.035 Å2/ps, respectively. As well as Si, increasing the amount of P ions in oxide melts leads to a more close slag structure. Therefore, the polymerization degree of the melts increased and all the self-diffusion coefficients decreased. On the contrary, with the increase of FeO content from 30 to 40 %, the self-diffusion coefficients of Ca, Si, P, Fe and O ions increase from 0.056 to 0.097 Å2/ps, 0.023 to 0.04 Å2/ps, 0.032 to 0.057 Å2/ps, 0.053 to 0.092 Å2/ps and 0.045 to 0.08 Å2/ps, respectively. This is because the Fe ion plays the role of network modifier in the oxide melts. The depolymerization of the slag structure decreases with increasing FeO content, thus, the self-diffusion coefficients increased.
Self-diffusion coefficients of different ions /(Å2/ps).
| No. | Ca | Si | Fe | P | O |
|---|---|---|---|---|---|
| 1 | 0.065 | 0.027 | 0.057 | 0.038 | 0.053 |
| 2 | 0.056 | 0.023 | 0.053 | 0.032 | 0.045 |
| 3 | 0.045 | 0.019 | 0.042 | 0.026 | 0.037 |
| 4 | 0.04 | 0.017 | 0.037 | 0.023 | 0.033 |
| 5 | 0.097 | 0.04 | 0.092 | 0.057 | 0.08 |
| 6 | 0.083 | 0.034 | 0.075 | 0.049 | 0.068 |
| 7 | 0.05 | 0.021 | 0.049 | 0.028 | 0.039 |
| 8 | 0.043 | 0.018 | 0.042 | 0.025 | 0.035 |
| 9 | 0.069 | 0.028 | 0.061 | 0.04 | 0.056 |
| 10 | 0.097 | 0.04 | 0.092 | 0.057 | 0.08 |
Viscosities
Table 5 shows the viscosities of Nos. 1~10 slags calculated by self-diffusion coefficients. It can be seen that the viscosities decrease from 0.26 to 0.15 Pa·s with the slag basicity increasing from 0.6 to 1.5. Similarly the viscosities decrease from 0.18 to 0.11 Pa·s with the FeO content in slag increasing from 30 to 40 %; and increase from 0.14 to 0.28 Pa·s with the P2O5 content in slag increasing from 5 to 14 %. It is apparent that increasing the amount of network formers (e. g., Si and P ions) in molten CaO-SiO2-P2O5-FeO system leads to larger viscosity while adding network modifiers (e. g., Fe and Ca ions) causes viscosity to decrease.
Viscosities calculated by self-diffusion coefficients /(Pa·s).
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| η | 0.15 | 0.18 | 0.2 | 0.26 | 0.14 | 0.15 | 0.19 | 0.28 | 0.14 | 0.11 |
In order to verify the validity of the calculated results, we measured the viscosities of above molten slags by the rotating cylinder method [22]. In the viscosity measurement test, both the crucible and spindle are made of pure iron. The comparisons of the measured and the calculated values for the viscosities are shown in Figure 2. The calculated values are in good agreement with the experimental ones.
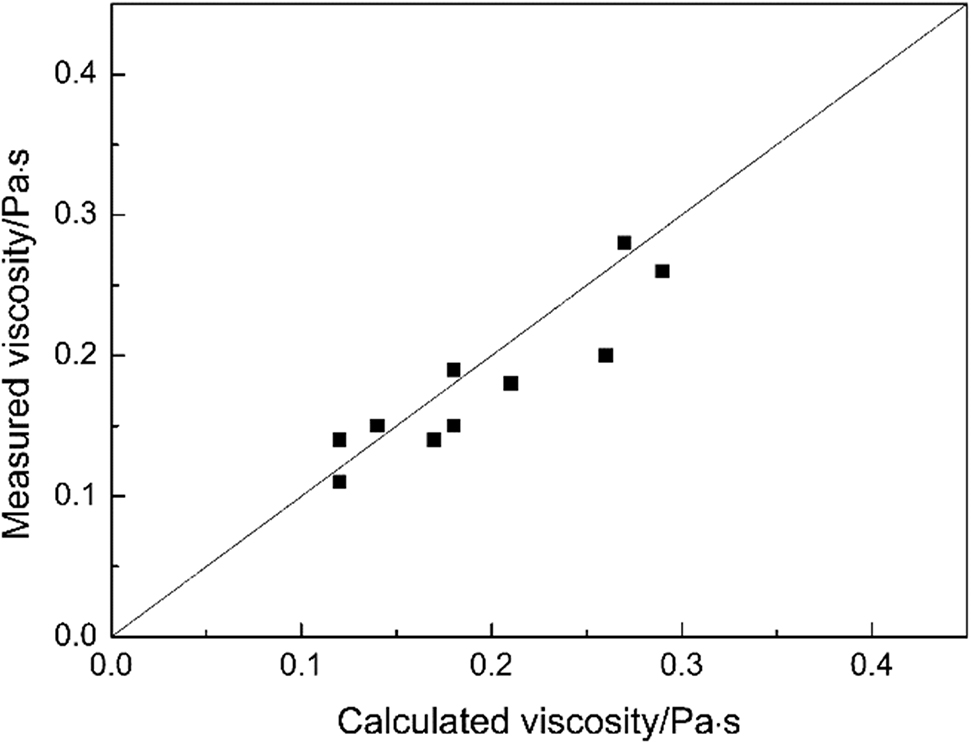
Calculated viscosities using MD simulations against experimental data.
Links between transport and structural properties
Each Si and P tetrahedron was classified into five types of structural units, i. e. Q0, Q1, Q2, Q3, and Q4, where the superscript referred to the number of bridging oxygen atoms in the unit [23]. Figure 3 shows the concentration variation of Qn with changing slag basicity, FeO content and P2O5 content, respectively. It is important to note that the Qn(Si+P) in present work includes both Qn(Si) and Qn(P). Seen from Figure 3(a), with the increase of slag basicity, the proportion of Q0(Si+P) shows a remarkable uptrend while the proportions of Q2(Si+P), Q3(Si+P) and Q4(Si+P) decrease obviously. It suggests that the degree of polymerization of the Si-O and P-O network structures is weakened. This phenomenon is also observed with the increase of FeO content in slag. At the same time, the proportions of Q0(Si+P) and Q1(Si+P) decrease slightly with the increase of P2O5 content in slag while the proportions of Q2(Si+P) and Q3(Si+P) increase slightly. It can be concluded that the network of both P and Si ions are more polymerized and tend to form complex anions.
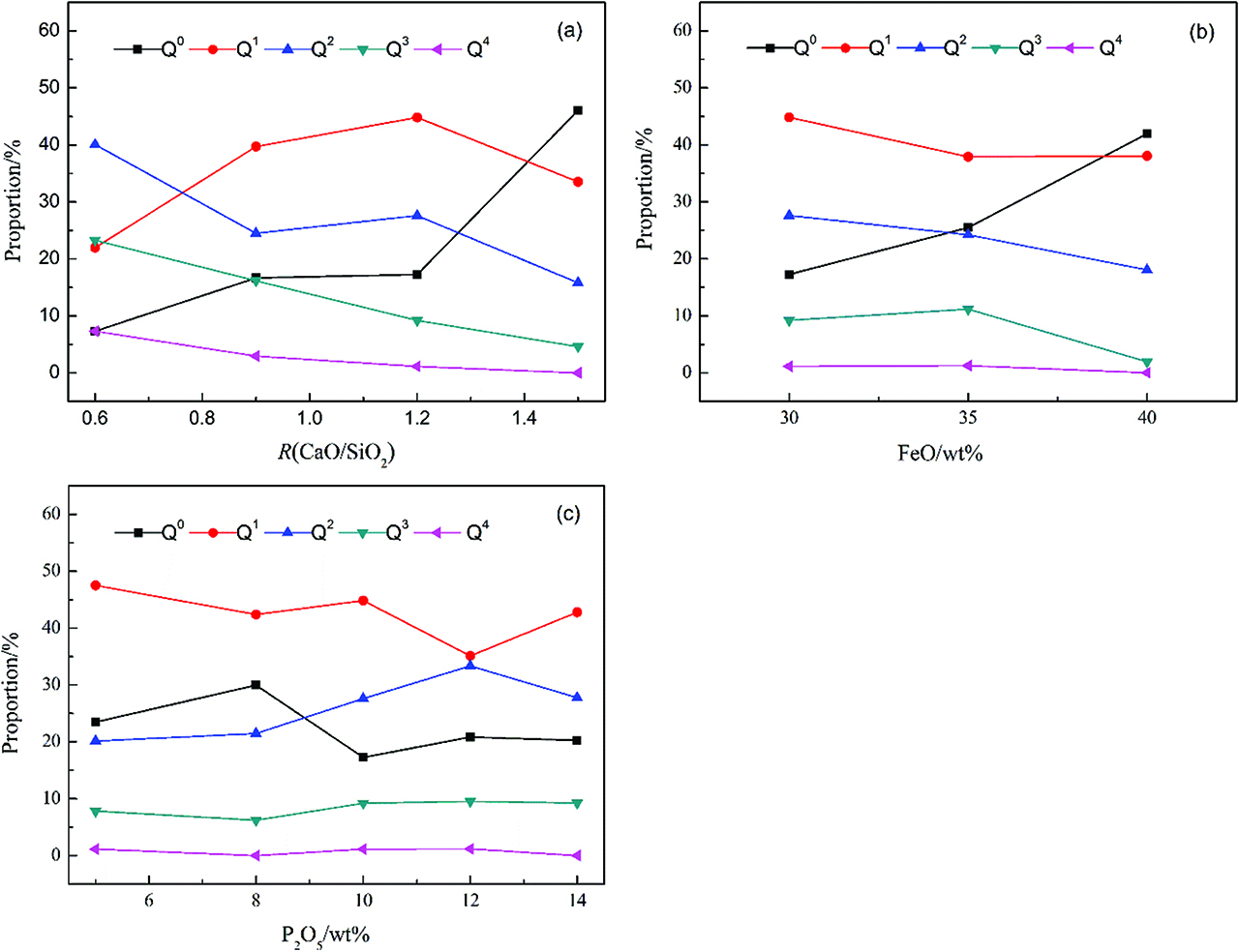
Effect of (a) basicity, (b) FeO content and (c) P2O5 content on Qn(Si+P).
The ratio of non-bridging oxygen/tetragonal oxygen (NBO/T) is a measure of the de-polymerization of the molten system. Mills et al. [24] proposed a relational expression between the polymerization of the molten CaO-Na2O-Al2O3-SiO2 slag and the mole fractions of different oxides.
Similarly, the parameter Q(Si+P), which is a measure of the polymerization of the molten CaO-SiO2-P2O5-FeO system and which can be calculated by
Figure 4 shows the relationship between the calculated viscosities and the parameter of Q(Si+P) at 1,673 K. It can be intuitively seen that the viscosities vs Q(Si+P) is a linear-related function. However, there is a special point that the deviation between the calculated data and the fitting data is pretty huge. The reason for this may be that the P2O5 content is extremely high, which going beyond the application of eq. (7). Without thinking about this special point, the coefficient of determination R2 increases from 0.65 to 0.92.
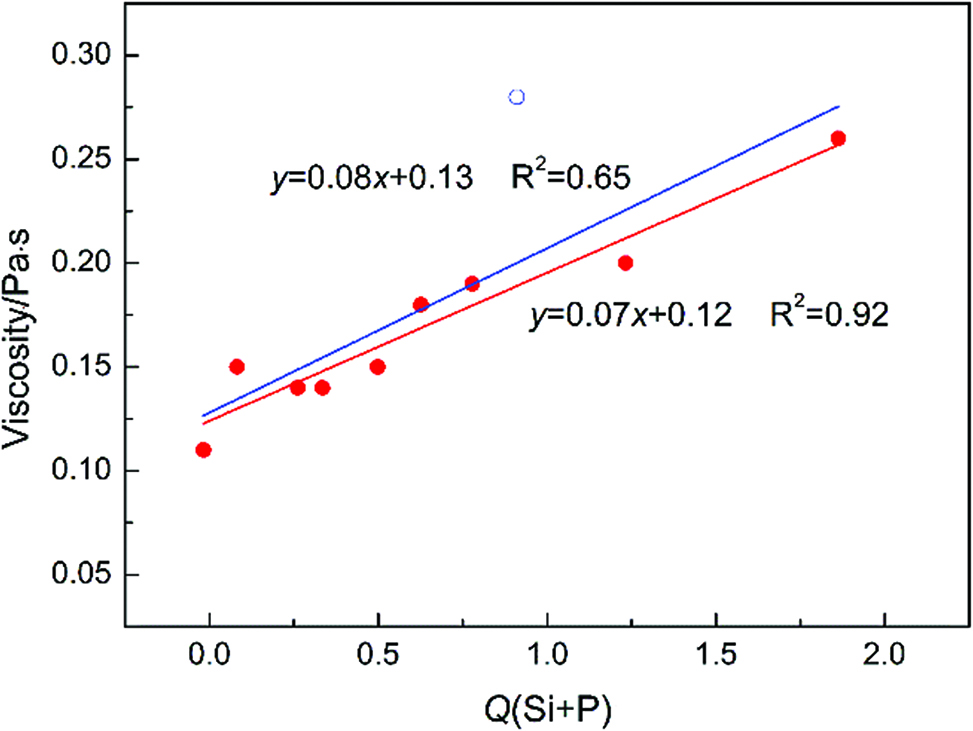
Relationship between the calculated viscosities and the parameter of Q(Si+P) at 1,673 K.
FT-IR spectra analysis
The structures of the slags were also detected by FT-IR spectroscopy (Nicolet 5DXC). Figure 5(a) shows the effect of slag basicity on the FT-IR spectra of the slags. In general, the spectra was composed of three regions, i. e. 800–1,200 cm–1 with strong intensity, 600–800 cm–1 with weak intensity and 400–600 cm–1 with middle intensity. The band in the 800–1,200 cm–1 range has been generally assigned to the symmetric stretching vibration of SiO4 and PO4 tetrahedra. The bands shift to lower wavenumber region with increasing slag basicities, which suggests that the proportions of Q2(Si+P) and Q3(Si+P) decreased. Therefore, the degree of polymerization of the slags decreased [25]. With the increase of FeO content, this phenomenon also showed in Figure 5(b). However, the bands shift from low wavenumber to high wavenumber in Figure 5(c), which indicates that more polymerized structures were formed with increasing P2O5 content. The weak 600–800 cm–1 bands represent the Si-O symmetry stretching [26, 27]. The characteristic peak near 695 cm–1 corresponds to the FeO4 tetrahedra stretching bands [28]. The medium intense band in the 400–600 cm–1 range represents the bending vibration of T-O-T (T denotes Si or P).
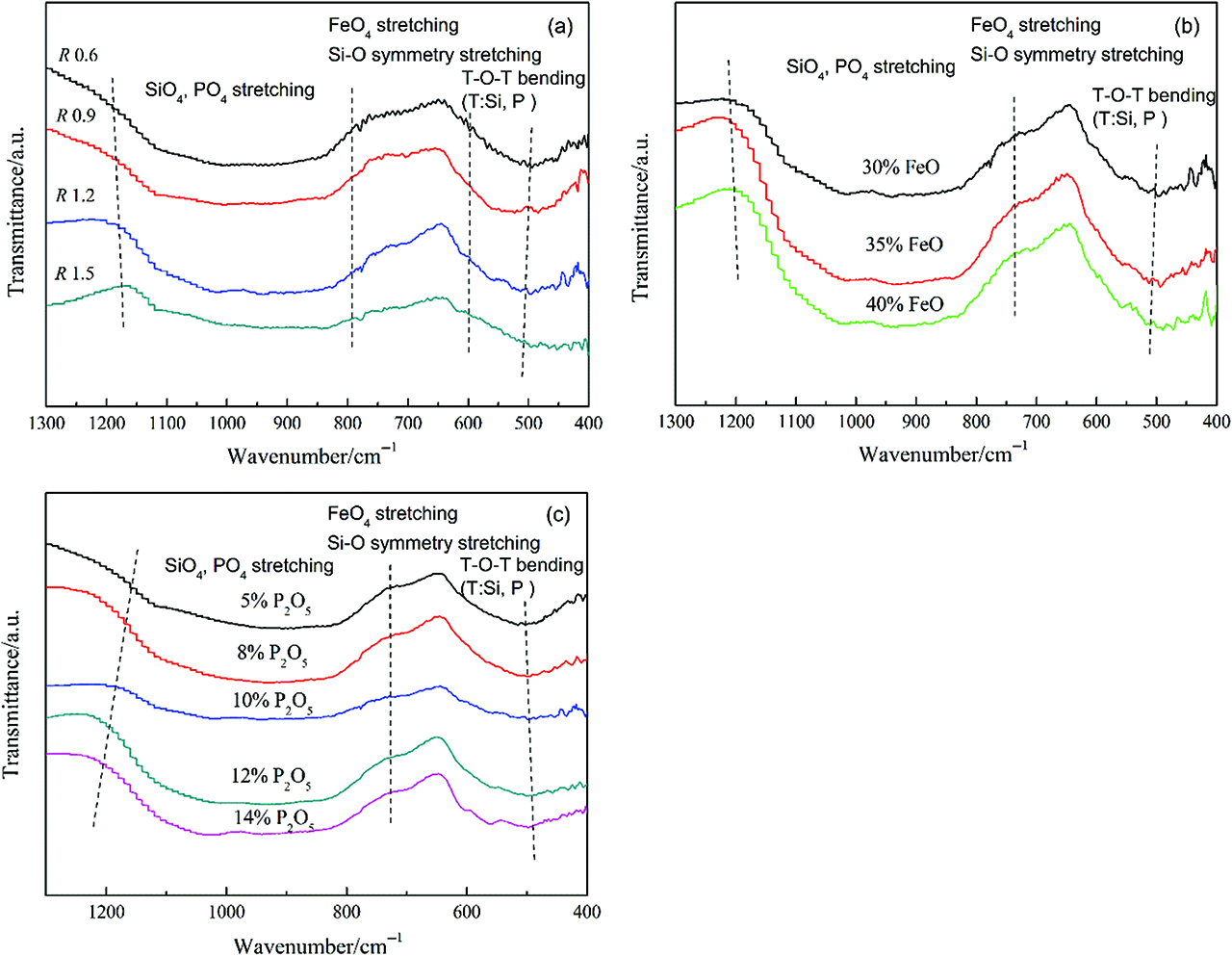
FT-IR spectra of slag samples with varying (a) basicity, (b) FeO content and (c) P2O5 content.
Conclusions
In the present theoretical study, the MSD of Ca, Si, P, Fe and O ions in quaternary CaO-SiO2-P2O5-FeO melts have been modeled by MD simulations. The self-diffusion coefficients of above ions and the viscosities of the melts were calculated. It was found that the diffusivity of above ions follow the sequence of Ca>Fe>O>P>Si. The self-diffusion coefficients of all ions increase with increasing slag basicity and FeO content, while decrease with increasing P2O5 content.
The calculated viscosities are in good agreement with the experimental values. It is apparent that increasing the amount of network formers (e. g., Si and P ions) in molten CaO-SiO2-P2O5-FeO system leads to larger viscosity while adding network modifiers (e. g., Fe and Ca ions) causes viscosity to decrease.
The links between transport properties and structural properties of the melts were also discussed. The degree of polymerization of the Si-O or P-O network structures weakened with increasing slag basicity and FeO content, while promoted with increasing P2O5 content. The FT-IR spectra of the slags also show the same structural informations. It is interesting to note that the viscosity vs Q(Si+P) shows a linear-related function.
We expect that this investigation of the transport properties of CaO-SiO2-P2O5-FeO system will encourage and motivate further experimental and theoretical investigations, and finally reveal the mechanism of viscosity change with slag composition.
Funding statement: This work was supported by the National Basic Research Program of China under Grant No. 2013CB632604; Fundamental Research Funds for the Central Universities under Grant CDJZR 14130001; and National Natural Science Foundation of China under Grants Nos. 51090382 and 51604047.
References
1 I. Kansal, A. Goel, D.U. Tulyaganov, R.R. Rajagopal and J.M.F. Ferreira, J. Eur. Ceram. Sco., 32 (2012) 2739–2746.10.1016/j.jeurceramsoc.2011.10.041Search in Google Scholar
2 U. Hoppe, G. Walter, R. Kranold and D. Stachel, J. Non-Cryst. Solids, 263&264 (2000) 29–47.10.1016/S0022-3093(99)00621-3Search in Google Scholar
3 G. Fan, J. Diao, L. Jiang, Z. Zhang and B. Xie, Mater. Trans., 56 (2015) 655–660.10.2320/matertrans.M2014363Search in Google Scholar
4 J. Diao, G.Z. Fan, X. Liu and B. Xie, Metall. Mater. Trans. B, 45 (2014) 1942–1947.10.1007/s11663-014-0092-1Search in Google Scholar
5 C. Mercier, C. Follet-Houttemane, A. Pardini and B. Revel, J. Non-Cryst. Solids, 357 (2011) 3901–3909.10.1016/j.jnoncrysol.2011.07.042Search in Google Scholar
6 H.W. Ni, H.J. Hui and G.S. Neumann, Rev. Geophys., 53 (2015) 715–744.10.1002/2015RG000485Search in Google Scholar
7 G.B. Martin, F.J. Spera, M.S. Ghiorso and D. Nevins, Am. Mineral, 94 (2009) 693–703.10.2138/am.2009.3087Search in Google Scholar
8 N. Sun, L. Stixrude, N. Koker and B.B. Karki, Geochim. Cosmochim. Ac., 75 (2011) 3792–3802.10.1016/j.gca.2011.04.004Search in Google Scholar
9 L. Woodcock, C. Angell and P. Cheeseman, J. Chem. Phys., 65 (1976) 1565–1577.10.1063/1.433213Search in Google Scholar
10 H. Luo, S. Xiao, S. Wang, P. Huai, H. Deng and W. Hu, Comp. Mater. Sci., 111 (2016) 203–208.10.1016/j.commatsci.2015.09.052Search in Google Scholar
11 H. Hirao and K. Kawamura, Material Design Using Personal Computer, Shokabo, Tokyo (1994).Search in Google Scholar
12 Verein Deutscher Eisenhuttenleute, Slag Atlas, 2nd edition, Verlag Stahleisen mBH, Dusseldorf (1995).Search in Google Scholar
13 D.J. Lacks, D.B. Rear and J.A. Van Orman, Geochim. Cosmochim. Ac., 71 (2007) 1312–1323.10.1016/j.gca.2006.11.030Search in Google Scholar
14 D. Nevins, F.J. Spera and M.S. Ghiorso, Am. Mineral, 94 (2009) 975–980.10.2138/am.2009.3092Search in Google Scholar
15 T. Matsumiya, A. Nogami and Y. Fukuda, ISIJ Int., 33 (1993) 210–217.10.2355/isijinternational.33.210Search in Google Scholar
16 W.G. Seo and F. Tsukihashi, ISIJ Int., 44 (2004) 1817–1825.10.2355/isijinternational.44.1817Search in Google Scholar
17 K. Shimoda and K. Saito, ISIJ Int., 47 (2007) 1275–1279.10.2355/isijinternational.47.1275Search in Google Scholar
18 T. Asada, Y. Yamada and K. Ito, ISIJ Int., 48 (2008) 120–122.10.2355/isijinternational.48.120Search in Google Scholar
19 W.G. Seo and F. Tsukihashi, Mater. Trans., 46 (2005) 1240–1247.10.2320/matertrans.46.1240Search in Google Scholar
20 D.K. Belashchenko and O.I. Ostrovskii, Inorg. Mater., 38 (2002) 958–963.10.1023/A:1014065127380Search in Google Scholar
21 D.K. Belashchenko and O.I. Ostrovskii, Inorg. Mater., 38 (2002) 196–203.10.1023/A:1020094325624Search in Google Scholar
22 L.J. Zhou and W.N. Wang, Metall. Mater. Trans. B, 47 (2016) 1548–1552.10.1007/s11663-016-0651-8Search in Google Scholar
23 Y. Sasaki and M. Iguchi, ISIJ Int., 49 (2009) 602–604.10.2355/isijinternational.49.602Search in Google Scholar
24 K.C. Mills, L. Yuan, Z. Li, G.H. Zhang and K.C. Chou, High Temp. Mater. Proc., 31 (2012) 301–321.10.1515/htmp-2012-0097Search in Google Scholar
25 Y. Sun, K. Zheng, J.L. Liao, X.D. Wang and Z.T. Zhang, ISIJ Int., 54 (2014) 1491–1497.10.2355/isijinternational.54.1491Search in Google Scholar
26 Y.Q. Sun and Z.T. Zhang, Metall. Mater. Trans. B., 46 (2015) 1549–1554.10.1007/s11663-015-0374-2Search in Google Scholar
27 Y.Q. Sun, Z.T. Zhang, L.L. Liu and X.D. Wang, J. Non-Cryst. Solids, 420 (2015) 26–33.10.1016/j.jnoncrysol.2015.04.017Search in Google Scholar
28 Z.J. Wang, Q.F. Shu, S. Sridhar, M. Zhang, M. Guo and Z.T. Zhang, Metall. Mater. Trans. B., 46 (2015) 758–765.10.1007/s11663-014-0270-1Search in Google Scholar
© 2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- Research Articles
- Catalytic Synthesis of n-Butyl Oleate by Cerium Complex Doped Y/SBA-15 Composite Molecular Sieve
- Effects of Vacancy Concentration and Temperature on Mechanical Properties of Single-Crystal γ-TiAl Based on Molecular Dynamics Simulation
- Experimental Study on Electrical Conductivity of FexO-CaO-SiO2-Al2O3 System at Various Oxygen Potentials
- Textural and Optical Properties of Ce-Doped YAG/Al2O3 Melt Growth Composite Grown by Micro-Pulling-Down Method
- Short Communication
- Aging of a Low Carbon Heat Resistant Cast Alloy
- Research Articles
- Computational Study of the Transport Properties of Molten CaO-SiO2-P2O5-FeO System
- Melting Features and Viscosity of TiO2-Containing Primary Slag in a Blast Furnace
- Development of Processing Maps for AZ81E Magnesium Alloy
- A Modified Johnson Cook Constitutive Model for Aermet 100 at Elevated Temperatures
- Cyclic Oxidation and Hot Corrosion Behavior of Nickel–Iron-Based Superalloy
- Flow Behavior and Dynamic Recrystallization of BT25y Titanium Alloy During Hot Deformation
Articles in the same Issue
- Frontmatter
- Research Articles
- Catalytic Synthesis of n-Butyl Oleate by Cerium Complex Doped Y/SBA-15 Composite Molecular Sieve
- Effects of Vacancy Concentration and Temperature on Mechanical Properties of Single-Crystal γ-TiAl Based on Molecular Dynamics Simulation
- Experimental Study on Electrical Conductivity of FexO-CaO-SiO2-Al2O3 System at Various Oxygen Potentials
- Textural and Optical Properties of Ce-Doped YAG/Al2O3 Melt Growth Composite Grown by Micro-Pulling-Down Method
- Short Communication
- Aging of a Low Carbon Heat Resistant Cast Alloy
- Research Articles
- Computational Study of the Transport Properties of Molten CaO-SiO2-P2O5-FeO System
- Melting Features and Viscosity of TiO2-Containing Primary Slag in a Blast Furnace
- Development of Processing Maps for AZ81E Magnesium Alloy
- A Modified Johnson Cook Constitutive Model for Aermet 100 at Elevated Temperatures
- Cyclic Oxidation and Hot Corrosion Behavior of Nickel–Iron-Based Superalloy
- Flow Behavior and Dynamic Recrystallization of BT25y Titanium Alloy During Hot Deformation

