Home Physical Sciences Phase Transition and Thermal Expansion of Ba3RB3O9 (R = Sm–Yb, and Y)
Article Open Access

Phase Transition and Thermal Expansion of Ba3RB3O9 (R = Sm–Yb, and Y)

  • Rayko Simura EMAIL logo , Shohei Kawai and Kazumasa Sugiyama
Published/Copyright: April 14, 2016
Download Article (PDF)
High Temperature Materials and Processes
From the journal High Temperature Materials and Processes Volume 36 Issue 8

Abstract

High temperature powder X-ray diffraction measurements of Ba3RB3O9 (R=Sm–Yb, and Y) were carried out at temperatures ranging from room temperature to just below the corresponding melting temperatures (1,200–1,300 °C). No phase transition was found for the H-type phase (R3‾) with R=Sm–Tb and the L-type phase (P63 cm) with R=Tm–Yb. On the other hand, phase transition from the L phase to the H phase was observed for R=Dy–Er, and Y at around 1,100–1,200 °C. The obtained axial thermal expansion coefficient (ATEC) of the a-axis was larger than that of the c-axis for the H phase, and the ATEC of the c-axis was larger than that of the a-axis for the L phase. The observed anisotropic nature of ATEC is attributed to the distribution of the BO3 anionic group with rigid boron–oxygen bonding in the structures of the H and L phases.

Keywords: borates; phase transition; thermal expansion; X-ray diffraction; high temperature
PACS: Thermal expansion; 65.40.De; Crystal structure inorganic compounds; 61.66.Fn

Introduction

The Ba3RB3O9 (R=rare earth element; REE) systems show two polymorphs corresponding to the type of REE. One is the H-type structure with the space group R3‾ in the case of lighter REEs (R=Nd–Dy) (Figure 1(a)), and the other is the L-type structure with the space group P63 cm reported for heavier REEs (R=Dy–Lu, and Y) (Figure 1(b)) [1, 2, 3, 4, 5]. The H-type structure of Ba3RB3O9 is a potential host material for non-linear optical, laser, and scintillator application [6, 7, 8, 9, 10]. In particular, H-type compounds with Gd, Lu, or Y as the REE attract much interest as a potential host crystal in optical applications, because the elements generally produce no unfavorable photoluminescence. In addition to the structural variation associated with the REE, the phase transition as a function of temperature was reported in systems with the middle rare earth elements and Y. For the practical use of the H-type structure, knowledge of the detailed conditions of chemistry and temperature for the phase stability in the Ba3RB3O9 systems, and the corresponding physical properties such as the thermal expansion coefficient, is strongly required. This prompted us to conduct a systematic study of Ba3RB3O9 compounds (R=Sm–By, and Y) with respect to their structure and high temperature behaviors. High temperature X-ray diffraction measurements were performed to confirm the crystal structural change and to clarify the axial thermal expansion coefficients (ATECs) of the H and L phases in the Ba3RB3O9 systems (R=Sm–Yb, and Y).

Figure 1: Schematic illustration of the crystal structures of the (a) H phase and (b) L phase. Oxygen-coordinated polyhedrons of cations (R=REE), Ba, and B) are drawn. The H phase is constructed of BO3 triangles, BaO8 polyhedrons, (Ba,R)O6 octahedrons, and RO6 octahedrons. The L phase is composed of three types of alternating layers; BO3 triangles, BaO9 polyhedrons, and RO6 octahedrons.
Figure 1:

Schematic illustration of the crystal structures of the (a) H phase and (b) L phase. Oxygen-coordinated polyhedrons of cations (R=REE), Ba, and B) are drawn. The H phase is constructed of BO3 triangles, BaO8 polyhedrons, (Ba,R)O6 octahedrons, and RO6 octahedrons. The L phase is composed of three types of alternating layers; BO3 triangles, BaO9 polyhedrons, and RO6 octahedrons.

Experimental

Sample preparation

Sample powders of Ba3RB3O9 compounds (R=Sm–Yb, and Y) were prepared by the high-temperature solid-state reaction. Stoichiometric mixtures of raw chemicals (4N R2O3, 3N BaCO3, and 3N H3BO3) were ground together and subsequently molded into pellets. Then, they were placed in alumina crucibles and sintered for 24 h at 1,000 °C in a muffle furnace. After the furnace was cooled down to room temperature (RT; 27 °C), the sintered pellets were crushed into powders for the following measurements.

Thermal analysis

Thermogravimetry-differential thermal analyses (TG-DTA) were performed for the prepared sample powders from RT to 1,350 °C using Pt pans with a Rigaku TG8120. Heating and cooling rates were 20 K/min. The obtained melting temperature was used for determining the temperature range for the high temperature powder X-ray diffraction (HT-XRD) measurements.

X-ray diffraction measurements

The HT-XRD measurements utilized the ordinary Bragg-Brentano optics, a diffracted-beam monochromator, and Cu Kα radiation. An electric furnace with a water-cooling device was placed at the center of a two-axes goniometer (Ultima III, Rigaku), and the temperature of the furnace was controlled using a R-type thermocouple. The temperature at the sample was calibrated using the result of high temperature X-ray diffraction for Al2O3 powder and the published standard data [11]. Temperatures of HT-XRD measurements during the heating period were set at RT, 200 °C, 400 °C, 600 °C, 800 °C, and 1,000 °C. In particular, intervals of 50 °C or 100 °C were also selected from 1,000 °C to the melting temperatures. For the cooling-down period over 800 °C, the HT-XRD measurements were performed at similar temperatures. In order to stabilize the temperature at the sample, HT-XRD measurements were started 5 min after reaching the target temperature. In our HT-XRD measurements, the heating rate was set at 10 K/min below 1,000 °C and 5 K/min above 1,000 °C, and the cooling rate was set at 20 K/min.

Unit cell parameters were calculated by the least-square refinement with the computer program JADE ver. 6.5. The variations of the obtained unit cell parameters were analyzed using a quadratic function (L=L0+ L1T + L2T2, where L = the values of a or c axis, T=temperature (°C), and L0, L1, and L2 are coefficients). The obtained coefficients are summarized in Table 1. ATEC (αT=1/L0dL/dT|T) of the a- and c-axis were calculated using the coefficients of L0, L1 and L3.

Table 1:

The fitted coefficients for the quadratic curve shown in Figure 5 (L=L0 + L1T + L2T2).

Ra-axisc-axis
ValueσValueσ
L phase
DyL09.426×1002×10−31.7642×1019×10−3
L19.0×10−58×10−61.7×10−44×10−5
L2−2.2×10−87×10−92.2×10−73×10−8
ErL09.431×1002×10−31.7580×1011×10−2
L18.0×10−58×10−61.2×10−46×10−5
L2−1.6×10−86×10−93.0×10−75×10−8
HoL09.434×1002×10−31.7613×1018×10−3
L19.3×10−57×10−62.1×10−43×10−5
L2−2.6×10−86×10−92.1×10−72×10−8
TmL09.409×1002×10−31.7478×1018×10−3
L15.8×10−57×10−62.2×10−43×10−5
L2−a−a2.2×10−72×10−8
YL09.430×1001×10−31.7609×1013×10−3
L17.6×10−54×10−61.7×10−41×10−5
L2−1.2×10−83×10−92.36×10−78×10−9
YbL09.400×1002×10−31.7470×1015×10−3
L16.3×10−59×10−61.8×10−42×10−5
L2–a–a2.4×10−72×10−8
H phase
DyL01.3049×1014×10−39.536×1002×10−3
L11.4×10−42×10−58.8×10−58×10−6
L21.2×10−72×10−8−7.8×10−87×10−9
EuL01.3079×1018×10−39.570×1004×10−3
L11.9×10−43×10−58.0×10−52×10−5
L21.0×10−72×10−8−6×10−81×10−8
GdL01.3078×1012×10−39.576×1003×10−3
L11.9×10−41×10−54×10−51×10−5
L21.0×10−78×10−9−4×10−81×10−8
HoL01.3061×1012×10−39.5451×1007×10−4
L11.4×10−41×10−59.2×10−53×10−6
L21.3×10−78×10−9−8.5×10−83×10−9
SmL01.3095×1016×10−39.576×1004×10−3
L11.9×10−43×10−58.0×10−52×10−5
L21.1×10−72×10−8−7.0×10−82×10−8
TbL01.3059×1013×10−39.565×1002×10−3
L11.9×10−41×10−56.4×10−59×10−6
L29.0×10−89×10−9−6.7×10−87×10−9

  1. Note: Note that the ATEC can be expressed by α=1/L0dL/dT=1/L0 (L1+L2T).

  2. aThe 2nd order coefficients, L2, for the a-axis of Tm and Yb are meaningless. As shown in Figure 5, they show an almost linear line.

Results

Sample and thermal analysis

The prepared sample powders were generally white in color except for the samples with R=Er, which was pink, R=Tb, which was brownish, and R=Ho, which was orange. No significant signals that indicate weight increase or decrease were observed in the TG analysis for all the samples, and the endothermic/exothermic peaks of melting, solidification, or phase transition were observed in the DTA signals.

The obtained melting temperatures for Ba3RB3O9 compounds (R=Sm–Yb, and Y) were summarized in Figure 2. They are consistent with the reported values of melting temperature for R=Dy–Yb and Y by Cox et al. [2], R=Y by Li et al. [4, 5], and R=Tm and Yb by Khamaganova et al. [3], but are inconsistent with those reported for R=Y, Ho, and Er by Khamaganova et al. [3]. It may be noted that the melting temperatures observed during the cooling-down period are different from those during the heating-up period, and the difference reached ~100 °C for Dy, in particular. The fact suggests the overcooled state during the cooling-down period. Additionally, the phase transition temperatures fluctuated in each measurement, suggesting the association of thermal hysteresis or kinetics.

Figure 2: Melting temperatures during heating-up and cooling-down period by DTA and phase transition temperatures during heating-up period by HT-XRD for the Ba3RB3O9 system are shown with the published temperatures [2–5]. The horizontal axis is the effective ionic radius of REE [12].
Figure 2:

Melting temperatures during heating-up and cooling-down period by DTA and phase transition temperatures during heating-up period by HT-XRD for the Ba3RB3O9 system are shown with the published temperatures [2–5]. The horizontal axis is the effective ionic radius of REE [12].

X-ray diffraction measurements

The XRD profiles at RT revealed that the samples with R=Sm–Tb and with R=Dy–Yb, Y showed the H type structures and the L type structures, respectively. In the HT-XRD, no phase transition was found for the H-type phase (R3‾) with R=Sm–Tb (Figure 3(a)) and the L-type phase (P63 cm) with R=Tm–Yb (Figure 3(c)). On the other hand, phase transition from the L phase to the H phase was observed for R=Dy–Er, and Y at around 1,100–1,200 °C (Figure 3(b)). It may be noted that the HT-XRD measurement with R=Dy and Ho did not show phase transition from the H phase to the L phase during the cooling-down period, in particular. The phase transitions for Ba3DyB3O9 and Ba3HoB3O9 are affected largely by thermal hysteresis or kinetics.

Figure 3: Representative patterns from the three types of typical XRD diffractions for Ba3RB3O9; (a) H phase only, R=Gd; (b) H and L phase, R=Y; and (c) L phase only R=Tm. The numbers in the graph show the measurement temperature and RT indicates room temperature.
Figure 3:

Representative patterns from the three types of typical XRD diffractions for Ba3RB3O9; (a) H phase only, R=Gd; (b) H and L phase, R=Y; and (c) L phase only R=Tm. The numbers in the graph show the measurement temperature and RT indicates room temperature.

Discussions

The unit cell parameters at room temperature

Figure 4 shows the cell parameters at RT as a function of rR+rO (the sum of the effective ionic radius of REE, rR, and that of oxygen, rO [12]). The c-axis of the L phase increases significantly with increasing rR+rO, which is associated with the structural features of the L-phase. The L type structure consists of the stacking the RO6 layers and BaO9 layers along the c-axis and the RO6 and BaO9 coordination polyhedra link together by sharing a triangle face. This unique linkage indicates a strong electrostatic repulsion along the c-axis and produces an appreciated effect of the length of the c-axis. In contrast, the no strong anisotropy was detected in the variation of cell parameters for the H phase as shown in Figure 4(a) and (b). These features are associated with the rather homogeneous arrangement of the RO6 and BaO9 polyhedra in the H-type structure.

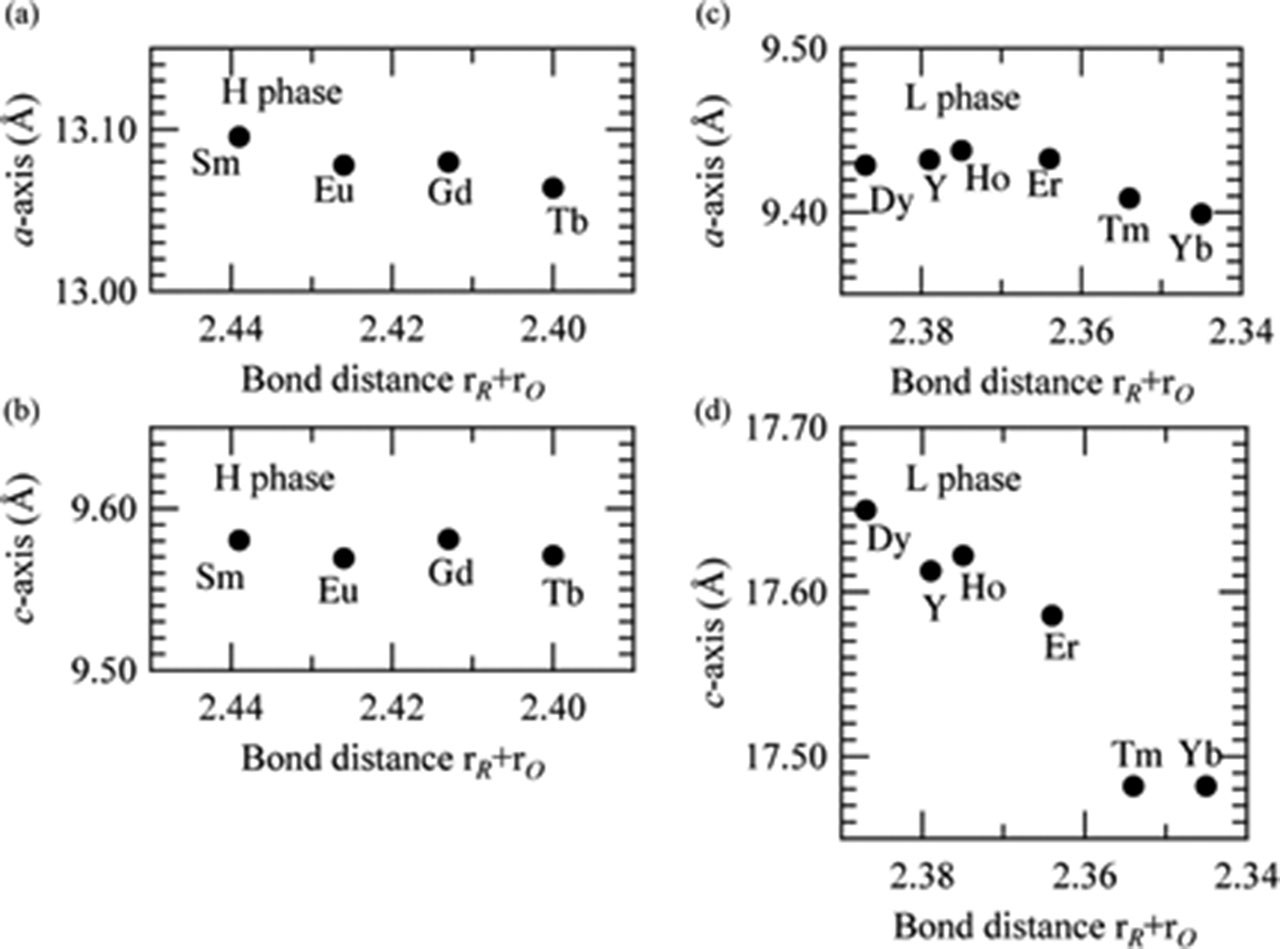
Figure 4: The unit cell parameters versus the sum of the effective ionic radius ratio, rR+rO, at room temperature; (a) a- and (b) c-axes of the H phase, and (c) a- and (d) c-axes of the L phase. Note that horizontal axes are reversed.
Figure 4:

The unit cell parameters versus the sum of the effective ionic radius ratio, rR+rO, at room temperature; (a) a- and (b) c-axes of the H phase, and (c) a- and (d) c-axes of the L phase. Note that horizontal axes are reversed.

Thermal expansion coefficients

Temperature dependences of unit cell parameters are shown in Figure 5, and the data can be approximated by quadratic curves.

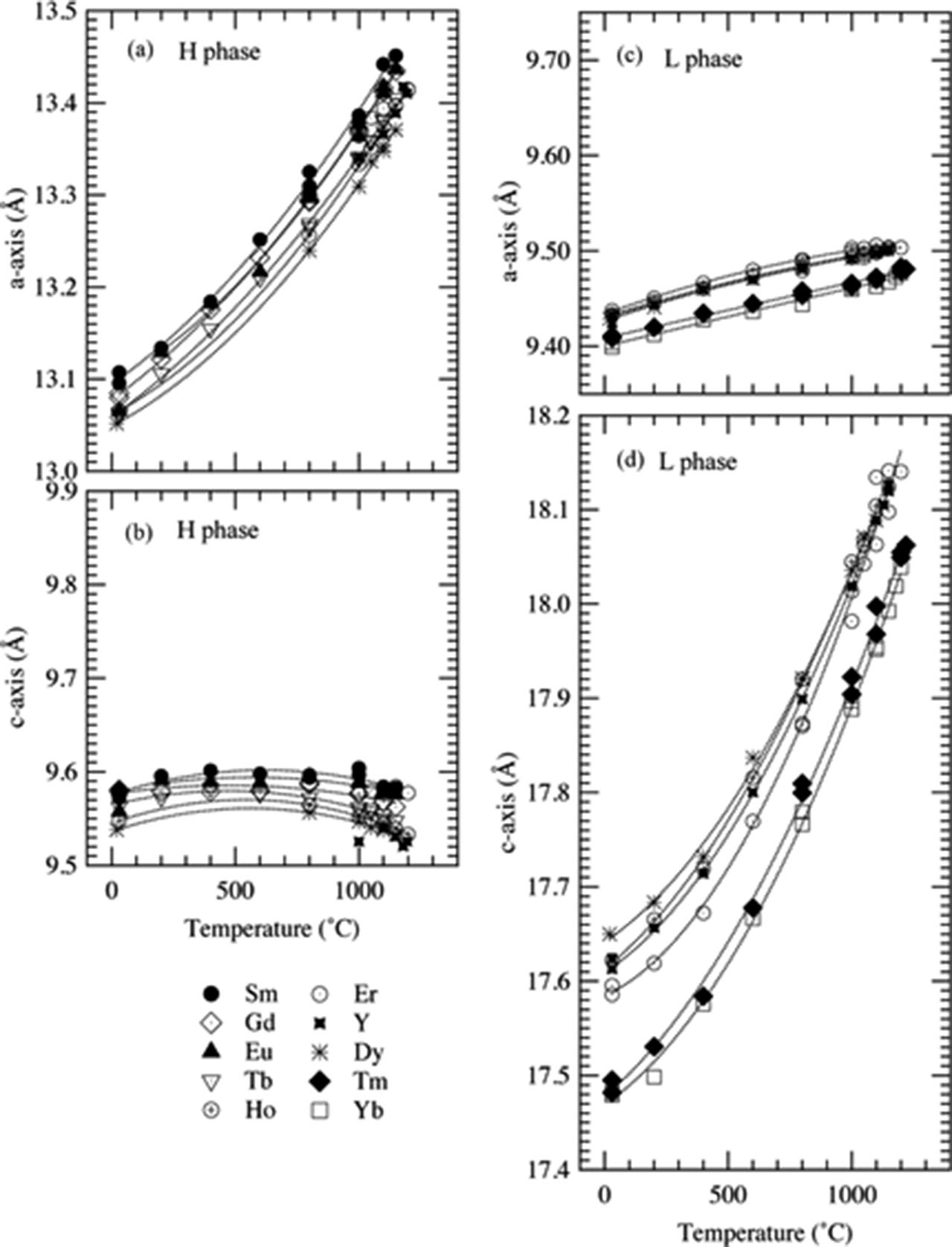
Figure 5: Temperature dependence of the unit cell parameters; (a) a- and (b) c-axes of the H phase, and (c) a- and (d) c-axes of the L phase. Dotted lines are the fitted quadratic curves. Fitted coefficients are shown in Table 1.
Figure 5:

Temperature dependence of the unit cell parameters; (a) a- and (b) c-axes of the H phase, and (c) a- and (d) c-axes of the L phase. Dotted lines are the fitted quadratic curves. Fitted coefficients are shown in Table 1.

In the case of the H phase, the ATEC of the a-axis increases linearly from ~15×10−6 °C−1 to ~30×10−6 °C−1 and that of the c-axis decreases linearly from ~10×10−6 °C−1 to ~ –10×10−6 °C−1 as a function of temperature. This anisotropic thermal expansion for the H phase can be attributed to the distribution of BO3 triangles and their thermal vibration at the high temperature [13, 14, 15, 16]. The normal vectors of BO3 triangles are almost perpendicular to the c-axis, as shown in the close-up figure of the H phase (Figure 6(a)) and then the expected thermal vibration of BO3 triangles perpendicular to the plane of the triangle encourages the larger ATEC of the a-axis in the present case.

Figure 6: Crystal structure of Ba3RB3O9 focused on the direction of the BO3 triangles illustrated in black triangles. Structures perpendicular to the (a) a- and (b) c-axes of the H phase and those perpendicular to the (c) a- and (d) c-axes of the L phase are shown.
Figure 6:

Crystal structure of Ba3RB3O9 focused on the direction of the BO3 triangles illustrated in black triangles. Structures perpendicular to the (a) a- and (b) c-axes of the H phase and those perpendicular to the (c) a- and (d) c-axes of the L phase are shown.

On the contrary, the ATEC for the a-axis of the L phase decreases linearly from ~10×10−6 °C−1 to ~5×10−6 °C−1 with increasing temperature, and increases linearly from ~10×10−6 °C−1 to ~40×10−6 °C−1 for the c-axis. This anisotropy can be discussed by using the structural features found in the alignment of BO3 triangles, again. As shown in Figure 6, the planes of BO3 triangles are perpendicular to the c-axis, and the anisotropic thermal vibration of the BO3 triangle could be associated with the larger ATEC along the c-axis. Similar distribution of BO3 triangles was also reported in the structure of LuBO3 (calcite modification), and the larger thermal expansion perpendicular to the BO3 triangles was demonstrated [13].

Summary

Features of the phase transition in the Ba3RB3O9 (R=Sm–Yb, and Y) systems were examined using TG-DTA and HT-XRD. The Ba3RB3O9 (R=Sm–Tb) system with the lighter REE indicates no solid–solid phase transition and remained as the H phase up to the melting temperature. The system (R=Tm–Yb) with heavier REE also indicates no solid–solid phase transition, and they remained as the L phase. In contrast, the system (R=Dy–Er, and Y) shows a solid–solid phase transition from L-type to H-type phases.

Features of the thermal expansion coefficient for the Ba3RB3O9 (R=Sm–Yb, and Y) systems were investigated by the HT-XRD measurements. The ATEC of the a-axis for the H phase was larger than that of the c-axis. On the contrary, the ATEC of the c-axis for the L phase was larger than that of the a-axis. These anisotropic thermal behaviors are associated well with the systematic distribution of the BO3 triangles in the crystal structures. The larger thermal expansion is realized in the direction perpendicular to the planes of BO3 triangles and this feature is in accordance with the thermal vibration of BO3 triangle.

Acknowledgements

One of the authors (R.S.) was supported by a Grant-in-Aid for Young Scientists (B) (2376003) from the Japan Society for the Promotion of Science (JSPS).

References

[1] A.B. Ilyukhim, B.F. Dzhurinskii and R.J. Inorg. Chem., 38 (1993) 1625–1630.Search in Google Scholar

[2] J.R. Cox, D.A. Keszler and J. Huang. Chem. Mater., 6 (1994) 2008–2013.10.1021/cm00047a021Search in Google Scholar

[3] T.N. Khamaganova, N.M. Kuperman and Zh.G. Bararova, J. Solid State Chem., 145 (1999) 33–36.10.1006/jssc.1999.8163Search in Google Scholar

[4] X.Z. Li, X.L. Chen, L. Wu, Y.G. Cao, T. Zhou and Y.P. Xu. J. Alloys Compd., 370 (2004) 53–58.10.1016/j.jallcom.2003.09.128Search in Google Scholar

[5] X.Z. Li, X.L. Chen, J.K. Jian, L. Wu, Y.P. Xu and Y.G. Gao, J. Solid State. Chem., 177 (2004) 216–220.10.1016/S0022-4596(03)00415-8Search in Google Scholar

[6] S. Pan, Z. Hu, Z. Lin and G. Wang. J. Cryst. Growth, 247 (2003) 452–456.10.1016/S0022-0248(02)02052-3Search in Google Scholar

[7] S. Pan, Z. Hu, Z. Lin and G. Wang. J. Cryst. Growth, 263 (2004) 214–217.10.1016/j.jcrysgro.2003.11.006Search in Google Scholar

[8] B. Han, H.B. Liang, H.H. Lin, J.P. Zhong, Q. Su, P. Dorenbos, M. Danang-Birowosuto, G.B. Zhang and Y.B. Fu. J. Appl. Phys., 101 (2007) #113530.10.1063/1.2743826Search in Google Scholar

[9] R. Sole, F. Guell, J. Gavalda, M. Aguilo and F. Diaz. J. Mater. Res., 23 (2008) 2512–2518.10.1557/jmr.2008.0313Search in Google Scholar

[10] R. Simura, T. Yagi, K. Sugiyama, T. Yanagida and A. Yoshikawa. J. Cryst. Growth, 362 (2013) 145–158.10.1016/j.jcrysgro.2011.11.086Search in Google Scholar

[11] T. Mitsunaga, M. Saigo and G. Fujinawa. Powder Diffr., 17 (2002) 173–177.10.1154/1.1471519Search in Google Scholar

[12] R.D. Shannon. Acta Cryst. A., 32 (1976) 751–767.10.1107/S0567739476001551Search in Google Scholar

[13] S.K. Filatov and R.S. Bubnova. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol. B, 56 (2015) 24–35.Search in Google Scholar

[14] W.-D. Stein, A. Cousson, P. Becker, L. Bohaty and M. Braden, Z. Kristallogr., 222 (2007) 680–689.Search in Google Scholar

[15] R.S. Bubnova and S.K. Filatov. Phys. Status Solid., 245 (2008) 2469–2476.10.1002/pssb.200880253Search in Google Scholar

[16] S.N. Volkov, S.K. Filatov, R.S. Bubnova, V.L. Ugolkov, T.N. Ugolkov, T.N. Svetlyakova and A.E. Kokh. Glass Phys. Chem., 38 (2012) 162–177.10.1134/S108765961201018XSearch in Google Scholar

Received: 2015-8-20
Accepted: 2016-2-6
Published Online: 2016-4-14
Published in Print: 2017-9-26

© 2017 Walter de Gruyter GmbH, Berlin/Boston

This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. High Temperature Mechanical Behavior of MgAl2O4-YAG Eutectic Ceramic In Situ Composites by Float Zone Method
  4. Phase Transition and Thermal Expansion of Ba3RB3O9 (R = Sm–Yb, and Y)
  5. Microstructure and Mechanical Properties of Heat-treated T92 Martensitic Heat Resistant Steel
  6. Short Communication
  7. Change in Microwave-Absorbing Characteristics during the Oxidation Processes of an Ilmenite Concentrate
  8. Research Articles
  9. FeAl2O4 Nanopowders; Structural Analysis and Band Gap Energy
  10. The Influence of Dwell Time on Low Cycle Fatigue Behavior of Ni-base Superalloy IC10
  11. Microwave-Assisted Preparation of Activated Carbon from Eupatorium Adenophorum: Effects of Preparation Parameters
  12. Kinetics of Evaporation of Alloying Elements under Vacuum: Application to Ti alloys in Electron Beam Melting
  13. Effect of Heat Treatment Technique on the Low Temperature Impact Toughness of Steel EQ70 for Offshore Structure
  14. Effect of B2O3 on Volume Stability and Strength of Corundum-based Castables
  15. Thermodynamic Analysis of the Selective Reduction of a Nickeliferous Limonitic Laterite Ore by Hydrogen
  16. The Analysis of Parametric Sensitivity Based on Designing and Optimization of a New Microwave Heating System
  17. Influence of Heat Treatment on the Mechanical Properties of Ni Films on 430 Stainless Steel Substrate
https://doi.org/10.1515/htmp-2015-0290
Keywords for this article
borates; phase transition; thermal expansion; X-ray diffraction; high temperature
Creative Commons
BY-NC-ND 3.0

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. High Temperature Mechanical Behavior of MgAl2O4-YAG Eutectic Ceramic In Situ Composites by Float Zone Method
  4. Phase Transition and Thermal Expansion of Ba3RB3O9 (R = Sm–Yb, and Y)
  5. Microstructure and Mechanical Properties of Heat-treated T92 Martensitic Heat Resistant Steel
  6. Short Communication
  7. Change in Microwave-Absorbing Characteristics during the Oxidation Processes of an Ilmenite Concentrate
  8. Research Articles
  9. FeAl2O4 Nanopowders; Structural Analysis and Band Gap Energy
  10. The Influence of Dwell Time on Low Cycle Fatigue Behavior of Ni-base Superalloy IC10
  11. Microwave-Assisted Preparation of Activated Carbon from Eupatorium Adenophorum: Effects of Preparation Parameters
  12. Kinetics of Evaporation of Alloying Elements under Vacuum: Application to Ti alloys in Electron Beam Melting
  13. Effect of Heat Treatment Technique on the Low Temperature Impact Toughness of Steel EQ70 for Offshore Structure
  14. Effect of B2O3 on Volume Stability and Strength of Corundum-based Castables
  15. Thermodynamic Analysis of the Selective Reduction of a Nickeliferous Limonitic Laterite Ore by Hydrogen
  16. The Analysis of Parametric Sensitivity Based on Designing and Optimization of a New Microwave Heating System
  17. Influence of Heat Treatment on the Mechanical Properties of Ni Films on 430 Stainless Steel Substrate
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/htmp-2015-0290/html
Scroll to top button