From continuous time random walks to the generalized diffusion equation

1 Introduction

Brownian motion, the classical model for normal diffusion, can be explained within random walk theory according to which the particle in equal time intervals performs steps in random direction (left or right) to the nearest neighbor site. From the master equation for such a stochastic process one can find that the probability density function (PDF) W(x, t) to find the particle at position x at time t satisfies the standard diffusion equation in the continuum limit. The corresponding solution for a point initial condition is the well-known Gaussian PDF, and the mean squared displacement (MSD) has a linear dependence on time. The continuous time random walk model (CTRW) represents a generalization of the Brownian random walk model. The mathematical theory of CTRW was developed by Montroll and Weiss (1965) [34], and first applied to physical problems by Scher and Lax (1973) [52]. Nowadays it has become a very popular framework for the description of anomalous, non-Brownian diffusion in complex systems, and even after its 50 years’ history the model is still trendy with applications in various fields [23]. The Brownian random walk model is the limit case of CTRW when the waiting time PDF ψ(t) is of Poisson form and the jump length PDF λ(x) is of Gaussian form. Moreover, in the more general case of any finite characteristic waiting time T = ∫0∞tψ(t) dt and any finite jump length variance Σ² = ∫−∞∞x²λ(x) dx, the corresponding process in the diffusion limit shows normal diffusive behavior with Gaussian PDF W(x, t), [19].

It has been shown that the CTRW process with a scale-free waiting time PDF of power-law form ψ(t) ≃ t^−1−α with 0 < α < 1, leads in the continuum limit to the time fractional diffusion equation, represented by a power-law dependence of the MSD on time of form 〈 x²(t)〉 ≃ t^α [1], 33]. Since 0 < α < 1 this process is subdiffusive. Processes for which the anomalous diffusion exponent is α > 1, are superdiffusive. An example is the case of Lévy walks with long tailed jump length PDF λ(x) ≃ |x|^−1−μ, μ < 2, and spatiotemporal coupling [33]. Anomalous diffusion, either subdiffusion or superdiffusion, has been observed, for example, in the charge carrier motion in amorphous semiconductors [54], in aquifer problems [53], in living biological cells [62], including superdiffusion [2, 43] and subdiffusion [14, 21], in weakly chaotic systems [20, 60], or turbulence [44], to name a few. Furthermore, from the CTRW theory one may obtain distributed order fractional diffusion equations for ultraslow diffusive processes [4, 6, 7], where the MSD has logarithmic dependence on time found for Sinai-type disorder [57, ageing CTRW [24] or interacting subdiffusive CTRW-walkers, [45].

In this work we consider a CTRW model whose corresponding diffusion equation is of general form in the Riemann-Liouville sense. In Section 2 we provide an introduction to the generalized derivatives in the Riemann-Liouville and Caputo sense. We derive the generalized diffusion equation in the Riemann-Liouville sense from the CTRW model in Section 3. Several special cases of the model are analyzed in Section 4. In Section 5 we compare the generalized diffusion equation in normal and modified form, and we show under which conditions both equations are equivalent. A summary is given in Section 6.

2 Generalized derivatives and Mittag-Leffler functions

A string of recent works that were summarized and discussed in [36, 63] concerned definitions of new operators of fractional calculus. Some of the newly introduced derivatives belong to a class of generalized derivatives with memory kernels either in modified (or Riemann-Liouville (R-L)) form

or in the normal (or Caputo) form

The R-L fractional derivative is a special case of the generalized derivative (2.1) in which the memory kernel is of power-law form η(t) = t^−α/Γ(1 − α), 0 < α < 1, [40],

Similarly, the Caputo fractional derivative is a special case of the generalized derivative (2.2) for γ(t) = t^−α/Γ(1 − α), 0 < α < 1, [40],

As we will see later, the distributed order and tempered fractional derivatives are special cases of these generalized derivatives (2.1) and (2.2) as well. An extensive study of the generalized derivatives is presented by Kochubei [22], Luchko and Yamamoto [26], and Sandev et al. [46, 47, 49], to name but a few. Such generalized derivatives have been used in anomalous diffusion modeling by fractional and generalized Langevin equations with memory kernels of power-law, exponential, Mittag-Leffler, and tempered form, or combinations thereof [27, 28, 41, 48, 50, 51, 58, 64, 65, 66].

The famed Mittag-Leffler (M-L) functions play an important role in the theory of fractional and generalized differential equations. Here we consider the three parameter M-L function, introduced by Prabhakar [42] as follows:

where (δ)_k = Γ(δ + k)/Γ(δ) is the Pochhammer symbol. The more familiar one parameter M-L function E_α(z) and the two parameter M-L function E_α,β(z) are special cases of the three parameter M-L function for β = δ = 1 and δ = 1, respectively, see e.g. [8, 29, 40]. Introducing the Laplace transform of a function f(t) as f̂(s) = 𝓛_s[f(t)] = ∫0∞f(t)e^−st dt, for the three parameter M-L function (2.5) we get [42]

The three parameter M-L function has many applications in the description of anomalous diffusion and non-exponential relaxation processes, see for example [11, 12, 13, 15, 46, 47, 49, 51, 61].

There are many generalizations of the M-L function. We will use here the multinomial M-L function [25] defined by

where

are the so-called multinomial coefficients. This function has been shown to play an important role in description of the MSD of anomalous diffusion processes [46, 47, 50].

3 CTRW theory and subordination

Here we give a brief introduction to the fundamental results of the continuous time random walk (CTRW) theory. This stochastic model is based on the fact that individual jumps are separated by independent, random waiting times. For the PDF W(x, t) a simple algebraic form for the Fourier-Laplace transform W^~(k, s) = 𝓕_k[𝓛_s[W(x, t)]] can be found. We note that the Fourier transform of f(x) is given by F̃(k) = 𝓕[f(x)] = ∫−∞∞f(x)e^ıkx dx, and the inverse Fourier transform is defined by f(x) = 𝓕⁻¹[F̃(k)] = 12π∫−∞∞F̃(k)e^−ıkx dk. With these definitions, one finds for the PDF in the Fourier-Laplace space [33, 54]

Here ψ̂(s) is the Laplace transform of the waiting time PDF ψ(t), and λ̃(k) is the Fourier transform of the jump length PDF λ(x). The Fourier transform of the Gaussian distribution of jump lengths with variance σ² is 1−12σ²k² for small k, where σ² has the dimension of length. To avoid dimensions, we set σ² = 2. Therefore, in this paper we assume λ̃(k) ≃ 1 − k², [33]. As it was already mentioned in the Introduction, the CTRW process with a scale-free waiting time PDF of a power law form ψ(t) ≃ t^−1−α, 0 < α < 1, and Gaussian distribution for the jumps leads to the subdiffusive time fractional diffusion equation exhibiting mono-scaling behavior [33]. In this paper we present a CTRW model with generalized waiting time PDF and Gaussian distribution of jump lengths, for which we can derive the corresponding generalized diffusion equation.

We introduce the generalized waiting time PDF

in Laplace space, where η(t) has the property

in order to ensure normalization of the waiting time PDF. To guarantee that this generalized function is a proper PDF its Laplace transform ψ̂(s) should be completely monotone [9, 55]. Here we note that the function g(s) is completely monotone if ( − 1ⁿg⁽ⁿ⁾(s) ≥ 0 for all n ≥ 0 and s > 0. An example of a completely monotone function is s^α, where α < 0. The requirement ψ̂(s) to be completely monotone is fulfilled if the function 1/ψ̂(s) = 1 + 1/η̂(s) is a Bernstein function, that is a non-negative function whose derivative is completely monotone. Here we employ the Theorem that the function f(g(s)) is competely monotone if the function f(s) is completely monotone, and the function g(s) is a Bernstein function [55]. In what follows we consistently check this requirement for all the specific examples considered in the paper. The waiting time PDF (3.2) together with a Gaussian jump length PDF with λ̃(k) ≃1 − k² yield the Fourier-Laplace form

of the PDF W(x, t). Rewriting Eq. (3.4) as

from inverse Fourier-Laplace transform we obtain the generalized diffusion equation

with the memory kernel η(t). In this generalized diffusion equation the memory kernel appears on the right hand side of the equation, i.e., this equation is of what we call the modified form in comparison to the generalized diffusion equation in normal form (or natural form) where the memory kernel appears on the left side of the equation. Special cases of the generalized equations in normal and modified forms have been extensively investigated in different contexts, for example, in [3, 4, 6, 7, 10, 22, 26, 46, 47, 59].

From Eq. (3.4) we derive the general form of the n-th moment (n ∈ N), by using

Therefore, we conclude that the PDF W(x, t) is normalized since

and the MSD is given by

Next we need to show the non-negativity of the PDF W(x, t) in order to have an appropriate stochastic process governed by the generalized CTRW model. For this reason, we employ the subordination technique. From Eq. (3.4) one finds that

where the function Ĝ(u, s) is given by

Thus, the PDF W(x, t) is given by [30, 31]

The PDF G(u, t) provides a subordination transformation, from time scale t (physical time) to time scale u (operational time). It is normalized with respect to u for any t,

Here we again use the definitions and properties of the completely monotone and Bernstein functions. Therefore, G(u, t) is positive if its Laplace transform Ĝ(u, s) is completely monotone on the positive real axis s [55]. This condition is satisfied if, [49]: (a) the function 1/[sη̂(s)] is a completely monotone function, and (b) the function 1/η̂(s) is a Bernstein function. The constraint (b) ensures that the function e^−u/η̂(s) is completely monotone, since the exponential function is completely monotone and the composition of a completely monotone and a Bernstein function is itself completely monotone [55]. Moreover, Ĝ(u, s) is completely monotone, as the product of the two completely monotone functions e^−u/η̂(s) and 1/[sη̂(s)]. Alternatively, we can check that 1/η̂(s) is a complete Bernstein function. This is an important subclass of the Bernstein functions [55]. An example is the function s^α with 0 ≤ α ≤ 1. This condition is enough for complete monotonicity of Ĝ(u, s) due to the property of the complete Bernstein function: if f(s) is a complete Bernstein function, then f(s)/s is completely monotone [55].

4 Specific examples

4.6 Tempered fractional diffusion equation

As a last example we consider a power-law memory kernel with truncation η(t) = e^−btt^α−1/Γ(α), 0 < α < 1, b > 0, i.e., the following equation

∂W(x,t)∂t=1Γ(α)ddt∫0te−b(t−t′)(t−t′)α−1∂2W(x,t′)∂x2dt′.(4.18)

By substitution of η̂(s) = (s + b)^−α, in the generalized waiting time PDF (3.2), we find

ψ(t)=Ls−111+(s+b)α=e−bttα−1Eα,α−tα.(4.19)

Therefore, the tempered M-L waiting time PDF (4.19) generates a stochastic process governed by the tempered time fractional diffusion equation in the modified form (4.18).

Since 1/η̂(s) = (s + b)^α is a complete Bernstein function, the solution of Eq. (4.18) is non-negative. Here we use that the function f(s) = s^α with 0 ≤ α ≤ 1 is a complete Bernstein function, and so is the function f(s + a), a = const, [55].

The MSD is represented by help of the three parameter M-L function

x2(t)=2Ls−1s−1(s+b)α=2tαE1,α+1α−bt,(4.20)

which in the short time limit encodes the subdiffusive behavior 〈 x²(t)〉 ≃ 2 t^α/Γ(α + 1), while in the long time limit one observes the saturation 〈 x²(t)〉 ≃ 2 b^−α = const.

A graphical representation of the MSDs (4.20) and (4.9) is given in Figure 1. From the figure one can see that in absence of a truncation (blue solid line) the MSD (4.20) behaves as for the mono-fractional diffusion equation, 〈 x²(t)〉 ≃ 2 t^α/Γ(1 + α). In presence of a truncation in the short time limit one has the same behavior as for the mono-fractional diffusion equation, and in the long time limit the saturation 〈 x²(t)〉 ≃ 2 b^−α is observed (red dashed and green dot-dashed lines). Accelerating diffusion from 〈 x²(t)〉 ≃ 2a₁t^α₁/Γ(1 + α₁) to 〈 x²(t)〉 ≃ 2a₂t^α₂/Γ(1 + α₂) in the case of the bi-fractional diffusion equation is observed from the figure (brown dotted line), as well.

Figure 1

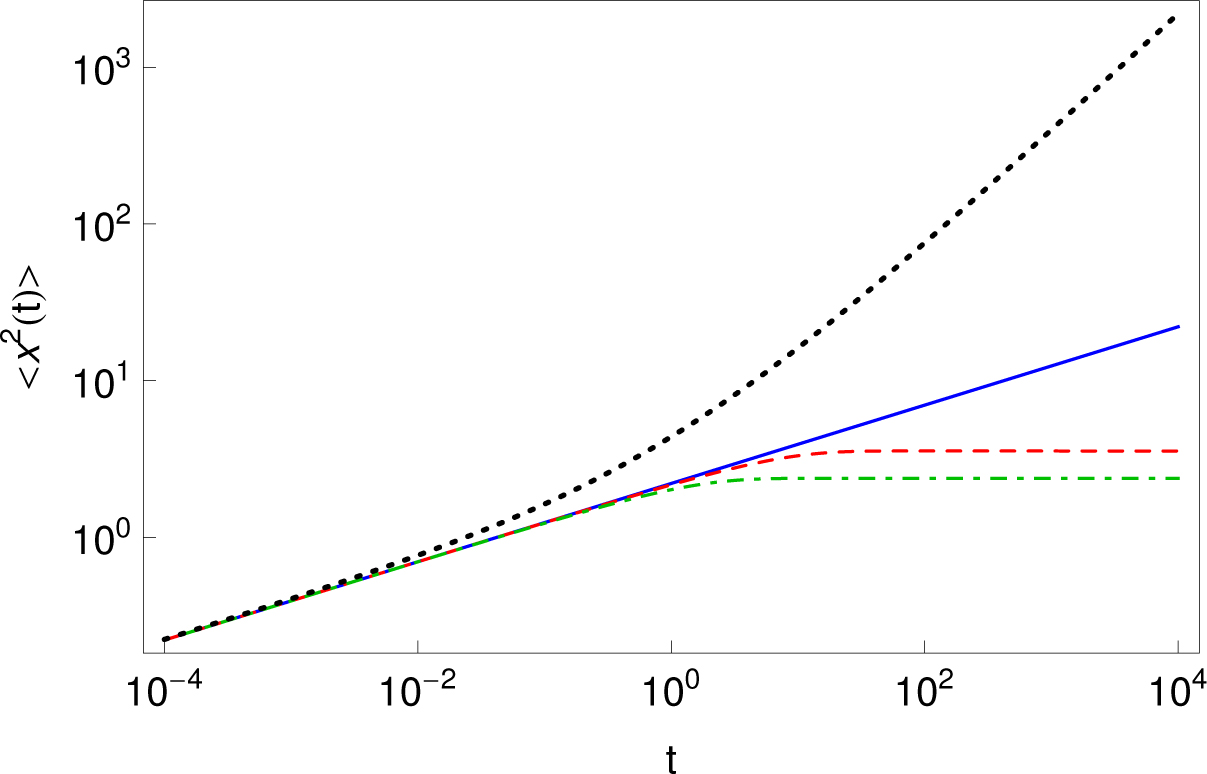
MSD for the fractional diffusion equation (4.6) with α = 1/4 (blue solid line), MSD for the tempered fractional diffusion equation (4.20) with α = 1/4 and b = 0.1 (red dashed line), b = 0.5 (green dot-dashed line). The MSD (4.9) for the bi-fractional diffusion equation in modified form with, a₁ = a₂ = 1/2, α₁ = 1/4 and α₂ = 3/4 is multiplied by factor 2 (black dotted line).

5 Normal versus modified generalized diffusion equation

In our previous work [46] we demonstrated that the CTRW model with waiting time PDF of form

where γ̂(s) is completely monotone and sγ̂(s) is a Bernstein function [49] (or alternatively, sγ̂(s) is a complete Bernstein function), and a Gaussian distribution of jump lengths yields the generalized diffusion equation in normal form

In comparison to the waiting time PDF (3.2) we conclude that there is a connection between both models simply by exchanging γ̂(s) → 1[sη̂(s)]. Thus, if this connection is fulfilled the solutions of both generalized diffusion equations in normal (5.2) and modified form (3.5) will be identical.

Let us illustrate this point. We saw that in the case of η(t) = 1 (η̂(s) = 1/s) we have a Poisson waiting time PDF (4.2) and the classical diffusion equation (4.1). So, if we use that γ̂(s) = 1/[sη̂(s)] = 1, i.e., γ(t) = δ(t), from relations (5.1) and (5.2) we obtain the same results.

Next, the memory kernel η(t) = t^α−1/Γ(α), 0 < α < 1, and η̂(s) = s^−α, corresponds to the M-L waiting time PDF (4.5) and the fractional diffusion equation (4.4). Therefore, by using γ̂(s) = 1/s^1−α, γ(t) = t^−α/Γ(1 − α), the generalized diffusion equation (5.2) becomes the time fractional diffusion equation in the Caputo sense,

which, as we know [46] is an equivalent formulation of the fractional diffusion equation (4.4) as long as the initial values are properly taken into account.

From the previous results [7, 47] we know that the bi-fractional diffusion equations in normal and modified form do not give the same results for the PDF and the MSD. The first one leads to decelerating subdiffusion, and the second one to accelerating subdiffusion. In order to find the equivalent formulation for the bi-fractional diffusion equation in modified form (4.7), we should use γ̂(s) = 1/[s(a₁s^−α₁ + a₂s^−α₂)], 0 < α₁ < α₂ < 1, from where, by inverse Laplace transform, we find that γ(t) is given by

Therefore, the equation in normal form corresponding to (4.7) in modified form is given by

We finally discuss one more example with the tempered memory kernel η(t) = e^−btt^α−1/Γ(α), 0 < α < 1, b > 0, which leads to the tempered fractional diffusion equation (4.18). Setting γ̂(s) = 1/[s(s + b)^−α], (η̂(s) = (s + b)^−α), we find that

and the corresponding diffusion equation in normal form becomes

Conversely, let us consider the memory kernel γ(t) = a₁t^−α₁/Γ(1 − α₁) + a₂t^−α₂/Γ(1 − α₂), 0 < α₁ < α₂ < 1, which leads to the bi-fractional diffusion equation in the normal form,

From the memory kernel we find that η̂(s) = [a₁s^α₁ + a₂s^α₂]⁻¹, i.e.,

Therefore, the equation corresponding to the bi-fractional diffusion equation in normal form turns into the following equation in modified form

In case of a tempered memory kernel γ(t) = e^−btt^−α/Γ(1 α), 0 < α < 1, b > 0, the corresponding equation of the tempered fractional diffusion equation in normal form

is

since

With these examples we show that many different equations with a wide range of memory kernels are special cases of the generalized diffusion equations (3.5) and (5.2).

6 Conclusion

We provided a CTRW model that corresponds to the generalized diffusion equation in modified form. We show that many different generalized derivatives are special cases of the generalized derivative considered in this paper. We also discuss the connection between the generalized diffusion equations in modified and normal form. We show that, for example, the bi-fractional diffusion equation and the tempered fractional diffusion equation in modified form can be represented in normal form by using Mittag-Leffler memory kernels. The need for better fitting of the experimental results [18, 35] requires introducing more flexible theoretical models as those analyzed in this work. Studying of ageing and weak ergodicity breaking [32, 56] often observed in experiments for this more general setting is left for future investigation.