On copulas with a trapezoid support

Piotr Jaworski

doi:10.1515/demo-2023-0101

Article Open Access

On copulas with a trapezoid support

Piotr Jaworski

Published/Copyright: August 14, 2023

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Dependence Modeling Volume 11 Issue 1

Abstract

A family of bivariate copulas given by: for v + 2 u < 2 , C ( u , v ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) , where F is a strictly increasing cumulative distribution function of a symmetric, continuous random variable, and for v + 2 u ≥ 2 , C ( u , v ) = u + v − 1 , is introduced. The basic properties and necessary conditions for absolute continuity of C are discussed. Several examples are provided.

Keywords: copulas; tail dependence function; Kendall τ; Spearman ρ; absolute continuity

MSC 2010: 62H05

1 Introduction

In recent years, the interest in the construction of multivariate stochastic models describing the dependence among several variables has grown. In particular, the recent financial crises emphasized the necessity of considering models that can serve to better estimate the occurrence of extremal events (see, e.g., [3,6,23] or [13]).

We introduce a new family of bivariate copulas, which are supported not on the whole unit square [ 0 , 1 ] 2 , but on its subset, a trapezoid with vertices ( 1 ∕ 2 , 1 ) , ( 0 , 1 ) , ( 1 , 0 ) , and ( 0 , 0 ) . The family consists of copulas parametrized by generators F , the symmetric cumulative distribution functions, with full support, which are convex on the negative half-line

C F ( u , v ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) , for v + 2 u ≤ 2 .

The interest in such copulas has aroused from the study of self-similar stochastic processes and the dependence between such processes and their running minima or maxima processes. See [4] or [1] for the Brownian motion case.

In Section 2, we recall the basic notation, the definition of the bivariate copula, and the formulas for its Kendall τ , Spearman ρ , and tail dependence parameters. The construction of the new family of copulas is presented in the next section. In addition, the absolute continuity of these copulas and the support are discussed.

In Section 4, we provide five examples of copulas introduced in the previous section. For each one, we calculate tail parameters and Kendall τ . For some, Spearman ρ as well.

The proofs of theorems and calculations are relegated to Section 5, which also contains some auxiliary results. In Section 5.1, we proved that the introduced family of functions is a family of copulas. Sections 5.2 and 5.3 deal with the support and absolute continuity. In Sections 5.4 and 5.5, the Kendall τ and Spearman ρ are characterized in terms of generator F and calculated for examples from Section 4. Sections 5.6, 5.7, and 5.8 deal with the tail dependence at the lower left, lower right, and upper left corners. We show that the tail dependence of C F is closely connected with the regular variation of the survival distribution function F ¯ ( t ) = 1 − F ( t ) .

2 Definitions and basic properties

We recall the definition of a bivariate copula; see [24] and [11] for more details.

Definition 1

The function

C : [ 0 , 1 ] 2 ⟶ [ 0 , 1 ]

is called a copula if the following three properties hold:

( c 1 ) ∀ u ∈ [ 0 , 1 ] C ( u , 0 ) = 0 = C ( 0 , u ) ; ( c 2 ) ∀ u ∈ [ 0 , 1 ] C ( u , 1 ) = u = C ( 1 , u ) ; ( c 3 ) ∀ u 1 , u 2 , v 1 , v 2 ∈ [ 0 , 1 ] , u 1 ≤ u 2 , v 1 ≤ v 2 V C ( ( u 1 , v 1 ) , ( u 2 , v 2 ) ) ≥ 0 ,

where the function

V C : [ 0 , 1 ] 2 × [ 0 , 1 ] 2 ⟶ R

is given as follows:

V C ( ( u 1 , v 1 ) , ( u 2 , v 2 ) ) = C ( u 1 , v 1 ) − C ( u 1 , v 2 ) − C ( u 2 , v 1 ) + C ( u 2 , v 2 ) .

Note that for u 1 ≤ u 2 , v 1 ≤ v 2 , V C ( ( u 1 , v 1 ) , ( u 2 , v 2 ) ) is equal to the so-called C -volume of the rectangle [ u 1 , u 2 ] × [ v 1 , v 2 ] .

By the celebrated Sklar’s theorem, the joint distribution function H of a pair of random variables X , Y defined on the probability space ( Ω , ℱ , P ) can be written as a composition of a copula C and the univariate marginals F and G , i.e., for all ( x , y ) ∈ R 2 ,

H ( x , y ) = C ( F ( x ) , G ( y ) ) .

Moreover, if F and G are continuous, then the copula C is uniquely determined, and the random variables

U = F ( X ) , V = G ( Y ) ,

which are uniformly distributed on [ 0 , 1 ] , are its representers.

The above is a special case of the more general fact: a bivariate copula C is a restriction to the unit square [ 0 , 1 ] 2 of a distribution function of a random pair ( U , V ) of uniformly distributed random variables on [ 0 , 1 ] , known as representers.

Furthermore, when the marginal distribution functions F X and F Y are continuous, then many concordance and dependence measures may be expressed in terms of the copula. For example,

Kendall τ and Spearman ρ are given by the following formulas ([24] s. 5.1.1, s. 5.1.2):

(1) τ ( C ) = 1 − 4 ∫ 0 1 ∫ 0 1 ∂ ∂ u C ( u , v ) ∂ ∂ v C ( u , v ) d u d v .

(2) ρ ( C ) = 12 ∫ 0 1 ∫ 0 1 C ( u , v ) d u d v − 3 .

We observe that since copulas are Lipschitz functions, they are differentiable on the complement of at most a zero measure set (Theorem of Rademacher, [21], Section 7.1), and the integral in the formula (1) is well defined for any copula. Similarly, the tail dependence parameters, lower left (LL), lower right (LR), upper left (UL), and upper right (UR), which describe the dependence of random variables in extreme cases, are defined as limits (providing they exist) as follows:

(3) λ LL = lim t → 0 P ( Y ≤ F Y ( − 1 ) ( t ) ∣ X ≤ F X ( − 1 ) ( t ) ) = lim t → 0 C ( t , t ) t ,

(4) λ LR = lim t → 0 P ( Y ≤ F Y ( − 1 ) ( t ) ∣ X ≥ F X ( − 1 ) ( 1 − t ) ) = lim t → 0 t − C ( 1 − t , t ) t ,

(5) λ UL = lim t → 0 P ( Y ≥ F Y ( − 1 ) ( 1 − t ) ∣ X ≤ F X ( − 1 ) ( t ) ) = lim t → 0 t − C ( t , 1 − t ) t ,

(6) λ UR = lim t → 0 P ( Y ≥ F Y ( − 1 ) ( 1 − t ) ∣ X ≥ F X ( − 1 ) ( 1 − t ) ) = lim t → 0 C ( 1 − t , 1 − t ) − 1 + 2 t t ,

where F X ( − 1 ) and F Y ( − 1 ) denote the quantile functions, i.e., the generalized inverses of the distribution functions. Compare with [24, Section 5.4], [10, Section 2.6.1], or [18, Section 2.18]. Note that the existence of the limits in formulas (3) and (6) implies that the diagonal section δ of the copula C , δ ( u ) = C ( u , u ) , admits one-sided derivatives, respectively, at the points 0 and 1 as follows:

λ LL = δ ′ ( 0 + ) , λ UR = 2 − δ ′ ( 1 − ) .

3 Novel construction

We introduce a new family of copulas characterized by a functional parameter F , where

F : [ − ∞ , + ∞ ] ⟶ [ 0 , 1 ]

is a strictly increasing continuous cumulative distribution function, which is furthermore symmetric

F ( − x ) + F ( x ) = 1

and convex on the half-line ( − ∞ , 0 ] . The set of all such distribution functions is denoted by ℱ .

Theorem 1

Let F ∈ ℱ , then the function

C F : [ 0 , 1 ] 2 ⟶ [ 0 , 1 ]

given by

C F ( u , v ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) f o r v + 2 u < 2 , u + v − 1 f o r v + 2 u ≥ 2

is a copula.

The proof is postponed to Section 5.1.

The above-introduced copulas are a close analogy of Archimedean copulas, which are also characterized by functions convex on a half-line, [18,22,24]. We recall that a bivariate copula C is said to be Archimedean if, and only if,

C ( u , v ) = ψ [ ( φ ( u ) + φ ( v ) ) ] ,

where ψ and φ are convex functions such that

ψ : [ 0 , + ∞ ] ⟶ [ 0 , 1 ] ,

is continuous and decreasing, ψ ( 0 ) = 1 , and ψ ( ∞ ) = 0 , and

φ : [ 0 , 1 ] ⟶ [ 0 , + ∞ ]

is a right-sided inverse of ψ

ψ ( φ ( t ) ) = t , φ ( 0 ) = inf { x : ψ ( x ) = 0 } .

Note that an Archimedean generator ψ is a restriction of a survival distribution function of a nonnegative random variable. Hence, for any F ∈ ℱ , the function

2 ( 1 − F ( x ) ) ∣ x ≥ 0

is a generator of an Archimedean copula.

The other example of a related family of copulas is left truncation invariant (LTI) copulas [5,8, 9,17]. For any F ∈ ℱ , the function

f ( x ) = ( 2 F ( x ) − 1 ) ∣ x ≥ 0 or f ( x ) = 2 ( F ( x ) − 1 ) ∣ x ≥ 0

is a generator of an LTI copula C f as follows:

C f ( u , v ) = u f ( f − 1 ( v ) ∕ u ) for u ≠ 0 , 0 for u = 0 .

Similarly as in the Archimedean or LTI case, the construction of C F copulas is scale invariant.

Let F 1 ( x ) = F ( x ∕ s ) , s > 0 . Then,

C F ( u , v ) = C F 1 ( u , v ) .

Indeed,

F 1 − 1 ( x ) = s F − 1 ( x ) .

For u + v ∕ 2 < 1 , we have

C F 1 ( u , v ) = F 1 ( 2 F 1 − 1 ( v ∕ 2 ) + F 1 − 1 ( u ) ) = F ( ( 2 s F − 1 ( v ∕ 2 ) + s F − 1 ( u ) ) ∕ s ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) = C F ( u , v ) .

As follows from the construction of C F copulas, they are supported on the trapezoid

Tr = ( u , v ) ∈ [ 0 , 1 ] 2 : u + v 2 ≤ 1 ,

as shown in Figure 1. We provide a bit stronger result.

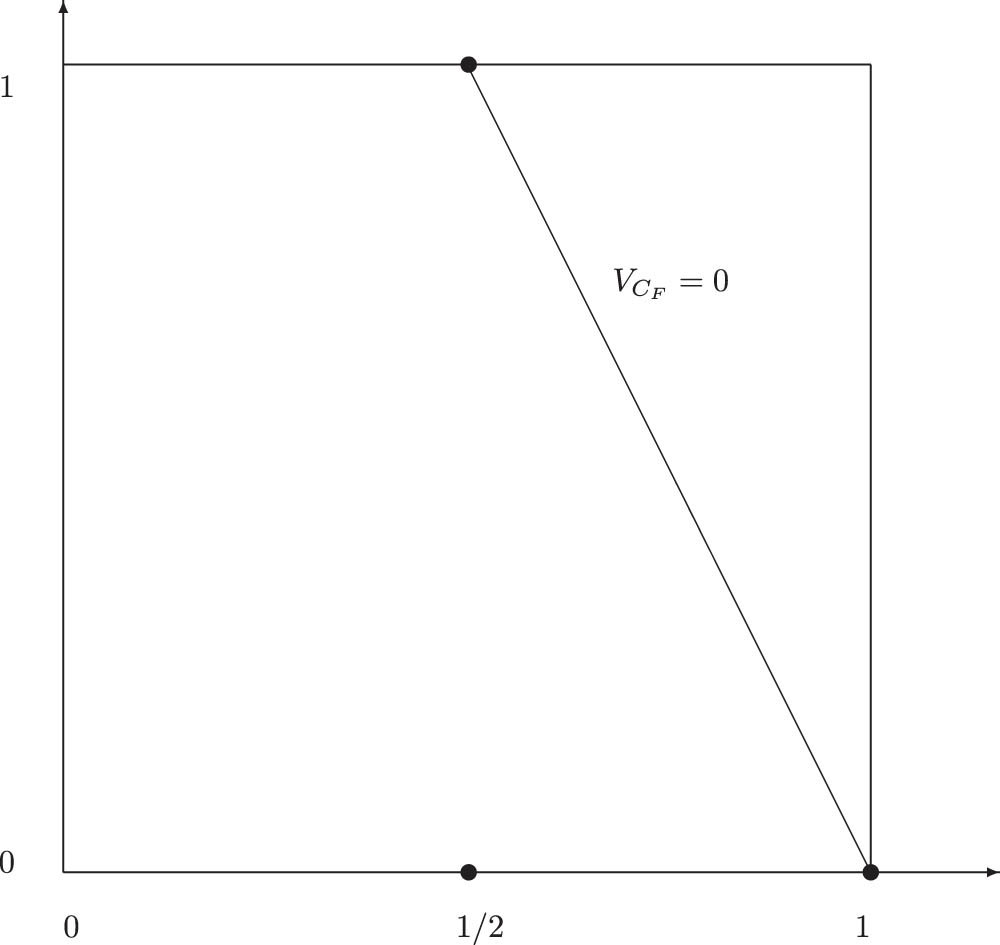
$Figure 1 Support of C F {C}_{F} .$

Figure 1

Support of C F .

Theorem 2

Let U and V be representers of a copula C F , F ∈ ℱ , then

P U + V 2 < 1 = 1 .

Under some additional slight assumptions, copulas C F are absolutely continuous and have a feasible density. Thus, they might be estimated via the maximum likelihood method.

Theorem 3

Let F ∈ ℱ . If, moreover, it has a locally absolutely continuous derivative f on the punctured line ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) , then the copula C F is absolutely continuous. If, moreover, F is differentiable at 0, then the density of the copula C F is given on the open square ( 0 , 1 ) 2 as follows:

c F ( u , v ) = g ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) f ( F − 1 ( v ∕ 2 ) ) f ( F − 1 ( u ) ) f o r 2 u + v < 2 , 0 f o r 2 u + v ≥ 2 .

If F is not differentiable at 0, then

c F ( u , v ) = g ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) f ( F − 1 ( v ∕ 2 ) ) f ( F − 1 ( u ) ) f o r 2 u + v < 2 , u ≠ 1 ∕ 2 , 0 f o r u = 1 ∕ 2 , 0 f o r 2 u + v ≥ 2 ,

where g is a nonnegative version of the density of f on the negative half-line, i.e.,

∀ y < 0 ∫ − ∞ y g ( ξ ) d ξ = f ( y ) .

The conditions in the above theorem are also sufficient.

Theorem 4

Let F ∈ ℱ . If the copula C F is absolutely continuous, then F is differentiable on the punctured line ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) , and its derivative is locally absolutely continuous.

The proofs of Theorems 2–4 are postponed to Sections 5.2 and 5.3.

4 Examples

To illustrate the concept of “trapezoid” copulas, we provide in this section several examples of the C F copulas and list their basic properties. The proofs of these properties are postponed to next sections (5.4 to 5.8).

The upper tail parameters are trivial for all C F s.

λ UL = λ UR = 0 .

The lower tail parameters, λ LL and λ LR , depend on the regular variation index of the survival distribution function F ¯ = 1 − F . We recall that F ¯ has a regular variation index equal to γ ∈ [ − ∞ , 0 ] when for any positive x , the limit

lim t → ∞ F ¯ ( t x ) F ¯ ( t )

exists and equals x γ . Here, x − ∞ is defined for x > 0 as follows:

x − ∞ = + ∞ for x < 1 , 1 for x = 1 , 0 for x > 1 .

For more details, the reader is referred, e.g., to [25]. Note that the regular variation was also studied in the context of the tail behavior of Archimedean copulas [2].

4.1 F ∼ N ( 0 , 1 )

Let F ( x ) = Φ ( x ) ∼ N ( 0 , 1 ) . Then,

C Φ ( u , v ) = Φ ( 2 Φ − 1 ( v ∕ 2 ) + Φ − 1 ( u ) ) for v + 2 u < 2 , u + v − 1 for v + 2 u ≥ 2 .

Regular variation index γ = − ∞ , tail parameters λ LL = 0 , λ LR = 3 ∕ 4 (Figure 2).

ρ = 6 π arccos 6 3 − 2 ≈ − 0.8245 , τ = − 2 π ≈ − 0.6366 .

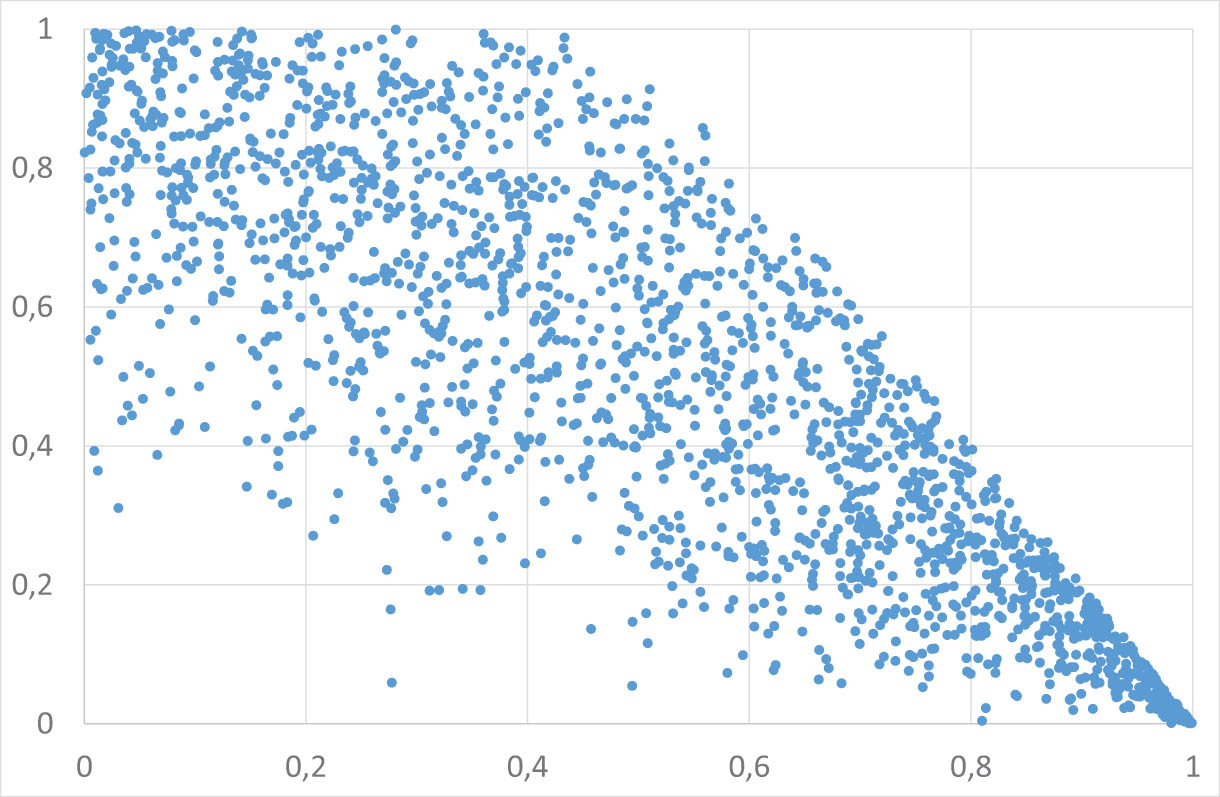
$Figure 2 Scatterplot of C F {C}_{F} , F ∼ N ( 0 , 1 ) F\hspace{0.33em} \sim \hspace{0.33em}N\left(0,1) .$

Figure 2

Scatterplot of C F , F ∼ N ( 0 , 1 ) .

Note that C Φ is the copula of the self-similar bivariate stochastic process ( W t , − M t ) t > 0 , where W t denotes a Wiener process and M t denotes its running maxima process as follows:

M t = max { W s , 0 ≤ s ≤ t } .

Compare [4] and [1], where the copula of the pair ( W t , M t ) is discussed.

4.2 Laplace (bi-exponential) La ( 0 , 1 ) = Exp ( 1 ) ⊕ ‒ Exp ( 1 )

Let

F ( t ) = 1 2 exp ( t ) for t ≤ 0 , 1 − 1 2 exp ( − t ) for t > 0 .

Since

F − 1 ( s ) = ln ( 2 s ) for s ≤ 1 ∕ 2 , − ln ( 2 − 2 s ) for s > 1 ∕ 2 ,

we obtain

C F ( u , v ) = u v 2 for 0 ≤ u ≤ 1 ∕ 2 , 0 ≤ v ≤ 1 , v 2 4 ( 1 − u ) for 1 ∕ 2 < u ≤ 1 , 0 ≤ v < 2 − 2 u , u + v − 1 for 1 ∕ 2 < u ≤ 1 , 2 − 2 u ≤ v ≤ 1 .

Regular variation index γ = − ∞ , and tail parameters λ LL = 0 , λ LR = 3 ∕ 4 , τ = − 1 ∕ 2 , and ρ = − 2 ∕ 3 (Figure 3).

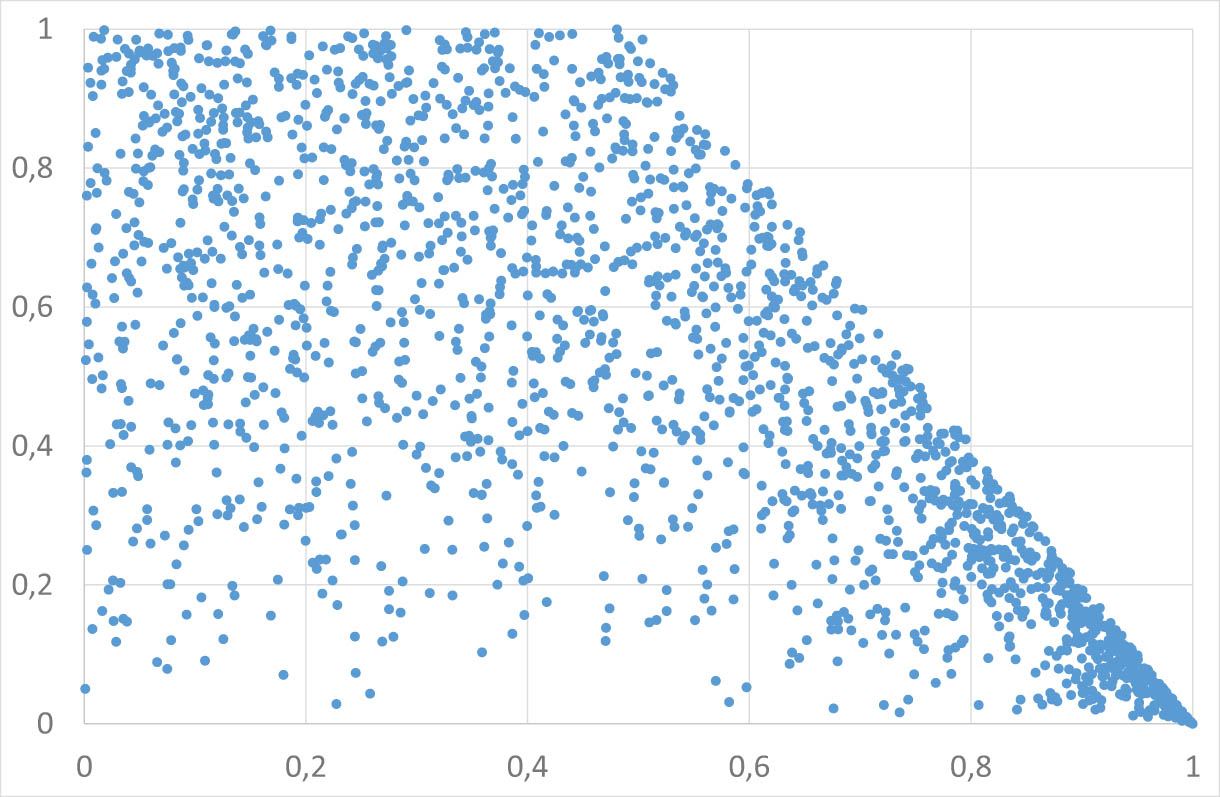
$Figure 3 Scatterplot of C F {C}_{F} , F ∼ La ( 0 , 1 ) F\hspace{0.33em} \sim \hspace{0.33em}{\rm{La}}\left(0,1) .$

Figure 3

Scatterplot of C F , F ∼ La ( 0 , 1 ) .

4.3 Bi-Pareto, P ( I I ) ( 0 , 1 , k ) ⊕ ‒ P ( I I ) ( 0 , 1 , k )

Let k > 0 and

F ( t ) = 1 2 ( 1 − t ) − k for t ≤ 0 , 1 − 1 2 ( 1 + t ) − k for t > 0 .

Since

F − 1 ( s ) = 1 − ( 2 s ) − 1 ∕ k for s ≤ 1 ∕ 2 , − 1 + ( 2 ( 1 − s ) ) − 1 ∕ k for s > 1 ∕ 2 ,

we obtain

C F ( u , v ) = 1 2 ( 2 v − 1 ∕ k + ( 2 u ) − 1 ∕ k − 2 ) − k for 0 ≤ u ≤ 1 ∕ 2 , 0 ≤ v ≤ 1 , 1 2 ( 2 v − 1 ∕ k − ( 2 ( 1 − u ) ) − 1 ∕ k ) − k for 1 ∕ 2 < u ≤ 1 , 0 ≤ v < 2 − 2 u , u + v − 1 for 1 ∕ 2 < u ≤ 1 , 2 − 2 u ≤ v ≤ 1 .

Regular variation index γ = − 1 ∕ k , and tail parameters λ LL = ( 2 + 2 − k ) − 1 ∕ k ∕ 2 , λ LR = 1 − ( 2 − 2 − k ) − 1 ∕ k ∕ 2 (Figure 4),

τ = − 1 2 + 1 ∕ k ,

ρ ≈ − 0 , 287 for k = 1 ∕ 2 ; − 0 , 413 for k = 1 ; − 0 , 517 for k = 2 .

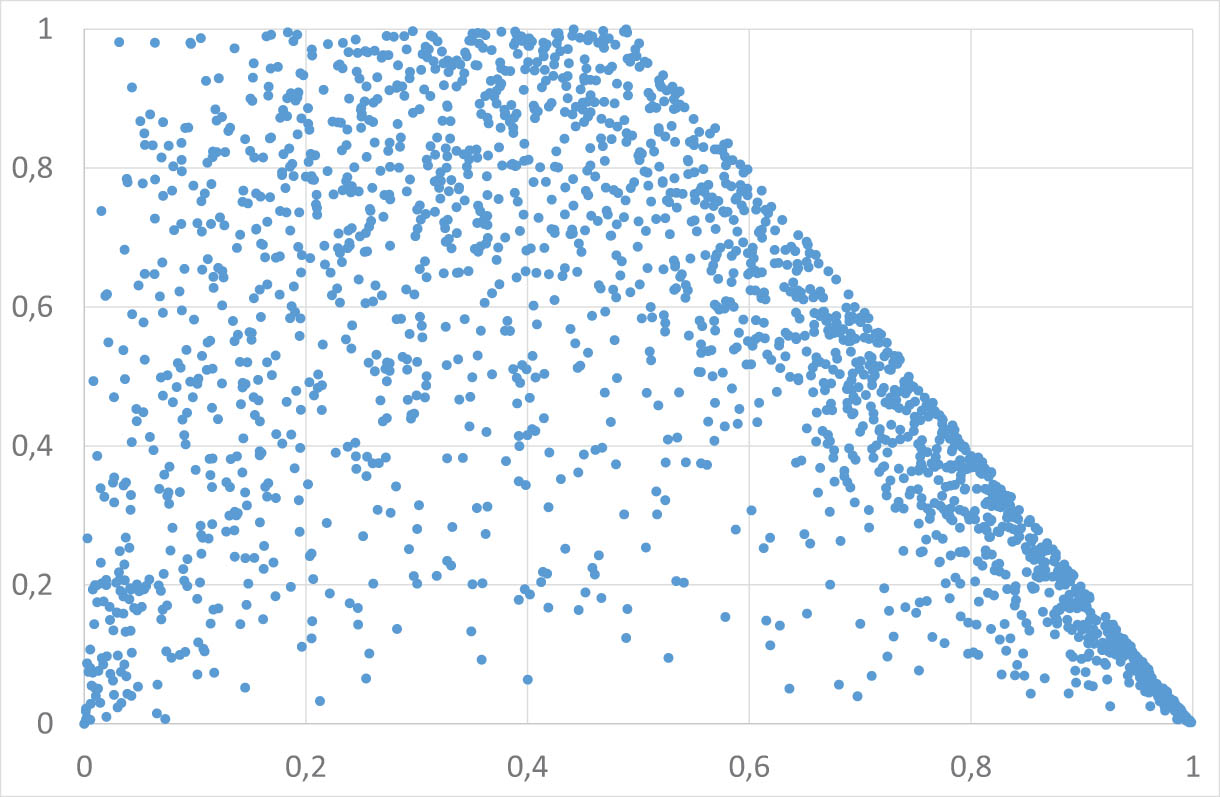
$Figure 4 Scatterplot of C F {C}_{F} , F ∼ biPareto ( 1 ) F\hspace{0.33em} \sim \hspace{0.33em}{\rm{biPareto}}\left(1) .$

Figure 4

Scatterplot of C F , F ∼ biPareto ( 1 ) .

4.4 t -Student, T ( n )

Let F ( x ) = T n ( x ) ∼ T ( n ) , n > 0 , and

C T n ( u , v ) = T n ( 2 T n − 1 ( v ∕ 2 ) + T n − 1 ( u ) ) for v + 2 u < 2 , u + v − 1 for v + 2 u ≥ 2 .

Regular variation index γ = − n , and tail parameters λ LL = ( 2 + 2 − 1 ∕ n ) − n ∕ 2 , λ LR = 1 − ( 2 − 2 − 1 ∕ n ) − n ∕ 2 (Figure 5),

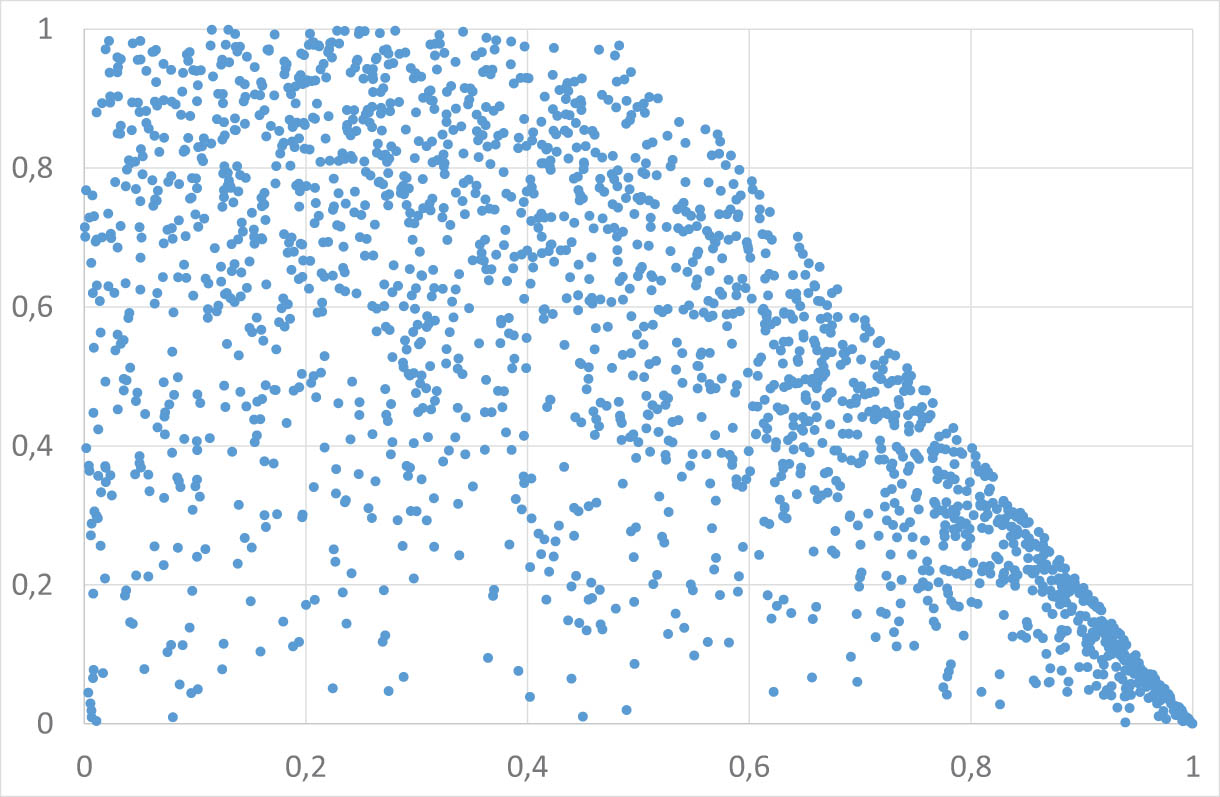
$Figure 5 Scatterplot of C F {C}_{F} , F ∼ t -Student ( 2 ) F\hspace{0.33em} \sim \hspace{0.33em}t\hspace{0.1em}\text{-Student}\hspace{0.1em}\left(2) .$

Figure 5

Scatterplot of C F , F ∼ t -Student ( 2 ) .

τ = − 4 Γ 2 ( ( n + 1 ) ∕ 2 ) π n Γ 2 ( n ∕ 2 ) ,

ρ ≈ − 0 , 499 for n = 1 ; − 0 , 643 for n = 2 ; − 0 , 789 for n = 10 .

4.5 Extra heavy tail

Let

F ( t ) = 1 2 ln 2 ln ( 2 − t ) for t ≤ 0 , 1 − 1 2 ln 2 ln ( 2 + t ) for t > 0 .

Since

F − 1 ( s ) = 2 − 2 1 2 s for s ≤ 1 ∕ 2 , − 2 + 2 1 2 ( 1 − s ) for s > 1 ∕ 2 ,

we obtain

C F ( u , v ) = ln 2 2 ln 2 1 + 1 v + 2 1 2 u − 4 for 0 ≤ u ≤ 1 ∕ 2 , 0 ≤ v ≤ 1 , ln 2 2 ln ( 2 1 + 1 v − 2 1 2 ( 1 − u ) ) for 1 ∕ 2 < u ≤ 1 , 0 ≤ v < 2 − 2 u , u + v − 1 for 1 ∕ 2 < u ≤ 1 , 2 − 2 u ≤ v ≤ 1 .

Regular variation index γ = 0 and tail parameters λ LL = λ LR = 1 ∕ 2 ,

τ = 2 3 ln 2 − 2 ln 2 ( 2 ) U ( 4 , 4 , ln 2 ) ≈ − 0.2234 , ρ ≈ − 0.236 .

U denotes the so-called Tricomi confluent hypergeometric function (Figure 6).

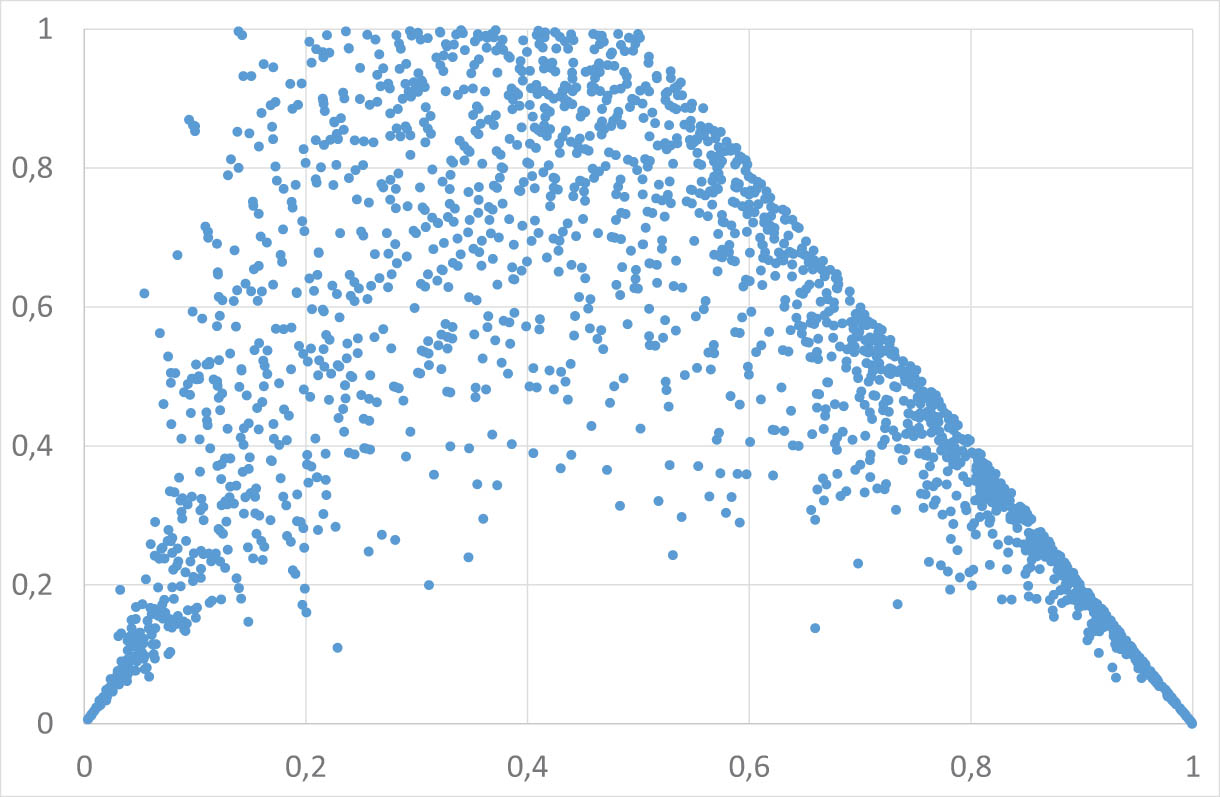
$Figure 6 Scatterplot of C F {C}_{F} , F F extra heavy tailed.$

Figure 6

Scatterplot of C F , F extra heavy tailed.

5 Proofs and auxiliary results

5.1 Proof of the Theorem 1

Step 1. Conditions (c1) and (c2) – the easy part.

By direct computation, we obtain

C ( 0 , v ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( 0 ) ) = F ( − ∞ ) = 0 , C ( u , 0 ) = F ( 2 F − 1 ( 0 ) + F − 1 ( u ) ) = F ( − ∞ ) = 0 , C ( 1 , v ) = 1 + v − 1 = v , for u < 1 ∕ 2 C ( u , 1 ) = F ( 2 F − 1 ( 1 ∕ 2 ) + F − 1 ( u ) ) = F ( 0 + F − 1 ( u ) ) = u , for u ≥ 1 ∕ 2 C ( u , 1 ) = u + 1 − 1 = u .

Step 2. Condition (c3).

We follow the approach from [7].

First, we check the continuity of C F .

We introduce an auxiliary function G : { ( u , v ) : 0 ≤ v ≤ 1 , 0 ≤ u ≤ 1 − v ∕ 2 } ⟶ [ 0 , 1 ]

G ( u , v ) = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) for u < 1 , 0 for v = 0 , u = 1 .

Since for u < 1 , the sum 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) is well defined (it is finite or is equal to − ∞ ) and G is continuous for u < 1 .

We show that G is continuous at the point ( 1 , 0 ) as well. Indeed, let v n → 0 and u n → 1 , then since v n ∕ 2 ≤ 1 − u n ,

0 ≤ F ( 2 F − 1 ( v n ∕ 2 ) + F − 1 ( u n ) ) ≤ F ( F − 1 ( v n ∕ 2 ) + F − 1 ( 1 − u n ) + F − 1 ( u n ) ) = F ( F − 1 ( v n ∕ 2 ) ) = v n ∕ 2 → 0 .

Since W ( u , v ) = ( u + v − 1 ) + = max ( 0 , u + v − 1 ) is continuous on [ 0 , 1 ] 2 and

G ( u , 2 − 2 u ) = F ( 2 F − 1 ( 1 − u ) + F − 1 ( u ) ) = F ( F − 1 ( 1 − u ) ) = 1 − u = u + ( 2 − 2 u ) − 1 = W ( u , 2 − 2 u ) ,

C F is continuous.

Next, we calculate the right-sided partial derivative of C F with respect to the second variable v , v ∈ ( 0 , 1 ) .

Let f be the right-sided derivative of F .

For 2 u + v < 2 , we obtain

∂ + ∂ v C F ( u , v ) = ∂ + ∂ v G ( u , v ) = f ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) ⋅ 1 f ( F − 1 ( v ∕ 2 ) ) .

On the other hand, for 2 u + v ≥ 2 , we obtain

∂ + ∂ v C F ( u , v ) = ∂ ∂ v ( u + v − 1 ) = 1 .

We check that for any fixed v , the function

u ⟼ ∂ + ∂ v C F ( u , v ) ,

is nondecreasing. In more detail:

Since for 0 ≤ 2 u < 2 − v ,

2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ≤ 2 F − 1 ( v ∕ 2 ) + F − 1 ( 1 − v ∕ 2 ) = F − 1 ( v ∕ 2 ) ≤ 0 ,

and F is convex on the negative half-line, we obtain that f is nondecreasing and so is the function

u ⟼ ∂ + ∂ v G ( u , v ) = f ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) ⋅ 1 f ( F − 1 ( v ∕ 2 ) ) .

Furthermore,

lim u → 1 − v ∕ 2 ∂ + ∂ v G ( u , v ) ≤ f ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( 1 − v ∕ 2 ) ) f ( F − 1 ( v ∕ 2 ) ) = 1 .

Thus, as required, for any v ∈ ( 0 , 1 ) , the function

u ⟼ ∂ + ∂ v C F ( u , v )

is nondecreasing on the interval [ 0 , 1 ] .

To prove the 2-monotonicity of C F , we consider an auxiliary function H (compare [7]).

For any fixed u 1 , u 2 , v 1 , 0 ≤ u 1 < u 2 ≤ 1 , 0 ≤ v 1 < 1 , we put

H : [ v 1 , 1 ] ⟶ [ 0 , 1 ] , H ( v ) = C F ( u 1 , v 1 ) + C F ( u 2 , v ) − C F ( u 1 , v ) − C F ( u 2 , v 1 ) .

We obtain H ( 0 ) = 0 and

d + d v H ( v ) = ∂ + ∂ v C F ( u 2 , v ) − ∂ + ∂ v C F ( u 1 , v ) ≥ 0 ,

which implies that H is nondecreasing, hence nonnegative.

5.2 Support – proof of Theorem 2

We show that the set

ω : U ( ω ) + V ( ω ) 2 < 1

contains subsets of the measure close to 1.

Let δ be a positive constant. We observe that for any v > 0 ,

F F − 1 v 2 + F − 1 1 + δ 2 > F F − 1 v 2 = v 2 .

Hence,

P U + V 2 < 1 = P U < 1 − V 2 ≥ P U ≤ 1 − F F − 1 V 2 + F − 1 1 + δ 2 .

But taking into account that for any u ∈ ( 0 , 1 ) ,

E ( 1 l U ≤ u ∣ σ ( V ) ) = a s ∂ C ∂ v ( u , V ) ,

and substituting v = 2 F ( y ) , we obtain by “disintegration”

P U + V 2 < 1 ≥ P U ≤ 1 − F F − 1 V 2 + F − 1 1 + δ 2 = E ( E ( 1 l U ≤ 1 − F ( F − 1 ( V ∕ 2 ) + F − 1 ( ( 1 + δ ) ∕ 2 ) ) ∣ σ ( V ) ) ) = ∫ 0 1 E ( 1 l U ≤ 1 − F ( F − 1 ( v ∕ 2 ) + F − 1 ( ( 1 + δ ) ∕ 2 ) ) ∣ V = v ) d v = ∫ 0 1 ∂ C ∂ v ( 1 − F ( F − 1 ( v ∕ 2 ) + F − 1 ( ( 1 + δ ) ∕ 2 ) ) , v ) d v = ∫ 0 1 f ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( 1 − F ( F − 1 ( v ∕ 2 ) + F − 1 ( ( 1 + δ ) ∕ 2 ) ) ) ) 1 f ( F − 1 ( v ∕ 2 ) ) d v = ∫ 0 1 f ( 2 F − 1 ( v ∕ 2 ) − F − 1 ( v ∕ 2 ) − F − 1 ( ( 1 + δ ) ∕ 2 ) ) 1 f ( F − 1 ( v ∕ 2 ) ) d v = ∫ 0 1 f ( F − 1 ( v ∕ 2 ) − F − 1 ( ( 1 + δ ) ∕ 2 ) ) 1 f ( F − 1 ( v ∕ 2 ) ) d v = v = 2 F ( y ) 2 ∫ − ∞ 0 f ( y − F − 1 ( ( 1 + δ ) ∕ 2 ) ) d y = 2 F ( y − F − 1 ( ( 1 + δ ) ∕ 2 ) ) ∣ − ∞ 0 = 2 F ( − F − 1 ( ( 1 + δ ) ∕ 2 ) ) = 2 F ( F − 1 ( ( 1 − δ ) ∕ 2 ) ) = 1 − δ .

Since δ might be “infinitely” small, P U + V 2 < 1 must be equal to 1.

5.3 Density – proofs of Theorems 3 and 4

Proof of Theorem 3

Since g is a density of f ,

∀ x , y ∈ ( − ∞ , 0 ] ∫ x y g ( ξ ) d ξ = f ( y ) − f ( x )

and changing the variables, we obtain that for 2 u + v ≤ 2 ,

∫ 0 v ∫ 0 u c F ( α , β ) d α d β = ∫ 0 v ∫ 0 u g ( 2 F − 1 ( β ∕ 2 ) + F − 1 ( α ) ) f ( F − 1 ( β ∕ 2 ) ) f ( F − 1 ( α ) ) d α d β { α = F ( x ) , β = 2 F ( y ) } = ∫ − ∞ F − 1 ( v ∕ 2 ) ∫ − ∞ F − 1 ( u ) 2 g ( 2 y + x ) d x d y = ∫ − ∞ F − 1 ( v ∕ 2 ) 2 f ( 2 y − F − 1 ( u ) ) d y = F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) .

Note that for 2 u + v = 2

∫ 0 v ∫ 0 u c F ( α , β ) d α d β = u + v − 1 = 1 − u = v 2 .

Similarly, for 2 u + v > 2 , we obtain

□ ∫ 0 v ∫ 0 u c F ( α , β ) d α d β = ∫ 0 2 ( 1 − u ) ∫ 0 u c F ( α , β ) d α d β + ∫ 2 ( 1 − u ) v ∫ 0 1 − β ∕ 2 c F ( α , β ) d α d β = 1 − u + ∫ 2 ( 1 − u ) v ∫ 0 1 − β ∕ 2 g ( 2 F − 1 ( β ∕ 2 ) + F − 1 ( α ) ) f ( F − 1 ( β ∕ 2 ) ) f ( F − 1 ( α ) ) d α d β { α = F ( x ) , β = 2 F ( y ) } = 1 − u + ∫ F − 1 ( 1 − u ) F − 1 ( v ∕ 2 ) ∫ − ∞ − y 2 g ( 2 y + x ) d x d y = 1 − u + ∫ F − 1 ( 2 ( 1 − u ) ) F − 1 ( v ∕ 2 ) 2 f ( y ) d y = 1 − u + 2 F ( F − 1 ( v ∕ 2 ) ) − 2 F ( F − 1 ( 1 − u ) ) = u + v − 1 .

Proof of Theorem 4

Let a nonnegative, Borel function c F be a density of the copula C F . Due to the Fubini theorem, we have

C F ( u , v ) = ∫ [ 0 , u ] × [ 0 , v ] c F ( α , β ) d α d β = ∫ 0 v ∫ 0 u c F ( α , β ) d α d β ,

where

β → ∫ 0 u c F ( α , β ) d α

is a Borel function. Hence, for a fixed u , the function v → C F ( u , v ) is almost everywhere differentiable with respect to v . Let U be a dense countable subset of the unit interval [ 0 , 1 ] . Since a countable union of zero measure sets is a zero measure set as well, then for any ε ∈ ( 0 , 1 ) , there exists v ∗ ∈ ( 1 − ε , 1 ) such that for any u ∈ U , the function v → C F ( u , v ) is differentiable at v ∗ . For u from U such that u ≤ 1 − v ∗ ∕ 2 , we obtain

∫ 0 u c F ( α , v ∗ ) d α = ∂ C F ( u , v ∗ ) ∂ v = f ( 2 F − 1 ( v ∗ ∕ 2 ) + F − 1 ( u ) ) f ( F − 1 ( v ∗ ∕ 2 ) ) ,

where f is a right-sided derivative of F . Substituting v ∗ = 2 F ( y ∗ ) α = F ( γ ) and u = F ( x ) and rearranging the above equation, we obtain that for x ∈ F − 1 ( U ) ∩ ( − ∞ , − y ∗ ) ,

f ( 2 y ∗ + x ) = ∫ − ∞ x c F ( F ( γ ) , y ∗ ) f ( y ∗ ) f ( γ ) d γ .

The right side of the equation is an absolutely continuous function of x . Since both sides are nondecreasing functions of x and are equal on the dense set, they are equal at every point, which implies that f is absolutely continuous on the set ( − ∞ , y ∗ ) . Since v ∗ may be chosen as close to 1 as necessary and y ∗ = F − 1 ( v ∗ ∕ 2 ) , f is absolutely continuous on the set ( − ∞ , 0 ) . Furthermore, since f is continuous, F is differentiable on the half-line ( − ∞ , 0 ) .□

5.4 Kendall τ

Theorem 5

Let F ∈ ℱ . The Kendall τ of the copula C F is given by

τ ( C F ) = − 4 E ( ∣ X ∣ f ( X ) ) = 8 ∫ − ∞ 0 x f 2 ( x ) d x ,

where X is a random variable with the cumulative distribution function F and the probability density f.

Proof

Indeed, for u = F ( x ) and v = 2 F ( y ) , we obtain

□ τ ( C F ) = 1 − 4 ∫ 0 1 ∫ 0 1 ∂ ∂ u C ( u , v ) ∂ ∂ v C ( u , v ) d u d v = 1 − 4 ∫ 0 1 ∫ 0 1 − v ∕ 2 f 2 ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) ⋅ 1 f ( F − 1 ( v ∕ 2 ) ) 1 f ( F − 1 ( u ) ) d u d v + ∫ 0 1 ∫ 1 − v ∕ 2 1 d u d v = − 8 ∫ − ∞ 0 ∫ − ∞ − y f 2 ( 2 y + x ) d x d y = − 8 ∫ − ∞ 0 ∫ − ∞ y f 2 ( x 1 ) d x 1 d y = − 8 ∫ − ∞ 0 ∫ x 1 0 f 2 ( x 1 ) d y d x 1 = 8 ∫ − ∞ 0 x f 2 ( x ) d x = − 4 ∫ − ∞ + ∞ ∣ x ∣ f 2 ( x ) d x = − 4 E ( ∣ X ∣ f ( X ) ) .

In the following, we show how to calculate Kendall τ for examples listed in Section 4.

5.4.1 Kendall τ for N ( 0 , 1 ) generator

We recall that

φ ′ ( x ) = − x φ ( x ) .

Hence,

τ = 8 ∫ − ∞ 0 x φ 2 ( x ) d x = − 4 φ 2 ( x ) ∣ − ∞ 0 = − 2 π .

5.4.2 Kendall τ for La ( 0 , 1 ) generator

We recall that for x < 0 ,

f ( x ) = 1 2 e x .

Hence,

τ = 8 ∫ − ∞ 0 x f 2 ( x ) d x = 2 ∫ − ∞ 0 x e 2 x d x = x e 2 x − 1 2 e 2 x ∣ − ∞ 0 = − 1 2 .

5.4.3 Kendall τ for bi-Pareto generator

We recall that for x < 0 ,

f ( x ) = k 2 ( 1 − x ) − ( k + 1 ) .

Hence,

τ = 8 ∫ − ∞ 0 x f 2 ( x ) d x = 2 ∫ − ∞ 0 x k 2 ( 1 − x ) − 2 ( k + 1 ) d x = − 2 ∫ − ∞ 0 k 2 ( 1 − x ) − 2 k − 1 d x + 2 ∫ − ∞ 0 k 2 ( 1 − x ) − 2 ( k + 1 ) d x = − 2 k 2 1 2 k − 1 2 k + 1 = − k 2 k + 1 .

5.4.4 Kendall τ for Student generator

We recall that

f ( t ) = Γ ( ( n + 1 ) ∕ 2 ) π n Γ ( n ∕ 2 ) 1 + t 2 n − ( n + 1 ) ∕ 2 .

Hence,

τ = 8 ∫ − ∞ 0 x f ( x ) 2 d x = 8 ∫ − ∞ 0 x Γ 2 ( ( n + 1 ) ∕ 2 ) π n Γ 2 ( n ∕ 2 ) 1 + x 2 n − ( n + 1 ) d x = − 4 Γ 2 ( ( n + 1 ) ∕ 2 ) π Γ 2 ( n ∕ 2 ) 1 + x 2 n − n − ∞ 0 = − 4 Γ 2 ( ( n + 1 ) ∕ 2 ) π Γ 2 ( n ∕ 2 ) .

5.4.5 Kendall τ for heavy-tailed F

We recall that for x > 0 ,

f ( x ) = − ln ( 2 ) 2 ( 2 + x ) 1 ln 2 ( 2 + x ) .

Hence,

τ = − 8 ∫ 0 ∞ x f 2 ( x ) d x = − 2 ∫ 0 ∞ x l n 2 ( 2 ) ( 2 + x ) 2 1 ln 4 ( 2 + x ) d x = − 2 ln 2 ( 2 ) ∫ 2 ∞ x − 2 x 2 1 ln 4 ( x ) d x = − 2 ln 2 ( 2 ) ∫ 2 ∞ 1 x 1 ln 4 ( x ) d x + 4 ln 2 ( 2 ) ∫ 2 ∞ 1 x 2 1 ln 4 ( x ) d x = − 2 3 ln 2 ( 2 ) ln 3 ( x ) 2 ∞ + 4 ln 2 ( 2 ) ∫ ln ( 2 ) ∞ 1 x 4 e x d x = − 2 3 1 ln ( 2 ) + 2 ln 2 ( 2 ) ⋅ U ( 4 , 4 , ln ( 2 ) ) ≈ − 0 . 2234 .

U denotes the so-called Tricomi confluent hypergeometric function as follows:

U ( a , a , z ) = e z ∫ z ∞ u − a e − u d u .

5.5 Spearman ρ

Theorem 6

Let F ∈ ℱ . The Spearman ρ of the copula C F is given as follows:

ρ ( C F ) = 24 P ( Y ≤ 0 , Y + X ≤ 0 , Z ≤ 2 Y + X ) − 1 . 5 = − 1 . 5 + 24 ∫ − ∞ 0 ∫ − ∞ − y ∫ − ∞ 2 y + x f ( z ) f ( x ) f ( y ) d z d x d y ,

where X, Y, and Z are independent and identically distributed (iid) random variables with distribution function F and probability density f.

Proof

We observe that for u = F ( x ) and v = 2 F ( y ) , we obtain

□ ρ ( C F ) = 12 ∫ 0 1 ∫ 0 1 C F ( u , v ) d u d v − 3 = − 3 + 12 ∫ 0 1 ∫ 1 − v ∕ 2 1 ( u + v − 1 ) d u d v + 12 ∫ 0 1 ∫ 0 1 − v ∕ 2 F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( u ) ) d u d v . = − 1 . 5 + 24 ∫ − ∞ 0 ∫ − ∞ − y F ( 2 y + x ) f ( x ) f ( y ) d x d y = − 1 . 5 + 24 ∫ − ∞ 0 ∫ − ∞ − y ∫ − ∞ 2 y + x f ( z ) f ( x ) f ( y ) d z d x d y .

5.5.1 Spearman ρ for F ∼ N ( 0 , 1 )

We observe that the joint distribution of independent random variables X , Y , and Z , each following the standard normal law N ( 0 , 1 ) , is normal N 3 ( 0 , I d 3 ) . Since such distribution is spherical, the probability P ( Y ≤ 0 , Y + X ≤ 0 , Z ≤ 2 Y + X ) can be expressed in terms of the volume of a spherical triangle (a subset of the unit sphere S 2 = { ( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 } cut by three half-spaces a i x + b i y + c i z ≤ 0 , i = 1 , 2 , 3 ).

We recall that due to Girard’s theorem such volume (taken with respect to the surface measure μ S 2 ) equals

(7) V o l = A + B + C − π ,

where A , B , and C are inner angles (in radians) of the triangle (see, e.g., [20] formula (1.12.2) in section 1.12). Since the inner angle increased by Π equals the angle between normal vectors (oriented outward), the cosine of the inner angle is given by the scalar product of normal vectors as follows:

(8) cos ( ∠ ( a 1 x + b 1 y + c 1 z ≤ 0 , a 2 x + b 2 y + c 2 z ≤ 0 ) ) = − a 1 a 2 + b 1 b 2 + c 1 c 2 a 2 2 + b 2 2 + c 2 2 a 1 2 + b 1 2 + c 1 2 .

Therefore,

P ( Y ≤ 0 , Y + X ≤ 0 , Z ≤ 2 Y + X ) = 1 μ S 2 ( S 2 ) μ S 2 ( { ( x , y , z ) ∈ S 2 : y ≤ 0 , y + x ≤ 0 , z − 2 y − x ≤ 0 } ) = 1 4 π ( ∠ ( y ≤ 0 , y + x ≤ 0 ) + ∠ ( y ≤ 0 , z − x − 2 y ≤ 0 ) + ∠ ( y + x ≤ 0 , z − x − 2 y ≤ 0 ) − π ) = 1 4 π 3 4 π + arccos 6 3 + 1 6 π − π = 1 4 π arccos 6 3 − 1 48 .

Finally, we conclude

ρ ( C F ) = 24 1 4 π arccos 6 3 − 1 48 − 1.5 = 6 π arccos 6 3 − 2 ≈ − 0 , 82452 .

5.5.2 Spearman ρ for Laplace F

We have

C F ( u , v ) = u v 2 for 0 ≤ u ≤ 1 ∕ 2 , 0 ≤ v ≤ 1 , v 2 4 ( 1 − u ) for 1 ∕ 2 < u ≤ 1 , 0 ≤ v < 2 − 2 u , u + v − 1 for 1 ∕ 2 < u ≤ 1 , 2 − 2 u ≤ v ≤ 1 .

Since

∫ 0 1 ∫ 0 1 ∕ 2 u v 2 d u d v = ∫ 0 1 ∕ 2 u d u ∫ 0 1 v 2 d v = u 2 2 0 1 ∕ 2 v 3 3 0 1 = 1 8 ⋅ 1 3 = 1 24 , ∫ 1 ∕ 2 1 ∫ 0 2 − 2 u v 2 4 ( 1 − u ) d u d v = ∫ 1 ∕ 2 1 1 4 ( 1 − u ) v 3 3 0 2 ( 1 − u ) d u = ∫ 1 ∕ 2 1 2 3 ( 1 − u ) 2 d u = − 2 9 ( 1 − u ) 3 1 ∕ 2 1 = 2 9 ⋅ 1 2 3 = 1 36 , ∫ 1 ∕ 2 1 ∫ 2 ( 1 − u ) 1 ( u + v − 1 ) d v d u = ∫ 1 ∕ 2 1 1 2 ( u + v − 1 ) 2 2 ( 1 − u ) 1 = ∫ 1 ∕ 2 1 1 2 ( u 2 − ( u − 1 ) 2 ) d u = 1 8 ,

we obtain

ρ ( C F ) = 12 ∫ 0 1 ∫ 0 1 C F ( u , v ) d u d v − 3 = − 3 + 12 ∫ 0 1 ∫ 0 1 ∕ 2 u v 2 d u d v + ∫ 1 ∕ 2 1 ∫ 0 2 − 2 u v 2 4 ( 1 − u ) d u d v + ∫ 1 ∕ 2 1 ∫ 2 ( 1 − u ) 1 ( u + v − 1 ) d v d u = − 3 + 12 1 24 + 1 36 + 1 8 = − 2 3 .

5.5.3 Spearman ρ by the Monte Carlo method

Thanks to Theorem 6, we may apply Monte Carlo methods to approximate Spearman ρ . Just draw N times a random vector ( X , Y , Z ) , where X , Y , and Z are iid and have a cumulative distribution function F . Next, check the percentage of cases when the drawing ( x i , y i , z i ) fulfills

y i ≤ 0 , x i + y i ≤ 0 , z i ≤ 2 y i + x i .

For N = 6 ⋅ 1 0 7 , we obtained the following approximated values:

biPareto k = 0.5 , ρ = − 0.287 ;

biPareto k = 1 , ρ = − 0.413 ;

biPareto k = 2 , ρ = − 0.517 ;

tStudent n = 1 , ρ = − 0.499 ;

tStudent n = 2 , ρ = − 0.643 ;

tStudent n = 10 , ρ = − 0.789 ;

Extra heavy tail, ρ = − 0.236 .

5.6 Lower left tail dependence

We say that a copula C admits the uniform tail decomposition when

C ( u , v ) = L ( u , v ) + R ( u , v ) ( u + v ) ,

where the leading part L : [ 0 , + ∞ ) 2 → [ 0 , + ∞ ) is positive homogeneous

L ( t u , t v ) = t L ( u , v )

and the tail R : [ 0 , 1 ] 2 → [ 0 , + ∞ ) is bounded and

lim ( u , v ) → ( 0 , 0 ) R ( u , v ) = 0 .

Note that

L ( u , v ) = lim t → 0 C ( t u , t v ) t ,

provided the limit exists. See [14–16] for more details. The leading part L is also called the tail dependence function [18,19].

Proposition 1

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ ∈ ( − ∞ , 0 ) . Then, the copula C F admits the tail decomposition with the leading part

L γ ( u , v ) = ( 2 ( v ∕ 2 ) 1 ∕ γ + u 1 ∕ γ ) γ .

Proof

Since F is symmetric, F ( − t ) = F ¯ ( t ) , and we have for x > 0 ,

F ( − t x ) F ( − t ) = F ¯ ( t x ) F ¯ ( t ) ⟶ t → ∞ x γ .

The above convergence is almost uniform in x (see [25] Proposition 2.4). Moreover,

F − 1 ( x ∕ t ) F − 1 ( 1 ∕ t ) = F ¯ − 1 ( x ∕ t ) F ¯ − 1 ( 1 ∕ t ) ⟶ t → ∞ 1 x − 1 ∕ γ = x 1 ∕ γ .

The regular variation of the function G ( t ) = F ¯ − 1 ( 1 ∕ t ) follows from [25] Proposition 2.6.v. Since

− F − 1 ( 1 ∕ t ) ⟶ t → ∞ + ∞ ,

and the function x γ is monotonic, we obtain

□ L γ ( u , v ) = lim t → ∞ t C F u t , v t = lim t → ∞ t F 2 F − 1 v 2 t + F − 1 u t = lim t → ∞ 1 F ( F − 1 ( 1 ∕ t ) ) F F − 1 ( 1 ∕ t ) 2 F − 1 ( v ∕ ( 2 t ) ) F − 1 ( 1 ∕ t ) + F − 1 ( u ∕ t ) F − 1 ( 1 ∕ t ) = lim t → ∞ 2 F − 1 ( v ∕ ( 2 t ) ) F − 1 ( 1 ∕ t ) + F − 1 ( u ∕ t ) F − 1 ( 1 ∕ t ) γ = ( 2 ( v ∕ 2 ) 1 ∕ γ + u 1 ∕ γ ) γ .

Proposition 2

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ = 0 . Then, the copula C F admits the tail decomposition with

L ( u , v ) = min u , v 2 .

Proof

Since F ( − t ) = F ¯ ( t ) and F ¯ is slowly varying, we have for x > 0 ,

F ( − t x ) F ( − t ) = F ¯ ( t x ) F ¯ ( t ) ⟶ t → ∞ 1 .

Since F − 1 is negative on the interval ( 0 , 1 ∕ 2 ) , we observe that for t < 1 ∕ 2 ,

F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≤ F ( F − 1 ( t u ) ) = t u and F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≤ F ( F − 1 ( t v ∕ 2 ) ) = t v ∕ 2 .

On the other hand,

u ≤ v 2 ⇒ 1 t F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≥ F ( 3 F − 1 ( t u ) ) F ( F − 1 ( t u ) ) ∕ u → u , u ≥ v 2 ⇒ 1 t F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≥ F ( 3 F − 1 ( t v ∕ 2 ) ) 2 F ( F − 1 ( t v ∕ 2 ) ) ∕ v → v 2 .

We apply the sandwich rule

□ min ( u , v ∕ 2 ) ≥ 1 t F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≥ 1 t F ( 3 F − 1 ( t min ( u , v ∕ 2 ) ) ) → min ( u , v ∕ 2 ) .

Proposition 3

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ = − ∞ . Then, the copula C F admits the trivial tail decomposition with L = 0 .

Proof

We apply the sandwich rule for small t , 0 < t < 1 ∕ 2 ,

□ 0 ≤ 1 t F ( 2 F − 1 ( t v ∕ 2 ) + F − 1 ( t u ) ) ≤ F ( 2 F − 1 ( t v ∕ 2 ) ) 2 F ( F − 1 ( t v ∕ 2 ) ) ∕ v → t → 0 2 − ∞ = 0 .

Since for the copulas with a uniform lower left tail decomposition, the lower left tail parameter exists and equals

λ LL = lim t → 0 C ( t , t ) t = L ( 1 , 1 ) ,

we obtain

Corollary 1

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ ∈ [ − ∞ , 0 ] . Then,

λ LL ( C F ) = 1 ∕ 2 f o r γ = 0 , ( 2 + 2 1 ∕ γ ) γ ∕ 2 f o r γ ∈ ( − ∞ , 0 ) , 0 f o r γ = − ∞ .

5.7 Lower right tail dependence

In order to simplify the calculations, instead of studying the tail behavior of a copula C F at point ( 1 , 0 ) , we deal with the lower left tail of the copula reflected with respect to the line u = 1 ∕ 2 .

Let ( U , V ) be generators of a copula C . We recall that the copula C ∗ of ( 1 − U , V ) is a reflected copula and

C ∗ ( u , v ) = v − C ( 1 − u , v ) .

Indeed,

P ( 1 − U ≤ u , V ≤ v ) = P ( U ≥ 1 − u , V ≤ v ) = P ( V ≤ v ) − P ( U < 1 − u , V ≤ v ) = v − C ( 1 − u , v ) .

Hence, the copula C F ∗ obtained by reflection of C F copula with respect to the u = 1 ∕ 2 line is given as follows:

C F ∗ ( u , v ) = v − C F ( 1 − u , v ) = v − F ( 2 F − 1 ( v ∕ 2 ) + F − 1 ( 1 − u ) ) for ( 1 − u ) + v ∕ 2 < 1 , v − ( ( 1 − u ) + v − 1 ) for ( 1 − u ) + v ∕ 2 ≥ 1 , = v − F ( 2 F − 1 ( v ∕ 2 ) − F − 1 ( u ) ) for v < 2 u , u for v ≥ 2 u .

Proposition 4

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ ∈ ( − ∞ , 0 ) . Then, the copula C F ∗ admits the tail decomposition with the leading part

L ∗ ( u , v ) = v − ( 2 ( v ∕ 2 ) 1 ∕ γ − u 1 ∕ γ ) γ f o r v < 2 u , u f o r v ≥ 2 u .

Proof

We apply the same approach as in the proof of Proposition 1. For v < 2 u , we have

□ L ∗ ( u , v ) = lim t → 0 C F ∗ ( t u , t v ) t = lim t → 0 t v − F ( 2 F − 1 ( t v ∕ 2 ) − F − 1 ( t u ) ) t = v − lim t → 0 F ( F − 1 ( t ) ( 2 F − 1 ( t v ∕ 2 ) ∕ F − 1 ( t ) − F − 1 ( t u ) ∕ F − 1 ( t ) ) ) F ( F − 1 ( t ) ) = v − ( lim t → 0 ( 2 F − 1 ( t v ∕ 2 ) ∕ F − 1 ( t ) − F − 1 ( t u ) ∕ F − 1 ( t ) ) ) γ = v − ( 2 ( v ∕ 2 ) 1 ∕ γ − u 1 ∕ γ ) γ .

Proposition 5

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ = 0 . Then, the copula C F ∗ admits the tail decomposition with the leading part

L ∗ ( u , v ) = min u , v 2 = v ∕ 2 f o r v < 2 u , u f o r v ≥ 2 u .

Proof

Indeed, for v < 2 u and t < 1 ∕ 2 , we have

C F ∗ ( t u , t v ) t = t v − F ( 2 F − 1 ( t v ∕ 2 ) − F − 1 ( t u ) ) t ≤ v − F ( 2 F − 1 ( t v ∕ 2 ) ) 2 F ( F − 1 ( t v ∕ 2 ) ) ∕ v → v − v ∕ 2 = v ∕ 2 .

On the other hand,

□ t v − F ( 2 F − 1 ( t v ∕ 2 ) − F − 1 ( t u ) ) t ≥ v − F ( F − 1 ( t v ∕ 2 ) ) t = v − v ∕ 2 = v ∕ 2 .

Proposition 6

Let F ∈ ℱ and let the survival distribution function F ¯ be regularly varying with index γ = − ∞ . Furthermore, let there exists a function w : R → R + such that

lim t → ∞ t w ( t ) = ∞ ,

and for any y ∈ R .

lim t → ∞ F ¯ ( t + y w ( t ) ) F ¯ ( t ) = exp ( − y ) .

Then, the copula C F ∗ admits the tail decomposition with the leading part

L ∗ ( u , v ) = v 1 − v 4 u f o r v < 2 u , u f o r v ≥ 2 u .

Proof

We observe that

F ( t − y w ( t ) ) F ( t ) = F ¯ ( − t + y w ( t ) ) F ¯ ( − t ) ⟶ t → − ∞ exp ( − y )

and

lim t → − ∞ w ( t ) ( F − 1 ( e − y F ( t ) ) − t ) = y .

Therefore, for v < 2 u and t = F ( x ) ∕ u , we have

□ lim t → 0 C F ∗ ( t u , t v ) t = v − lim t → 0 1 t F ( 2 F − 1 ( t v ∕ 2 ) − F − 1 ( t u ) ) = v − lim x → − ∞ u F 2 F − 1 v 2 u F ( x ) − x F ( x ) = v − u lim x → − ∞ F x − 2 ln ( v ∕ ( 2 u ) ) w ( x ) F ( x ) = v − u exp 2 ln v 2 u = v − v 2 4 u .

Since for the copulas, such that their reflections with respect to the line u = 1 ∕ 2 admit a uniform lower left tail decomposition, the lower right tail parameter exists and equals

λ LR = lim t → 0 t − C ( 1 − t , t ) t = L ∗ ( 1 , 1 ) ,

we obtain the following corollaries.

Corollary 2

Let the survival distribution function F ¯ be regularly varying with index γ ∈ ( − ∞ , 0 ] . Then,

λ LR ( C F ) = 1 ∕ 2 f o r γ = 0 , 1 − ( 2 − 2 1 ∕ γ ) γ ∕ 2 f o r γ ∈ ( − ∞ , 0 ) .

Corollary 3

Let the survival distribution function F ¯ be regularly varying with index γ = − ∞ and let the function w introduced in Proposition 6 exist. Then,

λ LR ( C F ) = 3 4 .

Note that for the normal standard distribution function and for Laplace L ( 0 , 1 ) distribution function, the required function w exists and equals, respectively,

w ( x ) = x and w ( x ) = 1 .

Furthermore, the existence of w implies that the distribution F belongs to the maximum domain of attraction of the Gumbel distribution (see [12] Theorem 3.3.27).

5.8 Left upper tail

The left upper tail of the copula C F is trivial, i.e., the leading part L ⋆ of the copula C F ⋆ , the reflection of C F with respect to the line v = 1 ∕ 2 , equals 0. In more detail:

Since F is increasing and convex on the half-line ( − ∞ , 0 ] and F ( 0 ) = 1 ∕ 2 , we have for h ≥ 0 and y ≤ 0

(9) F ( y ) ≥ F ( y − h ) ≥ F ( 0 ) + ( y − h ) F ( y ) − F ( 0 ) y = F ( y ) + h 2 y − F ( y ) h y > F ( y ) + h 2 y .

Since F − 1 is increasing and concave on the interval ( 0 , 1 ∕ 2 ] and F − 1 ( 1 ∕ 2 ) = 0 , we have for λ ∈ ( 0 , 1 ∕ 4 ) ,

(10) 0 > F − 1 ( 1 ∕ 2 − λ ) ≥ ( 1 − 4 λ ) F − 1 ( 1 ∕ 2 ) + 4 λ F − 1 ( 1 ∕ 4 ) = 4 F − 1 ( 1 ∕ 4 ) λ .

Inequalities (9) and (10) imply that for sufficiently small positive t ,

0 ≤ 1 t C F ⋆ ( u t , v t ) = u − 1 t C F ( u t , 1 − v t ) = u − 1 t F ( F − 1 ( u t ) + 2 F − 1 ( 1 ∕ 2 − v t ∕ 2 ) ) ≤ u − 1 t F ( F − 1 ( u t ) + 4 v t F − 1 ( 1 ∕ 4 ) ) ≤ u − 1 t F ( F − 1 ( u t ) ) − 2 v t F − 1 ( 1 ∕ 4 ) F − 1 ( u t ) = 2 v F − 1 ( 1 ∕ 4 ) F − 1 ( u t ) ⟶ t → 0 0 .

Acknowledgments

The author would like to thank the anonymous reviewers for their valuable suggestions and remarks.

Funding information: No funding is involved.
Conflict of interest: The author state that there is no conflict of interest.

References

[1] Adès, M., Dufour, M., Provost, S., Vachon, M.-C., & Zang, Y. (2022). A class of copulas associated with Brownian motion processes and their maxima. Journal of Applied Mathematics and Computation, 6(1), 96–120. 10.26855/jamc.2022.03.012Search in Google Scholar

[2] Charpentier, A., & Segers, J. (2009). Tails of multivariate Archimedean copulas. Journal of Multivariate Analysis, 100, 1521–1537. 10.1016/j.jmva.2008.12.015Search in Google Scholar

[3] Chavez-Demoulin, V., & Embrechts, P. (2011). An EVT primer for credit risk. In A. Lipton, & A. Rennie, (Eds.), The Oxford handbook of credit derivatives. Oxford UK: Oxford University Press. 10.1093/oxfordhb/9780199546787.013.0014Search in Google Scholar

[4] Da̧browski, K., & Jaworski, P. (2021). On the dependence between a Wiener process and its running maxima and running minima processes. 2021, arXiv:2109.02024 [math.PR]. Search in Google Scholar

[5] DiLascio, F. M. L., Durante, F., & Jaworski, P. (2016). Truncation invariant copulas and a testing procedure. Journal of Statistical Computation and Simulation, 86(12), 2362–2378. 10.1080/00949655.2015.1110820Search in Google Scholar

[6] Donnelly, C., & Embrechts, P. (2010). The devil is in the tails: Actuarial mathematics and the subprime mortgage crisis. Astin Bull., 40(1), 1–33. 10.2143/AST.40.1.2049222Search in Google Scholar

[7] Durante, F., & Jaworski, P. (2010). A new characterization of bivariate copulas. Communications in Statistics - Theory and Methods 39(16), 2901–2912. 10.1080/03610920903151459Search in Google Scholar

[8] Durante, F., & Jaworski, P. (2012). Invariant dependence structure under univariate truncation. Statistics, 46, 263–277. 10.1080/02331888.2010.512977Search in Google Scholar

[9] Durante, F., Jaworski, P., & Mesiar, R. (2011). Invariant dependence structures and Archimedean copulas. Statistics and Probability Letters, 81, 1995–2003. 10.1016/j.spl.2011.08.018Search in Google Scholar

[10] Durante, F., & Sempi, C. (2016). Principles of copula theory. Boca Raton FL: CRS Press. 10.1201/b18674Search in Google Scholar

[11] Embrechts, P. (2009). Copulas: A personal view. Journal of Risk and Insurance, 76, 639–650. 10.1111/j.1539-6975.2009.01310.xSearch in Google Scholar

[12] Embrechts, P., Klü ppelberg, C., & Mikosch, T. (1997). Modeling extremal events for finance and insurance. Berlin: Springer. 10.1007/978-3-642-33483-2Search in Google Scholar

[13] Genest, C., Gendron, M., & Bourdeau-Brien, M. (2009). The advent of copulas in finance. European Journal of Finance, 15, 609–618. 10.1080/13518470802604457Search in Google Scholar

[14] Jaworski, P. (2004). On uniform tail expansions of bivariate copulas. Applicationes Mathematicae, 31, 397–415. 10.4064/am31-4-2Search in Google Scholar

[15] Jaworski, P. (2006). On uniform tail expansions of multivariate copulas and wide convergence of measures. Applicationes Mathematicae, 33, 159–184. 10.4064/am33-2-3Search in Google Scholar

[16] Jaworski, P. (2010). Tail behaviour of copulas. In P. Jaworski, F. Durante, W. Härdle, & T. Rychlik (Eds.), Copula Theory and Its Applications, Proceedings of the Workshop Held in Warsaw, 25–26 September 2009, Lecture Notes in Statistics - Proceedings 198 (pp. 161–186). Berlin: Springer. 10.1007/978-3-642-12465-5_8Search in Google Scholar

[17] Jaworski, P. (2017). On truncation invariant copulas and their estimation. Dependence Modeling, 5, 133–144. 10.1515/demo-2017-0009Search in Google Scholar

[18] Joe, H. (2015). Dependence modeling with copulas. Boca Raton FL: CRS Press. 10.1201/b17116Search in Google Scholar

[19] Joe, H., Li, H., & Nikoloulopoulos, A. (2010). Tail dependence functions and vine copulas. Journal of Multivariate Analysis, 101, 252–270. 10.1016/j.jmva.2009.08.002Search in Google Scholar

[20] Korn, G., & Korn, T. (1968). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. Search in Google Scholar

[21] Łojasiewicz, S. (1988). An introduction to the theory of real functions. A Wiley-Interscience Publication. (3rd edn.). Chichester: John Wiley & Sons Ltd. Search in Google Scholar

[22] McNeil, A. J., & Nešlehová, J. (2009). Multivariate Archimedean copulas, d-monotone functions and l1-norm symmetric distributions. The Annals of Statistics, 37(5b), 3059–3097. 10.1214/07-AOS556Search in Google Scholar

[23] McNeil, A. J., Frey, R., & Embrechts, P. (2005). Quantitative risk management. Concepts, techniques and tools. Princeton Series in Finance. Princeton, NJ: Princeton University Press. Search in Google Scholar

[24] Nelsen, R. B. (2006). An introduction to copulas. Springer series in statistics (2nd edn.). New York: Springer. Search in Google Scholar

[25] Resnick, S. I. (2007). Heavy-Tail phenomena. Probabilistic and statistical modeling. New York: Springer. Search in Google Scholar

Received: 2023-03-17

Revised: 2023-07-01

Accepted: 2023-07-12

Published Online: 2023-08-14

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/demo-2023-0101

Keywords for this article

copulas; tail dependence function; Kendall τ; Spearman ρ; absolute continuity

Creative Commons

BY 4.0