Stability analysis of fractional order SEIR model for malaria disease in Khyber Pakhtunkhwa

Noor Badshah; Haji Akbar

doi:10.1515/dema-2021-0029

Article Open Access

Stability analysis of fractional order SEIR model for malaria disease in Khyber Pakhtunkhwa

Noor Badshah and Haji Akbar

Published/Copyright: November 5, 2021

Published by

Become an author with De Gruyter Brill

Author Information Explore this Subject

From the journal Demonstratio Mathematica Volume 54 Issue 1

Abstract

We discussed stability analysis of susceptible-exposed-infectious-removed (SEIR) model for malaria disease through fractional order and check that malaria is epidemic or endemic in Khyber Pakhtunkhwa (Pakistan). We show that the model has two types of equilibrium points and check their stability through Routh-Hurwitz criterion. We find basic reproductive number using next-generation method. Finally, numerical simulations are also presented.

Keywords: SEIR model; fractional order; Routh-Hurwitz criterion; next-generation method

MSC 2010: 92B15; 92B05

1 Introduction

Malaria is an infectious disease having large economic and health impact on society. Although malaria disease is interrogated for several years but still it is a serious health problem in many countries of the world [1]. Malaria is an infectious disease caused by the plasmodium parasite and transmitted between humans through the bite of the female Anopheles mosquito. There are four types of plasmodium parasite which infect humans, namely, Plasmodium falciparum, Plasmodium vivax, Plasmodium malariae and Plasmodium ovale [2]. P. falciparum can cause serious complications and can be fatal if untreated. Pregnant women and children under the age of five are most infected from malaria because they have a lower immunity as compared to others in the community. According to WHO there are 243 million malaria cases across the world and 7.8 million of deaths occur every year. Therefore, we also check whether the malaria disease is epidemic or endemic in Khyber Pakhtunkhwa (KP, Pakistan).

In the early twentieth century, mathematical models play important role in the study of analyzing the spread of infectious disease [3]. Although there is a lot of work on integer order in epidemiological models [4,5], due to the effective nature of fractional differential equation (FDE) many models in science such as physics, fluid mechanics, mechanical system, and other fields of engineering and epidemiology have been successfully formulated and analyzed [6]. Up to now many fractional results have been presented which are very useful [7,8]. There are three basic definitions of FDE which are the Grunwald-Letnikov, the Riemann-Liouville, and the Caputo formula [9]. We used the Caputo formula due to its convenience for initial condition of the FDE. The Caputo fractional derivative of order α for the function f ( t ) is expressed as:

(1) D t α a c f ( t ) = 1 Γ ( n − α ) ∫ a t f n ( T ) ( t − T ) α + 1 − n d T , n − 1 < α < n ,

where t > a and α , a , t , n ∈ R .

The rest of the paper is arranged as follows: in Section 2, the model derivation is given. The equilibrium points and basic reproductive number are given in Section 3. Stability of equilibrium points is analyzed in Section 4. In Section 5, numerical simulations of the model are given. In Section 6, conclusion is given.

2 Model formulation

In the following model [10], the total population is distributed into four classes with respect to disease. The classes consist of susceptible population S (the individuals who are able to catch the disease), exposed population E (the individuals who have been infected but eventually are not infectious), infectious population I (the individuals who are able to conduct the disease), and recovered population R (the individuals who are recovered from disease). Figure 1 shows the disease transmission of model.

Figure 1

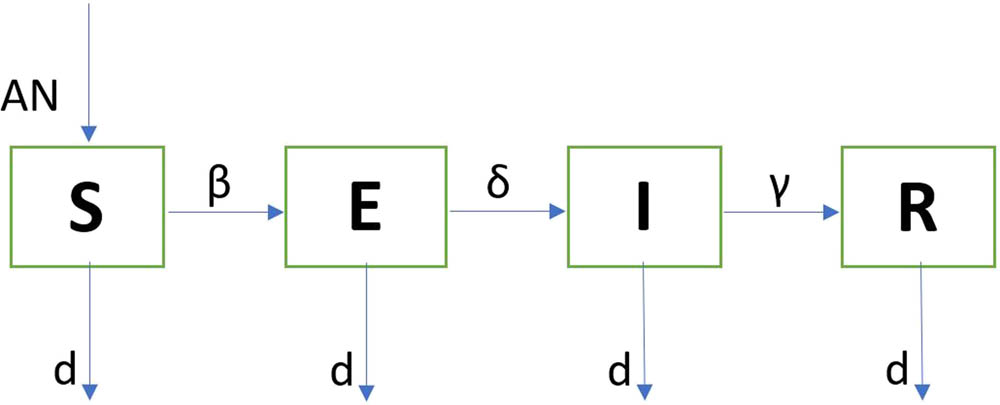
SEIR model for malaria disease.

The SEIR model can be expressed as a system of FDEs of order α given as:

(2) d α S d t = A N − β S I − d S , d α E d t = β S I − ( δ + d ) E , d α I d t = δ E − ( γ + d ) I , d α R d t = γ I − d R .

S ( 0 ) = S 0 , E ( 0 ) = E 0 , I ( 0 ) = I 0 , R ( 0 ) = R 0 , N = S + E + I + R ∈ R + 4 , and 0 < α ≤ 1 .

In the SEIR model, A is the natural birth rate, β denotes the infectious rate, δ denotes the incubation rate, γ is the recovery rate and d denotes the disease-related death. We take fractional order derivative instead of inter order derivative because fractional order derivative has a unique property called memory effect which does not exist in integer order derivative.

3 Equilibrium points and basic reproductive number of system (2)

To find the equilibrium points of the model consider:

(3) A N − β S I − d S = 0 ,

(4) β S I − ( δ + d ) E = 0 ,

(5) δ E − ( γ + d ) I = 0 ,

(6) γ I − d R = 0 .

Adding (3) and (4) we get A N − d S − ( δ + d ) E = 0 , then

(7) S = A N − ( δ + d ) E d .

From (5) we get

(8) I = δ E γ + d ,

while from (6) we obtain that

(9) R = γ I d .

Now putting (7) and (8) in (4) it follows that

(10) E [ β δ ( A N − ( δ + d ) E ) − ( δ + d ) ] d ( γ + d ) = 0 ,

so either E = 0 or

(11) E = β δ A N − d ( γ + d ) ( δ + d ) d ( δ + d ) .

For E = 0 , (7) becomes

(12) S = A N d .

While from (8) we obtain I = 0 . Also from (9) we get R = 0 . It follows that disease-free equilibrium points are given by

(13) X o = A N d , 0 , 0 , 0 .

From (11) there is another equilibrium with

(14) E ∗ = A N δ + d − ( γ + d ) d β δ .

By substituting the value of E ∗ in (7) we obtain

(15) S ∗ = ( δ + d ) ( γ + d ) β δ .

Again using the value of E ∗ in (8) we obtain

(16) I ∗ = δ A N ( δ + d ) ( γ + d ) − d β .

Finally, using the value of I ∗ in (9) we get

(17) R ∗ = γ d δ A N ( γ + d ) ( δ + d ) − d β .

So the endemic equilibrium point X ∗ = ( S ∗ , E ∗ , I ∗ , R ∗ ) is given by expressions (14)–(17).

To find basic reproductive number R 0 , we apply the next-generation method [11]. Suppose there are n disease compartments in the model (2). Let X = ( x 1 , x 2 , … , x n ) where i = 1 , 2 , 3 , … , n represent individuals in ith infected class. Further the rate of expression of new infections in ith compartment is denoted by F i and the rate of expression of disease progression in ith compartment is denoted by V i . Then we linearize the ith infected compartment about disease free equilibrium for finding the spreading of disease in the population. Next-generation matrix is made from partial derivative of F i and V i as:

(18) F = ∂ F i ( x 0 ) ∂ x j and V = ∂ V i ( x 0 ) ∂ x j , i = 1 , 2 , 3 , … , n ,

where x 0 is the disease-free equilibrium point. The R 0 will be found through the dominant eigenvalue of matrix F V − 1 . Note that for system (2) we have two classes that spread the infection which are E and I given as:

(19) d α E d t = β S I − ( δ + d ) E , d α I d t = δ E − ( γ + d ) I .

From (19), F 1 = β S I , F 2 = 0 , V 1 = ( δ + d ) E , V 2 = ( γ + d ) I − δ E , where

F = ∂ ( F 1 ) ∂ E ∂ ( F 1 ) ∂ I ∂ ( F 2 ) ∂ E ∂ ( F 2 ) ∂ I = ∂ ( β S I ) ∂ E ∂ ( β S I ) ∂ I 0 0 = 0 β S ∗ 0 0 = 0 β A N d 0 0

and

V = ∂ ( V 1 ) ∂ E ∂ ( V 1 ) ∂ I ∂ ( V 2 ) ∂ E ∂ ( V 2 ) ∂ I = ∂ ( δ + d ) E ∂ E ∂ ( δ + d ) E ∂ I ∂ ( γ + d ) I − δ E ∂ E ∂ ( γ + d ) I − δ E ∂ I ⇒ V = δ + d 0 − δ γ + d .

Now inverse of matrix V is given as:

V − 1 = 1 δ + d 0 δ ( δ + d ) ( γ + d ) 1 γ + d ,

F V − 1 = β A N δ ( δ + d ) ( γ + d ) d β A N ( γ + d ) ( d ) 0 0 .

We find basic reproductive number R 0 by dominant eigenvalue or spectral radius of ( F V − 1 ) that is ρ ( F V − 1 ) which is defined as:

ρ ( F V − 1 ) = β A N δ ( δ + d ) ( γ + d ) d − λ β A N ( γ + d ) ( d ) 0 − λ ,

this implies that either λ = 0 or λ = β A N δ ( δ + d ) ( γ + d ) d . Hence, the R 0 is given for system (2) as:

(20) R 0 = β A N δ ( δ + d ) ( γ + d ) d .

4 Stability of equilibrium points

In this section, we analyze the local stability of disease-free equilibrium point and endemic equilibrium point. The Jacobian matrix is calculated from equilibrium points as:

d S d t d E d t d I d t d R d t d I d t = A N − β S I − d S β S I − ( δ + d ) E δ E − ( γ + d ) I γ − d R ,

J ( X 0 or X ∗ ) = ∂ S ∂ S ∂ S ∂ E ∂ S ∂ I ∂ S ∂ R ∂ E ∂ S ∂ E ∂ E ∂ E ∂ I ∂ E ∂ R ∂ I ∂ S ∂ I ∂ E ∂ I ∂ I ∂ I ∂ R ∂ R ∂ S ∂ R ∂ E ∂ R ∂ I ∂ R ∂ R = − β I − d 0 − β S 0 β I − ( δ + d ) β S 0 0 δ − ( γ + d ) 0 0 0 γ − d ,

and evaluated equilibrium points to decide on the local stability which is directly determined from the eigenvalues λ as:

(21) ∣ J ( X 0 or X ∗ ) − λ I ∣ = 0 .

The eigenvalues of equation (21) will decide that the SEIR model of fractional differential equation is either stable (i.e., all the eigenvalues contain negative real part) or unstable (i.e., at least one of the eigenvalues contains positive real part).

4.1 Disease-free equilibrium points

Using disease-free equilibrium points, i.e., X 0 A N d , 0 , 0 , 0 , the Jacobian matrix J ( X 0 ) for system (2) is given as:

J ( X 0 ) = − d 0 − β A N d 0 0 − ( δ + d ) β A N d 0 0 δ − ( γ + d ) 0 0 0 γ − d ,

with eigenvalue λ

(22) ∣ J ( X 0 ) − λ I ∣ = 0 ,

J ( X 0 − λ ) = − d − λ 0 − β A N d 0 0 − ( δ + d ) − λ β A N d 0 0 δ − ( γ + d ) − λ 0 0 0 γ − d − λ .

The eigenvalue λ is found from the following polynomial:

(23) ( − d − λ ) ( λ 3 + k 1 λ 2 + k 2 λ + k 3 ) = 0 ,

where k 1 = γ + 2 d , k 2 = γ d + d 2 + δ β A N d , and k 3 = δ + d − β A N d .

From equation (23), one eigenvalue is λ 1 = − d and the remaining three eigenvalues λ 2 , λ 3 , and λ 4 are obtained from equation λ 3 + k 1 λ 2 + k 2 λ + k 3 = 0 . Routh-Hurwitz criterion is used for stability to check that eigenvalues have negative real parts, i.e., k 1 > 0 , k 3 > 0 , and k 1 k 2 > k 3 .

Clearly, k 1 = γ + 2 d > 0 , k 3 = δ + d − β A N d > 0 , and k 1 k 2 − k 3 = γ d + d 2 + δ β A N d − δ + d − β A N d γ + 2 d > 0 .

Therefore by Routh-Hurwitz criterion the disease-free equilibrium point X 0 A N d , 0 , 0 , 0 is locally stable.

4.2 Endemic equilibrium points

Using endemic equilibrium points i.e., X ∗ = ( S ∗ , E ∗ , I ∗ , R ∗ ) the Jacobian matrix J ( X 0 ) for system (2) is given as:

J ( X ∗ ) = − β δ A N ( γ + d ) ( δ + d ) − d β − d 0 β ( δ + d ) ( γ + d ) β δ 0 β δ A N ( γ + d ) ( δ + d ) − d β β − ( δ + d ) β ( δ + d ) ( γ + d ) β δ 0 0 δ − ( γ + d ) 0 0 0 γ − d ,

with eigenvalues λ

(24) ∣ J ( X ∗ ) − λ I ∣ = 0 .

J ( X ∗ − λ ) = − β δ A N ( γ + d ) ( δ + d ) − d β − d − λ 0 β ( δ + d ) ( γ + d ) β δ 0 β δ A N ( γ + d ) ( δ + d ) − d β β − ( δ + d ) − λ β ( δ + d ) ( γ + d ) β δ 0 0 δ − ( γ + d ) − λ 0 0 0 γ − d − λ ,

the eigenvalues λ are found from the following polynomial:

(25) ( d + λ ) 2 ( λ 2 + k 1 λ + k 2 ) = 0 ,

so either ( d + λ ) 2 = 0 ⇒ λ = − d or λ 2 + k 1 λ + k 2 = 0 , where k 1 = γ + δ + 2 d and k 2 = δ γ + δ d + d 2 + d ( δ + d ) ( γ d ) − γ A N β + 1 d ( δ + d ) ( γ d ) . From equation (25) one eigenvalue is λ 1 = − d and the other two eigenvalues λ 2 and λ 3 are obtained from equation λ 2 + k 1 λ + k 2 = 0 . Routh-Hurwitz criterion is used for stability to check that eigenvalues have negative real parts, i.e., k 1 > 0 and k 2 > 0 . Clearly, k 1 = γ + δ + 2 d > 0 and k 2 = δ γ + δ d + d 2 + d ( δ + d ) ( γ d ) − γ A N β + 1 d ( δ + d ) ( γ d ) > 0 , so that endemic equilibrium point X ∗ = ( S ∗ , E ∗ , I ∗ , R ∗ ) is locally stable for system (2).

5 Numerical method and simulation

For the numerical solutions of a system of FDE, we use fde12.m code [12].

For numerical simulations, we observe from malaria data taken from different hospitals of Khyber Pakhtunkhwa that 80% of the individuals are susceptible, 5% of the individuals are exposed, and 15% of the individuals are infected, i.e., S ( 0 ) = 0.80 , E ( 0 ) = 0.05 , I ( 0 ) = 0.15 . In the numerical simulations of the model (2), we assume that the natural birth A and death rates d are equal to 0.0086. The infectious rate β = 0.3 , the incubation rate δ = 0.1764 , and the recovery rate γ = 0.1 [10].

Now in Figure 2, we take fractional order α = 0.80 and observe that susceptible S is equal to 35.63%, exposed E is 3.31%, infected I is 5.65% and recovered R is equal to 55.54%. Next we take fractional order α = 0.90 in Figure 3 and observe that susceptible S is equal to 37.74%, exposed E is 3.04%, infected I is 5.01% and recovered R is equal 54.76%. Now we take fractional order α = 0.98 in Figure 4 and observe that susceptible S is equal to 38.37%, exposed E is 2.84%, infected I is 4.56%, and recovered R is equal to 54.18%. Similarly in Figure 5, we take fractional order α = 1 and observe that susceptible S is equal to 38.81%, exposed E is 2.84%, infected I is 4.59%, and recovered R is equal to 53.72%.

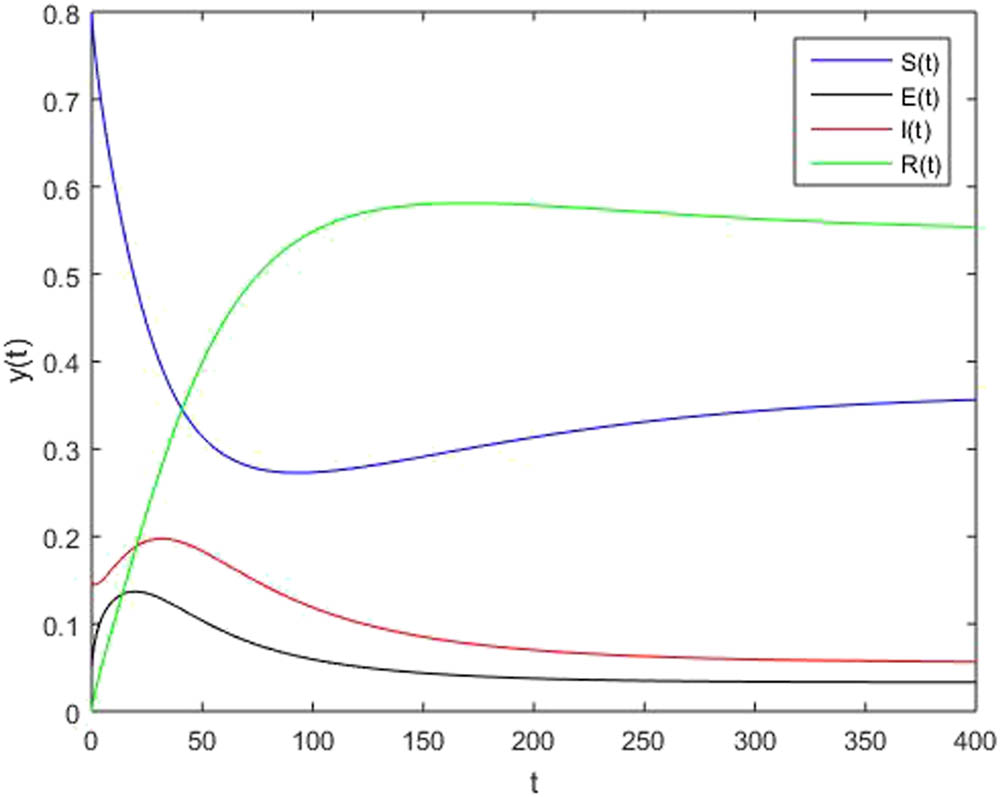
$Figure 2 A solution to the SEIR model with fractional order α \alpha = 0.80.$

Figure 2

A solution to the SEIR model with fractional order α = 0.80.

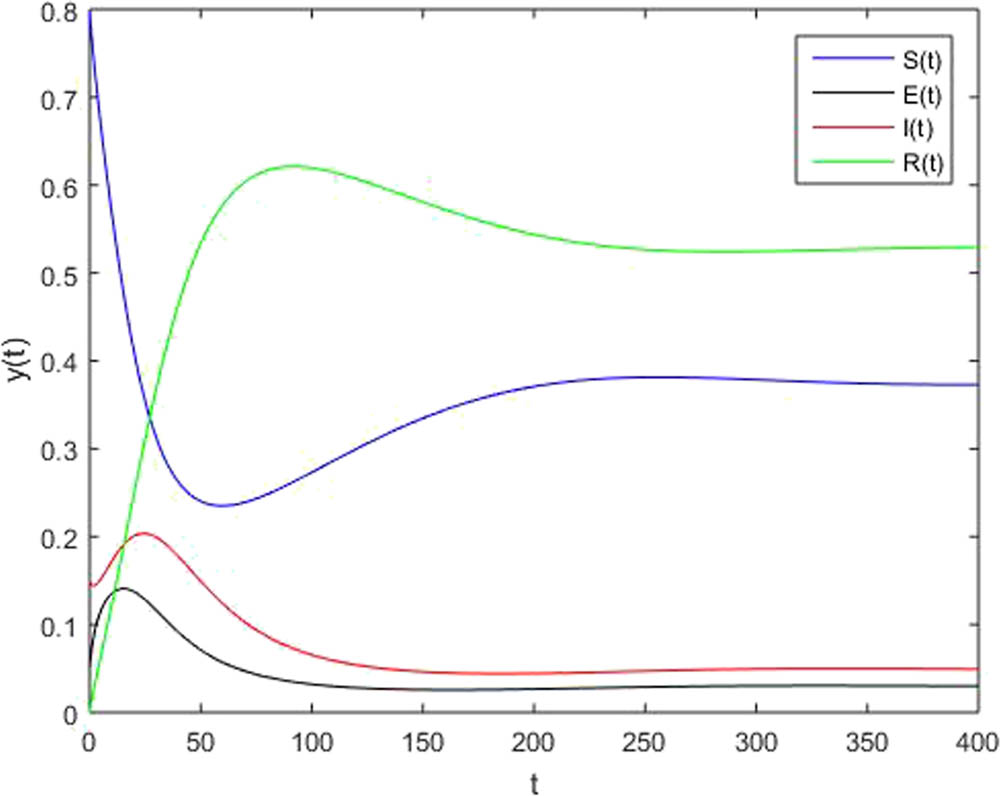
$Figure 3 A solution to the SEIR model with fractional order α \alpha = 0.90.$

Figure 3

A solution to the SEIR model with fractional order α = 0.90.

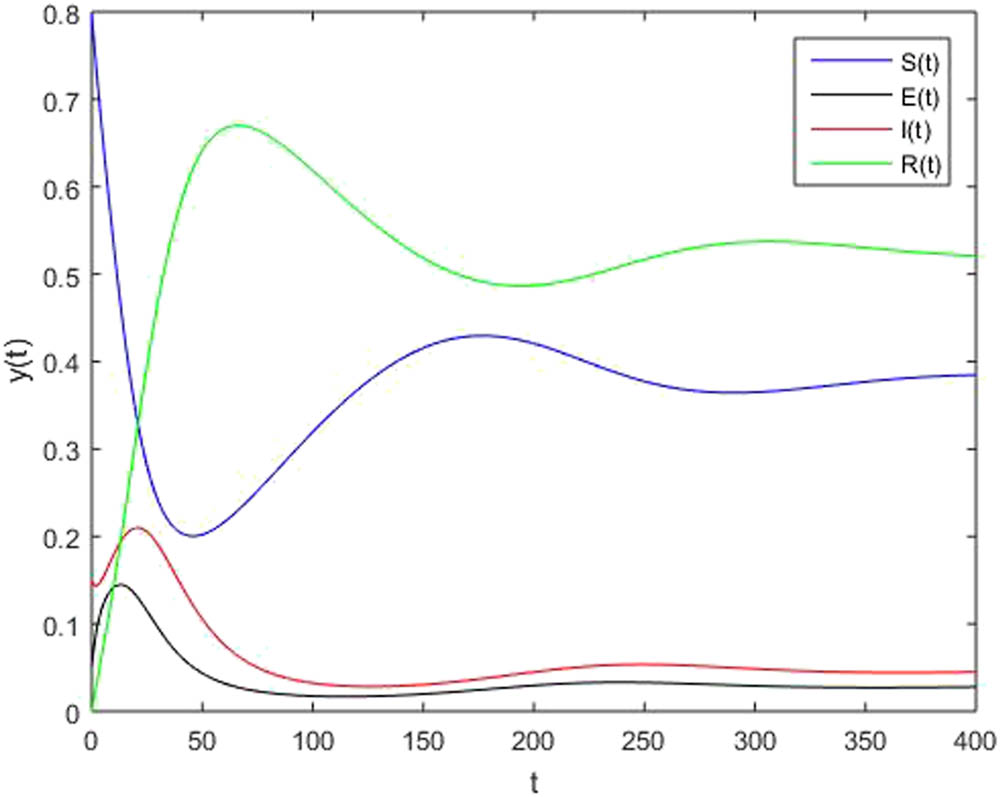
$Figure 4 A solution to the SEIR model with fractional order α \alpha = 0.98.$

Figure 4

A solution to the SEIR model with fractional order α = 0.98.

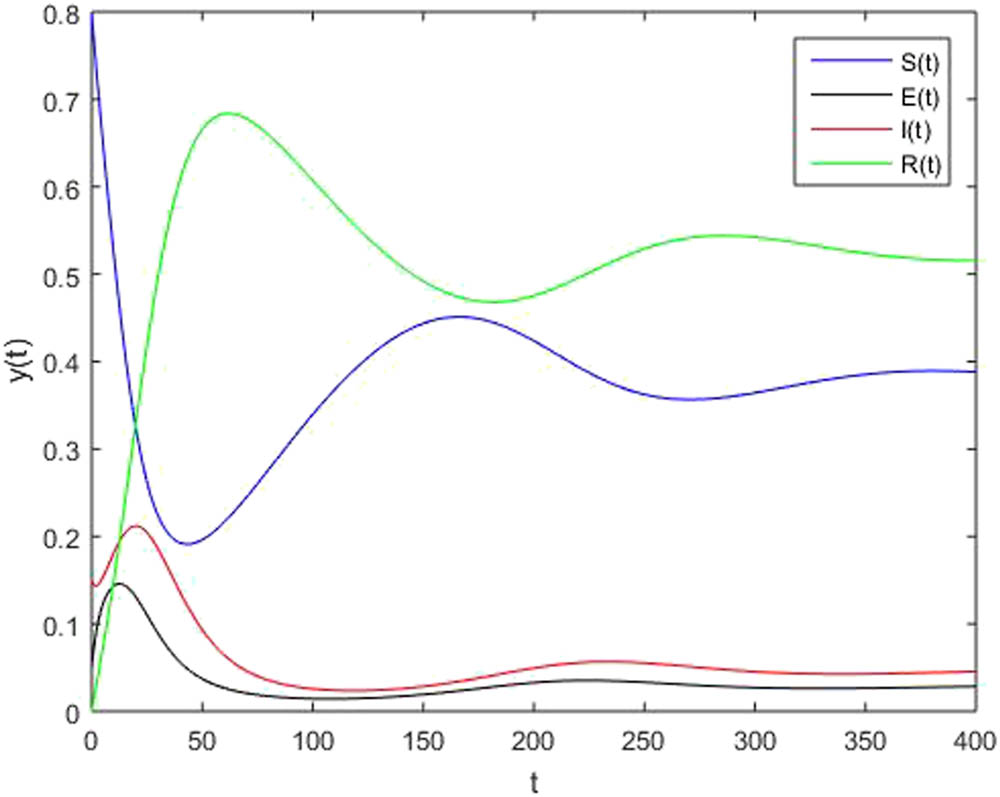
$Figure 5 A solution to the SEIR model with fractional order α \alpha = 1.$

Figure 5

A solution to the SEIR model with fractional order α = 1.

We compare all the above results of fractional order and notice that for fractional order α = 0.98 infected population decreases from 15% to 4.56% and recovered population reaches from 0% to 54.18%. So that the fractional order α = 0.98 gives good results than integer order. We also note from memory effect property that fractional order model behaves to particular point over a longer period of time.

6 Conclusion

We have formulated and analyzed the SEIR model for fractional order for malaria disease in KP. We observe that disease-free equilibrium points X 0 exist and are locally stable when R 0 < 1 and for R 0 ≥ 1 , and the endemic equilibrium points X ∗ exist and are locally stable. We find basic reproductive number R 0 from the SEIR model and its value by using malaria data of KP (Pakistan) for the year 2018. From the data the value of R 0 = 2.6340 , which is greater than one which means that malaria is endemic in KP. We also give a numerical example and observe that for fractional order α = 0.98 , the SEIR model of fractional differential equation gives good result than integer order. In the future, I will work on the fractional order SEIR model for epidemiological disease transmission with control strategies.

Conflict of interest: Authors state no conflict of interest.

References

[1] C. M. A. Pinto and J. A. Tenreiro Machado , Fractional model for malaria transmission under control strategies, Comput. Math. Appl. 66 (2013), no. 5, 908–916. 10.1016/j.camwa.2012.11.017Search in Google Scholar

[2] R. Almeida , Analysis of a fractional SEIR model with treatment, Appl. Math. Lett. 84 (2018), 56–62. 10.1016/j.aml.2018.04.015Search in Google Scholar

[3] M. Trawicki , Deterministic seirs epidemic model for modeling vital dynamics, vaccinations, and temporary immunity, Mathematics 5 (2017), no. 1, 7, https://doi.org/10.3390/math5010007 . 10.3390/math5010007Search in Google Scholar

[4] S. Javeed , S. Anjum , K. Saleem Alimgeer , M. Atif , M. S. Khan , W. A. Farooq , et al., A novel mathematical model for COVID-19 with remedial strategies, Results Phys. 27 (2021), 104248, https://doi.org/10.1016/j.rinp.2021.104248 . 10.1016/j.rinp.2021.104248Search in Google Scholar

[5] A. Sohail , M. Iftikhar , R. Arif , H. Ahmad , K. A. Gepreel , and S. Iftikhar , Dengue control measures via cytoplasmic incompatibility and modern programming tools, Results Phys. 21 (2021), 103819, https://doi.org/10.1016/j.rinp.2021.103819 . 10.1016/j.rinp.2021.103819Search in Google Scholar

[6] E. Demirici , A. Unal , and N. Ozalp , A fractional order SEIR model with density dependent death rate, Math. Stat. 40 (2011), 287–295. Search in Google Scholar

[7] F. Al-Basir , A. M. Elaiw , D. Kesh , and P. K. Roy , Optimal control of a fractional-order enzyme kinetic model, Control Cybernet. 44 (2015), no. 4, 443–461. Search in Google Scholar

[8] Z. Ul Abadin Zafar , K. Rehan , and M. Mushtaq , Fractional-order scheme for bovine babesiosis disease and tick populations, Adv. Difference Equ. 2017 (2017), 86. 10.1186/s13662-017-1133-2Search in Google Scholar

[9] I. Podlubny , Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, vol. 198, Academic Press, 1998. Search in Google Scholar

[10] A. Rachah and D. F. M. Torres , Analysis, simulation and optimal control of a SEIR model for Ebola virus with demographic effects, arXiv:http://arXiv.org/abs/arXiv:1705.01079 (2017). Search in Google Scholar

[11] P. van den Driessche and J. Watmough , Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci. 180 (2002), no. 1–2, 29–48. 10.1016/S0025-5564(02)00108-6Search in Google Scholar

[12] R. Garrappa , Numerical solution of fractional differential equations: A survey and a software tutorial, Mathematics 6 (2018), no. 2, 16, https://doi.org/10.3390/math6020016 . 10.3390/math6020016Search in Google Scholar

Received: 2020-12-15

Revised: 2021-03-25

Accepted: 2021-07-12

Published Online: 2021-11-05

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/dema-2021-0029

Keywords for this article

SEIR model; fractional order; Routh-Hurwitz criterion; next-generation method

Creative Commons

BY 4.0