Abstract
Offering virtual laboratories to chemical engineering students is likely to extend beyond the COVID-19 era. Thus, there is a need to develop more simulation-based tasks in a wide blend of subjects, spanning thermodynamics, chemical reactions, and unit operations. Molecular and material modeling based on density functional theory (DFT) calculations provides limitless opportunities to train students on how to obtain thermokinetic values that are typically measured experimentally. Through a series of illustrative cases, this contribution provides detailed procedures pertinent to calculating reaction rate constants, standard enthalpies of reactions, redox potentials, equilibrium reaction constants, and surface-assisted mechanisms. We hope that DFT-operated virtual labs will assist students in attaining learning outcomes and promote their self-learning in the above-mentioned subjects. From a broader prospective, the presented case studies are expected to encourage students to appreciate the practical applications of DFT, not only in the academic but also in the industrial domains.
1 Introduction
The recent lockdowns prompted by the global COVID-19 pandemic have trigged dramatic shifts in teaching methodologies away from the conventional class environment (Magana et al., 2022). In engineering subjects, these changes were mostly underpinned by the introduction of novel techniques in the demonstration, operation, and delivery of laboratory components (Bhute et al., 2022). The most common deployed approaches to shift lab work from reality to virtuality are simulation-based assignments, recorded videos, videoconferences, and synchronous sessions (Torre et al., 2013). A blended mixture of these methods has been applied in recent years. In many cases, typical experiments are recorded by instructors and students, and a sample of data is given to prepare reports. However, such an approach does not provide valuable hands-on experience in carrying out the experiments and cannot replace the educational value that stems from the physical interaction of the student with experimental rigs. Simple, real take-home experiments have also been suggested (Santiago et al., 2022), but such practices might be limited in terms of safety considerations.
The collection of data and performing the experiments are key elements in the learning experience for engineering students in general and chemical engineering students in particular. Nonetheless, running lab classes requires high operational costs (i.e., chemicals, acquiring space, and maintenance of equipment) and demands careful management of safety-related issues. Although the concept of virtual laboratories is not new and dates back to 2003 (Glassey & Magalhães, 2020), their implementations have skyrocketed over the last two years to supplement or replace physical laboratories. They have been utilized to deliver effective laboratory lessons in curricular courses in science, engineering, and technology domains (Casper et al., 2022; Mahaffey, 2020). As we are now fortunate to witness the end of the COVID-19 era and the return to face-to-face teaching worldwide, it is most likely that we will continue relying on remote virtual labs as an important teaching tool to address learning outcomes of courses and as a support to physical laboratories.
Continuous development of software and simulation packages that illustrate real scenarios is expected to be a chief pillar in the upcoming e-learning period (Garcia et al., 2014). Other merits of virtual labs in chemical engineering include flexibility in exploring the effect of changing parameters on the desired object or property and a more facile illustrative connection between the theory and the experiment (Liu et al., 2022). The concepts of virtual laboratories have even been extended to simulate visits to industrial plants (Seifan et al., 2019). Simulation work in general is now highly regarded as an essential chemical engineering graduate attribute and an important aspect in promoting the self-operated learning of students (Granjo & Rasteiro, 2020). As pointed out by Glassey and Magalhães (2020), the wide-scale implementation of virtual labs calls for the development of more robust and creative assessment methodologies that ensure the attainment of the outlined learning outcomes with likely limited physical interactions between the students and the instructor. Recent surveys have also indicated that within the chemical engineering curriculum, students largely prefer simulation labs rather than to work on data prepared by others (Larriba et al., 2021).
Virtual labs have been deployed to enhance students’ learning experiences; promote students’ autonomy in self-learning; complement traditional reactions, heat, and mass transfer, unit operations, fluid mechanics, and control laboratories (Botero et al., 2016); and facilitate data analysis and report writing (Domínguez et al., 2018). For instance, a group from the University of Minho (Portugal) has recently pioneered a set of simulation education tools to determine the residence time distribution in continuous stirred stank reactors and to investigate mechanisms that dictate catalytic reactions (Granjo & Rasteiro, 2020). These tools operate on web-platform engineering, making them universally accessible. Along the same line of inquiry, simulator-based laboratories have achieved similar learning outcomes in reference to real experimental tasks (Zendler & Greiner, 2020).
Through illustrative examples and exercises, we have advocated the introduction of density functional theory (DFT) and quantum chemical calculations in the curriculum of chemical engineering (Altarawneh & Dlugogorski, 2018), preferably as a few classes in the chemical reaction and thermodynamic units. Molecular modeling based on DFT calculations is now widely deployed in academia and industries in a wide range of strategic applications, most notably in the design of new catalysts, the optimization of the performance of a new material (Makkar & Ghosh, 2021), shortlisting of chemicals that warrant further experimental investigations, and the understanding of the mechanism of action of a new drug. The need to introduce DFT and molecular modeling flavors in the curriculum and pedagogy of chemical engineering reconciles with the recent trend of adding artificial intelligence (AI), advanced materials, and biotechnology to conventional process engineering (Altarawneh & Dlugogorski, 2018). The most exciting applications of predictive analysis and AI in chemical engineering have been driven by the ease of data generation using DFT computations (Wan et al., 2021). Thus, it is important to introduce students to an introductory level of DFT calculations during their studies. The implementation of this task has now become more feasible with the establishment of virtual labs as a reality in the teaching of chemical engineering through distance e-learning. Along the same line of inquiry, running DFT calculations through virtual labs was instrumental in achieving the learning outcomes in physical chemistry courses (Hamilton et al., 2022). In recent studies, computational tools have been used to train students on how to synthesize and model small molecules and investigate their properties (Melia et al., 2022), to understand phase diagrams in the solid phase (Beck et al., 2021), and to address the chemistry of electrophilic substitution reactions (Dong et al., 2021).
To this end, this contribution serves as an extension of our previous call for the introduction of DFT in the teaching of chemical engineering. The emphasis herein is on demonstrating a few case studies that can be executed in virtual labs that complement students’ learning in chemical engineering and thermodynamics. Several of these illustrated examples were introduced to the unit “Advanced Reactions Engineering, between 2019 and 2021” that Master’s students in United Arab Emirates University do. Nonetheless, they could also be extended to the undergraduate reaction engineering unit.
2 Illustrative cases
With the availability of easy-to-use graphical user interfaces to build structures and visualize results, running DFT calculations has become a feasible task for nonexpert users. Results from DFT computations can be obtained without full comprehension of the complex mathematical formulations underlying DFT formalism. Nonetheless, instructors are encouraged to briefly present the main equations and the optimization algorithm. Choosing the right set of DFT parameters for a given task can now be directly sourced from the accumulated wisdom in thousands of published articles (Altarawneh et al., 2022; Razmgar et al., 2022). In the following examples, Gaussian16 and its graphical user interval GaussView were used to investigate the reaction mechanisms of gas phase reactions and to calculate the redox potential. Whereas Gaussian16 and GaussView software (Frisch et al., 2016) are only commercially available, open-source alternatives, such as ORCA (Neese et al., 2020) and Avogadro (Hanwell et al., 2012), are also available. Packages that extract thermokinetic parameters from DFT codes are open-source software (such as ChemRate (Mokrushin et al., 2014) and KiSThelP (Canneaux et al., 2014), which are used herein). For the presented catalyzed reaction, CASTEP (Schleder et al., 2019) and VESTA codes (Momma & Izum, 2008) were used in the calculations. Both are freely available for academic users. Gaussian16 in particular is a versatile code that can be effectively utilized as a one-pack combined computational laboratory.
In performing these cases, the instructor is advised to explain to students that outcomes from computations shall always be confronted with the experiment and/or more accurate calculations that have already been benchmarked against experimental measurements. For instance, the thermodynamic cycle covered in Case 4 provides a simplified treatment, while the implementation in reality incurs several approximations pertinent to simulation of the solvent medium. Overall, the successful handling of each case requires a prior knowledge of the tested system to set an accuracy margin as the DFT-based outcome may not exactly reflect real conditions and parameters of the system at hand. Generally, results from DFT shall be explained and interpreted in view of the experimental findings as these in-silico treatments may not always represent the real systems where complex interactions between many parameters underpin the chemical or physical behavior of the materials or reactions under investigations. For this reason, we attempted herein to compare DFT findings in the illustrated cases with some available corresponding experimental results.
2.1 Case 1: Calculation of the reaction rate constant for a unimolecular reaction
In this example, students are trained on how to calculate the reaction rate constant k(T) for the decomposition reaction of acetic acid (CH3C(O)OH) in the gas phase:
The procedure requires the implementation of transition state theory (TST) and the Eyring equation (Truhlar et al., 1996):
The terms k B (1.38 × 10−23 J/K), h (1.05 × 10−34 J/s), ∆S # (in J/mol K), ∆H # (in J/mol), and R (8.314 J/mol K) denote Boltzmann’s constant, Planks’ constant, entropy of activation, enthalpy of activation, and the universal gas constant, respectively. The equation describes how the reaction progresses at the molecular level. Thermodynamic functions are derived from partition functions of the electronic, vibrational, and rotational components, as described in statistical thermodynamics formulations (Gilson et al., 1997). The two Arrhenius parameters, the pre-exponential A factor, and the activation energy E a can then be obtained from TST:
Experimentally, k(T) values are obtained (say, for a unimolecular irreversible elementary reaction) A → B by measuring the conversion, x, as a function of temperature:
First, students often miss the fact that the values of k(T) are only sensitive to the chemistry of the reaction itself, regardless of the type of reactor utilized. Nonetheless, a batch reactor model is often used to experimentally measure k(T) values. The concept of the transition state or the activated complex in the reaction kinetics can also be ambiguous for chemical engineering students, if not pre-covered in elementary physical chemistry. Using DFT to investigate reaction kinetics and mapping out mechanisms allows students to better grasp the physical meaning and importance of the transition state and how the underlying atomic movements determine the course of the reaction. Central to this aim is the display of atomic movements and their associated vibrational frequencies, a task that can be carried out by numerous graphical user interfaces, such as Avogadro and GaussView. Likewise, students are encouraged to appreciate the importance of the analysis of vibrational frequencies in determining the nature of a structure as a stable species (reactant or a product) or a transition state. In the latter, there should be only one imaginary frequency, which indicates the existence of a maxima energy point along the specified reaction pathway. The visualized atomic movements portray the pathway that the reactant(s) follow in their conversion into the product(s). Such important aspects could not be attained experimentally. An important point to highlight in this regard is the direct connection between macroscopic scales (i.e., moles) and microscopic scales. For example, the calculated heat capacity for a molecule from DFT applies to real-world quantities.
Figure 1 outlines the procedure for computing kinetic parameters for the dissociation reaction CH3C(O)OH → CO2 + CH4. Tutorial 1.a in the Supplementary Materials (SM) provides a detailed description of the steps involved. In summary, Gaussian16 code is used to compute the energy profile of the reaction along the Reactant → Transition state → Products pathway. Vibrational frequencies and rotational constants from the Gaussian16 output files are then used to calculate thermodynamic values (namely, the enthalpies of formation ∆H f o (T) and entropies of formation ∆S f o (T)) for all involved species, including the transition state. This task will be carried out using the ChemRate code. Once the transition state is optimized, students are to view the calculated vibrational frequencies to confirm the existence of a single imaginary frequency in the obtained transition state, which amounts to 1097.7i. Visualizing atomic movements associated with this particular vibrational frequency confirms the dissociation of the CH3C(O)OH into methane and water molecules. Figure 2 shows the potential energy diagram for the reaction. The computed rection enthalpy amounts to −27.7 kJ/mol and the activation enthalpy is 298.1 kJ/mol. As Tutorial 1 explains, the ChemRate code extracts thermodynamics values from which ΔH # and ΔS # are calculated:
where ∆H f (TS), ∆H f (R), ∆S f (TS), and ∆S f (R) denote the temperature-dependent values of the enthalpy of formation for the transition state, enthalpy of formation of reactant, entropy of formation of the transition state, and entropy of formation of the reactant, respectively. Table 1 enlists these values, whereas Figure 3 plots entropic and enthalpic values for the reaction and corresponding activation values. Finally, applying Equations (1) and (2) yield the two Arrhenius parameters as Figure 4 shows. The E a value is computed to be 302.4 kJ/mol, a value that matches the corresponding experimental value of 305.0 kJ/mol (Mackie & Doolan, 1984).
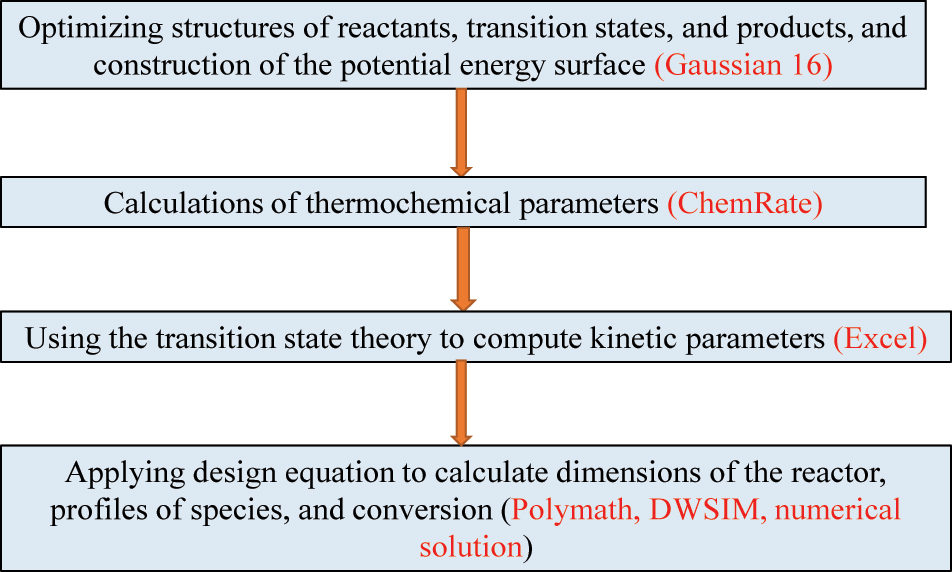
Computational procedure underlying Case 1.
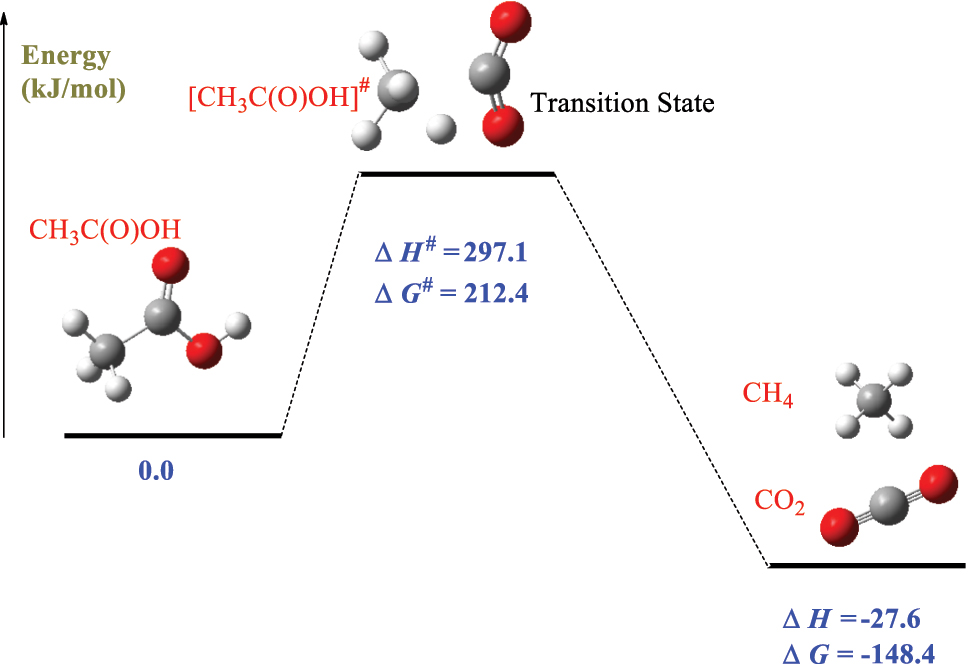
Plotted energy surface for the decomposition reaction CH3C(O)OH → CO2 + CH4.
Computed thermochemical parameters pertinent to the gas phase reaction CH3C(O)OH → CO2 + CH4.
| T (K) | CH3C(O)OH | Transition state | CO2 | CH4 | ||||
|---|---|---|---|---|---|---|---|---|
| ΔH f (kJ/mol) | ΔH f (J/mol. K) | ΔH f (kJ/mol) | ΔS f (J/mol. K) | ΔH f (kJ/mol) | ΔS f (J/mol. K) | ΔH f (kJ/mol) | ΔS f (J/mol. K) | |
| 300 | −433.1 | 296.9 | −135.9 | 292.1 | −392.9 | 228.9 | −74.4 | 216.5 |
| 400 | −425.5 | 318.6 | −128.1 | 314.3 | −389.1 | 240.1 | −70.7 | 227.3 |
| 500 | −416.6 | 338.4 | −119.1 | 334.4 | −384.8 | 249.5 | −66.4 | 236.8 |
| 600 | −406.5 | 356.9 | −108.9 | 352.9 | −380.3 | 257.8 | −61.6 | 245.6 |
| 700 | −395.3 | 374.0 | −97.9 | 369.9 | −375.5 | 265.1 | −56.2 | 253.9 |
| 800 | −383.4 | 390.0 | −86.0 | 385.8 | −370.5 | 271.8 | −50.3 | 261.8 |
| 900 | −370.7 | 404.9 | −73.5 | 400.5 | −365.4 | 277.9 | −43.9 | 269.3 |
| 1000 | −357.5 | 418.8 | −60.4 | 414.3 | −360.1 | 283.4 | −37.1 | 276.5 |
| 1100 | −343.6 | 432.0 | −46.8 | 427.3 | −354.7 | 288.6 | −29.8 | 283.4 |
| 1200 | −329.4 | 444.4 | −32.7 | 439.5 | −349.1 | 293.4 | −22.3 | 290.0 |
| 1300 | −314.7 | 456.1 | −18.3 | 451.0 | −343.5 | 297.9 | −14.4 | 296.3 |
| 1400 | −299.7 | 467.3 | −3.6 | 461.9 | −337.9 | 302.1 | −6.2 | 302.3 |
| 1500 | −284.4 | 477.8 | 11.3 | 472.2 | −332.1 | 306.0 | 2.2 | 308.1 |
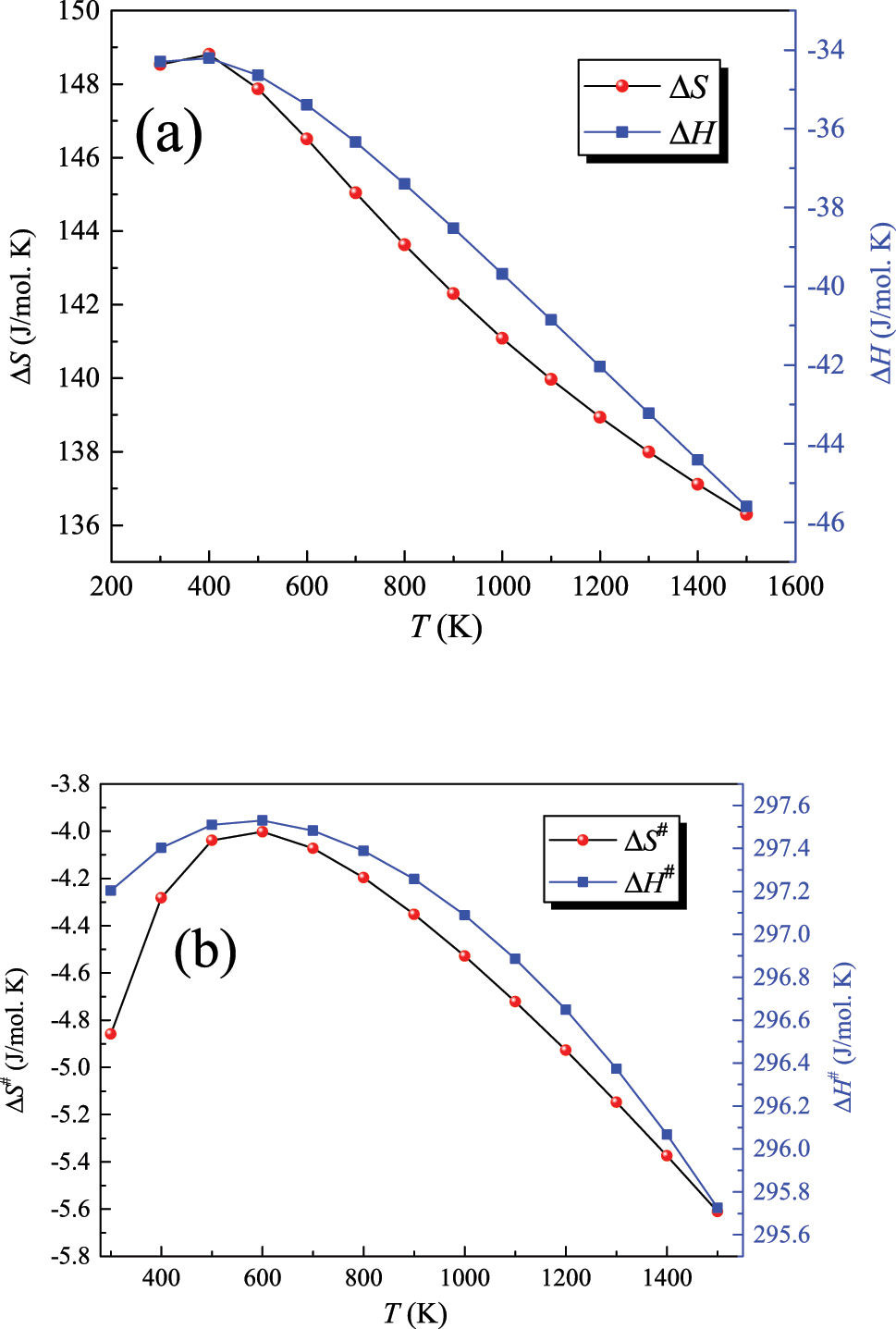
Computed ΔS and ΔH (a) and their corresponding ΔS # and ΔH # values (b) for the decomposition reaction CH3C(O)OH → CO2 + CH4. Entropic (S) and enthalpic (H) values are given in J/mol K and kJ/mol K; respectively.
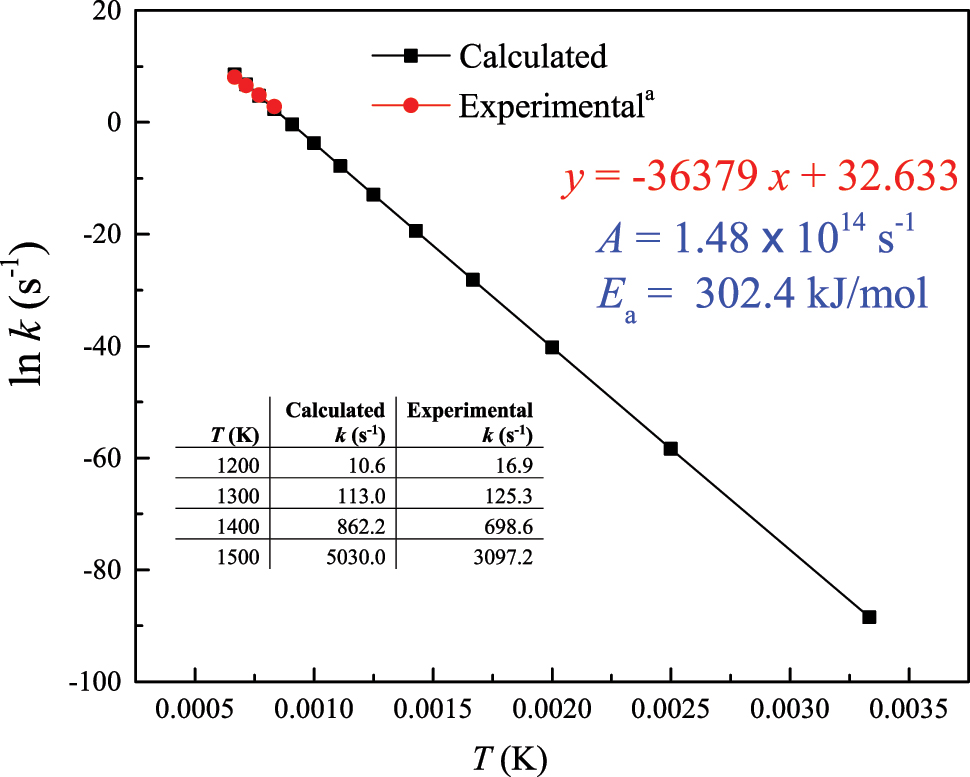
Computed Arrhenius parameters for the decomposition reaction CH3C(O)OH → CO2 + CH4. a Elwardany et al. (2015).
It is always advisable to ask students to attempt to compare computed thermo-kinetic parameters with analogous experimental findings from the literature so as to appreciate the expected accuracy margin of the DFT calculations. Figure 4 also compares computed and experimental reaction rate constants (Elwardany et al., 2015) for this reaction. As shown in Figure 4, the difference between the two sets of values remains within 0.62–1.50 between 1200 and 1500 K.
In this regard, students can also survey the effect of the deployed DFT methodology on the accuracy of the results. In this example, the M062X DFT method (Zhao & Truhlar, 2008) along with the basis set of 6-311+G(d,p) (McLean & Chandler, 1980) were deployed, for instance. Students may repeat the procedure in this case using other simple reactions, such as H + CH4 → H2 + CH3 or CH2=CHCH2Cl → CH2=C=CH2 + HCl. From a chemical engineering perspective, the calculated kinetic parameters can be used in the design equation of reactors (i.e., to find the length of a plug flow reactor necessary to attain a certain conversion). The literature provides comprehensive benchmarking of DFT-calculated thermodynamic parameters against analogous experimental values. For instance, we have previously illustrated that thermo-kinetic parameters for perfluorinated compounds could be accurately predicted by DFT calculations (Altarawneh et al., 2022). As an illustrative example, Table 2 contrasts computed and experimental values (Yu-Ran, 2002) of X–H (X = C, O, N) bond dissociation enthalpies in selected simple molecules. Detailed steps are given in Tutorial 1.b. The CBS-QB3 composite chemistry model is deployed in this case. Students were able to complete this task over three sessions (1 h each). The students appreciated the practical aspects of the case and started a discussion on how to compare kinetic petameters they typically obtain the laboratory segments of the Reaction class. Some of them indicated that a major obstacle in the design project in the final year would be to locate relevant sources of thermal and kinetic values. Hence, implementation of similar DFT calculations provide an alternative source of thermo-kinetic parameters.
Comparison between computed and experimental values of X–H bond dissociation enthalpies (BDH) in selected simple molecules. All values are in kJ/mol at 298.15 K. Tutorial 1.b provides the procedures and related Gaussian16 files.
| C–H Bond | BDH (computed) | BDH (experimental) (Yu-Ran, 2002) |
|---|---|---|
| H–CH3 (CH4 → CH3 + H) | 441.0 | 439.3 |
| CH 3 –CH3 (C2H6 → C2H5 + H) | 425.5 | 420.5 |
| CH3 CH 2 CH3 (CH3CH2CH3 → CH3CHCH3 + H) | 414.0 | 410.5 |
| H–NH2 (NH3 → NH2 + H) | 450.4 | 450.1 |
| CH3O–H (CH3OH → CH3O + H) | 436.7 | 440.2 |
2.2 Case 2: Finding the equilibrium constant for an isomerization reaction
All reactions are reversible, in principle. The direction of the reaction, either in the forward or the reverse direction, depends on its equilibrium constant, K c (T), from the Gibbs free energy ∆Gr(T) of the reaction:
Tutorial 2 (in SM) presents a procedure for computing the K c (T) values for the isomerization reaction n-butane ↔ i-butane based on Equation (5). The procedures involve using the standard enthalpies of formation of n-butane and i-butane and computed vibrational frequencies along with their rotational constants to derive thermochemical parameters (Gibbs free energies of formation ∆G f o (T) heat capacities, standard entropies, etc.) as a function of temperatures. Figure 5 plots the computed values of ∆Gr(T) and K c (T) between 300 and 1000 K. Lower ∆Gr(T) prefers the forward direction of the reaction as the temperature increases. Students may attempt to calculate K c (T) for other reactions, such as the decomposition of ammonia 2NH3 ⇄ 3H2 + N2 or water–gas–shift reaction CO + H2O ⇄ CO2 + H2. As demonstrated in Cases 1 and 2, the applied procedure affords a facile method to obtain thermochemical parameters. For example, Figure 6 presents the heat capacities of the i-butane molecule along with a comparison with pertinent experimental measurements (Pittam & Pilcher, 1972). The two sets of values are very close to each other. Supporting information provides the values and procedures applied in this case. The reaction rate parameters and equilibrium constants computed by DFT calculations often display excellent agreement with experimentally measured values. In a series of studies (Altarawneh, 2022; Altarawneh et al., 2022; Rawadieh et al., 2021), we thoroughly compared kinetic parameters obtained by DFT calculations with analogous experimental measurements. In many cases, the two set values reside within a factor of 1.0–3.0.
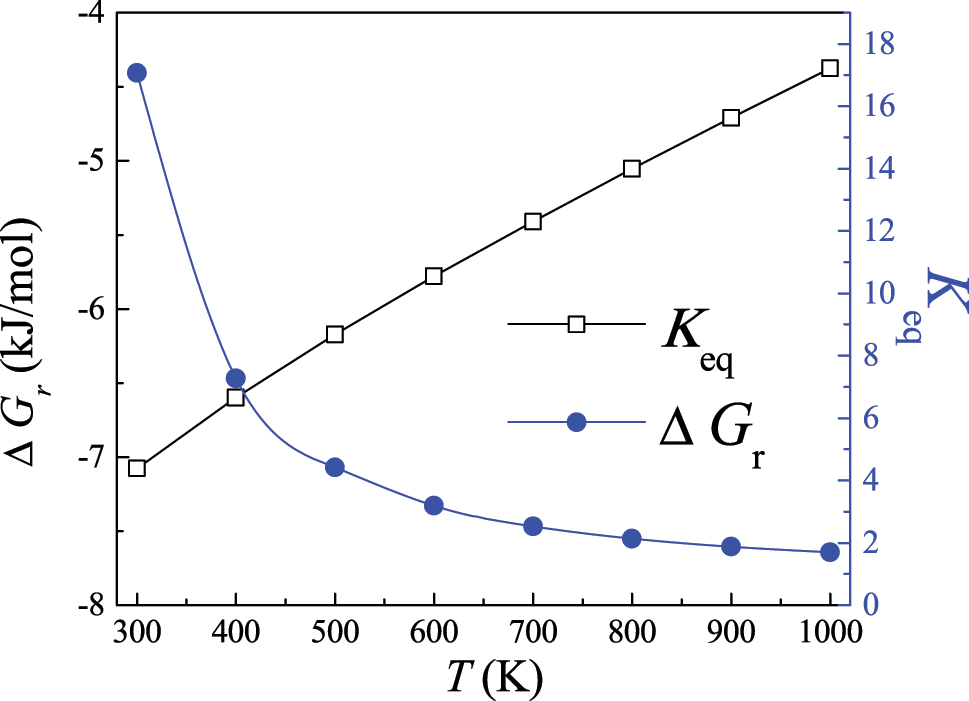
Calculated equilibrium constant K eq and the free energy ΔG r of the reaction n-butane ↔ i-butane.
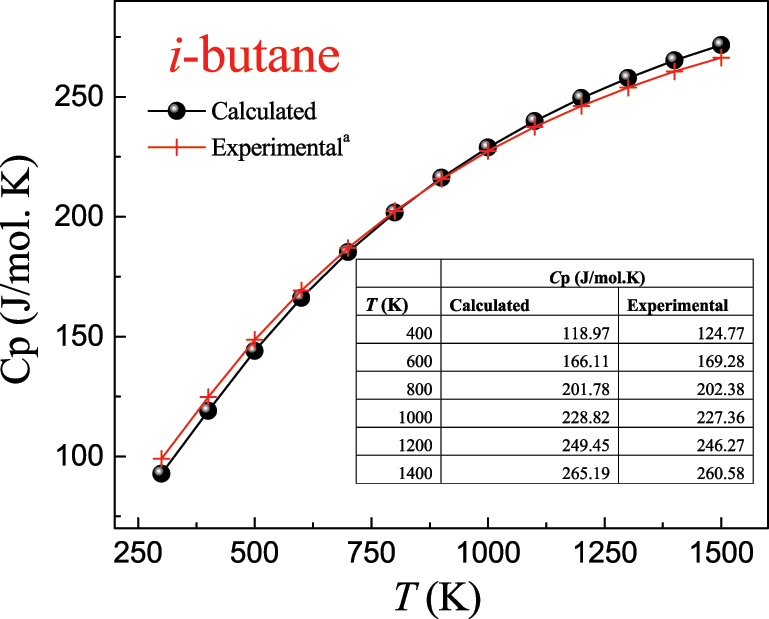
Obtained heat capacity for the n-butane molecule in the gas phase. a Pittam and Pilcher (1972).
2.3 Case 3: Estimation of the standard enthalpy of formation (∆H f o 298.15) of a compound
Students often find it challenging to locate thermochemical data at specific temperatures and pressures from the literature, or that such data simply do not exist. As Cases 1 and 2 demonstrate, DFT calculations are powerful for deriving an accurate estimation of thermochemical functions. Values of ∆H f o 298.15 are determined and measured from calorimetry experiments. Alternatively, isodesmic reaction schemes are readily used to estimate ∆H f o 298.15 values. Isodesmic reactions are hypothetical reactions that conserve the number and type of chemical bonds on two sides of the reaction. The procedure requires obtaining the standard enthalpy of the reaction from DFT calculations (∆H r 298.15) and then using this value to find a missing ∆H f o 298.15 that is not experimentally available. Scheme 1 presents an illustrative example in which the ∆H f o 298.15 value for the 1,4-dichlorobenzene molecule is computed. As Scheme 1 shows:
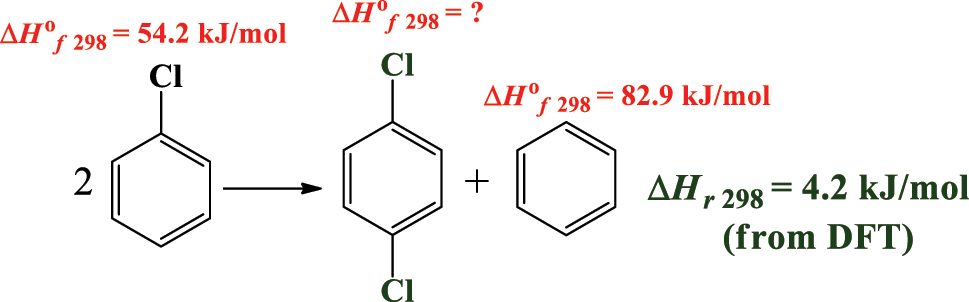
Isodesmic work reactions to obtain ∆H f o 298.15 value for 1,4-dichlorobenzene.
There are 10 aromatic C–H and two C–Cl bonds in the products and the reactants side. The experimental values for the chlorobenzene and benzene molecules are known to be 54.2 and 82.9 kJ/mol, respectively. These two compounds are referred to as “reference compounds”. ∆H r 298.15 for the reaction from the DFT calculations was calculated to be 4.2 kJ/mol. Hence, utilizing the two known ∆H f o 298.15 values with the computed ∆H r 298.15 gives 29.7 kJ/mol as the enthalpy of the formation of the 1,4-dichlorobenzene molecule. The students can then compare this computed value with the analogous experimental value of 24.6 kJ/mol (Platonov & Simulin, 1984) where a reasonable agreement is attained. Tutorial 3 in SM provides detailed procedures involved in Case 3. Students were able to successful complete this Case within an hour lab class. The instructor may advise students to consider other DFT methodologies or composite chemistry model to assess if agreement with the experimental value could be improved.
The procedure could be applied to more complex structures of pesticides and hydrocarbons with no available ∆H f o 298.15 values in the literature. The most important task is to write an Isodesmic reaction where the reference species entail known experimental ∆H f o 298.15 values. It is encouraged to ask students to compare. Literature provides satisfactory comparisons between the experimental and computed values of ∆H f o 298.15. For example, we have shown that the standard enthalpy of formation of o-thiophenoxy departs by less than 4.0 kJ/mol from the corresponding experimental value (Altarawneh et al., 2012).
2.4 Case 4: Calculation of redox potentials
The accurate determination of redox potentials is important in electrochemical and corrosion applications. In DFT calculations, the procedure requires implementing the Born–Haber cycle. Herein, we apply this cycle to calculate the standard one-electron redox potential E o /V based on the Nernest equation:
The standard Gibbs free energy change for the redox half ∆G ox,(sol) is calculated from the free energy change in the gas phase ∆G ox,(g), and the solvation free energies of the oxidized ∆G solv,(III) and reduced ∆G solv,(II) forms:
This example applies Equation (6) (the Born–Harber cycle (Heinz & Suter, 2004)) to calculate the half-redox potential of nickelocene, Ni(C5H5)2, as shown in Scheme 2:
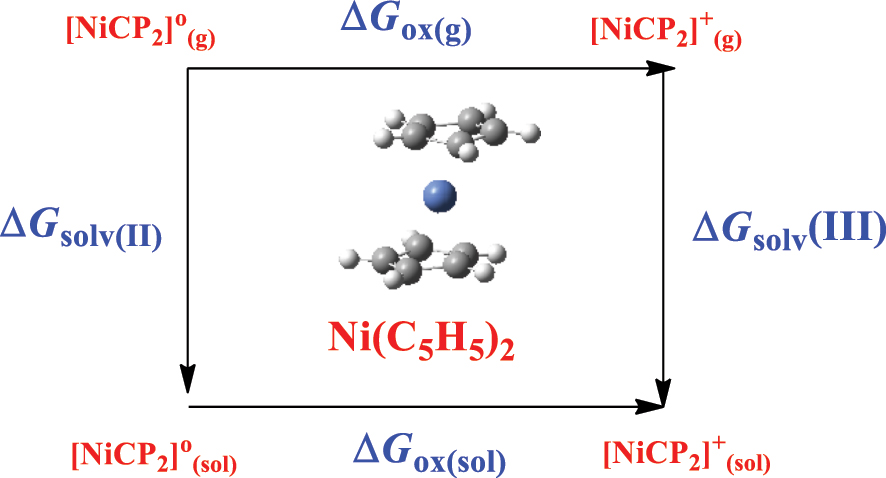
Born–Harber cycle for the II/III redox of Ni(C5H5)2.
Using the B3LYP/Lanl2dz level of theory, Table 3 enlists the calculated values in the thermodynamic cycle. The calculated ∆G ox,(sol) and E o are 4.25 and 0.18 V, respectively. Students are encouraged to see how these values compare with available experimental estimates and to re-apply the cycle for other compounds and complexes, such as nitrobenzene and Co(C5H5)2. Tutorial 4 in SM provides computed energies. As a benchmark of accuracy, values pertinent to the redox potential cycle (for copper complexes) obtained by DFT calculations were found to reside within 0.15 V from their analogous experimental values (Yan et al., 2016). Utilizing nickelocene in the example also encourages students to appreciate the effect of long-range interactions and oxidation states in metal–organic systems. Students may also revisit simple systems that involve the synthesis of hydrogen, as described by Matsui et al. (2013), where an equivalent procedure applies.
Calculated G and E o values in the Harber cycle for the II/III redox cycle of Ni(C5H5)2. All values are in V.
| ∆G solv,(III) | −1.91 |
| ∆G ox,(sol) | 6.00 |
| ∆G solv,(II) | −0.16 |
| ∆G ox,(sol) | 4.25 |
| E o | −0.18 |
2.5 Case 5: Computing material properties
The properties of materials are deployed throughout the chemical engineering curriculum (i.e., unit operations, heat transfer, corrosion, and plant design). DFT calculations have become the prime research tool for acquiring the accurate thermal, optimal, electronic, and mechanical properties of materials. Thus, it is important to train students in the use of DFT to derive the properties of materials and to investigate their structural properties. The latter are directly linked to their catalytic properties, for instance. The CASTEP program, along with the VESTA visualization code, was utilized to investigate the structural (Figure 7a), electronic (Figure 7b), and thermal (Figure 7c) properties of ceria (CeO2). The plotted density of states curve in Figure 5b determines the nature of the material as a conductor or semiconductor. A narrow band gap, for instance (1.0–3.0 eV), indicates semi-conducting behavior. As described in the literature, DFT calculations often yield very accurate band gaps for transition metal oxides (within 0.1–0.2 eV) in reference to experimental values (Widjaja et al., 2017).
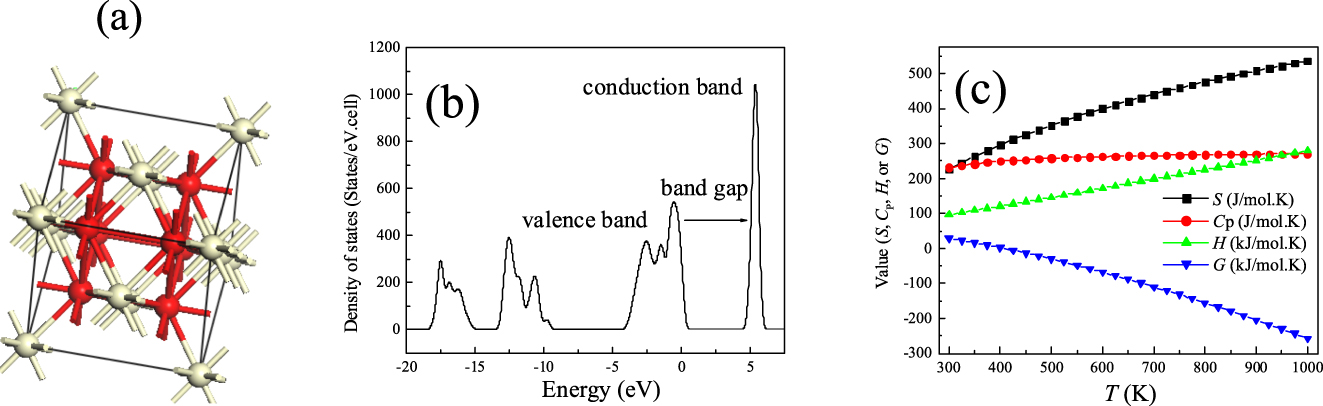
Structure (a), electronic (b), and thermal properties of ceria (CeO2).
2.6 Case 6: Mapping out a surface-catalyzed mechanism
Deriving a rate law for surface-catalyzed reactions from tabulated experimental data is an important aspect in attaining the learning outcomes of reaction courses in chemical engineering. The obtained rate law from the experimental data was then used to suggest potential reaction steps and mechanisms. This procedure produces overall kinetic parameters, that is, not for individual steps (adsorption, surface reactions, reactions between a gas phase species and an adsorbed one, and desorption). Reaction and activation energies for these initial steps in the catalyzed reaction cycle can be readily obtained by DFT calculations. This allows us to obtain a detailed reaction mechanism from which a comprehensive kinetic model can be deduced. Figure 8 provides a mechanism for the surface hydrogenation of ethene into ethane, showing all involved reactions: the dissociation of a hydrogen molecule, the adsorption of the ethene molecule, surface hydrogen transfer to adsorption species, and, finally, the desorption of the ethane molecule. The idea is to convey to students the atomic-base description of the catalyzed reactions—an aspect that has often been overlooked in the teaching of catalysis to undergraduate chemical engineering students. Other examples may include the surface oxidation of CO into CO2 or the synthesis of syngas from water and CO2. The literature presents insightful success stories in which DFT calculations satisfactorily account for the salient mechanistic and kinetic features of surface-mediated reactions in the interpretation of experimental observations (Li et al., 2022).
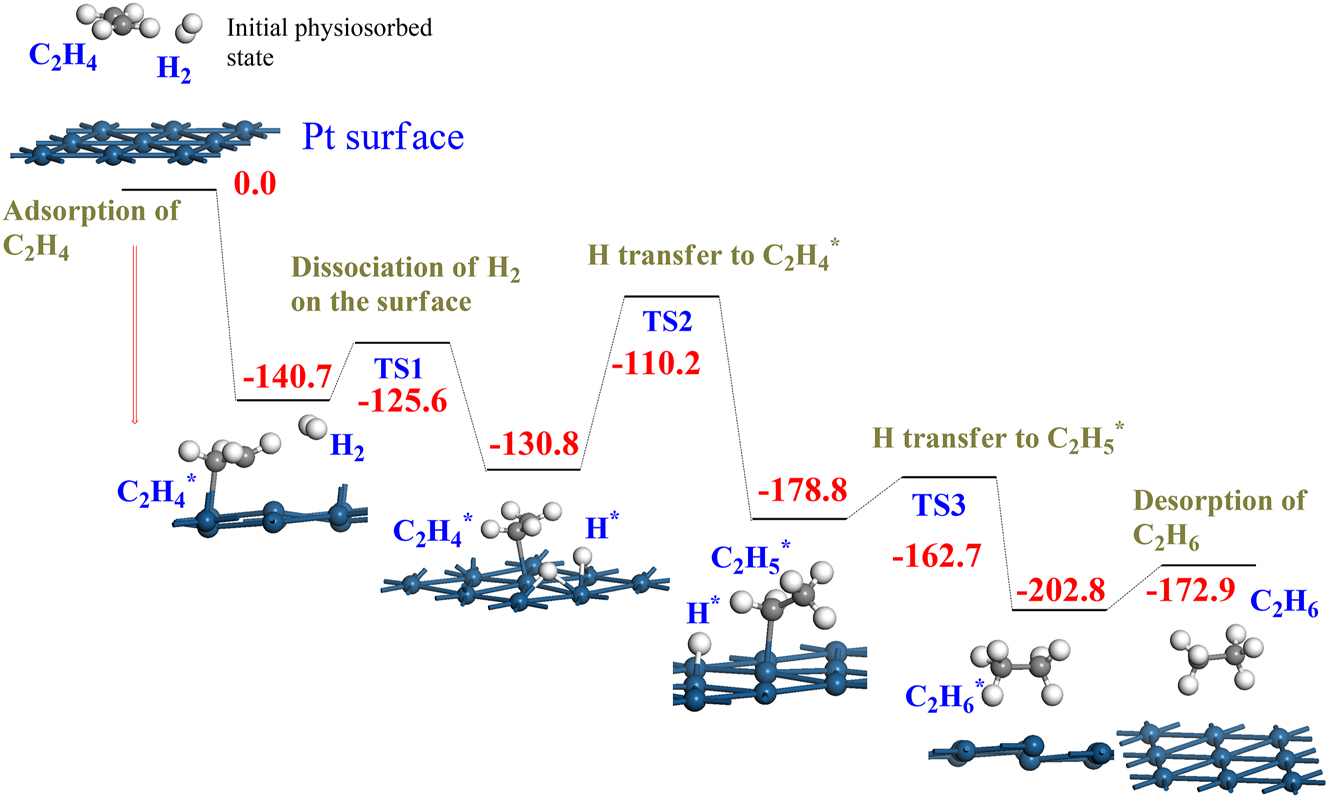
Surface catalyzed hydrogenation of ethene into ethane (C2H4 + H2 → C2H6) over Pt. All values are in kJ/mol in reference to the initial reactants. TS denotes a transition state.
3 Challenges and opportunity of teaching DFT
With the advancements in formulating accurate DFT methods, it has now become possible to obtain properties within a difference of 1–2 % from corresponding experimental measurements. As pointed out in the introduction, obtained properties span thermal, optical, mechanical, and kinetic parameters. Leading chemical firms around the world utilize molecular modelling in one way or another in the initial design of the products, to optimize operational conditions, and to provide fast testing of chemicals toward the desired properties. Thus, it is essential that chemistry and chemical engineering students to be exposed to DFT modelling during their studies. The domain of research topics that utilize DFT calculations are actually limitless, thus undergraduate students who did some DFT modelling, will find it very useful shall they choose to pursue a PhD degree afterword. The main challenge in teaching DFT could stem from two aspects. First of all is that students often use DFT software as a “black-box” without comprehending its mathematical formulations, assumptions, simplifications, and connection to reality. Thus, it is suggested that the instructor to at least cover the basic equations in DFT and their foundations and stress on the fact that not any DFT-obtainable value is correct or provides an insight. Secondly, obtaining a site-license for a commercial DFT code could be costly. Thus, instructors are advised to use open-source codes along with their visualization software.
4 Outlook
The presented cases in this contribution constitute a glimpse of how chemical engineering students can benefit from molecular and material modeling in their learning. Educational-based applications generally fall under chemical reactions and thermodynamics; however, they could also be extended to instrumental analysis, reactive distillation, strength of materials, and the chemistry of solution. We envisage that future directions in this regard may focus on a few aspects, such as the following:
Designing a combined experimental-modeling lab where students can compare experimentally obtained values with DFT prediction.
Introduce assessment items that are carefully tailored to meet the learning outcomes of the courses through molecular modeling.
Offering more representative examples of the industrial relevance of DFT calculations and their current uses in R&D departments in chemical industries.
Reaffirming to students (through illustrative cases) the capacity of DFT to predict properties that are not attainable in the lab, such as thermochemical functions at elevated temperatures and pressures, and the chemical reactivity of a very transient nature, such as intermediates.
Supplementary Materials (SM)
Tutorials 1–4 and Gaussian16 input and output files for Cases 1–4.
Funding source: United Arab Emirates University
Award Identifier / Grant number: 12R174
-
Research ethics: Not applicable.
-
Author contributions: The author has accepted responsibility for the entire content of this manuscript and approved its submission.
-
Competing interests: The author states no conflict of interest.
-
Research funding: This work is supported by a UAEU-AUA (grant number: 12R174) from the United Arab Emirates University.
-
Data availability: The raw data can be obtained on request from the corresponding author.
References
Altarawneh, M. (2022). Temperature-dependent profiles of dioxin-like toxicants from combustion of brominated flame retardants. Journal of Hazardous Materials, 422, 126879. https://doi.org/10.1016/j.jhazmat.2021.126879 Search in Google Scholar PubMed
Altarawneh, M., Almatarneh, M. H., & Dlugogorski, B. Z. (2022). Thermal decomposition of perfluorinated carboxylic acids: Kinetic model and theoretical requirements for PFAS incineration. Chemosphere, 286, 131685. https://doi.org/10.1016/j.chemosphere.2021.131685 Search in Google Scholar PubMed
Altarawneh, M., Dar, T., & Dlugogorski, B. Z. (2012). Thermochemical parameters and pKa values for chlorinated congeners of thiophenol. Journal of Chemical and Engineering Data, 57, 1834–1842. https://doi.org/10.1021/je3003173 Search in Google Scholar
Altarawneh, M., & Dlugogorski, B. Z. (2018). Introducing quantum chemistry in chemical engineering curriculum. Journal of Chemical Education, 95, 1562–1571. https://doi.org/10.1021/acs.jchemed.8b00422 Search in Google Scholar
Beck, H. P., Zhou, M., Hasanovic, P., Gießelmann, E., & Springborg, M. (2021). Course on the use of DFT calculations to improve understanding of phase diagrams in solid-state chemistry. Journal of Chemical Engineering, 98, 3207–3217. https://doi.org/10.1021/acs.jchemed.1c00510 Search in Google Scholar
Bhute, V. J., Sengupta, S., Campbell, J., Shah, U. V., Heng, J. Y. Y., & Brechtelsbauer, C. (2022). Effectiveness of a large-scale implementation of hybrid labs for experiential learning at Imperial College London. Education for Chemical Engineers, 39, 58–66. https://doi.org/10.1016/j.ece.2022.03.001 Search in Google Scholar
Botero, M. L., Selmer, A., Watson, R., Bansal, M., & Kraft, M. (2016). Cambridge weblabs: A process control system using industrial standard SIMATIC PCS 7. Education for Chemical Engineers, 16, 1–8. https://doi.org/10.1016/j.ece.2016.04.001 Search in Google Scholar
Canneaux, S., Bohr, F., & Henon, E. (2014). KiSThelP: A program to predict thermodynamic properties and rate constants from quantum chemistry results†. Journal of Computational Chemistry, 35, 82–93. https://doi.org/10.1002/jcc.23470 Search in Google Scholar PubMed
Casper, A. M. A., Rambo-Hernandez, K. E., Park, S., & Atadero, R. A. (2022). The impact of emergency remote learning on students in engineering and computer science in the United States: An analysis of four universities. Journal of Engineering Education, 111, 703–728. https://doi.org/10.1002/jee.20473 Search in Google Scholar
Domínguez, J. C., Miranda, R., González, E. J., Oliet, M., & Alonso, M. V. (2018). A virtual lab as a complement to traditional hands-on labs: Characterization of an alkaline electrolyzer for hydrogen production. Education for Chemical Engineers, 23, 7–17. https://doi.org/10.1016/j.ece.2018.03.002 Search in Google Scholar
Dong, L.-K., Li, Z.-H., & Zhang, S.-Y. (2021). Using computational chemistry to improve students’ multidimensional understanding of complex electrophilic aromatic substitution reactions: Further analysis of the solvent effect, temperature influence, and kinetic behaviors. Journal of Chemical Education, 98, 3226–3236. https://doi.org/10.1021/acs.jchemed.1c00252 Search in Google Scholar
Elwardany, A., Nasir, E. F., Es-sebbar, E., & Farooq, A. (2015). Unimolecular decomposition of formic and acetic acids: A shock tube/laser absorption study. Proceedings of the Combustion Institute, 35, 429–436. https://doi.org/10.1016/j.proci.2014.06.141 Search in Google Scholar
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Petersson, G. A., Nakatsuji, H., Li, X., Caricato, M., Marenich, A. V., Bloino, J., Janesko, B. G., Gomperts, R., Mennucci, B., Hratchian, H. P., Ortiz, J. V., … Fox, D. J. (2016). Gaussian 16 Rev. C.01. Gaussian, Inc.Search in Google Scholar
Garcia, I. A., Pacheco, C. L., & Garcia, J. N. (2014). Enhancing education in electronic sciences using virtual laboratories developed with effective practices. Computer Applications in Engineering Education, 22, 283–296. https://doi.org/10.1002/cae.20554 Search in Google Scholar
Gilson, M. K., Given, J. A., Bush, B. L., & McCammon, J. A. (1997). The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophysical Journal, 72, 1047–1069. https://doi.org/10.1016/s0006-3495(97)78756-3 Search in Google Scholar
Glassey, J., & Magalhães, F. D. (2020). Virtual labs – love them or hate them, they are likely to be used more in the future. Education for Chemical Engineers, 33, 76–77. https://doi.org/10.1016/j.ece.2020.07.005 Search in Google Scholar
Granjo, J. F. O., & Rasteiro, M. G. (2020). Enhancing the autonomy of students in chemical engineering education with LABVIRTUAL platform. Education for Chemical Engineers, 31, 21–28. https://doi.org/10.1016/j.ece.2020.03.002 Search in Google Scholar
Hamilton, N. B., Remington, J. M., Schneebeli, S. T., & Li, J. (2022). Outcome-based redesign of physical chemistry laboratories during the COVID-19 pandemic. Journal of Chemical Education, 99, 639–645. https://doi.org/10.1021/acs.jchemed.1c00691 Search in Google Scholar
Hanwell, M. D., Curtis, D. E., Lonie, D. C., Vandermeersch, T., Zurek, E., & Hutchison, G. R. (2012). Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. Journal of Cheminformatics, 4, 17. https://doi.org/10.1186/1758-2946-4-17 Search in Google Scholar PubMed PubMed Central
Heinz, H., & Suter, U. W. (2004). Atomic charges for classical simulations of polar systems. Journal of Physical Chemistry B, 108, 18341–18352. https://doi.org/10.1021/jp048142t Search in Google Scholar
Larriba, M., Rodríguez-Llorente, D., Cañada-Barcala, A., Sanz-Santos, E., Gutiérrez-Sánchez, P., Pascual-Muñoz, G., Álvarez-Torrellas, S., Águeda, V. I., Delgado, J. A., & García, J. (2021). Lab at home: 3D printed and low-cost experiments for thermal engineering and separation processes in COVID-19 time. Education for Chemical Engineers, 36, 24–37. https://doi.org/10.1016/j.ece.2021.02.001 Search in Google Scholar
Li, G., Shui, Z., Duan, X., Yang, H., Zhao, Z., Zhao, T., Zhang, Z., Jiang, G., Ren, H., Cheng, J., & Hao, Z. (2022). Unveiling the balance between catalytic activity and water resistance over Co3O4 catalysts for propane oxidation: The role of crystal facet and oxygen vacancy. ACS Catalysis, 13, 237–247. https://doi.org/10.1021/acscatal.2c05640 Search in Google Scholar
Liu, L., Ling, Y., Gao, Q., & Fu, Q. (2022). Supporting students’ inquiry in accurate precipitation titration conditions with a virtual laboratory tool as learning scaffold. Education for Chemical Engineers, 38, 78–85. https://doi.org/10.1016/j.ece.2021.11.001 Search in Google Scholar
Mackie, J. C., & Doolan, K. R. (1984). High-temperature kinetics of thermal decomposition of acetic acid and its products. International Journal of Chemical Kinetics, 16, 525–541. https://doi.org/10.1002/kin.550160504 Search in Google Scholar
Magana, A. J., Karabiyik, T., Thomas, P., Jaiswal, A., Perera, V., & Dworkin, J. (2022). Teamwork facilitation and conflict resolution training in a HyFlex course during the COVID-19 pandemic. Journal of Engineering Education, 111, 446–473. https://doi.org/10.1002/jee.20450 Search in Google Scholar PubMed PubMed Central
Mahaffey, A. L. (2020). Chemistry in a cup of coffee: Adapting an online lab module for teaching specific heat capacity of beverages to health sciences students during the COVID pandemic. Biochemistry and Molecular Biology Education, 48, 528–531. https://doi.org/10.1002/bmb.21439 Search in Google Scholar PubMed
Makkar, P., & Ghosh, N. N. (2021). A review on the use of DFT for the prediction of the properties of nanomaterials. RSC Advances, 11, 27897–27924. https://doi.org/10.1039/d1ra04876g Search in Google Scholar PubMed PubMed Central
Matsui, T., Kitagawa, Y., Okumura, M., Shigeta, Y., & Sakaki, S. (2013). Consistent scheme for computing standard hydrogen electrode and redox potentials. Journal of Computational Chemistry, 34, 21–26. https://doi.org/10.1002/jcc.23100 Search in Google Scholar PubMed
McLean, A. D., & Chandler, G. S. (1980). Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. Journal of Chemical Physics, 72, 5639–5648. https://doi.org/10.1063/1.438980 Search in Google Scholar
Melia, L. F., Barrionuevo, S. D., & Ibañez, F. J. (2022). Think outside the lab: Modeling graphene quantum dots in pandemic times. Journal of Chemical Education, 99, 745–751. https://doi.org/10.1021/acs.jchemed.1c00879 Search in Google Scholar
Mokrushin, V., Tsang, W., Zachariah, M. R., Knyazev, V. D., & McGivern, S. (2014). ChemRate. NIST.Search in Google Scholar
Momma, K., & Izum, F. (2008). VESTA: A three-dimensional visualization system for electronic and structural analysis. Journal of Applied Crystallography, 41, 653–658. https://doi.org/10.1107/s0021889808012016 Search in Google Scholar
Neese, F., Wennmohs, F., Becker, U., & Riplinger, C. (2020). The ORCA quantum chemistry program package. Journal of Chemical Physics, 152, 224108. https://doi.org/10.1063/5.0004608 Search in Google Scholar PubMed
Pittam, D. A., & Pilcher, G. (1972). Measurements of heats of combustion by flame calorimetry. Part 8.—Methane, ethane, propane, n-butane and 2-methylpropane. Journal of the Chemical Society, Faraday Transactions 1, 68, 2224–2229. https://doi.org/10.1039/f19726802224 Search in Google Scholar
Platonov, V. A., & Simulin, Y. N. (1984). Experimental determination of the standard enthalpies of formation of polychlorobenzenes. II. Standard enthalpies of formation of dichlorobenzenes. Russian Journal of Physical Chemistry, 58, 1630–1632.Search in Google Scholar
Rawadieh, S. E., Altarawneh, M., Altarawneh, I. S., Shiroudi, A., & El-Nahas, A. M. (2021). Exploring reactions of amines-model compounds with NH2: In relevance to nitrogen conversion chemistry in biomass. Fuel, 291, 120076. https://doi.org/10.1016/j.fuel.2020.120076 Search in Google Scholar
Razmgar, K., Altarawneh, M., Oluwoye, I., & Senanayake, G. (2022). Selective hydrogenation of 1,3-butadiene over ceria catalyst: A molecular insight. Molecular Catalysis, 524, 112331. https://doi.org/10.1016/j.mcat.2022.112331 Search in Google Scholar
Santiago, D. E., Pulido Melián, E., & Vaswani Reboso, J. (2022). Lab at home in distance learning: A case study. Education for Chemical Engineers, 40, 37–44. https://doi.org/10.1016/j.ece.2022.05.001 Search in Google Scholar
Schleder, G. R., Padilha, A. C. M., Acosta, C. M., Costa, M., & Fazzio, A. (2019). From DFT to machine learning: Recent approaches to materials science–a review. Journal of Physics: Materials, 2, 032001. https://doi.org/10.1088/2515-7639/ab084b Search in Google Scholar
Seifan, M., Dada, D., & Berenjian, A. (2019). The effect of virtual field trip as an introductory tool for an engineering real field trip. Education for Chemical Engineers, 27, 6–11. https://doi.org/10.1016/j.ece.2018.11.005 Search in Google Scholar
Torre, L. D. L., Heradio, R., Jara, C. A., Sanchez, J., Dormido, S., Torres, F., & Candelas, F. A. (2013). Providing collaborative support to virtual and remote laboratories. IEEE Transactions on Learning Technologies, 6, 312–323. https://doi.org/10.1109/tlt.2013.20 Search in Google Scholar
Truhlar, D. G., Garrett, B. C., & Klippenstein, S. J. (1996). Current status of transition-state theory. Journal of Physical Chemistry, 100, 12771–12800. https://doi.org/10.1021/jp953748q Search in Google Scholar
Wan, X., Zhang, Z., Yu, W., & Guo, Y. (2021). A density-functional-theory-based and machine-learning-accelerated hybrid method for intricate system catalysis. Materials Reports: Energy, 1, 100046. https://doi.org/10.1016/j.matre.2021.100046 Search in Google Scholar
Widjaja, H., Miran, H. A., Altarawneh, M., Oluwoye, I., Lim, H. N., Huang, N. M., Jiang, Z.-T., & Dlugogorski, B. Z. (2017). DFT + U and ab initio atomistic thermodynamics approache for mixed transitional metallic oxides: A case study of CoCu2O3 surface terminations. Materials Chemistry and Physics, 201, 241–250. https://doi.org/10.1016/j.matchemphys.2017.08.047 Search in Google Scholar
Yan, L., Lu, Y., & Li, X. (2016). A density functional theory protocol for the calculation of redox potentials of copper complexes. Physical Chemistry Chemical Physics, 18, 5529–5536. https://doi.org/10.1039/c5cp06638g Search in Google Scholar PubMed
Yu-Ran, L. (2002). Handbook of bond dissociation energies in organic compounds. CRC Press.Search in Google Scholar
Zendler, A., & Greiner, H. (2020). The effect of two instructional methods on learning outcome in chemistry education: The experiment method and computer simulation. Education for Chemical Engineers, 30, 9–19. https://doi.org/10.1016/j.ece.2019.09.001 Search in Google Scholar
Zhao, Y., & Truhlar, D. G. (2008). The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts, 120, 215–241. https://doi.org/10.1007/s00214-007-0310-x Search in Google Scholar
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles in the same Issue
- Frontmatter
- Editorial
- EDITORIAL for Volume 6
- Research Articles
- Virtual undergraduate chemical engineering labs based on density functional theory calculations
- From screen to bench: unpacking the shifts in chemistry learning experiences during the COVID-19 transition
- Good Practice Report
- Learning about Confucian ecological ethics to promote education for sustainable development in Chinese secondary chemistry education
- Research Article
- Interactive instructional teaching method (IITM); contribution towards students’ ability in answering unfamiliar types questions of buffer solution
- Special Issue Paper
- The times of COVID-19 and beyond: how laboratory teaching evolved through the Pandemic
- Research Article
- Development of a self-test for undergraduate chemistry students: how do students solve tasks on basic content knowledge?
- Good Practice Report
- IUPAC International Chemical Identifier (InChI)-related education and training materials through InChI Open Education Resource (OER)
- Everyday referenced use of a digital temperature sensor – how well do alternative ice cubes really cool a drink?
- Editorial
- List of reviewers contributing to volume 5, 2023
Articles in the same Issue
- Frontmatter
- Editorial
- EDITORIAL for Volume 6
- Research Articles
- Virtual undergraduate chemical engineering labs based on density functional theory calculations
- From screen to bench: unpacking the shifts in chemistry learning experiences during the COVID-19 transition
- Good Practice Report
- Learning about Confucian ecological ethics to promote education for sustainable development in Chinese secondary chemistry education
- Research Article
- Interactive instructional teaching method (IITM); contribution towards students’ ability in answering unfamiliar types questions of buffer solution
- Special Issue Paper
- The times of COVID-19 and beyond: how laboratory teaching evolved through the Pandemic
- Research Article
- Development of a self-test for undergraduate chemistry students: how do students solve tasks on basic content knowledge?
- Good Practice Report
- IUPAC International Chemical Identifier (InChI)-related education and training materials through InChI Open Education Resource (OER)
- Everyday referenced use of a digital temperature sensor – how well do alternative ice cubes really cool a drink?
- Editorial
- List of reviewers contributing to volume 5, 2023

