Home Inverse design of diffractive optical elements using step-transition perturbation approach
Article Open Access

Inverse design of diffractive optical elements using step-transition perturbation approach

  • Dong Cheon Kim ORCID logo EMAIL logo , Andreas Hermerschmidt , Pavel Dyachenko and Toralf Scharf
Published/Copyright: October 7, 2020
Download Article (PDF)
Become an author with De Gruyter Brill
Author Information
Advanced Optical Technologies
From the journal Advanced Optical Technologies Volume 10 Issue 1

Abstract

Diffractive optical elements are ultra-thin optical components required for a variety of applications because of their high design flexibility. We introduce a gradient-based optimization method based on a step-transition perturbation approach which is an efficient approximation method using local field perturbations due to sharp surface profile transitions. Step-transition perturbation approach be available to calculate the gradient of figure of merit straightforwardly, we implemented optimization method based on this gradient. This fast and accurate inverse design creates binary (2-level) diffractive elements with small features generating the wide angle beam arrays. The results of the experimental characterization confirm that the optimization based on the perturbation method is valid for 1-to-117 fan-out grating generating beam pattern of linear array.

Keywords: diffractive optical elements; fan-out gratings; gradient-based optimization; inverse design; step-transition perturbation approach

1 Introduction

Diffractive optical elements (DOEs) are used for a variety of optical systems because of their compact size, high design flexibility, and ease of mass production. A good example of this type of device is fan-out grating, often also referred to as diffractive beam-splitter which creates multi spots by deflecting an incident light into different diffraction orders. Applications of fan-out elements include multi-focal microscopy [1], [2], camera calibration [3], optical system distortion measurement [4], optical interconnects [5], and structured light projectors [6], [7]. In particular, wide angle DOEs are used in promising field of applications [7], [8], [9] with recent progress in fabrication technology realizing nanoscale features. When only small diffraction angles are required, the iterative Fourier transform algorithm (IFTA) [10], [11], [12] based on the thin element approximation (TEA) [13] is widely and successfully used for the design of the microstructure surface of the DOEs. However, this approach suffers from several severe shortcomings and is no more valid when larger angles are required [14]. One of the most severe problems is the insufficient modeling of the light field transmission through the DOE by the TEA [15]. A precise modeling can be obtained by rigorous electromagnetic diffraction theory, such as rigorous coupled-wave analysis (RCWA) [16], [17], [18]. However, the use of parametric optimization based on the rigorous analysis is often computationally heavy because the gratings with many parameters are leading to high-dimensional optimization problems. To overcome this limitation, we employ gradient-based algorithms [19] based on the step-transition perturbation approach (STPA) [20]. In gradient-based optimization of optical elements, within the overall design parameter space, one iteratively searches the maximum or minimum point based on calculated gradient [21], [22].

STPA enables rapid approximate calculation of diffraction intensity of wide angle DOEs, which is an approximate method based on local field perturbations generated by sharp transitions of the surface profile of diffractive elements. We can describe analytically the gradient of diffraction efficiency with respect to the design variables of optical elements using STPA. It thus is feasible to calculate the gradient straightforwardly with accuracy as much as the approach based on the rigorous electromagnetic diffraction theory if most of the features of the structure are bigger than the wavelength of the incident light.

Here, we introduce a design approach based on STPA for wide angle DOEs, yielding improvements in the uniformity of the created patterns while maintaining the total diffraction efficiency. We have focused our efforts on designing binary (i.e., 2-level) micro-structures because they are most easy to fabricate and thus obviously are very attractive for optical systems.

A schematic of DOE generating linear spot array is shown in Figure 1(a). In order to obtain a starting condition for our optimization, a one-dimensional (1D) diffractive fan-out DOE is designed by TEA-based IFTA (see Figure 1(b) inset). Figure 1(b) present the performance of this initial grating as a function of diffraction angle. Obviously, the performance of this initial fan-out element is very unsatisfactory with respect to uniformity even when the maximum diffraction angle is over 7°. We then apply our method to optimize large-angle 1D diffractive beam splitters but also compare to the results from parametric optimization based on RCWA. We measured the performance of fabricated samples based on the optimized designs and compared to calculated diffraction efficiency using RCWA simulation. Based on this analysis, we can show the excellent strengths of our design method.

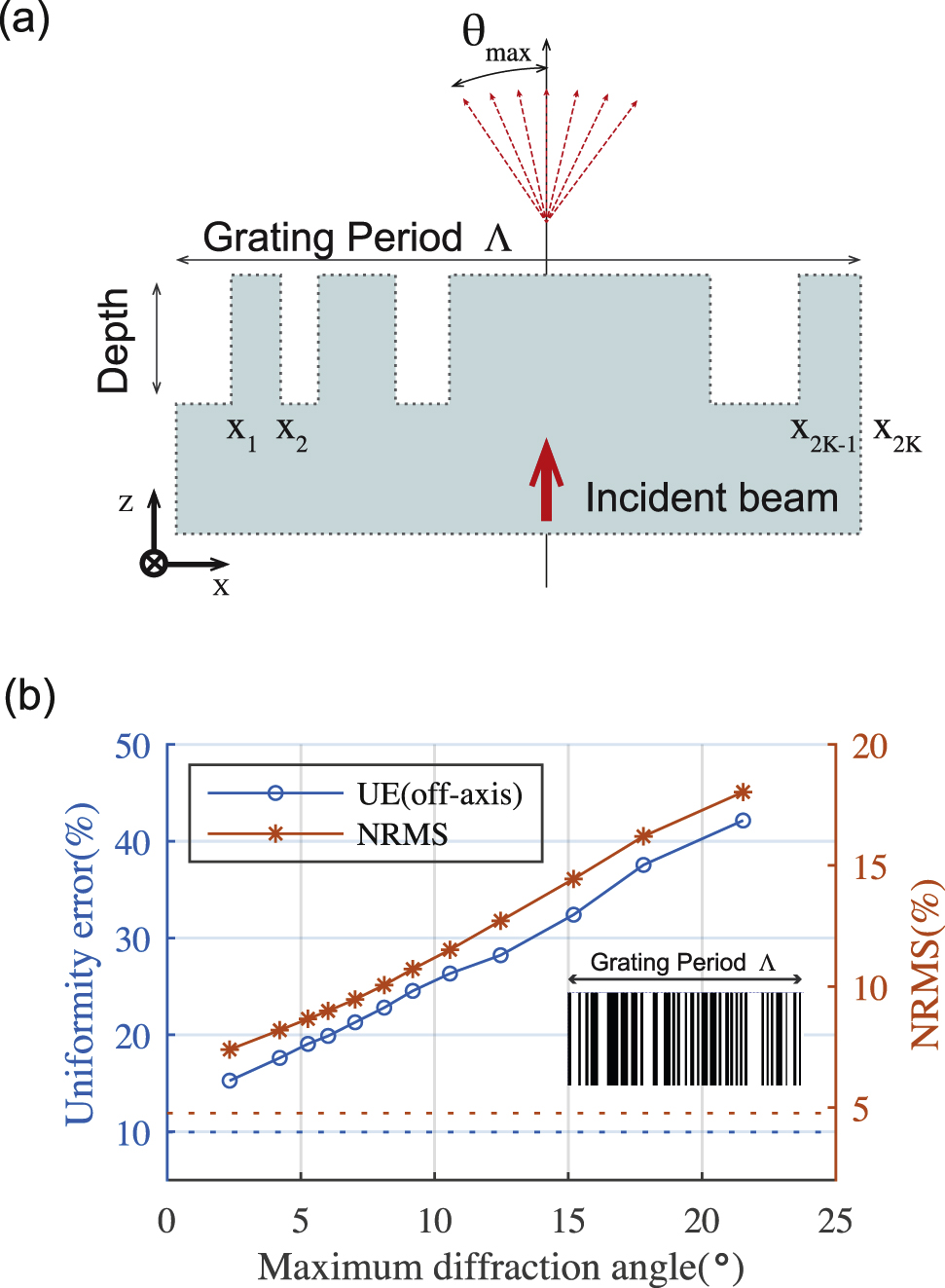
Figure 1: (a) The surface profile of a grating structure in a single period. (b) Uniformity of 1-to-117 diffractive beam splitter designed by TEA-based IFTA as a function of maximum diffraction angle when the grating period Λ${\Lambda}$ decreases. The uniformity error and normalized root-mean-square error (NRMS) calculated using Eqs. (9) and (10). The dashed lines indicate the uniformity values calculated based on TEA. The insets show the layout of the single unit cell with total 60 transition points.
Figure 1:

(a) The surface profile of a grating structure in a single period. (b) Uniformity of 1-to-117 diffractive beam splitter designed by TEA-based IFTA as a function of maximum diffraction angle when the grating period Λ decreases. The uniformity error and normalized root-mean-square error (NRMS) calculated using Eqs. (9) and (10). The dashed lines indicate the uniformity values calculated based on TEA. The insets show the layout of the single unit cell with total 60 transition points.

2 Inverse design methods

An important aspect of the optimization process is the parametrization used to describe the shape of the optical elements, which can significantly affect the performance and computational cost. Figure 1 illustrates an example of a 1D binary phase grating profile with 2K transitions in position xk within a single grating period. We use these positions of transition points as the set of design parameters x = [x1,…,xk,…,x2k] and define the figure of merit (FOM) to optimize DOEs creating diffraction pattern with uniform intensity distribution:

(1)F(x)=∑m=−MM[ηm(x)−ηobj]2

where F represents the difference between the calculated diffraction efficiency ηm and the target diffraction efficiency ηobj in diffraction orders. The gradient of the FOM with respect to transition positions ∇xF is crucial in determining the search direction to optima. For example, if the total number of transitions 2K is large, it may easily become computationally heavy to calculate the gradient by RCWA analysis. The STPA, however, allows expressing the variation for a diffraction efficiency with respect to transition positions as an analytical solution so that it can calculate the gradient straightforwardly.

It has been reported by T. Vallius et al. [20] that in fact the approximated method based on local field perturbations from sharp step-transitions enables rapid calculation of diffraction patterns of DOEs in the non-paraxial domain. The perturbations are observed in the field distribution directly after sharp vertical transitions of binary gratings. The TEA calculation, however, yields a constant amplitude and phase. This omission of perturbations in TEA makes computing inaccurate gratings with wavelength-scale structures, i.e., the gratings creating the wide angle arrays. Thus, we can accurately calculate the diffraction efficiency using the model which combines the TEA with field disturbances caused by sharp transitions in the surface profile calculated by RCWA. We define the field perturbation behind the kth sharp transition located at the point xk in the surface profile as

(2)pk(x)={UkR(x)−UkT(x)if |x|<ΔT0elsewhere

where UkR(x) and UkT(x) are field calculated by RCWA and TEA, respectively and ∆T is the truncation parameter that is chosen 10λ in the calculations [20]. In Figure 2(a), (b), the amplitude and phase of the field distribution directly after an isolated step transition determined by TEA and RCWA is presented. The field perturbations of binary gratings consist of only two kinds of oscillation corresponding to left-side and right-side transition point in a ridge. Therefore, the constructed field behind binary grating with many transition points is described by the x-axis shifts of the two field perturbations p1 (x) and p2 (x) in the following expression:

(3)U(x)=UT(x)+∑k=12Kpk(x)=UT(x)+∑k=1Kp1(x−x2k−1)+∑k=1Kp2(x−x2k)

where 2K is the total number of the transitions. The amplitude and phase of the field perturbation of right-side of a ringe p2 (x) is represented in Figure 2(c), (d). The diffraction amplitude of mth order in far field is given by mth Fourier coefficient of U (x) as

(4)Am=1Λ∫0ΛU(x)exp( −i2πmx/Λ) dx=Tm+Dm

where Λ is the grating period and Tm and Dm is the Fourier coefficient of the field calculated by TEA and a field perturbation contribution, respectively.

(5)Tm=1Λ∫0ΛUT(x)exp(−i2πmx/Λ)dx
(6)Dm=Pm∑k=1Kexp (−i2πmx2k−1/Λ)+P−m∑k=1Kexp (−i2πmx2k/Λ)

where the Fourier coefficient Pm of field perturbation p1 (x) is expressed as

(7)Pm=1Λ∫0Λp1(x)exp(−i2πmx/Λ) dx
Figure 2: The amplitude (a) and phase (b) of the electric field in TE-polarization and behind the sharp vertical surface profile with a transition point corresponding to a phase delay of π radians calculated by RCWA (red line) and TEA (blue dotted line). The corresponding perturbations in Eq. (2) are shown in (c) and (d).
Figure 2:

The amplitude (a) and phase (b) of the electric field in TE-polarization and behind the sharp vertical surface profile with a transition point corresponding to a phase delay of π radians calculated by RCWA (red line) and TEA (blue dotted line). The corresponding perturbations in Eq. (2) are shown in (c) and (d).

The Fourier coefficient of p2 (x) is P−m in Eq. (6) because the p2 (x) is an even function of p1 (x). We found Dm in Eq. (6) using the Fourier shifting theorem [23]. Up to here, T. Vallius et al. claimed that this is an efficient computation method compared with the calculation of RCWA to the entire profile. Once the Fourier coefficient of the step-transition perturbation Pm and P−m is calculated and no further RCWA calculations are necessary.

We furthermore focus on the fact that this Fourier-domain contribution from step transition Pm don’t contains explicit dependence on transition point xk. This point is highly useful when calculating the gradient of diffraction efficiencies with respect to transitions positions ∇xF=[∂F∂x1,⋯,∂F∂xk,⋯,∂F∂x2K] to optimize the structures. To find these derivatives, we apply chain rule when differentiating the FOM F (x):

(8)∂F∂xk=∑m=−MM∂F∂ηm⋅∂ηm∂xk=∑m=−MM∂F∂ηm⋅∂|Tm+Dm|2∂xk

where the first term ∂F∂ηm is easily calculated by using Eq. (1) and the second term ∂|Tm+Dm|2∂xk is also expressed by an analytical equation because because Pm and P−m don’t include the dependence on the position of transition point xk. Additional details on this are described in the Appendix. It is feasible to calculate the gradient straightforwardly with accuracy as much as the approach based on the rigorous method if most of the features of the structure are bigger than the wavelength of the incident light. The obtained gradient was used in optimization based on the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm [24], [25].

3 Simulation results

Using the proposed optimization approach, we can design various multi-spot array generators. In general, diffractive beam splitter creating larger number of spots require more complex structure, i.e. gratings with many features. To verify our method is valid in high dimensional optimization problems, we show the optimization results of fan-out grating generating many spots, for instance, 1-to-117 diffractive beam splitter.

To evaluate DOEs, we use two different metrics which are uniformity error (UE) and normalized root-mean-square error (NRMS) σ.

(9)UE=ηmax−ηminηmax+ηmin
(10)σ=1M∑(ηm−ηobjηobj)2

where ηmax and ηmin represent the maximal and minimum diffraction intensity and ηm is diffraction efficiency in orders and ηobj is target diffraction efficiency and M is the total number of diffraction orders. Lower values of both UE and NRMS indicate less residual variance so that our objective is to minimize UE and NRMS of a DOE design given uniform diffraction efficiency distribution.

To apply the optimization method, we prepared surface profiles of 1D fan-out grating designed by IFTA. The fused silica (SiO2) was selected as the material. The refractive index of SiO2 is assumed as n2 = 1.46. Transverse electric (TE)-polarized (i.e., E-field component along the y-axis) monochromatic light with a wavelength of λ = 633 nm is an incident plane wave from the substrate side with normal incidence angle. The depth of the grating was selected as d = 692 nm and the grating period is 200 µm. Thus, the maximal diffraction angle of 1-to-117 diffractive beam splitter are about 11° at 58th order from 0th order.

To optimize these 1-to-117 diffractive beam splitters, we use our figure of merit as in Eq. (1) with the uniform intensity distribution of target efficiency ηobj and find the local optima using the L-BFGS algorithm with the gradient calculated based on STPA. The uniformity of beam array created by elements designed from IFTA based on TEA, followed by optimization, are plotted in Figure 3 with different metrics. We also plot together with the uniformity of final design after gradient-based optimization based on RCWA, in this case, the gradient calculated by brute-force approaches. In other words, normally around 60 times (i.e., the number of transition points 2K + 1) RCWA simulation is required in an iteration during the optimization. We compared the optimized results by gradient-based on STPA and RCWA. For an accurate comparison, all diffraction efficiencies of final designs are calculated by RCWA. In most cases, the uniformity of these final elements is significantly improved and the uniformity of final design optimized based on STPA are as good as those of optimized based on RCWA. However, the performance of optimization based on STPA is much better than based on RCWA in terms of computation effort. The simulation and optimization steps were written using MATLAB scripts, and the optimization process took less than 20 s using gradient-based optimization by STPA, while taking over 6 h using gradient-based optimization by RCWA on a machine with 3.60 GHz clock rate and 32 GB RAM. During the optimization, the diffraction pattern for calculating UE and NRMS were evaluated with RCWA solver RETICOLO [26].

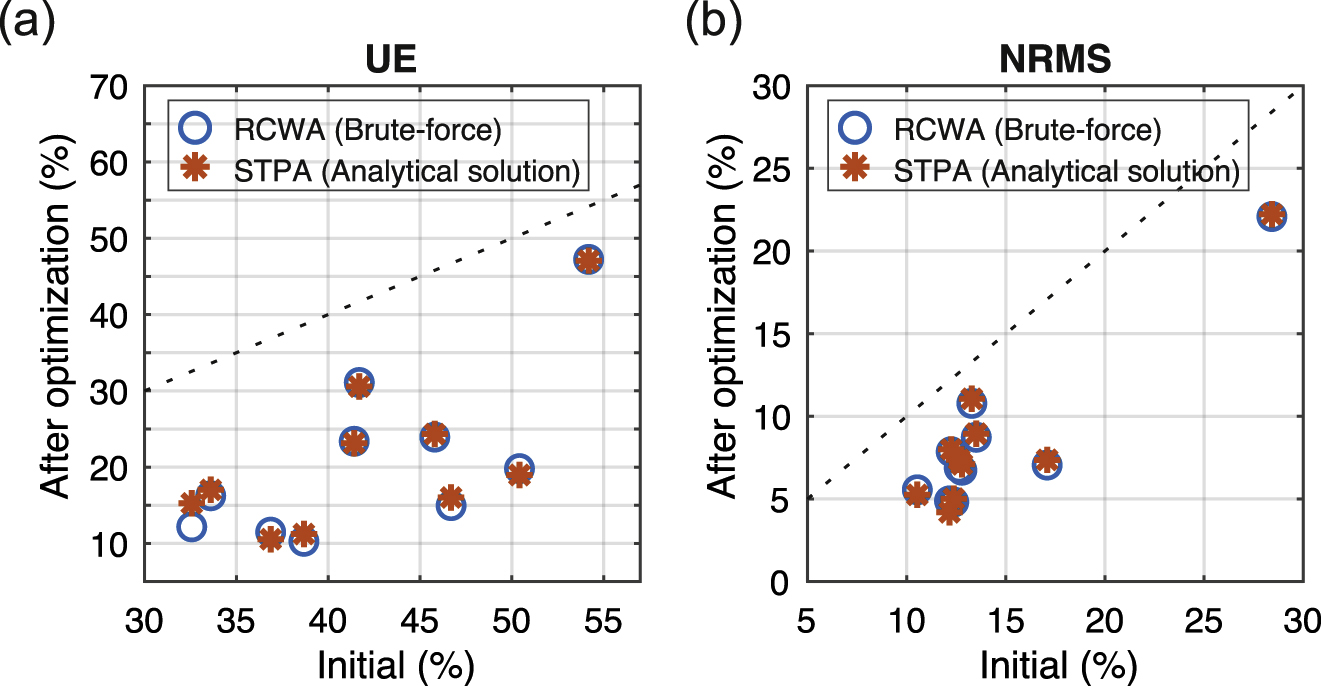
Figure 3: The uniformity of final elements (10 in total) obtained using gradient-based optimization by RCWA and STPA from initial TEA-based IFTA designs with different metrics: (a) UE, (b) UE without zero-th order, and (c) NRMS. The gradient-based on RCWA calculated by Brute-force search. The equal uniformity values of initial and optimized elements are indicated by the black dash line.
Figure 3:

The uniformity of final elements (10 in total) obtained using gradient-based optimization by RCWA and STPA from initial TEA-based IFTA designs with different metrics: (a) UE, (b) UE without zero-th order, and (c) NRMS. The gradient-based on RCWA calculated by Brute-force search. The equal uniformity values of initial and optimized elements are indicated by the black dash line.

To observe the changes of the FOM and transition positions during the optimization, we represent one optimized 1-to-117 diffractive beam splitter in Figure 4. Figure 4(a) shows the merit function as a function of the optimization iterations. The figure of merit converged well and the algorithm found the optimum point after 190 iterations. Through the optimization, the change of all transition positions of the structure is plotted in Figure 4(b). The total number of transitions is 66 and the average change of transition points is around 300 nm after optimization. The simulated diffraction efficiency distributions of DOEs after optimization is shown in Figure 4(c). We calculated the total diffraction efficiency, UE, and NRMS of optimized diffractive beam splitters. The total diffraction efficiency of 117 spots of optimized DOE is 77.35% and UE from 38.68 to 10.79% and NRMS from 12.16 to 04.18%, through gradient-based optimization using STPA. The surface profile of optimized design which has critical dimension (CD) (i.e., minimum feature size) is 700 nm and fill factor is 51.16% is represented in Figure 4(c) inset.

Figure 4: Theoretical analysis of 1-to-117 diffractive beam splitters. (a) the plot of the figure of merit over the course of the optimization process. (b) The variation of transition positions after optimization. The dash lines indicate the transition positions in the single grating period. (c) the calculated efficiency of diffractive beam splitter after optimization. The surface profile of the optimized element in the inset.
Figure 4:

Theoretical analysis of 1-to-117 diffractive beam splitters. (a) the plot of the figure of merit over the course of the optimization process. (b) The variation of transition positions after optimization. The dash lines indicate the transition positions in the single grating period. (c) the calculated efficiency of diffractive beam splitter after optimization. The surface profile of the optimized element in the inset.

4 Experimental results

The diffractive beam splitters were fabricated by direct laser writing to obtain SiO2 binary surface relief structures. The elements are optically characterized using a TE-polarized 636 nm wavelength beam from a diode laser. We detect the diffracted light beams using a mobile single-pixel detector with a high dynamic range. In Figure 5, a detector with a pinhole aperture is mounted on a translation stage under computer control. By scanning the detector to the center of each of the spots, it is possible to measure the power contained in each of the spots, i.e. diffraction orders in the output array.

Figure 5: Schematic of equipment used for diffractive array measurements.
Figure 5:

Schematic of equipment used for diffractive array measurements.

To focus on both the simulation and experiment to facilitate a quantitative comparison, we applied loss caused by Fresnel reflection from the interface between air and SiO2 substrate to simulate the overall efficiency of DOEs. The comparison between theoretical and experimental diffraction efficiencies are presented in Figure 6. We represent the total diffraction efficiency, UE, and NRMS of simulated and measured one in Table 1.

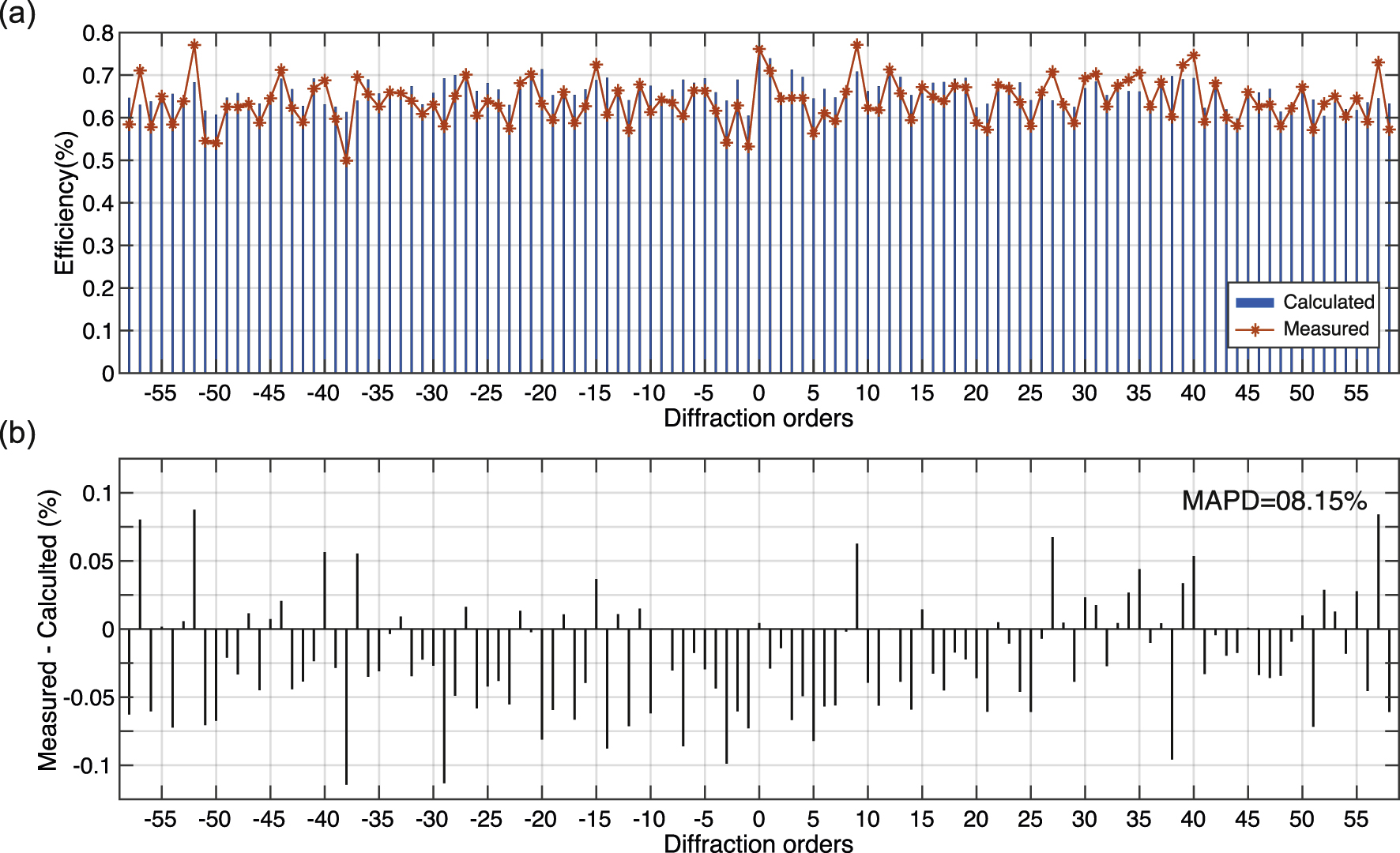
Figure 6: Experimental characterization of 1-to-117 diffractive beam splitter. (a) experimental data (orange star) from profile optimized base on STPA and the simulated data (blue bar). (b) difference between experimental and simulated data in orders.
Figure 6:

Experimental characterization of 1-to-117 diffractive beam splitter. (a) experimental data (orange star) from profile optimized base on STPA and the simulated data (blue bar). (b) difference between experimental and simulated data in orders.

Table 1:

Comparsion with the simulated and experimental properties of the 1-to-117 beam splitters. The simulated efficiency take into account the loss from Fresnel reflection in the air-SiO2 substrate interface.

SimulatedMeasured
Total efficiency (%)74.5674.65
UE (%)11.7421.42
NRMS (%)04.4508.07

The experimental data show that the DOE operates with high-performance. The UE and NRMS of beam splitters are 21.42 and 8.07%, respectively. For an accurate comparison between theoretical and measured results, we analyze the correlation of these data using mean absolute percentage deviation (MAPD) as a ratio defined by the formula:

(11)MAPD=1M∑|ηmS−ηmEηmS|

where ηmS, ηmE are simulated and experimental efficiency in (m)th diffraction orders and M is the total number of diffraction orders. The MAPD of 1-to-117 beam splitters are calculated to the 8.15%, which shows excellent reproducibility of the simulated results in a quantitative manner. The only noticeable deviation in the measurement is a small mismatch of diffraction efficiency in a few orders due to minor fabrication errors. In general the diffraction efficiency in orders often strongly depends on the errors in fabrication processes, e.g., etching depth, feature width, slope steepness, and feature rounding. Nevertheless, the fabricated samples based on optimized design overall display experimental performances which are better than the theoretical performances of initial designs before optimization.

5 Conclusion

In summary, we utilized the STPA in optimizing the optical elements, which is able to create wide angle diffractive optical elements at a very low computational cost. We explored properties of the optimization method, such as efficient computation for the gradient of the target function with respect to transition positions with Fourier-domain local field perturbation. As a case study, we applied gradient-based optimization with STPA to 1–117 beam splitter with a non-paraxial diffraction angle, i.e., maximal diffraction angle is 11° from the center, respectively. The optimized beam splitter show a considerable improvement of uniformity while maintaining the initial diffraction efficiency. The experimental results obtained by the illumination of the fabricated optical elements using a laser of 635 nm wavelength with a normal incidence have been compared with the numerical results. Numerical simulation and experimental results were found to be in good agreement and our optimization method can be considered proven to be an effective design tool for wide angle diffractive beam splitters.

Corresponding authors: Dong Cheon Kim, Nanophotonics and Metrology Laboratory (NAM), EPFL, 1015Lausanne, Switzerland, E-mail: .

Funding source: H2020 Marie Skłodowska-Curie Actions

Award Identifier / Grant number: 675745

  1. Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.

  2. Research funding: Horizon 2020 Framework Programme (675745).

  3. Conflict of interest statement: The authors declare no conflicts of interest regarding this article.

Appendix

In order to calculate the gradient of figure of merit in Eq. (8), we calculated the derivatives of the diffraction efficiencies ∂ηm∂xk.

(12)∂ηm∂xk=∂|Tm|2∂xk+∂|Dm|2∂xk+∂Tm∗ Dm∂xk+∂Tm Dm∗∂xk

where the diffraction efficiency ηm is a function with respect to transition point xk in binary grating. Thus we can partially differentiate each term of ηm with respect to xk. when m≠0, we can express the derivatives as

(13a)∂|Tm|2∂xk=2Φm2(C1m C1m′+S1m S1m′)
(13b)∂|Dm|2∂xk={|Pm|2(C2m Cm′+S2m Sm′)+2ℜ(PmP−m∗)(C3m Cm′+S3m Sm′)−2ℑ(Pm P−m∗)(S3m Cm′−C3m Sm′),for k=1,3,⋯,2K−1|P−m|2(C3m Cm′+S3m Sm′)+2ℜ(Pm P−m∗)(C2m Cm′+S2m Sm′)−2ℑ(Pm P−m∗)(C2m Sm′−S2m Cm′),for k=2,4,⋯,2K
(13c)∂Tm* Dm∂xk+∂Tm Dm*∂xk={2Φm[ℜ(Pm)(C1m Cm′+C2m C1m’+S1m Sm′+S2m S1m’)+ℑ(Pm)(C1m Sm′−S1m Cm′−C2m S1m’+S2m C1m’)+ℜ(P−m)(C3m C1m’+S3m S1m’)+ℑ(P−m)(S3m C1m’−C3m S1m’)],for k=1,3,⋯,2K−12Φm[ℜ(P−m)(C3m C1m’+C1m Cm′+S3m S1m’+S1m Sm′)+ℑ(P−m)(S3m C1m’+C1m Sm′−C3m S1m′−S1m Cm′)+ℜ(Pm)(C2m C1m’+S2m S1m’)+ℑ(Pm)(S2m C1m’−C2m S1m’)],for k=2,4,⋯,2K

where

(14a)Φm=sin(Δϕ/2)/πm
(14b)C1m=∑k=12K(−1)k cos(2πmxk/Λ)
(14c)S1m=∑k=12K(−1)k sin(2πmxk/Λ)
(14d)C2m=∑k=1Kcos(2πmx2k−1/Λ)
(14e)S2m=∑k=1Ksin(2πmx2k−1/Λ)
(14f)C3m=∑k=1Kcos(2πmx2k/Λ)
(14g)S3m=∑k=1Ksin(2πmx2k/Λ)
(14h)C1m′=−2πmΛ(−1)k sin(2πmxk/Λ)
(14i)S1m′=2πmΛ(−1)k cos(2πmxk/Λ)
(14j)Cm′=−2πmΛ sin(2πmxk/Λ)
(14k)Sm′=2πmΛ cos(2πmxk/Λ).

The ∆ϕ is the difference between phase ϕ1 and ϕ2 which are the phase of an electric field in the air and dielectric material, respectively and 2K is the number of transition point in structure. The Fourier coefficients Pm and P−m of field perturbation are given by Eq. (7), which are constant values with respect to transition point xk. Thus the values ℜ(Pm), ℜ(P−m), ℑ(Pm), ℑ(P−m), ℜ(PmP−m*) and ℑ(PmP−m*) also constant with respect to transition point xk.

If m = 0, the derivatives of the diffraction efficiency in zero order is expressed as

(15)∂η0∂xk=−4Q′(1−2Q) sin2(Δϕ/2)−8K⋅ℜ(Pm) sin(Δϕ/2) sin(ϕs/2)Q′+8K⋅ℑ(Pm) sin(Δϕ/2) cos(ϕs/2)Q′

where Q=∑k=12K(−1)k xk, Q′=(−1)kΛ, and ϕs=ϕ1+ϕ2. Therefore, we can express the gradient of diffraction efficiency with respect to transition points based on STPA as an analytical solution.

References

[1] J. E. Jureller, H. Y. Kim, and N. F. Scherer, “Stochastic scanning multiphoton multifocal microscopy,” Opt. Express, vol. 14, p. 3406, 2006. https://doi.org/10.1364/OE.14.003406.Search in Google Scholar PubMed

[2] Z. Chen, B. Mc Larney, R. Johannes, et al., “High-speed large-field multifocal illumination fluorescence microscopy,” Laser Photonics Rev., vol. 14, 2020, Art no. 1900070. https://doi.org/10.1002/lpor.201900070.Search in Google Scholar

[3] M. Bauer, D. Griessbach, A. Hermerschmidt, S. Krüger, M. Scheele, and A. Schischmanow, “Geometrical camera calibration with diffractive optical elements,” Opt. Express, vol. 16, pp. 20241–20248, 2008. https://doi.org/10.1364/OE.16.020241.Search in Google Scholar

[4] F. Wang, Z. Zhang, R. Wang, et al., “Distortion measurement of optical system using phase diffractive beam splitter,” Opt. Express, vol. 27, pp. 29803–29816, 2019. https://doi.org/10.1364/OE.27.029803.Search in Google Scholar PubMed

[5] D. F. Brosseau, F. Lacroix, M. H. Ayliffe, et al., “Design, implementation, and characterization of a kinematically aligned, cascaded spot- array generator for a modulator-based free-space optical interconnect,” Appl. Opt., vol. 39, p. 733, 2000. https://doi.org/10.1364/AO.39.000733.Search in Google Scholar PubMed

[6] R. Vandenhouten, A. Hermerschmidt, and R. Fiebelkorn, “Design and quality metrics of point patterns for coded structured light illumination with diffractive optical elements in optical 3D sensors,” in Digital Optical TechnologiesInternational Society for Optics and Photonics 2017, B. C. Kress and P. Schelkens, vol. 10335, 2017, pp. 264–276, SPIE.10.1117/12.2270248Search in Google Scholar

[7] O. Barlev and M. A. Golub, “Multifunctional binary diffractive optical elements for structured light projectors,” Opt. Express, vol. 26, p. 21092, 2018. https://doi.org/10.1364/OE.26.021092.Search in Google Scholar PubMed

[8] T. Simon, A. Arfaoui, and P. Desaulniers, “Cross-diffractive optical elements for wide angle geometric camera calibration,” Opt. Lett., vol. 36, p. 4770, 2011. https://doi.org/10.1364/OL.36.004770.Search in Google Scholar PubMed

[9] P. Twardowski, B. Serio, V. Raulot, and M. Guilhem, “Three-dimensional shape measurement based on light patterns projection using diffractive optical elements,” in in Micro-Optics 2010, H. Thienpont, P. Van Daele, J. Mohr, and H. Zappe, Eds., vol. 7716, International Society for Optics and Photonics, 2010, pp. 704–711, SPIE.10.1117/12.854906Search in Google Scholar

[10] W. Frank and O. Bryngdahl, “Iterative fourier-transform algorithm applied to computer holography,” J. Opt. Soc. Am. A, vol. 5, p. 1058, 1988. https://doi.org/10.1364/JOSAA.5.001058.Search in Google Scholar

[11] M. Skeren, I. Richter, and P. Fiala, “Iterative fourier transform algorithm: comparison of various approaches,” J. Mod. Opt., vol. 49, pp. 1851–1870, 2002. https://doi.org/10.1080/09500340210140542.Search in Google Scholar

[12] S. Bühling and W. Frank, “Improved transmission design algorithms by utilizing variable-strength projections,” J. Mod. Opt., vol. 49, pp. 1871–1892, 2002. https://doi.org/10.1080/09500340210140551.Search in Google Scholar

[13] J. W. Goodman, “Introduction to fourier optics,” in Introduction to Fourier Optics, vol. 1, 3rd ed., J. W. Goodman, Ed., Englewood, CO, Roberts & Co. Publishers, 2005 Chapter 5. p.10.1063/1.3035549Search in Google Scholar

[14] D. A. Pommet, M. G. Moharam, and E. B. Grann, “Limits of scalar diffraction theory for diffractive phase elements,” J. Opt. Soc. Am. A, vol. 11, p. 1827, 1994. https://doi.org/10.1364/JOSAA.11.001827.Search in Google Scholar

[15] T. Vallius, P. Vahimaa, and M. Honkanen, “Electromagnetic approach to the thin element approximation,” J. Mod. Opt., vol. 51, pp. 2079–2092, 2004. https://doi.org/10.1080/09500340408232515.Search in Google Scholar

[16] P. Lalanne and G. M. Morris, “Highly improved convergence of the coupled-wave method for TM polarization,” J. Opt. Soc. Am. A, vol. 13, p. 779, 1996. https://doi.org/10.1364/JOSAA.13.000779.Search in Google Scholar

[17] M. G. Moharam, E. B. Grann, D. A. Pommet, and T. K. Gaylord, “Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings,” J. Opt. Soc. Am. A, vol. 12, pp. 1068–1076, 1995. https://doi.org/10.1364/JOSAA.12.001068.Search in Google Scholar

[18] V. Liu and S. Fan, “S 4: A free electromagnetic solver for layered periodic structures,” Comput. Phys. Commun., vol. 183, pp. 2233–2244, 2012. https://doi.org/10.1016/j.cpc.2012.04.026.Search in Google Scholar

[19] S. Ruder, An overview of gradient descent optimization algorithms, CoRR abs/1609.04747, 2016.Search in Google Scholar

[20] T. Vallius, V. Kettunen, M. Kuittinen, and J. Turunen, “Step-discontinuity approach for non-paraxial diffractive optics,” J. Mod. Opt., vol. 48, pp. 1195–1210, 2001. https://doi.org/10.1080/09500340108231763.Search in Google Scholar

[21] F. J. Wen, and P. S. Chung, “2D optical beam splitter using diffractive optical elements (DOE),” in Passive Components and Fiber-based Devices III, Sang Bae Lee, Yan Sun, Kun Qiu, Simon C Fleming and IanWhite Ed., vol. 6351, International Society for Optics and Photonics, 2006, pp. 200–210, SPIE.10.1117/12.691058Search in Google Scholar

[22] S. Banerji and B. Sensale-Rodriguez, “A computational design framework for efficient, fabrication error-tolerant, planar THz diffractive optical elements,” Sci. Rep., vol. 9, p. 5801, 2019. https://doi.org/10.1038/s41598-019-42243-5.Search in Google Scholar PubMed PubMed Central

[23] R. L. Easton, Fourier Methods in Imaging, John Wiley & Sons, Ltd, Apr. 2010. https://doi.org/10.1002/9780470660102.Search in Google Scholar

[24] R. H. Byrd, P. Lu, J. Nocedal, and C. Zhu, “A limited memory algorithm for bound constrained optimization,” SIAM J. Sci. Comput., vol. 16, pp. 1190–1208, 1995. https://doi.org/10.1137/0916069.Search in Google Scholar

[25] C. Zhu, R. H. Byrd, P. Lu, and J. Nocedal, “Algorithm 778: L-BFGS-B: fortran subroutines for large-scale bound-constrained optimization,” ACM Trans. Math. Softw., vol. 23, pp. 550–560, 1997.10.1145/279232.279236Search in Google Scholar

[26] J.-P. Hugonin and P. Lalanne, Reticolo Software for Grating Analysis, Orsay, France, Institut d’Optique, 2005.Search in Google Scholar

Received: 2020-07-31
Accepted: 2020-09-17
Published Online: 2020-10-07
Published in Print: 2021-02-23

© 2020 Dong Cheon Kim et al., published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Editorial
  3. From the publisher Reviewer recognition and publisher’s note 2021
  4. Community
  5. News
  6. Views
  7. High quality diffractive optical elements (DOEs) using SMILE imprint technique
  8. Topical Issue: Diffractive Optics; Guest Editor: Reinhard Voelkel
  9. Editorial
  10. Diffractive optics
  11. Review article
  12. Diamond diffractive optics—recent progress and perspectives
  13. Research articles
  14. Narrowband transmission filters based on resonant waveguide gratings and conformal dielectric-plasmonic coatings
  15. Inverse design of diffractive optical elements using step-transition perturbation approach
  16. Diffractive optics based automotive lighting system
  17. Multifunctional materials for lean processing of waferscale optics
  18. Research article
  19. Stray light analysis and design optimization of geometrical waveguide
https://doi.org/10.1515/aot-2020-0046
Keywords for this article
diffractive optical elements; fan-out gratings; gradient-based optimization; inverse design; step-transition perturbation approach
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Editorial
  3. From the publisher Reviewer recognition and publisher’s note 2021
  4. Community
  5. News
  6. Views
  7. High quality diffractive optical elements (DOEs) using SMILE imprint technique
  8. Topical Issue: Diffractive Optics; Guest Editor: Reinhard Voelkel
  9. Editorial
  10. Diffractive optics
  11. Review article
  12. Diamond diffractive optics—recent progress and perspectives
  13. Research articles
  14. Narrowband transmission filters based on resonant waveguide gratings and conformal dielectric-plasmonic coatings
  15. Inverse design of diffractive optical elements using step-transition perturbation approach
  16. Diffractive optics based automotive lighting system
  17. Multifunctional materials for lean processing of waferscale optics
  18. Research article
  19. Stray light analysis and design optimization of geometrical waveguide
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 16.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/aot-2020-0046/html
Scroll to top button