Abstract
Metasurfaces with bound states in the continuum (BICs) have proven to be a powerful platform for drastically enhancing light–matter interactions, improving biosensing, and precisely manipulating near- and far-fields. However, engineering metasurfaces to provide an on-demand spectral and angular position for a BIC remains a prime challenge. A conventional solution involves a fine adjustment of geometrical parameters, requiring multiple time-consuming calculations. In this work, to circumvent such tedious processes, we develop a physics-inspired, inverse design method on all-dielectric metasurfaces for an on-demand spectral and angular position of a BIC. Our suggested method predicts the core–shell particles that constitute the unit cell of the metasurface, while considering practical limitations on geometry and available materials. Our method is based on a smart combination of a semi-analytical solution, for predicting the required dipolar Mie coefficients of the meta-atom, and a machine learning algorithm, for finding a practical design of the meta-atom that provides these Mie coefficients. Although our approach is exemplified in designing a metasurface sustaining a BIC, it can, also, be applied to many more objective functions. With that, we pave the way toward a general framework for the inverse design of metasurfaces in specific and nanophotonic structures in general.
1 Introduction
Bound states in the continuum (BICs) are non-radiating solutions to the wave equation with a spectrum embedded in the continuum of the propagating modes in the surrounding space. BICs are a general wave phenomenon that can exist in a variety of acoustic, hydrodynamic, quantum mechanical, and electromagnetic systems [1–3]. Because of their infinite radiative lifetimes, BICs are actively studied in optics and photonics, opening up enormous opportunities to realize compact planar high-Q metastructures necessary for biosensing, integrated nonlinear nanophotonics, and an enhancement of light–matter interactions [4]. In photonics, the most promising platform supporting BICs are metasurfaces [5]. Metasurfaces offer a vast number of designs with materials compatible with BIC. In particular, metasurfaces with BICs demonstrated their efficiency for lasing [6–10], biosensing [11–14], enhancing nonlinear optical effects [15–18] and polaritons [19–22], leading, recently, to the first experimental demonstration of room-temperature exciton–polariton condensation from a BIC [23].
Optical resonances in periodic metasurfaces radiate only into the open diffraction channels, while BICs remain non-radiating due to the vanishing coupling to all open diffraction channels. For subwavelength metasurfaces, there is only one open diffraction channel and, thus, one coupling coefficient. It can vanish due to symmetry reasons or due to a fine-tuning of the system’s geometrical or material parameters [24]. In the first case, the BICs are called symmetry-protected and usually exist in high symmetry points of the k-space. In the second case, BICs are called accidental or parametric, and they can exist at an arbitrary point in the k-space along the high-symmetry directions [25]. This explains the term “accidental”. The accidental BICs are extremely sensitive to changes in the geometry of the unit cell or the material parameters. Such a high sensitivity makes it challenging and time-consuming to design metasurfaces with a pre-required or fixed spectral and angular position of BIC.
As an expansion to the time-consuming and more classic optimization approach using analytical formulation tools [26, 27], an inverse design approach can be used [28–33]. The term “inverse design”, herein, refers to the process of designing a metasurface with optical properties by initially specifying the desired response rather than the structure of the metasurface itself. Such an inverse design involves dedicated algorithms, e.g., from Bayesian inference, topology optimization, or artificial neural networks. The purpose is always to find the optimal metasurface that provides a predefined optical response [34–37]. Inverse design can offer metasurfaces with a wide range of optical properties, including phase shifts, polarization conversions, and beam steering. It is a powerful tool for designing advanced optical devices and has applications in fields such as imaging, sensing, and telecommunications [38–41]. Despite the power of inverse design methods based on artificial neural networks, the underlying physics of the found optimum often remains vague.
In this work, we develop a physics-inspired inverse design procedure for all-dielectric metasurfaces sustaining an accidental BIC at a predefined frequency and incidence angle. Our framework is based on a smart combination of a semi-analytical approach and a dedicated machine-learning algorithm. Our procedure includes three steps schematically shown in Figure 1. In the first step, the problem is solved within a “toy” model. Here, we consider all-dielectric meta-atoms in dipole approximation and capture their response using a T-matrix. After representing the meta-atoms utilizing the electric/magnetic (dipole) polarizabilities, or, equivalently, the scattering (dipole) Mie coefficients, the metasurface model is set up. The existence condition for an accidental BIC at a predefined spectral position and angle of incidence is derived analytically as a function of the Mie coefficients of the constituting particle through the identification of the system’s eigenmodes. At the end of that first step, we know the polarizabilities of the particle such that the metasurface offers the predefined BIC. In the second step, using a dedicated artificial neural network, we identify the geometrical and material parameters of a core–shell, spherical particle that offers the desired and previously identified polarizabilities so that the metasurface sustains the predefined BICs. The neural network accounts for the practical limitations on the sizes of the spherical particle shells and refractive indices of the materials. In this way, a physically feasible meta-atom is found that provides the desired BIC when placed on an infinite 2D array. In the last step, we numerically verify the design. We also test the robustness of the designed BIC position in k-space if higher-order multipoles contribute besides the dipolar one, namely quadrupoles and octupoles. This entire process is described in the following.
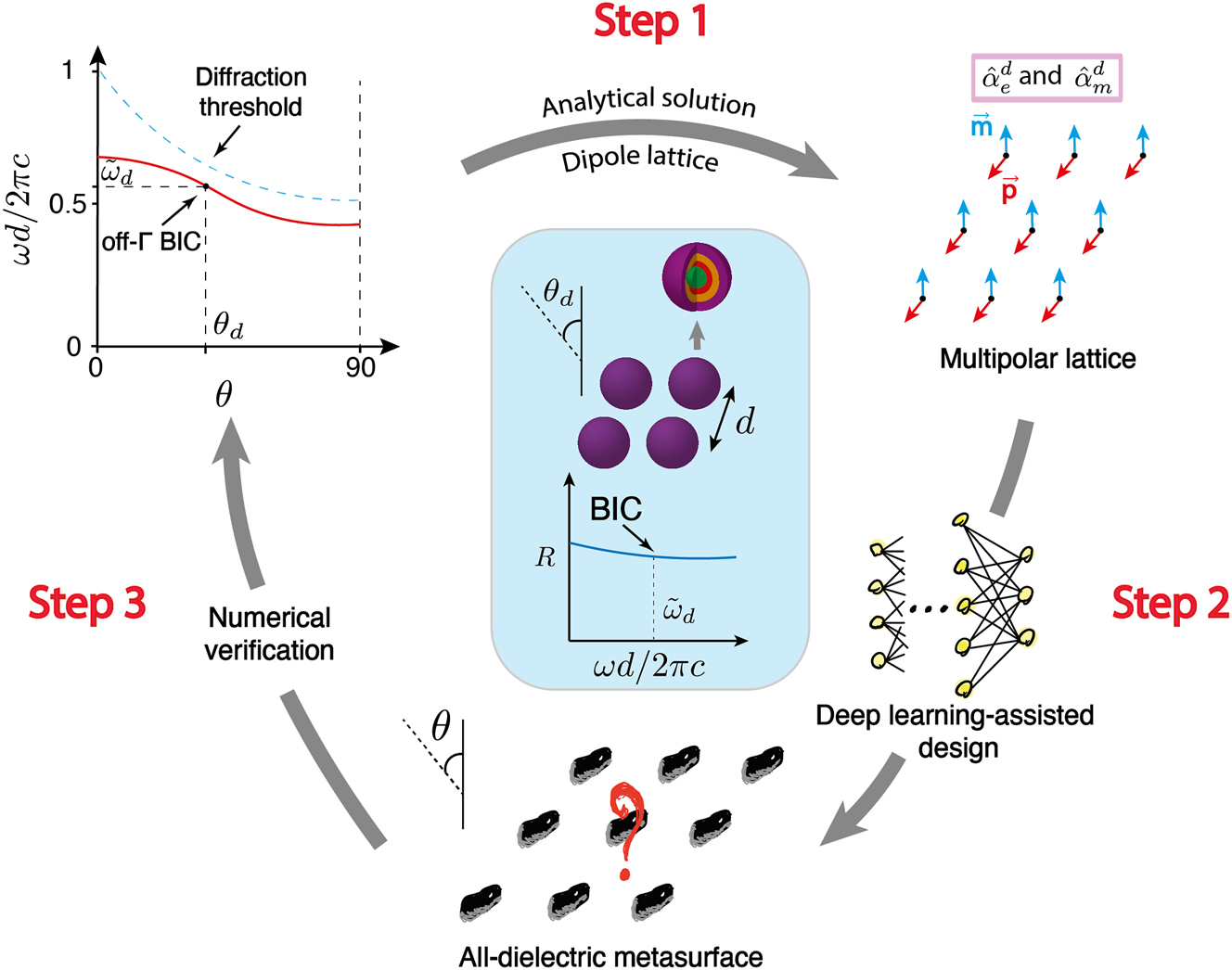
The concept of our proposed framework. Beginning from the top left, an accidental BIC sustained by a metasurface is desired at a specific normalized frequency and incidence angle given by
2 Results
2.1 Step 1: BIC in dipolar metasurface
Let us consider in our “toy” model a metasurface consisting of isotropic and non-absorbing particles described in dipole approximation. The particles are arranged on a square lattice with a subwavelength period, i.e. for any incidence angle, there is only a zeroth diffraction order. The considered unit cell is shown in Figure 2(a). The surrounding medium is a vacuum. The metasurface is illuminated by a time-harmonic linearly polarized plane wave in either TE (or s) or TM (or p) polarization.
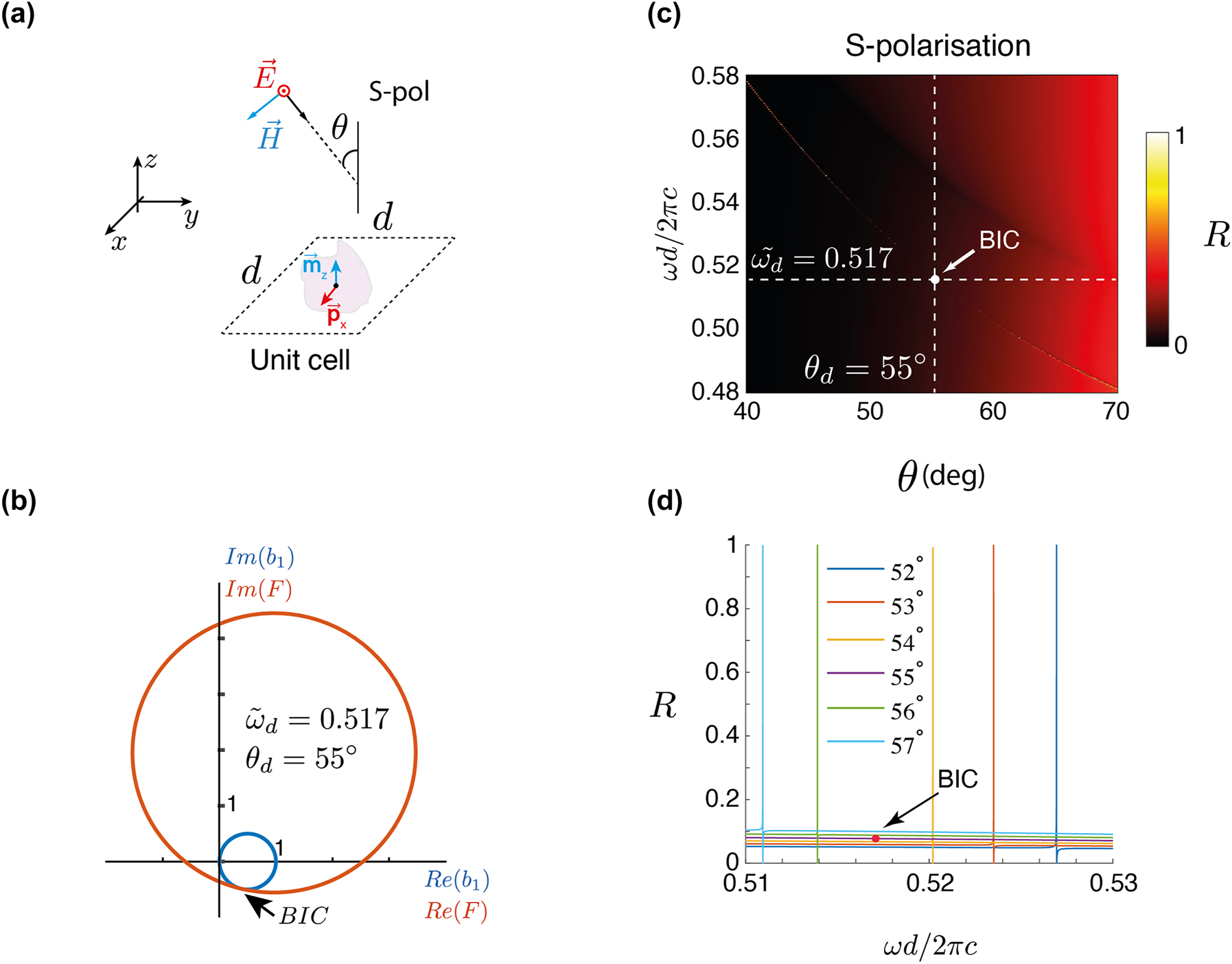
The toy model: (a) a unit cell of a metasurface made from a periodic arrangement of scatterers with electric and magnetic dipole polarizabilities in a square lattice. (b) A graphical representation of how the Mie coefficients are identified that leads to the desired response. The analytical expression for the Mie coefficient that needs to be satisfied to sustain a BIC at a predefined normalized frequency and incidence angle for a given period is plotted separately concerning its left- and right-handed sides. Each side depends only on one Mie coefficient. By parametrizing the Mie coefficients with the Mie angles, both sides of the expression in the complex plane have been plotted. From the point of crossing, the Mie coefficients that provide the desired BIC are identified. (c) The reflection R as a function of dimensionless frequency ωd/2πc and angle of incidence θ for a square lattice with period d = 450 nm. The lattice is decorated with particles that offer the previously identified Mie coefficients. The appearance of the BIC at the predefined frequency and incidence angle can be seen. (d) The reflection R as a function of dimensionless frequency ωd/2πc in close proximity to the off-Γ BIC.
Considering the renormalization of the particle’s polarizability due to the lattice interaction and imposing a condition that expresses the existence of a resonance, i.e., a denominator in the renormalized polarizability has to be zero, allows for the analytical identification of an equation that must be satisfied for the existence of a BIC. For a given lattice, frequency, polarization, and incidence angle, this equation expresses the necessary relation between the dipolar magnetic b 1 and electric a 1 Mie coefficients to encounter a BIC. A derivation is given in the METHODS section, but the final expressions read
where (1a) and (1b) refer to a TE/s-polarized or a TM/p-polarized incidence, respectively. The equations above are analogous to the equations found in [26, 27], but, now, we utilize the versatile Mie coefficients of the particles under study. The C
i
(i = 1, …, 5) are the elements of the lattice interaction coefficients matrix
The elements of
Hence, for the specific scenario considered, Eq. (1) provides the exact condition to encounter a BIC for s- or p-polarized incidences, respectively. To further simplify the design, the Mie coefficients are parametrized using what is called the Mie angles [45]. Note that we consider a system that possesses a time-reversal symmetry
The process of identifying the BIC graphically can be demonstrated by assuming an s-polarized incidence, as depicted in Figure 2(a). After expressing the right hand side of Eq. (1a) as F(a
1). All possible Mie angles in the range of [−π/2, π/2], which parametrize the magnetic and electric dipolar coefficients, are swept through. The left-hand side (only the b
1 coefficient) and the right-hand side of Eq. (1a) are shown in the complex plane in Figure 2(b). The left-hand side, i.e. only the b
1 coefficient, and the right-hand side of (1a) are shown in the complex plane in Figure 2(b). As required by lossless scatterers, all possible Mie coefficients, including the ones of b
1, lie on a circle in the complex plane with a center at the (0.5, 0) point and a radius of 1. It can be identified that the BIC is located where Re{b
1} = Re{F(a
1)} and Im{b
1} = Im{F(a
1)} for a specific wavelength, incidence angle, and lattice constant. Once the b
1 coefficient is known, the a
1 value can be explicitly calculated. If there were losses in the system, then in the expressions a
1 and b
1 (see METHODS) additional terms
As an example, we find a combination of Mie angles (θ
E1, θ
M1), or, in other words,
For the selected a
1 and b
1 dipole moments, a narrow resonant band is formed. This resonant band disappears precisely at the target parameters
2.2 Step 2: Deep learning-assisted engineering of spherical particles for BIC realization
In the previous subsection, a method was presented that provides the T-matrix for an isotropic particle to achieve an accidental BIC for a specific normalized frequency and incidence angle. Although this approach was successful, if one wants to provide a practical design of a metasurface that exhibits BICs, the calculated (a 1, b 1) values must be linked to a realistic scatterer. In this work, we employ a deep-learning scheme to assign the calculated Mie coefficients to a spherical core–shell nano-particle of realistic dimensions and made from existing materials for an operation at optical wavelengths.
To find a suitable scatterer that provides desired Mie angles, a gradient-based deep learning-assisted approach is performed, schematically explained in Figure 3(a). More details on the Artificial Neural Networks (ANNs) can be found in the article [46]. Initially, we train a set of ANNs to predict the Mie angles of coated dielectric spheres made from one to five shells and at 200 distinct wavelengths, between 800 nm and 1200 nm. A part of the ANNs is also a classifier that predicts the most probable number of shells to provide the requested Mie angles. Actually, the exemplarily shown core–shell particle in Figure 3(a) has only three shells. Our trained ANN simply predicted at the end a core–shell particle with three shells only as the most appropriate, which is illustrated here. The materials of the layers are restricted to discrete refractive indices classes ranging from 1.4–3.5, values that are realistic at optical wavelengths for specific materials (see Table 1). Note, that our goal, here, is to design a metasurface exhibiting a BIC at a specific frequency without examining what happens at neighboring frequency regions. Therefore, there is no need to include material dispersion and we utilize fixed real values of refractive indexes. Nevertheless, these values used in this work correspond to possible values of typical materials used in photonics, like GaAs, SiO2 etc. The radius of the core is limited to 20 nm–50 nm. The dimension of each shell is restricted to 20 nm–40 nm. The ANNs are used as a fully differentiable surrogate model in a gradient-based optimization algorithm, namely the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm including boundary constraints, or L-BFGS-B [47].
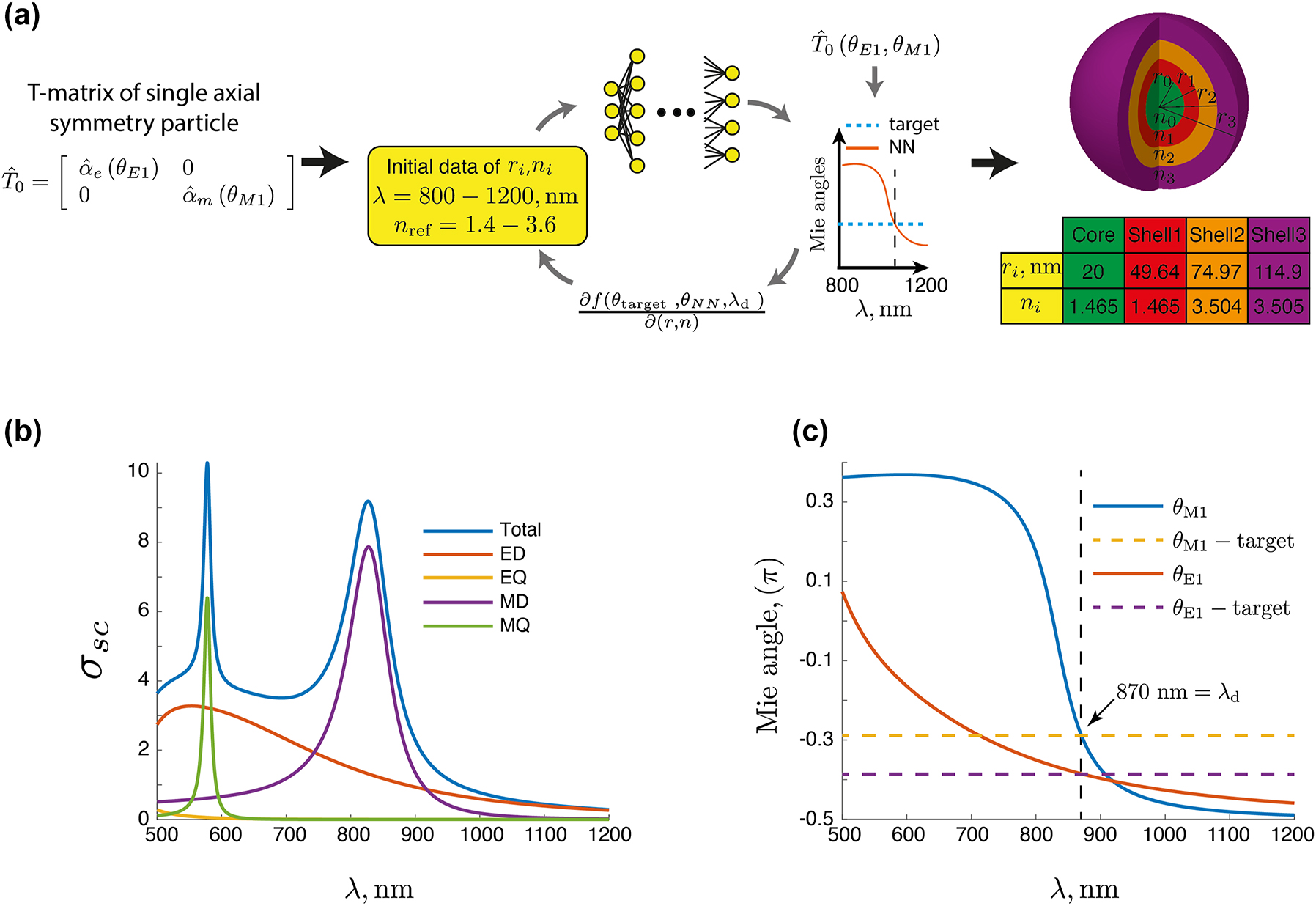
Inverse design: (a) scheme to find the geometrical and material parameters of a meta-atom (core–shell particle) with a target optical response. In the central part, there is a fully differentiable artificial neural network that can predict the Mie angles for a given core–shell particle. The network was trained within a given spectral region using discrete material classes and constrained geometrical dimensions for the core and the shell that make the design feasible for realization. A gradient descent is then used to identify the parameters characterizing the core–shell particle such that predefined dipolar Mie angles are provided at a design wavelength. At the very end, a second optimization is performed where the refractive indices of the considered materials are fine-tuned to reach an absolute precision. The table shows the design parameters for the example considered in the text. (b) Contribution of each multipole moment (up to quadrupolar order) to the scattering cross-section of the core–shell particle σ sc as a function of the wavelength λ for the final design. (c) Mie angles as a function of wavelength: the dotted line refers to the Mie angles of the optimized toy model, and the solid line refers to the Mie angles of the final design. The intersection of the dotted and solid lines in the λ d = 870 nm.
Diferent materials, associated classes and refractive indices.
| Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Refractive index | 1.4649 | 1.7196 | 1.9447 | 2.0745 | 2.4317 | 3.0 | 3.5 |
| Material | SiO2 | MgO | ZnO | ZrO2 | TiO2 | AlAs | GaAs |
The classification of modes by irreducible representations and the multipole composition of the eigenmode for C 2v symmetry group in direction ΓX in the dipole approximation for different bases.
| Irreducible representation | A 1 | A 2 | B 1 | B 2 |
| Cartesian basis | p y | m y | p z , m x | m z , p x |
| Spherical basis |
|
|
|
|
The actual solution to the inverse problem starts from random particle parameters as network input, for which we predict the spectral dependencies of the Mie angles with the trained ANN. From that output, we compute an objective function f, the Mean Absolute Error (MAE) of the ANN output and the target Mie angles at the desired wavelength, λ d, as
Subsequently, the gradients of f with respect to the particle parameters
Unfortunately, the discretization of the refractive index values naturally leads to a restriction of the possible design space. Thus, the design Mie angles and those of the optimized stricture do not match in a perfect sense after that procedure, i.e., we found an agreement only up to two digits after the comma. However, the BIC is very sensitive to slight changes in the Mie angles. Hence, we perform a second optimization using the actual analytical computation of the Mie angles and varied the refractive index of the involved materials slightly for fine-tuning. This approach alone is significantly slower than ANN-assisted design, especially for several initial trials. Fortunately, in this work, the designed particle can be fine-tuned to achieve the required accuracy (eight digits after the comma) and grant the appearance of the BIC, given the results of the first ANN-assisted optimization approach as a single starting point. The fine-tuning of the refractive index of the shells could be carefully done by suitable doping of the respective material, which should be within reach with existing technology [48–50]. In summary, this procedure provides a general scheme implemented, herein, by a physical core–shell spherical particle [51–53] that can be used to form a metasurface that offers the BIC at the predefined frequency and incidence angle. Furthermore, the Mie angle approach, as presented, herein, can be expanded with the proper modifications for the case of core–shell dielectric disks [54].
2.3 Step 3: Application of the design methodology
The procedure presented above will now be applied to propose a metasurface with a square unit cell decorated by core–shell dielectric spheres that realize a BIC for a predefined lattice, frequency, and incidence angle. For this purpose, let us begin with the theoretical setup depicted in Figure 2 with the resulting Mie coefficients from Eq. (1), a
1 = −0.4046 + 0.4908i and b
1 = −0.5508 + 0.4974i for
Finally, the designed core–shell spherical particle is placed on a 2D square array (Figure 4(a)) and the optical response from the metasurface is analyzed with a dedicated T-matrix-based full-wave solver (see Supplementary Material) [42, 43]. In Figure 4(b)–(d), the reflection depending on the normalized frequency, ωd/2πc, and the incidence angle, θ, are shown when only dipole (first order) and up to octupole (third order) multipoles are considered in the response calculation, respectively [43]. Please note that the dipolar approximation would correspond to the assumption in the design process. However, the actual particle does not, of course, have a purely dipolar response, but also small, yet non-negligible, higher-order multipolar coefficients. These higher-order multipolar contributions usually need to be considered when the response from an actual metasurface is predicted.
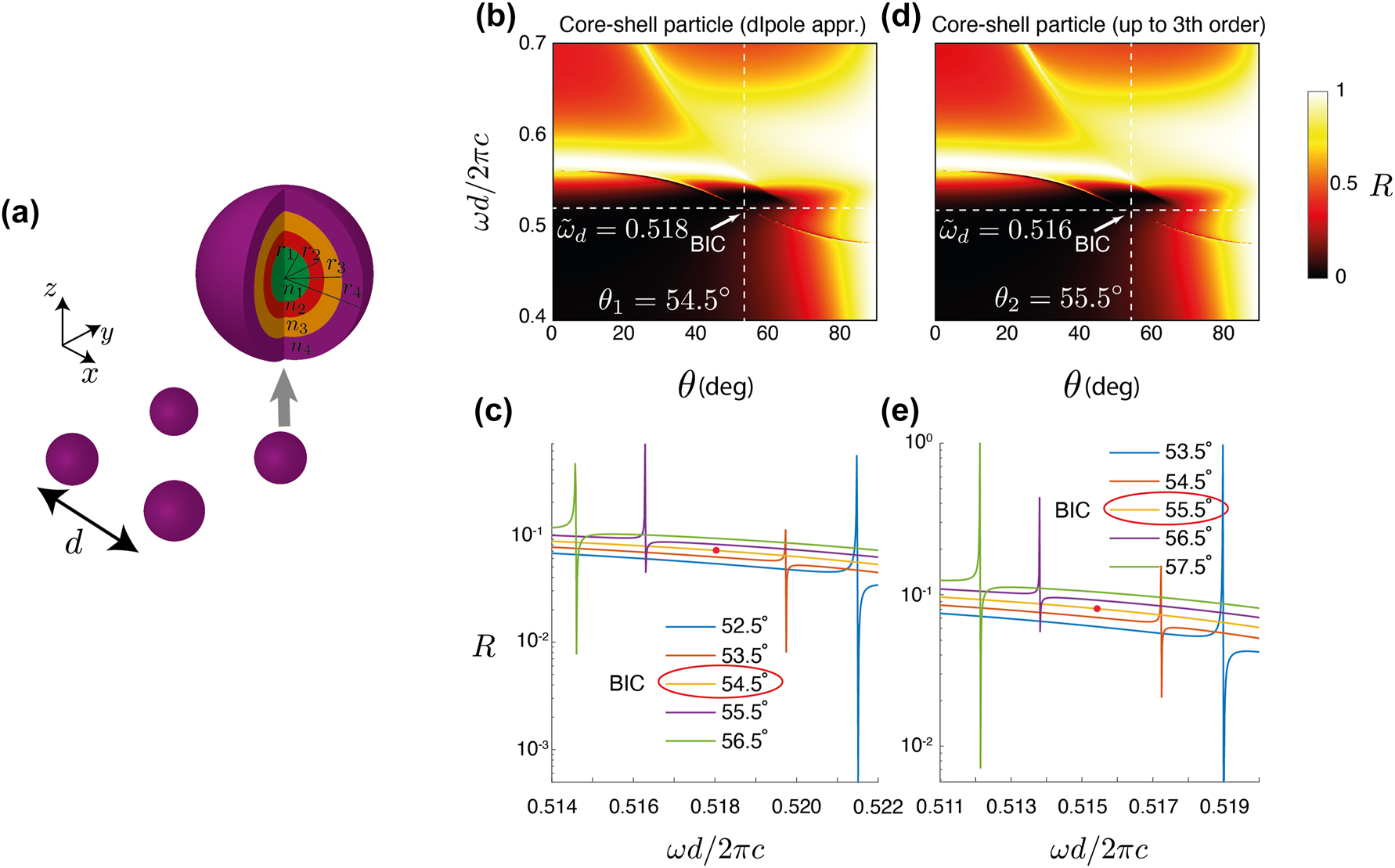
Designed metasurface: (a) The square lattice of core–shell particles. (b, d) Reflection coefficients of the actual metasurface as calculated with a full-wave Maxwell solver that exploits the T-matrix formalism. The reflection is shown as a function of the frequency and the incidence angle for a lattice dimension d = 450 nm. (b) Calculation in dipole approximation. (d) Calculation in octupole approximation. (c, e) The reflection coefficient versus the normalized frequency in proximity to the off-Γ BIC for a lattice dimension d and using the dipole or the octupole approximation, respectively.
Specifically, when only the dipolar response of the particle is considered (Figure 4(b)), a BIC is observed at the
3 Discussion
The sensitivity of the BIC against deviations in the Mie angles parameterizing the optical response of the scatterers will now be discussed. This step is important for certifying the stability of the proposed algorithm. In most of the previous – mainly theoretical – work on metasurface inverse design, the robustness of the proposed design to deviations of material or geometrical parameters is not guaranteed as most of the ANNs work as a black box. In this paper, we suggested a more transparent scheme, where the problem is initially solved semi-analytically via the dipole approximation and, afterward, an artificial particle with the required polarizabilities is designed with the ANN.
Figure 5 demonstrates how the position of the BIC for different angles θ and frequency
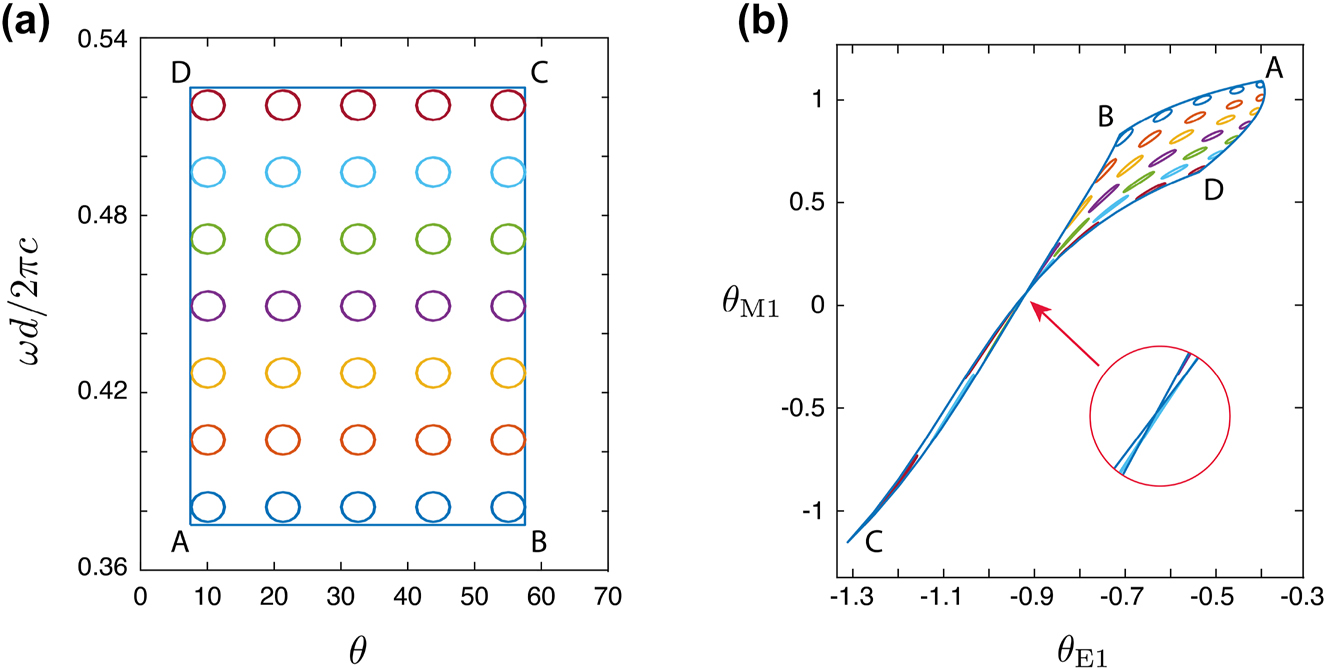
Robustness of the BICs. (a) The positions of the BICs for different angles θ (deg.) and normalized frequency
In Figure 5(b), the intersection of two lines of the bounding box occurs as a further interesting phenomenon. It means that for these Mie angles at the point of intersection, the metasurface sustains two distinct BICs for different pairs of frequency and incidence angles. This case is discussed in more detail in the Supplementary Material.
Although, in this work, we have utilized the dipole approximation to design the meta-atoms, i.e., only up to the first multipolar order, the core idea behind the presented methodology is general and can be applied to higher-order multipoles or more complex scatterers. Provided that the general eigenvalue problem (see (6) in METHODS) can be solved under some approximations and the solutions corresponding to the BIC resonances can be recognized, the Mie angles that lead to the desired BIC can be expressed. For example, in [43], for a square metasurface illuminated by a normally-incident plane wave and consisting of an isotropic particle with only a magnetic dipole and an electric quadrupole excited, a BIC point was identified, or the required (b 1, a 2) values. Then, a suitable inverse design technique can be used to identify an actual meta-atom that offers these desired Mie angles. In the work at hand, the acquired Mie coefficients were assigned to a core–shell particle via the deep learning algorithm. These considerations can be extended to more complex, e.g., anisotropic or bi-anisotropic scatterers and can accommodate an increasing number of multipolar orders. Approximate models for the T matrix could be utilized for that purpose [56, 57] or more advanced neural networks can be trained [58].
Moreover, the proposed scheme could be expanded within dipole approximation, in order to include material dispersion. If the dipole Mie coefficients are modeled for a Lorentzian dispersion [45], one can employ an optimization technique, to obtain a set of a Lorentzian resonant frequency and radiative losses (see Section 3 in Supplementary Material) that will provide a BIC via a metasurface for a given angle of incidence and operational frequency and, finally, try to associate the results with practical dispersive materials.
Furthermore, although “true” BICs with an infinite Q cannot exist in structures that not extend to infinity for at least one dimension [1], an expansion of the proposed procedure can be applied for finite arrays or non-periodic metasurfaces to design quasi-BIC resonances for a desired set (θ inc, ωd/λ), with a very high, yet finite Q [59]. Specifically, in finite structures, where the unit cells are not equivalent to each other, one could model the problem within dipole approximation, afterward, find the quasi-BIC conditions via the eigenvalues of the system and, finally, acquire the individual design of each consisting particle with the use of an optimization scheme.
Lastly, the same procedure as above could also be applied to metasurfaces with other functionalities, such as lenses or arbitrary holograms, where different types or shapes of scatterers form the final 2D array. Initially one has to acquire the scattering properties of each unit cell via Mie angles. Again, the unit-cells of the metasurface are different to each other, thus, solving the more complicated eigenvalue problem via the dipole approximation will, now, provide the quasi-BIC conditions.
In conclusion, the generalized design scheme presented, herein, for infinite, periodic structures composed of spherical, isotropic particles can be extrapolated to finite 2D arrays or 2D arrays with non-identical particles. The only difference would be the need to solve multiple-particle problems and parametrize each unit-cell with a required number of Mie angles. Nevertheless, the main idea presented in this work remains the same.
4 Conclusions
In summary, the physics-inspired inverse design procedure for all-dielectric metasurfaces sustaining an accidental BIC at a certain frequency and angle of incidence was developed in this work. The methodology utilized a smart combination of a semi-analytical approach and a dedicated machine-learning algorithm. Firstly, the problem was solved within a theoretical model considering all-dielectric meta-atoms using the dipole approximation and the T-matrix technique. The existence condition for an accidental BIC was derived in terms of Mie angles. Secondly, using a dedicated artificial neural network, the geometrical and material parameters of a core–shell, spherical particle that offered the desired optical response provided by the BIC condition were identified. In this way, a physically feasible meta-atom was found that provided the desired BIC when placed on an infinite 2D array. Finally, the design was numerically verified, and the robustness of the designed position BIC in k-space was tested by considering higher-order multipoles.
5 Methods
5.1 The T-matrix formulation for 2D arrays and BIC identification
Considering a metasurface composed of a square array of isotropic and non-absorbing particles, as shown in Figure 2(a). The surrounding medium is a vacuum.
If an arbitrary scatterer is placed in an infinite homogeneous background and the vector spherical harmonics (VSH) basis is employed to expand the fields, the scattering response to an incident electromagnetic wave can be described using the T matrix, or
Vectors q
{e,m} contain the incident wave electric or magnetic coefficients, respectively, while a
{e,m} contain the scattering electric or magnetic coefficients, respectively [60]. For each multipolar expansion order
For an isotropic particle, it is convenient to parameterize the coefficients with Mie angles [45]. In particular, for lossless particles and when only dipoles are considered, i.e., j = 1, all possible Mie coefficients can be expressed using two parameters θ E1 and θ M1, or
As a result, the optical response of the corresponding scatterer can be parameterized with the two Mie angles above, while still having a clear physical picture. This formulation is very important because the control parameters, namely θ E1 and θ M1, are placed between an upper and lower boundary, which will aid optimization methods and subsequent metasurface design. Furthermore, similar expressions involving Mie angles, like the ones of (4) above, exist for higher-order multipoles, the addition of absorption or Lorentzian dispersion for Mie coefficients (see Supplementary Material).
Let us now assume an infinite square array composed of arbitrary, identical, absorption-less, spherical particles placed in a homogeneous material, as depicted in Figure 1. The response of the metasurface can be calculated via the T matrix of the particle by employing microscopic models [42, 43, 63, 64]. An important aspect to be noted herein is that the T matrix of the particle within the metasurface is re-normalized due to the particle interaction. Thus, in 2D array models, the isolated particle’s T matrix,
where
It should be stressed that, although the scattering response of a single particle and of the subsequent 2D array is provided here using the spherical coordinates and the T matrix approach, the analysis that will follow is valid and interchangeable with the use of multipoles in Cartesian coordinates and the polarizability matrix. In particular, one can obtain the T matrix of a particle from the polarizability matrix, and vice versa using the appropriate transformation matrices for each multipolar order [43, 66] (Table 2). Additionally, modifications of the same matrices can transform multipoles of the same type and order from a spherical to a Cartesian basis and vice versa, as presented in the Supplementary Materials for multipoles up to the j = 3 order.
After defining the multipolar description of the electromagnetic response of 2D arrays composed of isotropic particles, next, we will present the procedure for identifying the presence of BICs after setting certain goals. First, let us theoretically acquire the BIC position using the multipolar expansion technique [43, 67–69]. If we again assume a square array composed of identical and isotropic particles, its response to an incident field can be described by substituting (3) and (5) into the equations that describe the response of a 2D array [42, 43] (see Supplementary Material), and, thus, a linear system of equations is formed. Solving the eigenvalue problem leads to the modes of the array, including, in this case, the trapped ones that do not couple with radiation channels, i.e., the BICs. Therefore, if we invert the square matrix of the system to the left side of (3) and set the excitation to zero, or q {e,m} = 0, the resulting homogeneous system will have a non-trivial solution if the determinant of the matrix is zero [26, 27, 43]. In particular, after some algebra, the BIC condition is reduced to
The symmetry of the resonators is tightly related to their mode structure and multipole content, which determine the linear and non-linear response of the resonator. Using group theory, it is possible to classify the eigenmodes into irreducible representations and understand their multipole content [70–72]. Our model is characterized only by the dipole response. Table 1 shows how the dipole moments correspond to different types of eigenmodes for a square array of particles outside the off-Γ point in a spherical basis. The system is characterized by the C
2v
symmetry group in direction ΓX. There are only 4 types of modes: A
1, A
2, B
1, and B
2. Destructive interference of the eigenmodes of one type is necessary for BICs formed by the Friedrich-Wintgen mechanism. It can be concluded that in this model, parametric BIC exists only in modes of types B
1 and B
2. The expression (6) is general in nature and can be used for any type of lattice or particle in a homogenous medium [43]. Due to its complexity, (6) can only be solved numerically in its general form, i.e., for higher-order multipoles or more diverse lattices. Nevertheless, for specific reduced cases, versatile analytic solutions can be found, as demonstrated in [43] for the case of the coupled electric dipole – magnetic quadrupole on a square lattice and a normal, TM wave incidence. In this work, we consider a square lattice decorated by isotropic and lossless particles, whose response is expanded only up to dipolar order, or j = 1. Then, because the elements of the lattice interaction matrix,
Funding source: Helmholtz-Gemeinschaft
Funding source: Karlsruhe School of Optics and Photonics
Funding source: Deutsche Forschungsgemeinschaft
Award Identifier / Grant number: EXC-2082/1-390761711
Funding source: Carl-Zeiss-Stiftung
Funding source: Karlsruhe Institute of Technology
-
Research funding: D.B. and C.R. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy via the Excellence Cluster 3D Matter Made to Order (EXC-2082/1-390761711) and by the Carl Zeiss Foundation. C.R. also acknowledges support by the Helmholtz Association via the Helmholtz program “Materials Systems Engineering” (MSE), and the KIT through the “Virtual Materials Design” (VIRTMAT). L.K. acknowledges support by the NHR@KIT program and the Karlsruhe School of Optics and Photonics. A.B. acknowledges BASIS Foundation and the Academic Leadership Program “Priority 2030”.
-
Author contributions: S. G. and T. K. contributed equally to this work and are the main authors; they created the analytical model to identify the BIC, performed the multipolar simulations and proposed the realistic metasurfaces to accomodate the predicted BIC via inverse design. L. K. designed the artificial neural network utilised for inverse design. D. B. assisted the calculation of the lattice coupling matrix and the metasurface multipolar response. T. W., C. R. and A. B. supervised the project. All authors discussed the results, contributed to writing parts of the manuscript and contributed to the final manuscript.
-
Conflict of interest: The authors declare no conflicts of interest.
-
Data availability: The data that support the findings of this study are available from the authors upon reasonable request.
References
[1] C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljačić, “Bound states in the continuum,” Nat. Rev. Mater., vol. 1, pp. 1–13, 2016. https://doi.org/10.1038/natrevmats.2016.48.Search in Google Scholar
[2] K. Koshelev, G. Favraud, A. Bogdanov, Y. Kivshar, and A. Fratalocchi, “Nonradiating photonics with resonant dielectric nanostructures,” Nanophotonics, vol. 8, no. 5, pp. 725–745, 2019. https://doi.org/10.1515/nanoph-2019-0024.Search in Google Scholar
[3] K. L. Koshelev, Z. F. Sadrieva, A. A. Shcherbakov, et al.., “Bound states in the continuum in photonic structures,” Phys.-Usp., vol. 93, pp. 528–553, 2023.10.3367/UFNr.2021.12.039120Search in Google Scholar
[4] S. I. Azzam and A. V. Kildishev, “Photonic bound states in the continuum: from basics to applications,” Adv. Opt. Mater., vol. 9, p. 2001469, 2021. https://doi.org/10.1002/adom.202001469.Search in Google Scholar
[5] C.-W. Qiu, T. Zhang, G. Hu, and Y. Kivshar, “Quo vadis, metasurfaces?” Nano Lett., vol. 21, pp. 5461–5474, 2021. https://doi.org/10.1021/acs.nanolett.1c00828.Search in Google Scholar PubMed
[6] A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman, and B. Kanté, “Lasing action from photonic bound states in continuum,” Nature, vol. 541, pp. 196–199, 2017. https://doi.org/10.1038/nature20799.Search in Google Scholar PubMed
[7] S. T. Ha, Y. H. Fu, N. K. Emani, et al.., “Directional lasing in resonant semiconductor nanoantenna arrays,” Nat. Nanotechnol., vol. 13, pp. 1042–1047, 2018. https://doi.org/10.1038/s41565-018-0245-5.Search in Google Scholar PubMed
[8] C. Huang, C. Zhang, S. Xiao, et al.., “Ultrafast control of vortex microlasers,” Science, vol. 367, pp. 1018–1021, 2020. https://doi.org/10.1126/science.aba4597.Search in Google Scholar PubMed
[9] M.-S. Hwang, H.-C. Lee, K.-H. Kim, et al.., “Ultralow-threshold laser using super-bound states in the continuum,” Nat. Commun., vol. 12, pp. 1–9, 2021. https://doi.org/10.1038/s41467-021-24502-0.Search in Google Scholar PubMed PubMed Central
[10] S. I. Azzam, K. Chaudhuri, A. Lagutchev, et al.., “Single and multi-mode directional lasing from arrays of dielectric nanoresonators,” Laser Photonics Rev., vol. 15, p. 2000411, 2021. https://doi.org/10.1002/lpor.202000411.Search in Google Scholar
[11] A. Ndao, L. Hsu, W. Cai, et al.., “Differentiating and quantifying exosome secretion from a single cell using quasi-bound states in the continuum,” Nanophotonics, vol. 9, pp. 1081–1086, 2020. https://doi.org/10.1515/nanoph-2020-0008.Search in Google Scholar
[12] A. Tittl, A. Leitis, M. Liu, et al.., “Imaging-based molecular barcoding with pixelated dielectric metasurfaces,” Science, vol. 360, pp. 1105–1109, 2018. https://doi.org/10.1126/science.aas9768.Search in Google Scholar PubMed
[13] A. Leitis, A. Tittl, M. Liu, et al.., “Angle-multiplexed all-dielectric metasurfaces for broadband molecular fingerprint retrieval,” Sci. Adv., vol. 5, 2019, Art. no. eaaw2871. https://doi.org/10.1126/sciadv.aaw2871.Search in Google Scholar PubMed PubMed Central
[14] S. Romano, G. Zito, S. Managò, et al.., “Surface-enhanced Raman and fluorescence spectroscopy with an all-dielectric metasurface,” J. Phys. Chem. C, vol. 122, pp. 19738–19745, 2018. https://doi.org/10.1021/acs.jpcc.8b03190.Search in Google Scholar
[15] N. Bernhardt, K. Koshelev, S. J. U. White, et al.., “Quasi-BIC resonant enhancement of second-harmonic generation in WS2 monolayers,” Nano Lett., vol. 20, pp. 5309–5314, 2020. https://doi.org/10.1021/acs.nanolett.0c01603.Search in Google Scholar PubMed
[16] G. Zograf, K. Koshelev, A. Zalogina, et al.., “High-harmonic generation from resonant dielectric metasurfaces empowered by bound states in the continuum,” ACS Photonics, vol. 9, pp. 567–574, 2022. https://doi.org/10.1021/acsphotonics.1c01511.Search in Google Scholar
[17] I. S. Sinev, K. Koshelev, Z. Liu, et al.., “Observation of ultrafast self-action effects in quasi-BIC resonant metasurfaces,” Nano Lett., vol. 21, pp. 8848–8855, 2021. https://doi.org/10.1021/acs.nanolett.1c03257.Search in Google Scholar PubMed
[18] Z. Liu, J. Wang, B. Chen, Y. Wei, and W. Liu, “Giant enhancement of continuous wave second harmonic generation from few-layer GaSe coupled to high-Q quasi bound states in the continuum,” Nano Lett., vol. 21, pp. 7405–7410, 2021. https://doi.org/10.1021/acs.nanolett.1c01975.Search in Google Scholar PubMed
[19] V. Kravtsov, E. Khestanova, F. A. Benimetskiy, et al.., “Nonlinear polaritons in a monolayer semiconductor coupled to optical bound states in the continuum,” Light: Sci. Appl., vol. 9, pp. 1–8, 2020. https://doi.org/10.1038/s41377-020-0286-z.Search in Google Scholar PubMed PubMed Central
[20] S. Cao, H. Dong, J. He, E. Forsberg, and Y. Jin, “Normal-incidence-excited strong coupling between excitons and symmetry-protected quasi-bound states in the continuum in silicon nitride–WS2 heterostructures at room temperature,” J. Phys. Chem. Lett., vol. 11, pp. 4631–4638, 2020. https://doi.org/10.1021/acs.jpclett.0c01080.Search in Google Scholar PubMed
[21] E. Maggiolini, L. Polimeno, F. Todisco, et al.., “Strongly enhanced light-matter coupling of a monolayer Ws2 from a bound state in the continuum,” 2022, arXiv Preprint arXiv:2209.00129.10.1038/s41563-023-01562-9Search in Google Scholar PubMed
[22] T. Weber, L. Kühner, L. Sortino, et al.., “Strong light-matter interaction with self-hybridized bound states in the continuum in monolithic van der waals metasurfaces,” 2022, arXiv preprint arXiv:2209.01944.10.1038/s41563-023-01580-7Search in Google Scholar PubMed PubMed Central
[23] A. M. Berghuis, G. W. Castellanos, S. Murai, et al.., “Room temperature exciton–polariton condensation in silicon metasurfaces emerging from bound states in the continuum,” Nano Lett., vol. 23, no. 12, pp. 5603–5609, 2023. https://doi.org/10.1021/acs.nanolett.3c01102.Search in Google Scholar PubMed PubMed Central
[24] B. Zhen, C. W. Hsu, L. Lu, A. D. Stone, and M. Soljačić, “Topological nature of optical bound states in the continuum,” Phys. Rev. Lett., vol. 113, p. 257401, 2014. https://doi.org/10.1103/physrevlett.113.257401.Search in Google Scholar PubMed
[25] C. W. Hsu, B. Zhen, J. Lee, et al.., “Observation of trapped light within the radiation continuum,” Nature, vol. 499, pp. 188–191, 2013. https://doi.org/10.1038/nature12289.Search in Google Scholar PubMed
[26] A. B. Evlyukhin, M. A. Poleva, A. V. Prokhorov, K. V. Baryshnikova, A. E. Miroshnichenko, and B. N. Chichkov, “Polarization switching between electric and magnetic quasi-trapped modes in bianisotropic all-dielectric metasurfaces,” Laser Photonics Rev., vol. 15, no. 12, p. 2100206, 2021. https://doi.org/10.1002/lpor.202100206.Search in Google Scholar
[27] D. R. Abujetas, J. Olmos-Trigo, and J. A. Sánchez-Gil, “Tailoring accidental double bound states in the continuum in all-dielectric metasurfaces,” Adv. Opt. Mater., vol. 10, no. 15, p. 2200301, 2022. https://doi.org/10.1002/adom.202200301.Search in Google Scholar
[28] P. R. Wiecha, A. Arbouet, A. Arbouet, and O. L. Muskens, “Deep learning in nano-photonics: inverse design and beyond,” Photonics Res., vol. 9, pp. B182–B200, 2021. https://doi.org/10.1364/prj.415960.Search in Google Scholar
[29] S. Molesky, Z. Lin, A. Y. Piggott, W. Jin, J. Vucković, and A. W. Rodriguez, “Inverse design in nanophotonics,” Nat. Photonics, vol. 12, pp. 659–670, 2018. https://doi.org/10.1038/s41566-018-0246-9.Search in Google Scholar
[30] M. Elizarov, Y. S. Kivshar, and A. Fratalocchi, “Inverse-designed metaphotonics for hypersensitive detection,” ACS Nanosci. Au, vol. 2, no. 5, pp. 422–432, 2022. https://doi.org/10.1021/acsnanoscienceau.2c00009.Search in Google Scholar PubMed PubMed Central
[31] P. R. Wiecha, A. Y. Petrov, P. Genevet, and A. Bogdanov, “Inverse design of nanophotonics devices and materials,” Photonics Nanostructures - Fundam. Appl., vol. 52, p. 101084, 2022.10.1016/j.photonics.2022.101084Search in Google Scholar
[32] W. Huang, S.-T. Cao, X. Qu, W. Zhang, S. Yin, and J. Han, “Inverse design of metamaterial bound states in the continuum device via coupled mode theory,” IEEE Trans. Microwave Theory Techn., pp. 1–9, 2023.10.1109/TMTT.2023.3305155Search in Google Scholar
[33] M. S. Molokeev, A. S. Kostyukov, A. E. Ershov, D. N. Maksimov, V. S. Gerasimov, and S. P. Polyutov, “Infrared bound states in the continuum: random forest method,” Opt. Lett., vol. 48, no. 17, p. 4460, 2023.10.1364/OL.494629Search in Google Scholar PubMed
[34] J. Jiang, M. Chen, and J. A. Fan, “Deep neural networks for the evaluation and design of photonic devices,” Nat. Rev. Mater., vol. 6, pp. 679–700, 2021. https://doi.org/10.1038/s41578-020-00260-1.Search in Google Scholar
[35] W. Ma, Z. Liu, Z. A. Kudyshev, A. Boltasseva, W. Cai, and Y. Liu, “Deep learning for the design of photonic structures,” Nat. Photonics, vol. 15, pp. 77–90, 2021. https://doi.org/10.1038/s41566-020-0685-y.Search in Google Scholar
[36] S. Krasikov, A. Tranter, A. Bogdanov, and Y. Kivshar, “Intelligent metaphotonics empowered by machine learning,” OEA, vol. 5, pp. 210147–1–210147–24, 2022. https://doi.org/10.29026/oea.2022.210147.Search in Google Scholar
[37] A. Estrada-Real, A. Khaireh-Walieh, B. Urbaszek, and P. R. Wiecha, “Inverse design with flexible design targets via deep learning: tailoring of electric and magnetic multipole scattering from nano-spheres,” Photon. Nanostruct: Fundam. Appl., vol. 52, p. 101066, 2022. https://doi.org/10.1016/j.photonics.2022.101066.Search in Google Scholar
[38] T. Zahavy, A. Dikopoltsev, D. Moss, et al.., “Deep learning reconstruction of ultrashort pulses,” Optica, vol. 5, pp. 666–673, 2018. https://doi.org/10.1364/optica.5.000666.Search in Google Scholar
[39] H. Kabir, Y. Wang, M. Yu, and Qi-Jun Zhang, “Neural network inverse modeling and applications to microwave filter design,” IEEE Trans. Microwave Theory Tech., vol. 56, pp. 867–879, 2008. https://doi.org/10.1109/tmtt.2008.919078.Search in Google Scholar
[40] T. Zhang, J. Wang, Q. Liu, et al.., “Efficient spectrum prediction and inverse design for plasmonic waveguide systems based on artificial neural networks,” Photonics Res., vol. 7, pp. 368–380, 2019. https://doi.org/10.1364/prj.7.000368.Search in Google Scholar
[41] Y. Rivenson, Z. Göröcs, H. Günaydin, Y. Zhang, H. Wang, and A. Ozcan, “Deep learning microscopy,” Optica, vol. 4, pp. 1437–1443, 2017. https://doi.org/10.1364/optica.4.001437.Search in Google Scholar
[42] D. Beutel, A. Groner, C. Rockstuhl, and I. Fernandez-Corbaton, “Efficient simulation of biperiodic, layered structures based on the t-matrix method,” J. Opt. Soc. Am. B, vol. 38, no. 6, pp. 1782–1791, 2021. https://doi.org/10.1364/josab.419645.Search in Google Scholar
[43] A. Rahimzadegan, T. D. Karamanos, R. Alaee, et al.., “A comprehensive multipolar theory for periodic metasurfaces,” Adv. Opt. Mater., vol. 10, no. 10, p. 2102059, 2022. https://doi.org/10.1002/adom.202102059.Search in Google Scholar
[44] D. Beutel, I. Fernandez-Corbaton, and C. Rockstuhl, “Unified lattice sums accommodating multiple sublattices for solutions of the helmholtz equation in two and three dimensions,” Phys. Rev. A, vol. 107, no. 1, p. 013508, 2023. https://doi.org/10.1103/physreva.107.013508.Search in Google Scholar
[45] A. Rahimzadegan, R. Alaee, C. Rockstuhl, and R. W. Boyd, “Minimalist mie coefficient model,” Opt. Express, vol. 28, no. 11, pp. 16511–16525, 2020. https://doi.org/10.1364/oe.390331.Search in Google Scholar PubMed
[46] L. Kuhn, T. Repän, and C. Rockstuhl, “Inverse design of core-shell particles with discrete material classes using neural networks,” Sci. Rep., vol. 12, p. 19019, 2022. https://doi.org/10.1038/s41598-022-21802-3.Search in Google Scholar PubMed PubMed Central
[47] R. H. Byrd, P. Lu, J. Nocedal, and C. Zhu, “A limited memory algorithm for bound constrained optimization,” SIAM J. Sci. Comput., vol. 16, no. 5, pp. 1190–1208, 1995. https://doi.org/10.1137/0916069.Search in Google Scholar
[48] M. Śmietana, M. Myśliwiec, P. Mikulic, B. Witkowski, and W. Bock, “Capability for fine tuning of the refractive index sensing properties of long-period gratings by atomic layer deposited al2o3 overlays,” Sensors, vol. 13, no. 12, pp. 16372–16383, 2013. https://doi.org/10.3390/s131216372.Search in Google Scholar
[49] S. K. Medda, S. De, and G. De, “Synthesis of au nanoparticle doped sio 2–tio 2 films: tuning of au surface plasmon band position through controlling the refractive index,” J. Mater. Chem., vol. 15, no. 32, pp. 3278–3284, 2005. https://doi.org/10.1039/b506399j.Search in Google Scholar
[50] B. Schwenzer, L. Wang, J. S. Swensen, et al.., “Tuning the optical properties of mesoporous tio2 films by nanoscale engineering,” Langmuir, vol. 28, no. 26, pp. 10072–10081, 2012. https://doi.org/10.1021/la301450h.Search in Google Scholar PubMed
[51] S. Muehlig, A. Cunningham, S. Scheeler, et al.., “Self-assembled plasmonic core–shell clusters with an isotropic magnetic dipole response in the visible range,” ACS Nano, vol. 5, no. 8, pp. 6586–6592, 2011. https://doi.org/10.1021/nn201969h.Search in Google Scholar PubMed
[52] R. Ghosh Chaudhuri and S. Paria, “Core/shell nanoparticles: classes, properties, synthesis mechanisms, characterization, and applications,” Chem. Rev., vol. 112, no. 4, pp. 2373–2433, 2012. https://doi.org/10.1021/cr100449n.Search in Google Scholar PubMed
[53] N. Vogel, M. Retsch, C.-A. Fustin, A. del Campo, and U. Jonas, “Advances in colloidal assembly: the design of structure and hierarchy in two and three dimensions,” Chem. Rev., vol. 115, no. 13, pp. 6265–6311, 2015. https://doi.org/10.1021/cr400081d.Search in Google Scholar PubMed
[54] A. Rahimzadegan, D. Arslan, D. Dams, et al.., “Beyond dipolar huygens’ metasurfaces for full-phase coverage and unity transmittance,” Nanophotonics, vol. 9, no. 1, pp. 75–82, 2019. https://doi.org/10.1515/nanoph-2019-0239.Search in Google Scholar
[55] X. G. Santiago, M. Hammerschmidt, S. Burger, C. Rockstuhl, I. Fernandez-Corbaton, and L. Zschiedrich, “Decomposition of scattered electromagnetic fields into vector spherical wave functions on surfaces with general shapes,” Phys. Rev. B, vol. 99, no. 4, p. 045406, 2019. https://doi.org/10.1103/physrevb.99.045406.Search in Google Scholar
[56] A. Serdyukov, I. Semchenko, S. Tretyakov, et al.., Electromagnetics of Bi-anisotropic Materials: Theory and Applications, Amsterdam, The Netherlands, Gordon and Breach Science Publishers, 2001.Search in Google Scholar
[57] R. Marqués, F. Martin, and M. Sorolla, Metamaterials with Negative Parameters: Theory, Design, and Microwave Applications, New York, USA, John Wiley & Sons, 2011.Search in Google Scholar
[58] T. Repän, Y. Augenstein, and C. Rockstuhl, “Exploiting geometric biases in inverse nano-optical problems using artificial neural networks,” Opt. Express, vol. 30, no. 25, pp. 45365–45375, 2022. https://doi.org/10.1364/oe.474260.Search in Google Scholar
[59] K. Koshelev, A. Bogdanov, and Y. Kivshar, “Meta-optics and bound states in the continuum,” Sci. Bull., vol. 64, no. 12, pp. 836–842, 2019. https://doi.org/10.1016/j.scib.2018.12.003.Search in Google Scholar PubMed
[60] M. I. Mishchenko, L. D. Travis, and A. A. Lacis, Scattering, Absorption, and Emission of Light by Small Particles, Cambridge, United Kingdom, Cambridge University Press, 2002.Search in Google Scholar
[61] G. Demésy, J.-C. Auger, and B. Stout, “Scattering matrix of arbitrarily shaped objects: combining finite elements and vector partial waves,” J. Opt. Soc. Am. A, vol. 35, no. 8, pp. 1401–1409, 2018. https://doi.org/10.1364/josaa.35.001401.Search in Google Scholar PubMed
[62] C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, New York, USA, John Wiley & Sons, 2008.Search in Google Scholar
[63] Y.-L. Xu, “Scattering of electromagnetic waves by periodic particle arrays,” J. Opt. Soc. Am. A, vol. 30, no. 6, pp. 1053–1068, 2013. https://doi.org/10.1364/josaa.30.001053.Search in Google Scholar PubMed
[64] T. Antonakakis, F. I. Baida, A. Belkhir, et al.., Gratings: Theory and Numeric Applications, Marseille, France, Université d’Aix-Marseille, 2014.Search in Google Scholar
[65] I. M. Fradkin, S. A. Dyakov, and N. A. Gippius, “Fourier modal method for the description of nanoparticle lattices in the dipole approximation,” Phys. Rev. B, vol. 99, no. 7, p. 075310, 2019. https://doi.org/10.1103/physrevb.99.075310.Search in Google Scholar
[66] J. Mun, S. So, J. Jang, and J. Rho, “Describing meta-atoms using the exact higher-order polarizability tensors,” ACS Photonics, vol. 7, no. 5, pp. 1153–1162, 2020. https://doi.org/10.1021/acsphotonics.9b01776.Search in Google Scholar
[67] K. Koshelev and Y. Kivshar, “Dielectric resonant metaphotonics,” ACS Photonics, vol. 8, no. 1, pp. 102–112, 2020. https://doi.org/10.1021/acsphotonics.0c01315.Search in Google Scholar
[68] D. R. Abujetas, J. Olmos-Trigo, J. J. Sáenz, and J. A. Sánchez-Gil, “Coupled electric and magnetic dipole formulation for planar arrays of particles: resonances and bound states in the continuum for all-dielectric metasurfaces,” Phys. Rev. B, vol. 102, no. 12, p. 125411, 2020. https://doi.org/10.1103/physrevb.102.125411.Search in Google Scholar
[69] A. B. Evlyukhin, V. R. Tuz, V. S. Volkov, and B. N. Chichkov, “Bianisotropy for light trapping in all-dielectric metasurfaces,” Phys. Rev. B, vol. 101, no. 20, p. 205415, 2020. https://doi.org/10.1103/physrevb.101.205415.Search in Google Scholar
[70] Z. Sadrieva, K. Frizyuk, M. Petrov, Y. Kivshar, and A. Bogdanov, “Multipolar origin of bound states in the continuum,” Phys. Rev. B, vol. 100, no. 11, p. 115303, 2019. https://doi.org/10.1103/physrevb.100.115303.Search in Google Scholar
[71] S. Gladyshev, K. Frizyuk, and A. Bogdanov, “Symmetry analysis and multipole classification of eigenmodes in electromagnetic resonators for engineering their optical properties,” Phys. Rev. B, vol. 102, no. 7, p. 075103, 2020. https://doi.org/10.1103/physrevb.102.075103.Search in Google Scholar
[72] Z. Xiong, Q. Yang, W. Chen, et al.., “On the constraints of electromagnetic multipoles for symmetric scatterers: eigenmode analysis,” Opt. Express, vol. 28, no. 3, pp. 3073–3085, 2020. https://doi.org/10.1364/oe.382239.Search in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/nanoph-2023-0373).
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Review
- Mid-infrared integrated electro-optic modulators: a review
- Research Articles
- High-fidelity optical fiber microphone based on graphene oxide and Au nanocoating
- Balancing detectivity and sensitivity of plasmonic sensors with surface lattice resonance
- Switchable dual-mode nanolaser: mastering emission and invisibility through phase transition materials
- On-chip wavefront shaping in spacing-varied waveguide arrays
- Twofold optical display and encryption of binary and grayscale images with a wavelength-multiplexed metasurface
- Direct tuning of soliton detuning in an ultrahigh-Q MgF2 crystalline resonator
- Inverse design of all-dielectric metasurfaces with accidental bound states in the continuum
- Gigantic blue shift of two-photon–induced photoluminescence of interpenetrated metal–organic framework (MOF)
- Feature-enhanced X-ray imaging using fused neural network strategy with designable metasurface
- Topological degeneracy breaking in synthetic frequency lattice by Floquet engineering
- Coupled harmonic oscillators model with two connected point masses for application in photo-induced force microscopy
- Theory of nonlinear corner states in photonic fractal lattices
- Dual channel transformation of scalar and vector terahertz beams along the optical path based on dielectric metasurface
- Erratum
- Erratum to: Black phosphorus nanosheets and paclitaxel encapsulated hydrogel for synergistic photothermal-chemotherapy
Articles in the same Issue
- Frontmatter
- Review
- Mid-infrared integrated electro-optic modulators: a review
- Research Articles
- High-fidelity optical fiber microphone based on graphene oxide and Au nanocoating
- Balancing detectivity and sensitivity of plasmonic sensors with surface lattice resonance
- Switchable dual-mode nanolaser: mastering emission and invisibility through phase transition materials
- On-chip wavefront shaping in spacing-varied waveguide arrays
- Twofold optical display and encryption of binary and grayscale images with a wavelength-multiplexed metasurface
- Direct tuning of soliton detuning in an ultrahigh-Q MgF2 crystalline resonator
- Inverse design of all-dielectric metasurfaces with accidental bound states in the continuum
- Gigantic blue shift of two-photon–induced photoluminescence of interpenetrated metal–organic framework (MOF)
- Feature-enhanced X-ray imaging using fused neural network strategy with designable metasurface
- Topological degeneracy breaking in synthetic frequency lattice by Floquet engineering
- Coupled harmonic oscillators model with two connected point masses for application in photo-induced force microscopy
- Theory of nonlinear corner states in photonic fractal lattices
- Dual channel transformation of scalar and vector terahertz beams along the optical path based on dielectric metasurface
- Erratum
- Erratum to: Black phosphorus nanosheets and paclitaxel encapsulated hydrogel for synergistic photothermal-chemotherapy


