Experimental demonstration of cylindrical vector spatiotemporal optical vortex

1 Introduction

Optical singularities are zero intensity points within a light field with undefined physical quantities, including scalar singularity arising from undefined phase and vector singularity arising from undefined state of polarization [1]. The commonly investigated scalar singularities are the optical vortex beams with orbital angular momentum (OAM) associated with a spatial spiral phase front [2, 3], whose applications have been widely explored in optical communications, optical trapping, super-resolution imaging, quantum information processing, metrology, etc. [4], [5], [6], [7], [8], [9], [10], [11]. Most previous research on optical vortex beams dealt with longitudinal OAM, whose angular momentum is parallel to the propagation direction. For example, plasmonic vortex cavities based on reflection from structural boundaries is constructed to generate and control plasmonic OAM in spatial domain with topological charge changing with time [12]. Optical vortex lattices are created by employing coherent beam combining for brightness enhancement and stochastic parallel gradient descent algorithm for dynamic phase noises compensation [13]. High efficiency focused vortex beam is generated by exploiting an all-fiber generator based on a kinoform spiral zone plate integrated on the facet of composite fiber structure [14]. Focused vortex-beam together with orthogonal linear-polarization conversion are implemented by taking advantage of gap-surface plasmon metasurfaces [15]. On the other hand, theoretical studies also reveal that the transverse OAM could be formed via introducing temporal variations of phase [16], resulting in OAM perpendicular to the propagation direction of the beam. Recently, a linear method to experimentally generate spatiotemporal optical vortex (STOV) with transverse OAM in a controllable way has been reported [17] and the propagation of STOV in free space are studied with single-shot supercontinuum spectral interferometry [18]. Later wavepackets embedded with multiple spatiotemporal phase singularities carrying different transverse OAM has been demonstrated [19]. Wavepackets that contain both spatiotemporal phase singularity and spatial phase singularity have also been generated very recently [20]. Subwavelength STOV at the focal plane of a high numerical aperture lens can be obtained through pre-conditioning the spatiotemporal structure of the incident wavepacket to overcome the so-called spatiotemporal astigmatism brought by the lens [21]. A close-loop characterization system that is capable of automatically reconstructing the three-dimensional intensity and phase structures of spatiotemporal wavepacket in the spatiotemporal domain has been demonstrated [22]. The second harmonic STOV is also generated and characterized to reveal the conservation of transverse OAM, during which the topological charge of the fundamental wavepacket is doubled along with the optical frequency [23]. Nevertheless, all these works are limited to the scalar singularities contained within the STOV wavepackets.

The most well-known vector singularity is the cylindrical vector beams, including radial polarization and azimuthal polarization [24]. Recently, a compact vectorial field generator based on high resolution reflective liquid crystal spatial light modulator (SLM) has been demonstrated to modulate the complete spatial degrees of freedom of optical field to generate arbitrarily complex vectorial fields [25]. Cylindrical vector beams are generated by the combination of an array of linearly polarized beams, in which each beam has sub-aperture and controllable polarization. Their focusing properties have been analyzed and utilized to tailor the distribution of the focused field [26]. Azimuthally polarized optical pulses with duration of 7.8 ps and average power up to 1.7 kW using a thin-disk multipass amplifier have been reported [27]. Collimated circularly polarized incident beam with plane wavefront can also be converted into cylindrically polarized vortex beam in the spatial domain after passing through a biconical glass rod [28]. Radially polarized vortex beam can be directly generated from a vertical semiconductor microcavity through the use of a polarization-selective subwavelength grating [29]. A cylindrically polarized vortex surface plasmon wave is experimentally demonstrated based on a meta-device, whose efficiency is about 34% [30]. Recently, researchers started to pay attention to vectorial properties of spatiotemporal optical vortex. For example, the coupling between longitudinal spin angular momentum and spatiotemporal OAM has been reported [31], leading to new coupling phenomena for the tailored photonics angular momentum states. Meanwhile, spin–orbit interaction between spin angular momentum and spatiotemporal OAM is also theoretically analyzed [32]. The inherent mathematical non-separability of spatiotemporally structured light makes it a natural candidate for the next forefront of entanglement studies [33, 34]. Despite these inspiring theoretical works, as far as we know, there have been no reports on cylindrical vector spatiotemporal optical vortex either theoretically or experimentally. In this paper, we experimentally generate and characterize cylindrically polarized STOV with transverse OAM, demonstrating the coexistence of spatiotemporal OAM singularity with the spatial polarization singularity for the first time. The vectorial STOV may find applications in light–matter interaction, optical tweezers, spatiotemporal spin–orbit angular momentum coupling, etc.

2 Principle and experimental setup

The experimental setup to generate and characterize radially and azimuthally polarized STOVs are shown in Figure 1(a). Figure 1(b) presents the three-dimensional (3D) perspective of the pulse shaper, indicating the x–ω coordinate in the SLM. The laser source emits chirped pulses of about 3 ps duration as the incident wavepackets, whose central wavelength is 1030 nm. The incident pulse is split into two pulses by the non-polarizing beam splitter (NPBS) 1. One is directed to the pulse shaper consisting of a diffraction grating (G1), a cylindrical lens (CL) and one two-dimensional SLM [35], [36], [37], in which the STOV is generated. Assuming that the optical field in the space-frequency domain (x–ω domain) is given by g _R (r) in the polar coordinates, where r = r 0 ( x / w ) 2 + [ ( ω − ω 0 ) / Δ ω ] 2 , and r ₀ is the beam size on the SLM, w is the waist width of the laser beam, ω ₀ is the center frequency of the laser pulse, Δω is the band width of the laser pulse. The SLM located in the x–ω plane is used to apply spiral phase e^−ilθ to the incident wavepacket, after a two-dimensional Fourier transformation, we can obtain the STOV in the x–t domain as the following [17]:

where θ = tan − 1 [ w ( ω − ω 0 ) / ( x Δ ω ) ] , ρ = x 2 + ( c t ) 2 and ϕ = tan − 1 ( x / ( c t ) ) , J _l (⋅) is the Bessel function of the first kind, l is the topological charge, c is the velocity of light. Then, the STOV output from the pulse shaper is directed by Mirror 1 (M1) to pass through polarizer 1 (P1) and vortex wave plate (VWP, LBTEK VR1-1030). The transmission axis of P1 is along the horizontal direction, thus the transmitted beam is horizontally polarized, which will be converted into radially or azimuthally polarized STOV by the VWP subsequently. The VWP has a constant retardance across the clear aperture, but its fast axis rotates continuously around the center of the aperture. When the 0° fast axis of the VWP is parallel with the polarization direction of the STOV, the transmitted wavepacket from the VWP is radially polarized, which can be expressed as

where β = tan − 1 ( y / x ) is the azimuthal angle in the spatial domain of the STOV, cos  β ⋅ G ( ρ , ϕ ) is the horizontal component of the radially polarized STOV, sin  β ⋅ G ( ρ , ϕ ) is the vertical component of the radially polarized STOV. On the other hand, when the 0° fast axis of the VWP is perpendicular to the polarization direction of the STOV, the transmitted wavepacket from the VWP is azimuthally polarized, as shown in the following:

where − sin  β ⋅ G ( ρ , ϕ ) is the horizontal component of the azimuthally polarized STOV, and cos  β ⋅ G ( ρ , ϕ ) is the vertical component of the azimuthally polarized STOV.

Figure 1:

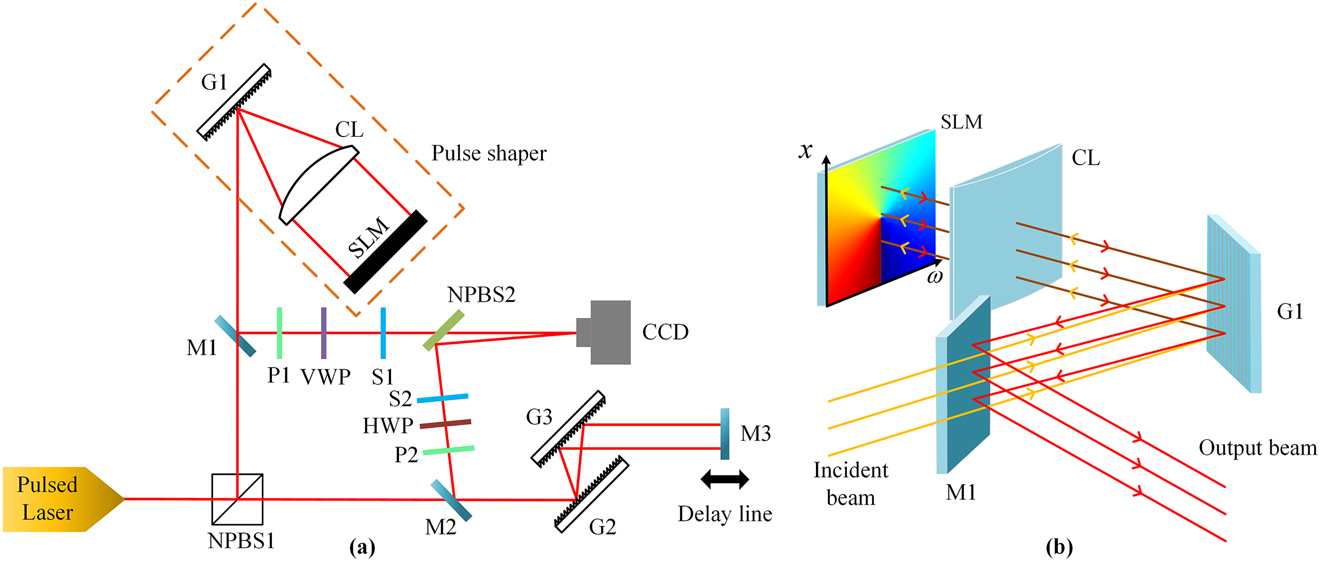
Schematic drawing of the experimental setup. (a) Experimental setup for generating and characterizing vectorial spatiotemporal vortices. (b) The 3D perspective of the pulse shaper. M: mirror; G: grating; CL: cylindrical lens; P: polarizer; NPBS: non-polarizing beam splitter; S: shutter; VWP: vortex wave plate and HWP: half-wave plate.

To characterize the generated vectorial STOVs, the other pulse divided by NPBS 1 is compressed to about 90 fs by a grating pair (G2 and G3) as the probe beam. Mirror 3 (M3) is used to adjust the time delay of the probe beam to make it interfere with the object beam at different time slice. Since both the radially and azimuthally polarized STOVs can be treated as a linear combination of vertically and horizontally polarized components, to reconstruct the 3D spatiotemporal structure of each STOV, the probe beam should interfere with both polarization components at a series of time slices of the corresponding STOV. The polarizer 2 (P2) is employed to make the probe beam be horizontally polarized. And the half-wave plate (HWP) is adopted to rotate the polarization direction of the probe beam. Meanwhile, the intensity distributions of the object beam, probe beam and background noise also need to be measured individually in the characterization process [38], [39], [40]. Shutters 1 and 2 are utilized to gate the object and probe beams.

3 Results

In the first experiment, we applied a spiral phase pattern with topological charge of 1 to the SLM within the pulse shaper, and rotate the 0° fast axis of the VWP to horizontal direction. To analyze the polarization distribution of the generated wavepacket, a linear polarizer together with a quarter wave plate is inserted between the NPBS 2 and CCD to conduct the Stokes parameters measurement. Noting that, shutter 1 is opened and shutter 2 is closed in this process. The experimental results are shown in Figure 2. The histogram of elevation angle in Figure 2(b) has a nearly uniform distribution in the range of [−90°, 90°], and the histogram of ellipticity in Figure 2(c) peaks around 0.01π. Combining with the polarization map in Figure 2(a), we can conclude that the generated wavepacket is radially polarized in spatial domain.

Figure 2:

Experimental results for the Stokes parameters measurement of radially polarized STOV.

(a) Intensity distribution of the object beam with polarization map. Histograms of elevation angle (b) and ellipticity (c).

Subsequently, we open both shutters 1 and 2 to measure the 3D spatiotemporal structure of the generated wavepacket. The time delay is electronically controlled to step the probe beam throughout the object beam automatically. The fast axis of the HWP is firstly rotated to horizontal direction, thus the transmitted probe beam is horizontally polarized, which just interferes with the x-polarized component of the object beam at each time slice, as shown in Figure 3(a). The interference patterns at several representative temporal locations of the object wavepacket are shown in Figure 3(b)–(e). We can see that there are no interference fringes near the vertical center line in all these patterns, which is due to the fact that the nearly vertical polarization within this area does not interfere with the horizontally polarized probe beam. The evolution of the fringe patterns could be understood as the following. As the probe pulse is overlapped near the head of the spatiotemporal vortex, smooth continuous vertical fringes are observed due to a phase difference close to 0 or 2π between the upper and lower parts of the beam in the spatial domain, as shown in Figure 3(b). As the probe pulse scans toward the center of the spatiotemporal vortex, the phase difference approaches to π due to the spatiotemporal vortex phase, the upper and lower fringes start to shift with respect to each other, as shown in Figure 3(c). At the center of the spatiotemporal vortex, the upper and lower fringes are totally misaligned with each other because of the π phase difference between the corresponding two parts, as shown in Figure 3(d). Just as the probe pulse passes the center, the phase difference becomes smaller than π, resulting the upper and lower fringes shifts in the opposite direction, as shown in Figure 3(e). As the probe pulse advances more toward the end of the spatiotemporal vortex wavepacket, the fringes become vertically aligned again, which is similar to that in Figure 3(b).

Figure 3:

Experimental results for characterizing radially polarized STOV.

(a) Diagram of the pattern for the horizontally polarized component within a radially polarized object beam. (b–e) The interference patterns at several representative temporal locations of the object wavepacket when the probe beam is horizontally polarized. (f) Diagram of the pattern for the vertically polarized component within a radially polarized object beam. (g–j) The interference patterns at several representative temporal locations of the object wavepacket when the probe beam is vertically polarized. The reconstructed 3D spatiotemporal wavepacket (k) and its cut-through view (l). (m) The experimentally reconstructed spatiotemporal phase distribution. The red arrows in (a) and (f) indicate the polarization direction of the probe beam, and the white arrows indicate the polarization direction of corresponding components within object beam. The black lines in (b)–(e) and (g)–(j) indicate the relative location between the upper and lower fringes in each interference pattern. The green arrows in (k) represent the radial polarization of the STOV. The green and black lines in (l) indicate the traces of the polarization and OAM singularities, respectively.

Then the fast axis of the HWP is rotated by 45° to make the transmitted probe pulse be vertically polarized, which is used to scan through the wavepacket again. In this case, the probe beam will just interfere with the y-polarization component of the object beam, as shown in Figure 3(f). The interference patterns at several representative temporal locations are shown in Figure 3(g)–(j). The differences from the former case are that there exist no fringes along the horizontal central axis, and the evolution of the fringe patterns also changes. Near the head or tail of the wavepacket, the upper and lower fringes totally misaligned with each other due to the π phase difference caused by the opposite polarization orientation in the upper-half and lower-half of the beam, while the phase difference contributed from the spatiotemporal phase pattern is near 0 or 2π. Toward the center of the spatiotemporal vortex, the fringes are aligned along the vertical direction. This is due to the contribution of π phase difference from the opposite polarization orientation and the π phase difference from the spatiotemporal vortex phase. Thus, at this location, the total phase difference across the upper-half and lower-half of the beam in Figure 3(i) is 2π or 0, making the interference fringes line up. Between the head and the center of the vortex or between the center and the tail of the vortex, the upper and lower fringes are misaligned but connected while the bending directions in these two transition regions are reversed.

Based on all the collected interference patterns corresponding to the two probe polarization, 3D spatiotemporal structure of the generated wavepacket can be reconstructed as shown in Figure 3(k). To reveal singularity structures within the wavepacket, Figure 3(l) demonstrates a cut-through view of the reconstructed wavepacket along the meridional plane. Two tunnels within the wavepacket marked by the green and black lines can be clearly seen. The transverse tunnel is caused by the phase singularity carried by the spatiotemporal spiral phase with topological charge of 1 (as shown in Figure 3(m)), while the longitudinal tunnel is caused by the polarization singularity carried by the radial polarization. Hereby, a radially polarized STOV with topological charge of 1 is generated.

In the next experiment, we applied the same spiral phase pattern to the SLM, and rotate the 0° fast axis of the VWP to vertical direction. The results of the Stokes parameters measurement for the transmitted wavepacket are shown in Figure 4. From the polarization map and histograms of the elevation angle and ellipticity, we can confirm that the transmitted wavepacket is azimuthally polarized. The interference patterns between the probe beam and several representative temporal slices of the object beam are shown in Figure 5(b)–(e) and 5(g)–(j), respectively. The patterns in the first row are obtained with a horizontally polarized probe pulse, while the patterns in the second row are collected with a vertically polarized probe pulse. Figure 5(a) and (f) give the diagram of the patterns for the horizontally and vertically polarized components of an azimuthally polarized object beam, respectively. The evolution of the interference fringe patterns can be explained similarly to the radially polarized STOV case. Separately, there exist no fringes near the horizontal center line in Figure 5(b)–(e) and no fringes near the vertical center line in Figure 5(g)–(j), which are opposite to what is observed in Figure 3. Likewise, the evolution of the fringe patterns are also contrary to those in Figure 3, indicating the azimuthal polarization of generated wavepacket again. As shown in Figure 5(k) and (l), the reconstructed 3D spatiotemporal structure and its cut-through view demonstrate that there are two types of optical singularity in the generated wavepacket. The reconstructed spatiotemporal phase distribution of the object wavepacket is demonstrated in Figure 5(m), indicating that the transverse OAM has a topological charge of 1. Therefore, the generated wavepacket is azimuthally polarized STOV.

Figure 4:

Experimental results for the Stokes parameters measurement of the azimuthally polarized STOV.

(a) Intensity distribution of the object beam with polarization map. Histograms of elevation angle (b) and ellipticity (c).

Figure 5:

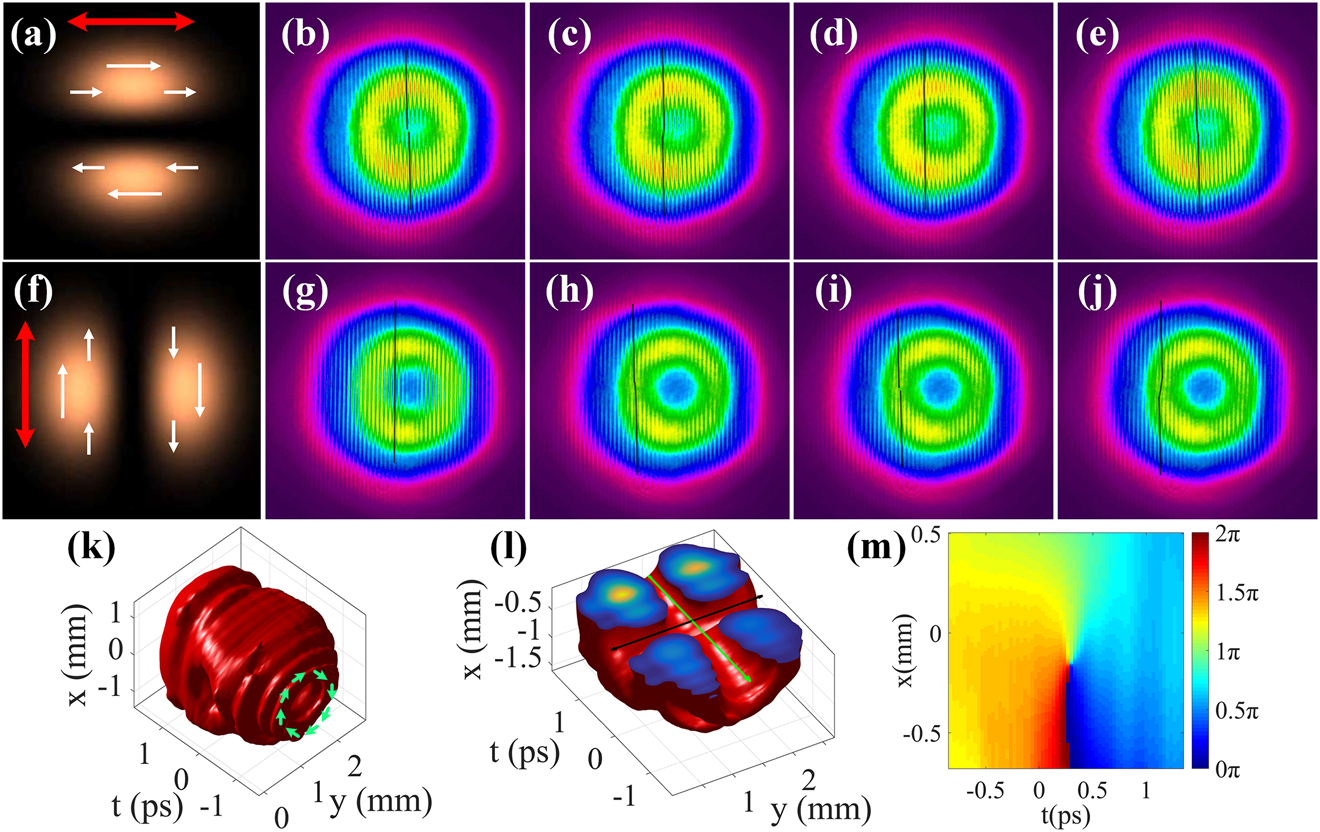
Experimental results for characterizing azimuthally polarized STOV. (a) Diagram of the pattern for the horizontally polarized component within an azimuthally polarized object beam. (b–e) The interference patterns at several representative temporal locations of the object wavepacket when the probe beam is horizontally polarized. (f) Diagram of the pattern for the vertically polarized component within an azimuthally polarized object beam. (g–j) The interference patterns at several representative temporal locations of the object wavepacket when the probe beam is vertically polarized. The reconstructed 3D spatiotemporal wavepacket (k) and its cut-through view (l). (m) The experimentally reconstructed spatiotemporal phase distribution. The red arrows in (a) and (f) indicate the polarization direction of the probe beam, and the white arrows indicate the polarization direction of corresponding components within object beam. The black lines in (b)–(e) and (g)–(j) indicate the relative location between the upper and lower fringes in each interference pattern. The green arrows in (k) represent the azimuthal polarization of the STOV. The green and black lines in (l) indicate the traces of the polarization and OAM singularities, respectively.

4 Conclusions

Here, we experimentally demonstrate the radially and azimuthally polarized STOV with topological charge of 1. Both Stokes parameters measurement and 3D spatiotemporal measurement are conducted to characterize the generated cylindrically polarized STOV. The results revealed that the spatiotemporal OAM singularity can coexist with the spatial polarization singularity. To our best knowledge, this is for the first time that optical wavepackets with both spatiotemporal singularity and polarization singularity have been reported. In the past two decades or so, there has been a tremendously increasing interest in the research and applications of spatial phase singularity such as OAM beams and vectorial singularity such as cylindrical vector beams. The discovery of spatiotemporal vortex and its controllable experimental creation and characterization, however, are very recent. The realization of optical wavepackets with both spatiotemporal phase singularity and spatial polarization singularity provides a completely new type of spatiotemporal optical field. We expect that further investigations into the properties of this new type of optical wavepackets and their interactions with matters will reveal more interesting findings and pave the way to a myriad of applications ranging from classical to quantum optics.