Photonic flat-band lattices and unconventional light localization

1 Introduction

Two-dimensional (2D) photonic systems with flat-bands have attracted increasing interest in recent years [1], [2], inspired by multiband Hubbard models earlier introduced in condensed matter physics [3], [4], [5]. A flat-band is a completely dispersionless energy band that extends in the whole Brillouin spectrum [6], [7], [8], [9]. As the kinetic energy is completely quenched, which suppresses wave transport, particle interaction becomes dominant, leading to some exotic or unconventional correlated ground states. Such enhanced interaction makes flat-band systems a perfect candidate for investigation of complex many-body quantum states and the physics of strongly correlated systems in the absence of a magnetic field [5], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]. One well-known example is the fractional quantum Hall effect, where the interaction induces nontrivial behavior of the electrons in topological flat-bands [20], [21], [22]. Numerous efforts have been made to understand the underlying flat-band physics within the community of ultracold atomic gases [23], [24] and exciton-polariton condensates [25]. It has also been predicated that the flat-band features can support nonlinear compactons [26], [27] and interaction-induced topological phases [28], which open up new avenues for studying the interplay between nonlinearity and spin-orbit coupling phenomena in topological flat-band systems. Thus far, flat-bands have been realized in a variety of systems including ultracold atoms, various metamaterials, electronic and other realistic materials, and photonic waveguide arrays [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41]. A detailed account on artificial flat-band systems and related discussions can be found in recent review articles [1], [2] (see, e.g. Ref. [42] for further articles related to flat-band magnetism in frustrated crystals, and Refs. [43], [44] for a review on topological flat bands).

Artificial photonic structures can provide controllable platforms to explore physical phenomena that are difficult to achieve in real materials. In particular, photonic lattices have proven to be extremely effective for investigating fundamental physics in simple optical settings. The underlying physics involved relies on the analogy between the paraxial equation for electromagnetic waves and the Schrödinger equation describing quantum phenomena. Photonic lattices offer exquisite control of initial conditions and allow for monitoring the actual wave functions (including phase). Therefore, it is possible to directly observe wave dynamics using classical light waves in photonic lattices. Over the past two decades, many intriguing fundamental phenomena have been demonstrated in evanescently coupled waveguide arrays created using either femtosecond (fs)-laser writing or optical induction technique, including discrete solitons, dynamical localization, and Anderson localization in disordered lattices [45], [46], [47], [48], [49], [50], [51], [52], [53]. These developments have opened up new avenues for the manipulation of light.

Femtosecond laser writing of photonic lattices was first implemented in 2004 for the fabrication of dielectric waveguide arrays [54]. Since then, many successful and fascinating examples of laser-written photonic structures have been realized with this technology. In the fs-laser-writing method, typically a focused laser pulse is sent into bulk fused silica, which creates a localized permanent increase in the refractive index of the material. Consequently, when moving the sample with respect to the writing beam, a longitudinally extended index modification (a waveguide) is created. This fabrication method has the advantage of supporting the generation of compact two-and high-dimensional lattices of nearly arbitrary geometries, leading to the observation of a variety of fundamental phenomena in such lattices.

In Figure 1, we show some typical examples of laser-written and engineered flat-band photonic lattices. Laser-written photonic Lieb lattices [58] were first created by two independent groups (Mukherjee et al. [30] and Vicencio et al. (Figure 1A) [32]) for the observation of compact localized states (CLSs). Recently, Hassan et al. reported the experimental realization of novel topological corner states of light in laser-written 2D photonic Kagome lattices (Figure 1B) [55]. Two-dimensional honeycomb-like lattices, known as photonic graphene [59], which have been used to explore photonic Landau levels [60] and Floquet topological insulators [61], [62], have recently been established with engineered micropillar photonic resonators for the demonstration of type-III Dirac cones that combine flat and linear dispersions (Figure 1C) [56]. As another example, losses can be introduced by rapid longitudinal bending of the waveguides or introducing scatters in the laser-writing technique, enabling the realization of non-Hermitian lattice Hamiltonians [63], which leads to the demonstration of PT (parity-time)-symmetric flat-bands (Figure 1D) [57].

Figure 1:

Examples of laser-written and engineered flat-band photonic lattices.

(A) A photonic Lieb lattice established by fs-laser-writing technique for demonstration of flat-band compact localized states [32]. (B) A photonic Kagome lattice established for demonstrating topological corner states exhibiting a remarkable degree of flexibility and control [55]. (C) A photonic honeycomb lattice of micropillars engineered with type-III Dirac cones that combine flat and linear dispersion bands [56]. (D) Schematic of the tripartite PT-symmetric photonic lattice and resulting dispersion relation showing the partially flat band around the exceptional point of the structure [57].

In this mini-review, we focus on novel phenomena in optically induced flat-band lattices established in nonlinear crystals. We mainly revisit our recent experimental and theoretical progress in the demonstration of flat-band states and novel light localization in engineered photonic flat-band lattices. In Section 2, we briefly summarize two kinds of flexible approaches based on the optical induction technique to obtain photonic flat-band lattices. In Section 3, we review the numerical method and theory for the calculation and simulation of flat-band light localization in photonic lattices. In subsequent sections, recent experimental work is summarized with respect to the demonstrations of conventional flat-band states – the so-called CLSs in Lieb and Kagome lattices as well as in driven rhombic lattices. Unconventional flat-band localized line states due to the flat-band touching dispersive bands in photonic Lieb and super-honeycomb lattices (sHCLs) are summarized in Section 5. These line states, independent of linear superpositions of conventional bulk CLSs, can be considered as an indirect illustration of the non-contractible loop states (NLSs). Furthermore, in Section 6 we discuss two alternative approaches to directly observe NLSs in photonic Kagome lattices: one is to realize the robust boundary modes spanning the whole boundary of a finite lattice, and the other is to achieve direct observation of the NLS in an annular-shaped Kagome lattice, which hosts such a loop state along the toroidal direction. These robust boundary modes and NLSs are direct manifestations of the real-space topology in such flat-band systems. Finally, in Section 7 we summarize our work and present some outlooks for future exploration of the field. This review is not intended to be a comprehensive account of the vast flat-band literature, nor to repeat the published reviews on this subject [1], [2], but it is rather a concise account of the study (mainly from our group) on flat-band phenomena in various photonic lattices.

2 Experimental method of lattice induction

Optical induction is a simple yet effective method for the creation of photonic waveguide lattices [45], [46]. The induction technique is based on optically induced nonlinear refractive index change in a bulk nonlinear crystal, somewhat similar to that in the generation of optical spatial solitons (see Ref. [51] for a detailed review). This technique, especially in photorefractive materials, allows the realization of reconfigurable (non-permanent) photonic lattice structures [46], [50], [64], [65], [66], in contrast to the fs-laser-writing technique that inscribes structures permanently in silica glass [67], [68]. In what follows, we discuss two main approaches for the realization of photonic lattices using optical induction in photorefractive crystals. The first one uses periodic nondiffracting waves, where the phase and amplitude of multiple interfering plane waves can be modulated to create different 2D periodic lattices. Many of the original studies on optically induced lattices were associated with this method. The other technique, developed more recently, is the site-to-site continuous wave (cw)-laser-writing technique, as shown in Figure 2. Compared with the former method, the latter has the advantage of flexibly establishing lattices with tailored boundaries, as well as aperiodic lattices of arbitrary structures.

Figure 2:

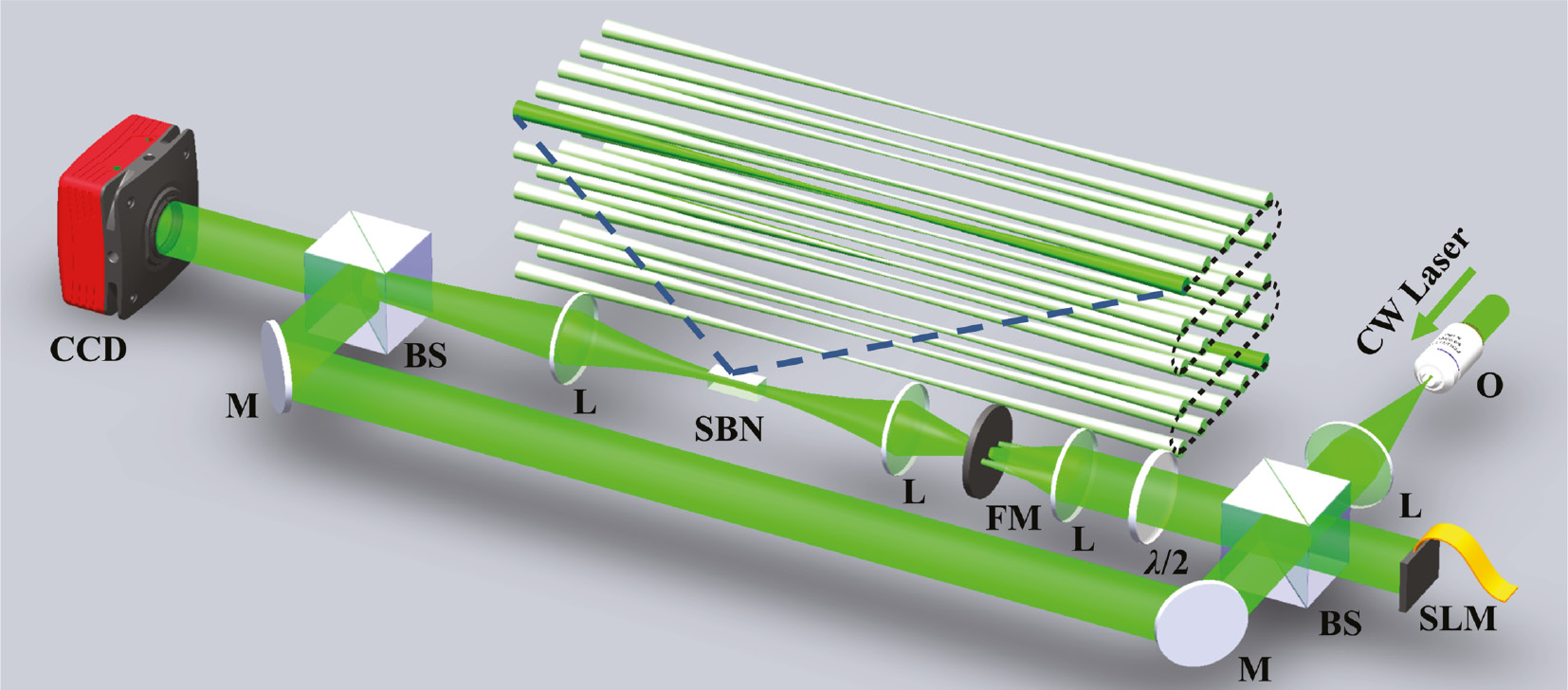
Experimental setup for site-to-site writing of a photonic lattice with a cw laser in a nonlinear photorefractive SBN crystal.

SLM, spatial light modulator; BS, beam splitter; FM, Fourier mask; SBN, strontium barium niobate.

2.2 Site-to-site cw-laser-writing technique

The methods mentioned above are used to fabricate different “unbounded” lattice structures without considering the lattice termination. However, sometimes we need to prepare some lattice patterns with specially tailored boundaries or edges. Like graphene, different edges support different edge states and have different characteristics. For instance, some flat-band states can only exist in lattices with appropriate boundaries, such as the extended flat-band line states [81], [84], [85], [86] discussed in later sections. In order to observe such states, we develop a simple cw-laser-writing technique which can establish finite-sized photonic lattices with desired boundaries. Figure 2 shows a schematic of the experimental setup. An ordinarily polarized quasi-nondiffracting beam from a solid-state laser (λ=532 nm) is used to illuminate a spatial light modulator (SLM), which creates a writing beam with reconfigurable input positions. The 4f system guarantees a quasi-nondiffracting zone of the beam as it propagates through the crystal. The technique relies on site-to-site inducing or writing waveguides in a nonlinear photorefractive (SBN) crystal. All the waveguides remain intact during the writing process due to the “memory” effect of the nonlinear photorefractive crystal. Different from the fs-laser-writing technique [67], a lattice written in the bulk crystal is readily reconfigurable, since one can easily erase it with white light and rewrite another lattice in the same crystal. In addition, since the crystal has strong photorefractive nonlinearity, one can study nonlinear wave dynamics in such lattices. Apparently, this method is not only limited to creating photonic Lieb lattices but also can be used to flexibly realize some flat-band lattices with virtually arbitrary lattice edges, any ribbon or aperiodic photonic lattices (see Figure 3 for some examples). However, although this method is very flexible, it also has the disadvantage that the period of the lattice cannot be too small (typically around 26 μm or more) due to the limitation of “nondiffracting” region of the writing beam [81], even when the writing beam is a Bessel beam [80].

Figure 3:

Typical examples of the flat-band photonic lattices created in a nonlinear bulk crystal with the cw-laser-writing technique.

(A, B) Lieb [81] lattices with different boundary terminations, (C–E) Kagome lattices with different boundary terminations [86], (F) a super-honeycomb lattice [85], and (G) a “driven” rhombic lattice with an index gradient [84].

3 Numerical method and flat-band classification

The evolution of a light beam through a photonic lattice is well described by the following Schrödinger-type equation under the paraxial approximation [46], [50], [51]:

where ψ corresponds the slowly varying electric field envelop of the probe beam, (x, y) are the transverse dimensions, z represents the longitudinal propagation distance into the photonic lattice, ∇⊥2 is the 2D transverse Laplacian operator, n₀ is the unperturbed refractive index of the nonlinear medium, k₀ is the wave number in the vacuum, Δn(x, y) represents the local refractive index change corresponding to a particular 2D photonic lattice under study, with Δn=n₀. Equation (1) has the form of the Schrödinger equation when the replacement is taken as z→t and Δn→V. The localization of flat-band states in lattices requires a stationary potential, implying that the index change Δn in Eq. (1) must be propagation-invariant; that is, Δn(x, y) must be z-independent. Experimentally, this corresponds to generation of a nondiffracting lattice-inducing beam pattern as described above.

Under the tight-binding approximation, the above continuous Schrödinger-like equation can be replaced by a discrete equation, considering only the nearest neighbour coupling effect. By Fourier transforming the tight-binding Hamiltonian into the k space, one readily obtains the band structure. A lattice of dispersionless energy band means that there exists at least one complete flat-band in its spectrum, and the corresponding linear Bloch modes are entirely compact localized due to the destructive interference of extended waves. That is, the eigenstate amplitudes strictly vanish except at a finite number of unit cells of the structure. This is particularly interesting because, in this case, waves can stay localized in the continuum. Additionally, these states may be robust against the presence of disorder in the system [87], [88].

Considering the properties of their eigenstates, flat-bands can be classified into three types [2]: “symmetry-protected” flat-bands, “accidental” flat-bands, and “topologically protected” flat-bands. In 1D settings, the CLS can be classified by the integer number U of unit cells they occupy [89]. “Symmetry-protected” chiral flat-bands, first introduced by Shima et al. [90], such as with the cross-stitch lattice (U=1), form an orthogonal set with the simplest CLSs occupying only one unit cell of the lattice. “Accidental” flat-bands can be regarded as the case of U≥2 with CLSs spanning over more than one unit cell formed by precisely adjusting the system parameters, such as with the sawtooth lattice [34], [91]. In such cases, the band is not always flat, as it only exists in some specific parameter regimes, while, the “topologically protected” flat-bands can be regarded as robust flat-bands, represented by a bipartite system such as the Lieb lattice with two sublattices. Bandcrossing is protected in a sense that it can only be removed by perturbations that also destroy the flatness of the band [92]. Like the protection of the Dirac points of graphene, the mechanism for this stability is topological. Very recently, Rhim and Yang [93] showed that flat-bands can be classified into two distinct classes, singular or nonsingular, based on whether the corresponding Bloch functions exhibit a discontinuity at the crossing points with other bands.

4 Compact localized states in flat-band lattices

The characteristic of flat-band lattices is the existence of the fundamental CLS. The first study of flat-band models started with the work by Sutherland [94]. In his paper, the existence of strictly localized states of a flat-band was demonstrated in a dice lattice. The localized states persist because of local topology even if the lattice periodicity is destroyed. The proposal of using CLSs to name the flat-band eigenmodes originated from the work by Aoki et al. [95].

In 2015, the first experimental demonstrations of stationary and transversely localized flat-band states were performed in photonic Lieb lattices [30], [32]. Such a flat-band in the Lieb lattices is protected by a chiral symmetry, and its intersection with the dispersive bands is said to be protected by real-space topology [77], [92], [96] (the topology of the inter-site couplings rather than their precise strengths, which will be discussed in detail in later sections), which is robust to the coupling disorder [87], [88]. The photonic Lieb lattice was produced early in 2014 by Guzman-Silva et al. [58], but that work focused more on the edge modes generated by stretching the lattice rather than the existence of the flat-band states (or whether the tight-binding condition is satisfied). In contrast, the work published in 2015 [30], [32] reported direct experimental observation of the fundamental flat-band states in photonic lattices, as demonstrated shortly afterward also with optical induced photorefractive lattices [35], [36]. These works attracted wide interest because they prove that waves can stay localized in the continuum, even in the absence of any defect [97], disorder [48], or nonlinearity [46]. Demonstrations of CLSs and a variety of associated phenomena have also been discussed in 1D and 2D lattices, including the Stub [39], sawtooth [34], [91], rhombic [31], [38], [84], [98], [99], [100], [101], [102], [103], Kagome [36], [86], super-honeycomb [85], [104], and Lieb [35], [81] lattices, thanks to the advanced techniques that allow for precise flat-band engineering. Figure 4 shows some typical experimental results of CLSs observed in the Lieb, rhombic, and sawtooth lattices fabricated by the fs-laser-writing technique. In the case of the sawtooth lattice, wave localization due to presence of an “accidental” flat-band was observed by fine-tuning the inter-site coupling coefficients [34].

Figure 4:

Examples of the compact localized states observed in fs-laser-written flat-band photonic lattices.

(A) The CLSs and their superimposed bound states observed in a Lieb lattice [32]. (B) The CLSs and the equal-phase modes observed in a rhombic lattice [31]. (C) Experimental output intensity for the bulk excitation under different regimes of wave transport in a sawtooth lattice [34].

In the tight-binding approximation, the Bloch modes of Lieb lattices are only distributed in three bands: a completely degenerate flat-band centered between two dispersive bands, with all three bands touching at the M points (k_x=k_y=π) (see Figure 5A) [23], [30], [32], [77], [105]. Similar to honeycomb lattices [61], [66], the intersection of the dispersive bands is characterized by a linear dispersion relation in the vicinity of Dirac-like points, leading to intriguing phenomena such as conical diffraction and pseudospin [79], [106]. Furthermore, taking advantage of the superposition of CLSs inherent in the Lieb lattices, flat-band-based text transmission through such 2D perovskite-like photonic structures was demonstrated [35], representing the experimental observation of distortion-free image transmission (Figure 5A) as predicted in Ref. [105]. In those experiments [35], the letter “L” (overlaid by a train of four fundamental modes) was constructed as a probe beam. For comparison, the probe beam with all the pixels being of equal phase is also launched under the same configuration. Obviously, the difference between distorted and undistorted image transmission is evident, as shown in Figure 5A.

Figure 5:

Examples of the compact localized states observed in optically induced flat-band photonic lattices.

Shown are experimental results of (A) linear image propagation through a Lieb photonic lattice [35] and (B) a bound-state transmission in a pyrochlore-like (Kagome) photonic lattice [36]. (C) Experimental observation of a quincunx-shaped CLS which spans over two unit cells in a photonic rhombic lattice [84]. From left to right: the lattice, calculated band structure in the tight-binding approximation, probe beam input, in-phase output, and out-of-phase output.

In addition to the light localization in Lieb lattices, many recent studies have been aimed at understanding the effect of this additional flat-band on various phenomena, including Floquet topological insulators [107], conical diffraction, and integer pseudospin states [79]. The near degeneracy of other bands with zero effective mass is ideal for switching applications and enables novel topological phases with protected edge states in resonance with flat-band states [62], [76], [107].

In the experiments of Zong et al., the first demonstration of CLSs in a Kagome lattice was carried out [36]. In those experiments, they also realized a high-fidelity bound-state transmission through the lattice by judiciously exciting a superposition of flat-band eigenmodes of the Kagome lattice (Figure 5B). Their work may provide inspiration for developing alternative light-trapping and image-transmission schemes in structured photonic materials without engineered disorder or nonlinearity. In addition, one can envisage the possibility for experimental demonstration of predicted novel phenomena such as discrete flat-band solitons and PT-symmetric phase in Kagome photonic lattices [57], [108], [109], and Aharonov-Bohm photonic caging with the implementation of a synthetic gauge field [31], [102], [110].

Flat-band states have also been demonstrated in a rhombic lattice that is robust in the presence of an external driving field (index gradient) along the lattice axis by Mukherjee and Thomson [38]. Recently, Xia et al. [84] demonstrated the existence of CLSs in a driven rhombic lattice ribbon with two distinct refractive index gradients acting as external dc fields. Such CLSs span over two unit cells with a quincunx shape under the action of a driving force. For the first time, the flat-band state of U=2 was experimentally realized (see Figure 5C). It is worth mentioning that the external drive added to the ribbon was achieved by modulating the relative intensity of the writing beam. We can see that the flat-band remains flat while the band gap is open, and does not diffract with the opening of the band gap. Comparing the influence of the direction of the index gradient on CLSs, they found that, with a y-gradient set perpendicularly to the ribbon, the undriven CLS turns into a quincunx-shaped CLS spanned over two unit cells (see Figure 5C). In this case, although the flat-band remains, the original flat-band state is no longer maintained, and a new flat-band state is generated that occupies two unit cells. Interestingly, when the index gradient is parallel to the ribbon, Bloch-like oscillation of flat-band states is observed in the momentum space [84].

Apart from the fundamental CLSs observed in the above experiments, there are many theoretical discussions and predictions about the flat-band phenomena under additional symmetry or perturbations. Earlier work of Sutherland reported on the persistence of localized states if the dice lattice periodicity is destroyed [94]. The tunability of the CLSs is another important aspect associated with the flat-band [111]. The robustness of the CLSs to disorder crucially depends on the flat-band feature, for instance, whether the flat-band touches the dispersive bands or not [88]. Bergman et al. discussed about band-touching from real-space topology in frustrated hopping models [92]. Examples of nontrivial and abrupt changes of the wavefunction properties of perturbed flat-band models are the appearance of the flat-band for Landau-Zener Bloch oscillations in the presence of external fields [99], the effect of chiral symmetry-breaking [84] on the flat-band in a partial chiral dimerized Lieb lattice [112], the localization of weakly disordered flat-band states [88], chiral flat-bands with double perturbations, including disorder and synthetic magnetic fields [96], and anomalous topological edge modes in a slowly driven photonic lattice [38], [100].

5 Line states in Lieb and super-honeycomb lattices

The conventional CLSs are compact and localized to a finite area in two dimensions, while the unconventional NLSs are a new type of flat-band eigenstates that are compact and localized in one direction but extended infinitely in the other direction. The existence of such NLSs is related to flat-band crossings with dispersive bands. Moreover, the NLSs are topologically different from the conventional CLSs in real space, as the NLSs cannot be continuously deformed into the conventional CLSs in a torus geometry representing the periodic boundary conditions.

In flat-band systems, one can always find a set of CLSs as degenerate eigenstates, whose energy is the same as that of the flat-band. The full sets of CLSs connected by lattice translation vectors are found to be linearly dependent on each other in certain flat-band systems. As such, the CLS sets are found to be incomplete. Bergman et al. [92] pointed out that in the majority of “frustrated” hopping examples, a flat-band always intersects with other dispersive bands at a number of discrete points in the momentum space. Such band degeneracy is related to the incompleteness of the CLSs in these models. That is to say, there exist some missing states that can complete the flat-band basis. Such missing states are accounted for by noncontractible loops around the torus under periodic boundary conditions (the so-called NLSs). More recently, Rhim et al. theoretically found that the NLSs are inherent to the singular flat-band, where an immovable singularity exists in the band-crossing of the Bloch wavefunctions [93]. Once the degeneracy at the band-crossing point is lifted, the flat-band becomes dispersive and may acquire a finite Chern number in general. Such real-space topology manifesting via the NLSs of the flat-band is in contradistinction with the recent and widely studied topological features of the Bloch wave functions defined in the momentum space [113], [114].

The NLSs in principle exist in infinite lattices which are experimentally nonfeasible. Recently, NLSs were found to exist even in finite lattices with specially tailored boundaries and satisfy the destructive interference conditions. Such NLSs appear as flat-band line states extended through the entire finite lattice that cannot be obtained by linear superposition of the bulk CLSs. As mentioned above, the band structure of photonic Lieb lattices contains a flat-band intersecting with the two dispersive bands at the Brillion zone (BZ) corners, and the CLSs in Lieb lattices are linearly dependent, which do not form the complete basis of flat-bands. One can find unusually extended flat-band line states, which are compact-localized in one direction but extended in the other direction as shown in Figure 6A. Xia et al. [81] reported the first realization of such unconventional flat-band line states in a finite photonic Lieb lattice with an appropriate termination.

Figure 6:

Demonstration of unconventional line states in a photonic Lieb lattice [81].

(A) Schematic illustration of two flat-band NLSs in an infinite Lieb lattice. (B–E) Experimental results of line states in a finite Lieb lattice with bearded edge. (B1) Out-of-phase input line beam. (B2) Out-of-phase output without the lattice. (B3) Out-of-phase output through the lattice. (B4) Measured k-space spectrum of (B3), with a dashed square marking the first BZ. (C1–C4) The same as in (B1–B4) but the line beam is in-phase. (D, E) Numerical simulation results showing the out-of-phase line beam remains intact but the in-phase line deteriorates after propagating a long distance through the lattice.

Typical experimental results of the flat-band line states in finite photonic Lieb lattices with the bearded edge are depicted in Figure 6. An input probe beam is shaped into a dotted line pattern with alternatingly opposite phase (see Figure 6B1) and is sent into the cw-laser-written photonic Lieb lattices, as shown in Figure 3B. In the absence of the lattice, the line shape cannot be preserved after free propagation because of the interference between pearls and diffraction of each pearl (see Figure 6B2). In contrast, when such a line beam is launched into the Lieb lattice, its overall intensity pattern is well maintained (Figure 6B3). For direct comparison, the corresponding results for an in-phase line beam (when all pearls are made with equal phase) are presented in Figure 6C1–C3. In the latter case, the line deteriorates as the energy couples to zero-amplitude lattice sites (Figure 6C3). Moreover, a dramatic difference is observed in the k-space spectrum between the out-of-phase and in-phase line beams (Figure 6B4 and C4): the spectrum of the out-of-phase line is distributed along the BZ edges where the flat-band touches with the dispersive bands, whereas that of the in-phase one goes to the center of the first BZ. One can see clearly the difference between the out-of-phase beam (intact as unconventional line states) and in-phase beam (strongly distorted). Such unconventional line states cannot be expressed as a linear combination of the previously observed boundary-independent bulk CLSs but rather arise from the nontrivial real-space topology as predicated by the theory [92], [93].

These line states not only represent a novel type of flat-band eigenstates but may also be useful for potential applications such as diffraction-free image transmission. Image transmission based on conventional CLSs has been demonstrated but is limited to a certain necklace-like shape as a superposition of “ring modes” [35]. By combining the features of the CLSs and the new line states, it is possible to realize large-scale image transmission with virtually any pattern extended to lattice boundaries [105]. To illustrate this, the transmission of three different letters based on the combination of the line states and the CLSs is realized with a bearded Lieb lattice [81].

Different from the Lieb lattice, where the flat-band touches the BZ edge, there are also flat-band lattices where the flat-band touching emerges at other high-symmetry points such as the sHCLs. sHCL was first studied more than two decades ago in the context of electronic systems [95], [115]. Recently Dirac cones and conical diffraction in such superlattices were also theoretically investigated [104], [116], [117] in cold atoms and optics, but experimental study is lacking because of the difficulty in constructing such sophisticated lattices. sHCL has five lattice sites (a–e) per unit cell, as shown in Figure 7A, and its tight-binding band structure consists of five bands, including a completely flat-band touching two dispersive conical bands at the center (Γ point) of the first BZ, which resembles the pseudospin-1 Dirac cone in the Lieb lattice. Interestingly, there are also additional graphene-like pseudospin-1/2 Dirac cones at the BZ corners in Figure 7B. Because the flat-band touches the BZ center, there are also NLSs in sHCLs. According to the geometry of sHCLs, there are two different types of line states in finite lattices with specially tailored boundaries, which manifest as the NLSs in infinite flat-band systems: straight line states along the x-direction and the zigzag line states along the y-direction, as shown in Figure 7C,D. Typical experimental results of the zigzag line states in a cw-laser-written finite sHCL with bearded edges are shown in Figure 7E–H. To excite the zigzag line state, the probe beam is shaped into the zigzag pattern and launched into the lattice vertically (see Figure 7E in which the white rectangle marks the input position). One clearly finds that only the out-of-phase beam can evolve into a flat-band zigzag line state with a localized intensity pattern (Figure 7F3) after exiting the lattice. It is worth mentioning that the zigzag line states realized here do not exist in either the Lieb or the Kagome lattices, which are unique because of the special geometry of sHCLs. More interestingly, the k-space spectra of the two line states reside in the higher order BZ and occupy the higher order BZ centers where the flat-band touches the dispersive bands (Figure 7H), which is also different from that in Lieb lattices (for which the band-touching is at the corners of the BZ). In addition, sHCL has a geometrical structure in real space that is different from that of the Lieb lattice. These differences make the distinct properties of the line states in sHCL, e.g. the zigzag line states that are absent in the Lieb lattice. These results again confirm that the line states are related to the flat-band touching the dispersive bands.

Figure 7:

Demonstration of unconventional line states in a finite photonic sHCL with bearded edges [85].

(A) Schematic of sHCL structure consisting of five sites (a–e) shown in dark-dashed square, with a flat-band mode (the CLS) shown in red-dashed square. Sites with zero amplitudes are denoted by gray color, and those with nonzero amplitudes of opposite phase are denoted by red and black colors. (B) Calculated band structure based on the tight-binding model. (C, D) sHCL with two different cutting boundaries that support (C) a “straight” line along x direction and (D) a “zigzag” line along y-direction. Red and black colors represent opposite phase. (E) The cw-laser-written sHCL. The white dashed line marks the position of the probe beam. (F) From left to right: (F1) the input of the out-of-phase probe beam, (F2) output without the lattice, (F3) output through the lattice, and (F4) simulated version of (F3). (G) Setup is as in (F) but with an in-phase probe. (H) Momentum space spectrum of (F3), where the dashed lines outline the first and second BZs.

6 Noncontractible loop states in Kagome lattices

As mentioned above, in finite Lieb or sHCL lattices, the straight or zigzag line states can be preserved under appropriately chosen boundaries. It is natural to ask whether this behavior is universal to all singular flat-band lattices. In fact, this is not always the case. Taking the Kagome lattices as an example, although these lattices have been the focus of numerous studies [24], [52], [105], [118], [119], [120], [121], the NLSs originally proposed have never been realized in the Kagome lattices, as it is not feasible to generate an infinite lattice or a torus lattice in experiments. For NLSs in the Kagome lattices, the initial research started with the line states in a truncated system, because Lieb and Kagome photonic lattices are both singular flat-band systems [93]. However, it was found that the line states in finite Kagome lattices are not stable, as their energy can easily dissipate into the bulk [86]. Further theoretical analysis revealed that the line states cannot preserve in truncated Kagome lattices, as a straight-line state cannot be the flat-band eigenmode regardless of the lattice edges, in sharp contrast to the case of Lieb lattices [81].

The experiments by Ma et al. [86] tackled the above problem in two ways. On one hand, they realized the robust boundary modes (RBMs) spanning the whole boundary of the finite lattice, as proposed already in Ref. [93]. The boundary modes arising from the NLSs are robust against perturbation and even possess the self-healing feature during propagation due to bulk-edge correspondence. On the other hand, a torus geometry with periodicities is difficult to be realized in real systems, but one can still preserve the periodicity at least along one direction by using a lattice with an annular (also known as Corbino) geometry. So they fabricated a Corbino-geometry Kagome lattice, and thereby directly observed the NLSs. We note that the Corbino geometry has well-known applications in physics [122], [123], [124], such as in the design of graphene heterostructures for detecting fractional quantum Hall states or superconducting waveguides for illustrating circuit quantum electrodynamics.

In Figure 8, the two alternative approaches are shown to reveal the NLSs. Two NLSs are shown in Figure 8A in an infinite Kagome photonic lattice and in Figure 8B on a torus. An RBM can be considered as a combination of the NLSs by cutting the torus in both toroidal and poloidal directions [93]. They create a space with four sides open as if it was a torus generated by truncation. If there are two pairs of NLSs on the torus (one in toroidal and the other in poloidal directions), then by cutting the torus along these directions one can expand it into a finite-sized lattice with four sides open. Then the state existing at the edge of finite size will be the superposition state of the four NLSs (Figure 8C). To observe this boundary mode, an input probe beam is shaped into a necklace of parallelogram shape with opposite phase. When such a probe beam is launched into the lattice boundary, we see clearly that the probe beam is preserved after passing through the lattice (Figure 8E1). The energy of the boundary mode couples into other sites out of the loop (Figure 8E2) if the neighboring sites are in-phase. As such, Kagome lattices with desired “cutting” edges can support RBMs, as an indirect illustration of the NLSs due to bulk-edge correspondence. Such RBMs also can be preserved during propagation in case of superposition with other modes, and possess “self-healing” features against perturbation in either the initial phase or amplitude [86].

Figure 8:

Demonstration of unconventional loop states in a photonic Kagome lattice [86].

(A) Illustration of two NLSs in an infinitely extended Kagome lattice. (B) Illustration of two NLSs winding around a torus, mimicking the 2D infinite lattice. (C) An RBM (orange loop) in a finite Kagome lattice with flat cutting edges. (D) Schematic diagram of a Corbino-shaped Kagome lattice, where the NLS is illustrated by the orange circle. In all figures, black sites are of zero amplitude, while the blue and red ones distinguish nonzero sites with opposite phases. (E) From left to right: (E1, E2) Experimental results of the RBM under out-of-phase and in-phase condition; (E3, E4) Simulation result corresponding to (E1, E2) but for a much longer propagation distance (40 mm). (F) Experimental realization of the Corbino-geometry lattice (F1) corresponding to (D), along with demonstration of the NLS in experiment (F2) and simulations after propagation distance of 10 mm (F3) and 40 mm (F4) under out-of-phase excitation condition. Insets are from input ring necklace of the probe beam.

Another more direct method to demonstrate NLSs is also shown in Figure 8, which is light localization for the NLSs in the Corbino-shaped photonic Kagome lattice. As illustrated in Figure 8D, with this lattice geometry one can realize the NLS along the toroidal direction, akin to an infinite system in one dimension. For this geometry, the distances between B and C sublattices are equivalent over each ring but increase with the ring diameter; the distances between A and B (or C) sublattices are also equal but these distances within and outside the ring are not dependent. Such a lattice is generated with site-by-site laser writing in a nonlinear crystal, and a typical written lattice is shown in Figure 8F1. Then, a ring-shaped necklace pattern under out-of-phase condition is launched to excite the NLS depicted in Figure 8D. The corresponding experimental results are shown in Figure 8F2, where one can clearly see that the necklace beam remains intact after 10 mm of propagation, as also verified by numerical simulations to even longer propagation distances (Figure 8F3,F4). If the input necklace beam does not have the required alternating phase, it is strongly distorted during propagation since such an input cannot evolve into the NLS. Therefore, these results represent the first demonstration of the NLS originally proposed for the infinite system in Kagome lattices as a direct manifestation of the real-space topology [86], [92], [93].

7 Summary and outlook

We have presented a brief overview of the recent experimental advances of light localization in 1D and 2D engineered flat-band photonic lattices, with an emphasis on the optical induction technique and unconventional flat-band states. Using optical induction, we have designed and realized photonic lattices with a variety of shapes and boundaries, such as Lieb lattices, Kagome lattices, super-honeycomb lattices, and rhombic lattices. The fine-tuned photonic structures can be established with the adjustment of lattice period, intensity and phase of the writing beam, and nonlinearity. Based on these flat-band micro-structured photonic platforms, we have demonstrated a variety of linearly localized states, such as the fundamental CLSs and the unconventional line states. The concept and techniques presented here could be developed for applications in other structured photonic media, such as photonic crystals and photonic crystal fibers. For example, such schemes could be used to make optical fibers with particular modal properties, or microscopic optical cavities if propagation in the third dimension can be blocked in a convincing way.

Before concluding, we briefly comment on a few notable directions related to flat-band phenomena pursued in other platforms. For instance, in flat-band topology, topological corner states have been realized in photonic Kagome lattices by El Hassan’s group [55]. This kind of corner modes relies on crystalline symmetries [125], [126], [127] and can be viewed as a variant of crystalline topological insulators [128]. Such simple and convenient means of implementation, in contrast to the much more complex designs with helical optical waveguides [62], drastically enhance the prospects of incorporating these ideas in photonic technological devices. Similar corner modes have also been explored in acoustic metamaterials [129], [130] and microwave circuits [131]. The report by Lim et al. [132] demonstrated that continuous transformations between Lieb and Kagome lattices are accompanied by the motion of Dirac point degeneracies through the Brilllouin zone. The successful implementation of 2D photonic Moiré lattices by Ye’s group [133] made it possible to realize the exciting characteristics of the “magic” twist angles (not merely in the field of light localization), and the existence of flat-bands at certain angles is the physical and fundamental physical origin of Mott insulators [16], [17], [18]. Moiré lattices may manifest as an almost arbitrary geometry that is consistent with the crystallographic symmetry groups of the sublattices, which provide a powerful tool for controlling the flow of light. Structured microcavities forming lattices for exciton-polaritons have been used to observe nonlinear localized modes in flat-bands [134] and the generation of flat-bands using strain [135]. In contrast to the above platforms, circuit quantum electrodynamics, which is not limited to planar Euclidean lattice geometries, was recently used to realize a variety of lattices including flat-band lattices on the hyperbolic space [123].

In summary, the study of artificial photonic flat-band lattices and flat-band states has provided and will continue to provide insights into understanding fundamental concepts and phenomena in interdisciplinary areas such as condensed matter physics, materials science, cold atoms, metamaterials, and photonics, which may also lead to new techniques to control the flow of light and to develop novel photonic devices.