Optimal Reciprocal Reinsurance under VaR or TVaR Constraint

Hung-Hsi Huang; Ching-Ping Wang

doi:10.1515/apjri-2021-0023

Article

Optimal Reciprocal Reinsurance under VaR or TVaR Constraint

Hung-Hsi Huang and Ching-Ping Wang

Published/Copyright: December 9, 2021

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Asia-Pacific Journal of Risk and Insurance Volume 16 Issue 2

Abstract

Most existing researches on optimal reinsurance contract are based on an insurer’s viewpoint. However, the optimal reinsurance contract for an insurer is not necessarily to be optimal for a reinsurer. Hence, this study aims to develop the optimal reciprocal reinsurance which satisfies the benefits of both the insurer and reinsurer. Additionally, due to legislative restriction or risk management requirement, the wealth of insurer and reinsurer are frequently imposed upon a VaR (Value-at-Risk) or TVaR (Tail Value-at-Risk) constraint. Therefore, this study develops an optimal reciprocal reinsurance contract which maximizes the common benefits (evaluated by weighted addition of expected utilities) of the insurer and reinsurer subject to their VaR or TVaR constraints. Furthermore, for avoiding moral hazard problem, the developed contract is additionally restricted to a regular form or incentive compatibility (both indemnity schedule and retained loss schedule are continuously nondecreasing).

Keywords: optimal reinsurance; VaR; TVaR; reciprocal reinsurance; moral hazard

Corresponding author: Hung-Hsi Huang, Professor, Department of Banking and Finance, National Chiayi University, No. 580, Sinmin Rd., Chiayi City 60054, Taiwan, E-mail: d86723002@ntu.edu.tw

Appendix A: Proof of Proposition 1

Given any outcome of x ̃ , the optimal reinsurance indemnity I * x in Expression (15) is equivalent to maximize the Hamiltonian. Mathematically,

(A1) Maximize 0 ≤ I ( x ) ≤ x H ≡ U I W I 0 − P − x + I x + λ U R W R 0 + P − I x f ( x ) .

The first and second derivatives of H with respect to I x are as follows.

(A2) ∂ H ∂ I = U I ′ W I 0 − P − x + I x − λ U R ′ W R 0 + P − I x f x , ∂ 2 H / ∂ I 2 = U I ″ W I 0 − P − x + I x + λ U R ″ W R 0 + P − I x f ( x ) < 0 ⋅

Let I ̂ x be the solution of ∂H/∂I = 0; that is,

(A3) U I ′ W I 0 − P − x + I ̂ x − λ U R ′ W R 0 + P − I ̂ x = 0 .

Based on Expressions (3) and (4), the solution in Eq. (A3) is existent and unique. Indeed, H has a peak at I ̂ x . Additionally, since H is globally concave in I (∂² H/∂I ² < 0), Eq. (A3) is a first order necessary and sufficient condition. Hence, I ̂ x can be viewed as the optimal reciprocal reinsurance without the constraint 0 ≤ I(x) ≤ x and any risk constraint. Next, differentiating Eq. (A3) with respect to x yields

(A4) U I ″ W I 0 − P − x + I ̂ x − 1 + I ̂ ′ x − λ U R ″ W R 0 + P − I ̂ x − I ̂ ′ x = 0 .

Incorporating with Equations (A3) and (A4) yields

(A5) U I ″ W I 0 − P − x + I ̂ x − 1 + I ̂ ′ x U I ′ W I 0 − P − x + I ̂ x − λ U R ″ W R 0 + P − I ̂ x − I ̂ ′ x λ U R ′ W R 0 + P − I ̂ x = 0 .

Since the ARA (absolute risk aversion coefficient) for a utility function U W is defined by − U ″ W / U ′ W , Eq. (A5) implies

(A6) 0 < I ̂ ′ x = ARA I W ̃ I ARA I W ̃ I + ARA R W ̃ R < 1 .

Based on Eq. (A6) and the constraint 0 ≤ I(x) ≤ x, the optimal reinsurance accordingly takes the form

(A7) I * x = min I ̂ x , x i f I ̂ 0 > 0 , I ̂ x i f I ̂ 0 = 0 , max I ̂ x , 0 i f I ̂ 0 < 0 ⋅

Subsequently, differentiating Eq. (A3) with respect to P yields

(A8) ∂ I ̂ x ∂ P − 1 U I ″ W I 0 − P − x + I ̂ x = λ − ∂ I ̂ x ∂ P + 1 U R ″ W R 0 + P − I ̂ x = 0 .

Equation (A8) implied that

(A9) ∂ I ̂ x ∂ P = 1 .

Equation (A7) is the same as Eq. (17), and combining Equations (A6) and (A9) yields Eq. (18). Thus, the proof of Proposition 1 is completed.

Appendix B: Proof of Proposition 2

Incorporating Expression (26a) and the fact of I ( x ) ∈ I , the optimal reciprocal reinsurance I * x should belong to I R defined by

(A10) I R = I x ∈ I | I x ̂ α R = v ̂ R , I x − v ̂ R ≤ x − x ̂ α R + , 0 ≤ x < ∞ .

Note that Expression (A10) implies that v ̂ R < x ̂ α R when the reinsurance’s VaR constraint is binding. Based on Expression (A10), the optimization problem of Expression (26) can be rewrite as follows,

(A11) Maximize I ( x ) ∈ I R E U I W I 0 − P − x ̃ + I x ̃ + λ U R W R 0 + P − I x ̃ .

Based on Expression (A10), we define F R as the feasible set of I * x , as follows,

(A12) F R = 0 ≤ I x ≤ x | v ̂ R ⋅ I x ≥ x ̂ α R ≤ I x ≤ v ̂ R + x − x ̂ α R + , 0 ≤ x < ∞ .

The feasible set F R is shown on the gray area in Figure 2, which contains the area that

(A13) 0 ≤ I x ≤ min x , v ̂ R f o r x ≤ x ̂ α R a n d v ̂ R ≤ I x ≤ v ̂ R + x − x ̂ α R f o r x ≥ x ̂ α R .

Appendix A shows that H is global concave with I x and has a peak at I ̂ x . This means that I ̂ x can be viewed as the optimal reciprocal reinsurance without the constraint 0 ≤ I x ≤ x and any risk constraint. On the other hand, if there imposes some constraints in I x , then the optimal reinsurance I * x should have the least difference between I ̂ x among these contracts which meet these constraints. Hence, the optimal reciprocal reinsurance problem in Expression (A11) can be shortly rewritten as follows,

(A14) I * x = arg min I ( x ) ∈ I R I x − I ̂ x .

Obviously, I R is a subset of F R . For convenience, this study finds the I * x in Expression (A14) via two steps, as follows.

Step 1: Find I * x = arg min I ( x ) ∈ F R I x − I ̂ x .

Step 2: Verify I * x ∈ I R .

This study employs the geometric analysis to find the I * x for Step 1. First, F R is shown as the gray area on the x − I x plane in Figure 2. Next, referring to Figure 1, I ̂ x is drawn on Figure 2 for the three situations ( I ̂ 0 = 0 , I ̂ 0 < 0 and I ̂ 0 > 0 ), respectively. Referring to Figure 2, we define E R , v ̂ R as the intersection of I ̂ x and I x = v ̂ R . Notably, since I ̂ ′ x ∈ ( 0,1 ) , the intersection point is existent and unique. If x ̂ α R ≤ v ̂ R , then the reinsurer’s VaR constraint is unbinding. Thus, Proposition 2 considers the situation of x ̂ α R > v ̂ R . Next, we define B R , v ̂ R + B R − x ̂ α R as the intersection of I ̂ x and I x = v ̂ R + x − x ̂ α R . Referring to Figure 2, three cases ( I ̂ 0 = 0 , I ̂ 0 < 0 and I ̂ 0 > 0 ) are separately analyzed as follows.

Case 1: I ̂ 0 = 0 shown on I A 1 x in Figure 2.

Since I ̂ ′ x ∈ ( 0,1 ) , we obtain the relationship v ̂ R < E R < x ̂ α R v ̂ R for x > E _R. Based the geometric analysis, the solution of I * x for Step 1 is expressed as follows,

(A15) I * x = I A 1 x ≡ I ̂ x ⋅ I 0 ≤ x < E R + v ̂ R ⋅ I E R ≤ x < x ̂ α R + v ̂ R + x − x ̂ α R ⋅ I x ̂ α R < x < B R + I ̂ x ⋅ I x ≥ B R .

Case 2: I ̂ 0 < 0 shown on I A 2 x in Figure 2.

Since I ̂ 0 < 0 and I ̂ ′ x ∈ ( 0,1 ) , the intersection d ̂ , 0 of I ̂ x and x-axis is existent and unique. Additionally, since I ̂ ′ x ∈ ( 0,1 ) , we obtain the relationship 0 < d ̂ < E R < x ̂ α R v ̂ R for x > E _R. Based the geometric analysis, the solution of I * x for Step 1 is expressed as follows,

(A16) I * x = I A 2 x ≡ I ̂ x ⋅ I d ̂ < x < E R + v ̂ R ⋅ I E R ≤ x ≤ x ̂ α R + v ̂ R + x − x ̂ α R ⋅ I x ̂ α R < x < B R + I ̂ x ⋅ I x ≥ B R .

Case 3: I ̂ 0 > 0 shown on I A 3 x and I A 4 x in Figure 2.

Define A , A as the intersection of I ̂ x and I x = x . I A 3 x and I A 4 x show the situations of A < v ̂ R and A > v ̂ R , respectively. Since I ̂ ′ x ∈ ( 0,1 ) , we obtain A > I ̂ 0 . Additionally, since I ̂ ′ x ∈ ( 0,1 ) , the reinsurance’s VaR is unbinding if I ̂ 0 > v ̂ R . Thus, Proposition 2 considers the situation of I ̂ 0 < v ̂ R . Hence, we have the relation of I ̂ 0 < min A , v ̂ R . Accordingly, I A 3 x and I A 4 x demonstrate the situations of 0 0 and I ̂ ′ x ∈ ( 0,1 ) , we obtain that I ̂ x > x for 0 < x < A, A ≤ I ̂ x < v ̂ R for A ≤ x < E _R, and I ̂ x > v ̂ R for x > E _R. Based the geometric analysis, the solution of I A 3 x for Step 1 is expressed as follows,

(A17) I * x = I A 3 x ≡ x ⋅ I 0 ≤ x < A + I ̂ x ⋅ I A < x < E R + v ̂ R ⋅ I E R ≤ x ≤ x ̂ α R + v ̂ R + x − x ̂ α R ⋅ I x ̂ α R < x < B R + I ̂ x ⋅ I x ≥ B R .

For I A 4 x , since I ̂ ′ x ∈ ( 0,1 ) , we obtain that 0 < E R < A < x ̂ α R x for 0 < x < A, I ̂ x < x for x > A, I ̂ x < v ̂ R for 0 < x < E _R, and I ̂ x > v ̂ R for x > E _R. Based on the geometric analysis, the solution of I A 4 x for Step 1 is expressed as follows,

(A18) I * x = I A 4 x ≡ x ⋅ I 0 ≤ x < v ̂ R + v ̂ R ⋅ I v ̂ R ≤ x ≤ x ̂ α R + v ̂ R + x − x ̂ α R ⋅ I x ̂ α R < x < B R + I ̂ x ⋅ I x ≥ B R .

For step 2, we can easily check that I A 1 x ∈ I R , I A 2 x ∈ I R , I A 3 x ∈ I R , and I A 4 x ∈ I R . Combining Expressions (A15) through (A18), the form of I * x can be solely expressed as follows.

(A19) I * x = max 0 , min x , v ̂ R , I ̂ x ⋅ I x < x ̂ α R + min I ̂ x , v ̂ R + x − x ̂ α R ⋅ I x ≥ x ̂ α R .

Expression (A19) is the same as Expression (27), and hence the proof is completed.

Appendix C: Proof of Proposition 3

Appendix A shows that I ̂ x can be viewed as the optimal reciprocal reinsurance without the constraint 0 ≤ I x ≤ x and any risk constraint. Restated, R ̂ x ≡ x − I ̂ x is optimal retained loss schedule without the constraint 0 ≤ R x ≤ x and any risk constraint.

Compared Expression (28) to Expression (26), we find that the programming problem for Expression (28) has similar mathematical form as that for Expression (23). Appendix B shows that the programming problem in Expression (26) is equivalent to the following program,

(A20) I * x = arg min I ( x ) ∈ I R I x − I ̂ x , I R = I x ∈ I | I x ̂ α R = v ̂ R , I x − v ̂ R ≤ x − x ̂ α R + , 0 ≤ x < ∞ .

Accordingly, the programming problem for Expression (28) can be rewritten as follows.

(A21) R * x = arg min R ( x ) ∈ I I R x − R ̂ x , I I = R x ∈ I | R x ̂ α R = v ̂ I , R x − v ̂ I ≤ x − x ̂ α I + , 0 ≤ x < ∞ .

Expression (A21) is analogous of Expression (A20), besides different notations. Referring to Expression (27), we can obtain the optimal retained loss schedule:

(A22) R * x = max 0 , min x , v ̂ I , R ̂ x ⋅ I x < x ̂ α I + min R ̂ x , v ̂ I + x − x ̂ α I ⋅ I x ≥ x ̂ α I .

Since I * x ≡ x − R * x , Expression (A22) implies that

(A23) I * x = min x , max 0 , x − v ̂ I , I ̂ x ⋅ I x < x ̂ α I + max I ̂ x , x ̂ α I − v ̂ I ⋅ I x ≥ x ̂ α I .

Expressions (A22) and (A23) are equal to Expressions (29) and (30), respectively. Thus, the proof is completed.

Appendix D: Proof of Proposition 4

For the case of I ̂ 0 = 0 , the optimal contractual forms are I A 1 x in Figure 2 and I B 1 x in Figure 4 when the reinsurer’s and the insurer’s VaR constraints are binding only, respectively. Thus, we guess that the optimal contractual form for both reinsurer’s and insurer’s VaR constraints binding is related to the combination of I A 1 x and I B 1 x . Referring to I A 1 x and I B 1 x , this study consider the following three situations: x ̂ α I < x ̂ α R , x ̂ α I > x ̂ α R and x ̂ α I = x ̂ α R .

Situation 1: x ̂ α I < x ̂ α R for I C 1 x in Figure 5.

In this situation, we will claim that the optimal contractual form can be represented as I C 1 x . Besides C ₁ = (B _I + E _R)/2, all the notations in I C 1 x have same definition as those in I A 1 x and I B 1 x . Now, we claim that the parameters in I C 1 x have the following order:

(A24) 0 < E I < x ̂ α I < B I < C 1 < E R < x ̂ α R < B R .

First, referring to I A 1 x , the reinsurer’s VaR binding implies the order of E R < x ̂ α R I ̂ B I and hence B _I < E _R. In sum, combining the above inferences and the equality of C ₁ = (B _I + E _R)/2 yields the Expression (A24). Additionally, according to the same analyses for I A 1 x and I B 1 x , we can obtain

(A25) I C 1 x = I B 1 x f o r 0 ≤ x ≤ C 1 a n d I C 1 x = I A 1 x f o r x > C 1 .

Situation 2: x ̂ α I > x ̂ α R for I C 2 x in Figure 5.

In this situation, we will claim that the optimal contractual form can be represented as I C 2 x . Besides C ₂ = (B _R + E _I)/2, all the notations in I C 2 x have same definition as those in I A 1 x and I B 1 x . Now, we claim that the parameters in I C 2 x have the following order:

(A26) 0 < E R < x ̂ α R < B R < C 2 < E I < x ̂ α I < B I .

First, referring to I A 1 x , the reinsurer’s VaR binding implies the order of 0 < E R < x ̂ α R x ̂ α R and both the insurer’s and reinsurer’s VaR constraints are binding, the line x − v ̂ I must be below the line v ̂ R + x − x ̂ α R and hence B _R < E _I. In sum, combining the above inferences and the equality of C ₂ = (B _R + E _I)/2 yields the Expression (A26). Additionally, according to the same analyses for I A 1 x and I B 1 x , we can obtain

(A27) I C 2 x = I A 1 x f o r 0 ≤ x ≤ C 2 a n d I C 2 x = I B 1 x f o r x > C 2 .

Situation 3: x ̂ α I = x ̂ α R = x ̂ α for I C 3 x in Figure 7.

According to the analyses for Situations 1 and 2, when both the insurer’s and reinsurer’s VaR constraints are binding, we can infer that the line x − v ̂ I must be above (below) the line v ̂ R + x − x ̂ α R if x ̂ α I < x ̂ α R ( x ̂ α I > x ̂ α R ). Now we consider the other case where the lines x − v ̂ I and v ̂ R + x − x ̂ α R exactly coincide. The possible contractual form is expressed as the graph of I C 3 x in Figure 7 below. First we depict the I ̂ x and the line x − v ̂ I = v ̂ R + x − x ̂ α R on the graph of I C 3 x . Since the reinsurer’s VaR constraint is binding, I * x = min I ̂ x , v ̂ R for x < x ̂ α . However, in this case, I * x never deviates from the insurer’s VaR constraint. Thus, the insurer’s and the reinsurer’s VaR are never simultaneously binding when x − v ̂ I = v ̂ R + x − x ̂ α R or x ̂ α I = x ̂ α R = x ̂ α . Finally, Expressions (A25) and (A27) are equivalent to Expressions (31a) and (31b), respectively. Thus, the proof is completed.

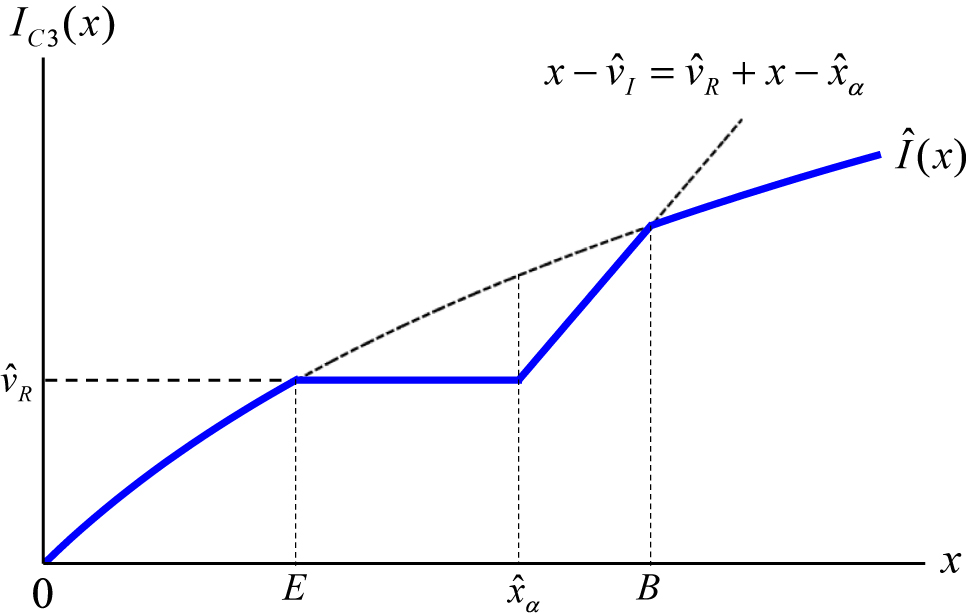
$Figure 7: Optimal reinsurance with x ̂ α I = x ̂ α R = x ̂ α ${\hat{x}}_{\alpha }^{\text{I}}={\hat{x}}_{\alpha }^{\text{R}}={\hat{x}}_{\alpha }$ .$

Figure 7:

Optimal reinsurance with x ̂ α I = x ̂ α R = x ̂ α .

Appendix E: Proof of Proposition 5

The Lagrange function for optimization problem in Expression (37) is as follows.

(A28) Maximize I ( x q ) ∈ I L ≡ ∫ 0 1 U I W I 0 − P − x q + I ( x q ) + λ U R W R 0 + P − I ( x q ) d q + μ 1 ∫ 0 1 I ( x q ) − x q + P − TVaR I I α I < q ≤ 1 d q + μ 2 ∫ 0 1 TVaR R + P − I ( x q ) I α R < q ≤ 1 d q

where μ ₁ > 0 and μ ₂ > 0 denote the Lagrange multiplier coefficients. For any quantile q, the above optimization problem is equivalent to maximize the Hamiltonian. Mathematically,

(A29) Maximize I ( x q ) ∈ I H ≡ U I W I 0 − P − x q + I ( x q ) + λ U R W R 0 + P − I ( x q ) + μ 1 I ( x q ) − x q + P − TVaR I I α I < q ≤ 1 + μ 2 TVaR R + P − I ( x q ) I α R < q ≤ 1 .

The first and second derivatives of H with respect to I(x _q) are as follows.

(A30) ∂ H ∂ I ( x q ) = U I ′ W I 0 − P − x q + I ( x q ) − λ U R ′ W R 0 + P − I ( x q ) + μ 1 I α I < q ≤ 1 − μ 2 I α R < q ≤ 1 , ∂ 2 H ∂ I ( x q ) 2 = U I ″ W I 0 − P − x q + I ( x q ) + λ U R ″ W R 0 + P − I ( x q ) < 0 ⋅

Similar to Eq. (16), I ̂ ( x q ) is the unique solution of the following equation.

(A31) U I ′ W I 0 − P − x q + I ̂ ( x q ) − λ U R ′ W R 0 + P − I ̂ ( x q ) = 0 .

Additionally, let I ̂ 1 ( x q ) , I ̂ 2 ( x q ) and I ̂ 3 ( x q ) respectively be the solutions of the following three equations.

(A32) U I ′ W I 0 − P − x q + I ̂ 1 ( x q ) − λ U R ′ W R 0 + P − I ̂ 1 ( x q ) + μ 1 = 0 .

(A33) U I ′ W I 0 − P − x q + I ̂ 2 ( x q ) − λ U R ′ W R 0 + P − I ̂ 2 ( x q ) + μ 1 − μ 2 = 0 .

(A34) U I ′ W I 0 − P − x q + I ̂ 3 ( x q ) − λ U R ′ W R 0 + P − I ̂ 3 ( x q ) − μ 2 = 0 .

Equation (A31) through (A34) implies that

(A35) ∂ I ̂ 1 ( x q ) ∂ x q = ∂ I ̂ 2 ( x q ) ∂ x q = ∂ I ̂ 3 ( x q ) ∂ x q = ∂ I ̂ ( x q ) ∂ x q , ∀ q .

Since H is global concave with x _q and has a peak at I ̂ ( x q ) , we obtain the relation:

(A36) I ̂ 1 ( x q ) > I ̂ 2 ( x q ) > I ̂ 3 ( x q ) a n d I ̂ 1 ( x q ) > I ̂ ( x q ) > I ̂ 3 ( x q ) .

Based on Equations (A35) and (A36), there exists positive numbers δ ₁ > 0, δ ₂ > 0 and δ ₃ > 0 such that

(A37) I ̂ 1 ( x q ) = I ̂ ( x q ) + δ 1 , I ̂ 2 ( x q ) = I ̂ ( x q ) + δ 2 − δ 3 a n d I ̂ 3 ( x q ) = I ̂ ( x q ) − δ 3 .

Similar to Appendix D, the three situations of α _I > α _R, α _I < α _R and α _I = α _R = α are considered to solve the optimization problem.

Situation 1: α _I > α _R

Since I ̂ 0 = 0 , I ̂ ( x q ) belongs to the regular form. Additionally, the optimal reinsurance I*(x _q) should belong to the regular form. Accordingly, based on Eq. (A30) through (A34) and Eq. (35), the optimal reinsurance contractual form can be expressed as follows.

(A38) I * ( x q ) = I ̂ ( x q ) f o r 0 ≤ q ≤ α R , max I ̂ x ̂ α R , I ̂ ( x q ) − δ 3 f o r α R < q < α I , min I ̂ x ̂ α I + x q − x ̂ α I , I ̂ x + δ 2 − δ 3 f o r α I ≤ q ≤ 1 ,

where δ ₂ and δ ₃ are selected such that both the insurer’s and reinsurer’s TVaR constraints are simultaneously binding.

Situation 2: α _I < α _R

Similar to the analysis in situation 1, we can obtain the optimal reinsurance contractual form as follows.

(A39) I * ( x q ) = I ̂ ( x q ) f o r 0 ≤ q ≤ α I , min I ̂ x ̂ α I + x q − x ̂ α I , I ̂ ( x q ) + δ 1 f o r α I < q < α R , max I ̂ x ̂ α R + δ 1 , I ̂ x + δ 1 − δ 3 f o r α R ≤ q ≤ 1 ,

where δ ₁ and δ ₃ are selected such that both the insurer’s and reinsurer’s TVaR constraints are simultaneously binding.

Situation 3: α _I = α _R = α

For 0 ≤ q ≤ α, incorporating Expressions (A30) and (A31) yields

(A40) U I ′ W I 0 − P − x q + I ̂ ( x q ) − λ U R ′ W R 0 + P − I ̂ ( x q ) .

Additionally, for α < q ≤ 1, incorporating Expressions (A30) and (A33) yields

(A41) U I ′ W I 0 − P − x q + I ̂ 2 ( x q ) − λ U R ′ W R 0 + P − I ̂ 2 ( x q ) + μ 1 − μ 2 = 0 .

Since H is global concave with x _q and has a peak at I ̂ ( x q ) , we obtain

(A42) I ̂ 2 ( x q ) ≥ I ̂ ( x q ) i f μ 1 ≥ μ 2 a n d I ̂ 2 ( x q ) < I ̂ ( x q ) i f μ 1 < μ 2 .

Since ∂ I ̂ 2 ( x q ) / ∂ x q = ∂ I ̂ ( x q ) / ∂ x q for all q, expression (A42) implies that there exists positive numbers δ _a ≥ 0 and δ _b ≥ 0 such that

(A43) I ̂ 2 ( x q ) ≥ I ̂ ( x q ) + δ a i f μ 1 ≥ μ 2 a n d I ̂ 2 ( x q ) = I ̂ ( x q ) − δ b i f μ 1 < μ 2 .

Incorporating Expressions (A40) and (A43) with the assumption of I * ( x q ) ∈ I yields

(A44) I * ( x q ) = I ̂ ( x q ) f o r 0 ≤ q ≤ α , min I ̂ x α + x q − x α , I ̂ ( x q ) + δ a f o r q > α a n d μ 1 ≥ μ 2 , max I ̂ x α , I ̂ ( x q ) − δ b f o r q > α a n d μ 1 < μ 2 ,

where δ _a and δ _b are selected such that both the insurer’s and reinsurer’s TVaR constraints are simultaneously binding. Expression (A44) implies that

(A45) TVaR α L ̃ R = TVaR α I * x ̃ − P ≥ TVaR α I ̂ x ̃ − P i f μ 1 ≥ μ 2 , TVaR α L ̃ R = TVaR α I * x ̃ − P < TVaR α I ̂ x ̃ − P i f μ 1 < μ 2 ⋅

Since the reinsurer’s TVaR constraint is binding, Expression (A45) implies that

(A46) TVaR α I ̂ ( x ̃ ) ≤ TVaR R + P i f μ 1 ≥ μ 2 , TVaR α I ̂ ( x ̃ ) > TVaR R + P i f μ 1 < μ 2 ⋅

Finally, Expression (38) can be directly obtained from Expressions (A38), (A39), (A44) and (A46), and hence the proof is completed.

References

Belles-Sampera, J., M. Guillén, and M. Santolino. 2014. “GlueVaR Risk Measures in Capital Allocation Applications.” Insurance: Mathematics and Economics 58 (5): 132–7. https://doi.org/10.1016/j.insmatheco.2014.06.014.Search in Google Scholar

Bernard, C., and W. Tian. 2009. “Optimal Reinsurance Arrangements under Tail Risk Managements.” Journal of Risk & Insurance 76 (3): 709–25. https://doi.org/10.1111/j.1539-6975.2009.01315.x.Search in Google Scholar

Borch, K. 1960. “Reciprocal Reinsurance Treaties.” ASTIN Bulletin 1 (4): 171–91. https://doi.org/10.1017/s0515036100009557.Search in Google Scholar

Borch, K. 1969. “The Optimal Reinsurance Treaties.” ASTIN Bulletin 5 (2): 293–7. https://doi.org/10.1017/s051503610000814x.Search in Google Scholar

Cai, J., Y. Fang, Z. Li, and G. E. Willmot. 2013. “Optimal Reciprocal Reinsurance Treaties under the Joint Survival Probability and the Joint Profitable Probability.” Journal of Risk & Insurance 80 (1): 145–68. https://doi.org/10.1111/j.1539-6975.2012.01462.x.Search in Google Scholar

Cai, J., C. Lemieux, and F. Liu. 2016. “Optimal Reinsurance from the Perspectives of Both an Insurer and a Reinsurer.” ASTIN Bulletin 46 (3): 815–49. https://doi.org/10.1017/asb.2015.23.Search in Google Scholar

Cai, J., H. Y. Liu, and R. D. Wang. 2017. “Pareto-Optimal Reinsurance Arrangements under General Model Settings.” Insurance: Mathematics and Economics 77: 24–37. https://doi.org/10.1016/j.insmatheco.2017.08.004.Search in Google Scholar

Cai, J., K. S. Tan, C. G. Weng, and Y. Zhang. 2008. “Optimal Reinsurance under VaR and CTE Risk Measures.” Insurance: Mathematics and Economics 43 (1): 185–96. https://doi.org/10.1016/j.insmatheco.2008.05.011.Search in Google Scholar

Cheung, K. C., H. K. Ling, Q. Tang, S. C. P. Yam, and F. L. Yuen. 2019. “On Additivity of Tail Comonotonic Risks.” Scandinavian Actuarial Journal 2019 (10): 837–66. https://doi.org/10.1080/03461238.2019.1626762.Search in Google Scholar

Cheung, K. C., F. Liu, and S. C. P. Yam. 2012. “Average Value-At-Risk Minimizing Reinsurance under Wang’s Premium Principal with Constraints.” ASTIN Bulletin 42 (2): 575–600.Search in Google Scholar

Chi, Y. 2012. “Reinsurance Arrangements Minimizing the Risk-Adjusted Value of an Insurer’s Liability.” ASTIN Bulletin 42 (2): 529–57.10.2139/ssrn.2039723Search in Google Scholar

Chi, Y. C., and K. S. Tan. 2021. “Optimal Incentive-Compatible Insurance with Background Risk.” ASTIN Bulletin 51 (2): 661–88. https://doi.org/10.1017/asb.2021.7.Search in Google Scholar

Chi, Y. C., and S. C. Zhuang. 2020. “Optimal Insurance with Belief Heterogeneity and Incentive Compatibility.” Insurance: Mathematics and Economics 92 (3): 104–14. https://doi.org/10.1016/j.insmatheco.2020.03.006.Search in Google Scholar

Chi, Y., and K. S. Tan. 2011. “Optimal Reinsurance under VaR and CVaR Risk Measures: A Simplified Approach.” ASTIN Bulletin 41 (2): 487–509.Search in Google Scholar

Chi, Y., and K. S. Tan. 2013. “Optimal Reinsurance with General Premium Principles.” Insurance: Mathematics and Economics 52 (2): 180–9. https://doi.org/10.1016/j.insmatheco.2012.12.001.Search in Google Scholar

D’Ortona, N. E., and G. Marcarelli. 2017. “Optimal Proportional Reinsurance from the Point of View of Cedent and Reinsurer.” Scandinavian Actuarial Journal 2017 (4): 366–75.10.1080/03461238.2016.1148627Search in Google Scholar

Fang, Y., and Z. Qu. 2014. “Optimal Combination of Quota-Share and Stop-Loss Reinsurance Treaties under the Joint Survival Probability.” IMA Journal of Management Mathematics 25 (1): 89–103. https://doi.org/10.1093/imaman/dps029.Search in Google Scholar

Gavagan, J., L. Hu, G. Y. Lee, H. Liu, and A. Weixel. 2021. “Optimal Reinsurance with Model Uncertainty and Stackelberg Game.” Scandinavian Actuarial Journal. https://doi.org/10.1080/03461238.2021.1925735.Search in Google Scholar

Golubin, A. Y. 2016. “Optimal Insurance and Reinsurance Policies Chosen Jointly in the Individual Risk Model.” Scandinavian Actuarial Journal 2016 (3): 181–97. https://doi.org/10.1080/03461238.2014.918696.Search in Google Scholar

Huang, H. H. 2006. “Optimal Insurance Contract under Value-At-Risk Constraint.” The Geneva Risk and Insurance Review 31 (2): 91–110. https://doi.org/10.1007/s10713-006-0557-5.Search in Google Scholar

Ignatov, Z. G., V. K. Kaishev, and R. S. Krachunov. 2004. “Optimal Retention Levels, Given the Joint Survival of Cedent and Reinsurer.” Scandinavian Actuarial Journal 2004 (6): 401–30.10.1080/03461230410020437Search in Google Scholar

Jiang, W. J., H. P. Hong, and J. D. Ren. 2021. “Pareto-Optimal Reinsurance Policies with Maximal Synergy.” Insurance: Mathematics and Economics 96 (1): 185–98. https://doi.org/10.1016/j.insmatheco.2020.11.009.Search in Google Scholar

Jorion, P. 2009. Value at Risk: The New Benchmark for Managing Financial Risk, 3rd ed. New York: McGraw-Hill International Edition.Search in Google Scholar

Lu, Z. Y., L. L. Meng, Y. Wang, and Q. Shen. 2016. “Optimal Reinsurance under VaR and TVaR Risk Measures in the Presence of Reinsurer’s Risk Limit.” Insurance: Mathematics and Economics 68 (5): 92–100. https://doi.org/10.1016/j.insmatheco.2016.03.001.Search in Google Scholar

Lu, Z. Y., L. P. Liu, and S. W. Meng. 2013. “Optimal Reinsurance with Concave Ceded Loss Functions under VaR and CTE Risk Measures.” Insurance: Mathematics and Economics 52 (1): 46–51. https://doi.org/10.1016/j.insmatheco.2012.10.007.Search in Google Scholar

Raviv, A. 1979. “The Design of an Optimal Insurance Policy.” The American Economic Review 69 (1): 84–96.10.1007/978-94-015-7957-5_13Search in Google Scholar

Wang, C. P., and H. H. Huang. 2016. “Optimal Insurance Contract under VaR and CVaR Constraints.” The North American Journal of Economics and Finance 37 (3): 110–27. https://doi.org/10.1016/j.najef.2016.03.007.Search in Google Scholar

Wang, C. P., D. Shyu, and H. H. Huang. 2005. “Optimal Insurance Design under a Value-At-Risk Framework.” The Geneva Risk and Insurance Review 30 (2): 161–79. https://doi.org/10.1007/s10713-005-4677-0.Search in Google Scholar

Wang, S. 1996. “Premium Calculation by Transforming the Layer Premium Density.” ASTIN Bulletin 26 (1): 71–92. https://doi.org/10.2143/ast.26.1.563234.Search in Google Scholar

Xu, Z. Q., X. Y. Zhou, and S. C. Zhuang. 2019. “Optimal Insurance under Rank‐dependent Utility and Incentive Compatibility.” Mathematical Finance 29 (2): 659–92. https://doi.org/10.1111/mafi.12185.Search in Google Scholar

Zhou, C. Y., and C. F. Wu. 2008. “Optimal Insurance under the Insurer’s Risk Constraint.” Insurance: Mathematics and Economics 42 (3): 992–9. https://doi.org/10.1016/j.insmatheco.2007.11.005.Search in Google Scholar

Zhou, C. Y., and C. F. Wu. 2009. “Optimal Insurance under the Insurer’s VaR Constraint.” The Geneva Risk and Insurance Review 34 (2): 140–54. https://doi.org/10.1057/grir.2009.3.Search in Google Scholar

Zhou, C. Y., W. F. Wu, and C. F. Wu. 2010. “Optimal Insurance in the Presence of Insurer’s Loss Limit.” Insurance: Mathematics and Economics 46 (2): 300–7. https://doi.org/10.1016/j.insmatheco.2009.11.002.Search in Google Scholar

Zhuang, S. C., T. J. Boonen, and K. S. Tan. 2017. “Optimal Insurance in the Presence of Reinsurance.” Scandinavian Actuarial Journal 2017 (6): 535–54. https://doi.org/10.1080/03461238.2016.1184710.Search in Google Scholar

Received: 2021-07-30

Revised: 2021-09-19

Accepted: 2021-11-22

Published Online: 2021-12-09

You are currently not able to access this content.

Articles in the same Issue

https://doi.org/10.1515/apjri-2021-0023

Keywords for this article

optimal reinsurance; VaR; TVaR; reciprocal reinsurance; moral hazard