Soliton turbulence in electronegative plasma due to head-on collision of multi solitons

1 Introduction

The presence of charged dust particles modifies the wave spectra as well as introduces a number of eigenmodes, such as dust acoustic mode [1], dust drift mode [2], Shukla–Varma mode [3], dust lattice mode [4], dust cyclotron mode [5], dust ion acoustic (DIA) mode [6] and dust Berstain–Green–Kruskal mode [7]. DIA waves are low frequency analogue of ion acoustic waves and can be observed in laboratory [8], [9] as well as in space environment [10], [11], [12], [13]. In recent years, a number of researches have been made to study linear and non linear DIA wave propagation [14], [15], [16], [17], [18], [19], [20]. Alinejad [14] studied the formation of large amplitude DIA waves in a multicomponent dusty plasma consisting of warm ions, two-temperatured trapped electrons and dust particles with negative charge and observe that the solitary structures are significantly affected by low and high temperature electrons. Khalid et al. [18] investigated the propagation of DIA cnoidal waves in a dusty plasma system where electron follows non-thermal distribution. They have shown that the non-linear ion flux depends significantly on dust concentration and non-thermality parameter. El-Bedwehy et al. [19] have investigated the modulational instability (MI) of DIA waves in a dusty plasma model containing warm ions fluid, generalized (r, q) distributed electrons and immobile dust grains.

A fairly large number of investigations consider distribution for the electrons and ions as Maxwell–Boltzmann. However, there are number of theoretical evidences that the space plasmas can have particle distribution with high energy tail, and they deviates from the Maxwellian distribution [21], [22], [23], [24], [25], [26]. Superthermal particle arises as a result of external forces acting on the natural space plasma environment or the presence of wave particle interaction. In general plasmas with excess amount superthermal electrons are characterized by a long tail in the high energy region. Generalized Lorentzian or kappa distributions [21], [27], [28], [29] are used to model such kind of space plasmas. The form of the three-dimensional isotropic kappa velocity distribution is [27]

where θ=((κ−3/2κ)(2kBTem))1/2 is the effective thermal speed, modified by spectral index κ (>3/2), T_e is the characteristic kinetic temperature, k_B is the Boltzmann constant and Γ(x) is the gamma function arises from the normalization of f_κ(v) such that ∫​fκ(v)d3v=1. For low values of κ the distribution function (1) represents a hard spectrum with a strong non-Maxwellian tail having a power law form at high speeds, while in the limit κ → ∞, the kappa distribution function reduces the well known Maxwell–Boltzmann distribution [21], [27]. Integration of Eq. (1) over velocity space gives the normalized form of electron number density as [29]

where ϕ is the electrostatic potential and is normalized by electron thermal energy k_BT_e/e.

Soliton is one of the most common non-linear structures in any weakly dispersive media and the dynamics of soliton are well understood in the framework of KdV equation [30], [31], [32]. Extensive studies on the collision of solitons in liquids have been reported in the studies by Maxworthy and Craig et al. [33], [34]. In one-dimensional system, the interaction of solitons may occur in two different ways: (i) the overtaking collision and exchange collision depending on the amplitude ratio of propagating solitons [35], when solitons are moving in the same direction with different velocities and (ii) the head-on interaction, when the angle between the propagating solitons is π and they approaches to each other. Zabusky et al. [36] studied the overtaking collision of solitons with different amplitudes and observed that after the interaction, the solitons reappear and move with same velocity, but their trajectories deviate from the straight line. Harvey et al. [37] experimentally studied the head-on collision of two solitons with equal amplitude and found that the phase shift depends on the initial amplitude of solitons. The head-on collision of ion acoustic solitons in an unmagnetized plasmas with Cairns non-thermal distributed electrons has been studied by Verheest et al. [38]. El-Labany et al. [39] examined the oblique interaction of two KdV solitons moving towards each other from opposite directions in an magnetized dusty electronegative plasma consisting of cold mobile positive ions, Boltzmann negative ions, Boltzmann electrons and dust particles of both polarities. They have observed that the angle of collision, the density and temperature of negative ions and the opposite polarity dust density have reasonable effects on the phase shift. Roy et al. [40] studied the features of the head-on collision and overtaking collision of four solitons in plasmas using extended PLK method. El-Labany et al. [41] have investigated the head-on collision of two, four and six solitons in an unmagnetized non-extensive plasma system. But none of the above studies on head-on collision of solitons reveals the changes in the statistical properties of the wave field during the head-on collision process of the solitons.

The interaction of a large number of random and weakly dispersive waves leads to the prediction of several stationary statistical states, such as weak turbulence, statistical equilibrium or integrable turbulence. Weak wave turbulence features an ensemble of non-linear interacting waves. The weak turbulence theory predicts an energy transfer through resonant interactions among waves and also provides analytical predictions of the statistical properties of turbulence such as the stationary wave spectrum. The interaction of number of solitons in a nonlinear integrable system changes the statistical properties of the wave field and leads to integrable soliton turbulence [42], [43]. One of the important aspect of turbulence theory is to know the distribution function of the wave field and statistical moments (mean, variance, skewness, kurtosis) of the wave field, which are obtained from the measurements in the studies [44], [45], [46], [47]. Recently, some works have been reported on the soliton interaction and the statistical properties of the wave field in integrable and non-integrable systems [48], [49], [50], [51], [52], [53], [54], [55], [56]. Pelinovsky et al. [48] showed that interaction of two-solitons in KdV equation leads to the decrease of third- and fourth-order moments of the wave field while the first and second moments remains invariant. Dutykh et al. [49] studied the collective behaviour of soliton ensembles using direct numerical simulations in integrable KdV and non-integrable KdV–BBM (Benjamin–Bona–Macon) equations. Redor et al. [54] experimentally observed the ensemble of bidirectional shallow water solitons in a 34 m long flume taking advantage of the process of fission of a sinusoidal wave train. The interplay between multiple solitons and dispersive radiation has been analysed by Fourier transform and the observed random soliton ensemble has been interpreted as representing a soliton gas. Didenkulova et al. [55] investigated soliton turbulence in the framework of Gardner equation and showed that the interaction of solitons with different polarities leads to the formation of extreme waves. Ali et al. [56] studied the interaction of three solitons and soliton turbulence in a dusty plasma system in the framework of KdV equation. But till today, there is no work on the statistical properties of the wave field due to the head-on collision of solitons. In this work, our goal is to investigate the properties of the resultant solitonic structure at the time of head-on interaction of four solitons and also the statistical properties of the wave field during the collision.

2 Model equations

We have considered a four component dusty plasma model comprising cold mobile inertial positive ions, negative ions following Maxwellian distribution, κ distributed electrons and stationary dust grains with positive charge. The DIA waves are governed by the following fluid equations in normalized form

where n_p represents the number density of positive ions, u_p is the speed of positive ions, μ_e = n_e0/n_p0, μ_d = Z_dn_d0/n_p0, with n_e0, n_p0, n_d0 representing the number densities of electron, positive ion and dust, respectively, and Z_d is the charge on the dust grains. The parameter α is the ratio of electron temperature (T_e) and negative ion temperature (T_n). The space variable x is normalized to the Debye wavelength λd=ϵ0kBTe/np0e2 and the time variable t is normalized to plasma period of positive ions ωpp−1=(np0e2/ϵ0mip)−1/2, m_ip is the mass of positive ions. The velocity u_p is normalized to the ion acoustic speed for positive ions Cip=kBTe/mip. The charge neutrality condition at the equilibrium gives

3 Derivation of two-sided KdV equations

In order to study the head-on collision of solitons in plasma model under consideration, the extended PLK perturbation method is used [38], [39], [40], [41], [57]. According to extended PLK perturbation method, the dependent variables expanded as

The independent variables x and t can be written as

where ξ and η refer to the directions of the solitary waves propagating in opposite directions with phase velocity λ. From Eqs. (11)–(13), one can obtain

Using Eqs. (8)–(15) into the set of Eqs. (3)–(5) and collecting the coefficients of the same powers of ϵ, the lowest order non-zero perturbed quantities are obtained as

The unknown functions ϕ1ξ(ξ,τ) and ϕ1η(η,τ) will be determined considering the next higher-order perturbed quantities [58]. The solvability condition (i.e. the condition to obtain uniquely defined n_p1 and u_p1 from Eqs. (17) and (18) assuming ϕ1 as Eq. (16)) gives the phase velocity as

where S=(aμe+αμn) with a=(κ−1/2κ−3/2).

The coefficients of the next order of ϵ give

After some algebraic calculation the coefficient of the next higher order of ϵ gives

where A=λ(3S2−2T)/2S, B=λ/2S, C=(3Sλ2+1),D=2Tλ2, T=(bμe+α2μn/2) and b=((κ−1/2)(κ+1/2)2(κ−3/2)2). The first and second terms in the right-hand side of Eq. (23) will be proportional to η and ξ, respectively, because the integrands are independent of η and ξ, respectively. The third and fourth terms in the right-hand side of Eq. (23) are non-secular and they would be secular in the next higher order of ϵ. Thus, to eliminate the secular terms from Eq. (23), we must have

Equations (24) and (25) represents the oppositely propagating two-sided KdV equations in the reference frame ξ and η, respectively. The solitary wave solutions of Eqs. (24) and (25) are

where U is the speed of both the solitary waves.

After the head-on collision the phase shift of the solitons can be determined as

The soliton (28) is traveling to the right and the soliton (29) is traveling to the left. Equations (30) and (31) indicate that the solitons (28) and (29) experience a negative phase shifts in their traveling direction. The negative phase shift after the collision means that the positions of the propagated solitons are behind the positions where they would have been if they just passed through each other without interacting [58].

4 Two-soliton solution

Using Hirota’s bilinear method [59], the two-soliton solutions of Eqs. (24) and (25) are obtained as

and

respectively. Where

and

The properties of the resultant soliton during the interaction of the four solitons given by Eqs. (32) and (33) propagating in opposite direction can be studied from

For |τ|>>1, the two-soliton solutions, Eqs. (32) and (33), of Eqs. (24) and (25) can asymptotically be expressed as the superposition of two single solitons [60]

and

respectively, where the soliton amplitudes are written as

and the phase shifts due to collision are

Therefore, before and after the head-on interaction of four solitons, Eq. (34) can be written as

It is well established that the KdV equation has infinite number of conserved quantities (Kruskal integrals) [30], [31], [32]. The first four conserved quantities of the KdV, Eqs. (24) and (25), are of the form

where γ=ξ,η, respectively.

The form of the Kruskal integrals for the resultant soliton (34) is

The integrals (44), (45) and (46) represent the mass, energy and moments of instability of wave field. It is evident from Eqs. (40)–(43) that for the resultant wave (34), only the integral (44) will be conserved as it is the sum of two conserved quantities (I₁ = I_1ξ + I_1η). The integrals I₂, I₃ and I₄ are not conserved as they cannot be expressed as the sum of conserved quantities.

5 Head-on collision and its impact on statistical properties of the wave field

The head-on collisions of four solitons given by Eqs. (32) and (33) are studied in this section. Monoley and Hodnett [61] showed that complete interaction of the solitons occurs at the point ξ = 0, τ = 0 for α1=−k1/2B1/3Δ1 and α2=−k2/2B1/3Δ2 and for the same choice of α₁ and α₂ the resultant wave profile is symmetric about the point ξ = 0, τ = 0. At the strongest interaction point, the profile of the resultant pulse is determined by the formula

and the amplitude of the resultant pulse at the point of strongest interaction is given by

Equation (48) determines the concavity of the resultant wave profile at the point ξ = 0, τ = 0. For 0 < R < 1/3 (where R = A₂/A₁ < 1), the resultant wave profile is concave downwards and hence, it will take the form of a single peak at the strongest interaction point. When 1/3 < R < 1, the wave profile is concave upwards and it will maintain a double peak status at the instant strongest interaction. Also, it is clear from Eq. (49) that the amplitude of the resulting impulse increases and exceeds the amplitude of the larger soliton due to head-on collision of four solitons two of which are moving from left to right and other two from right to left. The right moving solitons with amplitudes A₁ and A₂ (A₁ > A₂) collides at the point ξ = 0, τ = 0 and at that point the amplitude of the resultant pulse becomes (A₁ − A₂) [62]. Similarly the left moving solitons with amplitudes A₁ and A₂ (A₁ > A₂) collides at the point η = 0, τ = 0 and at the point of complete interaction, the resultant pulse amplitude become (A₁ − A₂). Finally, both the resultant pulses superimposed during the head-on collision and makes the resultant pulse amplitude 2(A₁ − A₂). Thus, there is a possibility of formation of large wave in the head-on interaction of four solitons. Figures 1 and 2 shows the head-on interaction process of four solitons.

Figure 1:

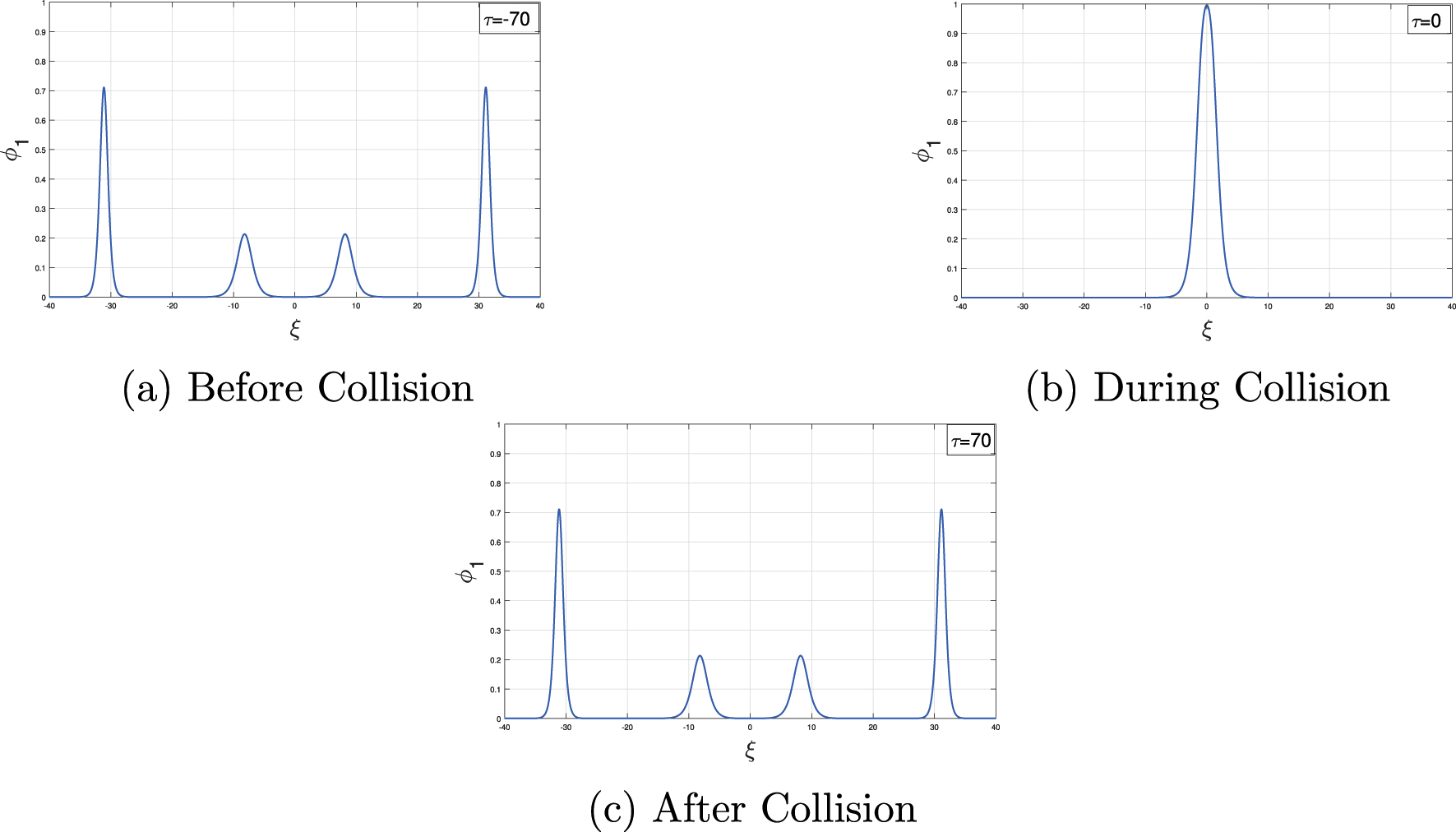
Head-on interaction process of four solitons with parameter values μ_e = 0.6, μ_d = 0.25, α = 3, κ = 2.3, R = 0.3, k₁ = 0.5.

Figure 2:

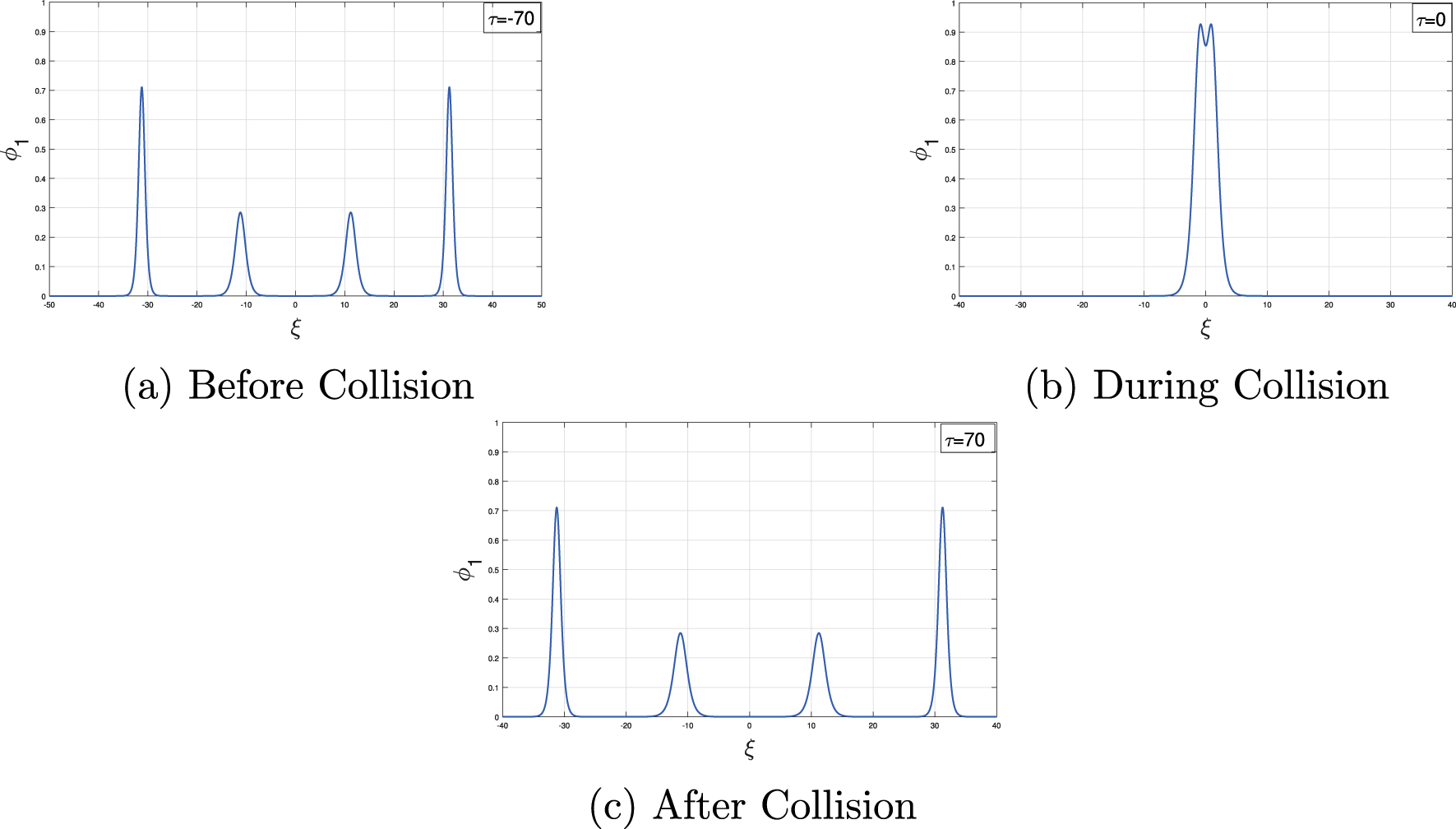
Head-on interaction process of four solitons with parameter values μ_e = 0.6, μ_d = 0.25, α = 3, κ = 2.3, R = 0.4, k₁ = 0.5.

The interaction of these solitons changes the statistical behaviour of the integrable system and leads to the theory of integrable turbulence or soliton turbulence which is an active field of research [42], [43] and is best described by the statistical theory [63], [64]. To study the effect of these collisions of solitons on the statistical properties of the random wave field, we consider the following four moments of the wave field

The moments M₁, M₂, M₃ and M₄ are related to the mean, variance, skewness and kurtosis of the probability distribution of the random wave field. Skewness represents the asymmetry of the probability distribution function of the random soliton amplitudes and kurtosis indicates the heaviness of the tails of the distribution function [49]. Using the non-interacting solitonic structure (39) the analytical calculation of Eqs. (50)–(53) are shown below:

The numerical evolution of M₂, M₃ and M₄ using the resultant solitonic structure (34) is depicted in Figure 3.

Figure 3:

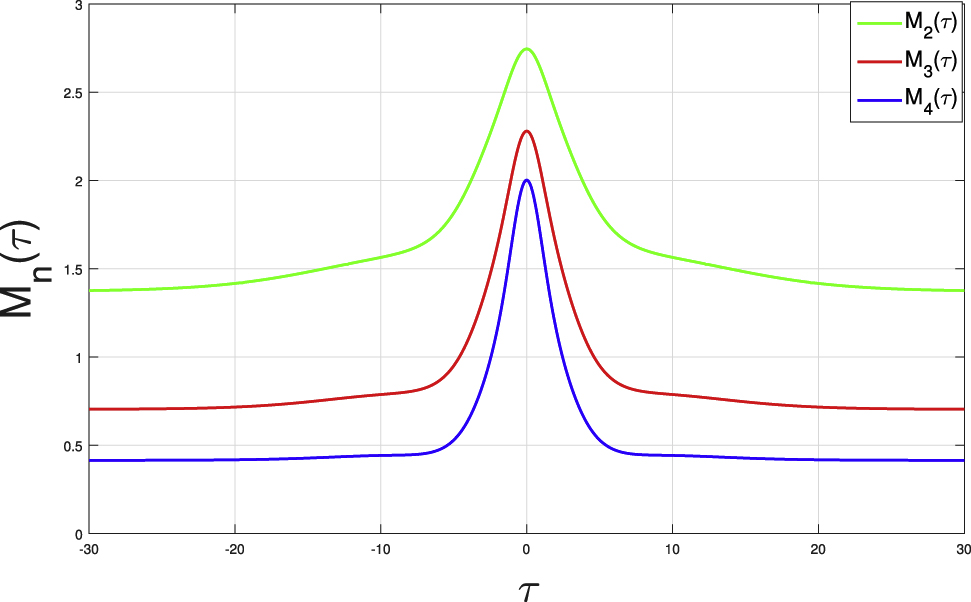
Variations of M₂, M₃ and M₄ in the head-on interaction process with the parameter values μ_e = 0.6, μ_d = 0.25, α = 3, κ = 2.3, R = 0.3, k₁ = 0.5.

From Figure 3, it is noticed that the second-order moment (M₂), third-order moment (M₃) and fourth-order moment M₄ increases due to the head-on collision of four solitons. The increase of M₂ says that the energy of the resultant soliton and hence its amplitude increases during the head-on collision of four solitons, which is observed from Figures 1(b) and 2(b). Figure 4 depicts the relative deviations Mn*=Mnmax−Mn0Mn0, (n=2,3,4) in second, third and fourth-order moments versus the amplitude ratio R (= A₂/A₁) with other parameter values as μ_e = 0.6, μ_d = 0.25, α = 3, κ = 2.3, R = 0.3, k₁ = 0.5. It is observed M2*=1, which means that the relative variation in energy due to collision of four solitons is 100%. In other word, the total energy of the system is accumulated in resultant soliton at the strongest interaction point. The graphs of M3* and M4* are non-monotonic and changes their nature (decreasing to increasing) at the points R = 0.33, which is a transition point of single peak to double peak status.

Figure 4:

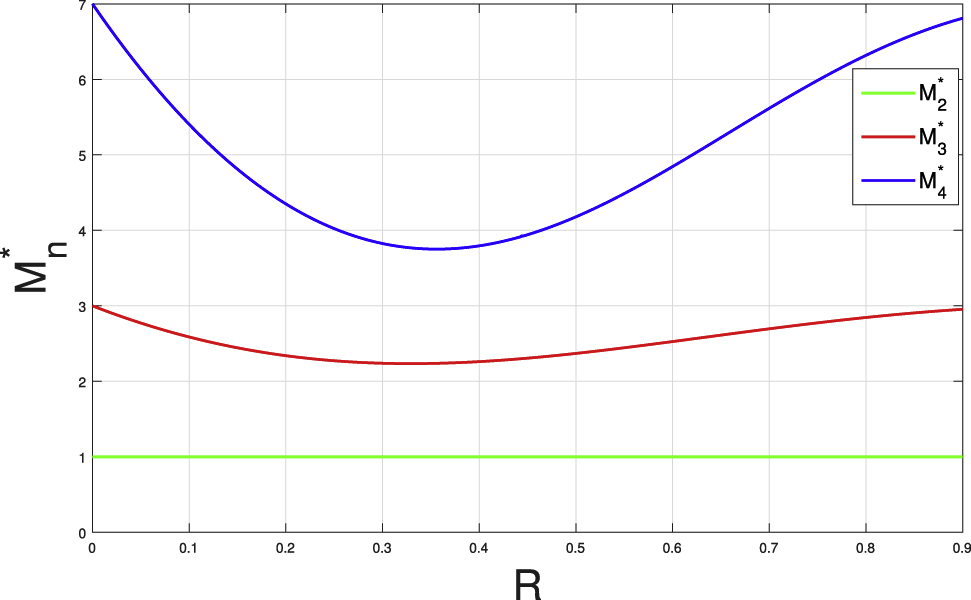
Dependence of the relative variations M2*,M3*,M4* on the amplitude ratio R during head-on collision of four solitons with the parameter values μ_e = 0.6, μ_d = 0.25, α = 3, κ = 2.3, k₁ = 0.5.

6 Conclusion

We have studied the head-on interaction of four DIA solitons in the framework of two oppositely propagating KdV equations in a dusty plasma comprising Maxwellian negative ions, cold mobile positive ions, κ-distributed electrons and positively charged dust grains. It is observed that the head-on collision leads to the increase of second-, third and fourth-order moments of the non-linear wave field while the first-order moment remains unaffected. Also, we have observed that the resultant wave amplitude increases at the strongest interaction point. The relative variation of second-order moment is monotonic and is a constant, which indicates the conservation of energy in the whole system. Also, the relative variations in third and fourth-order moments are non-monotonic and the change for both the curves occurs at R = 0.33, which is a transition point of single peak and double peak status. The findings of this investigation may be helpful to explain the interaction features of DIA waves in space plasma environment [65], [66], [67], [68] and in laboratory devices [69], [70], [71], [72], where electronegative dusty plasma with Boltzmann distributed negative ions and κ-distributed electrons exists.