Abstract
In their landmark 1969 study, Berlin and Kay challenged the longstanding assumption that each language had its own distinct color terminology. Instead, they posited that a core set of eleven basic color terms (or a subset thereof) are consistently recognized across languages globally. Although these basic color terms have largely endured over time, the underlying reason for this specific set of terms has remained elusive. This paper proposes an explanation grounded in the logical interconnections between C. S. Peirce’s Universal Categories, the geometric algebra of S3 symmetry transformations, and the spectral and saturation characteristics of color. It posits that this methodological framework, through a rigorous logical progression, accounts for the generation of each of the eleven basic color terms identified by Berlin and Kay, offering a systematic explanation for the universality observed in color naming through time and space.
1 Introduction
In has been fifty plus years since Berlin and Kay’s 1969 book on color naming was published. It has inspired many hundreds of studies across disciplines, including linguistic, anthropological, cultural, psychological, and neurobiological aspects of color naming. It has raised questions regarding why, given the linear nature of the visible spectrum, the colors are perceptually non-linear, as for example what we see in viewing Newton’s prismatic colors. Significantly, it has raised issues whether color naming is universal across languages, or whether it is influenced by aspects of culture, or whether it is fully shaped by the Sapir-Whorf theory of language relativity.
2 Universalism
2.1 Eleven perceived basic color terms
Acknowledging B&K’s findings introduces the concept of universalism in color perception. It is widely accepted by universalists that, with few exceptions, there are eleven universal basic color terms (BCTs), as proposed by Berlin and Kay (B&K; 1991 [1969]). It is agreed that non-industrial languages begin with fewer color terms, which can potentially later expand to include the full set of eleven BCTs. There are ongoing questions about how these new terms are incorporated – whether through universal processes, cultural influences, or other determining factors. Within the languages rigorously studied, eleven basic color terms (or a subset thereof) have been found to occur in the majority of world languages.[1] These colors represent a reorganization of the linear color spectrum into three distinct perceptual categories, which can be categorized as follows: (1) spectral, fully saturated colors closely reflecting the Newtonian spectrum – red, orange, yellow, green, blue, and violet/purple; (2) the non-spectral, but saturated colors – pink and brown; and (3) non-spectral, achromatic colors – black, gray, and white.
2.1.1 Truth functional values
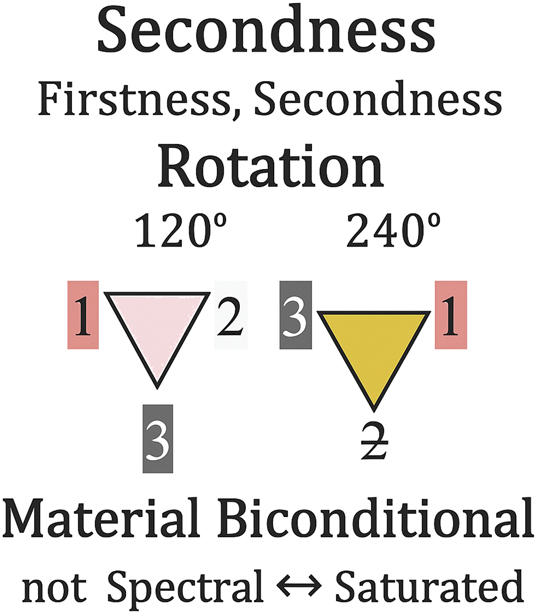
Unlike Newton’s categorization of 100 % spectral, fully saturated colors, a subset of B&K’s eleven colors considered here are red, orange, yellow, green, blue, purple, which are perceptually based. These colors do not quite process colors at the same level of purity or full saturation as Newton’s spectral colors. Nonetheless, in relative terms, B&K’s perceptual colors are purer and more saturated compared to less saturated shades like pink and brown, or as the fully unsaturated black and white. It is noteworthy that the classification of the eleven colors relies on the simple logic of truth functional values that define basic properties of colors, namely, ±spectral and ±saturated:
Basic properties of color Truth functional values
+Spectral → +Saturated Material Implication
–Spectral ↔ +Saturated Material Biconditional
–Spectral ← –Saturated Contrapositive of the Material Implication
+Spectral ↔ –Saturated Impossible
True: Material Implication: Any color that is spectral is also saturated, classifying red, orange, yellow, green, blue, purple
True: Material Biconditional: Any color that is not spectral may be saturated or unsaturated or any color that is unsaturated may be spectral or not spectral, classifying pink, brown
True: Contrapositive of the Material Implication: Any color that is not saturated cannot be spectral, classifying white, gray, black.
False: No color can be spectral and not saturated nor can any color be not saturated spectral.
2.1.2 Sound symbolism in English
We note that sound symbolism, evident in English color names, indicates varying levels of luminance (“brighter than” ↔ “darker than”), as illustrated in Figure 1.[2]
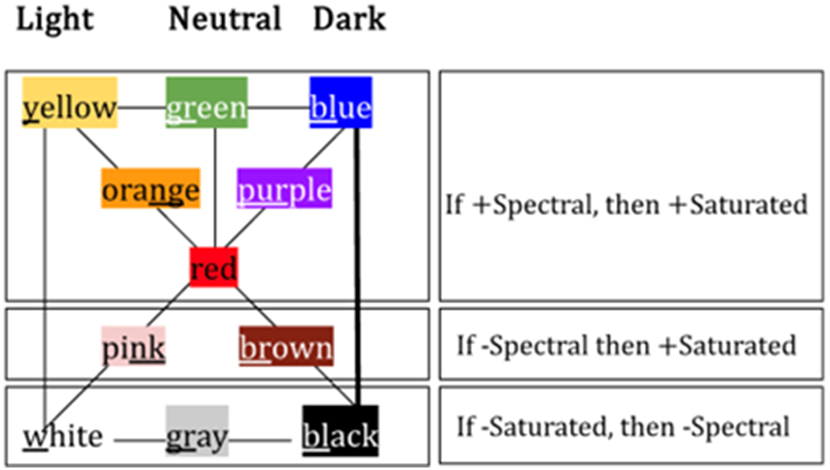
Categorizing Berlin and Kay’s eleven colors.
Colors such as white and yellow, which possess brighter luminosity, begin with the glides w/y. In contrast, black and blue, which exhibit darker luminosity, start with voiced labio-lateral blends, bl/bl. Neutral colors like gray and green are based on voiced velar-rhotic blends.
Derived colors exhibit similar patterns. Brown and purple begin with labio-rhotic blends, while pink and orange end with nasal, non-labial blends.
Furthermore, Kay et al. (1991) report that purple and brown typically occur in languages with a grue (the green-blue composite), whereas orange and pink are found in languages that separate grue into distinct green and blue, as noted by Dowman (2007).
Sound symbolism (Hinton et al. 1994) and color symbolism are pervasive in language. English is interesting because it merges sound symbolism with color. Specifically, English names for BCTs reflect an inherent property of color itself: luminosity.
2.2 The world color survey
Berlin and Kay (1991 [1969]) were criticized because there were only 20 languages surveyed, with informants who lived in the Bay area, who were bilingual, where in some cases there was only a single informant. It was thought that those BCTs could not be representative of the vast number of colors throughout the world’s languages (Lindsey and Brown 2021).
Owing to such criticisms, it was determined that Kay et al. (2010) would undertake the massive task of producing the World Color Survey (WCS).
The following describes the field workers’ research methodology, found representative of a worldwide distribution of largely unwritten languages:
In the WCS investigation, an average of 24 native speakers of each of 110 unwritten languages were asked (1) to name each of 330 Munsell chips, shown in a constant, random order, and (2), exposed to a palette of these chips and asked to pick out the best example(s) (‘foci’) of the major terms elicited in the naming task. (Cook et al. 2012)
At the conclusion of the project, it was found that there was a secure correlation between the World Color Survey and B&K’s (1991 [1969]) 11 universal colors found in the 110 unwritten languages, basically confirming the universality of the 11 categories. The ineffable consistency found in this collection of facts could not readily be written off as a mere haphazard coincidence (see Kay and Maffi 1999). The placement of the Saturated color terms are shown in Figure 2.

Showing the placement of the BCTs on the Munsell color chart (see MacEvoy 2015).
2.3 The six unique hues
Universal determination of the 11 BCTs typically relies on the supposition that color perception is biologically given, based on the framework of six unique hues, red/green, blue/yellow and black/white (Lindsey et al. 2015; Regier et al. 2005).
However, it has been widely believed that either the so-called unique hues are no different from any other colors, or that they are nonexistent because no direct neurophysiological evidence has been, or ever could be biologically confirmed. For example, Ocelák (2015: 1) concludes
that, contrary to the standard opinion, there is no solid reason to claim that the RYGB hues are unique among other colors, in a sense that would allow for direct neurophysiological explanation … Neurophysiologists have not managed to find specific mechanisms for what is called unique hues, and they will not – I bet – because there is nothing to search for; neither the focal RYGB nor any other colors are perceptually unique in the commonly acknowledged sense. (Ocelák 2015: 1, 3)
For similar arguments, see also Emery and Webster (2019); Saunders (2000); and Saunders and van Brakel (1988, 1997).
2.3.1 Neurobiological evidence of the unique hues
Rezeanu et al. (2023) have recently disputed these arguments:
In this paper, we propose a neurobiological three-stage color vision model to explain the neural basis of the unique hues without relying on any post hoc adjustments to fit the psychophysical data. By taking into account the wide variability in L:M cone ratios and normalizing second-stage cone-opponent mechanisms to equal-energy white, the model generates accurate color-opponent mechanisms that predict both the position and variability of the spectral unique hues – blue, green, and yellow – without any further adjustments. Furthermore, by taking differential adaptation of the S and the L cones at short and long wavelengths into account, we can explain the non-linearities in the R/G and B/Y color-opponent mechanisms demonstrated by Burns et al. (Greene et al. 2024; Rezeanu et al. 2023)
The eleven B&K categories, outlined in Figure 1, are based on the unique hues – black/white, red/green, and yellow/blue – as presented in Figure 3. If the neurological model proposed by Rezeanu et al. (2023) is accurate, it provides the long-sought neurological foundation for the B&K categories listed in Figure 3. In Figure 3, these same six opponent hues are achieved by excluding the five logically derived colors from Figure 1 orange, purple, pink, brown, and gray, leaving yellow/blue, red/green, and of course black/blue.
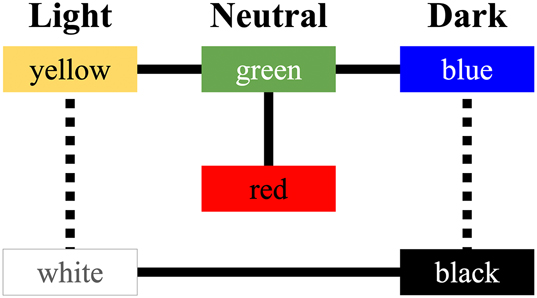
The unique hues.
2.3.2 The transition from six unique hues to a light/warm versus dark/cool color system
Building on the foundational work of Rezeanu et al. (2023) and Greene et al. (2024), the six unique hues can be realized as the three opponent pairs: black ↔ white, blue ↔ yellow, and green ↔ red. In turn, these oppositions can also exhibit properties that enable their grouping into two distinct categories with three members each: light/warm colors (white; red, yellow) and dark/cool colors (black; green, blue).
2.3.3 The evolutionary process based on light/warm, dark/cool colors
Based on the light/warm versus the dark/cool colors, whose source is the unique hues, there is an evolutionary process by which preindustrial languages with a limited number of BCTs gradually acquire additional color terms, eventually reaching the full complement of the 11 generally found in industrialized languages. This process was comprehensively detailed by Kay and Maffi (1999), derived from the 110 languages from the World Color Survey (WCS). Their findings reveal a systematic evolutionary process, as illustrated in Figure 4 (see Kay and Maffi 1999: 751 for a similar description of the process). According to their analysis, 92 % of the WCS languages follow the progression outlined in Figure 4.
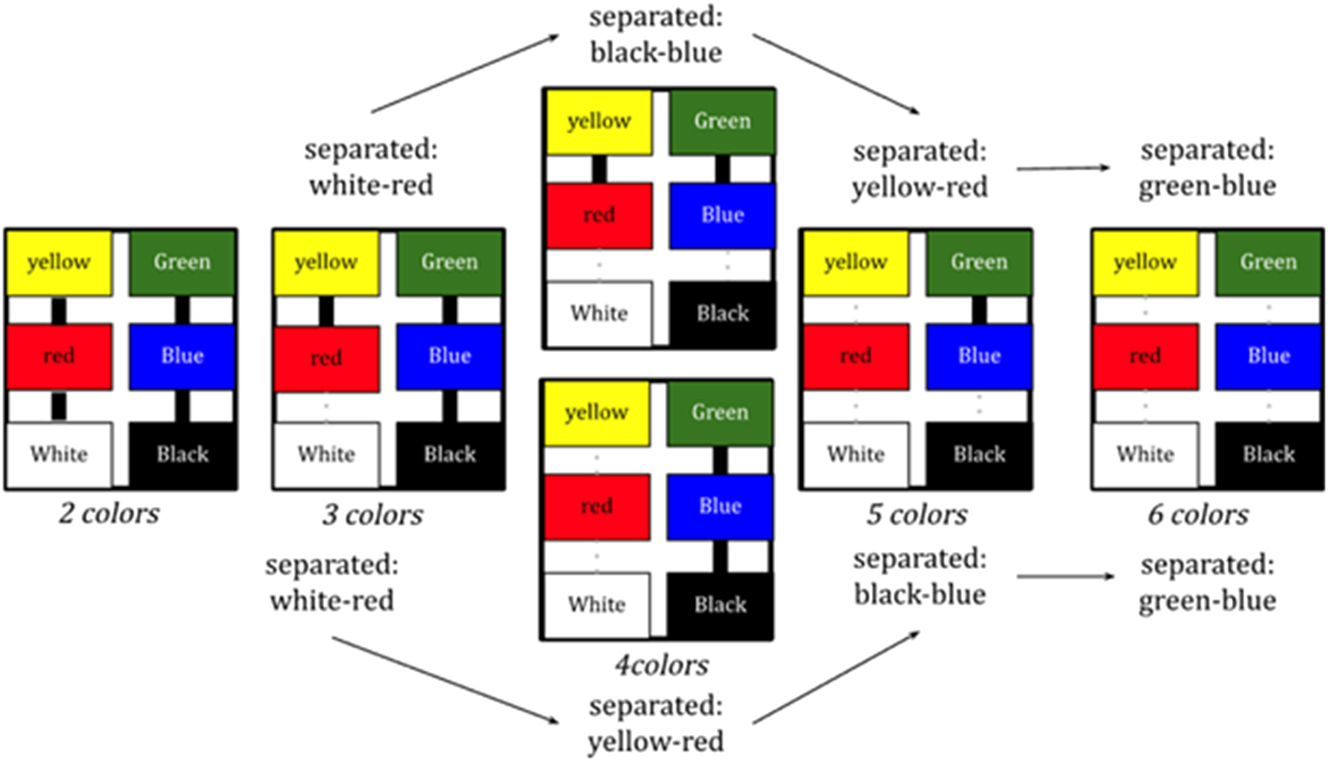
Showing the evolutionary process of going from two to eleven BCSs (after Kay and Moffi 1999).
2.4 Infant color discrimination occurring without naming
Preverbal children demonstrate color discrimination patterns that align with certain of the unique hues (Figure 5). These findings show that although language ultimately names colors, the perceptual foundations in children’s early discrimination patterns exist preverbally. The unique hues are perceptually and biologically real, even though infants cannot yet name them. Notably, “the red-green color mechanism develops first, and the blue-yellow mechanism develops around 4–8 weeks later” (Skelton et al. 2022). It is noteworthy that all languages that distinguish blue from green always distinguish red from yellow first, as shown in Figure 4.
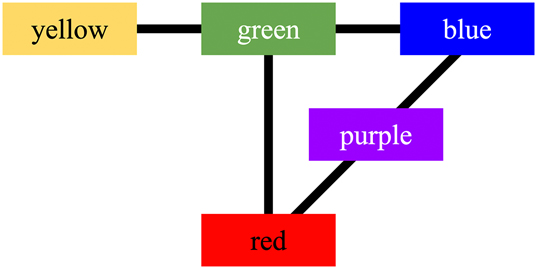
Infant, preverbal discrimination showing the unique hues plus purple.
Significantly, an article by Franklin et al. (2008), entitled, “Categorical perception of color is lateralized to the right hemisphere in infants, but to the left hemisphere in adults” shows the tight relationship between categorical perception and the later naming of such perceptual categories.
As Skelton et al. (2022) stated: “Overall, our findings suggest that infant memory parses the hue continuum at the lightness level tested into five categories: red, yellow, green, blue, and purple.” See also Franklin and Davies (2004) and Regier et al. (2005).
2.4.1 Computational evidence supporting the BCTs
McCarthy et al. (2019) eschewed using B&K’s celebrated basicness criteria to arrive at the same 11 BCTs. In doing so, they use computational linguistic criteria, using data from 2,491 languages of various quality to test the accuracy of B&K’s 11 basic color terms. Their “‘features’ aggregation correlates strongly with the Berlin and Kay basic/secondary color term partition (γ = 0.96). The aggregation also largely predicts the Berlin and Kay hypothesized universal acquisition sequence, which is in no way directly entailed by the basicness criteria.” In short, this computational methodology eluded the criticisms of the B&K’s basicness methodology (Lucy 1997; Roberson et al. 2005; Saunders and van Brakel 1988, 1997, and others). McCarthy et al.’s methodology did not rely on Berlin and Kay’s approach, but by using computational linguistics, they came up with largely the same results.
3 Questions of relativism
Whether or not Berlin and Kay’s (1991 [1969]) color categories are as universal as claimed, it is important to address questions of relativism regarding basic color terms (BCTs). Key issues include whether B&K’s framework overlooks cultural nuances of color naming across various societies. Are there more than eleven categories? Is there a biological basis of the unique hues – red/green, yellow/blue, black/white? Do the methods used to elicit color terms reflect Western biases, thereby neglecting non-Western perspectives? Are the Munsell colors a reasonable means of addressing color universalism? More broadly, do these proposed categories truly capture how perceptual color naming is structured across all languages?
3.1 Munsell color categories, psychological reality, the innate color space
Barbara Saunders (1999, 2000) has several concerns with the Munsell color system, and B&K’s proposed 11 universal color categories. Among others, is the notion that the Munsell color categories “cancel the life-world,” or “noticings,” meaning that the universal categories ignore expansive nature of the outside world, as in “there looks to me to be a little, shiny, red, square physical object over there.” Furthermore, the use of the Munsell color system is a function of Cartesianism, which “presupposes inferential use of concepts; empiricism cannot account for noticings.”
Another concern is that “neither neurophysiology nor psychophysics supports exactly two pairs of opponent hues or three pairs of opponent colors” (Saunders and van Brakel 1997), but see Section 2.3.1 in this paper. Saunders and van Brakel (1997) are also concerned about how many colors were seen in Newton’s spectrum: “But one thing is clear: the reported number of colors in the spectrum was not determined by what Newton or anyone else saw.” It might be pointed out, however, that the first perceptually viewed colors include red, orange, yellow, green blue, which are shared by Newton and B&K. Nonetheless, there is some question regarding the difference between purple (non-spectral) and violet (spectral).
Another of Saunders’s concerns has to do with innate color space, which, among others, is so-called Hering colors (Hering 1964), or the unique hues. Without either a lexical or other structural mark for the existence of color space, it “shows itself in the introspective uniqueness of red, green, yellow and blue, the opposition of red-green, yellow-blue.” These colors are “impingements” and “the phenomenological subject of Hering opponency,” whose mode of being does not exist in the inner world of color space because there is no such world. There has never been any neurobiological evidence that such opponency actually exists (but see 2.3.1 above) Also see Saunders and van Brakel (1988, 1997).
3.2 Focus on semantics and structure
The relativists, at bottom, share somewhat similar concerns. Whereas one of Saunders’s concerns focused on, among other things, the fact that B&K’s categories disregard the outside world, Lucy’s (1997) concern was B&K’s disregard of the semantics and structure of language. For him, if we choose to focus on the BCTs, and the Munsell array, we would then “want to know how the world’s languages structure [in] reference to color stimuli in their semantic systems – and the keywords here are structure and system [of Language.]”
For Saunders, using B&K’s method is like being subject to a “law-like relation,” and for Lucy, it is an “interpretive methodology readily skewed towards the theoretical expectations.”
For Saunders, universalists’ focus is on neurobiology, and for Lucy, what underlies our psychophysical experience of it is beside the point.
3.3 Focus on categorization of color naming: universally or linguistically determined?
Is it true that the continuous, linear color gradient is universally reorganized into the nonlinear BCTs, universally shared by all languages, as proposed by B&K – or are there exceptional languages that reorganize their color gradient into categories independent of the BCTs? Roberson et al. (2005) report on two languages, Himba and Berinmo, whose categories diverge from the BCTs. Culturally, their research found substantial evidence of cognitive color attributes in Himba and Berinmo that separates them from the normal, universal prototypes at the five-stage course of development (see Figure 4 for the next stage of development).
3.3.1 Cunén K’iche’ and Tz’utujil Mayan as an example of the shift from the fifth to the sixth-stage of development
Unlike Himba and Bernmo, Cunén K’iche’ (my data) is an example of a normal prototype with five colors, which includes ‘grue’ (green/blue). On the other hand, Tz’utujil (Mendoza and Mendosa 2001) innovated by splitting the historic ‘grue’ into the two categories, green and blue. The Tz’utujil term asuul was borrowed from Spanish, as shown in Figure 6. What is unusual about the fifth categorial division in Himba, is that it did not have the fixed category ‘grue’.

Comparing Cunén K’iche’ Maya with Tz’utujil Maya.
3.3.2 Possible reason for lack of universal prototypes in the Himba language
I would note here that Himba’s Burou is a recent borrowing: “This term is more recently borrowed from Afrikaans (blau) via Herero.” Because of its recentness, not “all observers spontaneously used the term ‘Burou’ in the naming task, but those who did not were able to select chips from the appropriate range when asked to indicate a ‘Burou’ stimulus.” It is interesting that for one of the tests, “[d]ata was excluded for two older participants who failed to use the term Burou to name any of the stimuli in the sets.” Apparently, older speakers had not fully absorbed Burou as a part of their speaking lexicon (quotes from Roberson et al. 2005).
These data suggest a language in the throes of change. This may explain why “[o]nly 35 % of Himba observers chose a black chip as best example [of zoozu]; other choices included light blue (10B 6/10), medium green (5G 5/10) and best example blue (5B 4/10). 2.6 % of observers used the term only for the black chip.” One wonders if zoozu might have historically been the word for grue before burou was borrowed, because, “light blue (6/10), medium green, and the best example blue, whereas only 35 % chose black”. The newly acquired burou is used “mostly in the blue/green/purple range. This corresponds to a grue term in Berlin and Kay’s (1969) stage theory.”
Could the newly borrowed burou’s increasing acceptance into the Himba language be the reason for the confusion regarding the universal prototypes, in particular grue as the referent? One suspects that for the rising generation, burou might be making its way to be the new word for grue presaging prototypical changes. Perhaps burou is adjusting the language to become the standard word for grue. Perhaps Roberson et al. captured Himba in an incomplete process of change.
4 Accounting for the BCTs
In the end, one thing that has never been fully accounted for is where the 11 categories begin – what is their genesis? Clearly, humans with normal color vision, with a repertoire of eleven colors, would plausibly be able to perceive Newton’s prismatic colors, and name them as least as far as red, orange, yellow, green, blue, with somewhat less certitude regarding violet/purple.
Since linearly given spectral colors are infinite, why do Newtons’ spectral colors, perceptually visible to humans, virtually match Berlin and Kay’s BCTs? Clearly the division of spectral colors would be wildly different for a pigeon or a frog. Pigeons and frogs surely divide their means of perceiving their world according to their needs for breeding and survival. But unlike humans, they do not have Broca’s and Wernicke’s areas in their brains to be able to name them.
But why pink and brown as members of the 11, and not other colors like magenta or cyan? Furthermore, is there a logical relationship between the full complement of red, orange, yellow, green, blue, purple, and pink and brown, black, white, and yellow? It is not difficult to see the relationship between red, orange, yellow, green, blue, purple, but where do pink, brown, black, white, and gray fit in?
This paper argues that the source of B&K’s categories is found in logic, as presented below, which rests on C. S. Peirce’s universal Categories, Firstness, Secondness, and Thirdness, the S3 Symmetry transformations, and the truth functional values of the Material Implication, the Material Biconditional, and the Contrapositive of the Material Implication.
4.1 The relationship between Peirce’s Universal Categories, the S3 symmetry transformations, and two immutable properties of color – spectral and saturated
The methodology presented in this paper focuses on the interaction of three key components:
Peirce’s Universal Categories, including Firstness, Secondness, and Thirdness
S3 symmetry transformations, including Identity, Rotation, and Reflection
The spectral and saturation properties of color, which include the implicational truth values of formal logic: the Material Implication, the Material Biconditional, and the Contrapositive of the Material Implication.
These three elements have a hierarchical, isomorphic relationship as shown below.
For clarification of these relationships, see Figures 7–9. Each figure builds upon the other, collectively demonstrating the underlying structures that mutually reinforce the argument for the emergence of the eleven BCTs prevalent across virtually all languages. In other words, the meanings of the Universal Categories effectively symbolize the S3 symmetry transformations, which in turn shape the implicational values of spectral and saturated colors, thereby generating each of the eleven colors found in languages of the world.
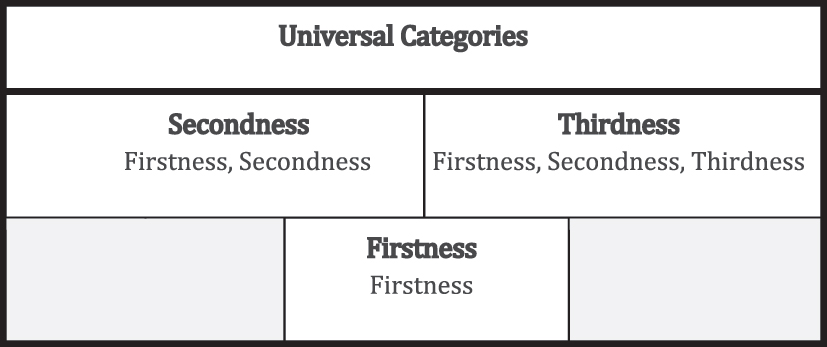
Peirce’s Universal Categories.
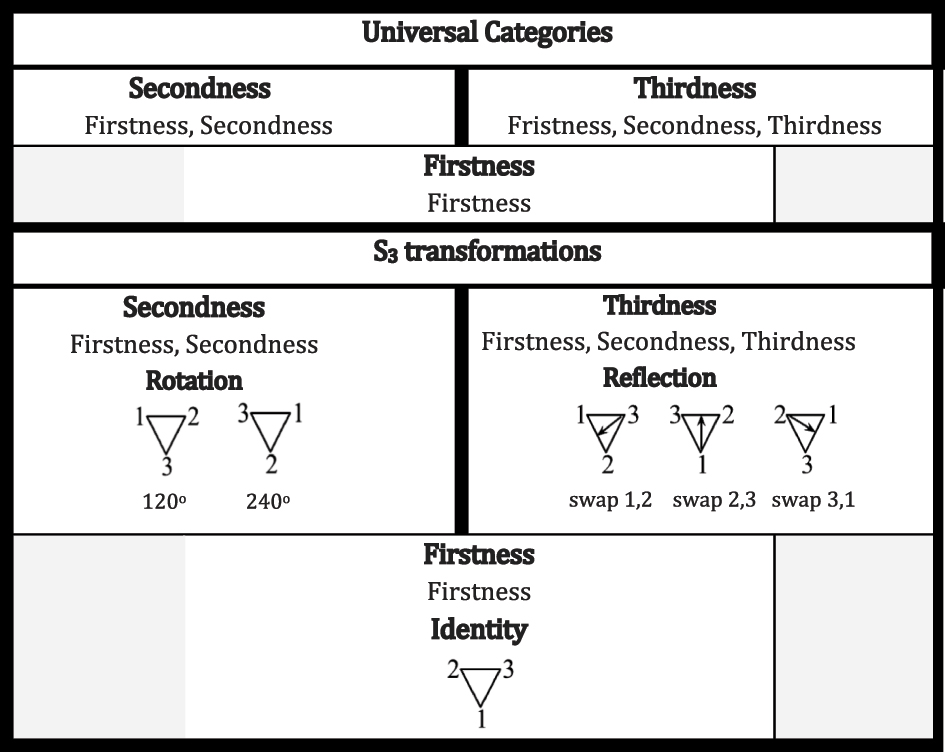
The isomorphisms between the Universal Categories and the S3 transformations.
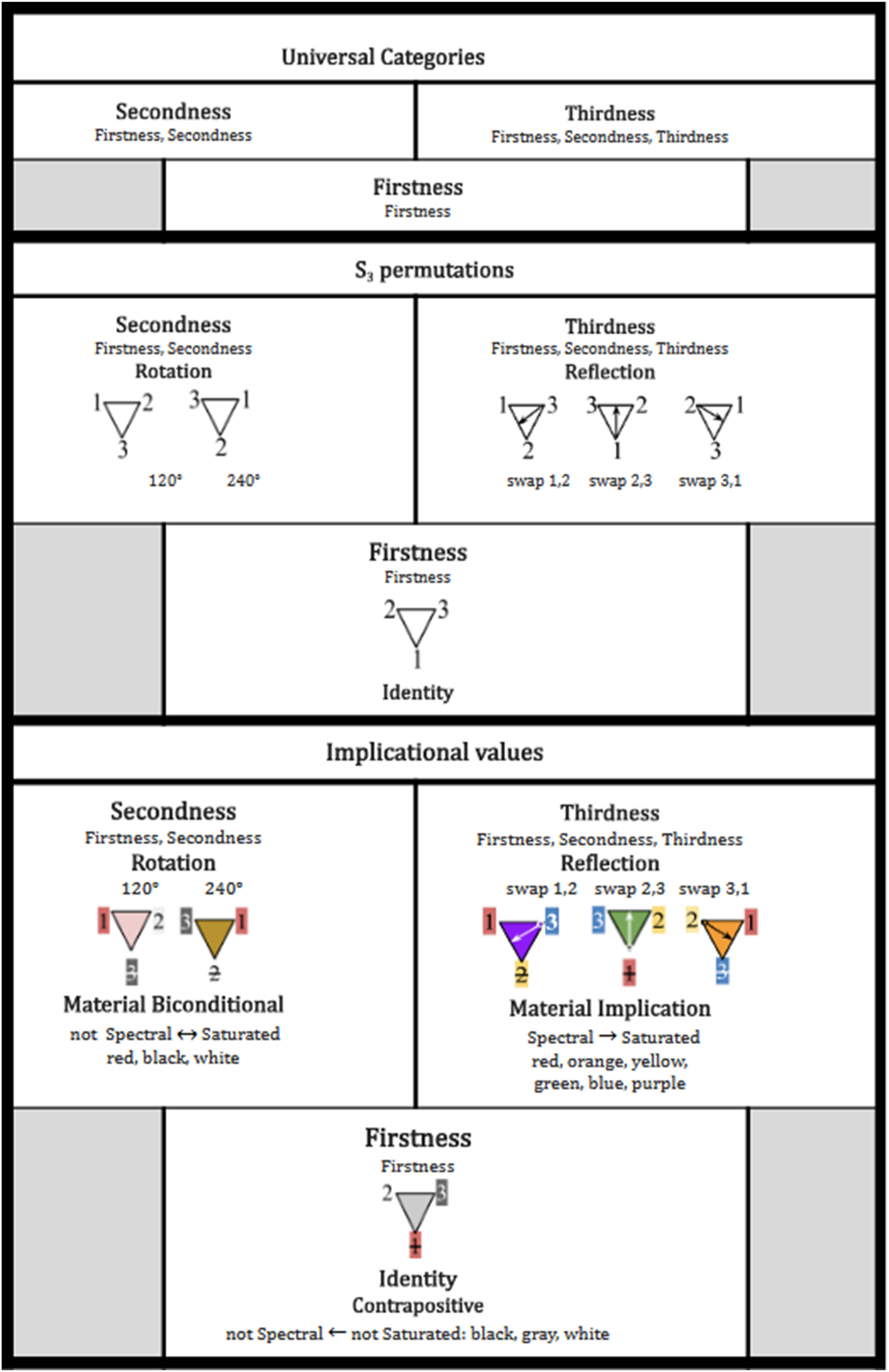
The Universal Categories, the S3 transformations, and the implicational values of the Spectral and Saturated colors.
4.1.1 Peirce’s Universal Categories
In Figure 7 Peirce’s Universal Categories, refer to the term “experience.” Please associate experience with the notion of perceptual awareness – that is, experiencing perceptions.
Firstness represents the immediate, qualitative aspects of experience – the sensations, feelings, and possibilities that arise in the present moment. Secondness encapsulates the realm of brute actuality – the resistances and reactions we encounter in the external world. Thirdness bridges the gap between the subjective and the objective, mediating between possibilities and necessities through signs, habits, and reasoned interpretation.
Firstness stands for “a monadic quality [that] is a mere potentiality, without existence” (CP 1.328). In other words, think of “ monadic experiences , or simples , [as] being elements [as] though there were nothing else in all experience.”
Secondness stands for a dyadic experience, which is an “experience of an opposing pair of objects.”
Thirdness stands for “ triadic experiences , or comprehensions , each a direct experience, which connects other possible experiences” (CP 1.328).
Peirce’s six Universal Categories – Firstness of Firstness, Firstness of Secondness, Secondness of Secondness, Firstness of Thirdness, Secondness of Thirdness, Thirdness of Thirdness – extend beyond their abstract philosophical foundations, providing a multifaceted framework for analyzing real-world experiences. Peirce sees his categories as representing or standing for different types of perceptual experiences. As symbolic representations, the six categories offer a lens through which to understand potentials, objects, and systems, rendering complex data transparent and accessible. As shown below, the categories provide the foundational framework for this proposed explanation for the widespread existence of the BCTs.
4.1.2 Structure and organization of S3 symmetry
Figure 8 shows significant isomorphisms (one-to-one relationships) comparing the Universal Categories with the S3 transformations: Firstness ≃ Identity, Secondness ≃ Rotation, and Thirdness ≃ Reflection.
These isomorphisms establish a thoroughgoing connection between Firstness, Secondness, and Thirdness. They suggest a nonrandom relationship between these concepts, further supported by six correlations. Compare the following:
Firstness of Firstness: The firstness of Identity represents the category on which the transformations of Rotation and Reflection must operate. Its mode of being is, therefore, a potential or a “firstness,” the subject to all transformations of the S3 symmetry group, including Rotation and Reflection.
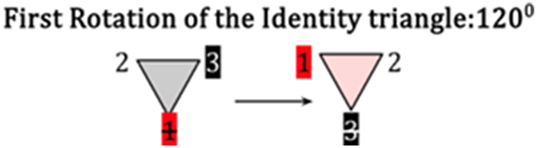
Firstness of Secondness: a first Rotation, representing the permutation of 120 degrees from Identity.
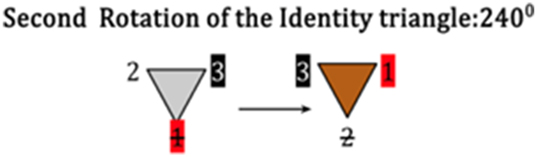
Secondness of Secondness: a second Rotation, representing the permutation of 240 degrees from Identity.
Firstness of Thirdness: a first Reflection represents swapping Identity’s 1 and 2.
Secondness of Thirdness: a second Reflection represents swapping Identity’s 2 and 3.
Thirdness of Thirdness: a third Reflection represents the swapping Identity’s 3 and 1.
Peirce’s Universal Categories offer a fundamental framework aligned with the conceptual structure of the symmetry and permutations associated with the S3 symmetry group. As Peirce noted, “the universal Categories … belong to every phenomenon, one being perhaps more prominent in one aspect of that phenomenon than another but all of them belonging to every phenomenon” (CP 5.43).[3]
The S3 group’s structure embodies the intuitive logic of the Universal Categories, underscoring the fact that these concepts and their corresponding isomorphisms are not merely abstract notions but are rather an intrinsic part of the fabric of reality. After all, Peirce defines Firstness, Secondness, and Thirdness in terms of perceptual “experiences” (CP 1.328). This group serves as a telling example of how abstract philosophical concepts can find tangible expression in the world around us, illustrating the connection between philosophical metaphysics and the actual physics of the material world.
Plainly put, “Geometric algebra is useful to a physicist because it automatically incorporates the structure of the world we inhabit, and accordingly provides a natural language for physics” (Gull et al. 1993).
As shown below, the formal relationship of Peirce’s Universal Categories and the algebra of the S3 symmetry transformations lays out the possibility of an abstract diagram produces each of the eleven BCTs. Peirce describes such possibilities in this way:
The purpose of a Diagram is to represent certain relations in such form that it can be transformed into another form, representing other relations involved in the first represented, and this transformed icon can be interpreted in the symbolic statement … No other kind of sign can make a Truth evident for the evidence is that which is presented in an image, leaving for the work of the understanding merely the interpretation of the image in a Symbol. (MS Am 1632 [339], 1906; emphasis added)
4.2 The isomorphisms among the Universal Categories, the S3 transformations, and the implicational values of the spectral and saturated colors
How does the isomorphic progression from Peirce’s Universal Categories (Firstness, Secondness, Thirdness) through the S3 Permutations (Identity, Rotation, Reflection), and finally to the three implicational truth values (Material Implication, Contrapositive, Material Biconditional) ultimately produce Berlin and Kay’s Basic Color Terms (BCTs)?
4.2.1 The relationship of the spectral and saturated colors
To understand the implicational values that lead to the generation of the BCTs, we must first explain the logic of Spectral and Saturated Colors relative to their relationship of the truth values mentioned above. For simplicity numbers will represent the structure of the three categories, Implication, Contrapositive, and Biconditional, represented in Figure 10.

The truth functional value of ±Spectral, ±Saturated.
In Figure 10, 2x represents Spectral colors, and 2y represents Saturated colors. 1x represents non-Spectral colors and 1y represents non-saturated colors.
A spectral color is monochromatic light composed of a single wavelength. Saturation is a measure of how vivid a color appears to the viewer. It describes the colors’ intensity, and purity. A highly saturated color is perceived as rich and vibrant, while a low saturation appears closer to a neutral shade of white, gray, black.
4.2.2 The contrapositive
The Contrapositive belongs to the category Firstness ≃ Identity ≃ Contrapositive. Please note: The Contrapositive has the truth value of –spectral ← –saturation of Figures 9 and 10. In both tables, the leftward arrow (1x ← 1y) represents the relationship “not Spectral ← not Saturated,” which is to be understood as “If any color is not Saturated, then it cannot be Spectral.” The Identity triangle of Figure 9 is the instantiation of the Contrapositive of the Material Implication: not Spectral ← not Saturated. The BCT colors Black, Gray, and White are neither Saturated nor Spectral.
The Identity triangle is a key focus of this paper because it lays the groundwork for the application of the Rotation and Reflexive transformations. The function of Identity is nothing more than to passively undergo transformations, to be transformed, i.e., to be Rotated, and then to undergo Reflection.
In Figure 11, Identity Triangle, red  is in the first position, and as potential it plays no part in what is in second position, namely, white, and in third position,
is in the first position, and as potential it plays no part in what is in second position, namely, white, and in third position,  , black. The combination of white + black yields gray, the color of the triangle.
, black. The combination of white + black yields gray, the color of the triangle.
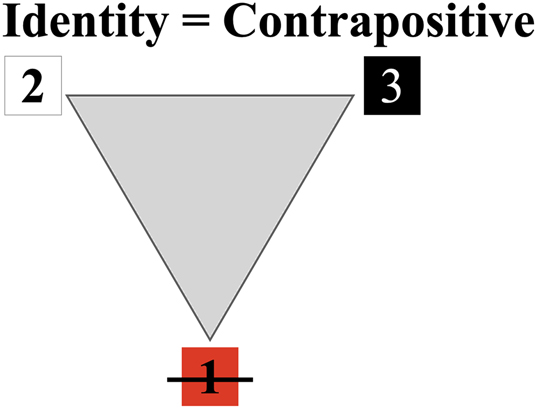
Identity triangle.
The color of the Contrapositive, white + black = gray, highlights a fundamental principle: a color that is not saturated cannot have a specific wavelength, making it fully non-spectral.
4.2.3 The material biconditional: rotation
In Figure 10, the left-right arrow (1x ↔ 1y) represents a biconditional reading: “If not Spectral, then Saturated” and “If not Saturated, then Spectral.”
It is the role of the Material Biconditional to determine the quality of colors that are Spectral (Red) and not Saturated, in this case, White. It is the rotation of 1200 that brings black to the hidden, first position, red to the second position, and white to the third position. As a consequence, red + white results in the pink and brown triangles, as shown in Figures 12 and 13.
Transformation from gray to pink.
Transformation from gray to brown.
The second rotation at 2400 brings white to the potential position, black the second position, and red to the third position, which results in black + red coloring the triangle to a brown color. It is the Material Biconditional that also determines the quality of colors that are not Saturated (Black) and Saturated (Red) = Brown, in that order.
In the second rotation at 2400, white moves to the potential position, black occupies the second position, and red takes the third position. The Material Biconditional also includes non-Saturated (Black) combined with Saturated (Red) yielding Brown, in that specific order.
Figure 14 summarizes.
Summary of rotation.
First reflection from gray to purple.
4.2.4 The material implication: reflection
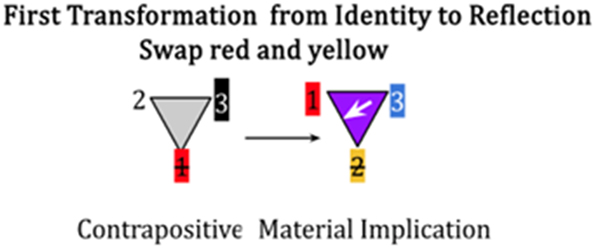
In every instance of transforming from the Contrapositive (white, gray, black) to the Material Implication (yellow, green, blue), we observe that white is substituted with yellow, gray with green, and black with blue. These substitutions arise from the transformation of the Contrapositive (–spectral ← –saturated; white, gray, black) to the Material Implication (+spectral → +saturated; yellow, green, blue). Notably, red remains unchanged throughout all transformations, because it begins as potential, absent from position 2 or 3, in the Contrapositive (see Figure 11).
In Figure 15, the Identity transformation undergoes the first Reflective transformation: Swap red and yellow, placing yellow in the first position, with red in second position, with blue remaining in third position, such that red + blue = purple.
In Figure 16, the Identity transformation undergoes the second Reflective transformation: swap red and yellow, which yields orange. The swap places blue in the second position and yellow in the third position with red remaining in the first position, where blue + yellow = green.

Second transformation from gray to green.
In Figure 17, the Identity transformation undergoes the third Reflective transformation: swap red and blue, which yields places red in third position and yellow remaining in second position with blue remaining the first position, where red + yellow = orange.
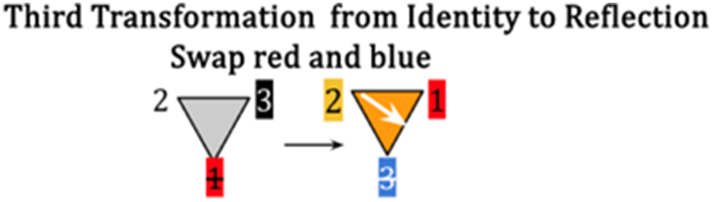
Third transformation from gray to orange.
Figure 18 summarizes.
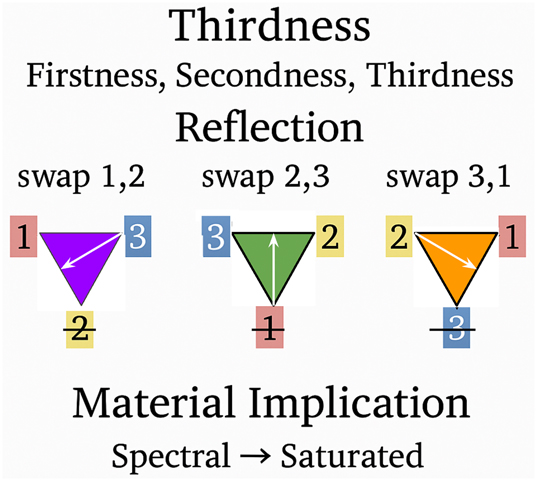
Summary of reflection.
In summary:
The Identity transformation i.e., –Spectral ← –Saturation, yields
red, white + black = gray.The Material Biconditional i.e., –Spectral ↔ +Saturation, yields
black, white + red = pink, andwhite, red + black = brown.The Material Implication i.e., +Spectral → +Saturation,
yellow, red + blue = purple,red, blue + yellow = green, andblue, yellow + red = orange.
4.3 Phenomenology
In his discussion of phaneroscopy (phenomenology), Peirce noted, “I never entertained a doubt that those features of the phaneron that I have found in my mind are present at all times and to all minds” (CP 1.40). Similarly, in their derived structure, the BCTs appear to be universally present in all minds, transcending time and space. The Identity triangle, therefore, is not just a mathematical construct; it is a phenomenological keystone that enables the derivation of the rest of the BCTs.
The crucial understanding is that the Universal Categories, along with their associated symmetry operations and the various manifestations of Spectral and Saturated colors, are not abstract notions existing as predicates in an immaterial realm. Instead, the application of the S3 symmetry group emerges as a tangible demonstration of the Universal Categories’ structure, as evidenced in Figure 9. In this context, the S3 symmetry transformations represent a specific instance showing how Peirce’s abstract philosophical categories find concrete expression within mathematical theory and the intrinsic qualities of color, Spectral and Saturation. Moreover, the application of the S3 transformations framed within the truth-functional logic of contrapositive, material biconditional, and material implication serves as a logical framework through which the eleven BCTs are generated and phenomenally manifested in the world’s languages.
5 Conclusions
Berlin and Kay’s (1991 [1969]) book served as a pivotal catalyst for exploring the nature of color, encompassing a deeper understanding of various constructs of the visible spectrum, even the unique color perceptions of belonging to various creatures such as monkeys, jumping spiders,[4] and bees. Significantly, it also brought attention to the construct of the human visible spectrum, including also how the resulting colors are named. This work also initiated an ongoing debate about whether color naming in humans is universal, relative, or a blend of both. It raised important questions regarding unique colors and whether they are biologically real or psychologically imagined. Additionally, it prompted inquiries into whether preverbal children worldwide can discern unique hues, particularly in the right hemisphere, and how the need for naming the basic color terms transition to the left hemisphere. Notably, while the language processing center in the left hemisphere aids in color discrimination, the right visual field shows superior color discrimination compared to the left (Pasmanter and Munakomi 2022).
These topics, among many others, have been extensively examined thanks to the contributions of Berlin and Kay. However, after fifty plus years of research, a crucial question remains unanswered: the origins of color naming. This paper addresses the central inquiry: Under what conditions do universal BCTs exist, and why have specific terms emerged?
This study’s proposed answer is available from three isomorphically related resources:
Peirce’s Universal Categories of Firstness, Secondness, and Thirdness provide a comprehensive structural predicate for directing the fundamental modes of human perception and experience.
The S3 symmetry group provides a fundamental method of scientific inquiry, which affords a robust framework not only for explaining the structure and organization of the natural world, but also for the perceptual experience of color naming.
The well-understood truth functional notions of the Material Implication, the Material Biconditional, and the Contrapositive of the Material Implication, which, by means of S3 Symmetry transformations, bring the eleven colors into the existing languages of the world.
By synthesizing these seemingly disparate fields – Peircean semiotics, geometric symmetry, and specific truth-functional elements – this research proposes a system of generative logic that underlies Basic Color Terms, while also suggesting broader possibilities for understanding the human mind’s capacity to comprehend the world around us.
References
Berlin, Brent & Paul Kay. 1991 [1969]. Basic color terms: Their universality and evolution. Berkeley: University of California.Suche in Google Scholar
Cook, Richard, Paul Kay & Terry Regier. 2012. World color survey: WCS data archives. International Computer Science Institute Berkeley. https://linguistics.berkeley.edu/wcs/data.html (accessed 25 May 2025).Suche in Google Scholar
Dowman, Mike. 2007. Explaining color term typology with an evolutionary model. Cognitive Science 31. 99–132. https://doi.org/10.1207/s15516709cog3101_4.Suche in Google Scholar
Emery, Kara J. & Michael A. Webster. 2019. Individual differences and their implications for color perception. Current Opinion in Behavioral Sciences 30. 28–33. https://doi.org/10.1016/j.cobeha.2019.05.002.Suche in Google Scholar
Franklin, Anna & Ian R. L. Davies. 2004. New evidence for infant color categories. British Journal of Developmental Psychology 22. 349–377. https://doi.org/10.1348/0261510041552738.Suche in Google Scholar
Franklin, Anna, Vicky G. Drivonikou, Laura Bevis, Ian R. L. Davies, Paul Kay & Terry Regier. 2008. Categorical perception of color is lateralized to the right hemisphere in infants, but to the left hemisphere in adults. Proceedings of the National Academy of Sciences of the United States of America 105(9). 3221–3225. https://doi.org/10.1073/pnas.0712286105.Suche in Google Scholar
Greene, Maxwell J., Alexandra E. Boehm, John E. Vanston, Vimal P. Pandiyan, Ramkumar Sabesan & William S. Tuten. 2024. Unique yellow shifts for small and brief stimuli in the central retina. Journal of Vision 24(6). 1–24. https://doi.org/10.1167/jov.24.6.2.Suche in Google Scholar
Gull, Stephen, Anthony Lasenby & Chris Doran. 1993. Imaginary numbers are not real – the geometric algebra of spacetime. Foundations of Physics 23(9). 1175–1201. https://doi.org/10.1007/bf01883676.Suche in Google Scholar
Hering, Ewald. 1964. Outlines of a theory of the light sense. Cambridge, MA: Harvard University Press.Suche in Google Scholar
Hinton, Leanne, Johanna Nichols & John J. Ohala (eds.). 1994. Sound symbolism. Cambridge: Cambridge University Press.10.1017/CBO9780511751806Suche in Google Scholar
Kay, Paul, Brent Berlin, Luisa Maffi, William R. Merrifield & Richard Cook. 2010. The world color survey. Stanford: CSLI.Suche in Google Scholar
Kay, Paul, Brent Berlin & William R. Merrifield. 1991. Biocultural implications of systems of color naming. Journal of Linguistic Anthropology 1. 12–25. https://doi.org/10.1525/jlin.1991.1.1.12.Suche in Google Scholar
Kay, Paul & Luisa Maffi. 1999. Color appearance and the emergence and evolution of basic color lexicons. American Anthropologist 101(4). 743–760. https://doi.org/10.1525/aa.1999.101.4.743.Suche in Google Scholar
Lindsey, Delwin T. & Angela M. Brown. 2021. Lexical color categories. Annual Review of Vision Science 7. 605–631. https://doi.org/10.1146/annurev-vision-093019-112420.Suche in Google Scholar
Lindsey, Delwin T., Angela M. Brown, David H. Brainard & Coren L. Apicella. 2015. Hunter-gatherer color naming provides new insight into the evolution of color terms. Current Biology 25(18). 2441–2446. https://doi.org/10.1016/j.cub.2015.08.006.Suche in Google Scholar
Lucy, John A. 1997. The linguistics of “color”. In Clyde Hardin & Luisa Maffi (eds.), Color categories in thought and language, 320–346. Cambridge, MA: Cambridge University Press.10.1017/CBO9780511519819.015Suche in Google Scholar
MacEvoy, Bruce. 2015. The geometry of color perception. Handprint. https://www.handprint.com/HP/WCL/color2.html (accessed 24 June 2023).Suche in Google Scholar
McCarthy, Arya D., Winston Wu, Aaron Mueller, Bill Watson & David Yarowsky. 2019. Modeling color terminology across thousands of languages. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), 2241–2250. Hong Kong: Association for Computational Linguistics. https://aclanthology.org/D19–1229.pdf (accessed 24 June 2023).10.18653/v1/D19-1229Suche in Google Scholar
Mendoza, Francisco Pérez & Miguel Hernández Mendoza (eds.). 2001. Diccionario Tz’utujil. Guatemala City: Proyecto Lingüístico.Suche in Google Scholar
Ocelák, Radek. 2015. The myth of unique hues. Topoi 34. 513–522. https://doi.org/10.1007/s11245-014-9249-4.Suche in Google Scholar
Pasmanter, Nathaniel & Sunil Munakomi. 2022. Physiology, color perception. StatPearls. https://www.ncbi.nlm.nih.gov/books/NBK544355/ (accessed 12 March 2025).Suche in Google Scholar
Peirce, Charles S. 1931–1966. The collected papers of Charles S. Peirce, 8 vols., Charles Hartshorne, Paul Weiss & Arthur, W. (eds.). Cambridge: Harvard University Press. [Reference to Peirce’s papers will be designated CP followed by volume and paragraph number.]Suche in Google Scholar
Peirce, Charles S. 1967. Manuscripts in the Houghton Library of Harvard University, as identified by Richard Robin, Annotated catalogue of the Papers of Charles S. Peirce. Amherst: University of Massachusetts Press. [Reference to Peirce’s manuscripts will be designated MS or L.]Suche in Google Scholar
Regier, Terry, Paul Kay & Richard S. Cook. 2005. Focal colors are universal after all. Proceedings of the National Academy of Sciences of the United States of America 102. 8386–8391. https://doi.org/10.1073/pnas.0503281102.Suche in Google Scholar
Rezeanu, Dragos, Maureen Neitz & Jay Neitz. 2023. From cones to color vision: A neurobiological model that explains the unique hues. Journal of the Optical Society of America A: Optics, Image Science, and Vision 40(3). A1–A8. https://doi.org/10.1364/josaa.477227.Suche in Google Scholar
Roberson, Debi, Jules Davidoff, Ian R. Davies & Laura R. Shapiro. 2005. Color categories: Evidence for the cultural relativity hypothesis. Cognitive Psychology 50(4). 378–411. https://doi.org/10.1016/j.cogpsych.2004.10.001.Suche in Google Scholar
Saunders, Barbara. 1999. The spectre of color: A sociobiobogical paradigm. Science as Culture 8(4). 473–496. https://doi.org/10.1080/09505439909526559.Suche in Google Scholar
Saunders, Barbara. 2000. Revisiting basic color terms. Journal of the Royal Anthropological Institute 6(1). 81–99. https://doi.org/10.1111/1467-9655.00005.Suche in Google Scholar
Saunders, Barbara & Jaap van Brakel. 1988. Re-evaluating basic color terms. Cultural Dynamics 1. 359–378. https://doi.org/10.1177/092137408800100306.Suche in Google Scholar
Saunders, Barbara & Jaap van Brakel. 1997. Are there nontrivial constraints on color categorization? Behavioral and Brain Sciences 20(2). 167–179. https://doi.org/10.1017/s0140525x97001428.Suche in Google Scholar
Skelton, Alice E., John Maule & Anna Franklin. 2022. Infant color perception: Insight into perceptual development. Child Development Perspectives 16(2). 90–95. https://doi.org/10.1111/cdep.12447.Suche in Google Scholar
Zurek, Daniel B., Thomas W. Cronin, Lisa A. Taylor, Kevin Byrne, Mara L. G. Sullivan & Nathan I. Morehouse. 2015. Spectral filtering enables trichromatic vision in colorful jumping spiders. Current Biology 25(10). R403–R404. https://doi.org/10.1016/j.cub.2015.03.033.Suche in Google Scholar
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Research Articles
- The six types of sign action
- Peirce’s Universal Categories in the S3 symmetry group: an analysis of the basic color terms
- The role of sentiment, aesthetic behavior, and narrative semiosis in the identification of selfhood from Peirce’s semiotic perspective
- From hieroglyphs to emoji: a spiral model for writing systems evolution
- The three states of mediatization: the case of war mediatization
- Challenging linguicentrism in translation: a semiotic approach to the emergence of a female counterculture in digital spaces
- TV series and the unveiling of the unknown: a semiology of strangeness
- Performance as discourse: a multimodal perspective on meaning-making in theater
Artikel in diesem Heft
- Frontmatter
- Research Articles
- The six types of sign action
- Peirce’s Universal Categories in the S3 symmetry group: an analysis of the basic color terms
- The role of sentiment, aesthetic behavior, and narrative semiosis in the identification of selfhood from Peirce’s semiotic perspective
- From hieroglyphs to emoji: a spiral model for writing systems evolution
- The three states of mediatization: the case of war mediatization
- Challenging linguicentrism in translation: a semiotic approach to the emergence of a female counterculture in digital spaces
- TV series and the unveiling of the unknown: a semiology of strangeness
- Performance as discourse: a multimodal perspective on meaning-making in theater

