Abstract
In this article, a number of smoothing methods were investigated to enhance the signal-to-noise (S/N) ratio of diverse methanol maser spectral data, encompassing variations in signal strength, multiplicity of peaks, and spectral complexity. The study aimed to improve the accuracy and reliability of astronomical measurements obtained with Irbene radio telescopes RT-16 and RT-32 at the Ventspils International Radio Astronomy Center. Comparing eleven different smoothing techniques, including moving average, Gaussian, Hanning, among others, the Savitzky–Golay smoothing method is identified as the optimal choice. The evaluation criteria included the preservation of spectral features, reduction of noise artifacts, and enhancement of S/N ratio metrics. The Savitzky–Golay method outperformed other techniques by effectively balancing noise reduction with the preservation of spectral details crucial for maser emission analysis.
1 Introduction
Cosmic, or astrophysical, masers are naturally occurring sources of stimulated spectral line emission in the radio wave part of the electromagnetic spectrum. They can be observed in star-forming regions, planetary atmospheres and systems, molecular clouds, late-type star atmospheres, comets, and more (Gray 2012, Strel’nitskii 1974).
Cosmic masers are large in volume, approximately
In the interstellar medium, masers consist of molecules with one to six atoms, most common being OH, CH3OH, H2O, and SiO (Gray 2012).
The study of astrophysical masers is crucial for enhancing our understanding of the universe. One of the institutes involved in observing galactic masers is Ventspils International Radio Astronomy Centre (VIRAC), utilizing the Irbene radio telescopes. These telescopes allow for resolution adjustments via computer settings, albeit with limitations. For instance, in the Ventspils monitoring program observing 6.7 GHz methanol masers (Aberfelds 2024, Aberfelds et al. 2023), a high velocity resolution of 0.017 km/s is used, even though the natural widths of the maser lines range from 0.2 to 0.3 km/s. As a result, the data are oversampled, leading to spectra with more noise than would be present with the appropriate velocity resolution.
The aim of this study is to find an optimal smoothing method, which in result increases the S/N value by not effecting the original peak values, keeping the original spectral form. It is hypothesized that the advanced mathematical functions will be better than the simple averaging down method.
Advanced mathematical methods differ from simple calculations like averaging over a number of spectral channels, they reduce noise via convolution-based filtering according to Fourier transform principles. Each convolution-based method applies various functions with specific parameters. For instance, the Savitzky–Golay method fits a polynomial with chosen polynomial order (p) to the central data point within a defined window (w) and replaces that point with the calculated polynomial value. Other parameters used are standard deviation (
Savitzky–Golay filtering has been previously applied in radio astronomy for spectral analysis, but past studies have only briefly explored its potential. Morabito et al. (2014) tested it alongside other smoothing methods for carbon radio recombination lines, while Stroe et al. (2015) mentioned its use without detailed results. More recently, Hussein and Mahdi (2024) applied it for radio signal enhancement but did not perform an extensive comparison. This study expands on previous work by systematically evaluating multiple smoothing techniques to determine the optimal approach for methanol maser spectra.
2 Method
In this article, VIRAC provided spectral data from nine different 6.7 GHz methanol maser sources (Aberfelds et al. 2023) and a pre-existing Python code for working with spectra, which included channel averaging smoothing method. The first course of action was to find additional smoothing methods for comparison. Ten more methods were identified, bringing the total to 11 methods (and their abbreviations):
Channel averaging (Average);
Savitzky–Golay (S-G) (Savitzky and Golay 1964);
Moving average (M-A);
Median (M);
Lorentzian (L) (Draine 2011);
Voigt (Draine 2011);
Hanning (H) (Essenwanger 1986);
Bartlett (B) (Proakis and Monolakis 1996).
Eilers Perfect Smoother (Eilers 2003)
The methods were compared based on their ability to preserve spectral details while smoothing the noise. Specifically, the radial velocity (
Each method was implemented in the Python code with source codes listed in Table A1, and required various parameters, including window sizes (how many points are included in the calculations), standard deviation (affecting the smoothing level), the polynomial degree, and smoothing factor. The parameters were empirically found, meaning by trial and error and observing which parameters gave the best result.
Following the determination of the parameters, three different graphs were generated to visualize the effect of the smoothing methods on the original spectra, and additional data were outputted in the console to compare.
A code was made that completes all the mentioned tasks earlier, which was then used for testing smoothing methods on a range of maser sources. These sources varied in intensity, with either one or multiple peaks, and demonstrated differing levels of spectral complexity.
The used maser sources in this article, naming according to Galactic coordinates, were: G78.122+3.633, G109.871+2.114, G133.947+1.064, G94.602-1.796, G22.357+0.066, G32.744-0.076, G111.26-0.77, G196.454-01.67, G121.298+0.659.
3 Result
The values of each parameter used in different smoothing methods are displayed in Table 1. These values were determined to be optimal, working with Irbenes radio telescopes RT-32 and RT-16, which had the velocity resolution set as 0.017 km/s. The Voigt smoothing method combines parameters from Gaussian and Lorentzian methods.
The parameters used for smoothing methods
| Method | F | S-G | M-A | H | B | M | G | L | E | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter |
|
m | w | p | w | w | w | w |
|
|
|
d |
| Value | 150 | 1 | 17 | 2 | 10 | 10 | 10 | 11 | 3 | 5 | 2 | 2 |
An example result list for each smoothing method is given in Table 2. The results are from maser source G78.122+3.633. In addition, from the same maser source, a graph displaying the effect of smoothing method on the original spectrum is shown in Figure 1. The formula used for the difference calculations is given as follows:
Original data and smoothed data for maser source G78.122+3.633 spectra
| G78.122+3.633 | Method | RMS, Jy |
|
|
|
Noise
|
S/N |
|---|---|---|---|---|---|---|---|
| Original | 0.77 |
|
65.37 | 3623.92 |
|
84.71 | |
| Average | 0.53 |
|
64.51 | 3621.04 |
|
121.84 | |
| Fourier | 0.45 |
|
62.75 | 3623.16 |
|
138.09 | |
| S-G | 0.46 |
|
64.50 | 3623.28 |
|
138.98 | |
| M-A | 0.40 |
|
60.82 | 3622.48 |
|
210.95 | |
| Median | 0.41 |
|
60.70 | 3618.72 |
|
198.85 | |
| Gaussian | 0.40 |
|
60.66 | 3622.85 |
|
151.39 | |
| Lorentz. | 0.42 |
|
61.69 | 3622.70 |
|
147.02 | |
| Voigt | 0.35 |
|
57.70 | 3622.18 |
|
164.75 | |
| Hanning | 0.49 |
|
63.76 | 3623.23 |
|
129.36 | |
| Bartlett | 0.48 |
|
63.43 | 3623.14 |
|
132.62 | |
| Eilers | 0.38 |
|
58.57 | 3622.85 |
|
153.73 |
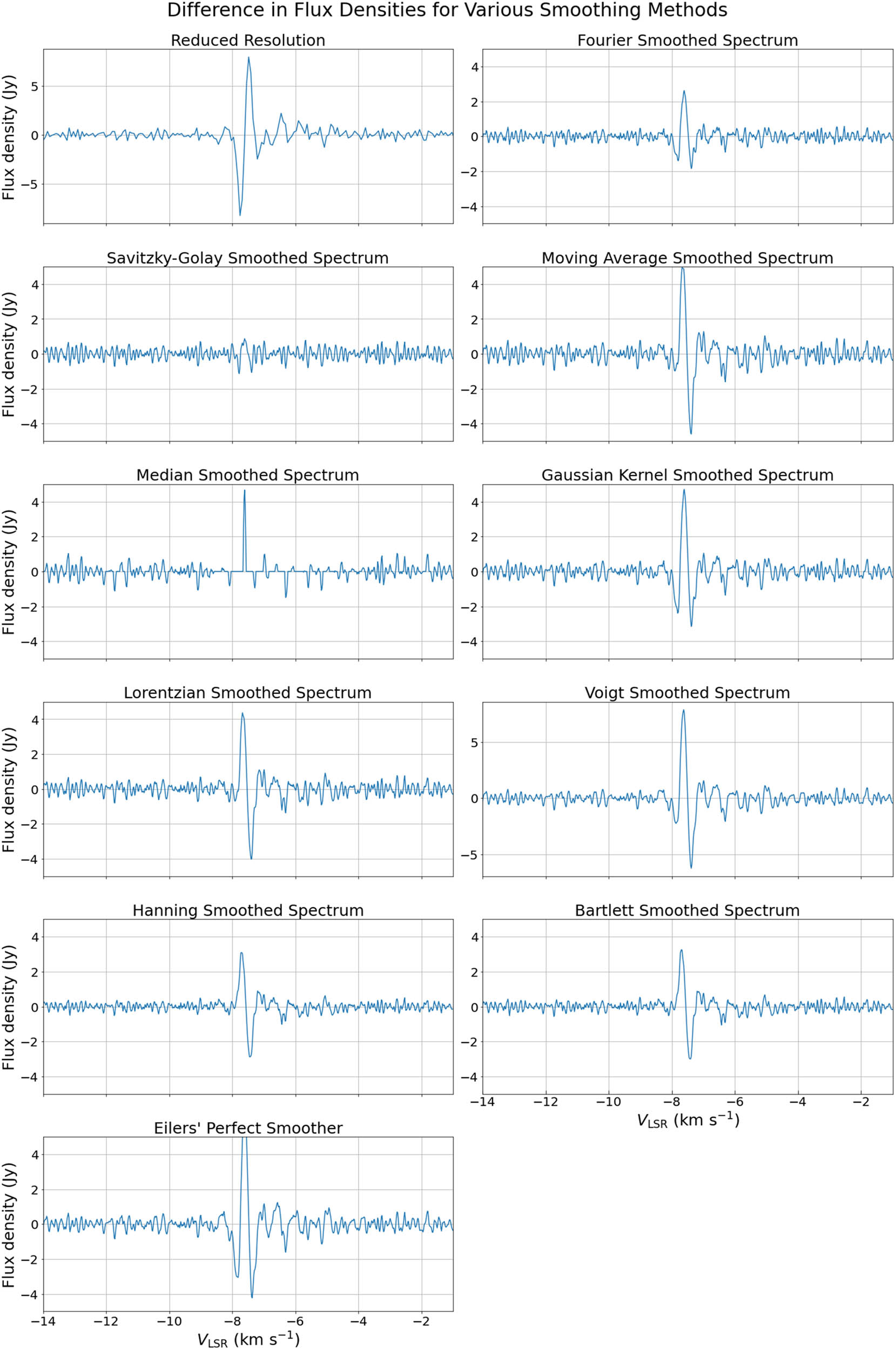
Difference in flux densities between the original spectrum and smoothed spectrum for maser source G78.122+3.633.
The optimal smoothing method is chosen by first examining the graphs and then comparing the values.
The results for maser source G78.122+3.633 show that the optimal smoothing method is Savitzky–Golay. This proves to be true comparing the values in Table 2: the peak radial speed does not change, while the flux density changes slightly by 0.87 Jy (1.33%) and integrated flux by 0.64 Jy km/s (0.02%). The noise RMS is smaller by 0.31 Jy (40.26%), integrated flux by 0.91 Jy km/s (1.61%), and the S/N value is 1.64 times larger compared to the original values. Also by examining the Figure 1, it is noticeable that the Savitzky–Golay method evenly affects the whole spectrum, while other methods affect the peak values more.
The same result was achieved for the other maser sources except G32.744-0.076 and G111.26-0.77. The former consists of multiple peaks, which noticeably hinders the quality of smoothing for the Savitzky–Golay method. The effect of smoothing methods on original data points is shown in Figure A4. However, it was still considered the best method together with the channel averaging method, which is shown in Figure A2.
4 Conclusion
Based on the evaluation of 10 methods, Savitzky–Golay was identified as the optimal method for improving the S/N ratio in cosmic maser spectra for 7 out of 9 maser sources.
Execution time is not a significant factor in determining the optimal method, as all methods have an execution time of less than 1/100th of a second. Therefore, it was not taken into account.
Although the Savitzky–Golay method was identified as the optimal method, it did not improve the S/N ratio for low signal spectra. No other method improved it either, indicating that further research and evaluation of different methods are needed to find an optimal solution for low signal spectra.
After determining the optimal parameters for each method, the differences between the smoothing methods are minimal. The Savitzky–Golay, Hanning, Bartlett, and channel averaging methods are quite similar, each having minimal effect on the peak values. In contrast, the Fourier, Gaussian, Lorentzian, Voigt, and Eilers Perfect Smoother methods impact the peak values more noticeably. Finally, moving average and median methods affect the peak values the most.
The fitting parameters for all smoothing methods demonstrate a strong alignment, as the point count within the chosen window size closely matches the point count corresponding to the natural line width of a 6.7 GHz methanol cosmic maser. If the line width differs, it is advisable to adjust the window size accordingly.
Acknowledgments
This publication has received funding from the Latvian Council of Science project “A single-baseline radio interferometer in a new age of transient astrophysics (IVARS)” (lzp-2022/1-0083). I would like to express my sincere gratitude to my supervisor, Artis Aberfelds, for his invaluable guidance and support during my research at the Engineering Research Institute “Ventspils International Radio Astronomy Center” (VIRAC), particularly in relation to my Bachelor thesis. I am also deeply thankful to Juris Kalvāns, my other colleague at VIRAC and my family for their motivation and encouragement throughout this process. I would also like to thank Daniel Pelliccia from Nirpy Research for his publicly available code examples and clear explanations of the Fourier and Savitzky–Golay smoothing methods, which provided valuable insights for this study.
-
Author contributions: Bibliographic research and analysis: A.E.; draft preparation: A.E.; writing, review, and editing: A.E., A.A.; supervision: A.A. All authors accepted the responsibility for the content of the manuscript and consented to its submission, reviewed all the results, and approved the final version of the manuscript.
-
Conflict of interest: The authors state no conflict of interest.
Appendix
| Algorithm 1: Function for reducing resolution | |
|---|---|
| Input: data - data array, factor - factor by which to reduce resolution | |
| Result: Data array with channel averaging | |
| 1 | Function reduce_resolution (data, factor): |
|
|
|
| 10 | average_xdata
|
| 11 | average_ydata
|
| Algorithm 2: Function for Lorentzian spectral smoothing | |
|---|---|
|
Input:
|
|
| Result: Smoothed spectral data using Lorentzian convolution | |
| 1 | Function lorentzian_kernel (size, gamma): |
|
|
|
| 7 | Function |
| lorentzian_spectral_smoothing (ydata, gamma): | |
|
|
|
| 12 |
|
| 13 | ; |
| 14 |
lorentzian_smoothed_spectrum
|
| Algorithm 3: Function for Eilers’ perfect smoother | |
|---|---|
|
Input
|
|
| Result: Smoothed spectral data using Eilers’ smoothing method | |
| 1 |
Function
eilers_smoothing (
|
|
|
|
| 9 |
|
| 10 |
|
| 11 |
eilers_smoothed_spectrum
|
Smoothing method source codes or mathematic algorithms
| Method | Source |
|---|---|
| Channel averaging | Algorithm 1 |
| Fourier | (Brandt 2019) |
| Savitzky–Golay | scipy.signal.savgol_filter (Press et al. 2002) |
| Moving-Average | np.convolve |
| Median | scipy.signal.medfilt |
| Gaussian | scipy.ndimage.gaussian_filter1d (Rudolph et al. 2023) |
| Lorentzian | Algorithm 2 (Draine 2011, Rudolph et al. 2023) |
| Voigt | (Draine 2011) |
| Hanning | np.hanning |
| Bartlett | scipy.signal.bartlett |
| Eilers | Algorithm 3 (Eilers 2003) |
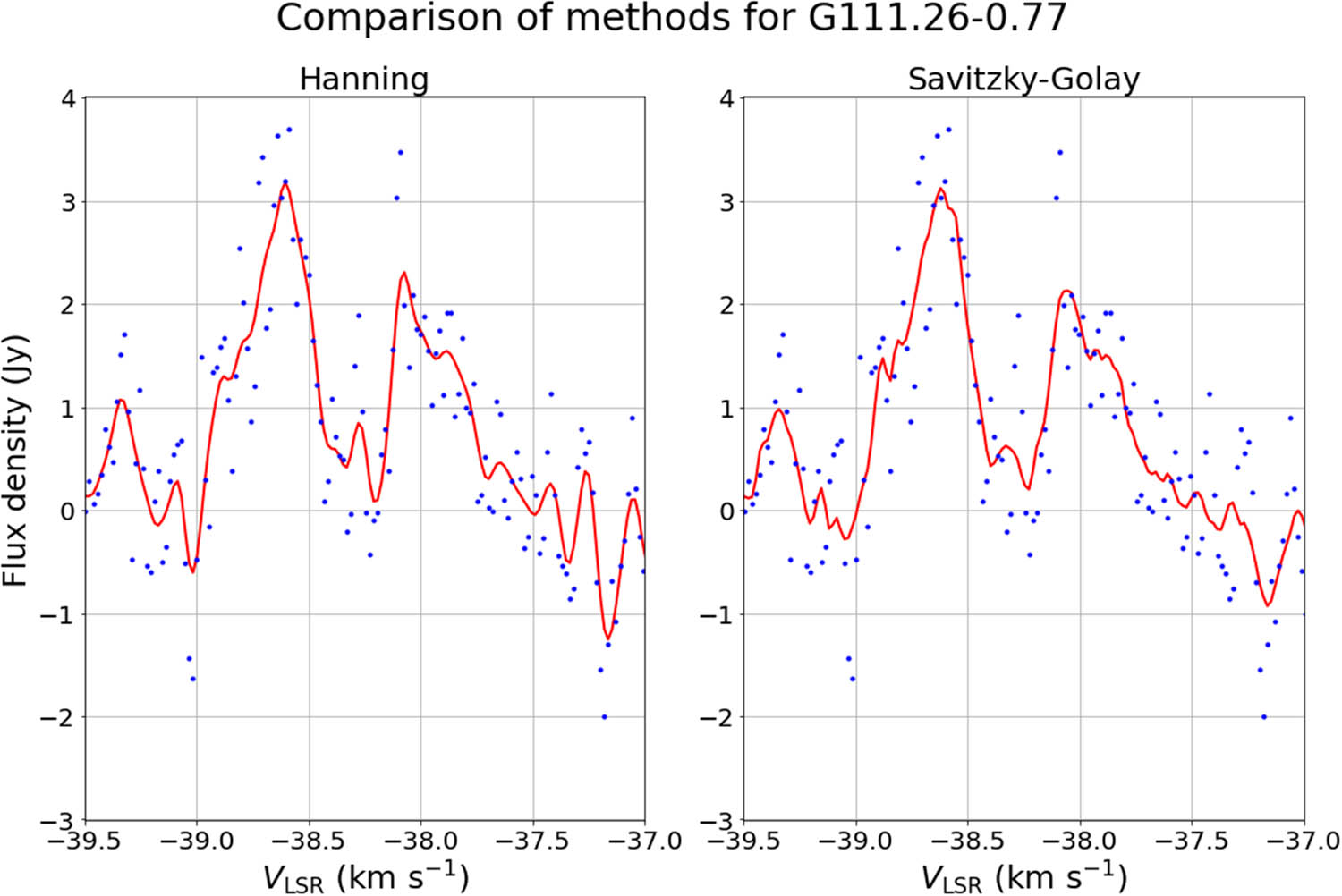
Comparison of Hanning, best smoothing method for G111.26-0.77, and Savitzky–Golay, overall best smoothing method, with G111.26-0.77 data. Red line - smoothing method result, blue points - original data.
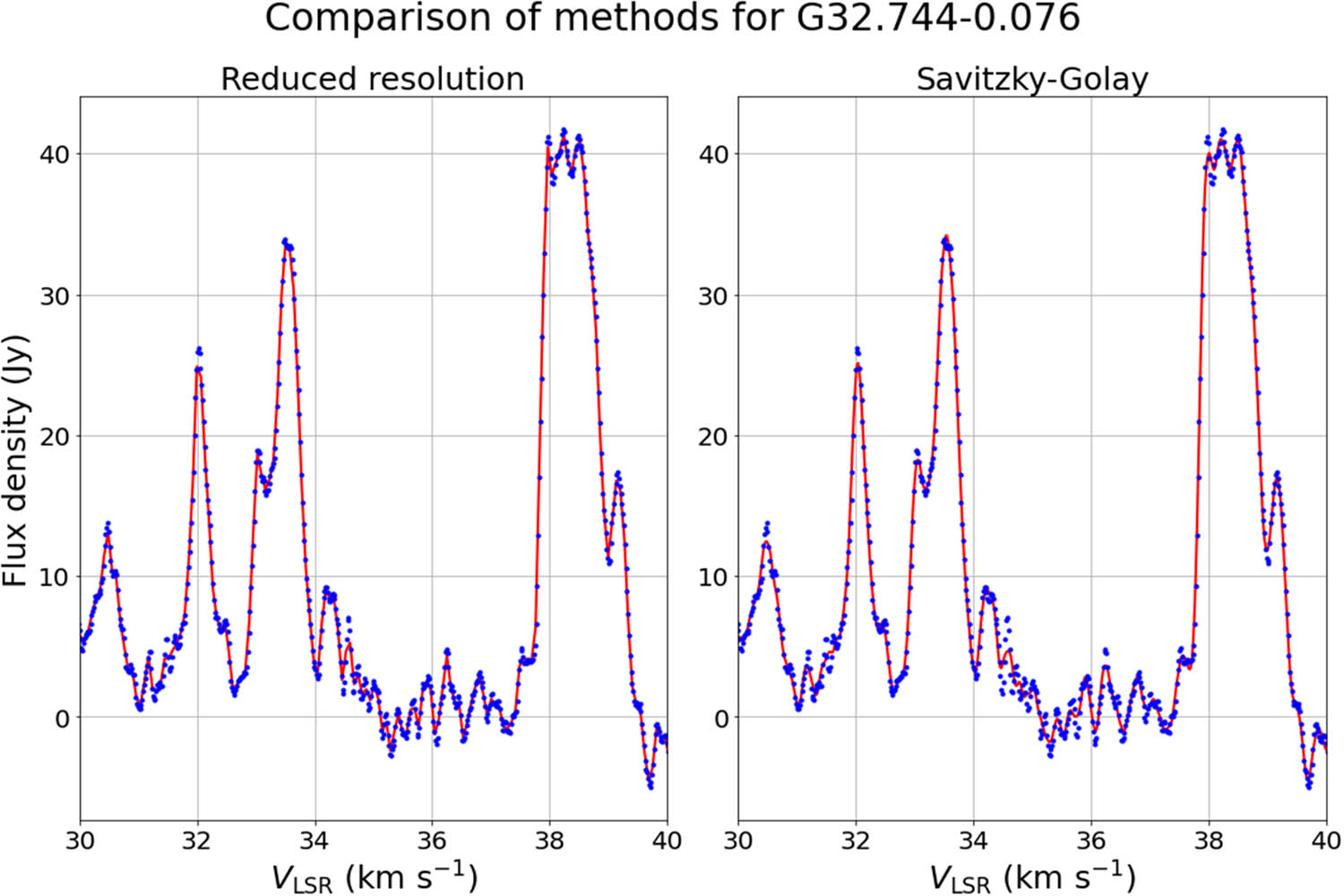
Comparison of channel averaging, best smoothing method for G32.744-0.076, where the window was 4 points, and Savitzky–Golay, overall best smoothing method, with G32.744-0.076 data. Red line - smoothing method result, blue points - original data.
The maser source G111.26-0.77 is a weak signal with a low S/N value. None of the mentioned 10 smoothing methods improved the S/N value; hence, there is no optimal method for this type of masers. The original data points with smoothing methods is shown in Figure A3. However, if we ignore the S/N not increasing above the original value, the best method is Hanning, which is made for dealing with high level noise. The comparison of Hanning and Savitzky–Golay methods can be observed in Figure A1
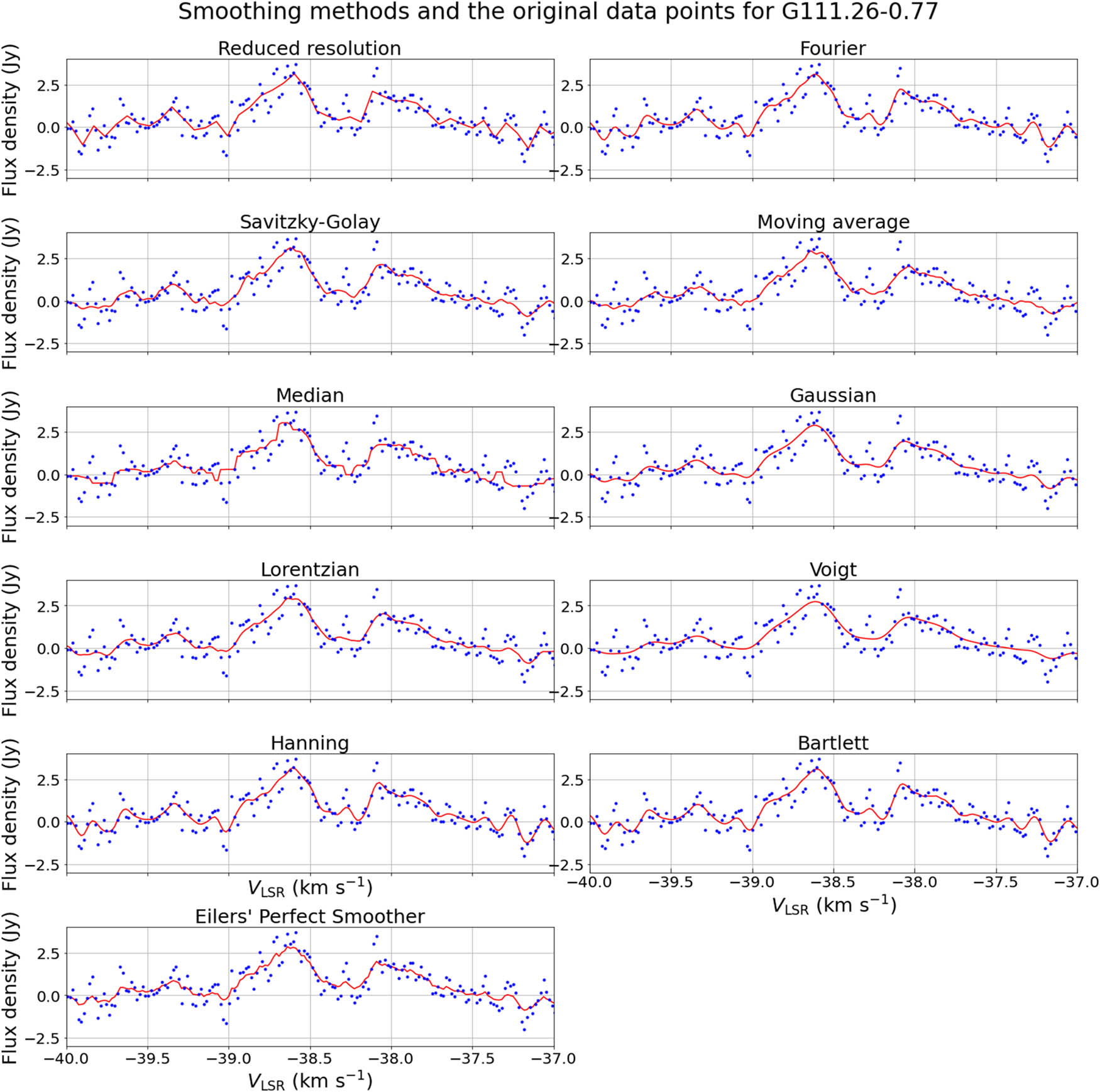
Smoothing methods (red) and the original data points (blue) for G111.26-0.77.
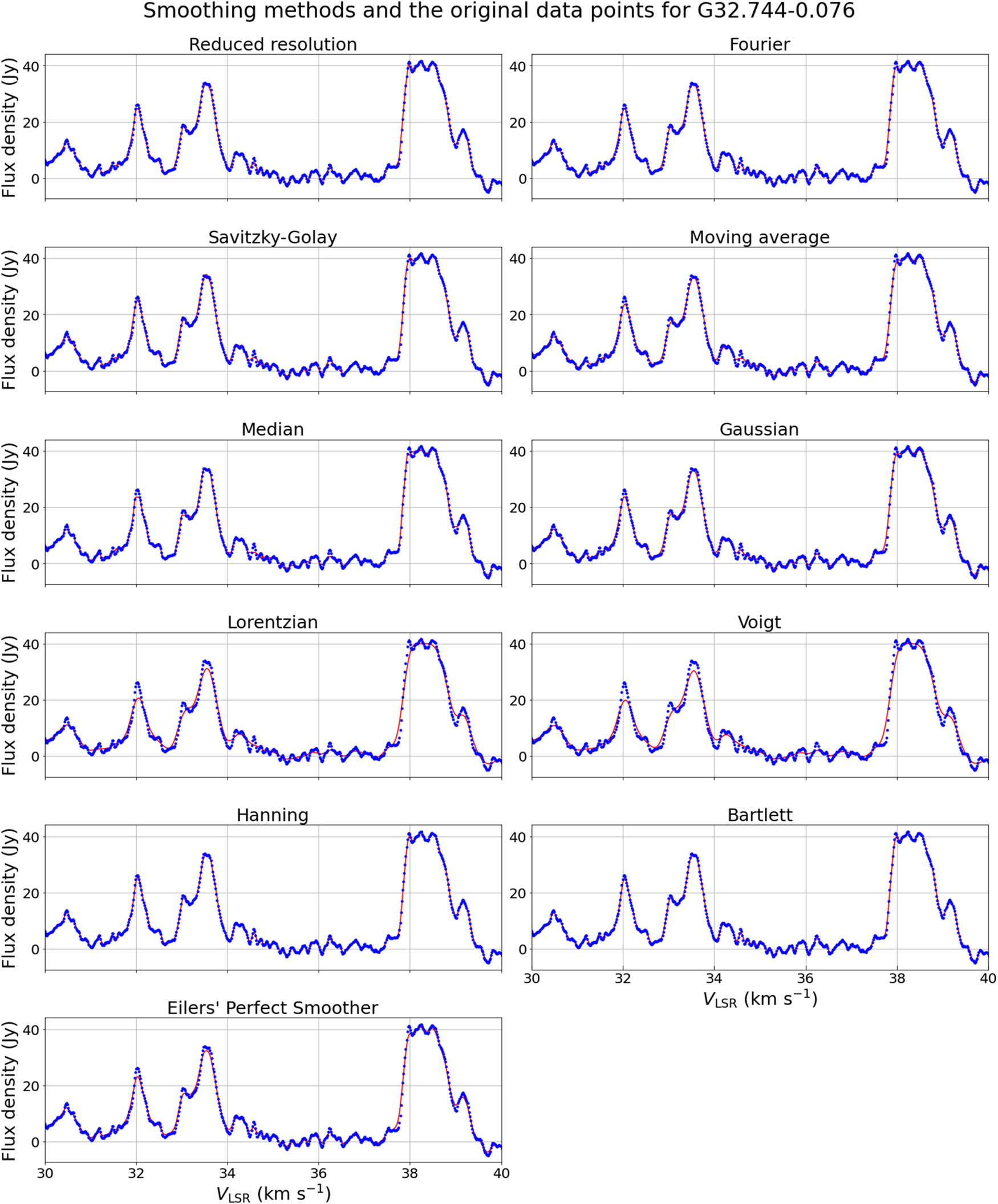
Smoothing methods (red) and the original data points (blue) for G32.744-0.076.
References
Aberfelds A. 2024. Research of 6.7 GHz Methanol Masers: Observation Methods, Monitoring and Source Morphology. PhD thesis. Riga (LV): Latvian University, Physics, MAthematics and Optometry Faculty. Suche in Google Scholar
Aberfelds A, Šteinbergs J, Shmeld I, Burns RA. 2023. Five years of 6.7 GHz methanol maser monitoring with Irbene radio telescopes. MNRAS. 526:5699–5714. 10.1093/mnras/stad3101. Suche in Google Scholar
Gray M. 2012. Maser sources in astrophysics. Cambridge: Cambridge University Press. 10.1017/cbo9780511977534. Suche in Google Scholar
Essenwanger OM. 1986. Elements of statistical analysis. Amsterdam-London-New York: Elsevier Science Publishing Co., Inc. Suche in Google Scholar
Kleinman Y, Korn-Lubetzki I. 1997. Understanding FFTs and windowing overview. Stroke. 28:7. Suche in Google Scholar
Kegel WH. 1975. Natural masers: maser emission from cosmic objects. Lehrstuhl für Theoretische Astrophysik, Universität, D-6900 Heidelberg, Fed. Rep. Germany. Suche in Google Scholar
Proakis JG, Monolakis DG. 1996. Digital signal processing: principles, algorithms, and applications. United States: Pentice Hall. Suche in Google Scholar
Savitzky A, Golay MJE. 1964. Smoothing and differentiation of data by simplified least squares procedures. Anal Chem. 36:1627–1639. 10.1021/ac60214a047. Suche in Google Scholar
Brandt SS. 2019. Smoothing of Noisy Spectra Using the Fast Fourier Transform. https://www.researchgate.net/publication/335517513_Smoothing_of_noisy_spectra_using_the_Fast_Fourier_Transform. accessed on 2025-02-17. Suche in Google Scholar
Draine BT. 2011. Physics of the Interstellar and Intergalactic Medium. Princeton: Princeton University Press, ISBN: 9780691122144. 10.1515/9781400839087Suche in Google Scholar
Rudolph A, Krois J, Hartmann K. 2023. Statistics and geodata analysis using Python (SOGA-Py). Department of Earth Sciences, Berlin: Freie Universitaet. https://www.geo.fu-berlin.de/en/v/soga-py/Advanced-statistics/time-series-analysis/Smoothing/Kernel-smoothing/index.html. accessed on 2024-05-14. Suche in Google Scholar
Smith SW. 2013. The scientist and engineer’s guide to digital signal processing. Digital Signal Processing. Suche in Google Scholar
Strel’nitskii VS. 1974. Cosmic masers. Usp Fiz Nauk. 113:463–502. 10.3367/UFNr.0113.197407c.0463Suche in Google Scholar
Press WH, Teukolsky SA, Vetterling WT, Flannery BP. 2002. Numerical Recipes in C++: The Art of Scientific Computing. 2nd Edition, Cambridge University Press. ISBN: 978-0521750332. [Section 14.8: Savitzky–Golay Smoothing Filters] https://phys.uri.edu/nigh/NumRec/bookfpdf/f14-8.pdf. Suche in Google Scholar
Morabito LK, Oonk JBR, Salgado F, Toribio MC, Röttgering HJA, Tielens AGGM, et al. 2014. Discovery of carbon radio recombination lines in M82. Astrophys J Lett. 795:L33. 10.1088/2041-8205/795/1/L33, https://arxiv.org/pdf/1410.1544. Suche in Google Scholar
Stroe A, Hardcastle MJ, Röttgering HJA, Hoeft M. 2015. Spectral properties of complex radio sources in the Double Radio Relic Cluster CIZA J2242.8.5301. Monthly Notices R Astron Soc. 452:2731–2750. 10.1093/mnras/stv1518. Suche in Google Scholar
Hussein MK, Mahdi RS. 2024. Improving radio signal from Baghdad University Radio Telescope Using the Savitzky–Golay filter. Iraqi J Phys. 22(3):60–66. 10.30723/ijp.v22i3.1274. Suche in Google Scholar
Eilers PH. 2003. A perfect smoother. Anal Chem. 75(14):3631–3636. 10.1021/ac034173t. Suche in Google Scholar PubMed
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Research Articles
- Deep learning application for stellar parameter determination: III-denoising procedure
- X-ray emission from hot gas and XRBs in the NGC 5846 galaxy
- Investigation of ionospheric response to a moderate geomagnetic storm over the mid-latitude of Saudi Arabia
- Constraining relativistic beaming model for γ-ray emission properties of jetted AGNs
- Radiogenic heating in comets: A computational study from an astrobiological perspective
- Search for the optimal smoothing method to improve S/N in cosmic maser spectra
- The stellar Mg/Si, C/O, Ca/Si, Al/Si, Na/Si, and Fe/Si ratios and the mineral diversity of rocky exoplanets
- Analogical education in times of virtuality: Back to the hands-on activities – 15 years of NASE program
- Physical conditions in spherical prestellar cores with analytical equations
- Special Issue: New Horizons in Astronomy Education
- Innovative practices in astronomy science education in China – A case study of BJP's science communication activities
- Enhancing astronomy literacy in Indonesia: Evaluating the impact of NASE training programs
- Democratizing Astronomy through teacher training in Portuguese-speaking contexts
Artikel in diesem Heft
- Research Articles
- Deep learning application for stellar parameter determination: III-denoising procedure
- X-ray emission from hot gas and XRBs in the NGC 5846 galaxy
- Investigation of ionospheric response to a moderate geomagnetic storm over the mid-latitude of Saudi Arabia
- Constraining relativistic beaming model for γ-ray emission properties of jetted AGNs
- Radiogenic heating in comets: A computational study from an astrobiological perspective
- Search for the optimal smoothing method to improve S/N in cosmic maser spectra
- The stellar Mg/Si, C/O, Ca/Si, Al/Si, Na/Si, and Fe/Si ratios and the mineral diversity of rocky exoplanets
- Analogical education in times of virtuality: Back to the hands-on activities – 15 years of NASE program
- Physical conditions in spherical prestellar cores with analytical equations
- Special Issue: New Horizons in Astronomy Education
- Innovative practices in astronomy science education in China – A case study of BJP's science communication activities
- Enhancing astronomy literacy in Indonesia: Evaluating the impact of NASE training programs
- Democratizing Astronomy through teacher training in Portuguese-speaking contexts

