Riccati Parametric Deformations of the Cornu Spiral

1 Introduction

One of the most famous spirals with important scientific and technological consequences is Euler’s spiral, also known as Cornu’s spiral in optics, and also as the clothoid, which means looking like Clotho, as proposed by the noted geometer Cesàro in 1890. Schwartzman, in his book “The Words of Mathematics” [1], mentions that Clotho was the youngest of the three fates “moirai” in ancient Greek mythology. The little sister Clotho was responsible for spinning the thread of human life. Presumably, Cesàro was inspired by the resemblance of the spiral to a spinning wheel. However, here we will call this spiral as Cornu’s spiral as it was Cornu who first drew the entire spiral with its two foci, while Euler drew only the positive arm.

Perhaps, the simplest mathematical definition of the Cornu spiral ℱ is the Argand plane representation, ℱ=X+iY, with X and Y as the two Fresnel integrals

which are parametrised by the arclength of the spiral s. In optics, the square modulus |ℱ|² is related to the intensity of light at a given point in diffraction patterns.

On the other hand, geometrically, the Cornu spiral is defined as the curve whose curvature increases linearly with the arclength, which means the radius of curvature ρ(t) times the arc length s(t) is constant at each point of the curve. This is represented by the Cesàro equation ρ(t)=c2s(t), with c as any constant. The other important property is related to the Fresnel integrals for which c=1π; both slowly approach the point (12, 12) as s→∞ in the first quadrant, and because both the functions are odd, the curve spirals towards (−12, −12) in the third quadrant [2].

Its most immediate technological use is in the layout of civil engineering works (roads, railways, pipelines among others) as road transitions to join straight sections with curved sections or to connect two circular sections [3], [4]. This is one of its most important engineering applications, as the radius of curvature decreases inversely proportional to the distance travelled on it, and this feature allows the driver a smooth change of trajectory. Other applications in which clothoids are considered useful are for the controlled trajectories of robots [5], for the design of roller coasters [6], and aesthetic shapes of industrial products [7].

Various generalisations of the Cornu spiral from the viewpoint of its different applications are found in literature [8], [9], [10], [11]. In this communication, we introduce a parametric generalisation which can be also considered as a deformation of the Cornu spiral. This is achieved by means of a complex parameter which appears in the general solution of the Riccati equation that corresponds to the Fresnel integrals. In Section 2, we show the reduction of the third-order ordinary differential equation (ODE) satisfied by the Fresnel integrals as particular solutions to the corresponding Riccati equation, whose general solution is obtained explicitly. We then write the solution of the third-order ODE based on the general Riccati solution and present the Argand plots of this solution. In Section 3, the similarity with supersymmetric quantum mechanics is emphasized by means of the factorization approach [12], [13], [14], [15], [16] which is applied to the second-order linear ODE that comes into play in the reduction process of Section 2.

2 From the Third-Order ODE to the Riccati Equation and Back

We start with the known linear third-order ODE satisfied by the Fresnel integrals [17]

which can be reduced by using w′(z)=v(z), with ′=ddz, to obtain

Letting z² = ζ we obtain the simple harmonic oscillator

Thus, the solution to (4) is

and by one integration the solution to (3) is

where C(z) and S(z) are the Fresnel integrals given by (1) and (2).

On the other hand, by using the logarithmic derivative y(z)=v′(z)v(z), (4) becomes the Riccati equation

with particular solution

As v(z)=c1e∫ypdz, then a particular solution to (4) is

which can be also obtained from (6) by setting c₂=ic₁. Thus, the particular solution of (3) for w(0)=0 is

To construct the general solution of Riccati equation (8) using any particular solution y_p we let

where u satisfies the linear equation

The solution of (13) is

where μ(z) is the integrating factor

which gives the general solution

with γ arbitrary constant.

We now use the particular solution given by (9) to construct the linear equation in u which becomes

By using the integrating factor

the general solution of Riccati equation (8) is

By redefining the constant γ=i(θ+1)2π, (19) takes the simpler form

Notice that for the limiting cases of θ→0, and θ→∞, y_g(z)→−iπz, and y_g(z)→iπz, respectively. When θ→1, and θ→−1, then yg(z)→−πztan(πz22), and yg(z)→πzcot(πz22), respectively.

To find the general solution to (4), we use vg(z)=Re∫yg(z)dz to obtain

By one integration, assuming w(0)=0 and using Euler’s formula, the deformed solution of (3) is given by

By writing the solution as

and letting θ=a+ib, we obtain

Comparing (7) with (23) and (24), one can see that we managed to replace the superposition constants c₁ and c₂ by the real and imaginary components of the parameters entering the general Riccati solution. This is not a trivial replacement because, as we will see next, one can disentangle an underlying supersymmetric structure of the solution expressed in this way. We present the Argand plots Y=w_ℐ(z), X=w_ℛ(z) in Figure 1 for various parameters a and b. All figures except a=0, b=0 are scaled by the factor R=1a2+b2.

Figure 1:

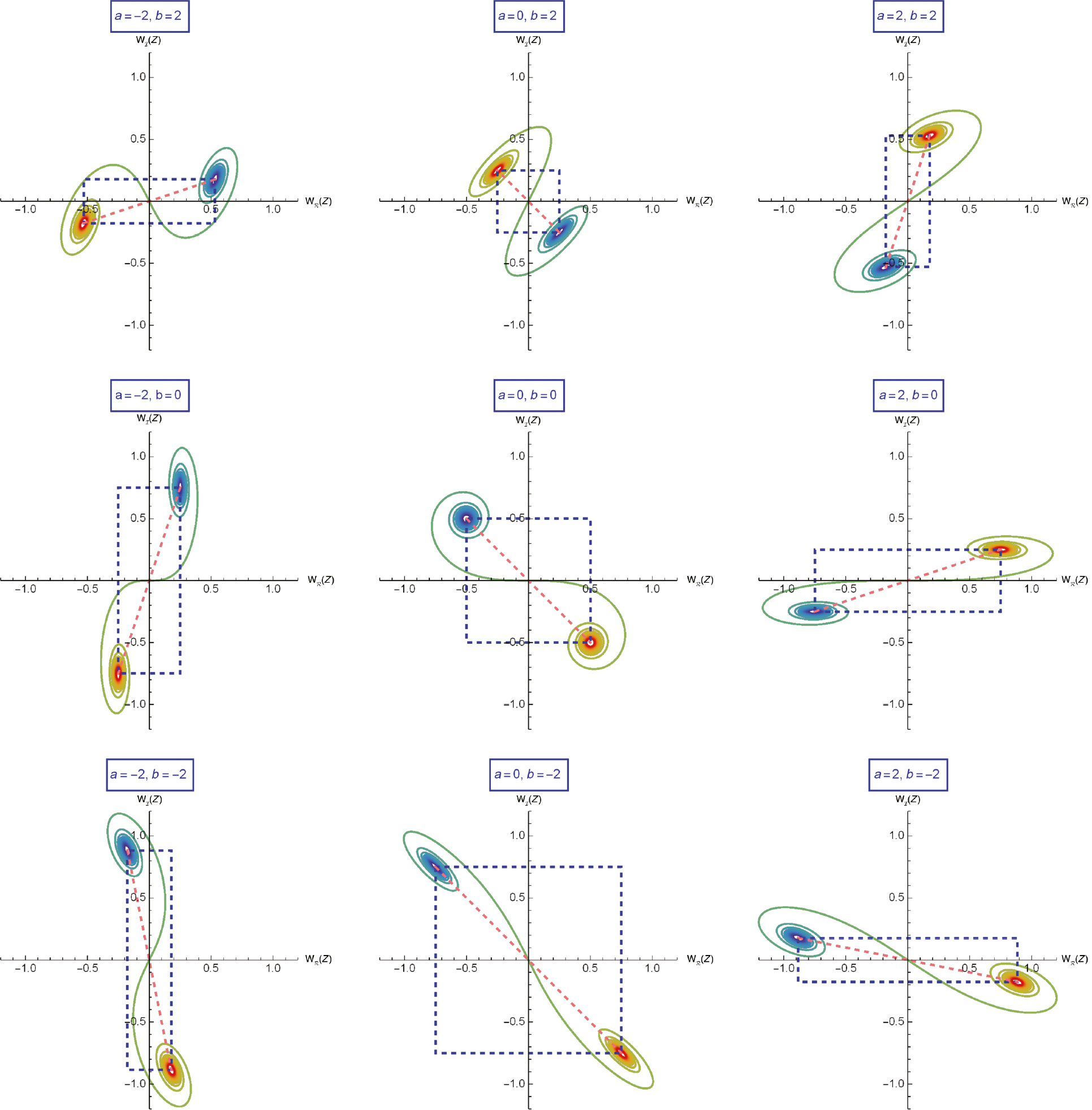
Argand plots for the Riccati-deformed Cornu spirals for different values of a and b. The a=0, b=0 case at the center corresponds to the supersymmetric partner equation (26), while all the other cases correspond to (30).

3 Factorization of (4) and Supersymmetric Approach

We will now demonstrate the supersymmetric features of the solution in which the complex Riccati parameter is used.

Equation (4) can be written in the factorized form A⁻A⁺v=0 using the differential operators given by

Proceeding as in supersymmetric quantum mechanics, the supersymmetric partner equation of (4) is

The extra term in (26) with respect to (4) is given by

which is the Darboux distortion of (4), and is presented in the first plot of Figure 2.

Figure 2:

Darboux distortion of (4) for various phases ϕ. The Darboux distortion of the supersymmetric partner of the Cornu spiral corresponds to ϕ=0. The other cases correspond to members of the parametric deformed family of spirals having the same supersymmetric partner.

To find out if the second-order linear ODE corresponds to the deformed Cornu spirals, we first write the general Riccati solution (20) in the trigonometric form

and simply substitute it instead of the particular Riccati solution in the factorization (26)

One obtains the equation

with the Darboux distortion depending parametrically on the phase shift ϕ

To find the general solution to (30), we let A−Ψ˜=Φ˜, thus the homogenous equation A+Φ˜=0 has the solution

By solving the non-homogeneous equation A−Ψ˜=Φ˜, we obtain the general solution of (30)

Denoting

and choosing the arbitrary constants to be b₁=2, b₂=0, (33) takes the compact form

In Figure 2, we display various cases of parametric Darboux distortions Δ_Darb(z;ϕ) of the deformed Cornu spirals presented in Figure 1. We notice the negative parabolic envelope as given by the first term in (31) together with the singularities due to the terms containing the tangents for nonzero z. The singularities at the origin are due to the 1/z² term except for the cases ϕ=±π/2 when the dominant contribution comes from the cotangent terms. For these values of the phase, the Darboux distortion simplifies to

ΔDarb(z;0)=34z2−π(sinπz2+4πz2)cosπz2+1,ΔDarb(z;±π/4)=34z2+π(cosπz2±4πz2)sinπz2∓1,ΔDarb(z;±π/2)=34z2−π(sinπz2−4πz2)cosπz2−1.

The factorization patterns discussed here unravel the Darboux origin of this deformation, which is a counterpart of the same construction in supersymmetric quantum mechanics, where the parametric families of supersymmetric isospectral potentials are obtained with the property that all the members of those families have the same supersymmetric partner potential [12], [13], [15]. The initial potential and its supersymmetric partners are reproduced for extremal values of the parameters. In the case of the Cornu spiral, our parametrization chosen is such that when a and b are nought, the supersymmetric partner spiral is obtained, whereas the standard Cornu spiral is obtained when a→∞ and b=0. This is graphically demonstrated in Figure 3 where even for the rather small values of a=10 and b=0, the spiral is very close to the standard one as known from textbooks [2].

Figure 3:

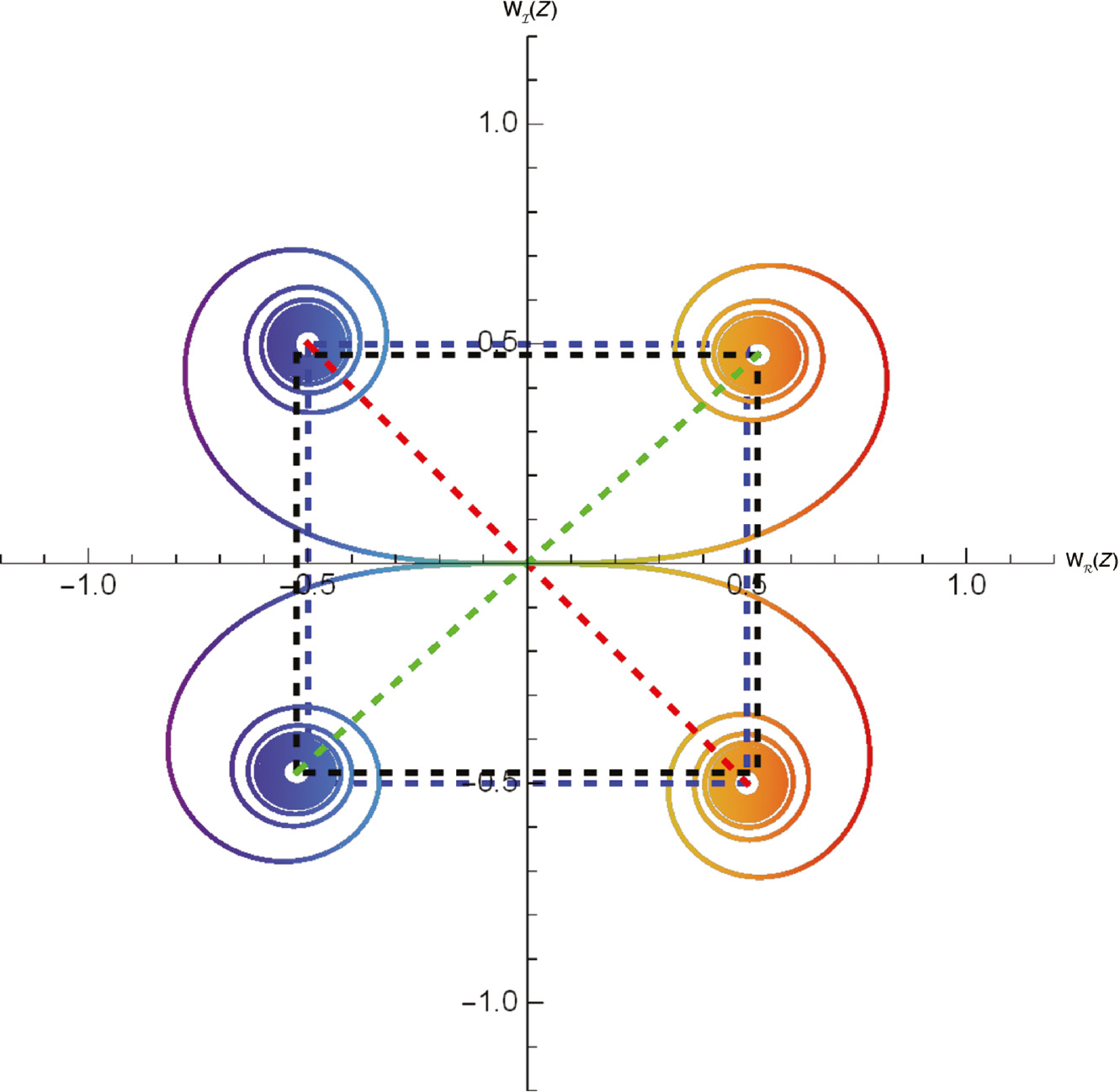
The Cornu supersymmetric partner spiral, a=0, b=0, from the center of Figure 1 and the parametric Cornu spiral for a=10, b=0 which is already very close to the standard Cornu spiral. Notice also that in the limit a→∞ the supersymmetric partner spiral is the image of the standard spiral under real axis reflection.

4 Conclusion

A parametric deformation of the Cornu spiral is introduced based on the usage of the corresponding general Riccati solution instead of the particular solution. Geometrically, the origin of this kind of deformation lies in the two independent scales, a and b, along the two orthogonal axes of the plane in which the spiral is plotted. These scales can generate not only the deformation of the rolls of the spiral, but also its global rotation as seen in the plots. Foreseen applications are in the same range as those of the standard Cornu spiral.