Analytical Solitary Wave Solution of the Dust Ion Acoustic Waves for the Damped Forced Korteweg–de Vries Equation in Superthermal Plasmas

1 Introduction

In addition to the usual electrons, ions and neutral particles, a dusty plasma contains charged and massive dust grains. This kind of dusty plasma opened up a new research area because of its tremendous applications in planetary rings, comet tails, asteroids zone, interstellar medium and the lower part of the Earth’s atmosphere and magnetosphere [1], [2], [3], [4], [5], [6], [7]. Recently, the applications of dusty plasmas have grown in many laboratory devices and experiments such as radio frequency discharges [8], plasma crystal [9], [10], plasma processing reactors, fusion plasma devices, etc. Because of the presence of heavy dust particles, dusty plasma supports different types of Eigen modes, such as dust acoustic mode [11], dust drift mode [12], Shukla-Varma mode [13], dust lattice mode [14], dust cyclotron mode [15], dust ion acoustic (DIA) mode [16] and dust Berstain-Green-Kruskal mode [17]. During the past few decades, the study of linear and nonlinear DIA waves in dusty plasmas was received with an enormous amount of interest [18], [19], [20], [21], [22], [23], [24]. The existence of low-frequency DIA waves in dusty plasma was theoretically observed by Shukla and Silin [18], and Barkan et al. [25] confirmed the existence of these waves experimentally. Nakamura et al. [26] studied linear and nonlinear DIA waves experimentally in a homogeneous unmagnetised dusty plasma. They found that in the linear regime, the phase velocity of the wave increases and the wave suffers heavy damping with increasing dust density. Anowar and Mamun [27] investigated the basic features of obliquely propagating DIA solitary waves (DIASWs) in a hot adiabatic magnetised dusty plasma containing adiabatic inertia-less electrons, adiabatic inertial ions and negatively charged static dusts. Duha and Mamun [28] studied DIA shock waves in dusty plasmas containing Boltzmann electrons, mobile ions and charge fluctuating stationary dusts. Ghorui et al. [29] investigated the head-on collision of DIASWs in a magnetised quantum dusty plasma. Recently, Pakzad et al. [30] studied the nonlinear amplitude modulation of DIA waves in the presence of nonextensive distributed electrons in dusty plasmas with stationary dust particles. They showed that the characteristics of the wave were affected by the nonextensive parameter and also the relative density of plasma constituents. Very recently, Sayyar et al. [31] investigated the oblique propagation of DIAWs in magnetised dusty plasmas.

It is well known that space and laboratory plasmas may contain substantial amounts of high-energy particles. These high-energy particles (superthermal particles) may arise due to the effect of external forces acting on the natural space environment plasmas or wave-particle interactions. Plasmas with an excess amount of superthermal electrons or positrons are generally characterised by a long tail in the high-energy region. Generalised Lorentzian or κ distribution [32], [33], [34], [35], [36] was used to model such space plasmas. The presence of a substantially large number of superthermal particles, which distinguish κ distribution from Maxwellian distribution, can significantly change the rate of resonant energy transfer between particles and plasma waves [37], [38], [39]. A three-dimensional generalised Lorentzian or κ distribution function [40], [41] can be written as follows:

where Γ is the gamma function, θ is the most probable speed or effective thermal speed connected to the usual thermal velocity V_t=(k_BT/m)^1/2 by θ=[(2κ−3)/κ]V_t, T is the characteristic kinetic temperature and k_B is the Boltzmann constant. The parameter κ is the spectral index, which is a measure of the slope of the energy spectrum of the superthermal particles forming the tails of the velocity distribution [42], [43]. The range of this parameter is 3/2<κ<∞. Low values of κ represent a hard spectrum with a strong non-Maxwellian (power law like) tail, an enhanced velocity distribution at low speeds and a depressed distribution at intermediate speeds [40]. In the limit κ→∞, the κ distribution function reduces the well-known Maxwell-Boltzmann distribution [38].

Recently, Saini and Kourakis [44] investigated the existence of arbitrary amplitude ion acoustic solitary waves in an unmagnetised plasma consisting of ions and excess superthermal electrons following the κ distribution in the presence of an electron beam. Very recently, Shalini and Saini [45] studied the properties of DIA rogue waves in an unmagnetised collisionless plasma system composed of charged dust grains, superthermal electrons and warm ions. It is noteworthy that the external periodic perturbation has significant effect in many real physical situations [46], [47]. Recently, a considerable interest has been shown towards the study of nonlinear travelling wave solution considering an external periodic perturbation [48], [49], [50]. This work presents an investigation of the DIASW solution in an unmagnetised collisional dusty plasma in the presence of external periodic perturbation.

The remaining part of the paper is organised as follows: in section 2, basic equations are presented. Nonlinear analysis is presented in Section 3. Section 4 presents the effects of different parameters on analytical solitary wave solution of the damped forced Korteweg–de Vries (DFKdV) equation. Section 5 states the conclusions.

2 Basic Equations

In this work, we consider an unmagnetised collisional dusty plasma that contains cold inertial ions, stationary dusts with negative charge and non-inertial κ-distributed electrons. The normalised ion fluid equations which include the equation of continuity, equation of momentum balance and Poisson equation, governing the DIA waves, are given by

The normalised superthermal electron number density [32] is given by

ne=(1−ϕκ−3/2)−κ+1/2.

where n is the number density of ions normalised to its equilibrium value n₀, and u is the ion fluid velocity normalised to ion acoustic speed Cs=(kBTemi), with T_e as the electron temperature, k_B as the Boltzmann constant and m_i as the mass of ions. The electrostatic wave potential ϕ is normalised to k_BT_e/e with e as the magnitude of electron charge. The space variable x is normalised to the Debye length λD=(Te4πne0e2)12, and the time t is normalised to ωpi−1=(mi4πne0e2)12, with ω_pi as ion-plasma frequency. Here ν_id is the dust ion collisional frequency and μ=Zdnd0n0.

3 Nonlinear Analysis

To study the nonlinear propagation of DIA waves in a collisional dusty plasma, the reductive perturbation technique (RPT) is applied to derive the damped KdV equation. According to the RPT, the independent variables are stretched as

where ε is the strength of nonlinearity, and v is the phase velocity of the DIA waves. The expansions of the dependent variables are as follows:

Substituting the above expansions along with stretching the coordinates into (2–4) and equating the coefficients of the lowest order of ε, the dispersion relation is obtained as

with a=κ−1/2κ−3/2.

Taking the coefficients of the next higher order of ε, we obtain the damped KdV equation

where A=(3−2b(1−μ)v42v),B=v32 and C=νid02, with b=κ2−1/42(κ−3/2)2.

It has been noticed that the behavior of nonlinear waves changes significantly in the presence of external periodic force [51], [52]. Resistive wall modes of the plasma with the presence of an external magnetic force have been discussed [47], and it has been shown that such a force can be produced by a flexible, high-speed waveform generator. Considering an external periodic force f₀cos(ωτ), the damped KdV (12) takes the form

which is termed as the DFKdV equation.

In the absence of C and f₀, that is, C=0 and f₀=0, (13) takes the form of the well-known KdV equation with the solitary wave solution

where ϕm=3MA and W=2BM, with M as the Mach number.

In this case, it is well established that

is a conserved quantity. For small values of C and f₀, let us assume that the solution of (13) is of the form

where M(τ) is an unknown function of τ and ϕm(τ)=3M(τ)A and W(τ)=2B/M(τ).

Differentiating (15) with respect to τ and using (13), one can obtain

Again,

From (17) and (21), the expression of M(τ) is obtained as

M(τ)=(M−8ACf016C2+9ω2)e−43Cτ+6Af016C2+9ω2(43Ccos(ωτ)+ωsin(ωτ)).

Therefore, the analytical solitary wave solution of the DIA waves for the DFKdV (13) is

where ϕm(τ)=3M(τ)A and W(τ)=2BM(τ).

4 Effects of Parameters

In this section, we present the effect of the different physical parameters κ, f₀ and ω on the DIASW solution of the DFKdV (13) through numerical computations.

In Figure 1, the rarefactive solitary wave solution of the DFKdV (13) is plotted for the different values of the strength of the external periodic force f₀ with special values of the other parameters M=0.1, κ=1.8, μ=0.5, ν_id0=0.01, ω=0.4 and τ=2. It is observed that the amplitude of the rarefactive solitary wave decreases and width increases as the force f₀ increases. Therefore, the rarefactive solitary wave becomes flatter as the strength f₀ of the external periodic force increases. Thus, the rarefactive solitary wave solution of the DFKdV (13) becomes smooth as the strength f₀ of the external periodic force grows rapidly.

Figure 1:

Variation of the solitary wave of the DFKdV (13) for the different values of f₀ with M=0.1, κ=1.8, μ=0.5, ν_id0=0.01, ω=0.4 and τ=2.

Figure 2 represents the variation of the rarefactive solitary wave solution for the DIA wave corresponding to the DFKdV (13) for different frequencies (ω) of the external periodic force with f₀=0.06, and the other parameters are the same as in Figure 1. The amplitude of the rarefactive solitary wave increases and the width decreases as the frequency ω of the external periodic force increases. Thus, the rarefactive solitary wave solution of the DFKdV (13) becomes non-smooth as the frequency ω of the external periodic force grows.

Figure 2:

Variation of the solitary wave of the DFKdV (13) for the different values of ω with M=0.1, κ=1.8, μ=0.5, ν_id0=0.01, f₀=0.06 and τ=2.

Figure 3 shows the variation of the rarefactive solitary wave profile of the DFKdV (13) for different values of the spectral index κ with fixed strength (f₀=0.03) of the external periodic force, and the other parameters are the same as in Figure 1. It is noticed that both amplitude and width of the DIA rarefactive solitary wave increase as the spectral index (κ) increases. Thus, the DIA rarefactive solitary wave flourishes as the spectral index κ moves far away from the Maxwellian equilibrium.

Figure 3:

Variation of the solitary wave of the DFKdV (13) for the different values of κ with M=0.1, μ=0.5, ν_id0=0.01, f₀=0.03, ω=0.4 and τ=2.

Figure 4 presents the variation of the compressive solitary wave of the DFKdV (13) for different strengths (f₀) of the external periodic force with μ=0.2, and the other parameters are the same as in Figure 1. The amplitude of the compressive solitary wave increases but the width decreases as the value of f₀ increases. Therefore, the DIA compressive solitary wave becomes spiky as the strength (f₀) of the external periodic force is enhanced. Thus, the compressive solitary wave solution of the DFKdV (13) becomes non-smooth as the strength (f₀) of the external periodic force grows.

Figure 4:

Variation of the solitary wave of the DFKdV (13) for the different values of f₀ with M=0.1, κ=1.8, μ=0.2, ν_id0=0.01, ω=0.4 and τ=2.

Figure 5 shows the variation of the compressive solitary wave profile of the DFKdV (13) for different frequencies ω of the external periodic force with μ=0.2, and the other parameters are the same as in Figure 2. It is seen that the amplitude of the DIA compressive solitary wave decreases but the width increases as ω increases. Thus, the compressive solitary wave solution of the DFKdV (13) becomes smooth as the frequency ω of the external periodic force grows.

Figure 5:

Variation of the solitary wave of the DFKdV (13) for the different values of ω with M=0.1, κ=1.8, μ=0.2, ν_id0=0.01, f₀=0.06 and τ=2.

The variation of the compressive solitary wave solution of the DFKdV (13) for the different values of the spectral index (κ) with μ=0.2 and the other parameters the same as in Figure 3 are presented in Figure 6. It is observed that both the amplitude and the width of the compressive solitary wave increase with the increasing value of the spectral index κ. Thus, the DIA compressive solitary wave diminishes as the spectral index κ moves far away from the Maxwellian equilibrium.

Figure 6:

Variation of the solitary wave of the DFKdV (13) for the different values of κ with M=0.1, μ=0.2, ν_id0=0.01, f₀=0.03, ω=0.4 and τ=2.

The dependence of the amplitude of the rarefactive solitary wave solution of the DFKdV (13) on the strength (f₀) of the periodic force is presented in Figure 7 for the different values of ω, and the other parameters are the same as in Figure 1. It is noticed that the amplitude of the rarefactive solitary wave decreases as the strength f₀ of the periodic force is enhanced. Also, it is observed that for the lower frequency (ω) of the external periodic force, the amplitude of the rarefactive solitary wave decreases more rapidly.

Figure 7:

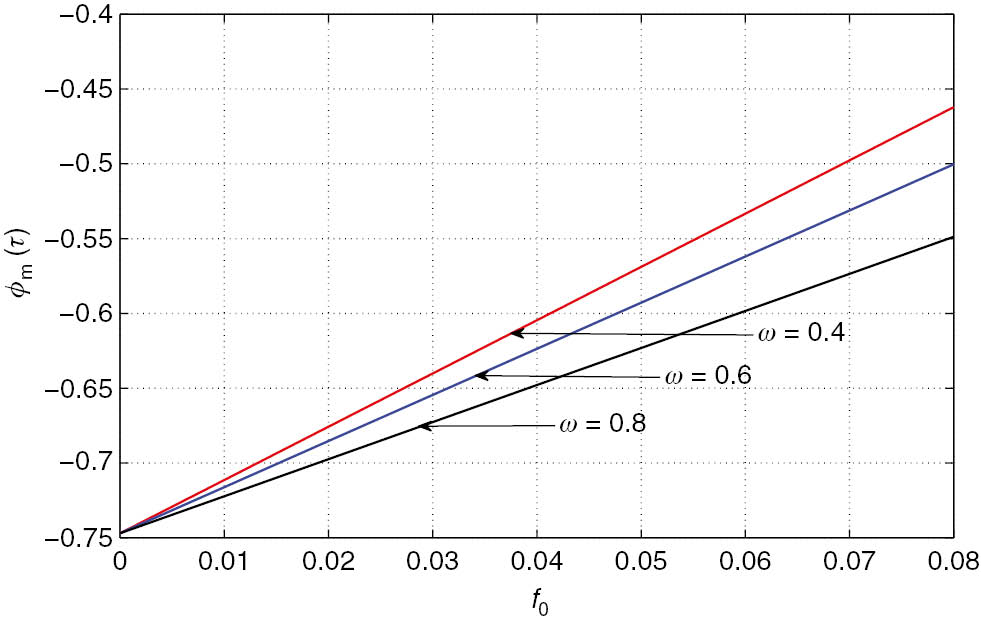
Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to f₀ of the DFKdV (13) for the different values of ω with M=0.1, κ=1.8, μ=0.5, ν_id0=0.01 and τ=2.

Figure 8 shows the variation of amplitude of the DIA rarefactive solitary wave with respect to the strength (f₀) of the external periodic force for the different values of the parameter κ. It is seen that the amplitude of the rarefactive solitary wave solution of the DFKdV (13) decreases as the strength (f₀) of the external periodic force increases. Also, it is observed that the rate at which the amplitude decreases is not affected by the spectral index κ.

Figure 8:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to f₀ of the DFKdV (13) for the different values of κ with M=0.1, μ=0.5, ν_id0=0.01, ω=0.4 and τ=2.

Figure 9 presents the variation of the amplitude of the DIA rarefactive solitary wave with respect to the frequency (ω) of the external periodic force for the different values of the spectral index κ. It is noticed that the amplitude of the rarefactive solitary wave increases smoothly as the frequency (ω) of the external periodic force is enhanced.

Figure 9:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to ω of the DFKdV (13) for the different values of κ with M=0.1, μ=0.5, ν_id0=0.01, f₀=0.02, ω=0.4 and τ=2.

The variation of amplitude of the rarefactive solitary wave solution of the DFKdV (13) with respect to frequency (ω) for the different strengths (f₀) of the external periodic force is presented in Figure 10. It is seen that the amplitude of the rarefactive solitary wave increases with the frequency (ω) of the external periodic force. Also, it is observed that the change in amplitude is more rapid for the higher value of the strength (f₀) of the external periodic force.

Figure 10:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to ω of the DFKdV (13) for the different values of f₀ with M=0.1, κ=1.8, μ=0.5, ν_id0=0.01, ω=0.4 and τ=2.

Figure 11 shows the variation of the amplitude of the compressive solitary wave solution of the DFKdV (13) with respect to the strength (f₀) of the external periodic force for the different values of the frequency ω. It is noticed that the amplitude of the DIA compressive solitary wave increases as the strength (f₀) of the external periodic force increases, but the rate is more for the lower frequency ω of the external periodic force.

Figure 11:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to f₀ of the DFKdV (13) for the different values of ω with M=0.1, κ=1.8, μ=0.2, ν_id0=0.01 and τ=2.

Figure 12 presents the variation of the amplitude of the compressive solitary wave solution of the DFKdV (13) with respect to the strength f₀ of the external periodic force for the different values of the spectral index κ. It is observed that the amplitude of the DIA wave of the DFKdV (13) increases with the strength (f₀) of the external periodic force.

Figure 12:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to f₀ of the DFKdV (13) for the different values of κ with M=0.1, μ=0.2, ν_id0=0.01, ω=0.4 and τ=2.

Figure 13 represents the variation of the amplitude of the compressive solitary wave solution of the DFKdV (13) with respect to the frequency (ω) of the external periodic force for the different values of the spectral index κ. It is observed that amplitude of the DIASW decreases smoothly as the frequency (ω) of the external periodic force increases.

Figure 13:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to ω of the DFKdV (13) for the different values of κ with M=0.1, μ=0.2, ν_id0=0.01, f₀=0.03, ω=0.4 and τ=2.

Figure 14 shows the variation of the amplitude of the compressive solitary wave solution of the DFKdV (13) with respect to the frequency (ω) of the external periodic force for different strengths (f₀). It is seen that the amplitude of the DIASW decreases as the frequency (ω) of the external periodic force increases, but the rate of change increases rapidly with the higher value of the strength (f₀) of the external periodic force.

Figure 14:

Variation of the solitary wave amplitude (ϕ_m(τ)) with respect to ω of the DFKdV (13) for the different values of f₀ with κ=1.8, M=0.1, μ=0.2, ν_id0=0.01, f₀=0.03, ω=0.4 and τ=2.

Figure 15 shows the variation of width of the rarefactive solitary wave solution of the DFKdV (13) with respect to strength (f₀) for the different frequencies (ω) of the external periodic force. It is seen that the width of the DIASW increases with the strength (f₀) of the external periodic force. It is also seen that the width of the solitary wave increases rapidly for the smaller frequency (ω) of the external periodic force.

Figure 15:

Variation of the solitary wave width (W(τ)) with respect to f₀ of the DFKdV (13) for the different values of ω with M=0.1, κ=1.8, μ=0.5, ν_id0=0.01 and τ=2.

Figure 16 represents the variation of width of the rarefactive solitary wave solution of the DFKdV (13) with respect to the strength (f₀) of the external periodic force for the different values of the special index (κ). It is observed that the width of the DIA rarefactive solitary wave increases with the strength (f₀) of the external periodic force, and it is also noticed that the width increases rapidly for the smaller value of the spectral index κ.

Figure 16:

Variation of the solitary wave width (W(τ)) with respect to f₀ of the DFKdV (13) for the different values of κ with M=0.1, μ=0.5, ν_id0=0.01, ω=0.4 and τ=2.

Figure 17 represents the variation of width of the compressive solitary wave solution of the DFKdV (13) with respect to frequency (ω) for the different strengths (f₀) of the external periodic force. It has been observed that the width of the DIA compressive solitary wave increases as the frequency (ω) of the external periodic force is increased. Also, it is observed that the width of the compressive solitary wave increases rapidly for the higher values of the strength (f₀) of the external periodic force.

Figure 17:

Variation of the solitary wave width (W(τ)) with respect to ω of the DFKdV (13) for the different values of f₀ with M=0.1, μ=0.2, ν_id0=0.01, ω=0.4 and τ=2.

In Figure 18, we present the variation of width of the compressive solitary wave solution of the DFKdV (13) with respect to the frequency ω of the external periodic force for the different values of the spectral index κ. It is noticed that the width of the compressive solitary wave increases smoothly as the frequency (ω) of the external periodic force increases.

Figure 18:

Variation of the solitary wave width (W(τ)) against f₀ for the different values of ν_id0 with M=0.1, κ=1.8, μ=0.5, ω=0.4 and τ=2.

5 Conclusions

Analytical DIASW solution has been studied in the presence of an external periodic perturbation in an unmagnetised collisional dusty plasma. Employing RPT, the DKdV equation is derived for DIASW. The effects of the parameters κ, f₀ and ω on the DIASW solution have been investigated through numerical simulation. The parameters κ, f₀ and ω have played a crucial role on the nonlinear structure of the DIASW in the presence of dust ion collision and external periodic force. The results of the present work may have relevance in laboratory plasmas as well as in space plasma environments where κ distributed electrons are present.