Home Hydrogen-bonding in mono-, di- and tetramethylammonium dihydrogenphosphites
Article Open Access

Hydrogen-bonding in mono-, di- and tetramethylammonium dihydrogenphosphites

  • Matthias Kogler and Berthold Stöger EMAIL logo
Published/Copyright: January 18, 2021
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Zeitschrift für Kristallographie - Crystalline Materials
From the journal Zeitschrift für Kristallographie - Crystalline Materials Volume 236 Issue 1-2

Abstract

The crystal structures of methylammonium and dimethylammonium dihydrogenphosphite (MA⋅H2PO3, I2/a and DMA⋅H2PO3, P21/c) are built of infinite chains of hydrogen bonded H2PO3− anions. The chains are connected by the ammonium cations via hydrogen bonding to di- (DMA⋅H2PO3) and triperiodic (MA⋅H2PO3) networks. Tetramethylammonium dihydrogenphosphite monohydrate (TMA⋅H2PO3⋅H2O) features temperature dependent dimorphism. The crystal structure of the high-temperature (HT, cubic P213) and low-temperature (LT, orthorhombic P212121) phases were determined at 150 and 100 K, respectively. The hydrogen bonding network in the HT phase is disordered, with H2PO3− and H2O being located on a threefold axis and is ordered in the LT phase. On cooling, the point symmetry is reduced by an index of 3. The lost symmetry is retained as twin operations, leading to threefold twinning by pseudo-merohedry. The hydrogen-bonding networks of the HT and LT phases can be represented by undirected and directed quotient graphs, respectively.

Keywords: hydrogen bonding; phase transition; symmetry relations; twinning; voltage graphs

1 Introduction

In our current line of research, we synthesized the 1:1 mono-, di-, tri- and tetramethylammonium salts of phosphorous acid H3PIIIO3 as precursors to fluorine containing PIII compounds in reactions of the type

(1)MH2PO3+5HF→MHPF5+3H2O

where M stands for a monovalent cation. The non-hydrous mono- and dimethylammonium (MA and DMA) salts crystallized at 280 and 255 K, respectively. In contrast, the trimethylammonium salt remained an oil even at 255 K. The tetramethylammonium (TMA) salt, on the other hand, crystallized at 280 K with one molecule of crystal water, which was introduced by the TMAOH⋅5H2O reactant.

As a routine analysis method, we determined the crystal structures of the crystalline salts at 100 K. In contrast to MA⋅H2PO3 and DMA⋅H2PO3, whose structures were trivially solved and refined, crystals of TMA⋅H2PO3⋅H2O were threefold twins of orthorhombic individuals with a pseudo-cubic symmetry. Since the crystals were optically isotropic at room temperature, we likewise determined their structure at higher temperatures. Indeed, at 150 and 200 K the crystals adopt a cubic symmetry.

The phase transition between the orthorhombic low-temperature (LT) and cubic high-temperature (HT) phases is due to the ordering of the hydrogen bonding network on cooling. Ordering of hydrogen bonding is one of the most important causes of order-disorder phase transitions in the solid state, the most well studied example probably being the potassium dihydrogen phosphate family of compounds [1]. The members of this family are ferroelectric below and paraelectric above the phase transition temperature.

In this work we present the order-disorder phase transition of TMA⋅H2PO3⋅H2O. It will be analyzed in the light of symmetry reduction and the topology of the hydrogen bonding network. Moreover, the hydrogen bonding networks MA⋅H2PO3 and DMA⋅H2PO3 are discussed briefly.

2 Experimental

2.1 Synthesis and crystal growth

2.1.1 MA⋅H2PO3

3.53 g (38 mmol) 33%wt ethanolic MeNH2 were added to 3.02 g (37 mmol) H3PO3 with stirring. The immediately precipitated white powder redissolved owing to heat of reaction. On cooling to 280 K, crystals of MA⋅H2PO3 formed. The sample was single-phase according to X-ray powder diffraction (XRPD).

2.1.2 DMA⋅H2PO3

4.26 g (38 mmol) 40%wt aqueous Me2NH was added to 3.01 g (37 mmol) H3PO3 with stirring. The solution was dried one day in vacuo over H2SO4. The residue crystallized at 255 K. Phase purity could not be established using standard XRPD procedures owing to the deliquescence of the sample.

2.1.3 Me3NH⋅H2PO3

6.19 g (37 mmol) 35%wt ethanolic Me3N was added to 3.07 g (37 mmol) H3PO3 with stirring. The solution was immediately attached to a vacuum pump (10−4 mbar) for two days. The resulting viscous liquid did not crystallize even at 255 K for a prolonged time. Cooling using liquid N2 led to formation of a glass, which melted when warming to 255 K. Analogous reaction from aqueous Me3N and drying for two days at 10−4 mbar likewise afforded an oil, which didn’t crystallize at 255 K. Likewise, drying in a vacuum desiccator over KOH followed by cooling did not result in crystallization.

2.1.4 TMA⋅H2PO3⋅H2O

3.09 g (37 mmol) H3PO3 and 6.64 g (37 mmol) TMAOH⋅5H2O were dissolved in MeOH. Excess MeOH and water was removed in vacuum (10−4 mbar) for two days. Crystallization was induced by cooling to 280 K. XRPD analysis was not attempted owing to the deliquescence of the crystals.

2.2 Data collection and reduction

The crystals were immersed in perfluorinated polyether oil and quickly attached to Kapton micro mounts under a polarizing microscope. Mounting crystals of TMA⋅H2PO3⋅H2O posed a challenge, because the cubic crystals are optically isotropic at room temperature and possess an index of refraction close to that of the employed polyether. Thus, the crystals were cut with a knife into reasonable sized fragments without visual feedback and then moved out of the oil to assess their shape and size.

Intensity data were collected in a dry stream of nitrogen on a Bruker Kappa Apex II diffractometer system equipped with a CCD detector using graphite monochromatized sealed tube MoKα radiation. Frame data were converted to intensity values using Saint-Plus and a correction for absorption effects was applied using the multi-scan approach implemented in Sadabs [2]. MA⋅H2PO3 and DMA⋅H2PO3 crystals were immersed directly into a 100 K N2 stream. TMA⋅H2PO3⋅H2O crystals diffracted poorly when cooled quickly below phase transition temperature. Therefore, the TMA⋅H2PO3⋅H2O crystal described herein was mounted at 250 K and then measured at 200, 150 and 100 K with a cooling rate of 240 K/h before each measurement.

The structures were solved with Shelxt [3] and refined against F2 using Shelxl [4]. H atoms attached to C were placed at calculated positions and refined as riding on their parent atoms. H atoms attached to P and N were refined freely and the P–H, N–H and O–H distances restrained to 1.350 (1) Å (P) and 0.870 (1) Å (N, O). The water and phosphonate O atoms in the HT structure of TMA⋅H2PO3⋅H2O were refined as positionally disordered about two positions. The total occupancy was constrained to 1 and the occupancy of both minor positions constrained to the same value. Likewise, a phosphonate O atom was refined as positionally disordered in DMA⋅H2PO3, owing to a distinct peak in the difference Fourier map, which could not be explained by other means.

Since the low-temperature (LT) structure of TMA⋅H2PO3⋅H2O has orthorhombic P212121 symmetry, the directions of three axes can in principle be chosen arbitrarily among the three directions of the 21screw axes. Formally, this is described by the affine normalizer [5] of P212121, which contains affine transformations that permutate the axes. However, the conventional cell choice fixes the orientation of the basis according to the a < b < c condition on the cell parameters, with the caveat that the b and c parameters are very close (ca. 9.61 vs. 9.63 Å or less than 0.2% difference) and their order might have been mis-determined owing to twinning. For consistency reasons, this setting was used for the LT phase.

In contrast, the high-temperature (HT) structure of TMA⋅H2PO3⋅H2O features the cubic P213 symmetry, which is devoid of the fourfold rotation of the cubic primitive (cP) lattice. Therefore, the structure can be described in two orientations, which are related by this fourfold rotation and the conventional cell choice does not give precedence over one of the two. In this case, the orientation was chosen in such a way that the coordinates of the HT phase are comparable to those of the LT phase. Thereto, the coordinate system had to be rotated by 90° about [100] with respect to the setting arbitrarily chosen by the diffractometer software.

More data collection and structure refinement data are collected in Table 1. Model data are deposited in the CIF format at the CCDC and can be retrieved using the deposition numbers listed at the bottom of Table 1.

Table 1:

Data collection and structure refinement details.

MA⋅H2PO3DMA⋅H2PO3TMA⋅H2PO3⋅H2OTMA⋅H2PO3⋅H2O
Crystal data
Chemical formulaCH8NO3PC2H10NO3PC4H16NO4PC4H16NO4P
Mr113.05127.08173.15173.15
Temperature (K)100100100150
Crystal system, space groupMonoclinic, I2/aMonoclinic, P21/cOrthorhombic, P212121Cubic, P213
a, b, c (Å)8.2503 (5), 12.5988 (7), 9.6822 (5)5.6086 (13), 11.554 (2), 9.544 (2)9.4907 (18), 9.6078 (19), 9.6270 (18)9.639 (2), 9.639 (2), 9.639 (2)
β (°)93.252 (4)96.556 (5)9090
V (Å3)1004.78 (10)614.4 (2)877.8 (3)895.6 (6)
Z8444
Radiation typeMo KαMo KαMo KαMo Kα
μ (mm−1)0.430.360.280.28
Crystal size (mm)0.30 × 0.17 × 0.020.40 × 0.25 × 0.120.32 × 0.30 × 0.170.32 × 0.30 × 0.17
Data collection
DiffractometerBruker KAPPA APEX II CCDBruker KAPPA APEX II CCDBruker KAPPA APEX II CCDBruker KAPPA APEX II CCD
Absorption correctionMulti-scan (SADABS)Multi-scan (SADABS)Multi-scan (SADABS)Multi-scan (SADABS)
Tmin, Tmax0.442, 0.4970.220, 0.2720.441, 0.4930.441, 0.493
No. of measured, independent and observed [I>2σ(I)] reflections12364, 2252, 20249350, 2739, 238510019, 2478, 23609200, 870, 847
Rint0.0290.0220.0320.028
Refinement
(sinθ/λ)max (Å−1)0.8110.8150.7060.704
R[F2>2σ(F2)], wR(F2), S0.022, 0.062, 1.060.025, 0.072, 1.060.038, 0.085, 1.240.021, 0.058, 1.08
No. of parameters728611349
No. of restraints5444
Δρmax, Δρmin (e Å−3)0.57, −0.350.43, −0.320.54, −0.490.20, −0.11
Twin operations––3[111]+, 3[111]−–
Twin volume fractions––63.9:25.5:10.6 (8)–
Flack parameter––−0.04(3)−0.08(3)
CCDC number2036785203678620367872036788

3 Results and discussion

3.1 General remarks

The structures of the crystals under investigation follow the expected building mechanisms. The H2PO3− dihydrogen phosphite anions exist as the HPO2(OH) tautomer, i.e. one H is attached directly to P. The ion adopts a distorted trigonal pyramidal geometry with the P–O distance of the OH group significantly longer than of the other two O atoms (ca. 1.57 vs. 1.50 Å, see Table 2), which compares well to neutron diffraction derived data published by [6]. Note that the standard uncertainty on the P–O1 distance of DMA⋅H2PO3 is distinctly larger owing to positional disorder of the O1 atom.

Table 2:

P–O distances in the crystals under investigation and LiH2PO3[6]. The O atom of the hydrogen bond donating hydroxyl fragment is O3. The hydrogen bond acceptor of the hydoroxyl group is O2. The HT phase of TMA⋅H2PO3⋅H2O is not listed because the H2PO3− anion is disordered.

CrystalP1–O1 (Å)P1–O2 (Å)P1–O3 (Å)
MA⋅H2PO31.5041 (5)1.5077 (5)1.5743 (6)
DMA⋅H2PO31.503 (2)1.4999 (6)1.5728 (6)
TMA⋅H2PO3⋅H2O, 100 K1.481 (4)1.496 (4)1.568 (4)
LiH2PO31.497 (2)1.506 (2)1.586 (2)

All structures are simple in the sense that the asymmetric unit contains at most one formula unit (Z′=1). In the HT phase of TMA⋅H2PO3⋅H2O, this number is even reduced to Z′=13. The structures are characterized by the maximization of hydrogen bonding, whereby the H atom attached to P does not partake in the hydrogen bonding. Indeed, with increased alkylation of the ammonium group (and thus less hydrogen bond donors), crystallization and handling owing to deliquescence became more difficult, with the trimethylammonium salt not crystallizing and the TMA salt crystallizing with water acting as hydrogen bond donor. All hydrogen bonds in the structures discussed herein are of moderate strength according to the classification of [7]; which means that their strength corresponds to the strength of hydrogen bonds of water at standard conditions.

3.2 MA⋅H2PO3 and DMA⋅H2PO3

The main building blocks of MA⋅H2PO3 and DMA⋅H2PO3 are infinite chains of H2PO3− ions connected by hydrogen bonding (Figure 1). In both cases, the chains are located on glide reflection planes. The shapes of the chains are overall similar, with the H atoms attached to P pointing in the same direction. The precise conformation though is dictated by the hydrogen bonding from the MA and DMA cations. Whereas in MA⋅H2PO3 the P–H bonds are virtually parallel to the glide plane, they are distinctly inclined in DMA⋅H2PO3 (arrows in Figure 1, left).

Figure 1: Chains of hydrogen bonded H2PO3−${\text{PO}}_{3}^{-}$ ions in (a) MA⋅H2PO3 and (b) DMA⋅H2PO3 extending along [100] viewed down [001] and [100] (left and right, respectively). P (pink), O (red) and C (gray) atoms are represented by ellipsoids drawn at the 50% probability levels, H atoms (white) by sphere of arbitrary radius. H⋯O hydrogen bonds are represented by dashed lines. In the [100] views, the direction of P–H-bonds are indicated by arrows. The minor (ca. 5%) positions of O1 in DMA⋅H2PO3 are omitted for clarity.
Figure 1:

Chains of hydrogen bonded H2PO3− ions in (a) MA⋅H2PO3 and (b) DMA⋅H2PO3 extending along [100] viewed down [001] and [100] (left and right, respectively). P (pink), O (red) and C (gray) atoms are represented by ellipsoids drawn at the 50% probability levels, H atoms (white) by sphere of arbitrary radius. H⋯O hydrogen bonds are represented by dashed lines. In the [100] views, the direction of P–H-bonds are indicated by arrows. The minor (ca. 5%) positions of O1 in DMA⋅H2PO3 are omitted for clarity.

Variations of such hydrogen-bonded chains of H2PO3− ions have been described for the non-hydrous salts LiH2PO3 [6], KH2PO3 [8] and (NH4)H2PO3 [9]. In all cases, the chains are located on a glide reflection plane. However, in the K salt the chains are built of two crystallographically independent H2PO3− ions. Finite hydrogen bonding networks of H2PO3− ions have been observed in non-hydrous salts of di- and trivalent metals. Trimers are observed in Fe(H2PO3)3 [10]; tetramers in Cu(H2PO3)2 [11] and Sr(H2PO3)2 [12].

In MA⋅H2PO3, the MA ion donates with all three ammonium H atoms to three distinct chains, thus forming a triperiodic network (Figure 2(a)). The DMA ion in DMA⋅H2PO3, on the other hand, possesses only two ammonium Hs, and each ion therefore connects only two chains, ultimately leading to a diperiodic hydrogen bonding network, which extends parallel to (100) (Figure 2(b)).

Figure 2: The crystal structures of (a) MA⋅H2PO3 and (b) DMA⋅H2PO3 viewed down [001]. a- and c-glide planes are represented by the usual symbols, viz. dashed (intrinsic translation parallel to the drawing plane) and dotted (perpendicular to the drawing plane) lines, respectively. Atom color codes as in Figure 1, N atoms are blue.
Figure 2:

The crystal structures of (a) MA⋅H2PO3 and (b) DMA⋅H2PO3 viewed down [001]. a- and c-glide planes are represented by the usual symbols, viz. dashed (intrinsic translation parallel to the drawing plane) and dotted (perpendicular to the drawing plane) lines, respectively. Atom color codes as in Figure 1, N atoms are blue.

In DMA⋅H2PO3, the DMA ion donates only to the O atom of H2PO3− that is not involved in inner-chain hydrogen bonding (O1, see Figure 1). In MA⋅H2PO3, the MA ion additionally donates to the acceptor of the H2PO3− to H2PO3− hydrogen bond (O2). The trend is continued by the unsubstituted ammonium salt [9], where the NH4+ ion donates to all three atoms of the H2PO3− ion. The result is a distinctly more twisted chain of H2PO3− ions.

3.3 TMA⋅H2PO3⋅H2O

3.3.1 HT phase

The HT phase of TMA⋅H2PO3⋅H2O crystallizes in the cubic P213 symmetry. The TMA cation, the H2PO3− anion and the H2O molecule are all located on the special position with threefold rotation symmetry. Note that all threefold rotation axes in P213 crystals are equivalent with respect to space group symmetry and they all belong to the unique special position.

Since the O atom of the water molecule is located (on average) on the threefold axis, it is formally connected to 3 H atoms, which therefore must feature an occupancy of 23 to satisfy the H2O stoichiometry. Likewise, since the HP fragment of the H2PO3− anion is located on the threefold axis, the hydroxyl H features an occupancy of 13.

Thus, every H2O molecule and every H2PO3− anion takes part in three disordered hydrogen bonds, whereby in two thirds of the cases H2O acts as donor and in the remaining third H2PO3− is the donor. A given H2O molecule thus switches between three states according to the schemeresulting on average in a site with 3 symmetry. The H2O molecules on a threefold axis in the [111]direction connects to three H2PO3− anions on axes precisely in the three other directions [1‾11], [11‾1], [1‾1‾1]. Note that in the P213 type of space group, these threefold rotation axes do not intersect, since such an intersection would correspond to a site with 23 symmetry, as it is found in the symmorphic P23 type of space group.

The situation is analogous for the H2PO3− anion, which switches between three states according toand likewise connects to H2O molecules located on threefold axes in precisely the other directions.

Combining these fragments, a rather complex triperiodic hydrogen bonding network is formed. In the free space of this network are located the TMA anions, which do not partake in hydrogen bonding owing to a lack of donor and acceptor groups (Figure 3). The view down [111] shows the threefold symmetry.

Figure 3: The cubic HT phase of TMA⋅H2PO3⋅H2O viewed down (a) [100] and (b) [111]. Atom colors as in Figure 2. The TMA ions are omitted in (b) for clarity. Threefold rotation and screw rotation axes in (b) are are indicated by the usual symbols [13]. The minor positions of the O atoms (ca. 7%) are omitted for clarity.
Figure 3:

The cubic HT phase of TMA⋅H2PO3⋅H2O viewed down (a) [100] and (b) [111]. Atom colors as in Figure 2. The TMA ions are omitted in (b) for clarity. Threefold rotation and screw rotation axes in (b) are are indicated by the usual symbols [13]. The minor positions of the O atoms (ca. 7%) are omitted for clarity.

The intricate triperiodic hydrogen bonding network can be conveniently represented using a labeled quotient graph [14], where every node represents an ion or molecule and all its translationally equivalents:Here, P and O nodes stand for H2PO3− anions and H2O molecules, respectively. Edges represent hydrogen bonds. A label (voltage) on an edge indicates that the representative H2O molecule in the unit cell is connected to an H2PO3− ion outside the unit cell and the label describes in fractional coordinates the vector of the lattice translation that moves the H2PO3− ion into the unit cell. Note that all labels are to be interpreted for O → P steps. When moving in the opposite direction, the translation vector has to be inverted.

The graph above is arranged in the form of a cube to highlight the cubic 23 point symmetry: P and O nodes on the same space diagonal of the cube are located on threefold axes in the same direction in the actual structure. However, to trace paths in the graph, a planarized version such asis more convenient. The dotted arrows in Eq. (5) indicate the walk around a face of the “cube”. However, such a cycle in the graph does not correspond to a cycle in the actual hydrogen bonding network. Indeed, summation of the voltages in the case above leads to a lattice translation in the [001] direction for every full cycle. Thus, the indicated path corresponds to a helicoidal structure with period four (with respect to translational equivalence) about an 21 axis. These helices extend in the three main directions ⟨100⟩. An example of each direction is shown in Figure 4 by blue ([100]), green ([010]) and yellow ([001]) backdrops. Each direction corresponds to a pair of opposing faces in the “cube” and each face of such a pair corresponds to two opposite orientations of the chain.

Figure 4: The HT phase of TMA⋅H2PO3⋅H2O viewed down [100], with TMA ions omitted for clarity. The same projection is given twice to avoid overlap of the colored regions. Atom colors as in Figure 1. 21 screw rotations axes are indicated by the usual symbols [13]. Examples of helicoidal chains of the hydrogen-bonding network with two H2PO3−$\mathrm{P}{\mathrm{O}}_{\mathrm{3}}^{-}$ ions and two water molecules per translation period are highlighted by green, blue and yellow regions. An example of a ten-node cycle is highlighted in red. The minor positions of the O atoms (ca. 7%) are omitted for clarity.
Figure 4:

The HT phase of TMA⋅H2PO3⋅H2O viewed down [100], with TMA ions omitted for clarity. The same projection is given twice to avoid overlap of the colored regions. Atom colors as in Figure 1. 21 screw rotations axes are indicated by the usual symbols [13]. Examples of helicoidal chains of the hydrogen-bonding network with two H2PO3− ions and two water molecules per translation period are highlighted by green, blue and yellow regions. An example of a ten-node cycle is highlighted in red. The minor positions of the O atoms (ca. 7%) are omitted for clarity.

The shortest actual cycle in the structure is obtained by combining two walks about two opposing faces of the “cube” as depicted inbecause paths on opposing faces screw in opposing directions. In this path, the sum of the voltages is the zero translation. Note that the edge that is crossed twice in the graph corresponds to two different bonds in the actual structure, which are related by a lattice translation. Such a ten-node cycle is highlighted by red color in Figure 4(b) and shown in Figure 5. The translationally equivalent H2PO3− ions and water molecules are connected by arrows.

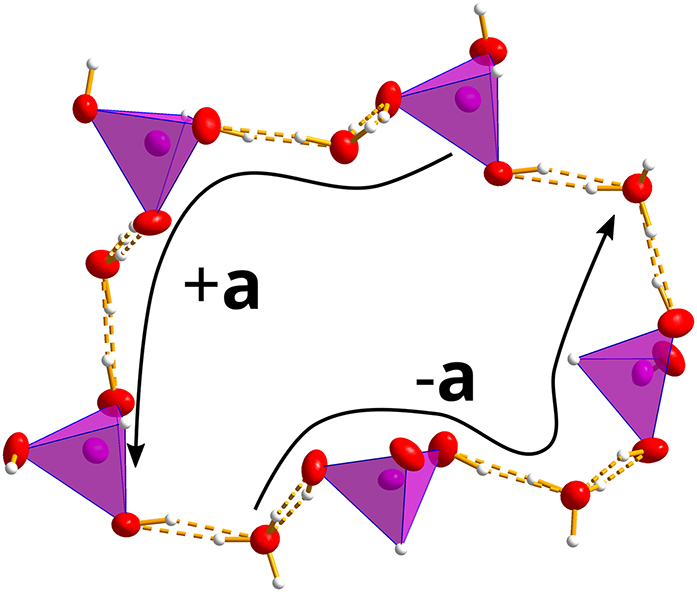
Figure 5: A ten-node cycle in TMA⋅H2PO3⋅H2O. Atom colors as in Figure 1. The two four-node helix fragments (from H2O to H2O and from H2PO3−$\mathrm{P}{\mathrm{O}}_{\mathrm{3}}^{-}$ to H2PO3−$\mathrm{P}{\mathrm{O}}_{\mathrm{3}}^{-}$) are indicated by arrows, which are marked with the translations relating the two end groups.
Figure 5:

A ten-node cycle in TMA⋅H2PO3⋅H2O. Atom colors as in Figure 1. The two four-node helix fragments (from H2O to H2O and from H2PO3− to H2PO3−) are indicated by arrows, which are marked with the translations relating the two end groups.

In addition to the disordered hydrogen bonding, distinct electron density in the difference Fourier maps showed that the H2O molecule features additional, most likely dynamical, disorder. Both positions are located on the three fold rotation axis. Refinement of the occupancies of both positions, while constraining the sum to 1 led to a 93:70 (5) ratio. The O atoms of the H2PO3− anions follow suit as shown in Figure 6 This minor positional disorder does not affect the overall hydrogen bonding network.

Figure 6: Disorder of a water molecule connecting two H2PO3−$\mathrm{P}{\mathrm{O}}_{\mathrm{3}}^{-}$ ions. The minor positions (ca. 7%) of the hydroxyl and water O atoms are labeled as O1′ and Ow′, respectively. Hydrogen bonding of the minor position is not shown, since the H atoms were not determined.
Figure 6:

Disorder of a water molecule connecting two H2PO3− ions. The minor positions (ca. 7%) of the hydroxyl and water O atoms are labeled as O1′ and Ow′, respectively. Hydrogen bonding of the minor position is not shown, since the H atoms were not determined.

3.3.2 LT phase

On cooling, both disorders of the HT phase (hydrogen bonding network and positional disorder) are “frozen”. The minor position of the positional disorder is never realized and for every H2PO3− ion and for every H2O molecule in the crystal precisely one of the three states given in Eqs. (2) and (3) is realized.

Under the assumption that the LT phase is fully ordered, all threefold rotation axes are lost on cooling, because a threefold rotation is incompatible with the symmetry of H2O and H2PO3−. Thus, the symmetry of the LT phase cannot be cubic, as all cubic space groups feature threefold rotations. It could either be trigonal (via P213→R3→P31/P32), orthorhombic (via P213→P212121) or of even lower symmetry. Note that the P31/P32 space groups possess only threefold screw rotations and such a structure could be ordered with respect to the hydrogen bonding. All trigonal space groups with a rhombohedral lattice, on the other hand, always contain threefold rotations and thus some disorder must still exist. However, experimentally a P31/P32 LT phase can be excluded, since the transition includes a symmetry descent of the klassengleiche type (R3→P31/P32). This corresponds to a reduction of translation symmetry and therefore appearance of superstructure reflections. However, no reflections compatible with such a hexagonal primitive (hP) lattice were observed.

A priori, we can of course not rule out that the LT phase is partially disordered and thus still features threefold rotations. The observed lattice is in principle compatible with R3 symmetry with with cell parameters analogous to the HT phase. However, overall the diffraction data was more consistent with an ordered orthorhombic P212121 structure than any other model. The point symmetry of the intensity data was more in line with an orthorhombic than a rhombohedral space group (Rint = 2.8% for P212121 vs. Rint > 10% for R3). Moreover, a very convincing model was obtained in the P212121 space group, featuring no disorder and the expected geometry of the ordered H2PO3− anion, with one distinctly longer P–O-bond (see Table 2). This model refined to lower residuals than R3 models. For the latter, even when modeling as a fourfold twin by fourfold rotation about [100], R[F2>2σ(F2)] could not be brought below 7%, in contrast to 3.8% for the P212121 model presented here.

The P212121 space group has no special positions, thus the symmetries of the TMA cation, the H2PO3− anion and the H2O molecule are decreased from 3 to 1. On the atomic level, as expected in a symmetry reduction, the atomic positions are split and/or the occupancies are increased [15], as summarized in Table 3. The H atoms of the water molecule feature both phenomena, namely the single HT position is split in two LT positions and the occupancy is increased from 23 to 1.

Table 3:

Site symmetry group and occupancy of atoms in the HT and LT phases of TMA⋅H2PO3⋅H2O. Methyl Hs are not listed and positional disorder of the O atoms is ignored. Ow designates the water molecule, other O atoms belong to the H2PO3− anion.

LTHT
AtomSite symmetry groupOcc.AtomSite symmetry groupOcc.
P131P111
Hp131Hp111
O111O111
O211
O311
Ho1113Ho311
Ow31Ow11
Hw1123Hw111
Hw211
N131N111
C131C111
C211C211
C311
C411

Since the hydrogen bonding is ordered in the LT phase, it can be represented by the directed graph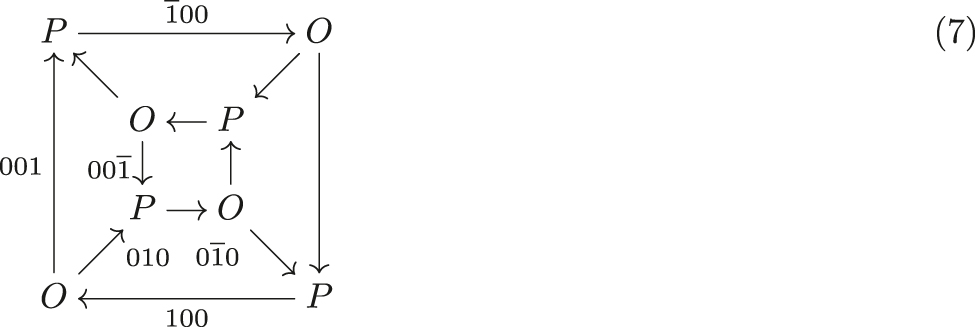where an → arrow indicates a directed O–H⋯O bond. Accordingly, every O (H2O) node has two outgoing and one incoming edge and vice-versa for P (H2PO3−) nodes. Again, the given voltages are to be read in the O → P direction and independent of the direction of the edges. From the graph one can immediately see the loss of the threefold rotations and therefore cubic symmetry. Moreover by tracing paths along the faces of the “cube”, one can see that by following hydrogen bonds in the donor → acceptor direction the helicoidal structures with 21 symmetry are retained in the [100], [1‾00], [001] and [001‾] directions (Figure 7). In the [010] and [01‾0] directions, on the other hand, hydrogen bonds have to be crossed in two different directions (green region in Figure 7).

Figure 7: Hydrogen bonding network in the LT phase of TMA⋅H2PO3⋅H2O viewed down [100]. Color codes of atoms and helices as in Figure 4. Directed hydrogen bonds in the highlighted areas are indicated by arrows.
Figure 7:

Hydrogen bonding network in the LT phase of TMA⋅H2PO3⋅H2O viewed down [100]. Color codes of atoms and helices as in Figure 4. Directed hydrogen bonds in the highlighted areas are indicated by arrows.

3.3.3 Twinning

The cubic 23 point group of the HT phase is a merohedry, which means that it is of a lower symmetry than the m3‾m point group of the cubic lattice. More precisely, it is a tetartohedry, i.e. the index of 23 in m3‾m is |m3‾m|:|23|=4. For a given cubic lattice, the structure can therefore appear in four orientations, which are derived by coset decomposition of 23 in m3‾m. In principle, crystalline domains of these orientations could be present in the same sample, which would then be a twin by merohedry [16]. However, in all experiments we could exclude twinning by fourfold rotation about 〈100〉 or by the corresponding fourfold rotoinversion. For the HT data set discussed here, the twin volume ratio of such a putative twin domain refined to −0.002 (6), i.e. to zero within the experimental error. Likewise, we did not find hints of twinning by inversion, though here the experimental uncertainty is larger by a factor of 5, since even the heaviest atom in the structure (P) is not a significant anomalous scatterer under the employed Mo Kα radiation [Flack parameter −0.04 (3)]. In summary, the TMA⋅H2PO3⋅H2O crystals are generally not twinned above the phase transition temperature.

For twinning to occur, there needs to be a continuity of either an arbitrary substructure [17] or in the form of full layers as in the order-disorder (OD) theory [18], which apparently is not the case here. Note that the OD theory is unrelated to the order-disorder type of phase transition described herein.

The 222 point group of the LT phase is a subgroup of index |23|:|222|=3 with respect to the 23 point group of the HT phase. Thus, on cooling of the HT phase, one can expect formation of threefold twins. Indeed, we invariably observed splitting of reflections in agreement with threefold twinning when measuring TMA⋅H2PO3⋅H2O at low temperatures. The twin laws are derived by coset decomposition of 222 in 23. The second and third orientation are related to the first by the representative 3[111]+ and 3[111]− operations, respectively. The remaining operations of the twin laws are threefold rotations about the other space diagonals, [1‾11], [11‾1] and [1‾1‾1]. The symmetry of the threefold twin is conveniently represented by the trichromatic point group (23(3))(3) [19]. This symbol indicates that the overall point symmetry of the twin is of type 23, whereby the 3 operations are trichromatic (interchanges domains in cycles of size 3) and the 2 operations are achromatic, as they are point operations of all three twin domains.

Since the translation lattice remains in principle unchanged during the phase transition (neglecting the small deviation from cubic metrics), the twinning is by pseudo-merohedry. This means that the twin index is n = 1, i.e. all three twin individuals possess diffraction spots at (approximately) the same location in reciprocal space. The deviation from cubic metrics causes a splitting of reflections, which is expressed by the twin obliquity ω, the angle of the three-fold [111] rotation axis to the normal of the (111) plane. For the orthorhombic lattice of the LT phase of TMA⋅H2PO3⋅H2O it calculates as

(8)ω=cos−1(3(1a2+1b2+1c2)(a2+b2+c2))

which, using the cell parameters of the LT phase, gives ω≈0.70°. However, this estimate is certainly smaller than the actual twin obliquity, because integration of frame data was performed using a single domain, which therefore represents an average of the three domains. To determine more reliable cell parameters, and thus a more precise twin obliquity, high-resolution (powder) diffraction would be needed.

3.4 Conclusion and outlook

The structure of TMA⋅H2PO3⋅H2O is seemingly trivial with only one third (HT) or one (LT) formula unit in the asymmetric unit. Nevertheless, owing to the cubic symmetry a surprisingly intricate hydrogen bonding network is formed. An analysis of the hydrogen-bonding topology and the symmetry relations clears the fog and simplifies these complexities, which arise from simple building principles. Tracing paths in a planarized voltage graph significantly facilitates the identification of infinite motifs in a triperiodic network. Moreover, in this case, the order-disorder phase transition can be represented by mapping directed and undirected graphs.

In general, for unsubstituted and methyl-substituted ammonium salts of dihydrogenphosphite the readiness to crystallize decreases with the number of hydrogens in the ammonium cation, showing the significance of hydrogen bonding in this system. In contradiction to this trend, we couldn’t crystallize the trimethylammonium salt, whereas TMA crystallized inside an extended hydrogen bonding network formed by water and H2PO3−. Interestingly, the exactly same behavior was observed for the hypophosphite (HPIO2−) salts. The ammonium, MA and DMA salts crystallize readily. However, we could not crystallize any trimethylammonium salt, and yet TMA crystallized as a hydrate. This similarity of the behavior does not extend to the structures themselves, which are unrelated to the dihydrogenphosphites described herein, and will be presented elsewhere.

Corresponding author: Berthold Stöger, X-Ray Centre, TU Wien, Getreidemarkt 9, 1060Vienna, Austria, E-mail

Acknowledgments

The constructive feedback of two anonymous referees is highly appreciated and distinctly improved the manuscript.

  1. Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.

  2. Research funding: None declared.

  3. Conflict of interest statement: The authors declare no conflicts of interest regarding this article.

References

1. Schmidt, V. H. Ferroelectrics 1987, 72, 157; https://doi.org/10.1080/00150198708017945.Search in Google Scholar

2. Bruker AXS Inc. APEXII, SAINT and SADABS: Madison, Wisconsin, USA, 2020.Search in Google Scholar

3. Sheldrick, G. M. Acta Crystallogr. A 2015, 71, 3; https://doi.org/10.1107/s2053273314026370.Search in Google Scholar

4. Sheldrick, G. M. Acta Crystallogr. C 2015, 71, 3; https://doi.org/10.1107/s2053273314026370.Search in Google Scholar

5. Koch, E., Fischer, W., Müller, U., Aroyo, M. I. Normalizers of space groups and their use in crystallography. In International Tables for Crystallography; IUCr: Chester, Vol. A, 2016; p. 826.10.1107/97809553602060000933Search in Google Scholar

6. Johansson, G. B., Lindqvist, O. Acta Crystallogr. B 1976, 32, 412; https://doi.org/10.1107/s0567740876003130.Search in Google Scholar

7. Jeffrey, G. A. An Introduction to Hydrogen Bonding; Oxford University Press: Oxford, 1997.Search in Google Scholar

8. Kratotochvíl, B., Podlahová, J., Hašek, K. Acta Crystallogr. C 1983, 39, 326.10.1107/S010827018300459XSearch in Google Scholar

9. Melichar, Z., Kratochvíl, B., Podlahová, J., Petříček, V., Malý, K., Císařová, I. Acta Crystallogr. C 1984, 40, 720; https://doi.org/10.1107/s0108270184005473.Search in Google Scholar

10. Sghyar, M., Durand, J., Cot, L., Rafiq, M. Acta Crystallogr. C 1991, 47, 8; https://doi.org/10.1107/s010827019000659x.Search in Google Scholar

11. Sghyar, M., Durand, J., Cot, L., Rafiq, M. Acta Crystallogr. C 1990, 46, 1378; https://doi.org/10.1107/s0108270189013703.Search in Google Scholar

12. Ouarsal, R., Tahiri, A. A., Bali, B. E., Lachkar, M., Bolte, M. Acta Crystallogr. E 2002, 58, i19; https://doi.org/10.1107/s1600536802000806.Search in Google Scholar

13. Hahn, Th., Aroyo, M. I. Space-group symmetry. In Aroyo, M. I., Ed. International Tables for Crystallography; IUCr: Chester, Vol. A, 2016; p. 144.10.1107/97809553602060000114Search in Google Scholar

14. Eon, J.-G. Acta Crystallogr. A 2011, 67, 68; https://doi.org/10.1107/s0108767310042832.Search in Google Scholar

15. Müller, U. Z. Anorg. Allg. Chem. 2004, 630, 1519; https://doi.org/10.1002/zaac.200400250.Search in Google Scholar

16. Grimmer, H., Nespolo, M. Z. Kristallogr. 2006, 221, 28; https://doi.org/10.1524/zkri.2006.221.1.28.Search in Google Scholar

17. Nespolo, M., Souvignier, B. Cryst. Res. Technol. 2015, 50, 442; https://doi.org/10.1002/crat.201400480.Search in Google Scholar

18. Dornberger-Schiff, K., Grell-Niemann, H. Acta Crystallogr. 1961, 14, 167; https://doi.org/10.1107/s0365110x61000607.Search in Google Scholar

19. Nespolo, M. Z. Kristallogr. 2004, 219, 57; https://doi.org/10.1524/zkri.219.12.773.55868.Search in Google Scholar

Received: 2020-10-14
Accepted: 2020-11-30
Published Online: 2021-01-18
Published in Print: 2021-02-23

© 2020 Matthias Kogler and Berthold Stöger, published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. In this issue
  3. Original papers
  4. Phase stability analysis of shocked ammonium dihydrogen phosphate by X-ray and Raman scattering studies
  5. Effect of solution acidity on the crystallization of polychromates in uranyl-bearing systems: synthesis and crystal structures of Rb2[(UO2)(Cr2O7)(NO3)2] and two new polymorphs of Rb2Cr3O10
  6. Novel tetrazole PtII and PdII complexes with enhanced water solubility: synthesis, structural characterization and evaluation of antiproliferative activity
  7. Hydrogen-bonding in mono-, di- and tetramethylammonium dihydrogenphosphites
  8. Photophysical property change of N-(5-bromo-salicylidene)-3-aminoethylpyridine monohydrated crystals via dehydration phase transition
https://doi.org/10.1515/zkri-2020-0088
Keywords for this article
hydrogen bonding; phase transition; symmetry relations; twinning; voltage graphs
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. In this issue
  3. Original papers
  4. Phase stability analysis of shocked ammonium dihydrogen phosphate by X-ray and Raman scattering studies
  5. Effect of solution acidity on the crystallization of polychromates in uranyl-bearing systems: synthesis and crystal structures of Rb2[(UO2)(Cr2O7)(NO3)2] and two new polymorphs of Rb2Cr3O10
  6. Novel tetrazole PtII and PdII complexes with enhanced water solubility: synthesis, structural characterization and evaluation of antiproliferative activity
  7. Hydrogen-bonding in mono-, di- and tetramethylammonium dihydrogenphosphites
  8. Photophysical property change of N-(5-bromo-salicylidene)-3-aminoethylpyridine monohydrated crystals via dehydration phase transition
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 18.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/zkri-2020-0088/html
Scroll to top button