Studying the nonlinear properties and strain-rate sensitivity of SiC short fiber-reinforced Al matrix composites

1 Introduction

As is well known, the mechanical properties of composite materials are related to their geometrical features, such as inclusion arrangement, inclusion fraction, inclusion dimension, and so on [1–4]. For the fiber-reinforced composites, it can be classified as continuous and short fiber-reinforced (SFR) composites. As a structural material, SFR composites are widely used in engineering area due to their superior mechanical properties and low manufacturing cost [5, 6].

By using the average stress coordinates of common intersection points of unloading-reloading loops in the tensile curves, the residual tensile stresses of SiC-fiber-reinforced ceramic matrix composites were directly measured by Dassios and Matikas [7]. By using the three different methods of experimental measurement, analytical calculation, and theoretical prediction, the thermal residual stress in composites was investigated by Mei [8]. Furthermore, relationships between the thermal residual stress state and macroscopic mechanical properties are discussed. Due to the requirements of a lot of test configurations, the experimental campaigns may be costly for acquiring different fiber arrangement and volume fraction influence on mechanical properties of the SFR composites. Therefore, the prediction theory becomes the most important method for studying and optimizing composite structures. Macro-mechanical method can be used to study mechanical behaviors. However, the complex failure characteristic from microscopic scale to macroscopic scale can hardly be revealed. Micromechanical method is a useful tool to reveal failure mechanisms of composites [9–12] because the complex microstructure can be easily and quickly obtained using electron microscope together with the micromechanical theory. Unterweger et al. [13] provided a comprehensive investigation of fiber influences on tensile strength, modulus, notched and unnotched impact resistance. The results indicate that a certain amount of adhesion is required for improving composite performance by increased fiber length. Mahmood et al. [14] developed a strain-rate-dependent micromechanical method to predict the strength of composites under various loading rates. A comparison between predicted results and experimental data under various strain rates shows the capability of the proposed model. Hashemi [15] investigated the effect of temperature fiber concentration and strain rate on the strength of short glass fiber-reinforced polymer composites. Mondali and Abedian [16] studied the creep deformation behavior of SFR composites by an approximate analytical model. The predicted strain rate and stress components by the method exhibit good agreement with the finite element results. Notta et al. [17, 18] presented an effective model of behaviors for SFR composites. The simulations are performed to investigate fiber length and interfacial shear strength. It revealed that the fiber orientation affects the stress state of composites and the plastic flow in matrix material. Ozkan et al. [19] investigated the effects of the sizing material type on the mechanical and electrical properties. Tensile test results showed that tensile modulus of sized short carbon fiber was higher than that of unsized short carbon fiber composites. In the literatures mentioned above, the studies focused on the fiber orientation distribution, fiber length, and interfacial strength influence on mechanical responses. Some important problems have not been adequately studied, e.g. without consideration of fiber shape, as well as thermal residual stress.

The generalized method of cells (GMC) has been established as a powerful tool to calculate microscopic local field for two-dimensional (2D) and three-dimensional (3D) composites [20–22]. Based on the homogenization theory, macroscopic stress-strain behaviors can be acquired. In addition, it has many advantages, such as explicit analytical expression for elastic constant and thermal expansion coefficient, no need to redefine the sub-cell grids with the variation of inclusion volume fraction, as well as high calculation efficiency. A method based on GMC and laminate analogy approach was proposed by Sun et al. [23] to predict the elastic properties of short sisal fiber-reinforced polypropylene composites. The results showed that the new model agrees better than other models do with the experimental data. Arnold et al. [24] employed GMC to investigate the microstructural influence on deformation and fatigue life of composites. However, in spite of their effectiveness in the above and other applications, GMC has not been applied in investigating the thermal residual stress influences on the macroscopic stress-strain characteristic of SFR composites. Considering its ability in dealing with the nonlinear deformation problems through incorporating unified constitutive model, GMC is employed to investigate the fiber off-axis orientation and thermal residual stress influence on the nonlinear response of SFR composites. In addition, most of the presented works focused on the mechanical behaviors investigation restriction to a certain loading rate. Therefore, another important factor, different applied loading rate effects on the mechanical properties, is also discussed.

The main objective of this paper is to establish a theory framework based on GMC for solving thermal residual stress and then investigate the fiber off-axis angle, thermal residual stress, and loading rate effects on the macroscopic nonlinear stress-strain response of SFR composites. Therefore, the outline of this paper is as follows. In Section 2, we present the theory framework of thermal residual stress based on GMC model for 3D composites. In Section 3, the fiber shape and fiber volume fraction (FVF) effect on elastic constant are discussed. Numerical simulation for investigating thermal residual stress influences on the nonlinear stress-strain response of the SFR composites is presented in Section 4. Furthermore, strain rate sensitivity of SFR composites is studied in Section 5. Conclusions can be found in Section 6.

2 Theory framework of thermal residual stress for SFR composites

It is no doubt that the mechanical properties and damage mechanism of composites are closely dependent on the thermal residual stresses in sub-cells. For the continuous fiber-reinforced composites (CFR), the reinforced fiber is assumed to be infinitely long. Through choosing a proper cross-section, that is, the representative volume element (RVE), the micromechanical model can be defined according to the continuous conditions among the adjacent sub-cells. For the SFR composites, they are considered to be reinforced with the finite length inclusions, as shown in Figure 1A. The thermal residual stress influences on the nonlinear mechanical response for the CFR composites based on GMC have been investigated [25]. Here, the theory framework of the thermal residual stress for SFR composites is developed. The RVEs with two typical short fibers, that is, cylinder short fiber and cuboid short fiber, are shown in Figure 1B and C, respectively. The values (x₁, x₂, x₃) and (y₁, y₂, y₃) indicate the global coordinate system and local coordinate system, respectively. Angle θ is defined as fiber orientation or fiber off-axis angle in the x₁-x₂ plane, as shown in Figure 1A. The relation between stiffness C^G in x₁-x₂ plane and stiffness C^L in y₁-y₂ plane can be written as:

Figure 1:

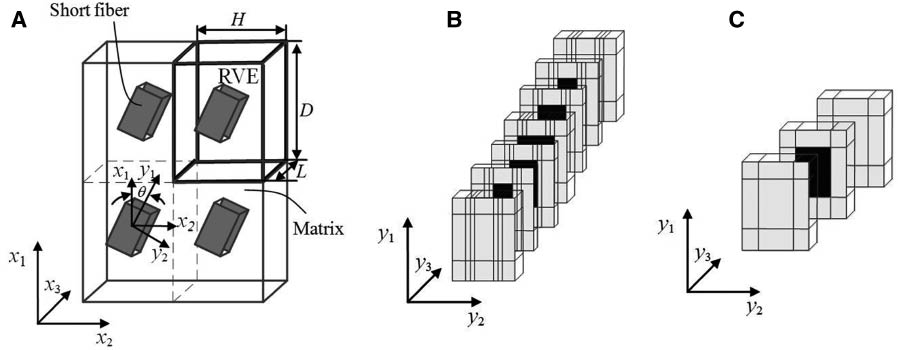
SFR composites and RVE (A) SFR composites, (B) Cylinder short fiber, (C) Cuboid short fiber.

For the sub-cell (αβγ) in local coordinate system, the constitutive equation can be written as follows [26]:

where σ¯ij(αβγ) and Cijkl(αβγ) indicate the sub-cell average stress and sub-cell stiffness components, respectively. The variations ε¯klE(αβγ) and ε¯klI(αβγ) are the sub-cell average elastic strain and plastic strain components, respectively. The variation ε¯klT(αβγ), which is related to thermal expansion coefficient and temperature difference between manufacturing temperature and working temperature, indicates the sub-cell average thermal strain component. The plastic strain can be acquired by yield criterion or unified constitutive model. For investigating the nonlinear deformation of SFR composites, the Bodner-Partom viscoplastic constitutive model [27] is introduced to describe nonlinear behaviors of matrix materials.

According to the interfacial displacement and traction continuity among adjacent sub-cells, the relations can be written in matrix forms, that is,

where A=[AMAG],B=[AM0],U=[0J].A_M refers to the sub-cell stiffness matrix with dimensions (6N_αN_βN_γ -N_αN_β -N_αN_γ -N_βN_γ +N_α +N_β +N_γ )*6N_αN_βN_γ . A_G contains the sub-cell size with the dimensions (N_α (N_β +N_γ +1)+N_β (N_γ +1) +N_γ )*6N_αN_βN_γ . J contains the RVE with the dimensions (N_α (N_β +N_γ +1)+N_β (N_γ +1)+N_γ )*6. ε¯s=(ε¯(111), …, ε¯(NαNβNγ)) indicates the sub-cell average strain components. εsT=(ε¯T(111), …, ε¯T(NαNβNγ)) denotes the sub-cell average thermal strain components. The components ε̅=(ε̅₁₁, ε̅₂₂, ε̅₃₃, 2ε̅₂₃, ε̅₁₃, ε̅₁₂) indicate the overall average strain of the composites.

By using matrix inversion operations in Eq. (3) for each sub-cell (αβγ) and substituting the transformation equation into constitutive equation of 3D composites as shown in Eq. (2), the sub-cell average stresses σ̅^(αβγ) can be expressed as follows:

where A̅=A^-1U. B̅=A^-1B.

Here, the matrices A̅^(αβγ) and B̅^(αβγ) indicate the N_αN_βN_γ six-order sub-matrices as follows:

A¯(αβγ)=[A(111)⋮A(NαNβNγ)] B¯(αβγ)=[B(111)⋮B(NαNβNγ)].

The detailed information in the expression above can be found in the study of Aboudi et al. [26]. From the sub-cell constitutive equation as shown in Eq. (4), it can be found that the thermal strain component ε¯sT can be easily acquired once the material properties and temperature difference between working temperature and manufacturing temperature are both confirmed. The sub-cell stiffness matrix C^(αβγ) is obtained when the RVE is confirmed. Therefore, once the macroscopic average strain ε̅ is confirmed, the thermal residual stresses in sub-cell can be acquired.

According to the homogenization theory, Eq. (4) can be expressed as follows:

It should be noted that the thermal residual stress of composites is introduced due to the thermal coefficient mismatch between inclusions and matrix materials. The dimensions of the RVE are defined as D, H, L along with the x₁-, x₂-, and x₃-direction, as shown in Figure 1A. In the initial condition, no mechanical loading is applied in composites. Therefore, overall stress component σ̅ is equal to 0. Through using matrix inversion operations in Eq. (5), the macroscopic average strain ε̅ can be acquired as follows:

Moreover, by substituting the tensor ε̅ in Eq. (4), the sub-cell thermal residual stresses for SFR composites can be acquired.

3 Elastic property of the SFR composites

3.2 The FVF variation

The predicted elastic constant and thermal expansion coefficient of 0° SFR composites are shown in Figure 2. For validating the micromechanical model, the ANSYS software (Ansoft Corporation, Pittsburgh, PA, USA) is used to calculate the longitudinal and transverse elastic modulus. An eighth of the finite element model can be seen in Figure 2D. In the RVE, solid186 element is employed. Moreover, the glue function is used to avoid debonding between fiber and matrix. Figure 2A shows the prediction results by using the micromechanical model and finite element method. It is true that a good consistency is obtained at low FVF, but a great gap can be found when the FVF is equal to 0.4 (5.88 GPa for the longitudinal elastic modulus and 6.65 GPa for the transverse elastic modulus). The relative errors for both longitudinal and transverse elastic moduli are less than 5%. Similarly with CFR composites, the elastic constant is closely dependent on FVF. It is shown in Figure 2A that longitudinal elastic modulus E₁₁ and transverse elastic modulus E₂₂ increase as FVF continues to increase, and E₁₁ presents linear increase tendency. This is due to the potentiation of short fiber in composites. Compared with matrix materials, the cuboid SFR composites provide 24.7% and 13.9% increase in longitudinal elastic modulus E₁₁ and transverse elastic modulus E₂₂ when the FVF increases to 0.1. In addition, it is hard to discern the difference between the cylinder SFR composites and cuboid SFR composites influence on longitudinal elastic modulus E₁₁. That is, fiber shape effects on E₁₁ can be ignored. However, the distinct difference can be found in transverse elastic modulus E₂₂. It is clearly seen that the cuboid SFR composites provide a higher transverse elastic modulus E₂₂ than cylinder SFR composites do.

Figure 2:

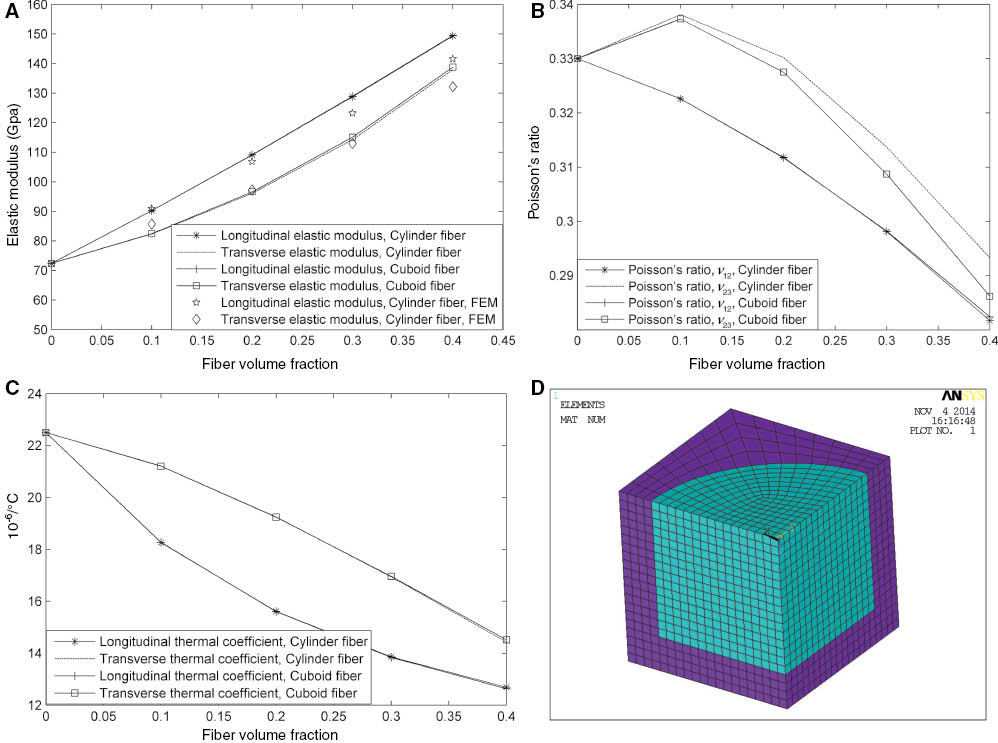
FVF influences on elastic constant of SFR composites. (A) Elastic modulus, (B) Poisson’s ratio, (C) Thermal expansion coefficient. (D) Finite element mesh.

Figure 2B indicates the relationship between Poisson’s ratio and FVF. Poisson’s ratio v₂₃ and v₁₂ present a different variation tendency. In detail, fiber shape effects on Poisson’s ratio v₂₃ can be easily discerned, while the fiber shape effects on Poisson’s ratio v₁₂ can be ignored. Moreover, the results show that FVF affects Poisson’s ratio v₁₂, and the value decreased as the FVF increased. However, Poisson’s ratio v₂₃ presents a distinct variation with the increasing FVF. When the FVF is <0.1, Poisson’s ratio v₂₃ increased with the increasing FVF. Opposite variation for Poisson’s ratio v₂₃ can be found when the FVF is more than 0.1. Figure 2C shows the results of longitudinal and transverse thermal expansion coefficients for SFR composites. Different fiber shapes influence on the longitudinal and transverse thermal expansion coefficients can hardly be discerned. Due to a higher thermal expansion coefficient of matrix materials, the longitudinal and transverse thermal expansion coefficients tend to decrease with the increase of FVF. It should be noted that the variation relationship between material parameters (elastic constant and thermal expansion coefficient) and FVF agreed with the conclusions of Caruso [30].

4 Nonlinear response of SFR composites

In order to analyze the effects of various fiber orientations on mechanical behaviors of SFR composites, five different fiber off-axis angles, that is, 0°, 15°, 45°, 60°, and 90°, were considered. Both cylinder SFR and cuboid SFR composites with 0.25 FVF were studied. The ratios of d/D and h/l were assumed to be 0.7 and 1, respectively. The RVE is a cube element. For investigating the influence of residual stress on SFR composites, the thermal residual stress was considered to be initial stress fields in sub-cells. And a decrease from manufacturing temperature of 820°C to room temperature of 20°C was considered. As well, the nonlinear behavior studies of the SFR composites were restricted to a constant strain rate 0.0005/s.

For describing nonlinear behavior, the Bodner-Partom viscoplastic model [27] is introduced and the material parameters for Al matrix are as follows [31]: Z₀=340 Mpa, Z₁=435 Mpa, m=300, n=10, D₀=10⁴/s. Here, parameter Z referred to material hardening. Parameters n and m indicate the material constant. D₀ indicates material limiting strain rate. In Eq. (2), the inelastic strain rate component ε¯˙klI and the flow function Λ in the Bodner-Partom viscoplastic model can be written as:

where s_ij indicates the deviatoric stress components. The hardening function of materials Z is as follows:

where W_p is the plastic work.

The reinforced phase is considered to be linear elasticity, and matrix materials are considered to be viscoplastic. Meanwhile, the elastic moduli of matrix and fiber are unrelated to strain rate. Figure 3A shows the prediction of longitudinal tensile behaviors of the SiC/Al composites with and without consideration of thermal residual stress. For CFR composites in the study by Chen et al. [32], the stress-strain behaviors tend to increase linearly in condition of longitudinal tensile loading, and the effect of interfacial debonding can be ignored. This is due to the huge difference of rigidity between the fibers and the matrix materials. It makes the matrix response in terms of stresses very low compared to that of the fibers. Therefore, a modification of the matrix behavior has a relatively low impact on the composite behaviors in the case of fiber off-axis angle 0°. However, it was concluded from Figure 3A that SFR composites present obvious nonlinearity in longitudinal loading due to the matrix plastic deformation when overall strain is increased to a certain degree. It is interesting to mention that the mechanical responses of SFR composites are closely dependent on fiber shape.

Figure 3:

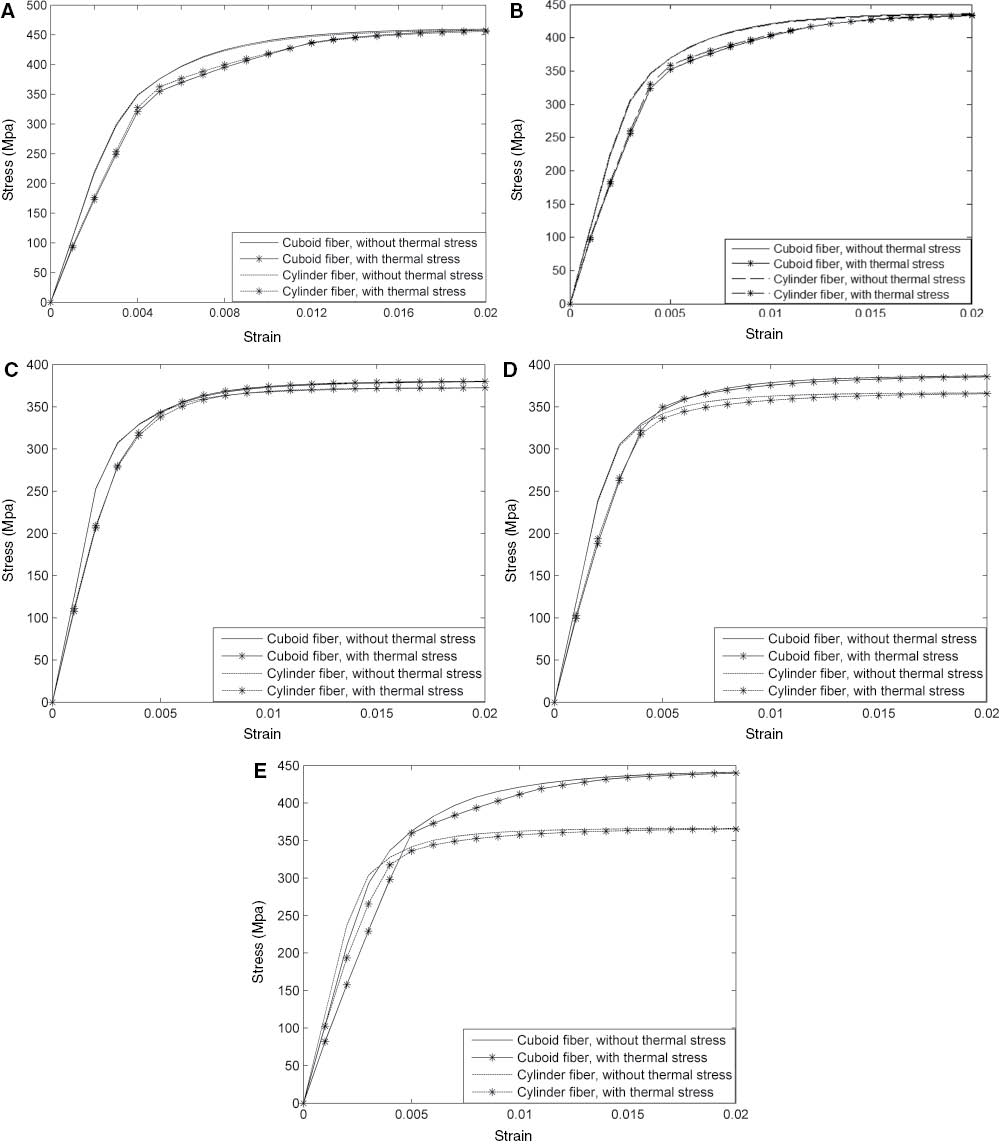
Thermal residual stress influences on stress-strain behaviors of SFR composites. (A) 0°, (B) 15°, (C) 45°, (D) 60°, (E) 90°.

Figure 3B–E shows the nonlinear stress-strain responses of the SFR composites when fiber off-axis angles are increased to 15°, 45°, 60°, and 90°. It can be concluded that the fiber shape influences on the nonlinear behaviors can be easily discerned whether the thermal residual stress is considered or not. Correlation research indicates that similar stiffness behaviors can be found at an early stage of loading for continuous fiber-reinforced composites with and without consideration thermal residual stress [25]. It is interesting to mention that the thermal residual stress influence on the mechanical behaviors appeared to have a greater effect at high rather than low off-axis angles, which is similar to the continuous fiber-reinforced composites [25]. In details, the thermal residual stress influences can hardly be discerned if the fiber off-axis angle is less than 60°, while obvious difference can be found when the fiber off-axis angle is equal to 90°. Furthermore, ignoring thermal residual stress effects will lead to overestimation of the stiffness behaviors in tensile loading. However, it should be emphasized that the stiffness behaviors tend to be consistent when overall strain is increased to 2%.

5 Strain-rate sensitivity of SFR composites

Composite structures, which show obvious strain-rate sensitivity, are always stated at dynamic loading in practical engineering application. Here, the model based on Section 2 is improved to investigate the strain rate influences on the mechanical properties of SiC short fibers and Al matrix composites. The reinforced phase is considered to be cylinder short fiber. Four different strain rates, that is, 0.1/s, 0.01/s, 0.001/s, and 0.0001/s, are considered. FVF is equal to 0.25, and thermal residual stresses in sub-cells are considered in all cases. The results of SFR composites with different off-axis angles are shown in Figure 4A–E. It should be explained that the sub-graph in each figure is the local enlargement of the original graph to describe the variance of each strain rate on mechanical response more distinctly.

Figure 4:

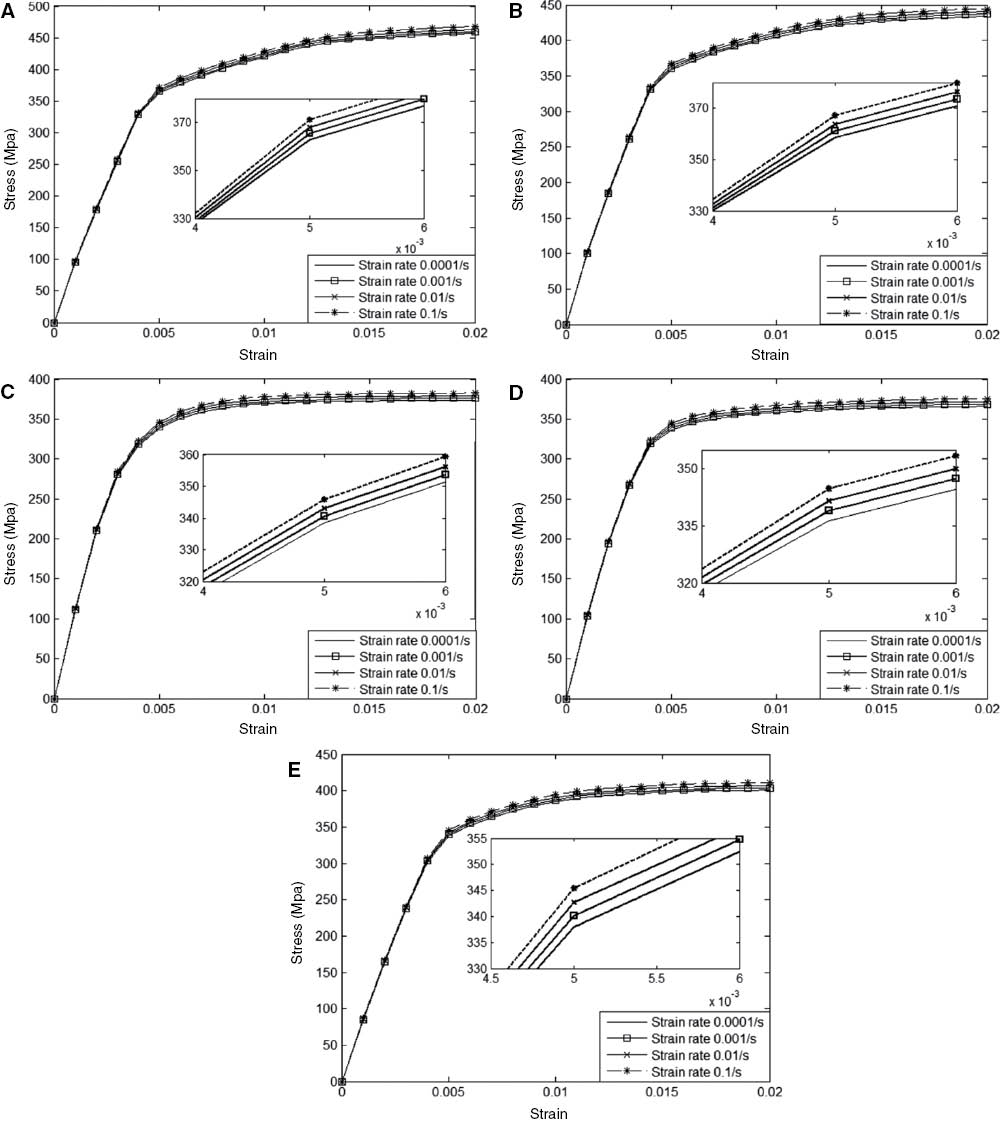
Strain rate influences on stress-strain behaviors of SFR composites. (A) 0°, (B) 15°, (C) 45°, (D) 60°, (E) 90°.

Figure 4A shows the longitudinal tensile results for SiC/Al composites. It can be easily seen that the stress-strain curves present obvious linear elasticity and nonlinearity. The strain rate effects on mechanical responses of SFR composites can hardly be discerned at the early stage of the loading. Only a little difference can be found at the stage of plastic deformation. Furthermore, the flow stress increased as strain rate continued to increase. Compared with the strain rate at 0.0001/s, the SFR composites provide a 2.17% increase in condition of strain rate at 0.1/s when overall strain increases to 1%. To further examine the effects of fiber off-axis angle, which is related to the nonlinear stress-strain behaviors, the SFR composites with various fiber off-axis angles are also calculated. From Figure 4B–E, similar conclusions can be obtained for SiC/Al composites with different fiber off-axis angles. In details, higher strain rate provides higher stiffness behaviors. Moreover, the effect of the strain rate on the stress-strain response is only evident and, to a very limited extent, in the initial yielding and inelastic deformation regions.

6 Conclusions

Short fibers are assumed to be periodic arrays in composite materials. On this basis, a micromechanical model is improved to calculate elastic constant, thermal expansion coefficient of the SFR composites. Furthermore, the thermal residual stress and short fiber off-axis angle are both considered to affect the nonlinear stress-strain responses. The results can be concluded as follows:

1. Fiber shape effects on elastic constant E₁₁ can be ignored. Cuboid SFR composites provide higher transverse elastic modulus E₂₂ than cylinder SFR composites do.

2. Ignoring thermal residual stress effects will lead to overestimation of the stiffness behaviors of SFR composites. However, it should be emphasized that the stiffness behaviors tend to be consistent when overall strain is increased to 2%.

3. Strain rate effects on mechanical response for SFR composites can hardly be discerned at the early stage of loading. Moreover, higher strain rate provides the higher stiffness behaviors.