Expressive Law and Escalating Penalties: Accounting for the Educational Function of Punishment

1 Introduction

The pervasiveness of law enforcement schemes that prescribe harsher penalties for repeat offenders continues to challenge scholars who seek an economic explanation for criminal justice policies. According to the conventional view, which is based on the Becker (1968) model,^[1] optimal deterrence is achieved by imposing a sanction equal to the harm from an illicit act. The characteristics of the defendant, including his or her offense history, are immaterial. Economic models of crime that rely on this Pigovian approach to punishment are therefore hard-pressed to explain penalties that depend on an offender’s record, though it is not for lack of trying. Indeed, something of a cottage industry has arisen around this question. Previous models have argued,^[2] for example, that escalating penalties avoid mistaken punishment,^[3] sort offenders according to the private or social value of a violation,^[4] prevent learning by doing among offenders,^[5] or offset the stigma of criminal conviction.^[6] On the other hand, some models have shown that there are circumstances in which declining sanctions may be optimal.^[7]

The current paper formalizes a different explanation, suggested by Dana (2001); namely, that escalating penalties promote the role of the law in educating people about wrongful behavior—the so-called “expressive function” of law.^[8] Dana (p. 738) specifically argued that

penalty escalation, through its expressive power to shape popular perceptions of moral wrongfulness, allows society to conserve its resources for investments other than law enforcement.

This mechanism relies on the existence of a certain fraction of the population who are receptive to this message (i.e., who look to the law for moral guidance), but are uninformed about the illegality of certain acts. Thus, they may sometimes violate the law unknowingly, but having done so, will be deterred from committing any future violations, regardless of the magnitude of the punishment they face. A token sanction will therefore suffice.

The idea is that a person’s conscience, reinforced by the shame and humiliation of being convicted of a crime, will be a sufficient deterrent going forward. People who respond this way are said to have “learned their lesson.”^[9] It may be, for example, that some fraction of the population is unaware of the illegality of a certain act, either due to immaturity or a temporary lapse, but if caught once will be sufficiently chastened so as never to commit the act again. The standard economic model of crime ignores such a mechanism,^[10] but it is likely that this effect operates on a substantial fraction of the population.^[11]

The downside of a lenient punishment for a first offense, however, is that it invites infractions by those rational offenders who act solely on the basis of a comparison of the costs and benefits of committing an act, regardless of its illegality—Becker’s rational offenders.^[12] Ideally, these potential career criminals would face a harsh punishment for any offense, thereby completely deterring them.^[13] Thus, in a world where such individuals can be readily distinguished from unknowing offenders, a form of price discrimination would be employed whereby a lenient sanction would be imposed on unknowing offenders, and a harsh sanction would be imposed on rational calculators. In this sense, ignorance of the law is a partial defense.

The problem, of course, is that the two types cannot be distinguished, and so all offenders must face the same sanction schedule. (An equal-treatment provision may also require this.) It follows that a uniformly harsh sanction that will deter rational calculators will impose an undue punishment on unknowing offenders, while a uniformly lenient sanction will fail to deter rational offenders. In a multi-period setting, I will show that an escalating structure that imposes a lenient sanction on all first-timers and a harsh sanction on repeaters represents a compromise solution that is (second best) optimal if the fraction of uninformed but essentially law-abiding people in the population of potential offenders is sufficiently large. As Dana (2001, p. 777) observes, the efficacy of such a structure depends on the fact that it

can rely on the deterrent effect of penalties (to the extent that people are expected penalty/expected gain calculators) and on the respect for moral authority of the law for compliance (to the extent that people are not expected penalty/expected gain calculators).

It is important to emphasize that the current explanation is different from arguments based on “accidental” offenses. For example, Rubinstein (1979) assumes individuals make decisions in each of two periods to commit or refrain from a prohibited act. Those who refrain, however, may commit the act accidentally (i.e., randomly). In the current model, by contrast, an individual who desires to be law-abiding may commit an offense out of ignorance (which is the same as committing it accidentally), but once convicted will never do so again. Emons (2007) assumes that people make a rational choice at the start of their two-period lives either to be law abiders or inveterate criminals, but the former may also commit accidental violations in each period. He derives the penalty structure that optimally deters people from choosing lives of crime. Finally, Chu and Huang (2000) assume all individuals are rational calculators, but those who refrain from committing a crime may be wrongfully convicted (i.e., the accident is on the enforcer’s side). This type of legal error does not happen in the current model.

The purpose of this paper is to formalize and verify the expressive-function argument for escalating penalties. The analysis is developed as follows. After setting up the basic two-period model, I first consider the case where apprehension is certain, as this benchmark scenario is sufficient to illustrate the logic of the mechanism in the simplest possible setting. Subsequent sections demonstrate the generality of the conclusions by considering imperfect detection, first with a fixed, and then an endogenous, apprehension rate. A final section concludes.

2 The Model

Consider an act that is definitely undesirable and which society therefore seeks to deter by means of a publicly-imposed sanction. Let the population of potential offenders consist of two types: those who are ignorant of the law and so may violate it “unknowingly,” but if caught will never do so again out of moral conviction; and those who are aware of the law and will violate it whenever the benefit exceeds the cost. The former type is therefore responsive to the expressive function of law in the sense that they will never knowingly violate the law, no matter what the punishment, simply because they believe that doing so is wrong. In other words, knowledge of the law is itself a deterrent. The latter type, by contrast, comprise rational calculators who act purely on cost-benefit principles and so can only be deterred by the threat of punishment.^[14]

To be more specific, suppose that there are two periods and that all potential offenders exist and can commit crimes in both periods. Unknowing offenders will commit a crime with certainty in the first period, and again in the second period if not caught. However, if caught in period one, they will not offend in period two no matter what the threatened punishment is. Rational offenders, by contrast, will weigh the cost and benefit of committing an illegal act over the two-period time horizon. Moreover, they are perfectly foresighted and so will anticipate any impact that their offense history will have on the second-period punishment. We will therefore need to derive their choices by backwards induction.

Notationally, let

b = a rational offender’s benefit from committing a crime, which is assumed to be the same for all such offenders and is constant over the two periods;

h = social harm from a crime regardless of who commits it and in which period;

s _j = cost of a sanction to an offender, where j = 1 indicates a first offense, and j = 2 indicates a second offense, s _j ≥ 0;^[15]

c = unit cost to society of imposing s;^[16]

α = fraction of unknowing offenders in the population of potential offenders, α ∈ [0,1].

As noted, we assume that crimes are socially undesirable so that h > b, and that the enforcer’s goal is to minimize the total cost of crime, consisting of the harm plus enforcement costs, over the two-period time horizon.^[17] Initially, we will consider the case of perfect detection of crimes as this will illustrate the key results in the simplest possible manner. A subsequent section will show that the qualitative results carry over to the case of imperfect detection.

2.1 The Optimal Sanction Structure with Perfect Detection

We consider two possible sanction levels, low (s _L ) and high (s _H ), where s _H ≥ b > s _L ≥ 0. Thus, in a one-shot decision, a high sanction will deter a rational offender but a low sanction will not.^[18] This results in four possible penalty structures of the form (s ₁, s ₂):^[19]

1. (s _L , s _L ) uniform low

2. (s _H , s _H ) uniform high

3. (s _L , s _H ) rising

4. (s _H , s _L ) falling

We first derive the optimal behavior of potential offenders under each structure, and then compare the resulting social costs to determine which is cost-minimizing. This yields the following result:

Proposition 1

Penalty structure III (the rising structure) is optimal if and only if α ≥ α ^*, where

(1) α * = h + c s L h + c s H

The intuition for this result is as follows (a formal proof is in the Appendix). Consider first the behavior of unknowing offenders. As noted, these individuals will commit an offense in period one, but after having been penalized (which occurs with certainty in the current version of the model), will be deterred in period two, regardless of the penalty structure. Thus, the total social cost for each of these offenders is h + cs ₁, where s ₁ = s _L under structures I and III, and s ₁ = s _H under structures II and IV.

Now consider the behavior of rational offenders. This is somewhat more complicated because we are assuming that these offenders consider their lifetime payoffs, and so we need to use backwards induction to ensure time-consistency of their decisions. Figure 1 shows the game tree, with the offender’s two-period payoffs and aggregate social costs, respectively, listed at each of the four terminal nodes. The realized magnitudes of these costs will depend on the values assigned to s ₁ and s ₂ under the various penalty structures.

Figure 1:

Game tree for rational offenders over the two-period time horizon.

Consider first penalty structure I, the uniformly low structure. In this case, s ₁ = s ₂ = s _L < b. It follows that offenders are not deterred in period two regardless of their choice in period one. Hence, they will offend in period one given their anticipation of their later choice. The unique optimum is therefore (Commit, Commit), which results in social costs of 2(h + cs _L ) per offender over the two-period time horizon. Combining this with the costs for accidental offenders from above and weighting them appropriately yields overall social costs of ^[20]

(2) T C I = α ( h + c s L ) + ( 1 − α ) 2 ( h + c s L ) = ( 2 − α ) ( h + c s L )

Consider next penalty structure II, the uniformly high structure, which has s ₁ = s ₂ = s _H ≥ b. It follows that rational offenders will be deterred in period two regardless of their period-one behavior, and, as a result, they will also be deterred in period one. The unique optimum is therefore (Not commit, Not commit), which results in zero social costs. Overall social costs in this case therefore consist solely of the period-one costs for unknowing offenders, which are

(3) T C I I = α ( h + c s L )

The advantage of this structure is that it completely deters rational offenders; the disadvantage is that it involves a high punishment cost in period one for unknowing offenders. Either of these first two structures may therefore be preferred on cost grounds, depending on α.

Now consider the rising, or escalating structure, where s ₁ = s _L and s ₂ = s _H . Beginning in period two, an offender who committed the crime in period one will commit it again in period two if 2b − s _L − s _H > b − s _L , or if b > s _H . But since this does not hold by assumption, the offender will be deterred. By contrast, if he did not commit the act in period one, he will commit it in period two because b > s _L . Given these results, we move back to period one and find that the offender will commit the act in period one if b > s _L , which is true. Thus, the unique optimum is (Commit, Not commit), and social costs per rational offender are h + cs _L . Combining this with costs for unknowing offenders in this case gives the following overall social costs under the escalating structure:

(4) T C III = α ( h + c s L ) + ( 1 − α ) ( h + c s L ) = h + c s L

Both types therefore commit period-one offenses but neither commits period-two offenses. Comparison of (2) and (4) shows that TC _III ≤ TC _I for all α ≤ 1, which is due to the deterrence of rational offenders in period two under structure III. This rules out structure I as long as α < 1.

Finally, consider the declining penalty structure, where s ₁ = s _H and s ₂ = s _L . Beginning in period two, an offender who committed the act in period one will commit it again in period two if 2b − s _H − s _L > b − s _H , or if b > s _L , which holds. Thus, the offender will repeat the act. Conversely, if an offender did not commit the act in period one he will not commit it in period two if b < s _H , which also holds, and so he will be deterred. Thus, either the offender will commit the act in both periods, or in neither period. Moving back to period one, we find that the offender will commit the act in both periods if 2b − s _L − s _H > 0, or if

(5) ( b − s L ) + ( b − s H ) > 0

which may or may not hold. Thus, two outcomes are possible here: if (5) holds, the optimum is (Commit, Commit), whereas if (5) does not hold, the optimum is (Not commit, Not commit). Intuitively, the offender may choose to commit the act in period one, despite the harsh initial punishment, in order to gain access to the lower punishment in period two.^[21] In other words, he “buys” the right to pay the lower price by paying the higher price up front. Whether or not this is desirable depends on how large the price differential is. Social costs under the two possible outcomes are as follows: for (Commit, Commit) we have

(6) T C I V C = α ( h + c s H ) + ( 1 − α ) ( 2 h + c s L + c s H ) = h + c s H + 1 ( 1 − α ) ( h + c s L )

while for (Not commit, Not commit) we have

(7) T C I V N C = α ( h + c s H )

Comparison of (6) to (2) shows that TC _IV ^C < TC _I, while comparison of (7) to (3) shows that T C I V N C = TC _II. Thus, structure IV is (weakly) dominated.

This leaves structure II, the uniformly high sanction, and structure III, the rising sanction, as candidates for an optimum. The trade-off between them is as follows. A uniformly high punishment will deter rational offenders over both periods, but will result in costly punishment of unknowing offenders in period one. Conversely, a rising penalty structure will induce rational offenders to commit period-one crimes but will result in low-cost punishment of unknowing offenders while deterring them in period two. The choice between these structures therefore turns on the fraction of each type in the population. The escalating structure will be preferred if the fraction of unknowing offenders is large enough; i.e., if α is large enough for (1) to hold. This reflects a large scope for the educational function of law. Conversely, if α is small, little learning is possible and so the law should be aimed primarily at deterring rational offenders.

It remains to derive the optimal sanction levels. This involves choosing s _L and s _H to minimize costs under the applicable penalty structure, subject to the constraints that 0 ≤ s _L < b and b ≤ s _H . Specifically, the problem is to

(8) min s L , s H α ( h + c s H ) , i f α < α *   h + c s L , i f α ≥ α *  

subject to the stated constraints, where α ^* depends on s _L and s _H according to (1). Thus, the choice of the sanctions itself determines the ranges over which each of the penalty structures is cost-minimizing.

Note first that, within each range, it is optimal to lower the sanction as much as possible. This gives s L * = 0 and s H * = b . The impact of this choice on the threshold separating the two structures is ambiguous: lowering s _L increases the range over which the escalating structure is optimal, while lowering s _H decreases that range. However, the resulting piecewise cost curve is unambiguously lowered by reducing the magnitude of both sanctions as much as possible. The resulting threshold is given by

(9) α * = h h + c b

which continues to be between zero and one. The results of this section are illustrated in Figure 2, where the relevant segments of TC _II and TC _III are darkened.

Figure 2:

An escalating penalty structure is preferred when α > α ^*.

2.2 The Optimal Structure with Imperfect Detection

We now turn to the case where detection is imperfect. In particular, suppose that an offender is only caught with probability p < 1, which we will assume is known and equal over the two periods.^[22] We will also initially assume that it is fixed.

The principal complication created by imperfect detection is that an offender who is not caught in period one but offends again in period two will be treated as a first-timer if caught.^[23] In addition, the lowest punishment that will deter an offender in a one-shot decision must now be scaled upward to b/p. Thus, in this section we will assume that s _H ≥ b/p > s _L ≥ 0.^[24] Except for this change, the possible penalty structures are the same as above.

As above, we first consider the behavior of unknowing offenders. They will again commit an offense with certainty in period one, but if caught, will refrain from committing it again in period two. However, if they are not caught in period one (and hence not informed about the illegality of the act), they will commit it again in period two. Thus, the total expected cost for an unknowing offender over the two-period horizon is now

(10) p ( h + c s 1 ) + ( 1 − p ) ( 2 h + p c s 1 ) = ( 2 − p ) ( h + p c s 1 )

Note that this reduces to h + cs ₁ when p = 1.

As for rational offenders, the decision tree over the two-period horizon is more complicated than that in Figure 1 because for each decision to commit the act, the offender is caught with probability p and not caught with probability 1 − p. Figure 3 shows the resulting tree, again with the offender’s and society’s costs (respectively) listed at each terminal node. As before, we employ backwards induction to derive the rational offender’s optimal behavior over the two periods under each penalty structure.

Figure 3:

Game tree for rational offenders with imperfect detection.

It turns out that the basic results from the certainty case carry over to this one. Thus, we have

Proposition 2

When detection is imperfect, penalty structure III (the rising structure) is optimal if and only if α ≥ α ^*, where^[25]

(11) α * = h + p c s L h + p c s H

The logic of the proof of this result is the same as for Proposition 1, and so the details are again relegated to the Appendix.

As above, the determination of the optimal penalty structure in this case involves a comparison of the uniformly high structure, which results in total costs of

(12) T C I I = α ( 2 − p ) ( h + p s c H )

and the rising structure, which results in total costs of

(13) T C III = ( 2 − p ) ( h + p c s L ) .

(Note that these expressions reduce to (2) and (3), respectively, when p = 1.) Equating these expressions and solving for α yields the threshold in (11).

We next derive the optimal sanction levels as the solution to

(14) min s L , s H α ( 2 − p ) ( h + p c s H ) , i f α < α *   2 − p h + p c s L , i f α ≥ α *  

subject to the constraints that s _L < b/p and s _H ≥ b/p. Again, it is optimal to minimize the sanction within each range, which gives s L * = 0 and s H * = b / p .

The resulting value of α ^* is identical to (9), and its determination is illustrated in Figure 4. For sake of comparison, the dashed lines show costs when p = 1, which are uniformly lower.

Figure 4:

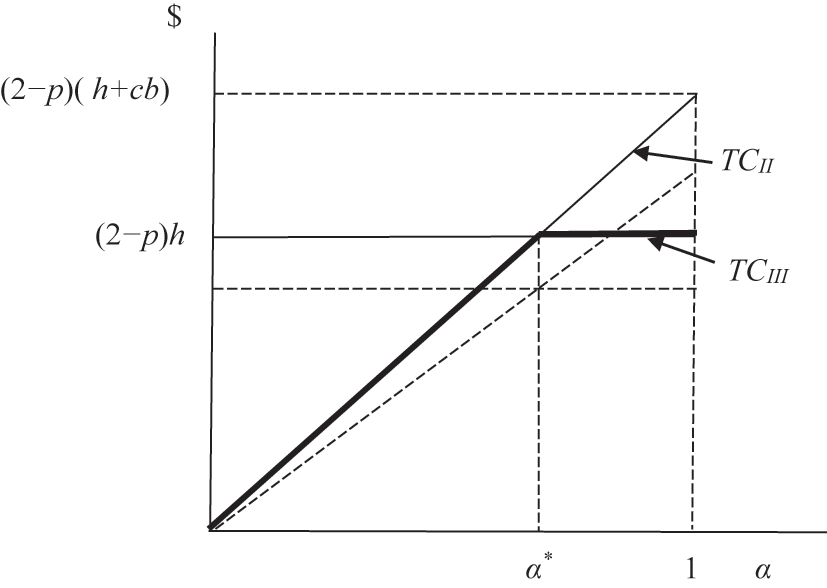
Ranges for the optimal penalty structure when p < 1.

3 Conclusions

This paper has explained the use of an escalating penalty structure as a device for informing otherwise law-abiding individuals about the illegality of certain acts, while simultaneously seeking to deter inveterate (rational) criminals from repeatedly committing those same offenses. Ideally, the latter would face a harsh punishment for a first offense as well, but given that the two types of offenders are indistinguishable, such a policy would subject unknowing offenders to excessive punishments when a slap on the wrist would adequately serve the educational purpose. An escalating scheme is therefore a second-best response when unknowing offenders who need only be caught once to deter future acts comprise a large enough fraction of all potential offenders. When optimal, such a scheme embodies the idea that ignorance of the law is at least a partial defense for wrongdoing, and that alerting these offenders to the illegality of their acts is sufficient to deter them forever after. It therefore achieves some deterrence at zero cost.

The relevance of this argument as an explanation for the pervasiveness of escalating penalty schemes is an empirical question as it depends on the extent of people’s lack of knowledge of the law, and the extent to which they are inclined to abide by it once they become informed. One suspects that this predominantly applies to non-violent offenses which are the by-product of risky but otherwise beneficial activities, where people are striving to pursue a private gain within the confines of the law but lack perfect knowledge of it. In other words, people are basically law-abiding. On the other hand, it seems inapplicable to individuals who, like the rational offender in Becker’s model, seek an advantage wherever one exists, including the commission of illegal acts when the punishment is light.

Although the current explanation is an appealing one, in all likelihood it misses some essential features of the issue. Possibly it is the case that the various explanations that have been put forth by economists collectively explain the popularity of rising sanctions. Alternatively, the policy may arise from a human impulse for forgiveness, coupled with a belief in (or hope for) redemption of wrongdoers, which are concepts that one usually associates with a moral rather than an economic basis for law.^[27]