Feasibility of multifunction calibration of H⁺-responsive glass electrodes in seawater (IUPAC Technical Report)

1 Introduction

Measurement of pH and the study of hydron transfer reactions in seawater are critical areas of marine chemistry, requiring a proper metrological approach.

Natural seawaters can be looked upon as multi-electrolyte solutions with typically high ionic strengths (I_m ≈ 0.67 mol kg⁻¹). Moreover, ion concentrations of the dissolved salts strongly influence the pH value, by changing both H⁺ concentration due to simultaneous equilibria (e.g., association with SO₄²⁻) and activity coefficients due to the complexity of the saline matrix.

The most common and fastest way of measuring pH in routine analysis is the classical potentiometric method. Glass electrodes are sensitive to H⁺. An electrochemical potential difference between the electrode surface and the sample solution is measured potentiometrically against a reference electrode of constant potential, also called an electrode of second kind, typically a silver–silver chloride electrode:

The potential difference which occurs in the cell varies linearly with pH according to the analytical law that relates the measured potential, E_cell, with the activity, a, of the ion H⁺, aH+, which is the Nernst equation [1], Eq. (1):

Here, k′ is the coefficient of lg(aH+) (slope), most commonly sub-Nernstian, implying that there might be a discrepancy between theory and fit, obtained from calibration of the setup with reference pH buffer solutions. Theoretically, the Nernst coefficient equals ln10RTnF ,where n represents the number of electrons exchanged per ion, F is the Faraday constant, R is the gas constant, and T is the thermodynamic temperature. Ecell0′ is the constant term (intercept), which corresponds to the sum of all constant terms that contribute to the cell potential and does not have the thermodynamic meaning of a standard potential, E⁰.

E 0 ′ and k′ are specific for each glass electrode and are determined through calibration with certified buffer solutions after linear regression of equation [1].

The cell potential is described by E_cell = (E_ref + E_lj) − E_g.el, where E_ref represents the reference electrode potential, E_lj is the liquid junction potential between the electrolytes of the two half-cells, and E_g.el is the glass electrode potential.

Buffer solutions recommended for calibration of pH instruments cover only pH measurements in dilute solutions (ionic strength, I_m ≤ 0.1 mol kg⁻¹ H₂O) [2]. Such certified reference buffers are widely available, and practitioners tend to use them for all-purpose measurements, i.e., even when they are not fit for the purpose of the measurement. Since seawater has a high ionic strength and ocean water pH varies worldwide in a very narrow range, instruments with well-adapted calibration strategies need to be used if exemplar pH data are to be obtained. The development of a rigorous calibration methodology is based on the availability of appropriate buffers in a matrix having a composition representative of the real samples. In such a way, the residual liquid junction potential appearing when standard solutions used for calibration are replaced by the tested real solution is minimized, thus reducing the uncertainty of pH measurement results.

Assignment of reference pH values to dilute (I_m ≤ 0.1 mol kg⁻¹) primary standard solutions relies on the measurement of Harned cell potentials, in conjunction with the Nernst equation and chloride ion activity coefficients, γCl−, assessed using the Debye–Hückel electrolyte solution theory complemented by the Bates–Guggenheim convention [2]. For high ionic strengths, the model fails, hence requiring other valid approaches for the calculation of mean and single-ion activity coefficients that consider enhanced electrostatic effects plus specific interactions, such as the Pitzer model, associated with a seawater matrix [3, 4]. A procedure parallel to the one adopted for dilute solutions is being followed, and experimental and model approaches (Pitzer) are undergoing validation. To this end, studies conducted since 1948 [5], [6], [7] until now [8], [9], [10] have led to the preference of 2-amino-2-(hydroxymethyl)propane-1,3-diol (Tris)–Tris·HCl buffers in a saline background.

Despite the importance of pH, conceptually defined as pH=−lg aH+ [2], measurement of seawater pH remains an issue for chemical oceanographers [1, 10, 11]. In this complex environment, various “pH” alternative quantities have been defined and measured in several ways by different users. Nevertheless the square quotes, “ ”, tend to be dropped and the same name, pH, has been mistakenly given to different measurands, e.g., pHT=− lg (mH+∗/m0), where m⁰ = 1 mol kg⁻¹ and mH+∗=limm→mSW[m(H+)+m(HSO4−)]. Here, mH+∗ represents the total hydrogen molality that is identical to the sum of the molalities of H⁺ and HSO₄⁻ in the limit of the pure synthetic seawater. The molalities m(H⁺) and m(HSO4−) are expressed in mol kg⁻¹ seawater. Sample measurement procedures, other than potentiometry, are increasingly being adopted, consequently hindering metrological traceability, leading to serious problems of the lack of comparability of results in time and in space.

The pH^T measurement option using UV–Vis spectrophotometry with m-cresol purple indicator has gained support as an alternative measurement procedure which, contrary to potentiometry which simply senses H⁺ (when electrodes have been properly selected in order to avoid interferences and mixed responses), senses both H⁺ and HSO4− species, the latter resulting from the association of H⁺ with SO₄²⁻ provided by the sodium sulfate Na₂SO₄, existing in seawater.

For the sake of harmonisation of seawater acidity measurements and to ensure the quality of results, it is urgent to clarify which are the recommended methods and procedures, thus avoiding the current unfortunate situation of confusion among oceanographers, chemists, and other experts and practitioners on which parameter is being considered, measured, reported, etc.

The Guide to Best Practices for Ocean CO₂ measurements [12] contains a reference procedure, SOP6a, describing the method to be used for the potentiometric determination of the pH of seawater on the total hydrogen ion concentration pH scale. However, the cited document recommends using in-house prepared Tris–Tris·HCl buffer solutions, and a measurement precision (i.e., not a total measurement uncertainty) that can reach 0.003 in pH^T is mentioned. Other studies [13] have been done using spectrophotometric calibration of electrodes but without an uncertainty statement. According to VIM [14], the metrological traceability is defined as a “Property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty.” It is thus clear that in the absence of a traceability chain, a complete uncertainty budget cannot be evaluated. That is why, for example, in the IOC/UNESCO Sustainable Development Goal Indicators, Methodology for 14.3.1 related to “Average marine acidity (pH) measured at agreed suite of representative sampling stations” [15] such measurements were identified as having an undefined quality but nevertheless considered useful in the identification of coastal ocean acidification hot spots and prioritizing future monitoring plans [16].

This work presents a study which aims to demonstrate the feasibility of using potentiometry to determine pH^T values by transposing the method applied for aqueous dilute media including an uncertainty budget evaluation. The proposed practice will contribute to establish comparability for the potentiometric assignment of both pH and pH^T values in the routine analysis of seawater samples by calculating the conversion factors between the different scales and also the equivalence of pH^T measurement results obtained with different techniques. The study is based on the use of high-order Tris–Tris·HCl reference buffer solutions prepared in a seawater background [8] and traceable to the Laboratoire de Métrologie et d’Essais (LNE) pH^T standard measurement procedure.

The assignment of such pH and pH^T values to reference buffer standards falls in the mission and scope of action of National Metrology Institutes, NMIs, which can certify the buffers for these kinds of quantities and make them available to the users who can then easily perform calibration of the pH meter setups in terms of the acidity parameter of their choice, E vs. pH or pH^T.

2 Experimental

3 Results and discussion

Three Tris–Tris·HCl buffer solutions were prepared in artificial seawater, S_p = 35. These buffers were characterized in terms of pH and pH^T using a primary pH system.

The pH values were calculated based on the experimentally measured acidity function and the Pitzer-modeled activity coefficient of chloride, represented in Eq. (2) by the first and second terms of the right side.

The free molalities of H⁺, HSO4− and SO₄²⁻ needed to apply the Pitzer model have been determined using the stoichiometric dissociation constant of hydrogen sulfate, K_m^*, with the literature value of 0.103 93 [20]. The asterisk denotes the constant’s representativeness for some specific ionic medium, here, the artificial seawater with the composition indicated in Table 2.

pH^T values were experimentally determined using the protocol described in the literature [17, 21], Eq. (3):

where E_cell is the potential of the Harned cell for the buffer, corrected to p(H₂) = 1 atm (101.325 kPa), the partial pressure of hydrogen gas used in electrochemistry in preference to 100 kPa; R and F are the gas and Faraday constants, respectively. E⁰* represents the standard potential of the Ag/AgCl electrode in pure ASW of the same nominal salinity. E⁰* differs from the well-known E⁰ defined as the standard potential of the Ag|AgCl electrode in pure water media and used for primary pH determinations. ωH2O represents the mass fraction of water and m⁰ is the standard molality, 1 mol kg⁻¹.

Table 3 presents the primary pH and pH^T values reported with assigned overall expanded uncertainty (k = 2, for a confidence level of approximately 95 %) that includes contributions from the characterization, long-term stability, and homogeneity of buffer solutions. For primary pH, the uncertainty contribution related to characterization neglects contribution coming from the activity coefficient of chloride.

The expanded uncertainty (k = 2) assigned to the measured pH values was estimated based on the global approach with the ISO 5725-2 document [19] using a pH 9 standard buffer solution as QA/QC. The different sources of uncertainty together with their estimation are given in Table 4. Intermediate precision [14] was issued from measurements performed on three series of three measurements.

The primary certified pH values were further compared with the results obtained using usual commercially available buffers with low ionic strength. This comparison revealed a difference greater than 0.1 pH, which is in good agreement with other published studies [22].

All pH values obtained with the pH meter are lower than the certified pH values, this difference being significantly greater than the expanded uncertainty. The existence of such a bias may come from an inappropriate calibration protocol and can be accounted for as a systematic error, due to the different ionic strengths affecting the liquid junction potential. Indeed, for calibration, several IUPAC documents recommend using buffer solutions that match the analyzed sample in terms of composition and ionic strength. However, when this is not possible, the users have two possibilities: (A) to integrate this bias into the result by performing the necessary correction or (B) to add it as a contribution to the overall uncertainty budget. The first option, (A), seams easier to apply, but in order to guarantee good data quality, several requirements must be satisfied:

1. ensure that the correction covers the range of seawater pH. To make this evaluation, measurements with solutions of different pH values need to be carried out.

2. choose a certified reference material representative of the seawater media and possibly traceable to SI [23], in order to ensure the SI traceability of the final pH results.

3. the operated correction has its own uncertainty that must be assessed and included in the overall pH uncertainty budget. The main sources contributing to the correction uncertainty would come from the standard solutions used to determine the correction, the reproducibility of measurement results, and the dispersion of the correction factors associated to their fluctuation in a studied pH range.

Table 6 summarizes the corrections to be applied for pH results in the seawater matrix and their associated expanded uncertainty (k = 2) for each studied glass electrode. The uncertainty of corrections is calculated with Eq. (4) and considers the uncertainty of the standard solution used to assess the value of correction and the repeatability obtained as standard deviation of the measured pH values.

Table 6 shows that for each studied electrode, the bias is constant within the studied range of pH between 7.8 and 8.4 and cannot be neglected as it is larger than the expanded uncertainty.

The second option, (B), applied mostly when the systematic errors are not completely understood or known, leading to much higher uncertainty, up to 0.2 pH, which is not fit for the intended purpose in several applications. The integration of the bias into the overall uncertainty budget could be done using the approaches described in different references [24], [25], [26].

A more rigorous approach would be to directly calibrate the pH meter with standard saline buffers, as recommended by the IUPAC. This was demonstrated with the second set of experiments.

Fig. 1:

Example of calibration curves for pH and pH^T potentiometric measurements with Unitrode 1. The symbols are used for (•) pH calibration with commercial dilute buffers, (○) pH calibration with Tris–Tris·HCl saline buffers and (□) pH^T calibration with saline Tris–Tris·HCl buffers. A zoomed version of the calibration curves is represented at the right-hand side of the figure.

The calibration slopes determined using this protocol showed that all the electrodes exhibit Nernstian behavior. To test the calibration efficiency, Buffer 2 solution was used as an unknown sample for pH and pH^T measurements.

Table 7 presents both pH and pH^T results obtained for Buffer 2 using the four electrodes and the associated expanded uncertainties calculated using the ISO 5725-2 document [19]. It shows excellent agreement between the values obtained with the combination electrodes for the reference primary values, which confirms that the selection of saline buffers to calibrate the pH electrode enables minimization of the systematic errors coming from liquid junctions. It has to be pointed out that measurements in the synthetic seawater matrix exhibit a good reproducibility, better than 0.002, and similar to the values attained for classical dilute buffers.

The consistency of the pH^T value with the reference primary pH^T value for this buffer documents the possibility to use the potentiometric method for direct determination of this quantity.

In 1988, an IUPAC recommendation [27] was published aiming at ensuring that measurements of different quantities used to assess seawater acidity, namely pH and pH^T, are comparable. Thus, it was recommended to calculate a parameter, f_H′, relating pH to pH^T, Eq. (5), that takes into account the systematic errors introduced by calibration with a low-ionic strength buffer solution.

In the present study, the dependency of the conversion factor between the acidity scales f_H′ to the electrode was evaluated.

Measurement results are sensitive to the type of liquid junction. The liquid junction potential is influenced by different factors, including the ionic strength (reflected by the difference of ionic strengths between reference buffer solutions and samples), geometry, and type of junction. Thus, the conversion factor should be calculated for each electrode, and based on the methodology proposed in the present work, a protocol can be relatively easily implemented for quality control of routine measurements.

Table 8 presents the f_H′ calculated based on the measurements done with the four combined glass electrodes and considering pH values obtained after calibration with saline buffers. The obtained values are represented graphically in Fig. 2.

Fig. 2:

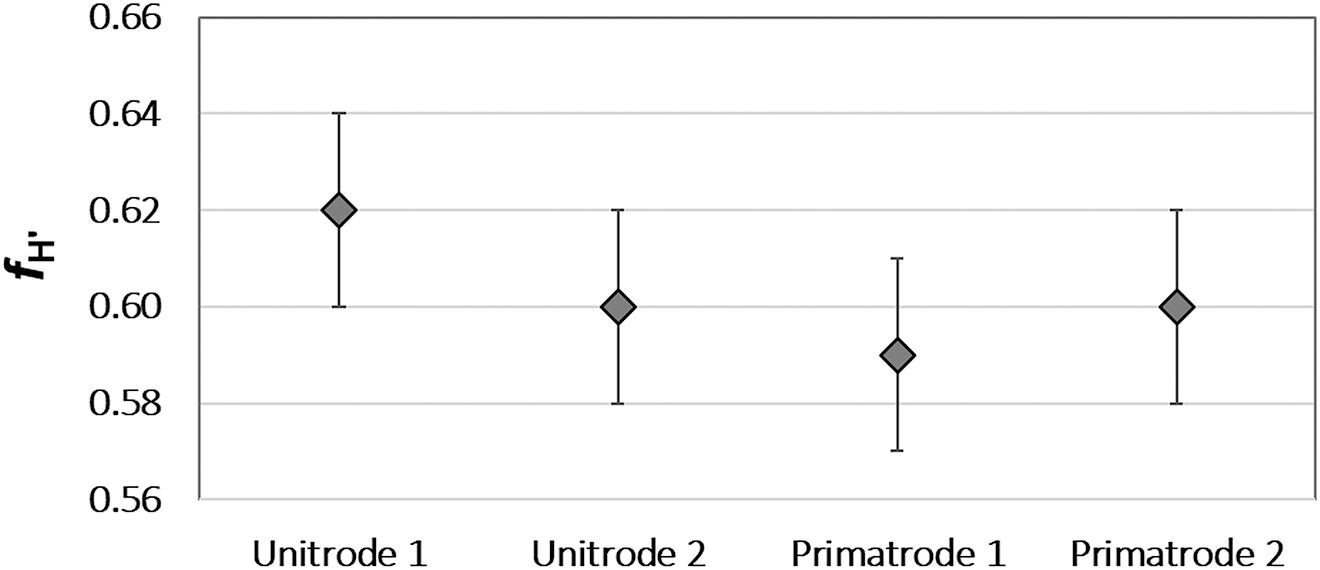
f _H′ values obtained by calibrating the combined glass electrodes used in this study with saline buffers. Error bars are expanded uncertainties (k = 2).

Table 8 and Fig. 2 show that f_H′ values obtained for the tested electrodes are not statistically different. Both pH and pH^T values are reported with uncertainties explained inter-alia by the control of the liquid junction, by perfectly matching the salinity of solutions used to standardize the electrodes to the salinity of the sample. The present study was conducted with new well-behaved electrodes. Quality of results is expected to decrease if aged electrodes and electrodes with different types of liquid junctions are used.

4 Conclusions

pH is one of the master variables that characterize seawater, used as an indicator of ocean acidification. Nevertheless, measurement of pH is still of major concern due, on one side, to the lack of recommended commercial buffer solutions to establish fit for purpose calibration for routine measurements and, on the other one, as a consequence of the proliferation of values pertaining to different measurands and different measurement procedures, often without clear identification.

The calibration with saline buffers characterized in terms of pH and ionic strength has not been a generalized practice so far because there is not yet such a recommendation supported on data and due to the lack of commercially available suitable calibrants. Also, the often indiscriminate use of different kinds of quantities for “pH” as well as potentiometric and spectrophotometric measuring methods and procedures has been hindering the traceability of values, hence making comparability of results in space and time impossible. The results of this study aim at overcoming these existing limitations.

For reliable QA/QC purposes, the availability of reference Tris–Tris HCl buffers in artificial seawater, of three different molality ratios, with assigned primary pH and pH^T values, provides the means for an adequate multi-point calibration approach to be used for pH meter setups, namely potentiometric devices equipped with quality assured, well-behaved glass electrodes. Conversion factors between the mentioned kinds of quantities can be applied to measurement results, thus solving the issues of comparability. Results with uncertainties of the same order of magnitude as those assessed for measurements in dilute solutions are reached.

Membership of sponsoring bodies

The membership of Division V (Analytical) at present is

President: Zoltán Mester; Past President: Jan Labuda; Vice President: Érico Marlon de Moraes Flores; Secretary: Takae Takeuchi; Titular Members: Medhat A. Al-Ghobashy, Derek Craston, Attila Felinger, Irene Rodriguez Meizoso, Sandra Rondinini, David Shaw. Associate Members: Jiri Barek, M. Filomena Camões, Petra Krystek, Hasuck Kim, Ilya Kuselman, M. Clara Magalhães, Tatiana A. Maryutina; National Representatives: Boguslaw Buszewski, Mustafa Culha, D. Brynn Hibbert, Hongmei Li, Wandee Luesaiwong, Serigne Amadou Ndiaye, Mariela Pistón Pedreira, Frank Vanhaecke, Winfield Earle Waghorne, Susanne Kristina Wiedmer.