Abstract
This study applies and compares different metrics and statistical methods to Paul’s letters and a variety of roughly contemporary texts also written in Greek. The primary objective is to elucidate the distinctions between several notable metrics and statistical methods of comparison to discern the relative impact of their application on our understanding of Paul’s letters vis-à-vis our comparanda. The secondary objective is to compare the findings from different statistical metrics in order to assess their relative merits as statistical tools for literary analysis. Such analysis extends to determining the statistical significance of different methods’ relative findings and extracting meaningful insights about each metric and method. We aim to determine which metrics are most accurate and provide the most useful information in comparing Paul’s letters to other types of literature such as Greco-Roman philosophy, formal oratory, and so-called Jewish apocalyptic literature. Such findings are especially salient when comparing these quantitative methods to qualitative conclusions from the biblical commentary traditions of literary analysis and comparison.
1 Introduction
This study applies and compares different metrics and statistical methods to Paul’s letters and a variety of roughly contemporary texts also written in Greek. The primary objective is to elucidate the distinctions between several notable metrics and statistical methods of comparison to discern the relative impact of their application on our understanding of Paul’s letters vis-à-vis our comparanda. The secondary objective is to compare the findings from different statistical metrics in order to assess their relative merits as statistical tools for literary analysis. Such analysis extends to determining the statistical significance of different methods’ relative findings and extracting meaningful insights about each metric and method. We aim to determine which metrics are most accurate and provide the most useful information in comparing Paul’s letters to other types of literature such as Greco-Roman philosophy, formal oratory, and so-called Jewish apocalyptic literature. Such findings are especially salient when comparing these quantitative methods to qualitative conclusions from the biblical commentary traditions of literary analysis and comparison.
By comparing computational methods and statistical techniques, this research enhances our understanding of stylometric analysis – a key approach in biblical and literary studies interested in empirical approaches – by suggesting the most effective applications for particular types of data and research questions, thereby yielding more accurate outcomes.[1] Its interdisciplinary approach bridges computational approaches with traditional biblical and literary scholarship, offering valuable insights into methodological strengths and limitations. To our knowledge, there is no such paper that engages such a mathematical comparison of methods. Appendices include a concise primer on our chosen methods as well as full results from each, for both the methodological novice and those seeking greater detail on our findings.
For these comparative analyses, this article uses the set of data features chosen and explicated in a 2016 monograph, Paul’s Letters and Contemporary Greco-Roman Literature: Theorizing a New Taxonomy.[2] In that monograph, Robertson makes the case for what are termed “top-down” features, namely features that are mostly second-order categories selected by the analyst trained in this area and hand-coded into Excel spreadsheets. This method is distinct from and contrasted to the so-called “bottom-up” feature selection comprised of vocabulary words and grammatical position, which can be machine-read and require no particular training or expertise in the text or culture in question. The latter (bottom-up) forms the foundation of traditional stylometry and related methods; the former (top-down) is mostly Robertson’s unique contribution to the field. Interested readers can find further discussion on theorizing second-order features in that monograph, where Robertson makes the case that top-down, second-order features both better capture an author’s distinct style and reveal interesting conclusions around comparing Paul’s letters with various contemporary texts.
The feature list is reproduced here, with all subsequent analyses using the hand-coded spreadsheets in Robertson 2016 that indicate the position of every feature occurrence in each text.
Appeals to Authority
Conversation
Prosópopoiia/Éthopoiia
Rhetorical Questions
Metaphors or Analogies
Anecdotes or Examples
Imperatives
Exhortation
Caustic Injunctions
Pathos
Irony or Satire
Hyperbole
Oppositions or Choices
Figurations of Groupness
Plural Inclusive versus Second Person Address
First Person Reflection
Analysis of Potential Questions or Objections
Systematic Argument
2 Methods Introduction
This section introduces each method, describing its function, relevant mathematical information, typical applications, and utility for our research questions, including strengths and limitations.
2.1 Euclidean Distance
A key method in author attribution, Euclidean distance aids stylometry by quantifying stylistic differences between texts and revealing textual patterns.[3] Euclidean distance calculates the separation between texts in a high-dimensional space, considering attributes like word frequency and sentence structure, both key stylometric criteria. Euclidean distance is defined by the following:
A simple example to illustrate: imagine you are standing at one corner of a room, and you want to get to the opposite corner. The Euclidean distance is the straight line that takes you directly to that corner. In a two-dimensional space, the formula to compute this straight-line distance between two points (say, Point 1(x 1, y 1) and Point 2(x 2, y 2)) is:
the Euclidean distance between two points P1(x 1, y 1) and P2(x 2, y 2) in a 3D space is given by the following formula:
So, the distance will be calculated as the square root of the sum of the squares of differences in both x and y coordinates.

In the context of stylometric analysis, Euclidean distance serves as a crucial tool for measuring the similarity or dissimilarity between texts based on their stylometric features.
Euclidean space is a geometric construct that provides a framework for understanding the relationship between texts in terms of their stylometric attributes. Stylometric features encompass various linguistic attributes such as word frequency, length, syntactic structures, and vocabulary richness. Each text can be represented as a point in a high-dimensional space, with each coordinate corresponding to the values of these stylometric features. Euclidean distance calculates the separation between these points, indicating the similarity or dissimilarity between texts.
Beyond stylometric analysis, Euclidean distance finds applications in various fields, including machine learning, data science, computer vision, image processing, GIS, and spatial analytics. It is used in algorithms like K-Nearest Neighbors, K-Means, and Principal Component Analysis for classification, clustering, and dimensionality reduction tasks. In computer vision, Euclidean distance aids in pattern recognition, similarity checks, and object detection. In GIS, it helps calculate geographical distances and perform spatial operations.
One of the most significant advantages of Euclidean distance is its simplicity and intuitive calculation method. It can be applied across different dimensions, making it highly versatile for multi-dimensional data analysis tasks, such as assessing the proximity of texts that are coded according to many different features. Additionally, it represents the most direct path between two points, facilitating easy interpretation and understanding.
Euclidean distance has limitations in stylometric analysis and other applications. One of its key limitations is that it is sensitive to scale. This means that the distances computed might be skewed depending on the units of the features. Another limitation is that as the dimensionality of the data increases, Euclidean distance tends to become less effective – a phenomenon known as the “curse of dimensionality.” Euclidean distance also does not work well when the data are sparse. The vectors should be non-zero in approximately 75% of attributes for Euclidean distance to be usable, a limitation that applies to any other norm-induced distance measures – such as Manhattan distance, discussed below. In textual data, other distance measures are typically preferred over Euclidean distance, because Euclidean distance depends on the vector’s magnitude instead of the angle between the vectors. The angle measure is more resilient to variations of occurrence counts between semantically similar terms, whereas occurrence counts and heterogeneity of word neighborhoods influence the magnitude of vectors. Even if the two text documents are far apart by Euclidean distance, in other words, there is still a chance that they are close to each other in terms of their context.
2.2 Cosine Similarity
Cosine similarity is a pivotal concept in mathematics and computational linguistics, measuring the similarity between vectors by calculating the cosine of the angle between them, commonly used in stylometry for comparing textual documents represented as Bag-of-Words (BoW) or Term Frequency-Inverse Document Frequency (TF-IDF) representations.[4] These representations transform textual documents into numerical vectors, where each element corresponds to the frequency or importance of a specific term within the document. By employing such representations, complex textual information is condensed into structured numerical formats, facilitating computational analysis and comparison. Cosine similarity operates by calculating the cosine of the angle between two non-zero vectors. Mathematically, it is expressed as the dot product of the vectors divided by the product of their magnitudes. This formulation enables the comparison of documents based on their directional similarity rather than their magnitudes, making it robust to variations in document lengths and word frequencies.
This similarity metric, ranging from −1 to 1, determines perfect alignment at 1, perfect dissimilarity at −1, and orthogonality at 0, making it robust for tasks like document clustering, authorship attribution, plagiarism detection, and information retrieval in natural language processing. In collaborative filtering-based recommendation systems, cosine similarity helps identify users or items having similar preferences. This technique is commonly used in movie, music, and product recommendations. Cosine similarity can also be used in text classification tasks such as spam detection, sentiment analysis, or topic modeling. Search engines use cosine similarity to match user queries with relevant documents by comparing the query vector to document vectors. This approach is commonly employed in information retrieval. Finally, cosine similarity is useful for clustering similar data points together, for example to group similar news articles or social media posts.
Cosine similarity is defined by the following:
Below is a simple example of cosine similarity:

Cosine similarity is a fundamental concept in mathematics and computational linguistics, offering a powerful tool for measuring the similarity between two vectors in an inner product space. In the context of stylometry, which concerns the quantitative analysis of literary style, cosine similarity serves as a cornerstone for comparing textual documents based on their vectorized representations.
Cosine similarity is easy to compute, especially with sparse matrices, and it can capture the overall similarity of the documents regardless of their length. Furthermore, cosine similarity is remarkably versatile. It can be applied not only to pairs of points but also to a diverse array of data types, including text documents, images, and numerical data. This versatility renders cosine similarity a powerful tool in various domains. However, it lacks consideration for the magnitude of vectors, focusing solely on their direction – it yields the same value regardless of the size of the vectors being compared as long as the angle between them is the same. This can be problematic when comparing vectors of different sizes, such as when comparing the risk profiles of different companies. It also does not capture the semantic meaning of words, making it less effective in understanding context. Additionally, in high-dimensional spaces where data are sparse, cosine similarity can be less reliable – it might not accurately reflect the true similarity between data points. Another limitation is that cosine similarity depends on vector normalization. Different normalization methods can yield different results, making comparisons sensitive to preprocessing choices.[5]
2.3 Jaccard Similarity
Jaccard similarity is a key tool in data analysis and information retrieval, quantifying the similarity between sets by comparing their overlap.[6] It calculates the ratio of intersecting elements to the total elements in the sets, providing a score from 0 to 1 where 1 signifies perfect similarity, and 0 indicates no common elements. It is defined by the following equation:
Here is a simple example of Jaccard similarity:

To calculate Jaccard similarity, the number of common elements (intersection) between two sets is divided by the total number of distinct elements (union) present in both sets. This ratio ranges from 0 to 1, where 1 signifies perfect overlap and 0 indicates no common elements.
Jaccard similarity is a fundamental concept in data analysis and information retrieval, offering a straightforward method to quantify the similarity between sets. Its applications span various domains, including text analysis, genomic analysis, social network analysis, and data deduplication. Jaccard similarity offers a different perspective in stylometric analysis, enabling the comparison of text documents based on their word content. By representing texts as sets of words and computing the ratio of intersection to union, analysts can discern similarities and differences in writing styles.
Jaccard similarity is a useful metric that has applications in various fields. One of its popular applications is in Natural Language Processing (NLP), where it is used to compare the similarity of two text documents. This technique is used in document clustering, plagiarism detection, and recommendation systems. Jaccard similarity is also used in recommendation systems based on collaborative filtering. It helps identify users with similar preferences by comparing the sets of items each user has interacted with. This way, recommendations can be made based on the preferences of similar users. In the field of genomic analysis, biologists use Jaccard similarity to measure the similarity between genetic sequences. By identifying common elements and mutations, Jaccard similarity aids in understanding evolutionary relationships. Social network analysis similarly uses Jaccard similarity to help analyze social networks by comparing the sets of friends or connections between individuals, thereby more easily identifying users with similar social circles. Finally, Jaccard similarity can also be used in data cleaning and preprocessing tasks. It can detect and remove duplicate records by comparing the sets of attributes within records to help in data deduplication, which is essential in maintaining data quality.
This metric is highly recommended for comparing sets of data for more conceptual reasons. One of the most significant advantages of using Jaccard similarity is that it is scale-invariant, which means that the size of the sets being compared does not affect the metric’s performance. This feature makes it a robust metric for comparing sets of varying sizes. Another advantage of Jaccard similarity is that it is easy to understand. Its simple concept makes it accessible to both data scientists and non-technical stakeholders. Finally, Jaccard similarity is versatile and can be applied to a wide range of data types and domains. This makes it a highly flexible metric for similarity measurement, from text data to biological data.
However, Jaccard similarity has certain limitations. First, it treats all elements equally without considering their frequency of occurrence. This means that words appearing multiple times in a text receive the same weight as words appearing only once, which can be a limiting factor as word frequency often carries important stylistic and authorial information. Second, Jaccard similarity is sensitive to the size of the sets being compared. Even slight variations in the size of the sets can lead to significant changes in the similarity score, which may not always accurately reflect the similarity between texts. Third, Jaccard similarity only considers the presence or absence of elements, completely ignoring their order or arrangement within the sets. This can be problematic in stylometric analysis, where the sequential arrangement of words, phrases, or stylistic features may carry important information about an author’s style. Finally, Jaccard similarity is based on set operations and does not capture semantic relationships between words, which is a significant limitation. Due to this, it may not effectively capture similarities between texts that use synonyms, paraphrasing, or related concepts.
2.4 Manhattan Distance
Manhattan distance is a practical measure in mathematics and computer science that is useful in grid-based systems where movement is constrained to horizontal and vertical paths. Stylometric analysis quantifies textual similarities by summing the absolute differences between corresponding linguistic features, aiding tasks like authorship attribution and route planning across various fields. It is defined by the following:
A simple example of Manhattan distance:

In stylometric analysis, Manhattan distance can be a valuable tool. By representing texts as vectors, with each element corresponding to the frequency of certain linguistic features (such as word occurrences, character n-grams, or syntactic structures), analysts can compute the Manhattan distance between these vectors to quantify the dissimilarity or similarity between texts.
Manhattan distance provides a straightforward and versatile method for measuring distance within grid-based systems, and its application extends beyond mathematical contexts to fields such as stylometry, where it facilitates the quantitative analysis of textual similarities and differences. Once the Pauline letters are represented as vectors in the feature space, the Manhattan distance can be calculated between pairs of letters. For each pair of letters attributed to different authors (e.g., Paul and another potential author), the Manhattan distance is computed by summing the absolute differences between the corresponding components of their feature vectors. Moreover, Manhattan distance is advantageous in scenarios where the data are naturally discrete or when the cost of movement along different dimensions is not uniform. This makes it a preferred choice in many practical applications, including route planning, image recognition, and clustering algorithms.
Manhattan distance is less affected by outliers compared to Euclidean distance. It assigns equal weight to each dimension and is more robust to variations in individual coordinates. If your data have outliers or you want to reduce the impact of extreme values, Manhattan distance might be a better choice. Also, you might want to consider the Manhattan distance if the input variables are not similar in type (such as age, gender, height, etc.). Due to the curse of dimensionality, we know that Euclidean distance becomes a poor choice as the number of dimensions increases. As it does not take any squares, it does not amplify the differences between any of the features. It also does not ignore any features.
Manhattan distance is a distance metric that treats each dimension or coordinate equally, regardless of the scale or importance of the feature. However, in cases where certain dimensions are more significant than others, this can lead to inaccurate distance measurements. Additionally, Manhattan distance restricts movement to horizontal and vertical paths, which can be inadequate for situations where diagonal movement is allowed or relevant. In such cases, other distance metrics like Euclidean distance might provide a better representation of true distances. It’s worth noting that while Manhattan distance excels in grid-based systems like city maps or game boards, it might not be the most appropriate metric for continuous or non-grid systems where movement is not constrained to specific paths.
2.5 Burrows’ Delta Method
Burrows’ Delta Method is a measure of the distance between a text whose authorship we want to ascertain and some other corpus. This method is designed to compare an anonymous text (or set of texts) to many different authors’ signatures at the same time.[7] More precisely, this method measures how the anonymous text and sets of texts written by an arbitrary number of known authors all diverge from the average of all of them put together.[8] Furthermore, the Delta Method gives equal weight to every feature that it measures, thus avoiding the problem of common words overwhelming the results.
There are several steps to execute Burrows’ Delta method. Initially, a reference corpus comprising texts authored by various individuals is essential. The corpus should represent a diverse array of writing styles and subjects to ensure its efficacy in capturing distinctive patterns of function word usage. Next, the text under examination, whose authorship needs identification, is compared to the reference corpus. This comparison involves calculating the frequency of function words in both the text being analyzed and the reference corpus. Common function words include “the,” “of,” “and,” “to,” “in,” “that,” “it,” “for,” “you,” and many others. Subsequently, statistical techniques are applied to gauge the discrepancy between the frequency distributions of function words in the analyzed text and the reference corpus. Burrows’ Delta, a statistical measure, is often utilized for this purpose. It quantifies the differences between the text’s function word usage and the average usage across the reference corpus.
A high delta (= difference) value suggests substantial dissimilarity between the text and the reference corpus in terms of function word frequency, indicating potential divergence in authorship. Conversely, a low delta value may imply similarity in writing styles and, thus, shared authorship characteristics. Finally, interpretation of the delta value demands careful consideration of contextual factors, including the size of the reference corpus, the genre and subject matter of the texts, and the potential presence of other linguistic features that could influence function word usage.
3 Data Analysis: Analyzing Paul’s Letters Using Multiple Methods
In this section, we outline the steps taken to compute and analyze the similarities and differences among various texts using the distance and similarity measures above: Euclidean distance, cosine similarity, Manhattan distance, Jaccard similarity, and Burrows’ Delta Method.
First, we defined the feature vectors for each text. These vectors represented the frequency of specific textual features. For instance, the feature vectors for texts like “1 Corinthians,” “2 Corinthians,” and others were compiled into a dictionary, allowing for structured and systematic analysis. Here is an example of the feature vectors defined for each text:

We then created DataFrames from this dictionary to facilitate computational analysis. Using the DataFrames, we calculated the Euclidean distance, cosine similarity, and Manhattan distance. The calculation of these metrics involved the following code:

The Jaccard similarity was calculated using a custom function designed to handle numerical arrays:

The code for Burrows’ Delta Method involved several steps, including calculating z-scores and delta scores:
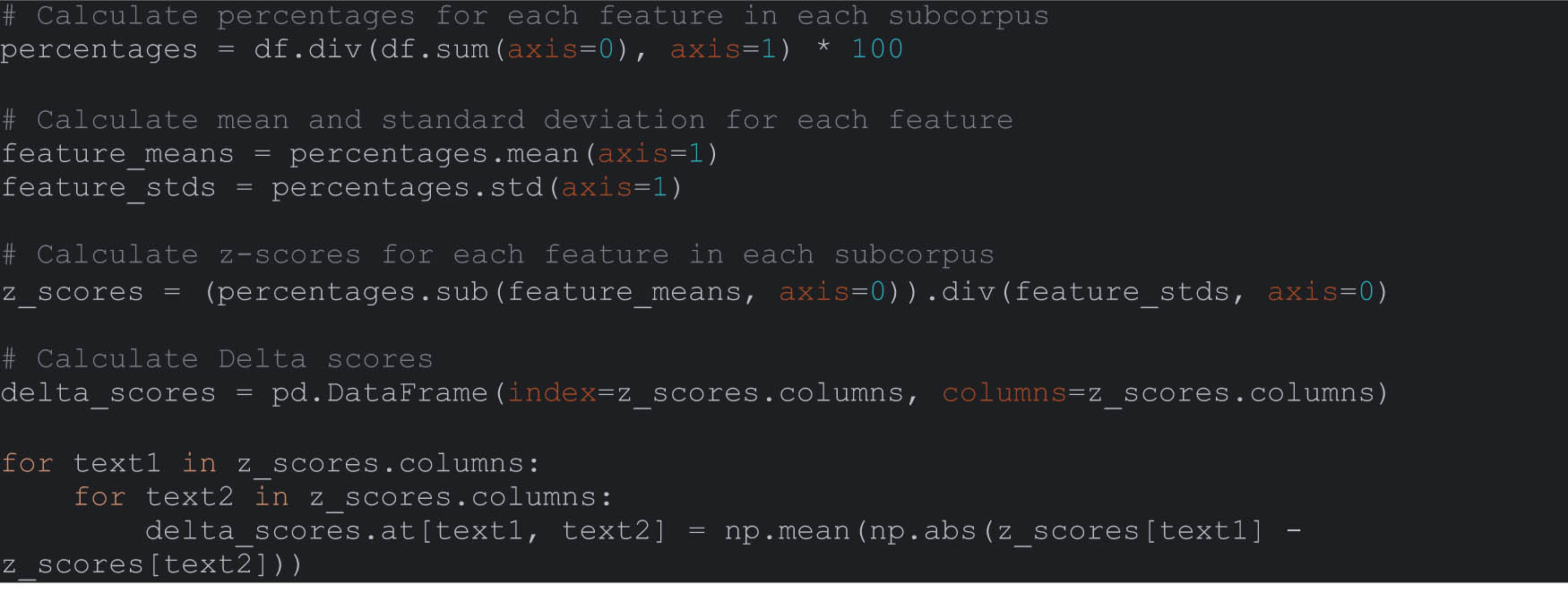
In this code, several Python libraries were used to allow for easy and accurate calculations.[9] , [10] The Pandas library was important for data manipulation and analysis, providing helpful data structures like DataFrame, which are essential for handling large datasets. NumPy was another library used in our code, supporting large, multi-dimensional arrays and matrices. It offers a collection of mathematical functions to operate on these arrays, which was needed for performing numerical operations and calculations necessary for the analysis. SciKit-Learn, a machine learning library, was used extensively to calculate the Euclidean distance, cosine similarity, and Manhattan distance. It offers simple and efficient tools, enabling ease of application of the various distance and similarity measures. Finally, the OS module, a standard utility in Python, was used to interact with the operating system. It aided with reading from and writing to files, ensuring smooth handling of input and output operations.
4 Discussion of Euclidean Distance Results
In analyzing the Euclidean distances between the various texts, we can draw several important conclusions about their relationships and differences. In our context, each text is represented as a point in a 20-dimensional space where each dimension corresponds to the frequency of a specific rhetorical feature – 20 features in all. By examining these distances, we can infer the degree of similarity or difference between the texts based on their rhetorical profiles.
The numerical range of Euclidean distances can vary significantly. We identify the maximum and minimum distances observed to set a context for what counts as high or low (Figure 1).

Euclidean distances.
Low distance pairs such as 1 Corinthians and Galatians, with a distance of 64.76, indicate a close relationship, suggesting that these texts share similar patterns and frequencies for the comparanda. Similarly, 2 Corinthians and 1 Thessalonians, with a distance of 30.54, show a high degree of similarity, indicating that their usage of the comparanda is quite alike.
Moderate distance pairs like Romans and 1 Corinthians, with a distance of 42.92, and Hebrews and 1 Corinthians, with a distance of 45.19, suggest some degree of similarity but also notable differences. These moderate distances imply that while there are commonalities between these texts, they are not as closely related as the low-distance pairs.
High-distance pairs, such as Epictetus’ Discourses, consistently show high distances from all other sets, with the smallest distance being 522.21 to 1 Corinthians. This indicates that Epictetus’ Discourses are quite distinct from the other texts in terms of the frequency and pattern of the comparanda. Additionally, Philemon and 1 Corinthians, with a distance of 89.32, suggest significant differences, making them less comparable.
Interpreting these distances, low numbers (0–30) indicate strong similarities between the sets, suggesting that the compared documents share a high frequency of similar comparanda. Moderate numbers (30–60) suggest a moderate level of similarity, implying that while there are commonalities, there are also notable differences. High numbers (60 and above) indicate significant dissimilarities. For instance, values above 500 suggest that the documents are quite different in terms of the chosen comparanda, which might reflect different authors, genres, or thematic focuses.
5 Discussion of Manhattan Distance Results
In the context of rhetorical feature analysis, Manhattan distance provides insights into the total difference in feature counts between texts. Unlike Euclidean distance, which considers the shortest path in a multi-dimensional space, Manhattan distance strictly follows the axes, offering a different perspective on textual similarity.[11]
Manhattan distances can range from 0 to a large number, depending on the feature counts. Lower values indicate greater similarity, while higher values denote greater dissimilarity. For practical analysis, distances closer to 0 can be considered indicative of high similarity, while larger values reflect more substantial differences (Figure 2).

Manhattan distances.
The low Manhattan distance of 98 between 1 Corinthians and Galatians suggests that these two texts have very similar frequency distributions of the selected comparanda, indicating a close thematic and rhetorical resemblance. This implies that these letters may share similar contexts or purposes, potentially reflecting common authorship or similar influences in their composition. Similarly, the distance of 110 between Romans and Galatians also reflects a high degree of similarity, supporting the notion that these letters are closely related in their use of rhetorical and thematic elements.
In the moderate distance category, the distance of 165 between 2 Corinthians and 1 Thessalonians suggests some differences in the frequency of comparanda, indicating that while there are shared themes, there are also divergent elements that differentiate these texts. This could reflect variations in the contexts or audiences addressed by these letters. The distance of 180 between Philippians and 1 Thessalonians further supports this, hinting at some shared rhetorical strategies but also distinct variations in content and style.
High Manhattan distances, such as the 1,236 between Epictetus’ Discourses and 2 Thessalonians, indicate significant differences in the frequency of comparanda. This suggests that these texts have distinct themes and rhetorical strategies, likely reflecting different genres, purposes, or authorship. Similarly, the high distance of 934 between Philodemus’ On Death and Epictetus’ Discourses highlights substantial differences in content and style, reinforcing the idea that these texts are markedly distinct in their rhetorical and thematic approaches.
The interpretation of these distance scores helps in understanding the degree of similarity and difference between the texts. Low distances (below 200) indicate high similarity in the frequency distributions of comparanda, suggesting thematic and rhetorical consistency. Moderate distances (200–600) suggest some similarities but also notable differences, reflecting a mix of shared and distinct elements. High distances (above 600) highlight significant differences in the frequency distributions, pointing to distinct themes, topics, and rhetorical strategies.
6 Discussion of Cosine Similarity Results
In analyzing the cosine similarity between the various texts, we can determine the degree of alignment or similarity in their rhetorical features. Cosine similarity measures the cosine of the angle between two vectors, which in this context are the rhetorical feature frequency vectors of the texts. Cosine similarity values range from −1 to 1, though in the context of text analysis, values typically range from 0 to 1. A similarity close to 1 indicates high similarity, while a value near 0 indicates low similarity. For example, values above 0.8 could be considered high, indicating strong similarity, whereas values below 0.3 could be considered low, indicating significant differences (Figure 3).

Cosine similarity scores.
High similarity pairs such as 1 Corinthians and Galatians, with a cosine similarity score of 0.945160, suggest a strong thematic and rhetorical congruence between these texts. This high score indicates that the frequency of the chosen comparanda in these letters is quite similar, pointing toward a consistently shared conceptual focus and rhetorical style. Similarly, the high similarity score of 0.900998 between Romans and Hebrews highlights a strong resemblance in the usage of comparanda, suggesting shared theological themes and rhetorical strategies, possibly indicative of similar authorship or common theological discourse. Another pair exhibiting high similarity is 1 Corinthians and Romans, with a score of 0.912127. This reinforces the idea that Paul’s letters share significant thematic and stylistic consistency. Such high similarity scores suggest that these letters might have been intended for similar audiences or contexts, emphasizing consistent theological teachings and rhetorical methods.
On the other hand, moderate similarity pairs such as 2 Corinthians and 1 Thessalonians, with a score of 0.782958, indicate some divergence in themes or rhetorical approaches while still maintaining notable similarities. This score suggests that while these letters share some common elements, there are also distinct differences possibly arising from different contexts or shifts in the author’s focus. Similarly, Philippians and Galatians, with a score of 0.724144, exhibit moderate similarity, suggesting shared rhetorical elements and theological points but also highlighting variations that could stem from different situational contexts.
Low similarity pairs, such as Philodemus’ On Death and 2 Thessalonians, with a score of 0.097214, indicate significant differences in the frequency of comparanda between these texts. This low score suggests that the rhetorical styles and themes in these works are very different, reflecting distinct genres or thematic focuses. Similarly, the low similarity score of 0.334328 between Epictetus’ Discourses and 2 Thessalonians perhaps underscores the contrast between the philosophical nature of Epictetus’ work versus the more religious content of 2 Thessalonians.
In interpreting these similarity scores, high similarity (0.8–1) indicates a high degree of thematic and rhetorical consistency, suggesting common authorship, similar audience, or consistent theological focus. Moderate similarity (0.5–0.8) suggests shared elements with notable differences, possibly arising from different writing contexts or shifts in rhetorical strategy. Low similarity (0–0.5) highlights significant differences in content and style, indicating distinct themes, purposes, or rhetorical techniques, and potentially different authors. It is important to note that there is no universally defined threshold for determining what constitutes a low or high cosine similarity score. The classification of a score as high or low is contingent upon the specific data being analyzed and is derived from internal comparison to other scores instead of an objective bar for significance.
7 Discussion of Jaccard Similarity Results
The Jaccard similarity index provides a different perspective on the relationship between texts by focusing on the presence or absence of specific features rather than their frequency. In this context, the sets are the rhetorical features present in each text. Jaccard similarity ranges from 0 to 1, where 0 indicates no common features and 1 indicates identical feature sets (Figure 4).

Jaccard similarity scores.
High similarity pairs include 1 Corinthians and Galatians with a Jaccard similarity score of 0.579618. This relatively high score indicates a significant overlap in the presence of comparanda between these two letters, suggesting that similar themes and rhetorical elements are prominent in both. Another high similarity pair is 4 Maccabees and Galatians, which have a Jaccard similarity score of 0.571429. This high similarity points to common rhetorical or thematic elements in these texts, despite their different contexts.
Moderate similarity pairs include 2 Corinthians and 1 Thessalonians, which have a Jaccard similarity score of 0.378571. This score suggests a moderate level of overlap in the comparanda used, indicating some shared themes or rhetorical strategies but also notable differences. Another moderate similarity pair is Philippians and 1 Thessalonians, with a Jaccard similarity score of 0.513158. This score reflects a moderate degree of overlap, hinting at shared but not identical themes or rhetorical approaches.
Low similarity pairs include Philodemus’ On Death and Epictetus’ Discourses, with a Jaccard similarity score of 0.019305. This very low similarity indicates minimal overlap in the comparanda, suggesting significant differences in content and style. Another low similarity pair is Philodemus’ On Death and 2 Thessalonians, which have a Jaccard similarity score of 0.148649. Similarly, a low similarity score highlights substantial differences between these texts.
High similarity scores (0.4–0.6) indicate a significant overlap in the presence of comparanda, suggesting shared themes, topics, or rhetorical strategies. Moderate similarity scores (0.2–0.4) suggest a moderate degree of overlap, indicating some common elements but also substantial differences. Low similarity scores (0–0.2) highlight minimal overlap, pointing to distinct differences in themes, topics, and rhetorical strategies.
8 Discussion of Burrows’ Delta Method Results
In Burrows’ Delta method, lower scores indicate greater stylistic similarity, while higher scores suggest more substantial stylistic differences. Each cell in the matrix represents the delta score between two texts (Figure 5).

Burrows’ delta method scores.
The delta score between 1 Corinthians and Galatians is 0.512, indicating a high degree of stylistic similarity. This suggests that the two texts share many stylistic features, possibly reflecting similar authorship or a close temporal or contextual relationship. The score between Hebrews and 1 Corinthians is 0.676, also suggesting a significant stylistic similarity. These low delta scores, ranging from 0.512 to 0.800, suggest that the texts compared have a high degree of stylistic similarity. For instance, texts like 1 Corinthians and Galatians (0.512) and 1 Corinthians and Hebrews (0.676) might have been written by the same author or in a similar style.
In the realm of moderate similarity pairs, the delta score between 1 Thessalonians and 2 Corinthians is 0.837, indicating a moderate stylistic difference. This suggests that while there are some differences in stylistic features, the two texts are still relatively similar compared to others. The score between Romans and Galatians is 0.656, showing moderate similarity, which might reflect shared authorship or thematic connections. These medium delta scores, ranging from 0.800 to 1.100, indicate moderate stylistic differences. Texts in this range, such as 2 Thessalonians and Romans (0.855), while not identical in style, share some common stylistic features. This might indicate that different authors are writing in a similar style or that the same author is writing in different contexts.
Low similarity pairs include Epictetus’ Discourses and 1 Thessalonians, with a delta score of 1.303, indicating substantial stylistic differences. This is expected as these texts likely belong to different genres and authors. Similarly, the score of 1.084 between Aelius Aristides’ Panathenaicus and 1 Corinthians reflects significant stylistic differences, which could be attributed to different authorships as well as the highly different contexts and social purposes. High delta scores, ranging from 1.100 and above, reflect significant stylistic differences. Examples such as Epictetus’ Discourses and 1 Thessalonians (1.303) or Aristides’ Panathenaicus and 1 Corinthians (1.084) suggest different authors, genres, or contexts, highlighting distinct stylistic features.
9 Notable Similarities and Divergences
The visualizations and detailed analysis of textual similarities and divergences across different metrics provide a comprehensive understanding of the relationships between the texts. By examining the top five and bottom five similarity and distance scores, we can draw several notable insights and conclusions.

Graph of the top five pairs of texts that are most similar according to each method.

Graph of the bottom five pairs of texts that are least similar according to each method.
The high similarity between 1 Corinthians and Galatians is evident across multiple metrics, including cosine similarity, Jaccard similarity, and Burrows’ Delta Method. This indicates that these texts share a significant number of common features and have a similar distribution of these features. For instance, the cosine similarity score between these texts is among the highest, reflecting their close alignment in terms of feature vectors. Similarly, the Jaccard similarity score shows a substantial overlap in features, while the Burrows’ Delta score indicates minimal stylistic differences. The consistent high similarity scores across different metrics suggest that 1 Corinthians and Galatians are thematically and stylistically close. This is consistent with the known historical and contextual connections between these letters, both written by Paul addressing similar issues in early Christian communities.
Conversely, Epictetus’ Discourses consistently shows high distances and low similarity scores with other texts across all metrics. For example, it has a high Euclidean distance of 522.21 with 1 Corinthians and a low Jaccard similarity of 0.061 with 2 Corinthians. This indicates that Epictetus’ Discourses is markedly different from the other texts in terms of both feature counts and distributions, as well as stylistic elements. The consistent identification of Epictetus’ Discourses as an outlier across multiple metrics highlights its unique characteristics and suggests that it may belong to a different genre or context compared to the other texts analyzed.[12]
The analysis also reveals that 1 Corinthians and 2 Corinthians have a close similarity across various metrics. For instance, their Euclidean distance is relatively small, indicating that the overall magnitude of differences in feature counts between these texts is minimal. Their high cosine similarity score further supports this, showing that the direction of their feature vectors is closely aligned. Additionally, the Jaccard similarity score indicates a substantial overlap in features, reflecting the shared themes and stylistic elements. This high degree of similarity is expected given that both letters were written by Paul to the same community, addressing related issues.
Another notable finding is the similarity between 1 Thessalonians and Philippians. These texts show high similarity across metrics, with particularly high Manhattan and Euclidean distance scores, suggesting minimal differences in feature magnitudes. The Jaccard similarity score highlights a significant overlap in features, consistent with the expectation that these letters, written by the same author to the same community, would be thematically and stylistically similar. Furthermore, Romans and Hebrews show a high similarity score across cosine similarity, Jaccard similarity, and Burrows’ Delta Method, indicating a significant overlap in themes and stylistic features. The Euclidean and Manhattan distances between these texts are moderate, suggesting that while there are differences in feature magnitudes, the overall distribution patterns are similar. This relationship may reflect shared theological themes or stylistic influences between these texts.
On the other hand, Philemon shows lower similarity scores and higher distance measures with most other texts. For instance, its Jaccard similarity with 1 Corinthians is very low, reflecting fewer shared features. The Euclidean and Manhattan distances are also relatively high, indicating more substantial differences in feature counts. This suggests that Philemon may have a unique set of features, or a different style compared to the other texts analyzed.
The bottom five similarity scores highlight texts with minimal overlap or significant differences. For example, the low similarity between Philemon and Seneca’s Natural Questions across multiple metrics underscores the distinct thematic and stylistic elements of these texts. Similarly, the high Euclidean and Manhattan distances between Epictetus’ Discourses and other texts further emphasize its unique characteristics and outlier status.
Triangulation, where three or more methods indicate high similarity between the same pairs of texts, further validates these findings. For instance, the high similarity between 1 Corinthians and Galatians is supported by cosine similarity, Jaccard similarity, and Burrows’ Delta Method, providing robust evidence of their close relationship. Similarly, the outlier status of Epictetus’ Discourses is consistently highlighted across all metrics, reinforcing its distinctiveness.
The visualizations illustrate these patterns clearly. The top five similarity scores graph shows texts like 1 Thessalonians with high similarity across multiple metrics, indicating its close relationship with multiple other texts. In contrast, the graph of the bottom five similarity scores highlights texts like Epictetus’ Discourses and Philemon, which show significant differences from others. The graphs are plotted on a log scale to effectively represent the wide range of similarity and distance scores, allowing for a clearer visualization of both small and large values. Using a log scale helps to compress the range, making it easier to compare values that vary by order of magnitude. This approach is particularly useful in text analysis, where the similarity and distance measures can differ significantly between text pairs. For those interested, Appendix B includes all pairs, providing a complete overview of the relationships among the analyzed texts.
10 Conclusion
The comprehensive analysis of Paul’s letters using multiple similarity and distance measures, including Euclidean distance, cosine similarity, Manhattan distance, Jaccard similarity, and Burrows’ Delta Method, reveals significant insights into the textual and stylistic characteristics of these epistles. This study underscores the importance of employing diverse analytical methods to capture the nuanced relationships between texts. Each metric highlighted different aspects of similarity and dissimilarity, which can provide a multi-faceted understanding of the letters attributed to Paul.
The application of Euclidean distance provided a measure of overall dissimilarity where magnitude matters, revealing significant differences between texts such as Epictetus’ Discourses and others, emphasizing the unique feature distribution of this text. Cosine similarity, which is ideal for documents with varying lengths, showed high similarity between 1 Corinthians and Galatians, suggesting strong thematic and rhetorical consistency. This consistency was further evidenced by high Jaccard similarity scores, indicating significant overlap in the presence of comparanda, such as between 1 Corinthians and Hebrews. Manhattan distance, known for its robustness to outliers, highlighted consistent feature count differences, particularly between 1 Corinthians and Philemon, suggesting divergent themes or rhetorical approaches. Burrows’ Delta Method, focusing on stylistic features, showed high similarity scores between Romans and Hebrews, indicating shared authorship or thematic connections.
These findings can usefully deeper insights into the Pauline corpus beyond what traditional qualitative analysis can offer. By quantitatively measuring the similarities and differences among Paul’s letters, we can make more informed assertions about their authorship, thematic coherence, and rhetorical strategies. For instance, the consistently high similarity scores between certain letters reinforce the argument for their inclusion in Paul’s authentic corpus. In contrast, others, like 2 Thessalonians, show significant stylistic differences, supporting the hypothesis of different authorship.
The implications of these findings extend to biblical scholarship, textual criticism, and historical theology. They offer a robust framework for analyzing ancient texts, combining computational methods with traditional literary analysis. This dual approach not only enhances our understanding of Paul’s letters but also provides a model for studying other corpora with similar complexity. Furthermore, putting these methods side by side allows us to triangulate findings, providing a more reliable and comprehensive view of the texts. The integration of various metrics reveals patterns and relationships that might be overlooked when using a single method. For example, while Euclidean distance highlights overall dissimilarities, cosine similarity, and Jaccard similarity focus on thematic and pattern overlaps, offering a balanced perspective. Ultimately, this study illustrates the value of combining quantitative and qualitative approaches in textual analysis. It shows that by leveraging multiple methods, researchers can uncover richer, more nuanced insights into ancient texts, enhancing our understanding of their historical and literary contexts.
Acknowledgements
Our thanks to the UNH College of Liberal Arts Dean’s Office, for consistent support around student-faculty undergraduate research. Additional thanks to Erich Pracht for his ongoing intellectual and logisical support.
-
Funding information: This project was partially supported by the UNH Hamel Center for Undergraduate Support, through an Undergraduate Research Award during the summer of 2024.
-
Author contributions: Alessandra Luce researched and compared the different statistical methods, ran the primary statistics, and drafted the majority of the paper. Paul Robertson provided the initial conceptual underpinnings, aided in the drafting and editing of Luce s sections, and drafted and edited other substantial sections of the paper.
-
Conflict of interest: Authors state no conflict of interest.
Euclidean Distance
What it provides: Euclidean distance measures the “straight-line” distance between two points in a multi-dimensional space. It is a straightforward, intuitive way to understand how similar or dissimilar two texts are based on their feature frequencies.
Why use it: It is widely used in various fields such as pattern recognition, machine learning, and bioinformatics due to its simplicity and interpretability. Ideal for continuous data where the magnitude of differences is important.
Where it is used: Clustering algorithms like k-means. Nearest neighbor searches.
How it calculates the score: By taking the square root of the sum of the squared differences between corresponding feature values in two vectors (texts).
Why it finds different things: Euclidean distance emphasizes the absolute differences in feature magnitudes, making it sensitive to large variations in any feature. It doesn’t consider the direction of differences, only their magnitude, so texts with similar feature distributions but different scales might appear very different.
Cosine Similarity
What it provides: cosine similarity measures the cosine of the angle between two vectors in a multi-dimensional space, reflecting the orientation rather than the magnitude.
Why use it: Effective for text analysis where the focus is on the similarity in the direction of feature vectors, regardless of their magnitude. Useful when dealing with high-dimensional sparse data, common in text mining.
Where it is used: Information retrieval and text mining. Document clustering and classification.
How it calculates the score: By dividing the dot product of two vectors by the product of their magnitudes.
Why it finds different things: cosine similarity captures the similarity in the shape of the feature distribution, making it robust to differences in text length. It is less affected by the absolute number of features, focusing instead on the relative distribution.
Jaccard Similarity
What it provides: Jaccard similarity measures the similarity between two sets, calculated as the size of the intersection divided by the size of the union of the sets.
Why use it: It is particularly useful for binary or categorical data where you want to know how many features are shared between two texts. Helps in scenarios where the presence or absence of features is more significant than their frequency.
Where it is used: Set-based comparisons, such as in market basket analysis and clustering.
How it calculates the score: By dividing the intersection of the sets (common features) by the union of the sets (total features present in either text).
Why it finds different things: Jaccard similarity focuses on shared features, ignoring how often they occur. Suitable for tasks where the overlap of features, rather than their frequency, is crucial.
Manhattan Distance
What it provides: Manhattan distance, also known as L1 distance or city block distance, measures the sum of the absolute differences between the features of two texts.
Why use it: Simple and intuitive, often used when data can have outliers or when the absolute differences are meaningful. It is robust to small changes in feature values and useful for categorical and ordinal data.
Where it is used: Various machine learning algorithms and optimization problems. Clustering and nearest neighbor searches in grid-based systems.
How it calculates the score: By summing the absolute differences between corresponding features in two vectors (texts).
Why it finds different things: Manhattan distance is more sensitive to individual feature differences than Euclidean distance. It is less affected by large differences in a single feature, providing a more balanced measure of overall dissimilarity.
Summary of Why Different Metrics Find Different Things
Data Emphasis: Different metrics emphasize different aspects of the data. Euclidean distance emphasizes overall magnitude, while cosine similarity focuses on distribution patterns, Jaccard similarity on shared features, and Manhattan Distance on absolute differences.
Sensitivity to Scale: Euclidean distance is sensitive to the scale of features, whereas cosine similarity is not. This can lead to different interpretations of similarity.
Feature Presence vs Frequency: Jaccard similarity considers only the presence of features, ignoring their frequency, which contrasts with the other metrics that consider both presence and frequency.
Handling of Variability: Manhattan distance handles variability differently than Euclidean distance, being less sensitive to large differences in any single feature, which can lead to different results in texts with outlier features.
Euclidean Distance
| 1 Thess & Phil: 11.0 | 1 Thess & Damascus: 56.089 |
| 1 Thess & Philem: 15.556 | Philo Piety & Seneca: 56.107 |
| Philem & Phil: 16.155 | Arist Pan & Gal: 56.205 |
| 1 Thess & Gal: 17.493 | Arist Pan & Romans: 56.93 |
| 4 Macc & Gal: 18.385 | Arist Pan & Seneca: 57.637 |
| Philem & Philo Death: 18.466 | Phil & Damascus: 57.922 |
| Gal & Phil: 19.875 | 1 Cor & 2 Cor: 58.898 |
| 1 Thess & Philo Death: 20.518 | Damascus & Hebrews: 59.515 |
| Gal & Seneca: 21.237 | Philem & Philo Piety: 60.175 |
| 1 Thess & 2 Thess: 21.817 | 2 Cor & Hebrews: 60.374 |
| Phil & Philo Death: 22.136 | Romans & Philem: 60.63 |
| 2 Thess & Philem: 22.316 | 2 Cor & Arist Pan: 61.27 |
| 2 Cor & Gal: 22.517 | 2 Thess & Philo Piety: 61.879 |
| 2 Thess & Phil: 23.087 | Philo Death & Damascus: 62.442 |
| 4 Macc & Philo Death: 23.302 | Gal & Hebrews: 62.738 |
| 4 Macc & Seneca: 24.434 | Seneca & Hebrews: 62.746 |
| 2 Thess & Gal: 24.454 | 4 Macc & Hebrews: 63.166 |
| 1 Thess & 4 Macc: 24.576 | Seneca & Damascus: 63.348 |
| Gal & Philo Death: 26.134 | 1 Cor & Seneca: 63.443 |
| Gal & Philem: 27.055 | 1 Thess & Arist Pan: 63.585 |
| 4 Macc & Phil: 27.875 | Arist Pan & Damascus: 64.117 |
| 2 Thess & Philo Death: 28.688 | Arist Pan & Philo Death: 64.234 |
| 2 Cor & Phil: 29.155 | Arist Pan & Philo Piety: 64.498 |
| 2 Thess & Seneca: 29.411 | Arist Pan & Hebrews: 64.645 |
| 1 Thess & Seneca: 30.545 | 1 Cor & Gal: 64.761 |
| 2 Cor & 1 Thess: 30.545 | Arist Pan & Phil: 66.257 |
| 2 Cor & Romans: 31.733 | Philem & Damascus: 67.335 |
| 2 Cor & 4 Macc: 31.859 | 2 Thess & Damascus: 67.35 |
| 4 Macc & Philem: 32.558 | Philo Piety & Hebrews: 68.666 |
| Phil & Seneca: 32.68 | 1 Cor & 4 Macc: 69.34 |
| Philo Death & Seneca: 33.347 | 2 Thess & Arist Pan: 70.05 |
| 2 Cor & Seneca: 34.351 | 1 Cor & Arist Pan: 70.534 |
| 2 Thess & 4 Macc: 34.756 | Arist Pan & Philem: 71.561 |
| Philem & Seneca: 36.565 | 1 Cor & Damascus: 72.979 |
| Gal & Romans: 37.31 | 1 Thess & Hebrews: 74.445 |
| 2 Cor & 2 Thess: 40.286 | 2 Thess & Hebrews: 76.105 |
| Romans & Seneca: 40.361 | Phil & Hebrews: 76.44 |
| 2 Cor & Philem: 40.583 | 1 Cor & Phil: 78.899 |
| 2 Cor & Philo Death: 40.841 | 1 Cor & 2 Thess: 79.145 |
| 4 Macc & Romans: 41.061 | 1 Cor & Philo Piety: 79.253 |
| 4 Macc & Philo Piety: 41.557 | 1 Cor & 1 Thess: 79.272 |
| Romans & Hebrews: 42.308 | Philo Death & Hebrews: 80.753 |
| 1 Cor & Romans: 42.919 | 1 Cor & Philo Death: 85.761 |
| 1 Cor & Hebrews: 45.188 | Philem & Hebrews: 86.983 |
| 4 Macc & Arist Pan: 45.266 | 1 Cor & Philem: 89.32 |
| Philo Death & Philo Piety: 46.195 | 1 Cor & Epict Disc: 522.208 |
| 2 Cor & Damascus: 46.765 | Epict Disc & Hebrews: 534.134 |
| Philo Piety & Damascus: 47.149 | Epict Disc & Romans: 551.57 |
| Gal & Philo Piety: 48.425 | Arist Pan & Epict Disc: 557.525 |
| Gal & Damascus: 50.695 | Epict Disc & Damascus: 558.563 |
| 4 Macc & Damascus: 51.498 | Epict Disc & Seneca: 560.835 |
| 1 Thess & Romans: 51.595 | Epict Disc & Philo Piety: 563.052 |
| Romans & Phil: 51.682 | 2 Cor & Epict Disc: 564.282 |
| Romans & Damascus: 51.807 | 4 Macc & Epict Disc: 566.762 |
| Romans & Philo Piety: 52.393 | Epict Disc & Gal: 569.678 |
| 1 Thess & Philo Piety: 53.038 | 1 Thess & Epict Disc: 581.917 |
| 2 Cor & Philo Piety: 53.74 | Epict Disc & Philo Death: 582.27 |
| 2 Thess & Romans: 53.889 | Epict Disc & Phil: 582.421 |
| Phil & Philo Piety: 54.406 | 2 Thess & Epict Disc: 584.33 |
| Romans & Philo Death: 55.651 | Epict Disc & Philem: 590.628 |
Cosine Similarity
| 1 Cor & Gal: 19.06 dg | 2 Thess & Seneca: 51.45 dg |
| Gal & Hebrews: 21.37 dg | 2 Thess & Hebrews: 51.56 dg |
| Gal & Romans: 22.84 dg | 1 Thess & Philem: 51.76 dg |
| 1 Cor & Romans: 24.2 dg | 1 Cor & Damascus: 52.04 dg |
| Romans & Hebrews: 25.71 dg | 1 Cor & Philem: 52.08 dg |
| 4 Macc & Arist Pan: 27.48 dg | Arist Pan & Seneca: 52.55 dg |
| 2 Cor & Romans: 28.0 dg | 1 Cor & 2 Thess: 52.89 dg |
| 1 Cor & Hebrews: 29.09 dg | 1 Thess & Seneca: 53.11 dg |
| 2 Cor & Gal: 30.12 dg | 1 Thess & Arist Pan: 54.0 dg |
| 1 Cor & 2 Cor: 30.54 dg | Arist Pan & Damascus: 54.03 dg |
| Philo Death & Philo Piety: 30.76 dg | 1 Thess & Philo Piety: 54.11 dg |
| 1 Thess & Hebrews: 31.9 dg | 1 Thess & Epict Disc: 54.28 dg |
| 4 Macc & Hebrews: 32.91 dg | 2 Thess & Gal: 54.8 dg |
| 4 Macc & Gal: 33.41 dg | Gal & Philem: 56.01 dg |
| Epict Disc & Seneca: 33.5 dg | 4 Macc & Phil: 56.67 dg |
| 1 Cor & Seneca: 33.82 dg | Arist Pan & Philo Piety: 57.11 dg |
| Gal & Seneca: 34.11 dg | 2 Cor & Arist Pan: 57.93 dg |
| 1 Thess & Gal: 34.8 dg | 2 Cor & Philem: 57.96 dg |
| 2 Cor & Phil: 35.51 dg | Arist Pan & Philo Death: 57.97 dg |
| 1 Thess & Phil: 35.79 dg | Epict Disc & Damascus: 58.16 dg |
| 2 Cor & Hebrews: 36.87 dg | Philem & Hebrews: 58.44 dg |
| Seneca & Hebrews: 37.06 dg | Arist Pan & Epict Disc: 58.51 dg |
| 1 Thess & Damascus: 37.2 dg | Epict Disc & Phil: 58.52 dg |
| 1 Cor & Epict Disc: 37.27 dg | Epict Disc & Philo Death: 58.56 dg |
| 4 Macc & Romans: 37.76 dg | Philem & Damascus: 58.79 dg |
| Epict Disc & Gal: 38.46 dg | 1 Cor & Philo Piety: 58.84 dg |
| 2 Cor & 1 Thess: 38.47 dg | 2 Cor & Philo Piety: 59.24 dg |
| Philem & Phil: 38.77 dg | 2 Thess & Romans: 59.27 dg |
| Romans & Seneca: 38.91 dg | Epict Disc & Philo Piety: 59.36 dg |
| 4 Macc & Seneca: 39.72 dg | Phil & Philo Piety: 59.84 dg |
| 4 Macc & Philo Piety: 39.82 dg | Philo Death & Hebrews: 59.84 dg |
| 4 Macc & Epict Disc: 40.26 dg | Phil & Seneca: 60.35 dg |
| Gal & Damascus: 40.68 dg | 2 Thess & Philem: 60.43 dg |
| 1 Cor & 4 Macc: 40.7 dg | Romans & Philem: 61.76 dg |
| 2 Cor & Damascus: 41.75 dg | Romans & Philo Death: 61.8 dg |
| Philo Piety & Damascus: 41.99 dg | 1 Thess & 2 Thess: 62.21 dg |
| Damascus & Hebrews: 42.17 dg | Philo Death & Seneca: 62.39 dg |
| 1 Cor & 1 Thess: 42.44 dg | Philo Death & Damascus: 62.48 dg |
| 4 Macc & Philo Death: 42.52 dg | Gal & Philo Death: 63.01 dg |
| Gal & Phil: 43.6 dg | Philo Piety & Seneca: 64.0 dg |
| 1 Cor & Phil: 43.81 dg | Arist Pan & Phil: 64.17 dg |
| Phil & Hebrews: 44.28 dg | 2 Thess & Phil: 65.25 dg |
| 1 Thess & 4 Macc: 45.5 dg | Seneca & Damascus: 65.58 dg |
| 4 Macc & Damascus: 45.84 dg | Epict Disc & Philem: 66.67 dg |
| Epict Disc & Hebrews: 46.0 dg | Philem & Philo Piety: 67.28 dg |
| Arist Pan & Gal: 46.03 dg | 1 Cor & Philo Death: 67.59 dg |
| Arist Pan & Hebrews: 46.07 dg | Philem & Seneca: 67.59 dg |
| 1 Thess & Romans: 46.23 dg | 2 Cor & 2 Thess: 69.16 dg |
| Romans & Damascus: 46.29 dg | 1 Thess & Philo Death: 69.48 dg |
| Phil & Damascus: 47.13 dg | 2 Thess & Epict Disc: 70.47 dg |
| Epict Disc & Romans: 47.2 dg | 4 Macc & Philem: 71.96 dg |
| 2 Cor & Epict Disc: 47.6 dg | 2 Thess & 4 Macc: 72.89 dg |
| 2 Cor & 4 Macc: 48.26 dg | 2 Cor & Philo Death: 73.25 dg |
| Romans & Phil: 48.51 dg | Phil & Philo Death: 73.27 dg |
| Arist Pan & Romans: 49.51 dg | 2 Thess & Arist Pan: 75.4 dg |
| 1 Cor & Arist Pan: 49.53 dg | 2 Thess & Damascus: 76.46 dg |
| Romans & Philo Piety: 50.3 dg | Arist Pan & Philem: 77.19 dg |
| Gal & Philo Piety: 50.56 dg | 2 Thess & Philo Piety: 80.38 dg |
| Philo Piety & Hebrews: 50.67 dg | Philem & Philo Death: 80.77 dg |
| 2 Cor & Seneca: 50.68 dg | 2 Thess & Philo Death: 84.42 dg |
Jaccard Similarity
| 1 Cor & Hebrews: 0.606 | Gal & Philo Death: 0.239 |
| 1 Cor & Romans: 0.58 | Philo Death & Philo Piety: 0.229 |
| 4 Macc & Gal: 0.571 | Romans & Phil: 0.229 |
| 2 Cor & Gal: 0.555 | 1 Thess & Philo Death: 0.228 |
| Romans & Hebrews: 0.542 | Seneca & Damascus: 0.218 |
| Gal & Seneca: 0.537 | Phil & Damascus: 0.217 |
| 1 Thess & Phil: 0.513 | 2 Thess & Romans: 0.2 |
| Romans & Seneca: 0.512 | Philo Death & Seneca: 0.197 |
| 2 Cor & Romans: 0.512 | 1 Thess & Philo Piety: 0.195 |
| 4 Macc & Seneca: 0.494 | 1 Thess & Arist Pan: 0.19 |
| Gal & Romans: 0.47 | 2 Cor & 2 Thess: 0.183 |
| Damascus & Hebrews: 0.466 | Phil & Philo Death: 0.181 |
| 4 Macc & Romans: 0.462 | Romans & Philo Death: 0.18 |
| 2 Cor & 4 Macc: 0.459 | 1 Cor & 1 Thess: 0.174 |
| 1 Thess & Gal: 0.446 | 1 Thess & Hebrews: 0.173 |
| 4 Macc & Arist Pan: 0.431 | 1 Cor & Phil: 0.17 |
| Romans & Damascus: 0.421 | Phil & Philo Piety: 0.168 |
| 2 Cor & Seneca: 0.421 | Phil & Hebrews: 0.168 |
| Philo Piety & Damascus: 0.406 | 2 Thess & 4 Macc: 0.168 |
| 4 Macc & Philo Piety: 0.402 | Arist Pan & Philo Death: 0.164 |
| 1 Cor & 2 Cor: 0.393 | Arist Pan & Phil: 0.161 |
| 2 Cor & Damascus: 0.389 | 2 Thess & Philem: 0.156 |
| 2 Cor & Hebrews: 0.384 | 2 Thess & Hebrews: 0.152 |
| Arist Pan & Hebrews: 0.384 | 2 Thess & Philo Death: 0.149 |
| Gal & Phil: 0.381 | 1 Cor & Epict Disc: 0.147 |
| 2 Cor & 1 Thess: 0.379 | 1 Cor & 2 Thess: 0.147 |
| 1 Thess & 4 Macc: 0.376 | 2 Cor & Philo Death: 0.143 |
| 2 Cor & Phil: 0.376 | Epict Disc & Hebrews: 0.139 |
| 1 Cor & Arist Pan: 0.369 | Philo Death & Hebrews: 0.134 |
| 1 Cor & Damascus: 0.363 | Philo Death & Damascus: 0.128 |
| 1 Cor & 4 Macc: 0.361 | 2 Thess & Arist Pan: 0.127 |
| Arist Pan & Romans: 0.349 | 1 Cor & Philo Death: 0.127 |
| 4 Macc & Philo Death: 0.348 | 1 Thess & Philem: 0.123 |
| Romans & Philo Piety: 0.347 | Philem & Phil: 0.121 |
| 1 Cor & Seneca: 0.347 | 2 Thess & Damascus: 0.099 |
| 4 Macc & Hebrews: 0.342 | Arist Pan & Epict Disc: 0.094 |
| 4 Macc & Damascus: 0.339 | Epict Disc & Damascus: 0.091 |
| 1 Cor & Gal: 0.325 | Epict Disc & Romans: 0.091 |
| Philo Piety & Hebrews: 0.321 | 2 Thess & Philo Piety: 0.083 |
| Seneca & Hebrews: 0.319 | Epict Disc & Philo Piety: 0.079 |
| Gal & Philo Piety: 0.319 | Gal & Philem: 0.067 |
| Arist Pan & Gal: 0.317 | 4 Macc & Philem: 0.061 |
| 1 Thess & Seneca: 0.312 | 2 Cor & Epict Disc: 0.061 |
| Gal & Hebrews: 0.309 | Epict Disc & Seneca: 0.06 |
| Arist Pan & Damascus: 0.307 | 4 Macc & Epict Disc: 0.056 |
| Gal & Damascus: 0.307 | 2 Cor & Philem: 0.051 |
| 2 Cor & Philo Piety: 0.304 | Epict Disc & Gal: 0.05 |
| Arist Pan & Philo Piety: 0.297 | Philem & Seneca: 0.048 |
| 1 Cor & Philo Piety: 0.294 | Philem & Philo Death: 0.044 |
| Arist Pan & Seneca: 0.293 | Romans & Philem: 0.037 |
| Philo Piety & Seneca: 0.286 | Philem & Damascus: 0.037 |
| 2 Thess & Gal: 0.282 | 1 Thess & Epict Disc: 0.026 |
| 1 Thess & 2 Thess: 0.275 | Arist Pan & Philem: 0.026 |
| 4 Macc & Phil: 0.272 | Epict Disc & Phil: 0.025 |
| 2 Thess & Phil: 0.272 | Philem & Hebrews: 0.024 |
| 2 Thess & Seneca: 0.271 | Philem & Philo Piety: 0.024 |
| 2 Cor & Arist Pan: 0.269 | 1 Cor & Philem: 0.023 |
| 1 Thess & Romans: 0.255 | 2 Thess & Epict Disc: 0.021 |
| Phil & Seneca: 0.247 | Epict Disc & Philo Death: 0.019 |
| 1 Thess & Damascus: 0.242 | Epict Disc & Philem: 0.003 |
Manhattan Distance
| 1 Thess & Phil: 37 | Phil & Damascus: 159 |
| 2 Thess & Philem: 38 | 2 Cor & Philo Piety: 160 |
| Philem & Philo Death: 43 | Philo Piety & Seneca: 160 |
| 1 Thess & Philem: 50 | Philem & Philo Piety: 163 |
| Philem & Phil: 51 | Arist Pan & Philo Death: 168 |
| 1 Thess & 2 Thess: 58 | Romans & Philo Piety: 171 |
| 2 Thess & Phil: 59 | 1 Thess & Arist Pan: 171 |
| 4 Macc & Gal: 60 | Arist Pan & Seneca: 174 |
| 1 Thess & Philo Death: 61 | Damascus & Hebrews: 174 |
| 1 Thess & Gal: 62 | Philo Death & Damascus: 177 |
| 2 Thess & Philo Death: 63 | 2 Thess & Philo Piety: 177 |
| Phil & Philo Death: 68 | Arist Pan & Phil: 182 |
| Gal & Seneca: 69 | Philem & Damascus: 182 |
| 2 Cor & Gal: 69 | Romans & Philem: 182 |
| Gal & Phil: 73 | Arist Pan & Romans: 185 |
| 4 Macc & Philo Death: 75 | 2 Thess & Arist Pan: 185 |
| 1 Thess & 4 Macc: 78 | 2 Cor & Hebrews: 189 |
| 4 Macc & Seneca: 81 | 2 Cor & Arist Pan: 190 |
| 2 Thess & Gal: 84 | Arist Pan & Philem: 191 |
| 2 Cor & 1 Thess: 87 | 2 Thess & Damascus: 192 |
| 2 Cor & Phil: 88 | 1 Cor & 2 Cor: 193 |
| Gal & Philo Death: 89 | Arist Pan & Philo Piety: 194 |
| 2 Cor & 4 Macc: 93 | 4 Macc & Hebrews: 198 |
| 1 Thess & Seneca: 95 | 1 Cor & 4 Macc: 198 |
| 2 Thess & Seneca: 97 | Seneca & Damascus: 201 |
| Gal & Philem: 98 | Arist Pan & Damascus: 203 |
| 4 Macc & Phil: 99 | Gal & Hebrews: 208 |
| Romans & Seneca: 101 | 1 Cor & Seneca: 209 |
| 2 Cor & Romans: 105 | 1 Cor & Gal: 210 |
| 2 Cor & Seneca: 106 | Seneca & Hebrews: 213 |
| Gal & Romans: 106 | Arist Pan & Hebrews: 215 |
| 4 Macc & Philem: 108 | 1 Cor & Arist Pan: 231 |
| Philo Death & Seneca: 110 | 1 Cor & Damascus: 232 |
| Phil & Seneca: 110 | Philo Piety & Hebrews: 233 |
| 4 Macc & Romans: 112 | 1 Thess & Hebrews: 244 |
| 2 Thess & 4 Macc: 114 | 2 Thess & Hebrews: 246 |
| 4 Macc & Philo Piety: 119 | Phil & Hebrews: 247 |
| Philem & Seneca: 119 | Philo Death & Hebrews: 251 |
| 4 Macc & Arist Pan: 123 | 1 Cor & 1 Thess: 256 |
| 2 Cor & 2 Thess: 125 | 1 Cor & Philo Piety: 257 |
| Philo Death & Philo Piety: 128 | 1 Cor & Phil: 259 |
| 2 Cor & Philem: 129 | 1 Cor & 2 Thess: 262 |
| 1 Cor & Romans: 132 | 1 Cor & Philo Death: 269 |
| 2 Cor & Philo Death: 132 | Philem & Hebrews: 282 |
| Gal & Philo Piety: 139 | 1 Cor & Philem: 300 |
| Romans & Hebrews: 142 | 1 Cor & Epict Disc: 1769 |
| 2 Cor & Damascus: 143 | Epict Disc & Hebrews: 1783 |
| 1 Cor & Hebrews: 146 | Arist Pan & Epict Disc: 1878 |
| 1 Thess & Romans: 146 | Epict Disc & Damascus: 1883 |
| 1 Thess & Philo Piety: 149 | Epict Disc & Romans: 1885 |
| Philo Piety & Damascus: 149 | Epict Disc & Philo Piety: 1908 |
| 1 Thess & Damascus: 150 | Epict Disc & Seneca: 1948 |
| 4 Macc & Damascus: 150 | 2 Cor & Epict Disc: 1956 |
| Romans & Damascus: 154 | 4 Macc & Epict Disc: 1957 |
| Romans & Phil: 155 | Epict Disc & Gal: 1969 |
| Arist Pan & Gal: 155 | 1 Thess & Epict Disc: 2023 |
| Gal & Damascus: 156 | Epict Disc & Phil: 2028 |
| 2 Thess & Romans: 156 | 2 Thess & Epict Disc: 2029 |
| Phil & Philo Piety: 158 | Epict Disc & Philo Death: 2032 |
| Romans & Philo Death: 159 | Epict Disc & Philem: 2065 |
Burrows’ Delta Method
| Romans & Hebrews: 0.464 | Gal & Philo Piety: 1.026 |
| 1 Cor & Gal: 0.512 | 1 Cor & Damascus: 1.045 |
| 1 Cor & Romans: 0.556 | 1 Thess & 2 Thess: 1.049 |
| Gal & Romans: 0.656 | 2 Thess & Philem: 1.05 |
| 1 Cor & Seneca: 0.66 | Arist Pan & Damascus: 1.067 |
| 2 Thess & Hebrews: 0.661 | 2 Cor & Epict Disc: 1.067 |
| Damascus & Hebrews: 0.666 | 2 Thess & Philo Death: 1.068 |
| 1 Cor & Hebrews: 0.677 | Epict Disc & Gal: 1.069 |
| 4 Macc & Hebrews: 0.694 | Phil & Philo Piety: 1.071 |
| 4 Macc & Gal: 0.704 | 2 Thess & Gal: 1.081 |
| Gal & Hebrews: 0.71 | Gal & Phil: 1.084 |
| Philo Death & Philo Piety: 0.724 | 1 Cor & Arist Pan: 1.084 |
| 2 Cor & Gal: 0.726 | Philo Death & Seneca: 1.089 |
| 1 Cor & 2 Cor: 0.731 | Gal & Philo Death: 1.097 |
| 2 Cor & Romans: 0.731 | 2 Thess & Seneca: 1.101 |
| 4 Macc & Romans: 0.742 | 1 Thess & Seneca: 1.113 |
| 1 Thess & Hebrews: 0.742 | 1 Cor & Philo Death: 1.117 |
| 4 Macc & Arist Pan: 0.771 | 2 Thess & 4 Macc: 1.137 |
| Romans & Seneca: 0.779 | 2 Cor & 2 Thess: 1.138 |
| 4 Macc & Philo Piety: 0.786 | 4 Macc & Phil: 1.15 |
| Phil & Hebrews: 0.792 | Arist Pan & Philo Death: 1.15 |
| Philem & Phil: 0.801 | 1 Thess & Arist Pan: 1.156 |
| 1 Cor & 4 Macc: 0.818 | 2 Thess & Damascus: 1.163 |
| 2 Cor & 4 Macc: 0.831 | 2 Thess & Philo Piety: 1.166 |
| 4 Macc & Philo Death: 0.834 | Philo Piety & Seneca: 1.18 |
| 1 Thess & Phil: 0.837 | Romans & Philem: 1.181 |
| 2 Cor & 1 Thess: 0.838 | Philem & Hebrews: 1.183 |
| 1 Cor & 1 Thess: 0.84 | 1 Cor & Philem: 1.183 |
| 1 Thess & Damascus: 0.844 | Philem & Damascus: 1.19 |
| 2 Thess & Phil: 0.846 | 1 Thess & Philo Piety: 1.201 |
| 2 Thess & Romans: 0.855 | 2 Cor & Philo Piety: 1.201 |
| 4 Macc & Seneca: 0.857 | Epict Disc & Hebrews: 1.203 |
| 2 Cor & Hebrews: 0.857 | Epict Disc & Philo Death: 1.221 |
| Gal & Seneca: 0.875 | Arist Pan & Gal: 1.231 |
| 4 Macc & Damascus: 0.876 | Epict Disc & Romans: 1.232 |
| Romans & Damascus: 0.877 | Arist Pan & Phil: 1.254 |
| Epict Disc & Seneca: 0.88 | 2 Thess & Arist Pan: 1.264 |
| Seneca & Hebrews: 0.91 | Philem & Philo Piety: 1.264 |
| Philo Piety & Damascus: 0.92 | Arist Pan & Philo Piety: 1.272 |
| Romans & Phil: 0.926 | Phil & Philo Death: 1.28 |
| 1 Cor & Phil: 0.926 | Arist Pan & Seneca: 1.282 |
| 1 Cor & Epict Disc: 0.927 | Epict Disc & Philo Piety: 1.296 |
| Philo Death & Hebrews: 0.928 | 1 Thess & Epict Disc: 1.304 |
| Romans & Philo Death: 0.942 | 2 Cor & Arist Pan: 1.304 |
| 4 Macc & Epict Disc: 0.944 | 1 Thess & Philem: 1.313 |
| Arist Pan & Hebrews: 0.947 | 1 Thess & Philo Death: 1.331 |
| 2 Cor & Phil: 0.948 | Phil & Seneca: 1.34 |
| Romans & Philo Piety: 0.966 | Epict Disc & Damascus: 1.369 |
| Philo Death & Damascus: 0.971 | Philem & Philo Death: 1.37 |
| 1 Thess & Gal: 0.976 | 2 Cor & Philo Death: 1.372 |
| 1 Cor & 2 Thess: 0.979 | Arist Pan & Philem: 1.389 |
| 1 Thess & Romans: 0.99 | Seneca & Damascus: 1.396 |
| 1 Cor & Philo Piety: 0.993 | 2 Thess & Epict Disc: 1.408 |
| Arist Pan & Romans: 0.995 | Gal & Philem: 1.434 |
| 2 Cor & Damascus: 0.995 | 2 Cor & Philem: 1.514 |
| Philo Piety & Hebrews: 0.997 | Epict Disc & Phil: 1.524 |
| Phil & Damascus: 1.002 | Arist Pan & Epict Disc: 1.542 |
| 1 Thess & 4 Macc: 1.009 | 4 Macc & Philem: 1.554 |
| 2 Cor & Seneca: 1.011 | Philem & Seneca: 1.625 |
| Gal & Damascus: 1.013 | Epict Disc & Philem: 1.85 |
References
Al-Anazi, Sumayia, Hind AlMahmoud, and Isra Al-Turaiki. “Finding Similar Documents using Different Clustering Techniques.” Procedia Computer Science 82 (2016), 28–34. 10.1016/j.procs.2016.04.005.Search in Google Scholar
Ale (https://stats.stackexchange.com/users/152762/ale). Drawbacks with Cosine Similarity. Cross Validated, 2017, March 12. https://stats.stackexchange.com/q/266979.Search in Google Scholar
Argamon, Shlomo. “Interpreting Burrows’s Delta: Geometric and Probabilistic Foundations.” Literary and Linguistic Computing 23:2 (2007), 131–47. 10.1093/llc/fqn003.Search in Google Scholar
Al-Hagery, Mohammed Abdullah Hassan. “Google Search Filter using Cosine Similarity Measure to Find All Relevant Documents of a Specific Research.” ResearchGate, 2016. https://www.researchgate.net/publication/309312557_Google_Search_Filter_Using_Cosine_Similarity_Measure_to_Find_All_Relevant_Documents_of_a_Specific_Research_Topic.Search in Google Scholar
Evert, Stefan, Thomas Proisl, Fotis Jannidis, Isabella Reger, Steffen Pielström, Christof Schöch, and Thorsten Vitt. “Understanding and Explaining Delta Measures for Authorship Attribution.” Digital Scholarship in the Humanities 32:suppl_2 (2017), ii4–16. 10.1093/llc/fqx023.Search in Google Scholar
Liberti, Leo, Carlile Lavor, Nelson Maculan, and Antonio Mucherino. “Euclidean Distance Geometry and Applications.” SIAM Review 56:1 (2014), 3–69. 10.1137/120875909.Search in Google Scholar
Pedregosa, Fabian, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, Jake Vanderplas, Alexandre Passos, David Cournapeau, Matthieu Brucher, Matthieu Perrot, Édouard Duchesnay. SciKit-Learn: Machine Learning in Python, 2011. https://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html.Search in Google Scholar
Robertson, Paul Mark. Paul’s Letters and Contemporary Greco-Roman Literature: Theorizing a New Taxonomy. Leiden: Brill, 2016.10.1163/9789004320260Search in Google Scholar
Shtovba, Serhiy and Mykola Petrychko. “Jaccard index-Based Assessing the Similarity of Research Fields in Dimensions.” ResearchGate, 2019. https://www.researchgate.net/publication/338458200_Jaccard_index-Based_Assessing_the_Similarity_of_Research_Fields_in_Dimensions.Search in Google Scholar
Suwanda, Rizki, Zulfahmi Syahputra, and Elvi M. Zamzami. “Analysis of Euclidean distance and Manhattan Distance in the K-Means Algorithm for Variations Number of Centroid K.” Journal of Physics. Conference Series 1566:1 (2020), 012058. 10.1088/1742-6596/1566/1/012058.Search in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Special issue: Mathematically Modeling Early Christian Literature: Theories, Methods and Future Directions, edited by Erich Benjamin Pracht (Aarhus University, Denmark)
- Mathematically Modeling Early Christian Literature: Theories, Methods, and Future Directions
- Comparing and Assessing Statistical Distance Metrics within the Christian Apostle Paul’s Letters
- Something to Do with Paying Attention: A Review of Transformer-based Deep Neural Networks for Text Classification in Digital Humanities and New Testament Studies
- Paul’s Style and the Problem of the Pastoral Letters: Assessing Statistical Models of Description and Inference
- Seek First the Kingdom of Cooperation: Testing the Applicability of Morality-as-Cooperation Theory to the Sermon on the Mount
- Modelling the Semantic Landscape of Angels in Augustine of Hippo
- Was the Resurrection a Conspiracy? A New Mathematical Approach
- Special issue: Reading Literature as Theology in Islam, edited by Claire Gallien (Cambridge Muslim College and Cambridge University) and Easa Saad (University of Oxford)
- Reading Literature as Theology in Islam. An Introduction and Two Case Studies: al-Thaʿālibī and Ḥāfiẓ
- Human Understanding and God-talk in Jāmī and Beyond
- Was That Layla’s Fire?: Metonymy, Metaphor, and Mannerism in the Poetry of Ibn al-Fāriḍ
- Divine Immanence and Transcendent Love: Epistemological Insights from Sixteenth-Century Kurdish Theology
- Regional and Vernacular Expressions of Shi‘i Theology: The Prophet and the Imam in Satpanth Ismaili Ginans
- The Fragrant Secret: Language and Universalism in Muusaa Ka’s The Wolofal Takhmīs
- Love as the Warp and Weft of Creation: The Theological Aesthetics of Muhammad Iqbal and Rabindranath Tagore
- Decoding Muslim Cultural Code: Oral Poetic Tradition of the Jbala (Northern Morocco)
- Research Articles
- Mortality Reimagined: Going through Deleuze’s Encounter with Death
- When God was a Woman꞉ From the Phocaean Cult of Athena to Parmenides’ Ontology
- Patrons, Students, Intellectuals, and Martyrs: Women in Origen’s Life and Eusebius’ Biography
- African Initiated Churches and Ecological Sustainability: An Empirical Exploration
- Randomness in Nature and Divine Providence: An Open Theological Perspective
- Women Deacons in the Sacrament of Holy Orders
- The Governmentality of Self and Others: Cases of Homosexual Clergy in the Communist Poland
Articles in the same Issue
- Special issue: Mathematically Modeling Early Christian Literature: Theories, Methods and Future Directions, edited by Erich Benjamin Pracht (Aarhus University, Denmark)
- Mathematically Modeling Early Christian Literature: Theories, Methods, and Future Directions
- Comparing and Assessing Statistical Distance Metrics within the Christian Apostle Paul’s Letters
- Something to Do with Paying Attention: A Review of Transformer-based Deep Neural Networks for Text Classification in Digital Humanities and New Testament Studies
- Paul’s Style and the Problem of the Pastoral Letters: Assessing Statistical Models of Description and Inference
- Seek First the Kingdom of Cooperation: Testing the Applicability of Morality-as-Cooperation Theory to the Sermon on the Mount
- Modelling the Semantic Landscape of Angels in Augustine of Hippo
- Was the Resurrection a Conspiracy? A New Mathematical Approach
- Special issue: Reading Literature as Theology in Islam, edited by Claire Gallien (Cambridge Muslim College and Cambridge University) and Easa Saad (University of Oxford)
- Reading Literature as Theology in Islam. An Introduction and Two Case Studies: al-Thaʿālibī and Ḥāfiẓ
- Human Understanding and God-talk in Jāmī and Beyond
- Was That Layla’s Fire?: Metonymy, Metaphor, and Mannerism in the Poetry of Ibn al-Fāriḍ
- Divine Immanence and Transcendent Love: Epistemological Insights from Sixteenth-Century Kurdish Theology
- Regional and Vernacular Expressions of Shi‘i Theology: The Prophet and the Imam in Satpanth Ismaili Ginans
- The Fragrant Secret: Language and Universalism in Muusaa Ka’s The Wolofal Takhmīs
- Love as the Warp and Weft of Creation: The Theological Aesthetics of Muhammad Iqbal and Rabindranath Tagore
- Decoding Muslim Cultural Code: Oral Poetic Tradition of the Jbala (Northern Morocco)
- Research Articles
- Mortality Reimagined: Going through Deleuze’s Encounter with Death
- When God was a Woman꞉ From the Phocaean Cult of Athena to Parmenides’ Ontology
- Patrons, Students, Intellectuals, and Martyrs: Women in Origen’s Life and Eusebius’ Biography
- African Initiated Churches and Ecological Sustainability: An Empirical Exploration
- Randomness in Nature and Divine Providence: An Open Theological Perspective
- Women Deacons in the Sacrament of Holy Orders
- The Governmentality of Self and Others: Cases of Homosexual Clergy in the Communist Poland

