Abstract
The laminar boundary layer MHD three-dimensional mixed convective flow of Maxwell nanofluid towards a bidirectional stretching sheet with non-linear radiation is analyzed. A constant magnetic field is implemented normal to the fluid flow direction. A numerical technique of Runge-Kutta-Fehlberg (RFK45) is utilized to obtain the numerical solution of the dimensionless coupled ODEs with associated boundary conditions. The various pertinent dimensionless parameters on the flow are examined with the help of graphs and tables. Results shows that, nonlinear thermal radiation is more influential o on temperature profile when compared to linear thermal radiation.
1 Introduction
The common heat transfer fluids like as water, ethylene glycol and oil have small thermal conductivity and they are unable to fulfill the growing demand of new advanced heat modern technologies. To overcome this aspect, thermal conductivity these convectional fluids are enhanced by addition of small solid nanoparticles. Therefore, nanofluids are the fluids acquired by suspending small volumetric quantities of nanometer-sized particles in the base conventional fluids. Improving the thermal conductivity of in convectional fluids with nanoparticles has initially studied by Choi [1]. The interaction of hydromagnetic motion in nanofluids has favorable applications in physical engineering, modern metallurgical process, applied chemistry and the polymer industry. There is also a great importance to the analysis and magnetohydrodynamic fluid flow problems in physiological fluids like as blood pump machines and peristaltic plasma pumping. Recently, many authors analyzed various boundary layer flow problems of a nanofluid in the presence and absence of applied magnetic field over a flat surface under different geometries [2, 3, 4, 5, 6, 7, 8, 9].
The importance of thermal radiation has obtained much attention of various scholars due to its numerous applications in physics, industrial chemistry and practical engineering applications such as nuclear reactors, polymer processing, furnace design, furnace design, gas cooled, glass production, and space technology. Electromagnetic waves are plays most responsible to transfer heat via radiation. Thermal radiation in flow and heat transfer processes is of major interest in the design of many advanced energy conversion systems operating at high temperature. Thermal radiation effect becomes important when the difference between the surface and the ambient temperature is large. Many authors studied the effect of linear thermal radiation on heat transfer of both Newtonian and non-Newtonian fluids over a stretching surface [10, 11]. But a linear radiation is not valid for high temperature difference and also dimensionless parameter that is used in the linearized Rosseland approximation is only the effective Prandtl number [12], whereas in the non-linear approximation the problem is governed by three parameters, Prandtl number, the radiation parameter and the temperature ratio parameter. The interaction of three dimensional nonlinear thermal radiation on Jeffrey fluid flow studied by Raju et al. [13] and reveals that the mass transfer rate on the flow in shrinking sheet is lower than stretching sheet. Khan et al. [14] presented non-linear radiative flow of three dimensional Burgers nanofluid with convective boundary conditions. They observed that for enhancing values of the Brownian motion parameter lead to a rising in the concentration field as well as associated thickness of concentration boundary layer. Mixed convection Al2O3–water nanofluid flow inside a vertical micro annulus by various modes of nanoparticle migration has recently investigated by Moshizi and Malvandi [15].
Heat and mass transfer flows with Soret (thermal-diffusion) and Dufour (diffusion-thermo) effects have been substantial attraction among many researchers owing to various grown engineering applications such as manufacture for rubber and plastic sheets, chemical production engineering, geophysical processes, Catalytic process, compact heat insulation exchangers and design of nuclear reactor. A considerable amount of research work has been done to show the importance of diffusion-thermo and thermal-diffusion and effects for the different aspects. Postelnicu [16] presented influence of soret and dufour effects on heat and mass transfer over vertical surface with magnetic field. Interaction of Soret and Dufour effects on radiative and hydromagnetic flow in nanofluids over a vertical non-linear sheet was recently investigated by Pal et al. [17]. They found that an increase in Soret number diminish the friction factor and rate of heat transfer.
The explore of non-Newtonian fluids are very significant important topic for many researchers because of it has various applications which include in fabric glass production, starch suspensions, petroleum production process, paper pulp, polymer production, cement slurry, polymer processing industry and Biological fluids. Some of non-Newtonian fluids are Casson fluid, viscoelastic fluid, tangent hyperbolic fluid and Williamson fluid in which reporting the nonlinearity behavior. Maxwell fluid is simplest suitable rheological fluid model for the nonlinear reaction of shear thinning fluids. Many researchers studied non-Newtonian fluid flows over different aspects and dimensions due to the important quoted applications [18, 19, 20]. Although nanofluids have been studied almost completely as Newtonian fluid, recently, their rheological properties have been established by non-Newtonian modeling of nanofluid transport phenomena. Recently many authors studied the flow and heat transfer phenomena of nanofluids with non-Newtonian fluids as a base fluid [21, 22, 23, 24, 25].
Simultaneous effect of heat and mass transfers will also cause a cross diffusion effect. Both Brownian diffusion and thermophoresis give rise to cross-diffusion terms that are in some ways analogous to the familiar Soret and Dufour cross-diffusion terms. Due to much attention in many fields that includes solid state physics, chemical engineering, geophysics, and oceanography, the research on the double diffusive convective boundary layer has become a topic of great interest. The flow problem of triple-diffusion type comprising of heat, nanoparticles and solute has been scrutinized by Kuznetsov and Nield [26]. They used nanofluid model which incorporates the effects of Brownian motion and thermophoresis, in Darcy porous medium. Khan et al. [27] employed Runge-Kutta Fehlberg method to investigate the stagnation point flow of nanofluid with thermo-diffusion effect. Goyal and Bhargava [28] considered second grade fluid as a base fluid with suspension of nanoparticles in the boundary layer flow problem in the presence of thermo-diffusion effects. Satyaban et al. [29] described the thermal diffusion and diffusion thermo effects in the Powell-Eyring fluid flow over a nonlinear stretching surface. Kandasamy et al. [30] explained the mechanisms of heat and mass transfer in the MHD flow of nanofluid in the presence of mixed convection, thermo-diffusion and convective boundary conditions and showed that, existence magnetic field controls the features of flow, heat and mass transfer. Akbar et al. [31] investigated the double-diffusive boundary layer flow of nanofluid with the consideration of magnetic effect and obtained dual solutions for the stretching parameter.
The flow of non-Newtonian nanofluids submerged with nanoparticles is significance to industrial applications specifically in nuclear reactors and nuclear systems cooling for rising energy efficiency. The application of non-Newtonian nanofluids in water-cooled nuclear systems could result in a significant improvement of their economic performance and/or safety margins. Non-Newtonian fluid mechanics has been an important subject of research due to its applications in food processing, petroleum, chemical and polymer industries. Furthermore, the features of the flow of the common fluid in industry like biological fluids, motor oils and polymeric liquids can be described by using non-Newtonian fluid. In view of these applications, the main objective of the present paper is to investigate the interaction of double-diffusive on three dimensional Maxwell nanofluid flow by including the effects of thermophoresis and Brownian motion with non-linear radiation. The governing basic equations for the present flow are modeled and transformed to couple non-linear ODEs by impose the suitable transformations. Local similarity solution is obtained numerically by RKF-45 method with Shooting technique. The influence of various physical fluid dynamical parameters on the flow are presented and analyzed by using the graphical aid.
2 Mathematical Analysis
Consider a three dimensional steady, incompressible, laminar flow of a Maxwell nanofluid over a stretching surface at z = 0. The sheet is aligned with the xy-plane (z = 0) and the flow takes place in the domain z > 0. Let u = Uw(x) = ax and v = Vw (y) = by be the velocities of the stretching sheet along the x- and y- directions respectively. The sheet is saturated by a binary fluid with dissolved solutal and containing nanoparticles in suspension. Let Tw, Cw and γw be the constant values of the temperature, nanoparticle concentration and solutal concentration of the sheet and these constant values are assumed to be larger than the ambient temperature, nanoparticle concentration and solutal concentration which are represented by T∞, C∞ and γ∞ respectively. Brownian motion, thermophoresis, nonlinear thermal radiation, Dufour effects are employed in the energy equation whereas solutal equation includes Soret effect. Conservation of mass, momentum, thermal energy, nanoparticles and solute are as follows [18],
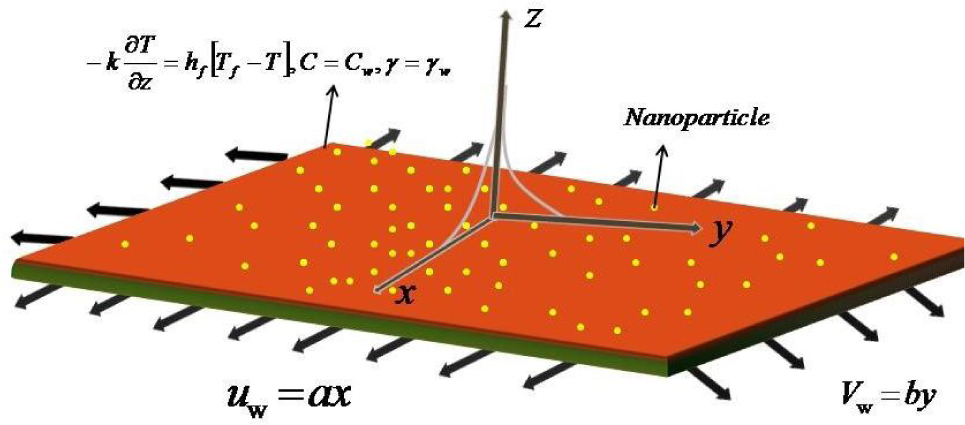
Schematic representation of the flow diagram.
where u, v and w are the velocity components along the x and y direction respectively, v is the kinematic viscosity of the fluid, ρf is the fluid density, λ is the relaxation time, g is the acceleration due to gravity, βT and βγ are the volumetric thermal expansion coefficient and volumetric solutal expansion coefficient of the nanofluid respectively, ρp is the density of the particles, σ is the electrical conductivity of the fluid, α is the thermal diffusivity of the fluid,
The boundary conditions for the present flow analysis are,
where subscript w denotes the wall condition, a and b are constants.
By using the Rosseland approximation, the radiative heat flux is given by,
where σ* is the Stefan-Boltzmann constant and k* is the mean absorption coefficient.
We introduce the non-dimensional similarity variables as,
with
Using equation (10), equation (1) is satisfied and the nonlinear partial differential equations (2) to (6) are reduced to nonlinear ordinary differential equations as below.
Corresponding boundary conditions are,
where λ* is the mixed convection parameter, Nc is the regular buoyancy ratio parameter, Nr is the nanofluid buoyancy ratio parameter, β is the Maxwell parameter, Rd is the radiation parameter, Pr is the Prandtl number, Nb is the Brownian motion parameter, Nt is the thermophoresis parameter, Nd is the modified Dufour parameter, Le is the nanofluid Lewis number, Ln is the regular Lewis number, Ld is the Dufour solutal Lewis number, c is the stretching ratio parameter.
These parameters are defined as
Because
The local Nusselt number is defined as,
Using equations (10), equation (18) is reduced as,
where
3 Numerical Method and accuracy
The system of equations (11) to (15) with boundary conditions of (16) have been solved using Runge-Kutta-Fehlberg fourth-fifth order method along with shooting technique. In the first step, Eqs. (11) to (15) are discretized to a system of simultaneous differential equations of first order by introducing new dependent variables. Missed initial conditions are obtained with the help of shooting technique. Afterward, a finite value for η∞ is chosen in such a way that all the far field boundary conditions are satisfied asymptotically. Our bulk computations are considered with the value at η∞ = 6, which is sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters considered. For the present problem, we took the step size Δη = 0.001 and accuracy to the fifth decimal places.
To minimize the truncation error, the grid independency test is performed and numerical values are tabulated in Table 1. The present code is tested for grid independency by calculating Nux with different mesh sizes. It is found that a grid size of 200 ensure the grid independent solution for the present case.
Comparison of Nux for different grid resolution, at Ld = 0.5, Le = 4, Ln = 0.2, Nd = 0.5, Nr = 0.2, Nt = 0.1, Pr = 5, β = 0.01, C = 0.3, λ* = 0.01, Nc = 0.5, θw = 1, Rd = 0.9
| Mesh size | 50 | 100 | 150 | 200 | 300 |
|---|---|---|---|---|---|
| Nux | 0.412440912 | 0.412340109 | 0.412340110 | 0.412340124 | 0.412340124 |
To have a check on the accuracy of the numerical approach used, we have computed f″(0) and g″(0) that are carried out for viscous fluid for various values of stretching rate parameter and compared with the available published results of Liu and Anderson [32] and Mushtaq et al. [33] in Table 2 and they are found to be in excellent agreement.
Comparison table for −f″(0) and −g″(0) with λ* = 0, β = 0, M = 0.
| c | Liu and Anderson [32] | Mushtaq et al. [33] | Present(RKF45Method) | |||
|---|---|---|---|---|---|---|
| −f″(0) | −f″(0) | −f″ (0) | −g″ (0) | −f″ (0) | −g″ (0) | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0.25 | 1.048813 | 0.194565 | 1.048811 | 0.194564 | 1.048834 | 0.194565 |
| 0.50 | 1.093096 | 0.465206 | 1.093095 | 0.465205 | 1.093105 | 0.465206 |
| 0.75 | 1.134486 | 0.794619 | 1.134486 | 0.794618 | 1.134491 | 0.794615 |
| 1 | 1.173721 | 1.173721 | 1.173721 | 1.173721 | 1.173723 | 1.173721 |
4 Result and Discussion
Numerical computation is carried out for several set of values of the Maxwell parameter (β), mixed convection parameter (λ*), Prandtl number (Pr), radiation parameter (Rd), regular buoyancy ratio parameter (Nc), nanofluid buoyancy ratio parameter (Nr), Brownian motion parameter (Nb), thermophoresis parameter (Nt), temperature ratio parameter (θw), modified Dufour parameter (Nd), nanofluid Lewis number (Le), regular Lewis number (Ln), Dufour solutal Lewis number (Ld) and stretching ratio parameter (c). In order to analyze the salient features of the problem, the numerical results are presented in Figures 2–19.
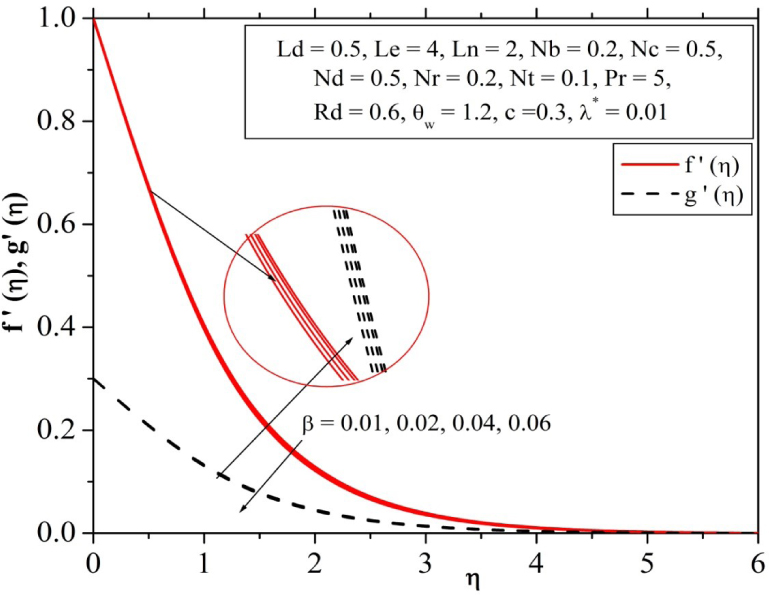
Influence of Maxwell parameter on velocity profile.
The influence of Maxwell parameter on axial velocity f′(η) and transverse velocity g′(η) are plotted in Fig. 2. It is revealed from the figure that with an increase in Maxwell parameter β, it produce resistance in the fluid axial velocity flow and transverse velocity. Furthermore, the magnitude of velocity curves and the boundary layer thickness diminishes for larger values of β. It is further concluding that when we boost the Maxwell fluid parameter β indefinitely, current phenomena trivially reduce to the case of Newtonian fluid.
Fig. 3 plotted for influence of the stretching parameter c on dimensionless velocity profiles. It can be seen that the usual downturn occurs to the horizontal velocity for distinct larger values of stretching parameter, while transverse velocity is enhanced with the higher in the stretching parameter. It further note that for c = 0, present problem reduced to the case of two-dimensional flow.
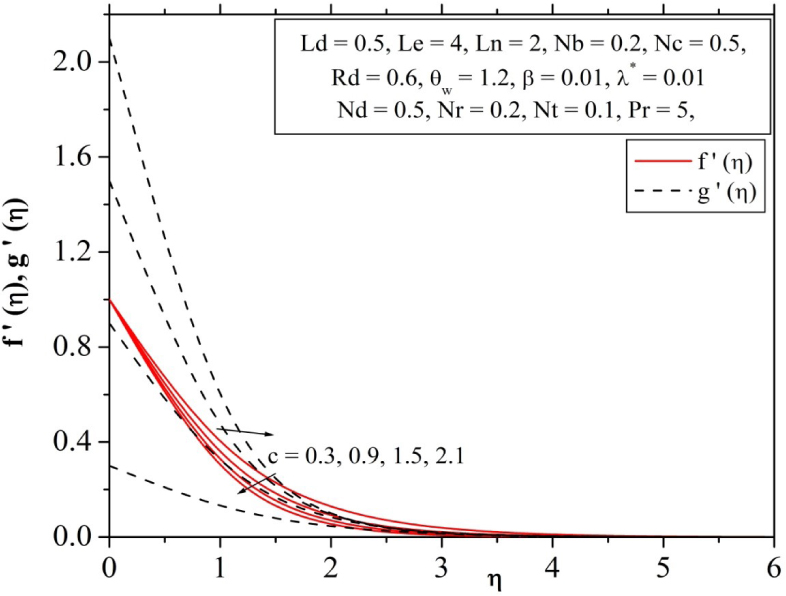
Influence of stretching ratio parameter on velocity profile.
The effect of mixed convection parameter λ* to the two velocities are depicted in Fig. 4. From the figure, here we can observed that as λ* increases, the velocity profile f′(η) and associated momentum boundary layer thickness increases. It is because of combined effects of mixed convection parameter due to the thermal, concentration and solutal gradients behaves as a pressure gradients which enhances the velocity along x-direction. While the quite opposite effect can be observed for the velocity profile g′(η).
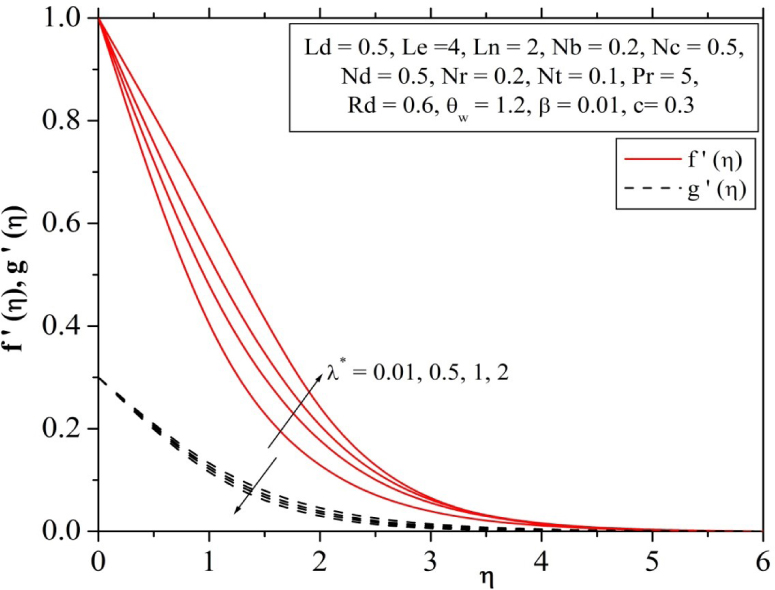
Influence of mixed convection parameter on velocity profile.
The temperature profile for different values of Prandtl number is shown Fig. 5. It is obvious that an increase in the Prandtl number results in deteriorate in the energy boundary layer thickness. This is due to fact that the thermal diffusion rate declines with increase of the Prandtl number.
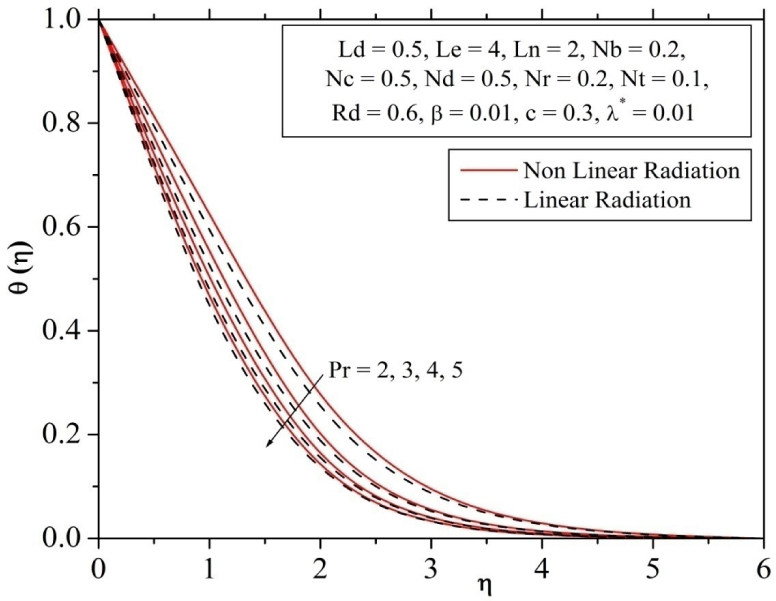
Influence of Prandtl number on temperature profile.
The thermal radiation impact is principally the occurrence of diffusion flux owing to temperature gradient and as a result the dimensionless energy function and the thermal boundary layer thickness is enhanced which is evidently shown in Fig. 6. Here we have considered both linear and nonlinear radiation effect to study the rate of heat transfer for the existing parameter. From, the obtained result we conclude that nonlinear radiation has more influence as compared to linear radiation. The effect of temperature ratio parameter θw on dimensionless temperature function θ(η) can be seen in Fig. 7. It illustrates that, with an increase in the temperature ratio parameter θw correspondingly magnify the temperature near the surface and hence the thermal boundary layer thickness. This is because fluid temperature is much higher than the ambient temperature for increasing values of θw, which increases the thermal state of the fluid. Further observation proves that the temperature profile for nonlinear stretching sheet is more influenced than linear stretching sheet for increasing values of θw.
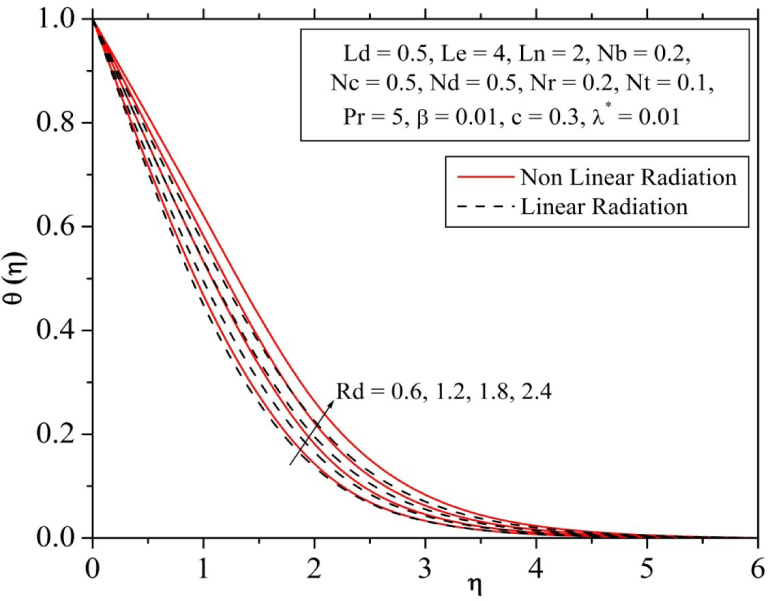
Influence of radiation parameter on temperature profile.
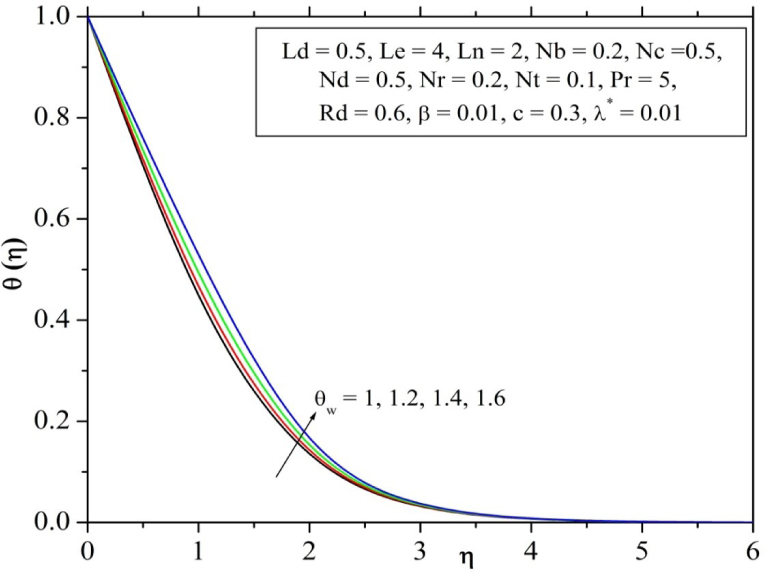
Influence of temperature ratio parameter on temperature profile.
The temperature and concentration profiles for the distinct values of Brownian number Nb are shown in Fig. 8 and Fig. 9. From these plots we found that the temperature and concentration have opposite behavior for boosted values of Nb and simultaneously the strengthen energy boundary layer thickness but reverse to the species boundary layer. The impact of Dufour solutal Lewis number Ld on Solute profile is presented in Fig. 10. The solute distribution h(η) hiked with an increase in Dufoursolutal Lewis number Ld. It is observed that for increasing values of Dufour solutal Lewis number Ld, with in the solute boundary layer, it enhances the solute function.
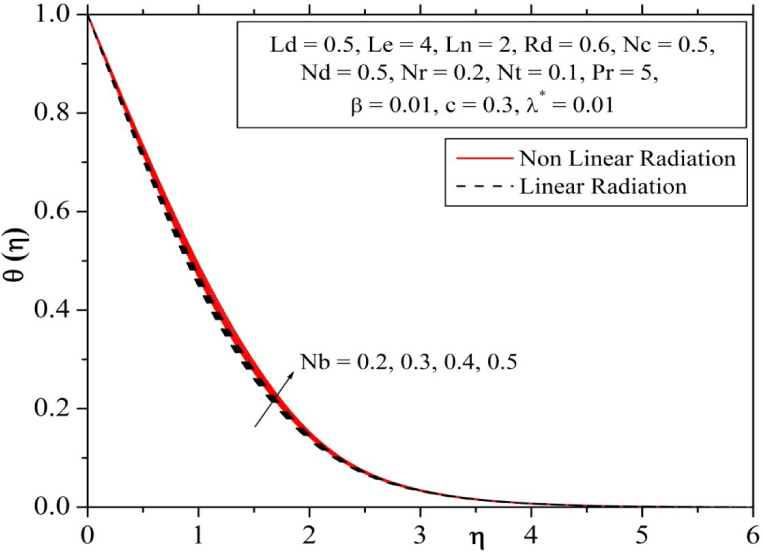
Influence of Brownian number on temperature profile.
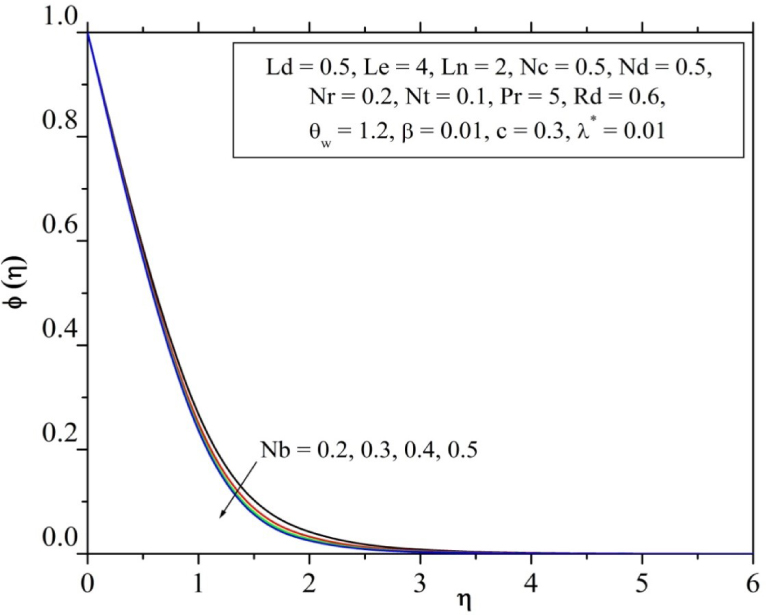
Influence of Brownian parameter on concentration profile.
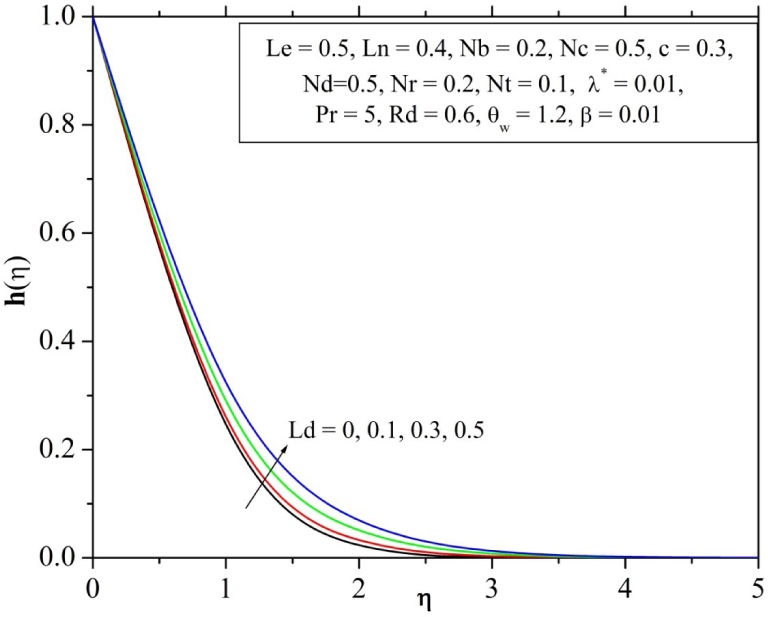
Influence of Dufour solutal Lewis number on Solute profile.
Variation of nanofluid concentration profile for the varying values of Lewis number can be seen in Fig. 11. It illustrates that, increase of Lewis number makes the profile to decrease due to dependency of Lewis number on Brownian diffusion coefficient. Effect of regular Lewis number on solutal concentration profile is analyzed in Fig. 12. It emphasizes that, increase of Lewis number makes the profile to decrease again due to dependency of this number on Brownian diffusion coefficient. Physically Le expresses the relative contribution of thermal diffusion rate to species diffusion rate in the boundary layer regime. An increase in Le values will reduce thermal boundary layer thickness and will be accompanied with a decrease in solutal concentration profile
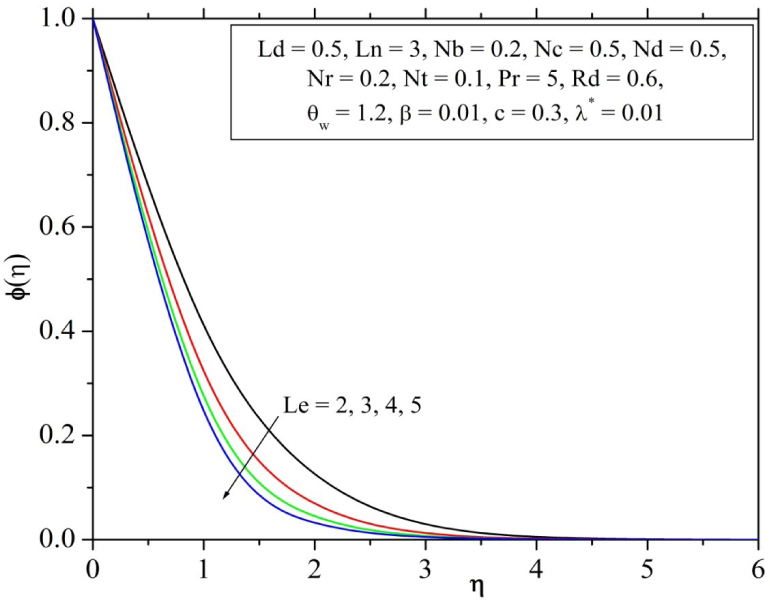
Influence of nanofluid Lewis number on concentration profile.
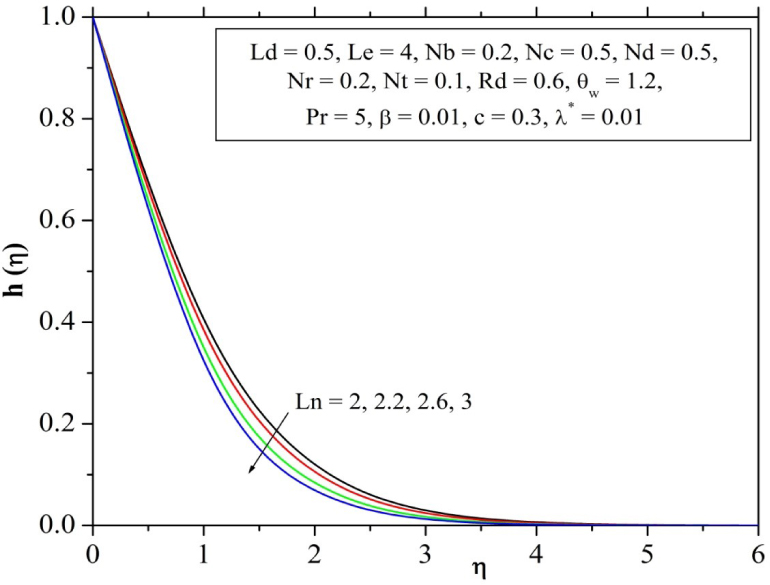
Influence of regular Lewis number parameter on Solute profile.
The characteristics of the influence of modified Dufour parameter Nd on the curves temperature displayed in Fig. 13. It is recognized that, increasing values of Dufour parameter increases the temperature profile. It is cleared that non-dimensional temperature function are magnify for the enhancing values of Nd. Fig. 14 and 15 we have been depicted to demonstrate the effects of thermophoresis parameter Nt on the dimensionless temperature and concentration profiles. It is revealed that as the thermophoresis parameter Nt increases there is a rise in the three profiles temperature and concentration of the fluid.
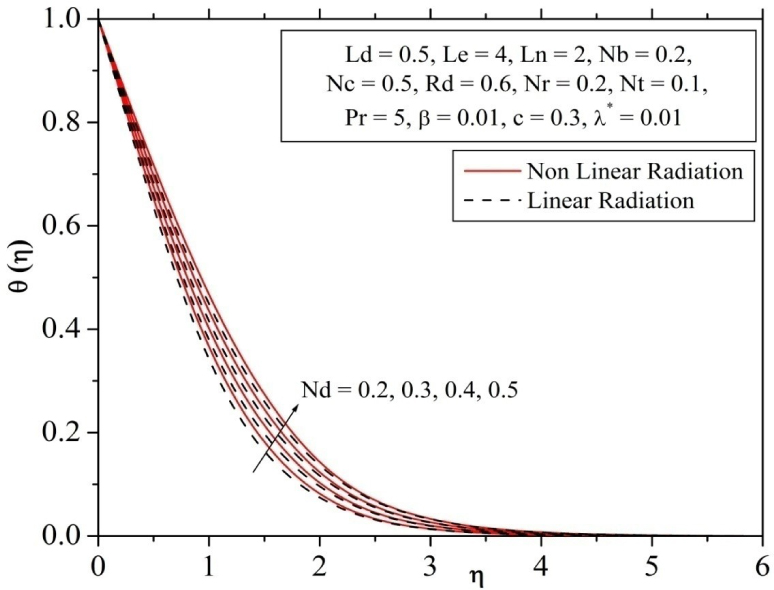
Influence of modified Dufour parameter on temperature profile.
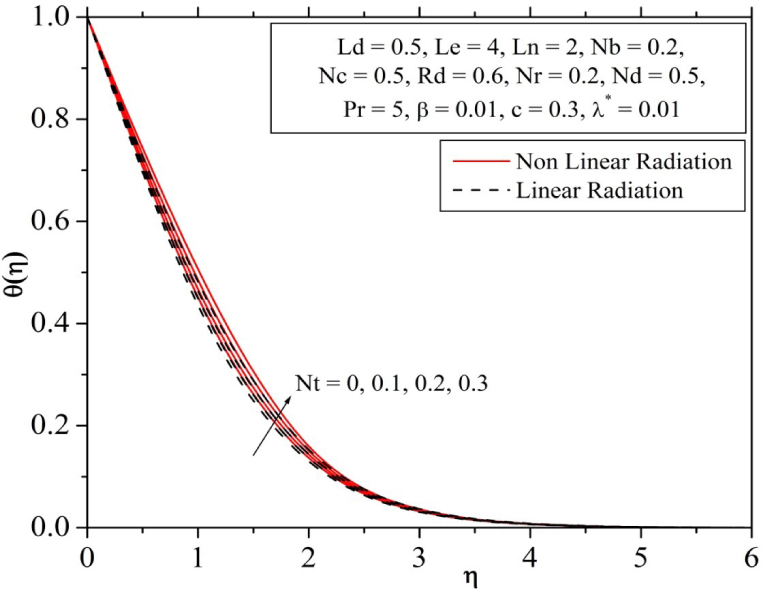
Influence of thermophoresis parameter on temperature profile.
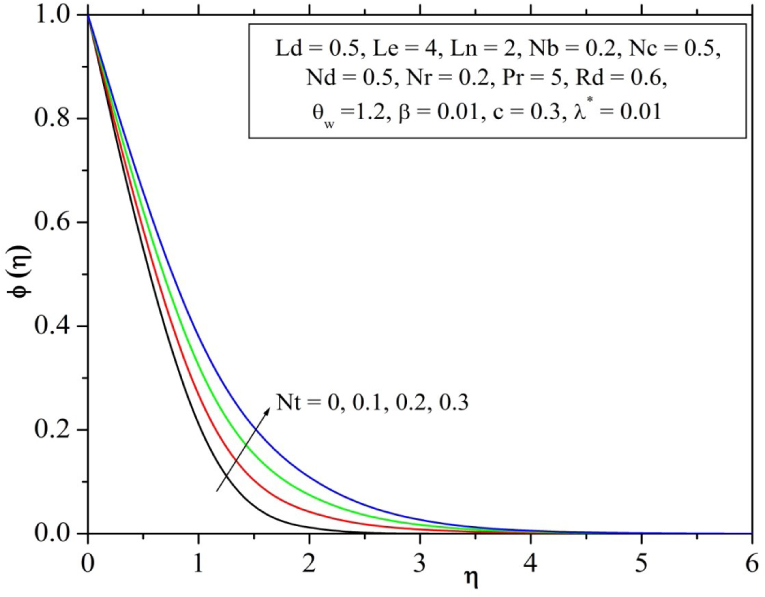
Influence of thermophoresis parameter on concentration profile.
The effect of nanofluid buoyancy ratio parameter (Nr) on velocity profile depicted in Fig. 16. Here we can notice that, increase of the parameter Nr makes the velocity profile f′(η) to decrease and g′(η) to increase. An increase in Nr increases the difference of particle density and fluid density, this parameter makes the velocity profile f′(η) to decrease along the x-direction.
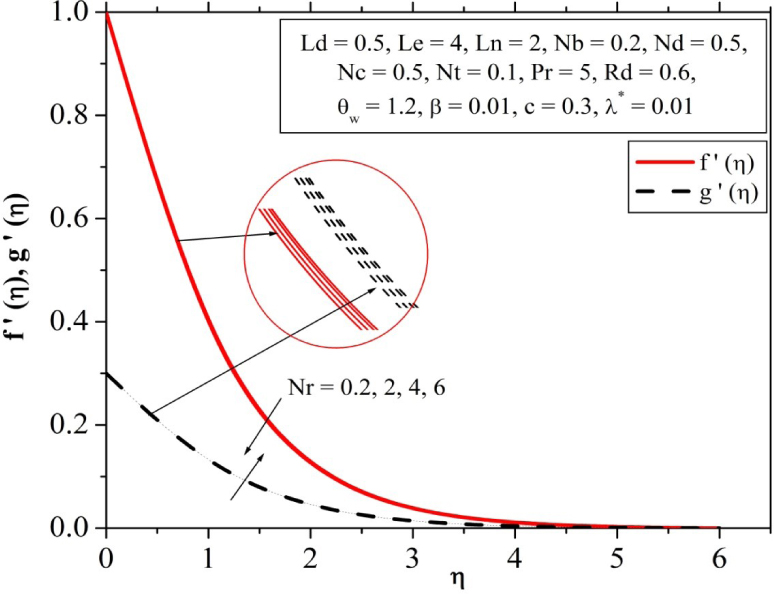
Influence of nanofluid buoyancy ratio parameter on velocity profile.
The description of the regular buoyancy ratio parameter (Nc) for the velocity profile depicted in Fig. 17. It is evident from this figure that, the velocity profile is an increasing function of f′(η), whereas is a decreasing function of g′(η). Because, increase of Nc makes the volumetric solution expansion coefficient to increase which makes the velocity profile to increase along the direction.
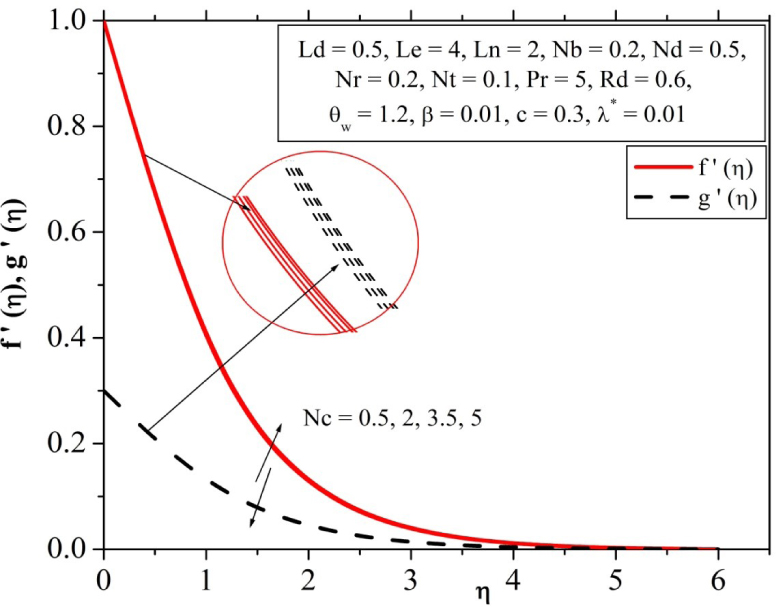
Influence of regular buoyancy ratio parameter on velocity profile.
Fig. 18 depicts the effect Brownian parameter and thermophoresis parameter on Nusselt number. Nusselt number increases with increase of these parameters respectively. It can be concluded that Nusselt number is a increasing function of Brownian parameter and thermophoresis parameter. Fig. 19 depicts the effect of Temperature ratio parameter and Radiation parameter on Nusselt number. Effect of Temperature ratio parameter and Radiation parameter on Nusselt number is similar to effect Brownian parameter and thermophoresis parameter on Nusselt number. It can also be concluded that Nusselt number is a increasing function of Temperature ratio parameter and Radiation parameter.
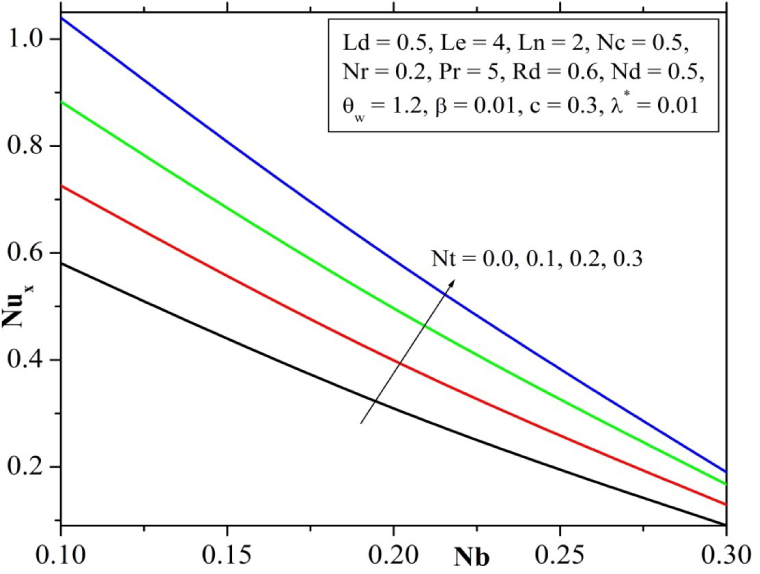
Effect of Brownian parameter and thermophoresis parameter on Nusselt number.
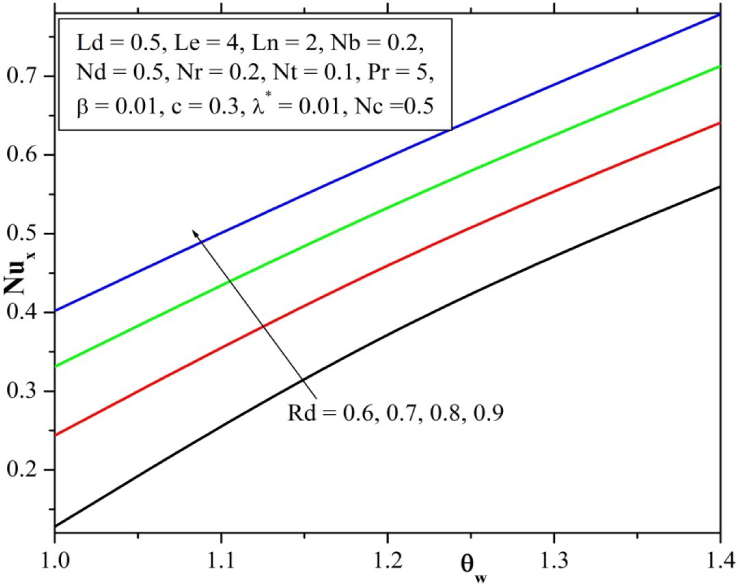
Effect of Temperature ratio parameter and Radiation parameter on Nusselt number.
5 Conclusion
Double diffusive hydromagnetic three dimensional boundary layer flow of Maxwell nanofluid is scrutinized in the presence of non-linear thermal radiation with Soret and Dufour effects. The impact of various physical parameters are reviewed on different profiles and are summarized as follows:
Velocity profiles decreases for the increasing values of Maxwell parameter.
Velocity profile f′(η) and corresponding momentum boundary layer thickness decreases for the stretching rate and nanofluid buoyancy ratio parameter, whereas it exhibits opposite behaviour for the profile g′(η). Reverse variations of these results are observed for the mixed convection and regular buoyancy ratio parameters.
Thermal boundary layer is thicker for the effect of Brownian motion, thermophoresis, radiation, temperature ratio and modified Dufour parameters.
Concentration boundary layer thickness is a decreasing function of Brownian motion parameter and nanofluid Lewis number whereas it is an increasing function for thermophoresis parameter.
Solutal profile increases for Dufour solutal Lewis number but adverse effect can be seen for regular Lewis number.
Acknowledgement
This research is supported by the University Grants Commission, New Delhi, India under the Major research project Scheme [F. No-43-419/2014(SR)].
References
[1] S. U. S. Choi and J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, The Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, USA, ASME, FED 231/MD., 66 (1995) 99–105.Suche in Google Scholar
[2] M. Turkyilmazoglu, Nanofluid flow and heat transfer due to a rotating disk, Comp. Fluids., 94 (2014) 139–146.10.1016/j.compfluid.2014.02.009Suche in Google Scholar
[3] H. S. Takhar, A. J. Chamkha and G. Nath, Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field, Int. J. of Eng. Sci. 37(13) (1999) 1723–1736.10.1016/S0020-7225(98)00144-XSuche in Google Scholar
[4] A. J. Chamkha and A. M. Aly, MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects, Chem. Eng. Comm. 198(3) (2010) 425–441.10.1080/00986445.2010.520232Suche in Google Scholar
[5] R. S. R. Gorla and A. Chamkha, Natural convective boundary layer flow over a nonisothermal vertical plate embedded in a porous medium saturated with a nanofluid, Nanoscale and Microscale Thermophysical Eng. 15(2) (2011) 81–94.10.1080/15567265.2010.549931Suche in Google Scholar
[6] A. J. Chamkha, S. Abbasbandy, A. M. Rashad and K. Vajravelu, Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid, Meccanica, 48(2) (2013)275–285.10.1007/s11012-012-9599-1Suche in Google Scholar
[7] C. Ram Reddy, P. V. S. N.Murthy, A. J. Chamkha and A. M. Rashad, Soret effect on mixed convection flow in a nanofluid under convective boundary condition, Inte.Journal of Heat and Mass Transfer, 64 (2013) 384–392.10.1016/j.ijheatmasstransfer.2013.04.032Suche in Google Scholar
[8] M. Gnaneswara Reddy, Influence of thermal radiation on natural convection boundary layer flow of a nanofluid past a vertical plate with uniform heat flux, Int. J. Heat and Tech., 32(12) (2014)1–7.Suche in Google Scholar
[9] G. K. Ramesh, B. C. Prasannakumara, B. J. Gireesha and Rama Subba Reddy Gorla, MHD Stagnation Point Flow of Nanofluid Towards a Stretching Surface with Variable Thickness and Thermal Radiation, J. of Nanofluids, 4(2) (2015) 247–253.10.1166/jon.2015.1144Suche in Google Scholar
[10] A. J. Chamkha, S. Abbasbandy, A. M. Rashad, and K. Vajravelu, Radiation effects on mixed convection over a wedge embedded in a porous medium filled with a nanofluid, Transport in Porous Media, 91(1) (2012) 261-279.10.1007/s11242-011-9843-5Suche in Google Scholar
[11] M. Gnaneswara Reddy, P. Padma, B. Shankar, and B. J. Gireesha, Thermal radiation effects on MHD stagnation point flow of nanofluid over a stretching sheet in a porous medium, J. Nanofluids, 5 (2016) 753–764.10.1166/jon.2016.1252Suche in Google Scholar
[12] E. Magyari and A. Pantokratoras, Note on the effect of thermal radiation in the linearized Rosseland approximation on the heat transfer characteristics of various boundary layer flows, Int. Comm. Heat Mass Transf., 38: (2011) 554–556.10.1016/j.icheatmasstransfer.2011.03.006Suche in Google Scholar
[13] C. S. K. Raju, N. Sandeep and M. Gnaneswara Reddy, Effect of nonlinear thermal radiation on 3D Jeffrey fluid flow in the presence of homogeneous–heterogeneous reactions, Int. J. of Eng. Research in Africa, 21 (2016) 52–68.10.4028/www.scientific.net/JERA.21.52Suche in Google Scholar
[14] M. Khan, W. A. Khan and A. S. Alshomrani, Non-linear radiative flow of three dimensional Burgers nanofluid with new mass flux effect, Int. J. Heat Mass Transf., 101 (2016) 570–576.10.1016/j.ijheatmasstransfer.2016.05.056Suche in Google Scholar
[15] S. A. Moshizi and A. Malvandi, Different modes of nanoparticle migration at mixed convection of Al2O3–water nanofluid inside a vertical microannulus in the presence of heat generation/absorption, J. Therm Anal Calorim, 126: (2016) 1947–1962.10.1007/s10973-016-5560-1Suche in Google Scholar
[16] A. Postelnicu, Influence of a magnetic field on heat and mass transfer by natural convection from vertical surface in porous media considering Soret and Dufour effects, Int. J. Heat Mass Transf., 47(67) (2004) 1467–1472.10.1016/j.ijheatmasstransfer.2003.09.017Suche in Google Scholar
[17] D. Pal, G. Mandal and K. Vajravalu, Soret and Dufour effects on MHD convective–radiative heat and mass transfer of nanofluids over a vertical non-linear stretching/shrinking sheet, Appl.Math. and Comp. 287–288 (2016) 184–200.10.1016/j.amc.2016.04.037Suche in Google Scholar
[18] Rahimah Jusoh, Roslinda Nazar and Ioan Pop, Flow and Heat Transfer of Magnetohydrodynamic Three-Dimensional Maxwell Nanofluid over a Permeable Stretching/Shrinking Surface with Convective Boundary Conditions, International Journal of Mechanical Sciences, 124-125,(2017), 166-173.10.1016/j.ijmecsci.2017.02.022Suche in Google Scholar
[19] S. A. Shehzad, A. Alsaedi, T. Hayat, Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux, PLOS One.8(7) (2013) e68139.10.1371/journal.pone.0068139Suche in Google Scholar PubMed PubMed Central
[20] M. E. M. Khedr, A. J. Chamkha and M. Bayomi, MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption, Nonlinear Analysis: Modelling and Control, 14(1) (2009) 27–40.10.15388/NA.2009.14.1.14528Suche in Google Scholar
[21] A. J. Chamkha, A. M. Aly and M. A. Mansour, Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects, Chem. Eng. Comm. 197(6) (2010) 846–858.10.1080/00986440903359087Suche in Google Scholar
[22] M. R. Krishnamurthy, B. C. Prasannakumara, B. J. Gireesha, Rama Subba Reddy Gorla, Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium, Eng. Sci. and Tech. an Int.J., 19(1) (2016)53–61.10.1016/j.jestch.2015.06.010Suche in Google Scholar
[23] B. C. Prasannakumara, B. J. Gireesha, Rama Subba Reddy Gorla and M. R. Krishnamurthy, Effects of Chemical Reaction and Nonlinear Thermal Radiation on Williamson Nanofluid Slip Flow over a Stretching Sheet Embedded in a Porous Medium, J. Aerosp. Eng., (2016) 10.1061/(ASCE)AS.1943-5525.0000578, 04016019.10.1061/(ASCE)AS.1943-5525.0000578Suche in Google Scholar
[24] B. C. Prasannakumara, M. R. Krishnamurthy, B. J. Gireesha and Rama Subba Reddy Gorla, Effect of Multiple Slips and Thermal Radiation on MHD Flow of Jeffery Nanofluid with Heat Transfer, J. of Nanofluids, 5(1) (2016) 82–93(12).10.1166/jon.2016.1198Suche in Google Scholar
[25] A. Rauf, M. K. Siddiq, F. M. Abbasi, M. A. Meraj, M. Ashraf and S. A. Shehzad, Influence of convective conditions on three dimensional mixed convective hydromagnetic boundary layer flow of Cassonnanofluid, J. of Magnetism and Magnetic Materials, 416 (2016) 200–207.10.1016/j.jmmm.2016.04.092Suche in Google Scholar
[26] A. V. Kuznetsov and D. A. Nield, The onset of double-diffusive nanofluid convection in a layer of a saturated porous medium, Transp. Porous Med., 85 (2010) 941–951.10.1007/s11242-010-9600-1Suche in Google Scholar
[27] U. Khan, N. Ahmed, S. I. U. Khan and S.T. Mohyud-din, Thermo-diffusion effects on MHD stagnation point flow towards a stretching sheet in a nanofluid, Propulsion and Power Res., 3(3) (2014) 151–158.10.1016/j.jppr.2014.07.006Suche in Google Scholar
[28] M. Goyal and R. Bhargava, Finite element solution of double-diffusive boundary layer flow of viscoelastic nanofluids over a stretching sheet, Comp. Math. and Mathematical Phy., 54(5) (2014) 848–863.10.1134/S0965542514050029Suche in Google Scholar
[29] S. Panigrahi, M. Reza and Akshya Kumar Mishra, Mixed convective flow of a Powell-Eyring fluid over a non-linear stretching surface with thermal diffusion and diffusion thermo, Procedia Eng., 127 (2015) 645 – 651.10.1016/j.proeng.2015.11.356Suche in Google Scholar
[30] R. Kandasamy, C. Jeyabalan and K. K. Sivagnana Prabhu, Nanoparticle volume fraction with heat and mass transfer on MHD mixed convection flow in a nanofluid in the presence of thermo-diffusion under convective boundary condition, Appl. Nanosci. 6 (2016) 287–300.10.1007/s13204-015-0435-5Suche in Google Scholar
[31] N. Akbar, Z. Khan, S. Nadeem and W. Khan, Double-diffusive natural convective boundary-layer flow of a nanofluid over a stretching sheet with magnetic field, I. J. of Numerical Methods for Heat & Fluid Flow, 26(1) (2016) 108–121.10.1108/HFF-01-2015-0019Suche in Google Scholar
[32] I. C. Liu, H.I. Andersson, Heat transfer over a bidirectional stretching sheet with variable thermal conditions, Int. J. Heat Mass Transf. 51 (2008) 4018–4024.10.1016/j.ijheatmasstransfer.2007.10.041Suche in Google Scholar
[33] A. Mushtaq, M. Mustafa, T. Hayat, A. Alsaedi, A numerical study for three-dimensional viscoelastic flow inspired by nonlinear radiative heat flux, Int. J. Nonlinear Mech. 79 (2016) 83–87.10.1016/j.ijnonlinmec.2015.11.006Suche in Google Scholar
Nomenclature
- C
nanoparticle volume fraction
- DB
Brownian diffusion coefficient
- DT
thermophoresis diffusion coefficient (m2/s)
- DTC
Dufour diffusivity
- DS
solutal diffusivity
- DCT
Soret diffusivity
- Le
nanofluid Lewis number
- Ln
Regular Lewis number
- Ld
Dufour Solutal Lewis number
- Nc
Regular buoyancy ratio parameter
- Nr
Nanofluid buoyancy ratio parameter
- Nb
Brownian motion parameter
- Nd
Modified Dufour parameter
- Nt
thermophoresis parameter
- Nux
local Nusselt number
- Pr
Prandtl number
- Rd
radiation parameter
- Rex
local Reynolds number
- T
fluid temperature
- Tw
Temperature at the wall surface
- T∞
ambient fluid temperature
- Uw, Vw
velocity of the stretching sheet along x and y direction (m/s)
- a, b
stretching velocity (m/s)
- C
stretching ratio parameter
- cf
specific heat coefficient of fluid (J/kgK)
- cp
specific heat coefficient of nanoparticles (J/kgK)
- f, g
dimensionless velocity components
- g
acceleration due to gravity (m/s2)
- h
heat transfer coefficient (W/m2K)
- k
Thermal conductivity (W/mK)
- k*
mean absorption coefficient (1/m)
- qr
radiative heat flux (W/m2
- u, v, w
velocity components along, and directions (m/2)
- x, y, z
Cartesian Co-ordinates (m)
Greek Letters
- λ
relaxation time
- λ*
Mixed Convection parameter
- β
Maxwell parameter
- βT
volumetric thermal expansion coefficient (K−1)
- βγ
volumetric solutal expansion coefficient
- γ
solutal concentration
- α
Thermal diffusivity of the fluid (m2/s)
- η
similarity variable
- τ
ratio of effective heat capacity of the nanoparticle material to heat capacity of the fluid
- θw
temperature ratio parameter
- μ
dynamic viscosity (kg/ms)
- v
kinematic viscosity (m2/s)
- ρf
density of the fluid (kg/m3)
- ρp
density of the particles (kg/m3)
- σ*
Stefan–Boltzmann constant (W/m2 K4)
- ϕ
dimensionless nanoparticle volume fraction
Superscript
- ′
derivative with respect to η
Subscript
- w
wall
- ∞
ambient
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- B-spline Wavelet Method for Solving Fredholm Hammerstein Integral Equation Arising from Chemical Reactor Theory
- Numerical Techniques for Unsteady Nonlinear Burgers Equation Based on Backward Differentiation Formulas
- Numerical Analysis of Peristaltic Transport of Casson Fluid for non-zero Reynolds Number in Presence of the Magnetic Field
- MHD Double-diffusive boundary-layer flow of a Maxwell nanofluid over a bidirectional stretching sheet with Soret and Dufour effects in the presence of radiation
- Diffusion-Chemotaxis Model of Effects of Cortisol on Immune Response to Human Immunodeficiency virus
- An efficient hybrid computational technique for solving nonlinear local fractional partial differential equations arising in fractal media
- Cattaneo -Christov heat flux model for magnetohydrodynamic flow in a suspension of dust particles towards a stretching sheet
- Exponential Stability of Impulsive Delay Differential Equations by using Weight Function
Artikel in diesem Heft
- Frontmatter
- B-spline Wavelet Method for Solving Fredholm Hammerstein Integral Equation Arising from Chemical Reactor Theory
- Numerical Techniques for Unsteady Nonlinear Burgers Equation Based on Backward Differentiation Formulas
- Numerical Analysis of Peristaltic Transport of Casson Fluid for non-zero Reynolds Number in Presence of the Magnetic Field
- MHD Double-diffusive boundary-layer flow of a Maxwell nanofluid over a bidirectional stretching sheet with Soret and Dufour effects in the presence of radiation
- Diffusion-Chemotaxis Model of Effects of Cortisol on Immune Response to Human Immunodeficiency virus
- An efficient hybrid computational technique for solving nonlinear local fractional partial differential equations arising in fractal media
- Cattaneo -Christov heat flux model for magnetohydrodynamic flow in a suspension of dust particles towards a stretching sheet
- Exponential Stability of Impulsive Delay Differential Equations by using Weight Function

