Abstract
Electromagnetic devices with multiple polarization modes are urgently needed in remote sensing detection and radar imaging due to their ability to obtain scattering information from targets through manipulation of full-parametric Jones matrix components (J xx , J xy , J yx , J yy ). Although metasurfaces exhibit exceptional capability for polarization control, they typically facilitate conversion between specific linearly polarized (LP) and circularly polarized waves on Poincaré sphere. Here, we find that identical phases in two co-polarized components is exactly half of the sum of phases in two cross-polarized components by deriving Jones matrix J AAL with full-parametric Aharonov–Anandan (AA) phase Jones matrix. On this basis, a novel spin-decoupled paradigm is proposed by merging of AA phase and Pancharatnam–Berry (PB) phase mechanisms. Such a paradigm in diatomic metasurface is promised to achieve elegant amplitude-phase controlling and generate arbitrary polarized waves. For verification, two types of meta-devices were designed, fabricated, and experimentally characterized. Compared to the combination of propagation and PB phase, the proposed method enables simultaneous broadband arbitrary LP-to-LP conversion and wavefront control with a relative bandwidth of 43.5 %. Our strategy establishes theoretical foundation for spin-decoupled phase manipulation and amplitude-phase control of AA phase, providing a solid platform and guidance for the design of devices with arbitrary polarization and wavefront control.
1 Introduction
The ability to arbitrarily manipulate polarization states has become essential for applications such as remote sensing [1], [2], [3], [4], and imaging [5], [6], [7], enabling effective resolution of target signatures. Such a control fundamentally requires complete engineering of the full-parametric Jones matrix (J xx , J xy , J yx , J yy ) to generate desired polarization response [8], [9], [10], [11]. Metasurfaces have emerged as integrated polarization control platforms [8], [9], [10], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], achieving on-demand polarization tailoring through manipulation of two orthogonal Jones matrix components [25], [26], [27], [28], [29], [30] via diverse strategies including space-time coding [31], [32], [33], [34], multi-phase interference [23], [35], and lossy absorption [36]. Among these approaches, meta-atoms incorporating multi-phase mechanisms such as Pancharatnam–Berry (PB) phase, propagation phase, or detour phase [19], [37], [38] were not limited by spectral constraints and can be further extended to high frequencies [39], [40]. Researchers have attempted to employ multiple pure PB phase meta-atoms to form pixel for arbitrary polarization conversion and wavefront manipulation [41], [42]. However, PB phase emerges under CP wave illumination through rotating meta-atoms by θ, suffering from spin-locking constraints and yielding a phase difference of Δφ = ±2σθ (where σ = +1/−1 corresponds to right/left-handed polarization, RCP/LCP) [43]. Therefore, PB phase-based metasurfaces produce conjugate images at symmetric mirrored positions [44]. In contrast, the propagation phase leverages dimension variations within LP basis [42], [44], [45], [46], [47], [48], and thus their intrinsic resonant dispersion effects severely restrict operational bandwidth.
To address spin-locking and bandwidth limitations, the Aharonov–Anandan (AA) phase in chiral meta-atoms achieves spin-decoupled functionality via non-adiabatic cyclic evolution of waves carrying spin angular momentum in meta-atoms. This geometric mechanism yields phase shifts governed by asymmetric arc length, achieving broadband operation (1.245 μm – 1.55 μm, 21.8 % fractional bandwidth) [49], [50], [51], [52], [53] via asymmetric evolution arcs by mimicking Aharonov–Bohm ring [54], [55]. However, most prior studies on chiral meta-atoms have focused primarily on the cross-circularly polarized Jones matrix components, resulting in limited polarization states (specific x/y-polarized or CP state) and thus making manipulation of AA phase particularly co-CP phase components (
Here, we report a novel strategy for generating arbitrary polarization state by combining full-parametric AA phase of chiral meta-atoms and PB phase. The contribution of our concept to EM wave manipulation is that a general amplitude-phase relationship for each scattering component of Jones matrix of AA phase is derived based on unitarity, symmetry, and lossless features, and then the extended Jones matrix with AA phase is further developed for broadband amplitude-phase controlling. The importance and significance of our work can be inspected from Figure 1a, which shows that the input LP or CP wave on a meta-device with our proposed integrated AA and PB phases can be converted into output wave with arbitrary polarization state and phase. For verification and potential applications, two types of proof-of-concept meta-devices have been designed to achieve arbitrary polarization. The first meta-device converts y-polarized wave into ±45° LP waves and focuses their energy to different positions, while the second one transfers CP wave into arbitrarily polarized state with elegant ability of wavefront control. Our approach not only opens an alternative avenue for conversion between arbitrary polarization states and complicated wavefront shaping, but also provides a general approach to analyzing the complete EM properties of metasurface platforms. This method holds promise for applications in integrated systems, such as polarization multiplexing, polarization detection and communication, etc.
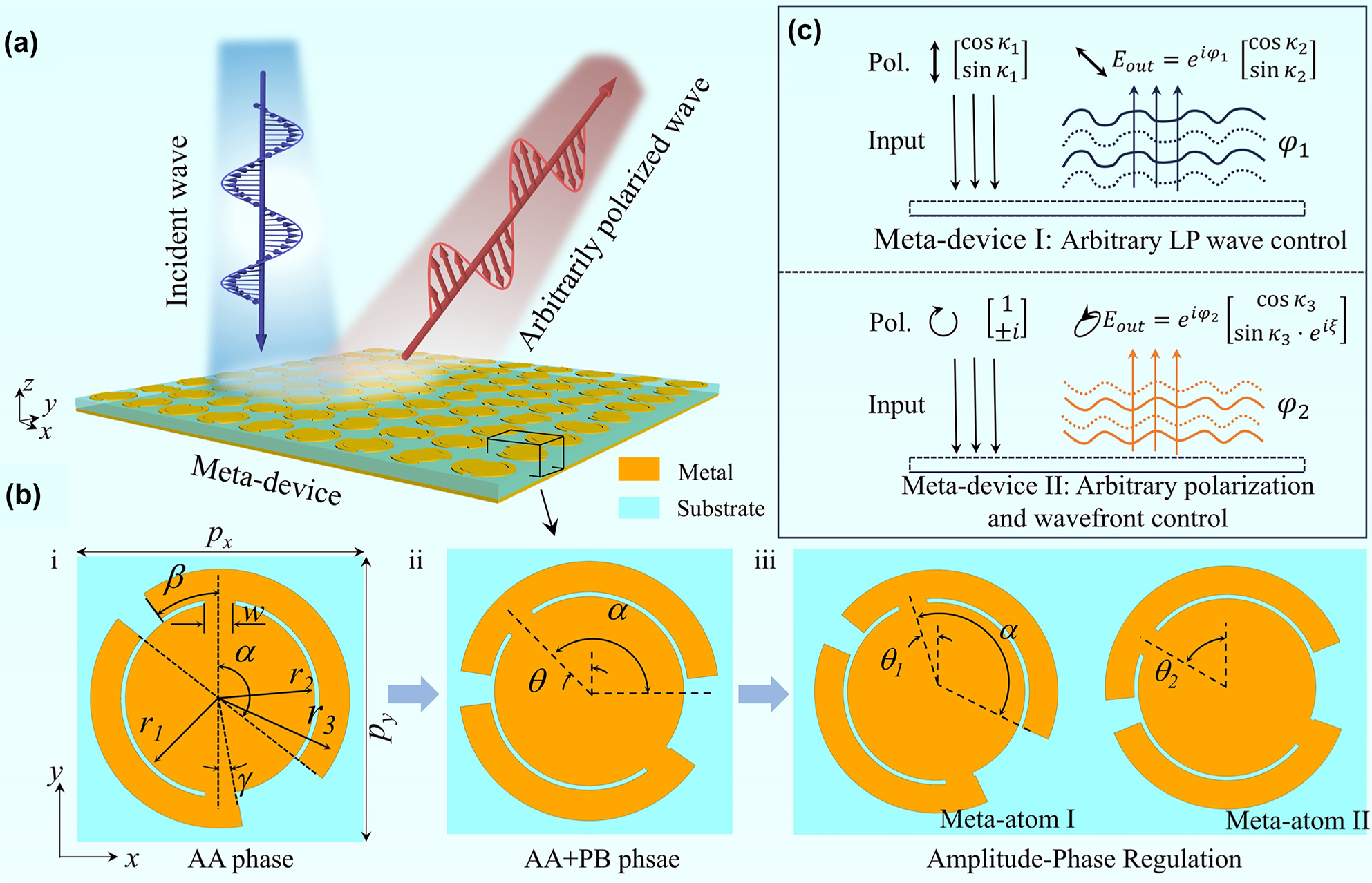
Schematic function of meta-devices based on AA phase. (a) Schematic function of AA phase polarization conversion meta-device. (b) Evolution of basic chiral meta-atom to spin-decoupled and diatomic spin-decoupled with amplitude-phase control based on AA phase. Detailed geometric parameters are p x = p y = 10 mm, w = 1 mm, β = 36°, γ = 8°, r 1 = 3.1 mm, and r 2 = 3.25 mm. Here, w denotes the width of connecting rod between metallic arc and inner disk, p x and p y represent the periodicity of meta-atom in x- and y-directions, respectively, and θ, θ 1, and θ 2 denote orientation angles of the top metal patch of meta-atoms. (c) Schematic function of two types of arbitrary polarization conversion and wavefront control.
2 Results and discussions
Theoretically, an arbitrarily polarized wave can be decomposed into two orthogonal CP components with distinct amplitude and phase response. To synthesize arbitrary states of polarization, we designed a chiral meta-atom leveraging AA phase for spin-dependent phase control, enabling independent manipulation of two cross-CP components, as seen in inset (i) of Figure 1b. The reflective meta-atom comprises a 2-mm-thick F4B substrate sandwiched by top metal patch and bottom metal ground. To increase cross-polarized scattering coefficients across a wide bandwidth, the top patch is designed consisting of a centered metallic disk and dual identical arc-shaped metallic patterns attached to the disc with rectangular patches. Parameters β and γ were meticulously optimized through full-wave electromagnetic simulations and subsequently fixed at 36° and 8°, respectively. The arc angle α of the left upper and right bottom arm is dynamically adjusted in accordance with different phase requirements.
For arbitrary LP-to-LP wave conversion, AA phase and PB phase are synergistically integrated to decouple EM waves of two cross-CP components (
2.1 Concept and fundamentals
2.1.1 AA phase mechanism
The realization of arbitrary polarization conversion through Aharonov–Anandan (AA) phase demands precise control over both amplitude and phase responses of each Jones matrix element. While previous chiral metamaterials have achieved spin-dependent phase manipulation, our framework advances this paradigm by analyzing the relationships within the Jones matrix components of chiral meta-atom and achieving elegant amplitude-phase control. Firstly, we analyze a reflective meta-atom’s EM properties through the linear Jones matrix
where
A basic chiral meta-atom prototype was designed and numerically characterized to validate above theory, as shown in inset (i) of Figure 1b. Figure 2 and Table S1 presents the reflected amplitude and phase response of the proposed meta-atom under normal LCP wave illumination, demonstrating |r
rl
| > 0.75 across 9–14 GHz while satisfying the lossless condition (|r
ll
|2 + |r
rl
|2 ≈ 1). Similar behavior is observed under RCP wave excitation (Figure 2d), where |r
lr
| = |r
rl
| and |r
rr
|2 + |r
lr
|2 ≈ 1. A larger phase cover of 270° with quasi-nondispersive properties is achieved in
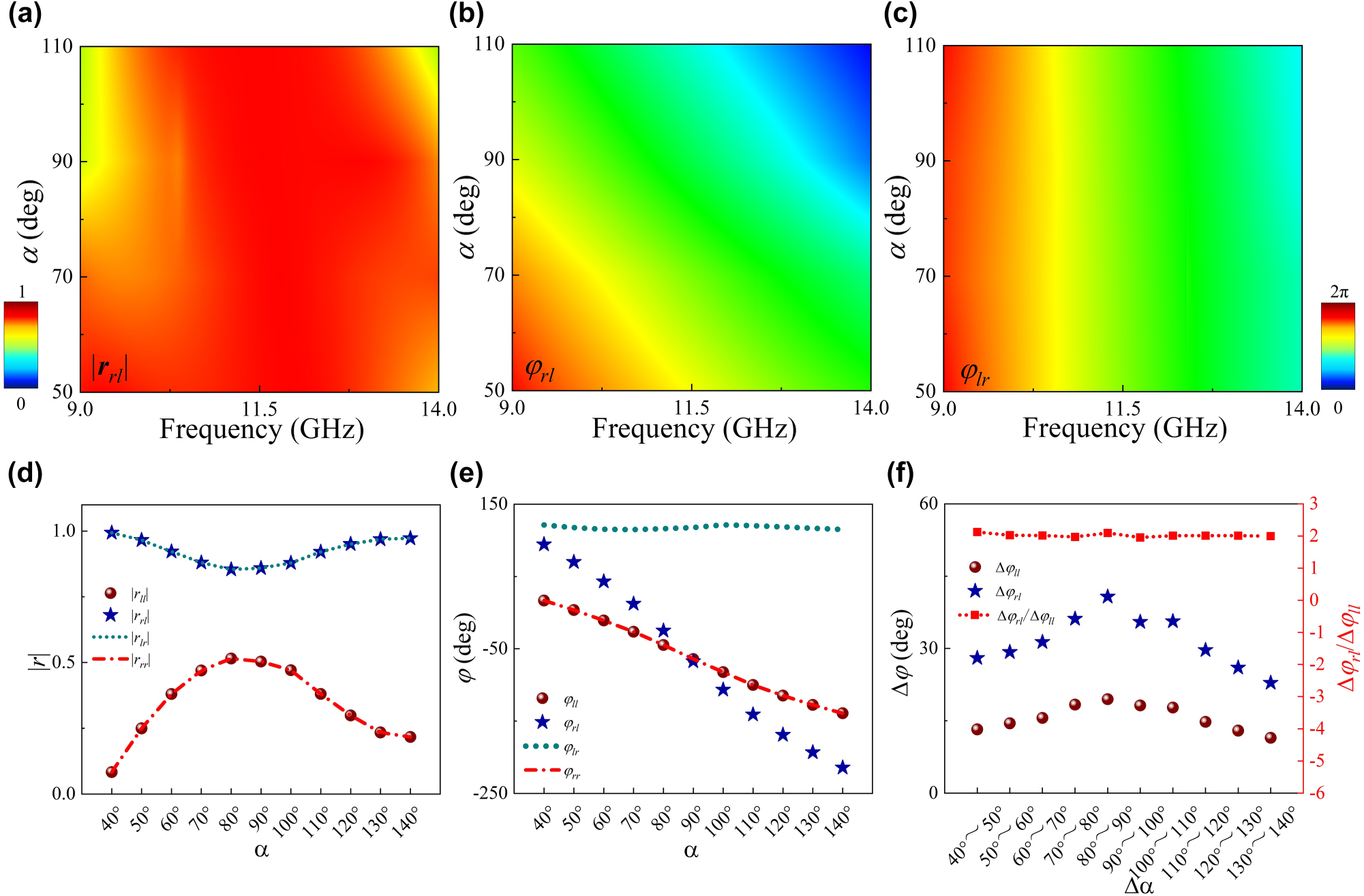
EM characterization of proposed chiral meta-atom based AA phase mechanism. Numerically calculated reflection magnitude and phase response at 9–14 GHz for (a–b)
2.1.2 Jones matrix of phase and amplitude-phase control based on synergetic AA and PB phase mechanisms
To independently adjust the phase φ
ll
, φ
lr
, and φ
rl
, the methods of spin-decoupled phase and amplitude-phase manipulation are proposed by simultaneously manipulating α and θ of meta-atoms. For amplitude-phase manipulation, a diatomic meta-atom is designed which consists of two spin-decoupled chiral meta-atoms (meta-atom I and II) with the same α but different θ, as illustrated in inset (iii) of Figure 1b. Cross- and co-polarized scattering coefficients are controlled by the angle difference between two meta-atoms under excitation of CP wave based on far-field interference, as shown in
For verification, reflection amplitude and phase response of diatomic meta-atom as orientation angle difference Δθ (Δθ = θ
2 − θ
1, θ
1 = 0) varying from 0° to 90° were numerically simulated within 9–13 GHz, as illustrated in Figure S7 (Supporting Information). The results demonstrate that |r
rl
| and |r
lr
| decrease from near unity to 0.24 (−12.4 dB) as Δθ increases within a wide frequency band 9.8–11.8 GHz, while the trend is opposite for |r
ll
| (Figure S7a and b). The numerically calculated reflection intensity |r
rl
| are consistent with counterparts of theoretically calculated by Eq. (3), as shown in Figure S7c. It is evident that phase shifts occurs in both
2.2 Arbitrary LP wave control using spin-decoupled phase manipulation
To achieve arbitrary LP-to-LP conversion and wavefront control, we implement spin-decoupled phase manipulation via meta-atoms (Figure 3a) featuring simultaneous modulation of arc angle α for AA phase control and orientation angle θ for PB phase engineering. As indicated from Eq. (S7), this equation can be further simplified as
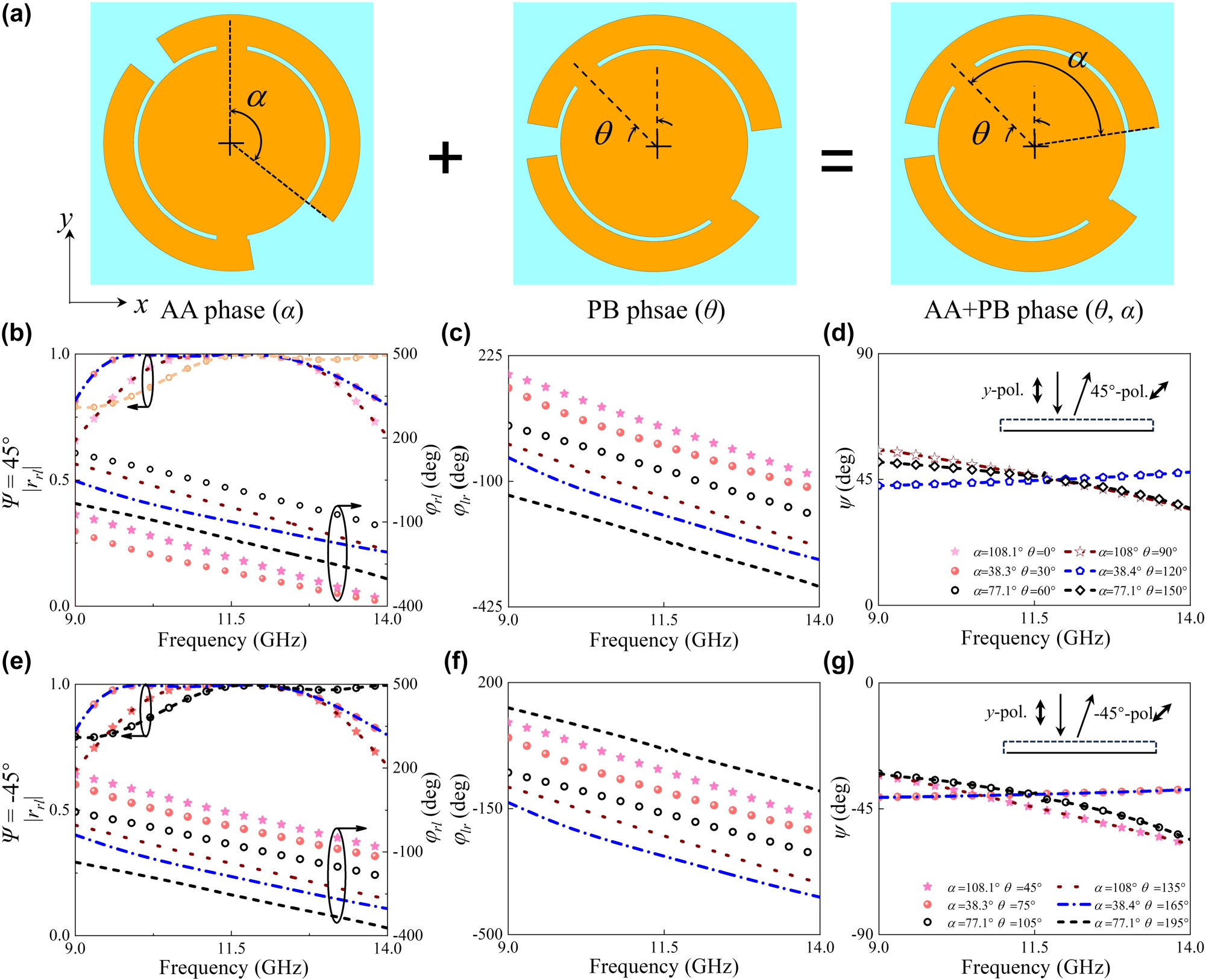
Structure and EM response of spin-decoupled meta-atoms with synergetic AA and PB phase mechanisms. (a) Structural evolution of meta-atoms implementing from geometric phase to synergetic AA and PB phases, where AA phase is tuned via arc angle α while PB phase is controlled through orientation angle θ, respectively. Numerically calculated amplitude (|r rl | and |r lr |) and phase response (φ rl and φ lr ) of cross-circular polarization components for meta-atoms A (b–c) and B (e–f) under LCP and RCP wave illumination, where meta-atoms A and B represent structures transforming y-polarized wave to 45° and −45°-LP waves, respectively. Polarization angle of meta-atoms for y-polarized wave to (d) 45° and (g) −45° LP waves, where ψ = (φ rl – φ lr )/2.
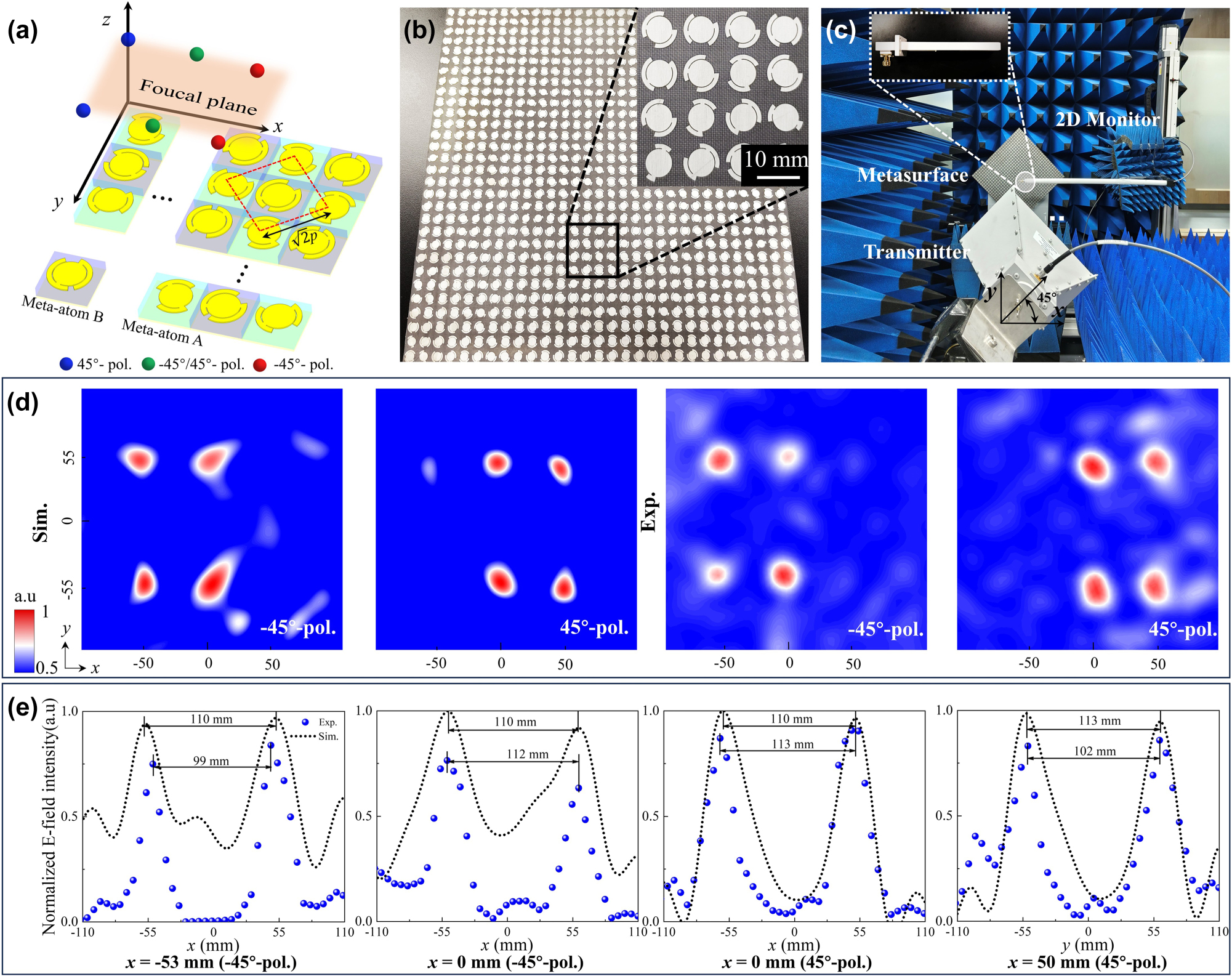
Experimental characterization of the spin-decoupled planar multifocal lens for arbitrary LP states. (a) Meta-device array layout, where dashed line represents real periodicity p r of meta-atoms A and B. (b) Photograph of the fabricated sample of planar multifocal lens. (c) Near-field experimental setup. (d–e) Simulated and measured normalized 2D electric field intensity |E 45°| and |E −45°| at 11.1 GHz in xoy plane (z = 204 mm), with cross-sectional profiles along y at x = −53, 0, 0, and 50 mm.
For experimental demonstration, a porotype of planar multifocal lens was fabricated with sample shown in Figure 4b and characterized using the near-field experimental setup illustrated in Figures 4c and S12a, where LP horn antenna and sample were turned around 45° clockwise. Two horizontally and vertically oriented waveguide probes were employed to capture reflected static EM signals from −45° and 45° LP waves, respectively. Upon interaction with meta-atom A, the y-polarized incident wave was transformed into a −45° LP wave, generating four localized energy foci at coordinates (−53, −49.5 mm), (−53, 49.5 mm), (0, −56 mm), and (0, 56 mm) within xoy plane (z = 204 mm). These measured foci characterized by 0.6 power beam width of field pattern normalized to the maximized intensity exhibited a size of 8.3, 19.3, 19.4 and 2.8 mm, respectively. Similarly, meta-atom B achieved conversion of y-polarized waves to 45° LP state with energy foci at (0, −55.5 mm), (0, 55.5 mm), (50, −56.5 mm), and (50, 56.5 mm) in the same plane. The corresponding focal sizes are 16.6 mm, 24.9 mm, 11.1 mm, and 19.3 mm. Simulated and experimental focal positions at 11.1 GHz align closely with theoretical predictions, as demonstrated in Figure 4d and e. Furthermore, two-dimensional (2D) electric field distributions in yoz planes at x = −53 mm, 0 mm, and 50 mm (Figures S9 and S10) clearly illustrate the designed multi-focus behavior with high spatial resolution and cross-polarization suppression across 10–12 GHz. The discrepancy between the simulated and measured multiple foci observed in Figure 4e may have resulted from differences in the selection of the focal plane (Figures S9 and S10). Relatively narrower bandwidths between meta-atoms in Figure 3 and array originate primarily from phase errors induced by near-field coupling and resonant frequency shift of meta-atoms as the periodicity increases from p to p r (Figures S11 and S12). Additionally, laterally distributed multifoci inherently induce chromatic dispersion under broadband operation, resulting in undesired focal elongation along x axis. The measured focusing efficiency, defined as the ratio between the powers carried by the focal spot of 45° (−45°) LP and the incident beam, was calculated as 91 % (89 %). Large signal intensity is received based on simultaneous matching of polarization states and spatial position, confirming the meta-device’s capability for arbitrary LP-to-LP conversion and high-precision wavefront control.
2.3 Arbitrary polarization and wavefront control using amplitude-phase control
To enable arbitrary polarization detection and communication, the polarization state of incident EM wave needs to be converted into arbitrary states of polarization. Here, we demonstrated the conversion of CP states to arbitrary states of polarization alongside wavefront control via the amplitude-phase manipulation. As shown in Eq. (S4), the co-polarized phase response follows φ
rr
= φ
AA/2, while the cross-polarized phase shifts are governed by θ
1 + θ
2 under RCP wave illumination. This configuration enables precise polarization engineering through the derived polarization angle ψ = φ
AA/4 − (θ
1 + θ
2)/2 and phase retardation Δφ = φ
AA/4 + (θ
1 + θ
2)/2. The ellipticity manipulation of the anisotropic diatomic meta-atom is dictated by the orientation angle difference Δθ = θ
2 − θ
1, establishing a mapping between geometric parameter space and full-Stokes polarization control. Furthermore, we validate the applicability of this strategy through the design and characterization of functional meta-device. According to the relationship between arbitrary polarization parameters and components of CP wave (
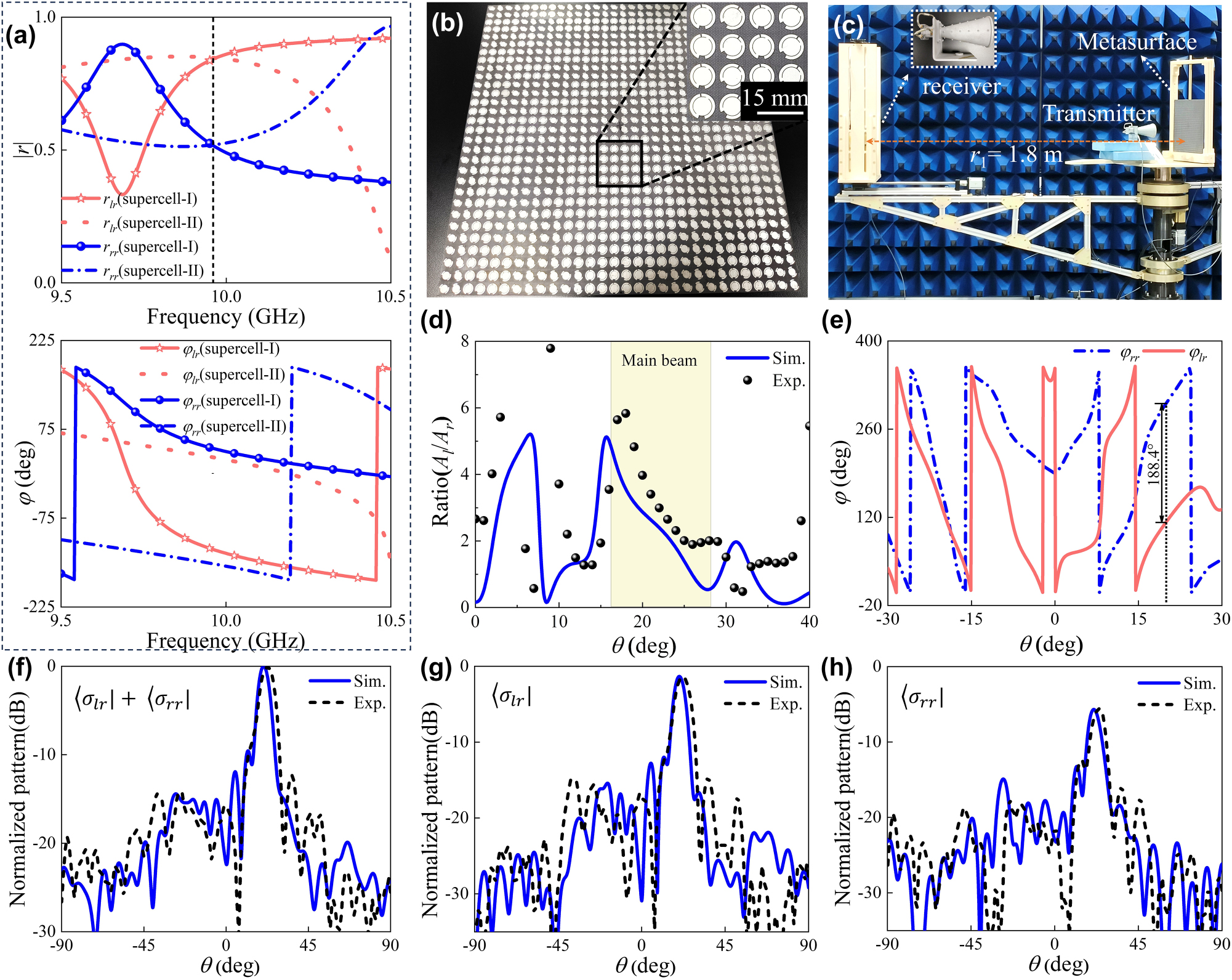
Experimental characterization of diatomic meta-device with amplitude-phase control for arbitrary polarization and wavefront manipulation. (a) Simulated amplitude (|r lr | and |r rr |) and phase (|φ lr | and |φ rr |) responses of the 1-bit meta-atoms under RCP wave illumination. (b) Photograph of the fabricated sample. (c) Far-field experimental setup. (d) Amplitude ratio and (e) phase difference between LCP and RCP components. (f–h) Simulated and experimental 1D far-field scattering patterns at f = 10 GHz in xoz plane. Here (f), (g), and (h) correspond to that of total, LCP, and RCP components of scattered wave.
For proof-of-principle verification, a 15 × 15 beam-steering diatomic meta-device was designed with linear phase distribution shown in Figure S14. The porotype was fabricated with sample shown in Figure 5b and measured using the far-field experimental setup shown in Figures 5c and S10b. For quantitative and intuitive characterization, the linear amplitude ratio and phase difference of
3 Conclusions
In summary, we have proposed a phase-amplitude manipulation strategy by synergistically combining full-parametric AA phase and PB phase. This approach is established based on unitary, symmetric, and lossless features of the Jones matrix, and validated through a meta-atom platform that simultaneously achieves arbitrary LP-to-LP conversion and wavefront manipulation across 9–14 GHz with 43.5 % fractional bandwidth. Two proof-of-concept meta-devices were designed: A planar multifocal lens converting y-polarized wave to ±45° LP waves and generating four predefined foci with >89 % efficiency; A diatomic meta-device transforming RCP wave into left-handed elliptically polarized wave with beam steering, exhibiting 83.1 % anomalous reflection efficiency. Both numerical simulations and experimental measurements confirm the effectiveness of our strategy. More importantly, theoretical derivation establishes a foundation for advanced applications of AA phase in arbitrary polarization synthesis.
4 Experimental section
For verification, the meta-devices were designed, numerically characterized and experimentally fabricated and measured. Both meta-devices (30 × 30 array, 300 × 300 mm2) were designed using CST Microwave Studio with open boundary conditions in xyz directions. The prototypes were fabricated via standard PCB processing, and the near- and far-field EM performances were measured by an AV3672B vector network analyzer (Figure S16 in Supporting Information). For near-field measurements, an LP horn antenna was positioned 1.6 m from the meta-device to ensure planar wavefront illumination. A 2D motor-mounted waveguide probe scanned a 350 × 350 mm2 area to map field intensities. For far-field characterization, an RCP transmitter was fixed at z = 205 mm (focal-diameter ratio F/D = 0.7) and dual LCP/RCP receivers were placed 1.8 m away, sweeping an angle from 0° to 180°.
Funding source: Innovation Capability Support Program of Shaanxi
Award Identifier / Grant number: 2025ZC-KJXX-81
Funding source: Research Program Project of Youth Innovation Team of Shaanxi Provincial Education Department
Award Identifier / Grant number: 24JP221
Funding source: Shaanxi Youth Science and Technology New Star
Funding source: Innovative Talents Cultivate Program for Technology Innovation Team of Shaanxi Province
Award Identifier / Grant number: 2024RS-CXTD-08
Funding source: National Natural Science Foundation of China
Award Identifier / Grant number: 62171459
Award Identifier / Grant number: 62571546
-
Research funding: This work was supported by the National Natural Science Foundation of China (No. 62171459 and 62571546), Innovative Talents Cultivate Program for Technology Innovation Team of Shaanxi Province (No. 2024RS-CXTD-08), the Special Talents Support Program of Shaanxi Province for Young Top Talents, Shaanxi Youth Science and Technology New Star, Innovation Capability Support Program of Shaanxi (No. 2025ZC-KJXX-81), Research Program Project of Youth Innovation Team of Shaanxi Provincial Education Department (No. 24JP221), and Youth Innovation Team of Shaanxi Universities.
-
Author contributions: All co-authors have made significant contributions to this work. TL, YW, and WF contributed equally to this work. TL and HXX proposed the idea and wrote the manuscript with input from all authors. YW analyzed the results and made additional efforts in preparing the manuscript. WF wrote the program code for array design. ZW and HW participated in the experiments. HL and FZ contributed to the methodology and data visualization. HXX and XGL supervised the project. All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript.
-
Conflict of interest: Authors state no conflicts of interest.
-
Data availability: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
[1] T. L. Ainsworth, J. P. Kelly, and J. S. Lee, “Classification comparisons between dual-pol, compact polarimetric and quad-pol SAR imagery,” ISPRS J. Photogramm. Remote Sens., vol. 64, no. 5, pp. 464–471, 2009, https://doi.org/10.1016/j.isprsjprs.2008.12.008.Search in Google Scholar
[2] S. Wang, W. Feng, and M. Sato, “Polarimetric calibration for a ground-based synthetic aperture radar system,” in PIERS, 2019, pp. 632–639.10.1109/PIERS-Fall48861.2019.9021317Search in Google Scholar
[3] S. Wang, W. Feng, K. Kikuta, G. Chernyak, and M. Sato, “Ground-based bistatic polarimetric interferometric synthetic aperture radar system,” in IGARSS, 2019, pp. 8558–8561.10.1109/IGARSS.2019.8900455Search in Google Scholar
[4] Z. Dong, X. Feng, H. Zhou, C. Liu, M. Zhang, and W. Liang, “Effects of uniaxial bianisotropic media on full-polarimetric GPR signatures,” IEEE Trans. Geosci. Remote Sens., vol. 61, pp. 1–20, 2023, https://doi.org/10.1109/tgrs.2023.3286945.Search in Google Scholar
[5] C. He, H. He, J. Chang, B. Chen, H. Ma, and M. J. Booth, “Polarisation optics for biomedical and clinical applications: a review,” Light Sci. Appl., vol. 10, no. 1, p. 194, 2021, https://doi.org/10.1038/s41377-021-00639-x.Search in Google Scholar PubMed PubMed Central
[6] M. M. S. Hossain, N. K. Nahar, and K. Sertel, “Resolution-enhanced polarimetric terahertz imaging,” IEEE Trans. Terahertz Sci. Technol., vol. 14, no. 5, pp. 675–690, 2024, https://doi.org/10.1109/tthz.2024.3430040.Search in Google Scholar
[7] R. S. Gurjar et al.., “Imaging human epithelial properties with polarized light-scattering spectroscopy,” Nat. Med., vol. 7, no. 11, pp. 1245–1248, 2001, https://doi.org/10.1038/nm1101-1245.Search in Google Scholar PubMed
[8] Z. Liu et al.., “Dual jones matrices empowered six phase channels modulation with single-layer monoatomic metasurfaces,” Laser Photonics Rev., vol. 19, no. 7, p. 2401526, 2025, https://doi.org/10.1002/lpor.202401526.Search in Google Scholar
[9] Y. Bao, F. Nan, J. Yan, X. Yang, C.-W. Qiu, and B. Li, “Observation of full-parameter Jones matrix in bilayer metasurface,” Nat. Commun., vol. 13, no. 1, p. 7550, 2022, https://doi.org/10.1038/s41467-022-35313-2.Search in Google Scholar PubMed PubMed Central
[10] Y. Bao, L. Wen, Q. Chen, C.-W. Qiu, and B. Li, “Toward the capacity limit of 2D planar Jones matrix with a single-layer metasurface,” Sci. Adv., vol. 7, no. 25, p. eabh0365, 2021, https://doi.org/10.1126/sciadv.abh0365.Search in Google Scholar PubMed PubMed Central
[11] H. Qin et al.., “Sphere of arbitrarily polarized exceptional points with a single planar metasurface,” Nat. Commun., vol. 16, no. 1, p. 2656, 2025, https://doi.org/10.1038/s41467-025-57737-2.Search in Google Scholar PubMed PubMed Central
[12] W. Tang et al.., “MIMO transmission through reconfigurable intelligent surface: system design, analysis, and implementation,” IEEE J. Sel. Areas Commun., vol. 38, no. 11, pp. 2683–2699, 2020, https://doi.org/10.1109/jsac.2020.3007055.Search in Google Scholar
[13] C. X. Huang, J. Zhang, Q. Cheng, and T. J. Cui, “Polarization modulation for wireless communications based on metasurfaces,” Adv. Funct. Mater., vol. 31, no. 36, p. 2103379, 2021, https://doi.org/10.1002/adfm.202103379.Search in Google Scholar
[14] H. Li et al.., “Metasurfaces for polarization-insensitive and directional backscatter communication,” IEEE Trans. Antenn. Propag., vol. 72, no. 10, pp. 8082–8087, 2024. https://doi.org/10.1109/TAP.2024.3439887.Search in Google Scholar
[15] H. Zhong et al.., “Gigahertz-rate-switchable wavefront shaping through integration of metasurfaces with photonic integrated circuit,” Adv. Photonics, vol. 6, no. 1, p. 016005, 2024, https://doi.org/10.1117/1.ap.6.1.016005.Search in Google Scholar
[16] X. Hu et al.., “Metasurface-based computational imaging: a review,” Adv. Photonics, vol. 6, no. 1, p. 014002, 2024, https://doi.org/10.1117/1.ap.6.1.014002.Search in Google Scholar
[17] S. Colburn, A. Zhan, and A. Majumdar, “Metasurface optics for full-color computational imaging,” Sci. Adv., vol. 4, no. 2, p. eaar2114, 2018, https://doi.org/10.1126/sciadv.aar2114.Search in Google Scholar PubMed PubMed Central
[18] B. Xiong et al.., “Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise,” Science, vol. 379, no. 6629, pp. 294–299, 2023, https://doi.org/10.1126/science.ade5140.Search in Google Scholar PubMed
[19] Z.-L. Deng et al.., “Diatomic metasurface for vectorial holography,” Nano Lett., vol. 18, no. 5, pp. 2885–2892, 2018, https://doi.org/10.1021/acs.nanolett.8b00047.Search in Google Scholar PubMed
[20] X. Zhang et al.., “Spatial varying vectorial holography and polarization encryption based on birefringent metasurface,” Adv. Funct. Mater., vol. 34, no. 41, p. 2404196, 2024, https://doi.org/10.1002/adfm.202404196.Search in Google Scholar
[21] C. Wang, H.-X. Xu, T. Liu, and F. Zhang, “Hybrid-phase assisted amplitude and phase control using full-space metasurface,” Adv. Opt. Mater., vol. 12, no. 10, p. 2302153, 2023, https://doi.org/10.1002/adom.202302153.Search in Google Scholar
[22] C. Feng et al.., “Diatomic metasurface for efficient six-channel modulation of Jones matrix,” Laser Photonics Rev., vol. 17, no. 8, p. 2200955, 2023, https://doi.org/10.1002/lpor.202200955.Search in Google Scholar
[23] X. Mu et al.., “Chirality-free full decoupling of Jones matrix phase-channels with a planar minimalist metasurface,” Nano Lett., vol. 25, no. 4, pp. 1322–1328, 2025, https://doi.org/10.1021/acs.nanolett.4c04577.Search in Google Scholar PubMed
[24] Q. Song et al.., “Bandwidth-unlimited polarization-maintaining metasurfaces,” Sci. Adv., vol. 7, no. 5, p. eabe1112, 2021, https://doi.org/10.1126/sciadv.abe1112.Search in Google Scholar PubMed PubMed Central
[25] Y. Zhang, H. Liu, H. Cheng, J. Tian, and S. Chen, “Multidimensional manipulation of wave fields based on artificial microstructures,” Opto-Electron. Adv., vol. 3, no. 11, p. 200002, 2020, https://doi.org/10.29026/oea.2020.200002.Search in Google Scholar
[26] H.-X. Xu, G. Hu, X. Kong, Y. Shao, P. Genevet, and C.-W. Qiu, “Super-reflector enabled by non-interleaved spin-momentum-multiplexed metasurface,” Light Sci. Appl., vol. 12, no. 1, p. 78, 2023, https://doi.org/10.1038/s41377-023-01118-1.Search in Google Scholar PubMed PubMed Central
[27] A. Arbabi, E. Arbabi, Y. Horie, S. M. Kamali, and A. Faraon, “Planar metasurface retroreflector,” Nat. Photonics, vol. 11, no. 7, pp. 415–420, 2017, https://doi.org/10.1038/nphoton.2017.96.Search in Google Scholar
[28] S. Im Sande, Y. Deng, S. I. Bozhevolnyi, and F. Ding, “Spin-controlled generation of a complete polarization set with randomly-interleaved plasmonic metasurfaces,” Opto-Electron. Adv., vol. 7, no. 8, p. 240076, 2024, https://doi.org/10.29026/oea.2024.240076.Search in Google Scholar
[29] H.-X. Xu et al.., “Polarization-insensitive 3D conformal-skin metasurface cloak,” Light Sci. Appl., vol. 10, no. 1, p. 75, 2021, https://doi.org/10.1038/s41377-021-00507-8.Search in Google Scholar PubMed PubMed Central
[30] Y. Wang et al.., “Detection and anti-detection with microwave-infrared compatible camouflage using asymmetric composite metasurface,” Adv. Sci., vol. 11, no. 43, p. 2410364, 2024. https://doi.org/10.1002/advs.202410364.Search in Google Scholar PubMed PubMed Central
[31] Q. Hu et al.., “Arbitrary and dynamic poincaré sphere polarization converter with a time-varying metasurface,” Adv. Opt. Mater., vol. 10, no. 4, p. 2101915, 2022, https://doi.org/10.1002/adom.202101915.Search in Google Scholar
[32] Q. Hu et al.., “Dynamically generating diverse multi-beams with on-demand polarizations through space-time coding metasurface,” Adv. Opt. Mater., vol. 12, no. 6, p. 2300093, 2023, https://doi.org/10.1002/adom.202300093.Search in Google Scholar
[33] G.-B. Wu et al.., “A universal metasurface antenna to manipulate all fundamental characteristics of electromagnetic waves,” Nat. Commun., vol. 14, no. 1, p. 5155, 2023, https://doi.org/10.1038/s41467-023-40717-9.Search in Google Scholar PubMed PubMed Central
[34] X. G. Zhang, Y. L. Sun, B. Zhu, W. X. Jiang, Z. Zhang, and T. J. Cui, “Light-controllable time-domain digital coding metasurfaces,” Adv. Photonics, vol. 4, no. 2, p. 025001, 2022, https://doi.org/10.1117/1.ap.4.2.025001.Search in Google Scholar
[35] T. Wu et al.., “Spin-decoupled interference metasurfaces for complete complex-vectorial-field control and five-channel imaging,” Adv. Sci., vol. 9, no. 35, p. 2204664, 2022, https://doi.org/10.1002/advs.202204664.Search in Google Scholar PubMed PubMed Central
[36] Z. Chu et al.., “Generic vectorial hologram based on simultaneous and independent amplitude and phase modulation of orthogonal polarization states via single completely spin-decoupled meta-particles,” Laser Photonics Rev., vol. 18, no. 1, p. 2300609, 2024, https://doi.org/10.1002/lpor.202300609.Search in Google Scholar
[37] Z.-L. Deng et al.., “Facile metagrating holograms with broadband and extreme angle tolerance,” Light Sci. Appl., vol. 7, no. 1, p. 78, 2018, https://doi.org/10.1038/s41377-018-0075-0.Search in Google Scholar PubMed PubMed Central
[38] K. Zhang, Y. Wang, S. N. Burokur, and Q. Wu, “Generating dual-polarized vortex beam by detour phase: from phase gradient metasurfaces to metagratings,” IEEE Trans. Microwave Theory Tech., vol. 70, no. 1, pp. 200–209, 2022, https://doi.org/10.1109/tmtt.2021.3075251.Search in Google Scholar
[39] A. Zaidi et al.., “Metasurface-enabled single-shot and complete Mueller matrix imaging,” Nat. Photonics, vol. 18, no. 7, pp. 704–712, 2024, https://doi.org/10.1038/s41566-024-01426-x.Search in Google Scholar
[40] Y. Bao, J. Ni, and C.-W. Qiu, “A minimalist single-layer metasurface for arbitrary and full control of vector vortex beams,” Adv. Mater., vol. 32, no. 6, p. 1905659, 2020, https://doi.org/10.1002/adma.201905659.Search in Google Scholar PubMed
[41] Q. Song et al.., “Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces,” Nat. Commun., vol. 11, no. 1, p. 2651, 2020, https://doi.org/10.1038/s41467-020-16437-9.Search in Google Scholar PubMed PubMed Central
[42] Q. Song et al.., “Broadband decoupling of intensity and polarization with vectorial Fourier metasurfaces,” Nat. Commun., vol. 12, no. 1, p. 3631, 2021, https://doi.org/10.1038/s41467-021-23908-0.Search in Google Scholar PubMed PubMed Central
[43] D. Wen et al.., “Helicity multiplexed broadband metasurface holograms,” Nat. Commun., vol. 6, no. 1, p. 8241, 2015, https://doi.org/10.1038/ncomms9241.Search in Google Scholar PubMed PubMed Central
[44] N. Mao et al.., “Nonlinear vectorial holography with quad-atom metasurfaces,” Proc. Natl. Acad. Sci. U. S. A., vol. 119, no. 22, p. e2204418119, 2022, https://doi.org/10.1073/pnas.2204418119.Search in Google Scholar PubMed PubMed Central
[45] H. X. Xu, Y. Shao, H. Luo, Y. Wang, and C. Wang, “Janus reflective polarization-division metadevices with versatile functions,” IEEE Trans. Microwave Theory Tech., vol. 71, no. 8, pp. 3273–3283, 2023, https://doi.org/10.1109/tmtt.2023.3267539.Search in Google Scholar
[46] A. Arbabi, Y. Horie, M. Bagheri, and A. Faraon, “Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission,” Nat. Nanotechnol., vol. 10, no. 11, pp. 937–943, 2015, https://doi.org/10.1038/nnano.2015.186.Search in Google Scholar PubMed
[47] R. Zhao et al.., “Polarization and holography recording in real- and k-space based on dielectric metasurface,” Adv. Funct. Mater., vol. 31, no. 27, p. 2100406, 2021, https://doi.org/10.1002/adfm.202100406.Search in Google Scholar
[48] Y. Yuan, K. Zhang, Q. Wu, S. N. Burokur, and P. Genevet, “Reaching the efficiency limit of arbitrary polarization transformation with non-orthogonal metasurfaces,” Nat. Commun., vol. 15, no. 1, p. 6682, 2024, https://doi.org/10.1038/s41467-024-50560-1.Search in Google Scholar PubMed PubMed Central
[49] K. Qu et al.., “Interference-assisted independent amplitude and phase manipulation with broadband chiral meta-mirror,” Adv. Opt. Mater., vol. 12, no. 19, p. 2400312, 2024, https://doi.org/10.1002/adom.202400312.Search in Google Scholar
[50] F. Zhang et al.., “Holographic communication using programmable coding metasurface,” Nanophotonics, vol. 13, no. 8, pp. 1509–1519, 2024, https://doi.org/10.1515/nanoph-2023-0925.Search in Google Scholar PubMed PubMed Central
[51] C. Wang, F. Zhang, H. X. Xu, T. Liu, and Z. Wang, “Dynamical multi-polarized reflectarray antenna using spin-decoupled programmable metasurface,” IEEE Antennas Wirel. Propag. Lett., vol. 23, no. 7, pp. 1–5, 2024, https://doi.org/10.1109/lawp.2024.3378227.Search in Google Scholar
[52] T. Liu et al.., “Six-channel programmable coding metasurface simultaneously for orthogonal circular and linear polarizations,” Photonics Res., vol. 11, no. 6, pp. 1047–1056, 2023, https://doi.org/10.1364/prj.486185.Search in Google Scholar
[53] Z. Wang et al.., “Spin-decoupled metasurface by hybridizing curvature- and rotation-induced geometrical phases,” Laser Photonics Rev., vol. 18, no. 9, p. 2400184, 2024. https://doi.org/10.1002/lpor.202400184.Search in Google Scholar
[54] G. D. Bai et al.., “Spin-symmetry breaking through metasurface geometric phases,” Phys. Rev. Appl., vol. 12, no. 4, p. 044042, 2019, https://doi.org/10.1103/physrevapplied.12.044042.Search in Google Scholar
[55] R. Ji et al.., “Chirality-assisted Aharonov–Anandan geometric-phase metasurfaces for spin-decoupled phase modulation,” ACS Photonics, vol. 8, no. 6, pp. 1847–1855, 2021, https://doi.org/10.1021/acsphotonics.1c00505.Search in Google Scholar
[56] C. Menzel, C. Rockstuhl, and F. Lederer, “Advanced Jones calculus for the classification of periodic metamaterials,” Phys. Rev. A, vol. 82, no. 5, p. 053811, 2010, https://doi.org/10.1103/physreva.82.053811.Search in Google Scholar
[57] J. Li et al.., “Hybrid dispersion engineering based on chiral metamirror,” Laser Photonics Rev., vol. 17, no. 3, p. 2200777, 2023, https://doi.org/10.1002/lpor.202200777.Search in Google Scholar
[58] W. Yang et al.., “Direction-duplex Janus metasurface for full-space electromagnetic wave manipulation and holography,” ACS Appl. Mater. Interfaces, vol. 15, no. 22, pp. 27380–27390, 2023, https://doi.org/10.1021/acsami.3c04382.Search in Google Scholar PubMed
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/nanoph-2025-0357).
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Reviews
- What is next for LLMs? Pushing the boundaries of next-gen AI computing hardware with photonic chips
- Application of metasurface in future displays
- Research Articles
- Transmissive hybrid metal–dielectric metasurface bandpass filters for mid-infrared applications
- A self-assembled two-dimensional hypersonic phononic insulator
- Long-metallic-strip array with parasitic rings: an efficient metasurface for dual-broadband electromagnetic window at large angles
- Polarization Raman spectra of graphene driven by monolayer ReS2
- POST: photonic swin transformer for automated and efficient prediction of PCSEL
- Nonreciprocal transmission based on quasi-bound states in the continuum via scaled lattice constants
- Chat to chip: large language model based design of arbitrarily shaped metasurfaces
- Azimuth-controlled multicolor shifting based on subwavelength sinusoidal grating
- Transparent metafilms for enhanced thermal regulation in energy-efficient windows
- Synergetic full-parametric Aharonov–Anandan and Pancharatnam–Berry phase for arbitrary polarization and wavefront control
- Label free super resolution imaging with photonic nanojets from tunable tapered optical fibers
- Defect-insensitive bound states in the continuum in antisymmetric trapezoid metasurfaces in the visible range
Articles in the same Issue
- Frontmatter
- Reviews
- What is next for LLMs? Pushing the boundaries of next-gen AI computing hardware with photonic chips
- Application of metasurface in future displays
- Research Articles
- Transmissive hybrid metal–dielectric metasurface bandpass filters for mid-infrared applications
- A self-assembled two-dimensional hypersonic phononic insulator
- Long-metallic-strip array with parasitic rings: an efficient metasurface for dual-broadband electromagnetic window at large angles
- Polarization Raman spectra of graphene driven by monolayer ReS2
- POST: photonic swin transformer for automated and efficient prediction of PCSEL
- Nonreciprocal transmission based on quasi-bound states in the continuum via scaled lattice constants
- Chat to chip: large language model based design of arbitrarily shaped metasurfaces
- Azimuth-controlled multicolor shifting based on subwavelength sinusoidal grating
- Transparent metafilms for enhanced thermal regulation in energy-efficient windows
- Synergetic full-parametric Aharonov–Anandan and Pancharatnam–Berry phase for arbitrary polarization and wavefront control
- Label free super resolution imaging with photonic nanojets from tunable tapered optical fibers
- Defect-insensitive bound states in the continuum in antisymmetric trapezoid metasurfaces in the visible range

