Spatiotemporal optical vortex reconnections of loop vortices

2.1 One paraboloid amplitude null

To study vortex reconnection phenomena, we begin with the field in the space-time domain, which is given by the Fresnel transform of the particular function in the spatial frequency–frequency k x , k y , ω domain as shown in Equation (1). In this manuscript, we will refer the k x , k y , ω domain as the Fourier domain.

where ℱ_3D represents the 3D Fourier transform, u = exp − k x 2 w k x 2 − k y 2 w k y 2 − ω 2 Δ ω 2 is the spatial and temporal frequency envelope, w is the spatial frequency bandwidth, Δω is the temporal frequency bandwidth, d = w/Δω is a factor that compensates the frequency/spatial frequency bandwidth mismatch, and the l = l 1 , l 2 , l 3 are the paraboloid powers. Additionally, the coefficients A k x , A k y , A ω control diffraction and dispersion effects for various propagations conditions. For example, focusing along x by a cylindrical lens would have A k x = λ z while A _ω would be constant and A k y approximately constant.

It is worth noting the meaning of the first three terms. For instance, when the first term is set to zero k x 2 + k y 2 + d ω = 0 , it defines a paraboloid. On the paraboloid surface, the electric field becomes zero and, therefore, the amplitude will be null. At the same time, there is a sign change from the inside of the paraboloid to the outside, indicating the π phase shift on the paraboloid surface for odd powers of l. Consequently, the first three terms represent three perpendicular paraboloids with amplitude null and a π phase shift in the Fourier domain.

From this simple Fourier domain representation, complex reconnections occur in space-time with propagation under various combinations of the paraboloid powers, spatial diffraction effects, and temporal dispersion effects. For the simplest case of l   =   1,0,0 , there is a single paraboloid that gives one ring vortex in space-time. For simplicity, we assume a circular symmetric beam with bandwidth w = w k x = w k y and frequency bandwidth Δ ω   =   w d   =   w (e.g., d = 1 mm⁻¹/1 THz), which results in equation (1) at the focus A = 0 becoming

This is a single closed-loop vortex with size dependent on the bandwidth. As an example, if this loop vortex was created at the focus of a focusing lens, the input before the lens would be E i n ∝ x 2   +   y 2   +   i t u ′ , which has phase Γ = a t a n x 2   +   y 2 t (Figure 1a). This has an intensity null centered around a point and is roughly ellipsoidal in shape. Additionally, the phase only advances with varying the polar coordinate θ   =  atan x 2 + y 2 / t , which reveals the loop with poloidal increasing phase evolves to a point with spherical-like phase profile. As another example, if the optical wavepacket is temporally focused during propagation in dispersive media, with the temporal focus effect coinciding with the spatial focus effect, the input wavepacket would be highly chirped with a paraboloid amplitude null (Figure 1b).

Figure 1:

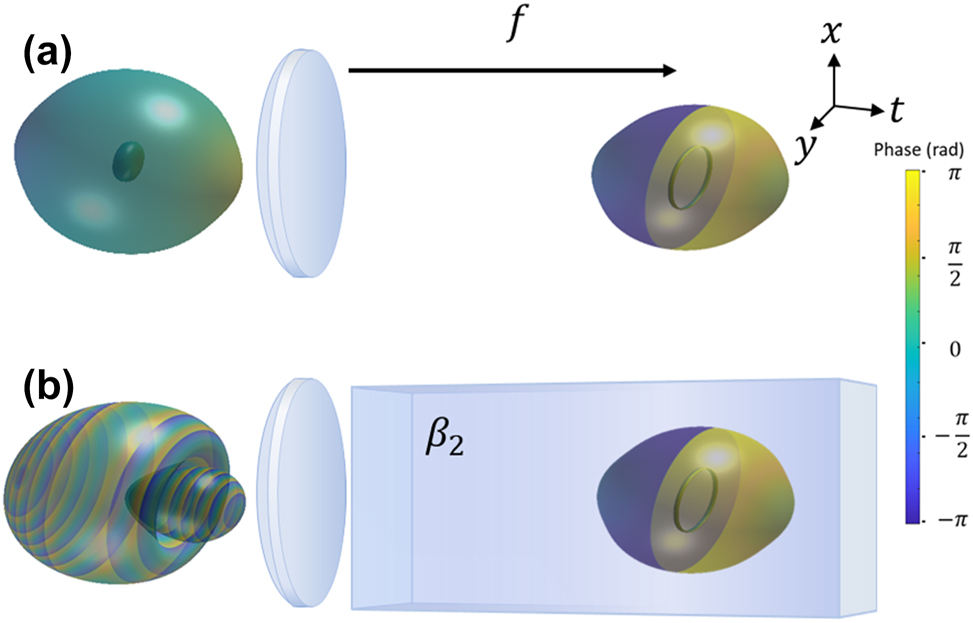
Illustrative examples of generating single loop vortices, highlighting an input wavepacket’s relationship to the resulting loop’s frequency domain profile. (a) A ring vortex forming at a spatial focus arises from an intensity null centered around a point. (b) A ring vortex forming at the spatial and temporal focus starts from a highly chirped paraboloid amplitude null.

2.2 Two perpendicular paraboloid amplitude nulls

With two paraboloid amplitude nulls in the Fourier domain l   =   l 1 , l 2 , 0 , multi-loop arrays are generated, leading to complex reconnections during propagation.

In the first example, we consider spherical focusing in dispersive media with simultaneous spatial and temporal focusing. For simplicity, we assumed the same propagation (focusing) effect in all directions with A   =   A k x   =   A k y   =   A ω where A = 0 represents the wavepacket at the focus, and for now set the bandwidths to w k x   =   w k y   =   1 m m − 1 and Δω = 1 THz.

Figure 2a shows the iso-intensity surface profile with two perpendicular paraboloid amplitude nulls in the Fourier domain. Figure 2b presents the corresponding space-time iso-intensity plot at large negative A. We remove the wavepacket envelope for clarity by using a filter and display the resulting processed intensity shown at a 20 % iso-value. The two paraboloidal sheets merge and collapse into a closed-loop vortex as A increases from A = −3 to A = −0.3 (Figure 2b and c). From A = −0.15 to A = 0, a two-step reconnection sequence occurs via folding and releasing of multiple loops. The set of reconnections are labeled in the figures along with each individual reconnection being highlighted with arrows. In this process, one loop shifts away and shrinks until it disappears (Figure 2h and i). This process is referred to as vortex death [14]. Figure 2i shows that at the focus a multi-loop connection forms. As A increases further, the reverse process occurs, leading to the birth of a vortex loop on the opposite side of the wavepacket (Figure 2j–o). For a clearer perspective, a video of the entire process is available in Video 1. The multi-loop array at the focus resembles the results presented in self-focused nonlinear pulse propagation [16].

Figure 2:

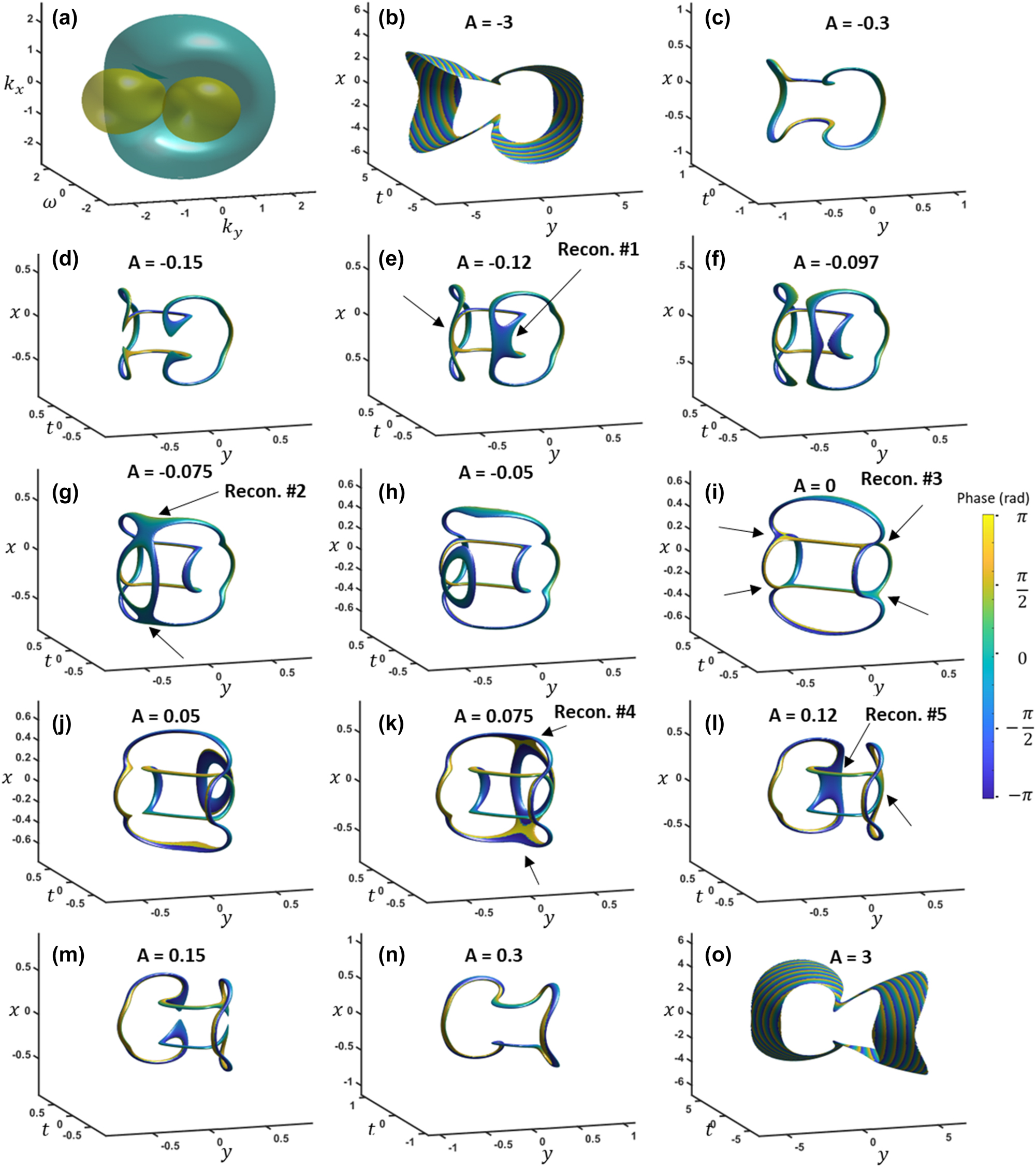
Reconnections resulting for simulteanous spatial and temporal focusing for the case of two paraboloids in the frequency domain. (a) The two paraboloids in the frequency domain. (b)–(o) Inside the wavepacket envelope for different values of A for spatiotemporal focusing, with (g) showing the focus. The iso-surface values are 20 % normalized intensity. Phase is shown from −π to π. k _x and k _y units are in inverse millimeters and ω units are in THz, while x and y units are in millimeters and t is in picoseconds. A is in units of mm² and ps² for the spatial and temporal components, respectively. Also shown in Video 1.

These ring vortices have spiral phases as shown in the cross section phase plots of Figure 3a, where the coordinates are rotated to y ′ = 1 2 y − t and t ′ = 1 2 y   +   t to obtain the best cross-sectional views. Due to the symmetry of the rings, the total orbital angular momentum (OAM) calculated by L = ∫ r ⃗ × E * ∇ E d r with r ⃗   =   [ x , y , t ] is always zero, independent of propagation parameter A. Despite of the local OAM conservation, there can be motion of these vortices. For example, during a reconnection in fluids, the distance between vortices scales with time according to d ∝ t ^0.5 [2]. It will be valuable to see if such motion occurs with spatiotemporal optical reconnections.

Figure 3:

Cross-sections of loop vortices and their trajectories during reconnecting with propagation. (a) The iso-intensity at A = −0.04 in coordinates rotated by 45° in the y-t plane. Phase cross sections are displayed for x = 0, t′ = 0, and y′ = 0. (b)–(d) The trajectory of the top and bottom of the ring vortex is shown by plotting the iso-intensity of the t′ = 0 cross section over A. (e)–(g) The trajectory of the sides of the ring vortex is shown by plotting the iso-intensity of the x = 0 cross section over A. The iso-surface values are 20 % normalized intensity.

To analyze the trajectories, we plot the cross sections over the propagation dimension, A, to create a 3D trajectory. The t′ = 0 cross section trajectory is plotted in Figure 3b–d, which shows the trajectory of the top and bottom parts of each of the rings. With the 3D visualization of the cross section with propagation, the second and fourth sets of reconnections (shown in Figure 2g and k) are evident. One vortex from the initial reconnection shrinks until it disappears, while the other crosses the center, eventually reconnecting with another vortex that just appeared from a point. In total, this process maps out a closed loop. The trajectory approaching the vortex death or leaving the vortex birth scales to the half power, with a fit shown in Figure 3d, matching the motion of vortices in fluids. Likewise, the x = 0 cross section is plotted over A in Figure 3e and f. In this, the vortex trajectories don’t form a closed loop, but the motion approaching a vortex death or leaving a vortex birth still scales to the half power.

To understand how the spatial frequency and temporal frequency bandwidths affect the field, we look at the equation of the electric field at the spatial and temporal focus (A = 0), again assume w = w _x = w _y and Δω = w/d = 1,

Equation (3) has several terms that depend on the bandwidth, w, which occurs because terms of different power in equation (1) (i.e., k x 3 , k x 2 , k x ) are multiplied by the bandwidth to a higher power (e.g., w ³, w ², w) with a Fourier transform. This is visualized in Figure 4. At a small bandwidth, the B term given by equation (3.1) dominates, which is approximately a single vortex along the x axis (Figure 4a). As the bandwidth increases, this vortex line splits and two loops form. Further increasing the bandwidth, what was shown Figure 2i, causes the C term given by equation (3.2) to dominate. At large bandwidth, the D term given by equation (3.3) now begins to dominate equation (3), as two holes form.

Figure 4:

Varying the spatial and frequency bandwidth. (a)–(c) The iso-intensity at A = 0 for small to large bandwidths. (d)–(f) The x = 0 cross sections plotted over A for two different bandwidths. The iso-surface values are 20 % normalized intensity.

It is also valuable to understand how bandwidth alters the vortex trajectory. Figure 4d–f shows the x = 0 cross section plotted over A for larger bandwidths. As the bandwidth increases, the initial reconnection is by reconnecting to other vortices (Figure 4d). With further increase in bandwidth, four symmetric rings form (Figure 4e and f). This shows that there are four simultaneous vortex births at large bandwidth, while these vortices then reconnect at eight locations at A = 0. Based on our analysis of varying the bandwidth in the range where term D dominates, the rings tend to follow the equation of an ellipse where one ring is defined as

where e is the Euler number, w is the bandwidth, and the offset of the loop from the center is y ′ = 1 2 w . While locally there is a half power scaling with propagation, when there is a sequence of vortex birth, reconnection, and death, the trajectory generally can follow an elliptical path. Although the bandwidth can affect loop arrangements and trajectories, it is worthy to note that this can be compensated by changing relative coefficients on the terms in Equation (1). For example, if a coefficient a is added to Equation (1) so that the first two set of terms are k x 2 + k y 2 + a d ω l 1 k x 2 + d 2 ω 2 + a k y l 2 , the coefficient can be increased as bandwidth increases to offset this change.

Next, we show spherical focusing along the x-axis and y-axis, where we set A   =   A k y   =   A k x while assuming no dispersion effect, with A _ω = 0, and also again using bandwidths of w k x = w k y = 1 m m − 1 and Δω = 1 THz. Since the reconnections after the focus are simply the reverse process, we illustrate the propagation up to the focus (Figure 5). As the complexity of reconnections has increased significantly, we will also only present a few vortex profiles near the focus, while Video 2 captures the entire range of the process. Initially, two loop vortices reconnect and break apart into two (Figure 5a and b). They reconnect with each other and split apart again (Figure 5c–f). Near the focus, another set of reconnections occurs that leads to a similar process of vortex death (Figure 5f–i). It is also intriguing to observe how loop vortex reconnection behaves in the case of one-dimensional diffraction (i.e., cylindrical lens focusing). While we have not provided figures for such a case, we provided Video 3 and Video 4 for clearer visualization of cylindrical focusing along the x-axis and the y-axis exhibiting their unique reconnection behaviors.

Figure 5:

Spherical focusing to the focus for (a)–(i) increasing values of A, where (i) is at the focus. The iso-surface values are 20 % normalized intensity. x and y units are in millimeters while t is in picoseconds. A is in units of mm². Also shown in Video 2.

We now examine the effect of increasing the l powers on the Fourier-space paraboloids. Figure 6 shows the result of spherical focusing with l = {2, 2, 0}, and the process is also shown in Video 5. Although much more complicated patterns emerge, at the focus, a well-organized collection of intersecting loops appears (Figure 6d). Cylindrical focusing along the y-axis is shown in Video 6, while spherical focusing with l = {2, 1, 0} is shown in Video 7. All cases exhibit distinct loop vortex reconnections.

Figure 6:

Spherical focusing with l = {2, 2, 0} for (a)–(d) increasing value of A. l 1 , l 2 = { 3,3 } from a (e) front and (f) side perspective. l 1 , l 2 = { 6,6 } from a (g) front and (h) side perspective. The iso-surface values are 20 % intensity for (a)–(d) and 15 % intensity of (e)–(h). A is in units of mm². x and y units are in millimeters while t is in picoseconds. Also shown in Video 5.

We have also investigated increasing the powers on the paraboloids even further. Figure 6e and f shows front and side perspectives of l = {3, 3, 0} loop vortex reconnections at the focus. The case of powers of l = {6, 6, 0} at the focus is presented in Figure 6g and h. A ladder-like pattern of loops appears aligned with the x-axis, accompanied by two ladder patterns appear along ±45° between the y- and t-axes. We find it quite intriguing to observe these complex arrangements of loop vortices emerging from simple paraboloid amplitude null patterns.

2.3 Three perpendicular paraboloid amplitude nulls

Next, we investigate reconnections when three perpendicular paraboloid amplitude nulls are present in the Fourier domain using Equation (1) with l = {1, 1, 1}. Unique vortex reconnections occur when both spatial and temporal focusing occur simultaneously with A = A k x = A k y = A ω .

Figure 7a shows the iso-intensity plot with large negative A, where the three paraboloids have collapsed into a single closed loop vortex, similar to the one paraboloid case (Figure 2). As A increases, the first loop shrinks, and three loops appear below the first loop (Figure 7b). The three small loops then reconnect into two loops, where one of the two remains while the other collapses to a point (Figure 7c and d). As it approaches the focus, the smaller loop grows in size to match the original loop while remaining separated (Figure 7d and e). At the same time, an outer loop also formed undergoes reconnections with itself, eventually transforming into a similar shape as the inner two loops. The outer loop reconnections are highlighted with red arrows and the inner loop reconnections highlighted with black arrows.

Figure 7:

Spatiotemporal focusing of l = {1, 1, 1} shown from a side view (a)–(i), with (e) being at the focus. The iso-surface values are 20 % normalized intensity. k _x and k _y units are in inverse millimeters and ω units are in THz, while x and y units are in millimeters and t is in picoseconds. A is in units of mm² and ps² for the spatial and temporal components, respectively. See also in Video 8 and 9.

After the focus, the vortex reconnection evolution is simply the reverse process seen before the focus (Figure 7f–i). The entire process is presented in more detail in Video 8 for the front perspective and Video 9 for the side perspective. The wavy closed-loop vortices that form around the focus resemble the experimental results of colliding ring vortices in viscous fluids [3]. In that case, several fluid ring vortices were propagated toward each other. After the collision, reconnected wavy ring vortices formed and quickly dissipated into turbulence. In contrast, our case of linear free-space propagation of an optical wavepacket allows reconnected loops to remain stable. This, in turn, can provide clearer visualization of the dynamics of reconnections.

Just like in the two-paraboloid case, spherical or cylindrical focusing results in more complex sequences of reconnections. The spherical focusing case can be observed in Video 10 and Video 11 from different perspectives. The cylindrical focusing along the y-axis also results in additional unique reconnections (Video 12 and 13).

Finally, we examine the impact of the paraboloid powers at the focus of the spatiotemporal focusing. With l = 2,1,1 , an additional outer loop appears while the shape and orientation of all the loops shift (Figure 8a). Increasing the powers to l = {2, 2, 1} results in an additional loop vortex (Figure 8b). Up to this point, it appears that the total number of loops is proportional to the sum of the powers N = l ₁ + l ₂ + l ₃. However, increasing the paraboloid powers to l = {2, 2, 2} drastically changes the number and arrangement of loops, with six small loops emerging around the center (Figure 8c and d). As all the powers are increased together to l = {3, 3, 3} (Figure 8e and f) and l = {6, 6, 6} (Figure 8g and h), circularly symmetric kaleidoscope-like patterns emerge. Again, we find it intriguing to observe these intricate arrangements of vortices emerge by simple linear propagation.

Figure 8:

The corresponding vortex arrays at the focus for three orthogonal paraboloid profiles in the Fourier domain with paraboloid powers l ₁, l ₂, and l ₃, shown from a front perspective and side perspective. x and y units are in millimeters while t is in picoseconds.

Although generating such paraboloid null patterns experimentally in the Fourier domain can be challenging, we believe current technology advancement provides a promising opportunity for their experimental realization. For example, a recently proposed time-reversal method for arbitrary 2D+1 amplitude and phase control may be capable of generating these paraboloid null profiles, thereby facilitating loop vortex reconnections [18].