High-quality CMOS compatible n-type SiGe parabolic quantum wells for intersubband photonics at 2.5–5 THz

3.1 Sample design and structural characterization

In biaxially strained high Ge content Si_1−x Ge _x alloys (x > 0.8), L, Δ₂, and Δ₄ conduction valley minima feature very similar energies whose precise value depends on the Ge content x and on the strain status [34]. By using a multivalley self-consistent code in the parabolic k·p envelope function approximation, we have calculated the three conduction band edges E c L , Δ 2 , Δ 4 ( x ) as a function of the Ge content x in the 0.8–1 range, assuming that the in-plane lattice parameter is coherent to that of a relaxed Si_0.1 Ge_0.9 VS to account for the need of a strain compensation strategy when growing Ge-rich multi-quantum well samples. In Figure 1(a), the L and Δ point band edges as a function of x in the Ge-rich alloys are reported showing that for x > 0.85 the conduction band minimum is at L. Consequently, in compositional graded Ge-rich Si_1−x Ge _x quantum wells where the Ge content x = x(z) is changed along the growth direction z, the potential V(z) felt by electrons in the well is determined by the L conduction minimum profile E c L ( x ( z ) ) [34]. The maximum achievable band-offset at L in the range x = [0.8, 1] is 126 meV and in this range E c L x exhibits a linear behavior. We point out that in our modeling, E c L ( x ) includes nonlinear terms, quadratic contributions being for instance related to the product of the L-point deformation potential with the strain field, since both these two quantities depend linearly on x. Nevertheless, Figure 1(a) indicates that those terms are practically negligible. This is confirmed by the inspection of Figure 1(b) where the potential V(z) = E c L ( x ( z ) ) calculated assuming the parabolic compositional profile of Figure 1(c) (well width W = 72 nm and Si_0.18Ge_0.82 barrier layers as in most of our samples) features a quadratic behavior with a depth D ₀ = 112 meV. It follows, as highlighted in Figure 1(d), that the calculated energy spacing of subsequent levels ΔE _j = E _j − E _j−1 is practically constant up to j = 7, in good agreement with the spacing expected in an infinite parabolic potential ℏω ₀ = ℏ(8D ₀/W ² m _z ^*)^1/2 where m _z ^* = 0.13m ₀ is the electron effective confining mass along the growth direction z. As a final remark, Figure 1(b) shows that the Δ₂ edge profile features a reversed parabolic shape with a minimum in the barrier region where the relative Δ₂ subband states are confined. We point out that in Ge-rich doped QWs, the coupling of Δ₂ states in the barriers with the populated L ones in the wells is negligible, as discussed in Ref. [35].

Figure 1:

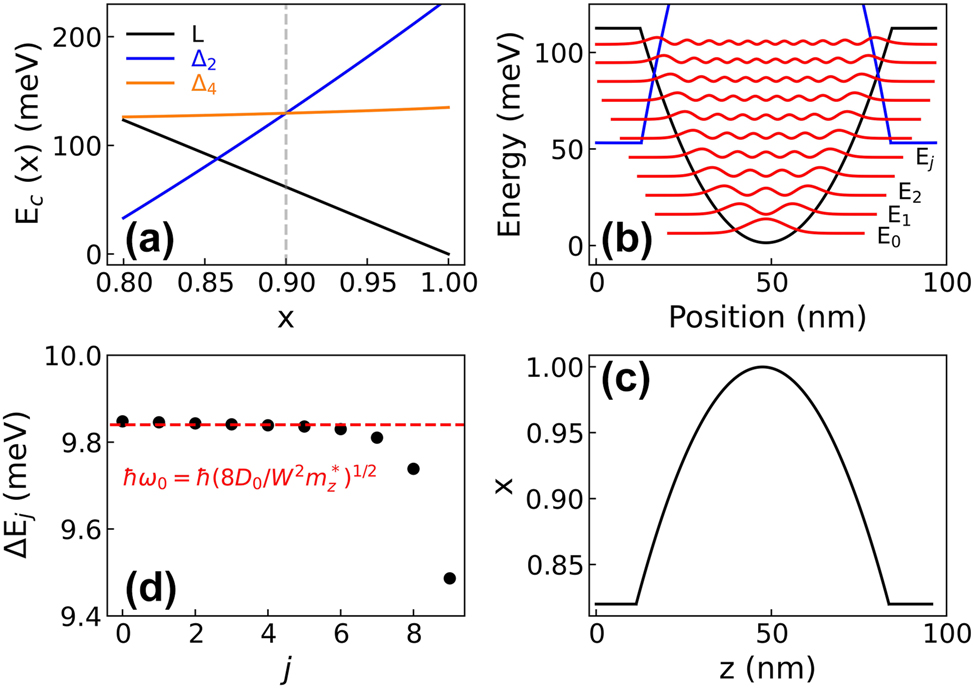
Bandstructure calculations. (a) Conduction band energy at the L, Δ₂, and Δ₄ valley edges as a function of the Ge content x in the alloy at 10 K. The energies are referred to the E c L ( 1 ) value, set to 0. In the calculation, the in-plane lattice parameter was set equal to that of a relaxed Si_0.1 Ge_0.9 VS to account for the need of a strain compensation strategy when growing Ge-rich multi-quantum well samples. In this condition, the Si_1−x Ge _x alloy is tensile strained for x < 0.9 and compressively strained for x > 0.9. Notice that the in-plane tensile strain shifts upward the Δ₂ edge with respect to the Δ₄ one, while the opposite holds for compressive strain. Conversely, the energy of L valleys, being controlled by the hydrostatic component of the strain tensor only, keeps their fourfold degeneracy. (b) Potential V(z) = E c L ( x ( z ) ) (black line) for a PQW having the graded compositional profile shown in panel (c); energy levels E _j and squared wavefunctions of the quantized states (red lines) are also reported. The edge profile at Δ₂, E c Δ 2 ( x ( z ) ) (blue line) is also displayed. (c) Ge content x in a PQW as a function of the position along the growth direction z. (d) Energy spacing of subsequent levels ΔE _j = E _j+1 − E _j .

To investigate the properties of SiGe parabolic quantum wells, we have deposited a series of samples (see Table 1) having a parabolic compositional graded Si_1−x(z) Ge _x(z) profile (0.82 < x < 1), with different well width W and doping levels n _2D.

The well width W has been varied in the range 76–46 nm to achieve transition energies in the range 10–20 meV (2.5–5 THz). We deposited a stack of N _QW = 20–25 identical wells for an overall thickness of the active region of ∼1.5–2 μm. These values have been selected envisioning the embedding of the parabolic QW stacks into microcavities to test the strong coupling limit [36]. As for the doping, we varied the phosphorus concentration in the central part of the barrier in order to tune the electron sheet densities n _2D in the [1 × 10¹¹ − 5 × 10¹¹] cm⁻² range.

The complete multilayered structure deposited on the Si(001) substrate is sketched in Figure 2(a) and the STEM image acquired on sample 2452 is shown in Figure 2(b). A reverse graded SiGe VS with a final Ge content y = 0.91 has been deposited in all the samples. To reach this final Ge content y, two 150 nm thick layers with increasing Si content have been deposited on the Ge buffer layer, as evidenced by the SIMS Ge content profile of the graded region of the virtual substrate and of the first 4 PQWs reported in Figure 2(c). To fulfill the strain-compensation conditions, the thickness of the SiGe barriers in the active region has been varied in order to maintain the average Ge content x _av close to 0.91. In our growth conditions, misfit and threading dislocations resulting from plastic relaxation of the Ge buffer and of the SiGe layers are mostly confined in the bottom part of the RG-VS, i.e., in its graded region [27]. The threading dislocation density in the topmost part of the sample has been quantified by Secco etching pit count measurements performed on similar samples [27], being ∼3 × 10⁶ cm⁻², a state of the art value for high Ge content SiGe heterostructures deposited on Si substrates.

Figure 2:

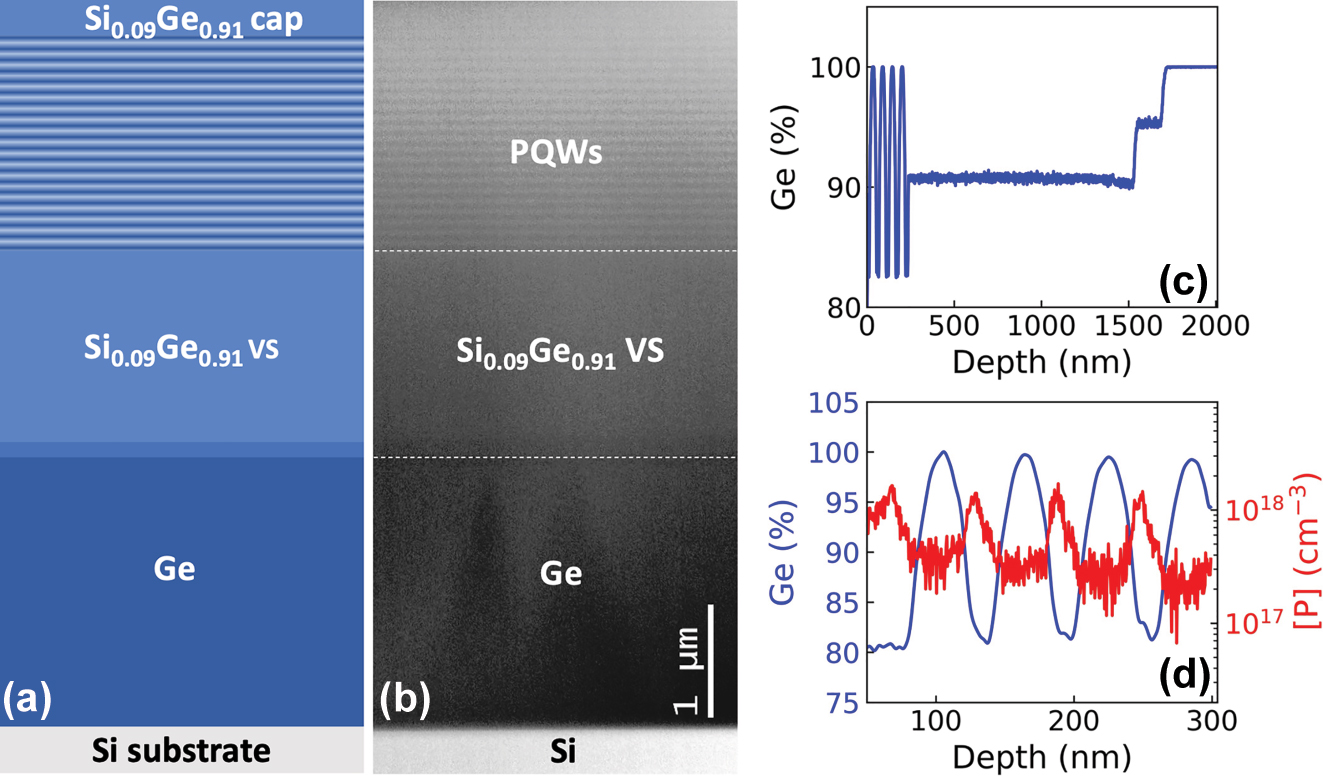
Structural characterization. (a) Sketch of the deposited multilayered structure. (b) STEM image of the 2452 PQW sample. (c) SIMS Ge content profile showing the RG VS region and the first 4 PQWs of the stack. (d) SIMS P and Ge content profiles of 4 periods acquired on a PQW sample with p _nom = 60 nm. The central 5 nm of the SiGe barriers are doped with a nominal P concentration N _3D = 1 × 10¹⁸ cm⁻³.

In Figure 2(d), the P and Ge SIMS content profiles of 4 periods of the active region of a sample featuring p _nom = 60 nm and nominally doped with a concentration of phosphorus atoms N _3D = 1 × 10¹⁸ cm⁻³ in the central 5 nm of the SiGe barriers are reported. The measurements demonstrate that in our growth conditions dopants remain well confined in the barriers with only a slight shift upwards of the P distribution with respect to the barrier center. This is a very important and not trivial achievement due to the P atoms tendency to float on Ge during the growth that could have conflicted with the need of confining donor atoms in the barriers to exploit the unique characteristic of the compensation of electron correlation effects in parabolic QWs.

The structural characterization of the samples has been performed by means of high-resolution STEM and XRD measurements. The data acquired on sample 2452, having a nominal period in the multi-quantum well stack p _nom = 90 nm, are reported in Figure 3. In panel (a), the STEM image of 5 periods of the active region of the sample is shown. The resulting intensity profile is in excellent agreement with the parabolic fit, demonstrating the capability of our UHV-CVD reactor in controlling at the nm scale the continuous grading of the SiGe alloy compositional profile. This achievement represents a significant step forward with respect to the previous attempt of growing graded Si_1−x Ge _x PQW samples by plasma-enhanced CVD reported in Ref. [30]. The 224 XRD reciprocal space map around asymmetric reflections of the layers is displayed in Figure 3(b). The positions of the VS spots associated to the Ge and the Si_0.09Ge_0.91 layers reveal the presence at room temperature of a tensile strain of about +0.15 %, which can be ascribed to the difference between the coefficients of thermal expansion in Ge and Si [37], [38]. Multiple orders of superlattice (SL) satellites, resulting from the PQW periodicity, that are perfectly vertically aligned to the Si0_0.09Ge_0.91 spot are present in the map, indicating that the entire PQW stack is coherent with the in-plane lattice parameter of the underlying VS. In Figure 3(c), we show the XRD ϑ/2ϑ curves around the 004 Ge and 004 Si Bragg peaks together with a simulation curve calculated using the parabolic fit of the STEM image as input for the well compositional profile. The sharp superlattice peaks confirm the high crystalline quality and the regular periodicity of the PQWs in the stack. Moreover, the good agreement between XRD data and simulations confirms the parabolic symmetry of the compositional profile over a relatively large area of the sample (∼4 mm²). Finally, the likeness of the XRD ϑ/2ϑ curves acquired on two nominally identical samples and reported in Figure 3(d) demonstrates the reproducibility in our reactor of the growth of different samples.

Figure 3:

Measure of parabolic concentration profile. (a) STEM image of sample 2452. The intensity profile and its parabolic fit are superimposed on the image. (b) Reciprocal space map of asymmetric 224 reflections of sample 2452. The dashed white line represents the reference values for relaxed Si_1−x Ge _x alloys. (c) 004 XRD ϑ/2ϑ curve of sample 2452 (blue curve) and dynamical simulation of the curve (green line) calculated assuming the well compositional profile resulting from the parabolic fit of the STEM data reported in (a). (d) 004 XRD rocking curves of samples 2454 and 2456 deposited using identical conditions.

The MQW stack period and the average Ge content in the stack measured by XRD on all the investigated samples are reported in Table 1. A very good agreement with respect to the nominal values has been found demonstrating once more the control acquired in the deposition process.

3.2 Optical properties of doped Si_1−x Ge _x PQWs

Intersubband transition absorption spectra have been measured on a subset of the doped samples of Table 1. The linear dichroic spectra have been acquired at different temperatures in the energy range where intersubband transitions are expected from numerical calculations. Although in this region several absorption lines are observed in the TM and TE spectra, the dichroic transmission signal is characterized in all the investigated samples by a single pronounced dip, which is due to a reduced transmission of the TM mode and which monotonically blue-shifts upon decreasing the well width (see Figure 4). Following the procedure reported in Ref. [33], the dimensionless single well absorption coefficient α _2D(E) has been determined and the central absorption energy ℏω _abs , the full width half maximum FWHM of the absorption peak, and the electron sheet density n _2D* are extracted by fitting the resulting α _2D(E) spectrum with a Lorentzian curve. The values estimated from the experimental data acquired at 100 K on all the measured samples are reported in Table 1.

Figure 4:

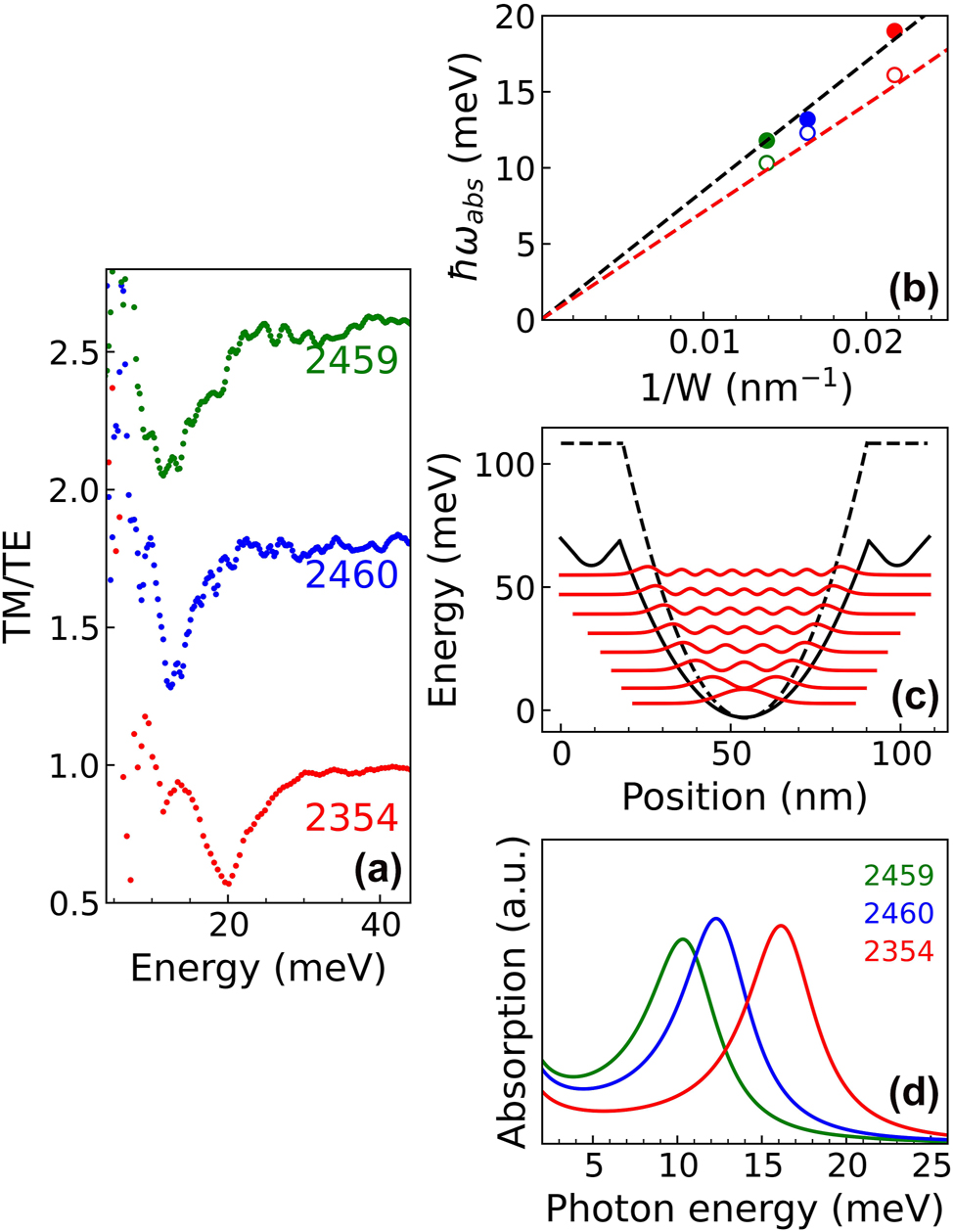
Terahertz spectroscopy measurements. (a) Dichroic transmission spectra acquired at 100 K of samples 2459, 2460, and 2354 having an electron sheet density ∼3 × 10¹¹ cm⁻² and well width 72 nm, 61 nm, and 46 nm, respectively. (b) Experimental (full circles) and theoretical (open circles) absorption energies as a function of W ⁻¹. Black dashed line represents the linear fit of the experimental data and the red dashed line the parabolic bare energy behavior ℏω ₀ (W) = ℏ(8D ₀ /m _z *)^1/2/W. (c) Potential V(z) (continuous black line) for sample 2459 along the growth direction; energy levels E _j and squared wavefunctions of the quantized states are also reported; the potential calculated for an undoped PQWs with the same shape is displayed as a dashed black line. The two potential curves have been aligned in energy at their minimum: (d) Theoretical absorption spectra for the samples in panel (a).

We point out that the absolute values of both nominal (n _2D) and measured (n _2D*) sheet densities are affected by a relative error of ∼30 %, due to the difficulties of a precise calibration of the N _3D phosphorus concentration confined in very thin doped layers, and to the uncertainty in the evaluation of the single well absorbance from the FTIR dichroic spectra acquired in multilayered samples with the side-illuminated single-pass waveguide configuration [1]. However, since the same doping procedure and FTIR data analysis have been used systematically, the relative variations of both n _2D and n _2D* among different samples are much more accurate. Despite these uncertainties, the fact that n _2D* values are always lower than the n _2D ones may be due to the small energy difference between donor levels originating from the Δ₂ edge states confined in the tensile strained SiGe barriers and the fundamental L subband state in the well, which can limit the effectiveness of the transfer doping mechanism [33]. Interestingly, the largest difference between n _2D and n _2D* is observed in sample 2354 which, having the thickest barrier, features the lowest energy difference between the fundamental L subband state and the Δ₂ donor level.

The low temperature dichroic transmission spectra of samples 2459, 2460, and 2354 having different well width and comparable electron sheet densities in the well n _2D* ∼ 3 × 10¹¹ cm⁻² are reported in Figure 4(a). As expected, the transmission dip energy blue-shifts by decreasing the well width W. As shown in Figure 4(b), the dependence of the measured absorption energy hω _abs (full circles) on 1/W follows the typical linear behavior foreseen for electron ISBTs in a harmonic potential. The electronic band structure and the absorption spectra of the samples have been calculated self-consistently. In modulation doped samples, the electrostatic (Hartree) charge effects influence the L band profile decreasing the depth of the effective potential felt by electrons as shown in Figure 4(c), where the effective potential profile, the electron energy levels, and the square modulus of the wavefunctions calculated for sample 2459 at 10 K are reported. The bare potential calculated for an undoped PQW with the same compositional profile is also reported for comparison. The simulated absorption spectra of the three samples are displayed in Figure 4(d). Estimated absorption energies in Figure 4(b) (open symbol) have been calculated correcting the subband transition energy, obtained considering the Hartree potential, to account for the depolarization shift effect, following Ref. [39]. Minor contributions stemming from band nonparabolicity and other many-body effects have been neglected. The shrinking of the energy level separation due to the Hartree potential is compensated by the depolarization shift so that the calculated absorption energies result in good agreement with the bare harmonic energy ℏω ₀ (red dashed line). However, the theoretical energies are slightly smaller with respect to the experimental data suggesting that the ratio D ₀/m _z could be slightly underestimated in our simulations.

In Figure 5 the dichroic transmission spectra as a function of temperature of samples 2433 and 2420 having the same well profile but different doping ((a) n _2D* ∼ 1.5 × 10¹¹ cm⁻², (b) n _2D* ∼ 3 × 10¹¹ cm⁻²) are reported. The transmission dips in these two samples are practically at same energy, the one featuring the larger carrier density being blueshift by 1 meV only. Remarkably, we find that in each sample the absorption energy is almost temperature independent despite in this THz range the subband population strongly depends on T. As already pointed out, this is a unique “fingerprint” of parabolic quantum wells, whose absorption energy is independent on the distribution of electron in subbands. This contrasts with terahertz ISB absorption in square QWs, where the lineshape and peak absorption energy vary with temperature [40]. Consistently, we have observed a significant variation of the ISB absorption spectrum with temperature when the PQWs is directly doped in the well, since in this case the cancellation of electron correlation effects does not occur [31].

Figure 5:

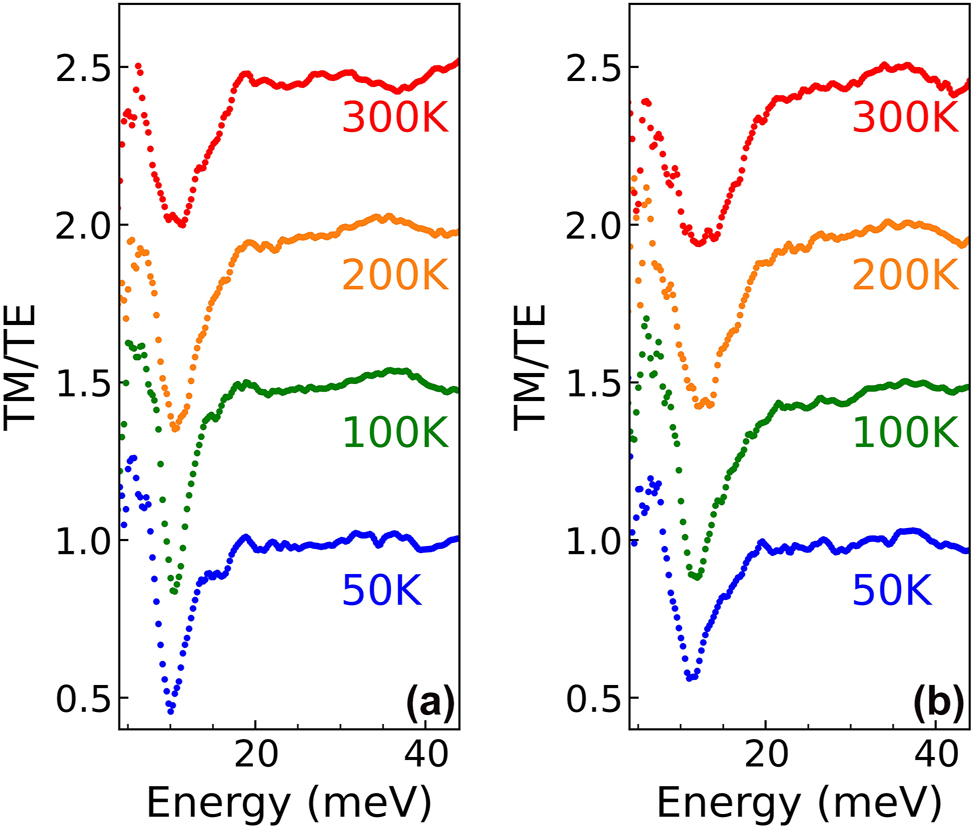
Dichroic transmission spectra acquired at different temperatures for two samples with the same well profile but different doping. (a) Sample 2433 with n _2D* ∼ 1.5 × 10¹¹ cm⁻². (b) Sample 2420 with n _2D* ∼3 × 10¹¹ cm⁻².

The main difference between the spectra of the two samples of Figure 5 is the increased linewidth observed at higher doping: in sample 2433 (n _2D* ∼ 1.5 × 10¹¹ cm⁻²), a narrow FWHM of about 2.3 meV has been measured at 100 K, increasing to 5 meV at 300 K. On the contrary, sample 2420 (n _2D* ∼ 3 × 10¹¹ cm⁻²) shows a FWHM ∼ 5.5 meV, almost constant with temperature. As shown in Table 1 where the FWHM at 100 K of all the investigated samples are reported, FWHMs ∼ 2 meV and ∼ 5 meV are typical values for these doping levels, independently on the well width and absorption energy. The observed increase of the linewidth as a function of the electron sheet density is in good agreement with previous results obtained in rectangular quantum wells. Interestingly, we notice that the values here reported at low doping are sensitively smaller with respect to those previously measured in rectangular Ge/SiGe QWs [41] typically featuring FWHM slightly larger than 4 meV. This effect may be attributed to a reduction of the scattering associated to the interface roughness occurring in systems without sharp interfaces.

The linewidth analysis, we performed with square QWs samples in [41] highlighted the presence of a non-negligible contribution of about 1–2 meV to the total width, attributed to structural crystal defects brought about by the fraction of treading defects which, overcoming the RG-VS region, penetrates in the QWs one. Although the crystalline quality of the SiGe heteroepitaxy in our reactor has been significantly improved in the last few years [27], the same mechanism can affect the lineshape of the PQW spectra here investigated, resulting in larger low temperature FWHM values with respect to III–V ones [19]. Considering the superior capability of achieving a sharp delta-like donor profile in III–V heteroepitaxy, also the spatial broadening of the P concentration along the growth direction, associated to the surface kinetics of donor atoms in the SiGe environment, can contribute to the enlargement of the absorption peak. We point out here that, in order to achieve a high filling factor of quantum wells in the stack, barrier thicknesses <18 nm have been deposited in our samples. We believe that the narrowness of the absorption resonance of Si_1−x Ge _x PQW samples could be improved by depositing thicker barriers and decreasing the growth temperature during the phosphine codeposition step, so to increase the spacer layer thickness between the doped region and the well [40]. Finally, we notice that in III–V QWs, a larger temperature dependence of the linewidth has been observed, so that the two material systems exhibit more similar value of the FWHM/E _abs ratio at room temperature [31].

The absorption spectra of our PQWs represent a promising starting point to achieve and investigate strong radiation-matter coupling in this technologically relevant material system. Following Ref. [8], [42], [43], in a photon cavity of thickness L _cav with a stack of N _QW PQWs doped with an electron sheet density n _2D, the intersubband polariton energy splitting E _up-down at the matching condition ω ₀ = ω _cav is:

Therefore, using an oscillator strength value f = 1, L _cav = 2 μm and N _QW = 25, n _2D = 2 × 10¹¹ cm⁻², as in our samples, we estimate an ISB polariton energy splitting E _up-down ∼ 5 meV and a strength ratio η = Ω R ω 0 ∼ 0.2 at 2.5 THz, well within the ultra-strong coupling regime. This estimated splitting value, which is larger than the measured FWHM, make feasible the future demonstration of ISB polaritons in Ge-rich PQWs.

Different approaches have been pursued to realize optical cavities aimed at the observation of the strong coupling regime with ISBTs. Most of them rely on lithographic patterning of metal structures directly on the epitaxial wafer, with or without etching the surrounding material. It is well known that the most important constraint in the comparison of different cavity designs is related to the dipole orientation, which requires a radiative electric field with polarization orthogonal to the quantum well plane. A second important parameter is the cavity volume that must be small, possibly subwavelength sized. To meet these requirements, the active region is usually placed within nondispersive metal–insulator–metal (MIM) microresonators, which are typically fabricated with the substrate-transfer technique. Among them, we mention the one-dimensional periodic grating [36], the capacitor-inductor cavities of Ref. [11], [18], [44], and the patch-antenna cavity discussed in Ref. [43], where the extension of the cavity in the vertical direction is accompanied by a small volume and a totally vertical and homogeneous electric field. The implementation of the substrate transfer technique is more complicated in SiGe epitaxial layers with respect to III–V materials, because of the difficulties related to the material-selective etching processes and owing to the lattice strain (thermal and epitaxial) featured by SiGe heterostructures. Planar microcavities relying, e.g., on deep-etched split-ring resonators, previously realized for III–V materials [45], are not efficient in the SiGe case due to the presence of the thick Ge virtual substrate with high dielectric constant that traps most of the electromagnetic energy density in an inactive layer. The solution may come again from epitaxy: while noble metals such as gold or aluminum have almost always been used for the cavity mirrors, in the THz range it is also possible to employ epitaxially grown, heavily doped degenerate semiconductors as substitutes for the metal layers. Indeed, the complex dielectric function of n-Ge with n > 10¹⁹ cm⁻³, measured in [46], indicates that a reflectivity R ∼ 1 can be achieved up to the mid-IR. For example, a plasma edge at 30 THz has been observed in epitaxial n-Ge with activated electron densities ∼2 × 10¹⁹ cm⁻³ and used to produce all-semiconductor nanoantennas [47]. We thus suggest that THz ISB polariton with SiGe PQWs can be demonstrated avoiding the substrate-transfer procedure and leveraging on a plasmonic-conductor ground plane below the quantum well stack, realized P-doping at ∼2 × 10¹⁹ cm⁻³ the Si_0.09Ge_0.91 VS layer.