Linear-polarized terahertz isolator by breaking the gyro-mirror symmetry in cascaded magneto-optical metagrating

2.1 Theoretical analysis

When the external MF is applied along the z-axis, the InSb shows a strong gyrotropy property. If a light propagating through the InSb also along the z-axis with Faraday configuration, Maxwell’s wave equation can be written as [17, 24]:

The detailed model of ε ₁ and ε ₂ above can be seen in Part 1 of Supplementary Information. Therefore, two eigen photonic spin states can be solved from Eq. (1):

Here, the first solution E _y  = −iE _x is the counter-clockwise (CCW) state, and the second one E _y  = iE _x is the clockwise (CW) state. The CCW state also means the forward left-handed circularly polarized light (LCP+) or backward right-handed circularly polarized light (RCP−), meanwhile, the CW state denotes the RCP+ or LCP−. According to Eq. (3), we can theoretically calculate the transmittance of CW state through InSb as follows [24]:

where d = 300 μm is the thickness of the InSb layer, T _CCW has the same form as the ε _CCW replaces the ε _CW. The detailed results can be seen in Part 1 of Supplementary Information. Since ε _CW ≠ ε _CCW in the same biased MF, so the time-reversal symmetry is broken to realize a nonreciprocal transmission for CW or CCW light. Moreover, when the direction of the MF or the propagating direction is inversed, ε _{CW+(or CCW+)} = ε _{CCW−(or CW−)} in the two reversed MFs, indicating a gyro-mirror symmetry for these two conjugated spin states with the positive and negative MF. It also shows that changing the MF direction is equivalent to changing the propagating direction in this work.

However, if an LP wave is incident into the InSb as shown in Figure 1(a), it can be decomposed into two conjugated spin states in the same phase. The transmission matrix for the LP state incident into the InSb on the x–y vector basis can be written as:

Figure 1:

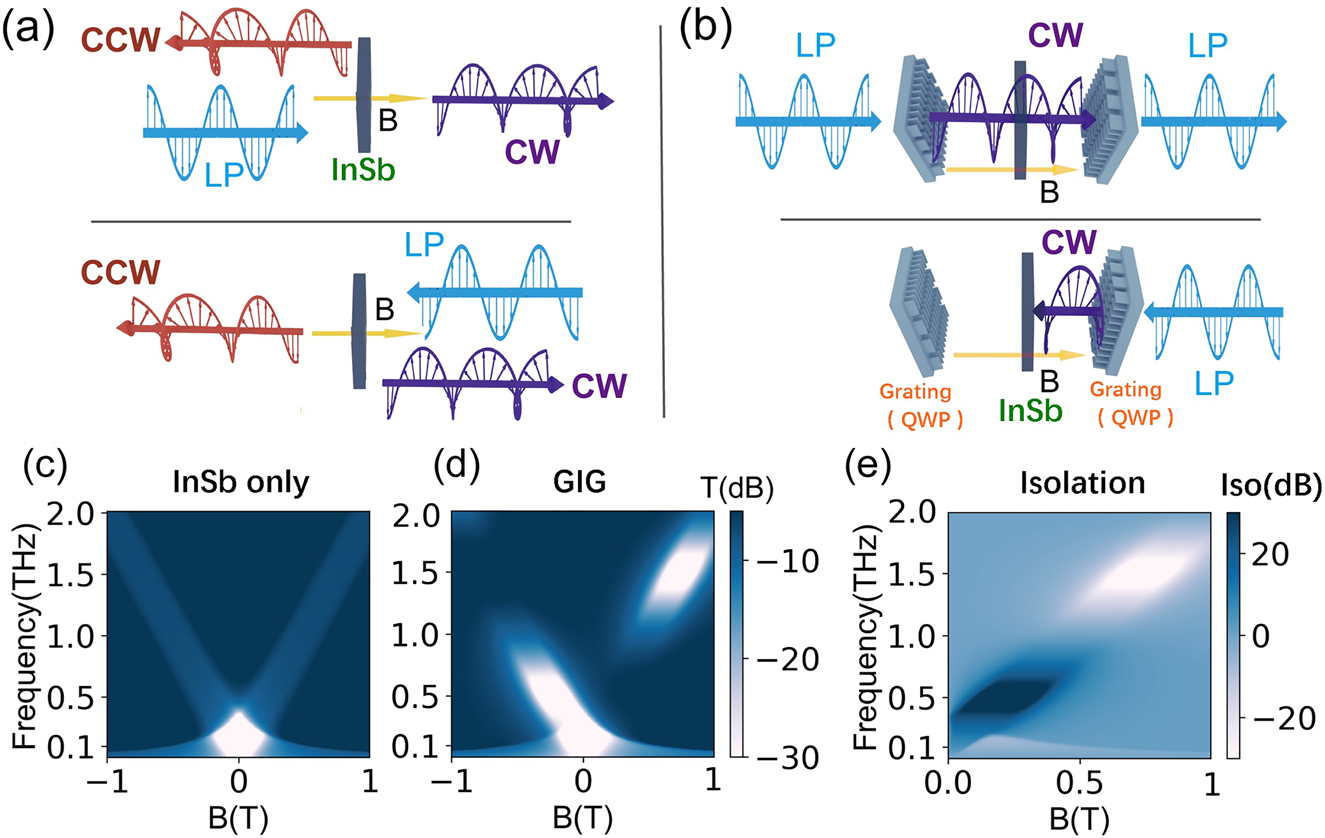
Schematic diagram of THz nonreciprocal one-way transmission based on InSb: the forward and backward LP waves incident into (a) the longitudinally magnetized InSb and (b) the InSb sandwiched in between two orthogonal meta-gratings. The theoretically calculated transmittance map as a function of frequency and the MF for the LP incidence of (c) the bare InSb and (d) GIG structure. (e) The calculated isolation for the LP incidence of GIG structure. In all the calculations, the carrier density of InSb is set to 4 × 10¹⁴ cm⁻³ as the temperature is 80 K.

According to Eqs. (3) and (4), we calculate the transmittance map of LP incidence for the single InSb as shown in Figure 1(c), and the white area is an opaque band in the figure. When B = 0 T, there is a cutting-off frequency around 0.4 THz that the transmittance is less than −30 dB. With the increase of the MFs, the forward wave only transmits CW wave, and the reflected wave only permits CCW wave in the cyclotron resonance frequency band. Figure 1(c) is mirror-symmetric for B = 0. Therefore, as shown in Figure 1(a), when the LP propagates forward through the InSb, the CW light transmits T _CW+ ≠ 0, and the CCW is reflected, T _CCW+ = 0. When the LP propagates backward through the InSb (the MF direction is still unchanged), the CCW light transmits T _CCW− ≠ 0, and the CW is reflected T _CW+ = 0. Due to the gyro-mirror symmetry of the InSb, the transmitted waves T _CW+ = T _CCW− in the above two cases, so T _Xout is a reciprocal component with the positive and negative MF (T _Xout(B) = T _Xout(−B)), half of the LP energy cannot transmit and the polarization becomes one chiral spin state. Therefore, the LP state could not be well isolated by the single InSb crystal.

Since our goal is to achieve efficient isolation for the LP waves without changing the polarization state, it is necessary to introduce a dielectric asymmetry to break the gyro-mirror symmetry while maintaining the nonreciprocity of InSb. Here, we consider utilizing the subwavelength dielectric meta-grating structure with artificial uniaxial anisotropy to introduce the dielectric asymmetry into this nonreciprocal transmission system. As shown in Figure 1(b), a couple of meta-gratings are placed before and after the InSb, forming a cascaded grating–InSb–grating (GIG) structure, where the grating direction of two gratings are orthogonal to each other and 45° to the incident LP direction. In this case, the transmission matrix of the whole system can be written as:

where δ is the phase difference between the x- and y-polarized LP state brought by the meta-grating. For the sake of simplicity, we assume the meta-grating has the linear dispersion as δ = 0.5πf THz⁻¹ where f is the frequency of the wave in the theoretical analysis. According to Eqs. (3) and (5), we calculate the transmittance map of LP incidence for the GIG structure as shown in Figure 1(d). Unlike Figure 1(c), Figure 1(d) is no longer mirror-symmetric for B = 0, and the isolation can be also calculated as follows:

where T(B) and T(−B) are the intensity transmission for the positive MF and negative MF (i.e. equivalent to the forward and backward transmission), respectively. Figure 1(e) shows the isolation map as the frequencies and MFs corresponding to the dark blue and white regions can realize efficient one-way transmission.

In special, when this meta-grating works as a perfect quarter wave-plate (QWP) (δ = 0.5π), the transmission matrix can be simplified as:

Thus, the output wave only depends on the T _CW and has one-way transmission property since the T _CW is nonreciprocal as discussed above. Moreover, there is no y-component output, which means the output wave is a pure x-LP, so the frequency points that satisfy Eq. (7) can be defined as the perfect isolation case. Figure 1(b) intuitively shows the working principle of the device: when the x-LP propagates forward through the GIG structure, after passing through the first grating, the CW wave is output; then, the CW wave can pass through the magnetized InSb within the cyclotron resonance band; finally, the CW wave is transformed into x-LP wave after passing through the second grating with orthogonal orientation. When the x-LP propagates backward through the GIG structure, the CW wave is still converted, but this backward CW wave cannot pass through the InSb. In this way, the perfect one-way isolation is achieved in theory, while keeping the input–output LP unchanged. Therefore, the efficient one-way isolation band occurs in the overlapping frequency band between the cyclotron resonance of InSb and circular polarization conversion of the meta-gratings.

2.2 Experimental results

Based on the above analysis, we designed and fabricated an MO meta-grating with GIG structure as shown in Figure 2(a). Our InSb single crystal wafer was purchased from Klamar-Reagent Corporation, which was prepared by the liquid phase epitaxial method. The InSb wafer is single-side polished, 300 μm in thickness, 〈111〉 orientation, n-doped with the intrinsic carrier concentration of 4 × 10¹⁴ cm⁻³ and the mobility of 4 × 10⁵ cm² V⁻¹·s⁻¹ at 80 K. Two Si meta-gratings with orthogonal grating orientations were fabricated on both sides of the InSb. The high resistivity Si wafer was tightly bonded to the InSb crystal. The Si was thinned by the plasma etching, and then the Si grating structures on the InSb substrate were fabricated by UV lithography and plasma etching. The meta-grating consists of two-dimensional periodic long rectangular column arrays, and its scanning electron microscope (SEM) image and the detailed geometries are shown in Figure 2(b). The structure of the backside is the same as that of the front side, but the long axis direction of the grating is orthogonal to that of the front side.

Figure 2:

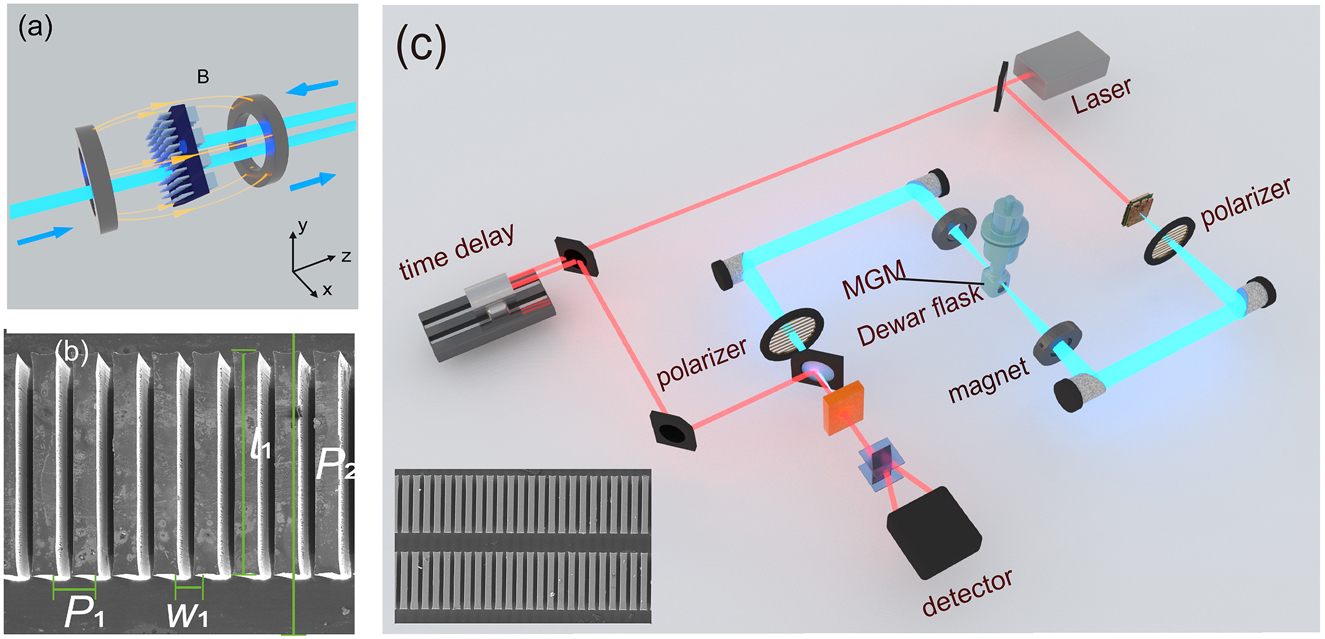
(a) The illustration of the transmission process for the designed GIG. (b) The SEM image of the Si meta-grating structure on the surface of the InSb substrate. The parameters of the structure are as follows: the transverse period P ₁ = 77 μm, the width of the Si bar is W ₁ = 54 μm, the length of the Si bar l ₁ = 350 μm, the longitude period P ₂ = 500 μm, and the etching depth of the grating is 170 μm. (c) The sketch map of the THz-TDMPS experiment setup. Inserted: the extended SEM image of the meta-grating with a larger field of view.

We use the terahertz time-domain magneto polarization spectroscopy (THz-TDMPS) system to experimentally demonstrated the property of the GIG as shown in Figure 2(c). Compared with the traditional THz-TDS system, the GIG sample is placed in a vacuum cryogenic Dewar bottle (T = 80 K in our work) with a pair of adjustable longitudinal magnets on both sides (B = 0–170 mT). There is one rotatable THz polarizer behind the THz source and the other one in front of the THz detector, which is used to generate and detect arbitrary THz polarization states, respectively. The details of the experimental system and the related data processing can be found in Part 2 of Supplementary Information.

At first, we investigated the transmission and polarization properties of the single meta-grating without InSb substrate. We measured the transmittance and phase difference along the major axis (along the y-axis) and minor axis (along the x-axis) of the grating. Meanwhile, we also obtained the numerical simulation results of the finite difference time domain (FDTD) method. The numerical modeling method can be found in Part 4 of Supplementary Information. As shown in Figure 3(a), the transmittance T _x and T _y for x-LP and y-LP are almost the same around 0.1–1 THz. And in Figure 3(b), the phase difference between x- LP and y-LP is decreasing with the frequency. In particular, the phase difference comes to 90° near 0.5 THz, so the grating is close to an ideal QWP. According to the above theoretical analysis, the GIG structure is expected to achieve efficient one-way transmission near this frequency point under the MF.

Figure 3:

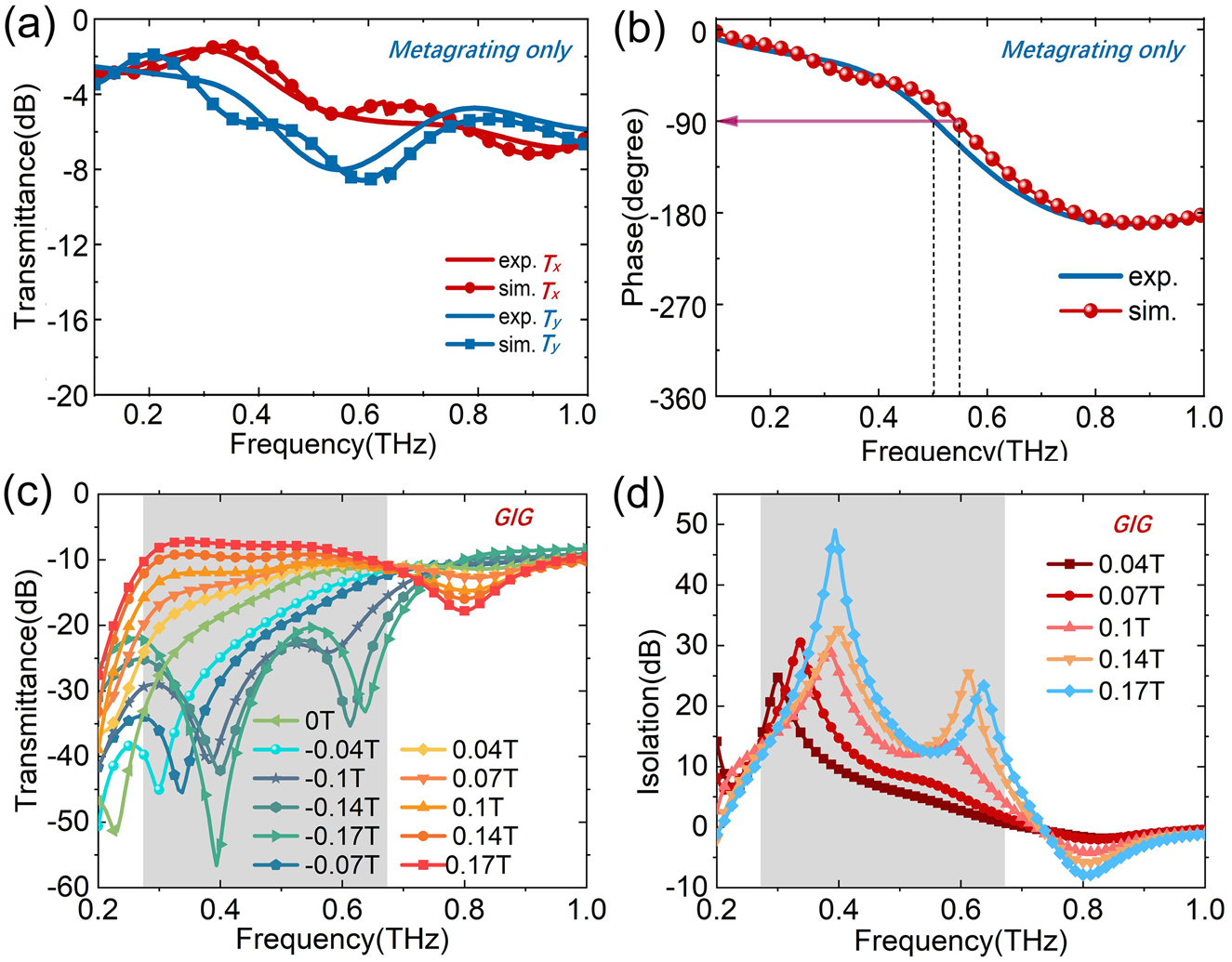
The simulative and experimental transmission spectra of the meta-grating on the Si substrate of x-LP (along with the minor axis) and y-LP (along with the long axis of grating); (b) the simulative and experimental phase difference of the grating between two orthogonal x-LP and y-LP. (c) The experimental transmission spectra from LP input to LP output of the GIG device under different MFs; (b) isolation of the GIG under different MFs.

Then, we focus on the nonreciprocal transmission property of the MO meta-grating with the GIG structure. We placed both THz polarizers to 0°, that is y-LP wave is incident into the GIG device, and the experimental system detects the y-LP component of the output wave. The transmission spectra of the LP wave passing through the GIG are shown in Figure 3(c). When B = 0 T, the transmittance is less than −10 dB in the frequency range of f < 0.7 THz. With the increase of the positive MFs, the cutting-off frequency gradually moves to the lower frequency as the transmittance increasing. On the contrary, when the negative MFs are applied, the cutting-off frequency gradually moves to a higher frequency with the decrease of transmittance. The experimental results are in good agreement with the theoretical calculation in Figure 1(d), and they are also verified by numerical simulations (see Part 4 of Supplementary information). Therefore, there is a nonreciprocal transmission band for the LP waves in the frequency range of 0.38–0.68 THz. Figure 3(d) shows the isolation between forward and backward transmission defined as Iso = T(+B) − T(−B) in dB. The isolation peak moves to high frequency and the isolation band (>10 dB) expands with the increase of MFs. Although the QWP point for the Si grating is 0.5 THz, when we combined the grating with the InSb, the impedance match condition of the grating is changed, thus making the QWP point of the GIG structure moves to the lower frequency. Therefore, when B = 0.17 T, the best isolation point can reach 50 dB at 0.42 THz with the 10 dB isolation bandwidth of 400 GHz.

Moreover, we analyzed the complete polarization state output through the GIG. When the frequency band deviates from the ideal QWP, the actual output wave will be an elliptical polarization state. We calculate the polarization ellipse as shown in Figure 4, we select two frequency points: f = 0.42 and 0.8 THz. When f = 0.42 THz, for the forward MFs, the amplitude growing with the MFs, and when B = 0.17 T, the output wave is almost the perfect LP state. However, for the backward MFs, the amplitude decreasing with the MFs, showing the isolation effect. For f = 0.8 THz, for the forward MFs, the polarization state turns counter clock-wise, but for the backward MFs, the polarization state rotates clockwise. Thus, in the higher frequency range of f > 0.8 THz, this structure shows the Faraday rotation effect which means the rotation angle can be turned by the MFs. For the details of related experimental measurement and data processing, please refer to Part 3 of Supplementary Information.

Figure 4:

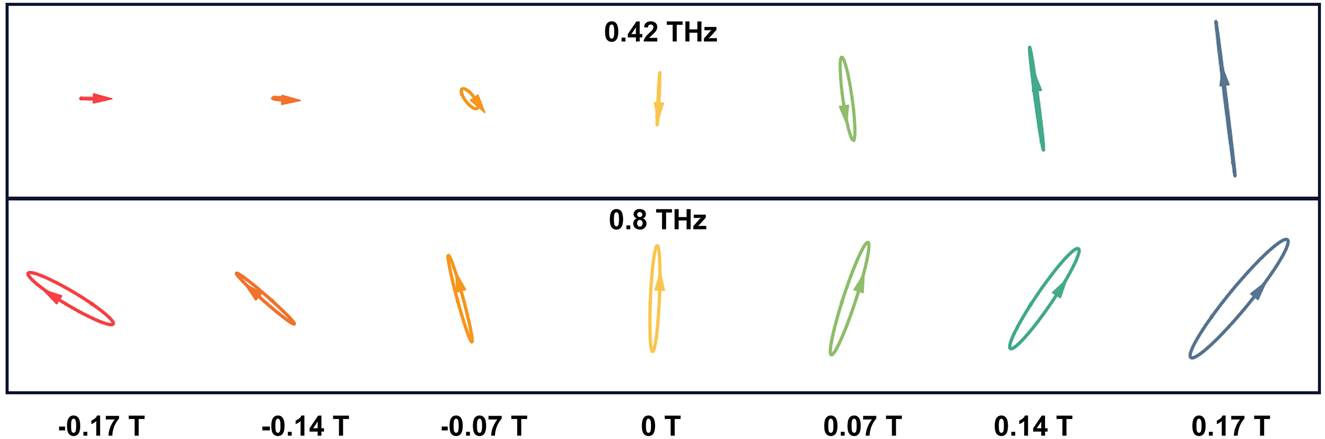
The polarization ellipse for the output wave for different MFs and frequencies.

2.3 Discussion for loss and bandwidth

Finally, as shown in Figures 3(c) and 5(c), the transmittance also reflects the total insertion loss of the device, and the lowest insertion loss is 6.7 dB for the first GIG structure and 6.9 dB for the second GIG structure, respectively. Two main factors contribute to the total loss of the device: the intrinsic absorption loss of the InSb and the surface reflection loss from the grating structure and interfaces. We think there are two ways to reduce the insertion loss in the future: one is to fabricate the InSb wafer with a lower intrinsic carrier concentration, and the second is to design a more optimized microstructure to achieve better impedance matching on the interfaces of the air/grating and grating/InSb.

Figure 5:

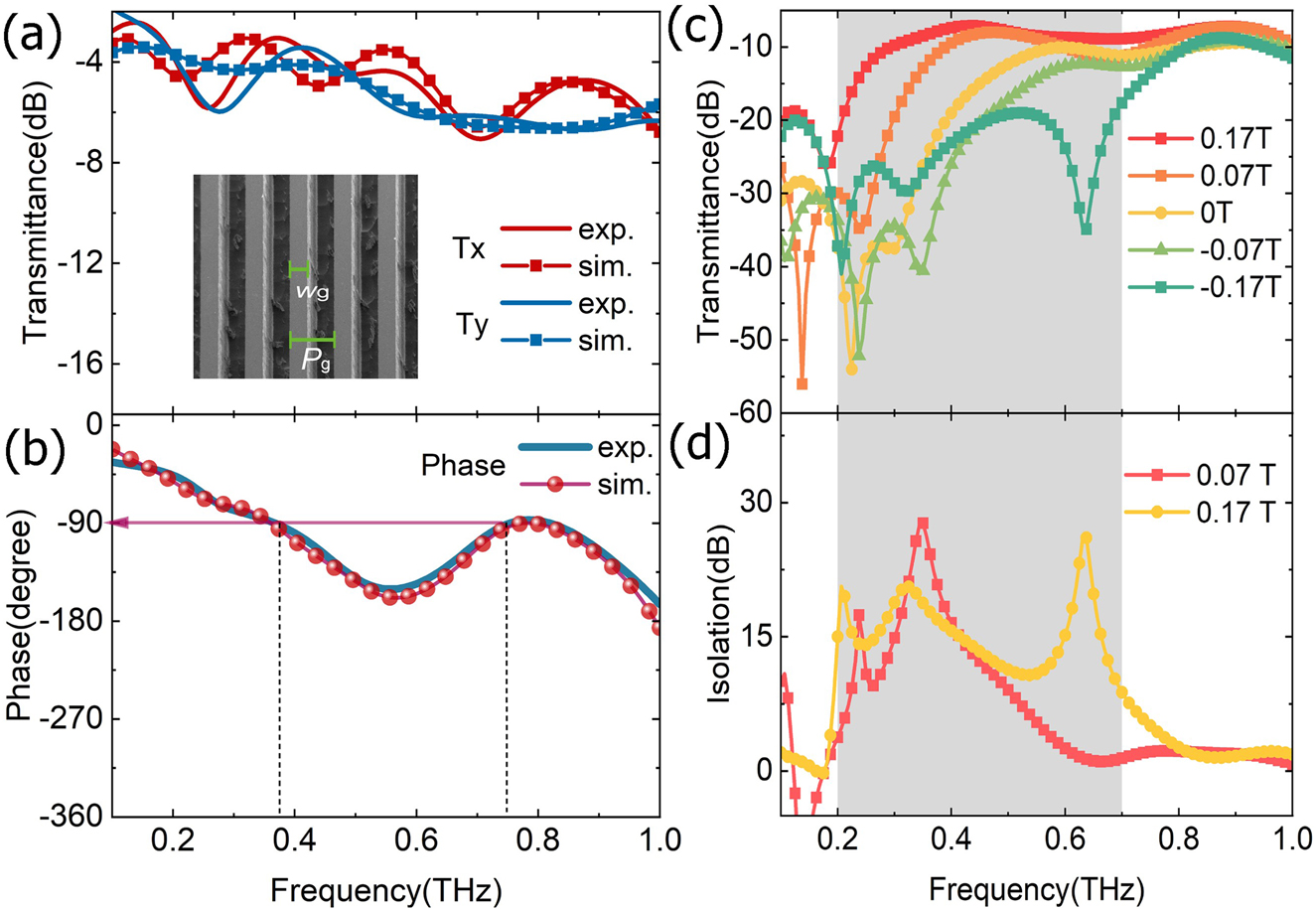
The simulative and experimental transmission spectra of the meta-grating without the InSb for x-LP (along with the minor axis) and y-LP (along with the long axis of grating); the parameters of the structure are as follows: the grating period P _g = 200 μm, the width of the Si bar is W _g = 75 μm and the etching depth of the grating is 200 μm. (b) The simulative and experimental phase difference of the grating between two orthogonal x-LP and y-LP. (c) The experimental transmission spectra from LP input to LP output of the GIG under different MFs; (d) isolation of the GIG under different MFs.

According to the nonreciprocity mechanism discussed in Section 2.1, the bandwidth of the device is determined by two factors: (1) the frequency band of InSb cyclotron resonance (including the position of resonance frequency determined by the MF and the resonance bandwidth determined by carrier collision frequency); (2) the frequency band of π/2 phase shift is realized by meta-grating as a THz QWP. When these two frequency bands are overlapped in the same frequency range, the perfect isolation case described in Eq. (7) can be achieved. The larger the overlap range is, the larger the 10 dB isolation bandwidth is. For a specific MO material, the cyclotron resonance bandwidth is constant, and the resonance center frequency can be tuned by the external magnetic field. Under these conditions, if a meta-grating can be designed as the THz QWP with enough broad bandwidth, a broadband LP isolator can be realized.

Therefore, we also designed and fabricated a subwavelength grating as a broadband QWP to obtain a broadband GIG. As shown in Figure 5(a), the transmittances of x- and y-LP components are almost the same. However, the phase difference between them has two 90° points at 0.38 and 0.75 THz as shown in Figure 5(b). By combining these grating with InSb, the transmittance and the isolation spectra under the different MFs can be seen in Figure 5(c) and (d). With the growth of the MFs, the transmittance increases under the positive MFs, while the transmittance decreases under the negative MFs. Different from the above results in Section 2.2, for the large MF (B = 0.17 T), the 10 dB isolation bandwidth is broader because these meta-gratings have two perfect QWP points which satisfy Eq. (7), its isolation band is located from 0.2 to 0.7 THz with the relative bandwidth of Δf/f _cen > 110%, where f _cen is the center frequency of this device.