True- and quasi-bound states in the continuum in one-dimensional gratings with broken up-down mirror symmetry

1 Introduction

The interaction of light and matter within subwavelength volumes is an important phenomenon in numerous branches of physics and technology, including light detectivity [1], stimulated emission in lasers [2], nonlinear optics [3], single-photon generation [4], observation of polariton–excitons [5], quantum electrodynamics, and others. A prominent example is Bose–Einstein condensation in photonic systems [6], which is observed along with coherent lasing below population inversion [7]. Strong light–matter interaction occurs in metallic periodic structures that utilize subwavelength localization of the light by means of surface plasmon polaritons [8]. However, light localization in these structures is inevitably associated with light absorption by metal in the visible and infrared region, which deteriorates the efficiency of plasmonic devices. In dielectric high refractive index periodic structures, strong light confinement in a small volume is enabled in the absence of absorption by means of Fano resonance [9, 10]. Fano resonance is manifested by an abrupt transition from total reflection to total transmission in the spectrum of the light interacting with a structure. When the spectral width of the dissipative Fano resonance becomes infinitely narrow, its quality factor tends to infinity and the resonance becomes a bound state in the continuum (BIC) [11, 12]. A BIC is a nonradiating resonant state of infinite quality (Q) factor localised in an open photonic system. Other resonant states of the system correspond to the continuum of optical states that carry electromagnetic energy away from the photonic structure. BICs have been found theoretically in infinite structures that are periodic in at least one dimension and symmetric in two other dimensions. When there is a lack of vertical symmetry [13], [14], [15] or in periodic structures with finite dimensions, which is the case with real-world realizations, the BIC transforms into a so-called quasi-BIC (qBIC) [16, 17] of finite but still very high quality factor.

In this paper, we investigate qBICs of finite Q-factor and BICs of infinite Q-factor (also known as true BICs, to emphasize their difference with respect to qBICs) in binary subwavelength gratings implemented on the surface of a semi-infinite substrate (Figure 1). In this configuration, the stripes are positioned periodically along the y direction and are infinite along the x direction (see the coordinate system in Figure 1). The wavevectors ( k ₀ ) of the resonant states (modes) are composed in general of k _x , k _y and k _z components. However, due to the infinite x dimension in our analysis, the wavevector is composed of two nonzero components: k ₀  = (0, k _y , k _z ). The norm of k ₀ is a wave number (k ₀) related to the resonant wavelength λ = 2π/k ₀. We limit our study to the modes at Γ-point (k _x  = k _y  = 0). We consider transverse-electric (TE) polarization of the electromagnetic wave, in which the electric component of the electromagnetic field is parallel to the grating stripes. We name the modes TE _nm , where n indicates the number of zeros in the distribution of the electric field in the vertical direction of the mode in a single grating segment (the segment is defined in Section 2) and m is the number of zeros in the lateral direction perpendicular to the stripes. Zeroes at the segment boundaries (if present) are regarded as one. We do not consider transverse magnetic (TM) polarization that is orthogonal to TE, as it would require a separate analysis and conclusions from the analysis of TE polarization cannot be directly applied to TM polarization. Modes propagating in the grating of which the lateral distribution (along y direction) of the electric field is symmetric with respect to all symmetry x–z planes of the grating are referred to as symmetric modes (s-TE) (see Figure 4 for examples of symmetric modes). Analogously, modes with antisymmetric lateral distribution of the electric field with respect to all symmetry x–z planes of the grating are referred to as antisymmetric (a-TE) (see Figure 7 for examples of antisymmetric modes). When the refractive index of the substrate (n _s) is equal to the refractive index of superstrate (n _a), the grating is vertically symmetric (VS). A VS grating with a superstrate and substrate both with a refractive index of 1 is a special case referred to as a membrane. The gratings with broken up-down mirror symmetry we call vertically nonsymmetric (VN) gratings. In the case of the VN grating, the subwavelength regime relative to air is referred to as the air-subwavelength (1 < L/λ) and subwavelength regime relative to substrate is referred to as substrate-subwavelength (n _s ⁻¹ < L/λ), where L is period of the grating.

Figure 1:

Schematic 3D picture of a grating with broken up–down mirror symmetry, consisting of a high refractive index periodic membrane (n _g) placed on a substrate with a refractive index n _s, where n _g > n _s. L is the width of the grating segment, H is the height of the grating stripes, a is the width of the stripes and F is the duty cycle determined as the ratio a/L.

In VS gratings, three types of BICs can be formed at k _y  = 0. The first appears when the mode is antisymmetric and the grating is subwavelength. The grating admits only a single leaky channel, related to zero diffraction order emission. Zero diffraction order emission is prohibited in the case of antisymmetric modes; hence, antisymmetric modes cannot be radiated from the grating. This type of BIC is called symmetry-protected (SP) [16] and is robust against changes in the grating parameters as long as the grating is subwavelength and k _y  = 0. In the case of antisymmetric modes in the grating with a period larger than the wavelength (diffraction regime), or in the case of symmetric modes regardless of the period size, at least one emission channel is open and symmetry protection is no longer possible [12, 18]. When there is only a single radiation channel, judicious tuning of the grating parameters can lead to destructive interference at both interfaces of the grating, producing an IB BIC [19, 20]. When tuning the grating parameters leads the dispersion curves of strongly coupled nonorthogonal resonances to approach each other, inducing avoided crossing with noticeable separation of the frequencies [21], the FW BIC appears [22]. The IB and FW types of BIC (that are also named accidental BICs) may occur for modes with k _y  = 0 as well as k _y  ≠ 0 [23].

VS gratings in which BICs are observed are very often impractical, as they are thin membranes suspended in air [24] or implemented on a low refractive index substrate and then covered with a material that has an identical or almost identical refractive index to the substrate [16]. Such designs make it difficult to fabricate electrically driven devices, since the air or low refractive index materials (typically dielectrics) are nonconducting. In comparison, all-semiconductor structures with broken vertical symmetry, such as for example a grating implemented on a bulk substrate, offer several advantages. Such structures can be robust and immune to mechanical failure. They can also be used as electrically driven devices. In contrast to suspended structures, their fabrication does not require sophisticated critical point drying after selective wet etching to release the membrane during processing. A given periodic structure on a solid semiconductor substrate can cover an arbitrarily large area, whereas large area suspended structures are always at risk of collapsing [25]. The spatial parameters of the grating can be precisely controlled via electron beam lithography for research applications or via nanoimprint lithography [26] on a mass production scale. However, such all-semiconductor structures have the obvious disadvantages of broken vertical symmetry and lower contrast between the refractive index of the periodic structure and the substrate, which contribute to light leakage into the substrate.

To the best knowledge of the authors, this is the first study to investigate the influence of up–down symmetry breaking and refractive index contrast on the creation of BICs and high Q-factor Fano resonances in a one-dimensional grating. Analyses of high Q-factor resonances in VN configurations are sparsely documented in the literature. Two studies have provided valuable insights into the mechanisms that cause BICs to collapse into finite Q-factor Fano resonances, due to lack of vertical symmetry [13, 14]. Neither of these studies, however, showed that true IB and FW BICs can be formed in VN gratings. The main purpose of the numerical analysis presented in the present paper is to investigate the influence of up–down mirror symmetry breaking and refractive index contrast on the creation of accidental (IB and FW) true and quasi BICs in a one-dimensional grating. The gratings with broken up–down mirror symmetry and reduced contrast between the refractive index of the grating and surroundings represent real-life realizations of gratings implemented directly on a substrate in all-semiconductor configurations. Although our work concerns a one-dimensional grating as an example structure, the conclusions are expected to be of more general significance and may be applicable to various one- and two-dimensional periodic configurations implemented on substrates with broken up–down mirror symmetry.

In Section 2, we present the grating configurations considered in this work and the numerical method used for their analysis. In Section 3, we investigate VN grating in the case of modes with symmetric lateral distribution of the electric field in a single segment (s-TE). In Section 4, we consider modes with antisymmetric lateral distribution of the electric field (a-TE) in a single segment of a VN grating. In Section 5, we provide a broad overview of high Q-factor resonances for all mode symmetries in VN gratings with substrate refractive indices varying from 1 to the refractive index of the grating. The structures analysed in Sections 3–5 are infinitely periodic gratings. In Section 6, we give an example of a configuration with a finite number of grating stripes and a low refractive index contrast between the grating and the substrate, corresponding to the contrast achieved in arsenide-based materials in the near infrared region. This example compares the Q-factors of two finite configurations with parameters corresponding to true BIC and qBIC in infinite arrangement. It demonstrates the possibility of achieving a very high Q-factor in a finite all-semiconductor VN grating and shows a possible way of constructing current injection devices.

2 Methods and structures

The method we used to numerically solve Maxwell equations is based on the Admittance Method [27], which is applied for the z direction, combined with Fourier series expansion of the electromagnetic field and refractive index in the lateral y direction of the structure. We assume that the structure and the electromagnetic field are homogeneous along the x axis. Consequently, the structure is periodic along the y axis and consists of infinitely repeated copies of the rectangular (in the (y, z) plane) computational window of width W in the y direction in which the structure is defined. The computed electromagnetic wave along the y direction is in the form given by Bloch’s theorem:

where f(y) is a periodic function with the period W as the computational window and k _y is an arbitrarily chosen number ranging from –π/W to π/W. We simulate two types of configuration. The first, which we call infinite, the computational window W is equal to the period of the grating structure (L). In the second case, referred to as finite, the computational window comprises numerous segments of the same width (L) of the grating structure. Therefore, L is not a period of the whole structure. Unless stated otherwise, the calculations are performed for k _y  = 0. We use two models that represent the electromagnetic field in the form of Bloch waves, as shown in (1). The Plane Wave Reflection Transformation Method (PWRTM) [28] is used to determine the power reflectance and transmittance of each diffraction order. The Plane Wave Admittance Method (PWAM) [27] is used to find electromagnetic resonances occurring in the structure. The complex wavenumbers of the modes (k ₀ = k _0re + ik _0im) can be determined by PWAM, with real parts (k _0re) corresponding to the values of the free space wavevectors of the optical modes and imaginary parts (k _0im) that are proportional to the optical losses of the modes. The Q-factor of the modes is defined as Q = 0.5k _0re/k _0im. In both methods, the only approximation used is truncation of the basis size. Our model has been shown to have high reliability by comparison with experimental results [29, 30]. In Sections 3 and 4, the computational window comprises a single grating segment. To simulate structures with finite gratings, the computational window in the lateral direction contains a finite number of grating stripes and a region with imposed absorbing boundary conditions is positioned at a distance of three segment widths from the grating. The number of plane waves used in the method (the size of the basis) was approximated according to the formula W/L × 30, where L is the width of the grating segment and W is the computational window.

In the calculations, the refractive index of the grating (n _g) is 3.52 (Figure 1). This level of refractive index corresponds to GaAs at 1 µm. It is also close to silicon and numerous alloys of phosphide- and antimonide-based materials in the infrared region. The refractive index of the substrate (n _s) varies. In Sections 3 and 4 we consider a VN grating where n _s = 2.5. In Section 5, n _s is varied in the range from 1 to values approaching 3.52. Finally, in Section 6, the refractive index of the substrate is n _s = 2.95, which corresponds to the refractive index of Al-rich AlGaAs at 1 µm. We consider possible variations in all the grating parameters shown in Figure 1: the grating segment (L), the etching depth (H) and the grating duty cycle (F) defined as the ratio of the grating stripe width (a) to the segment width (L).

3 Laterally symmetric modes

The modes propagating in the grating can be described according to waveguide theory [31], by determining their wavelength range within the slab periodic waveguide:

In formula (2), the short wavelength limit of L/λ is the cutoff (C _m) of the TE _nm modes. The cutoff is determined by the refractive index of the substrate (n _s) and is equal for all s-TE _nm and a-TE _nm modes with equal m. The long wavelength limit corresponds to H → ∞ and depends on the effective refractive index of the grating ( n g e f f ). The effective refractive index is the weighted refractive index over the normalized optical field intensity of the mode [32]. Therefore, its value is smaller than n _g. When F is 1, then n g e f f  = n _g for H → ∞ and all the modes in the range expressed by formula (2) are bound states with infinite Q. When F < 1, there is a reduction in n g e f f compared to F = 1. In addition, the s-TE modes can couple to the free space, turning them into dissipative modes with a finite Q-factor [11]. The light intensity maximum of these dissipative modes is located in the grating and the light does not vanish outside the grating. We restrict our considerations to air-subwavelength gratings (L < λ), which limits m to 6 in our example (since m 2 n g eff > 1 for m ≥ 8 and n _g ^eff ≤ n _g). In this spectral region, in the case of VS grating although the modes couple with the plane wave in air, light dissipation can be eliminated by tuning the grating parameters and BICs of two types emerge: FW and IB (see Figure S1b in the Supplementary Materials). The FW BICs appear in the vicinity of avoided crossing, between pairs of nonorthogonal modes [21]: s-TE _n2 and s-TE _n4, as well as s-TE _n4 and s-TE _n6. The other BICs are IB BICs, which are present in the dispersion curves of s-TE _nm modes for m ≥ 2.

Figures 2 and S1b in the Supplementary Materials illustrate the dispersion curves of s-TE modes for the VN grating and membrane, respectively. The Q-factors vary along the curves and reach maxima at the points indicated by circles. Colours correspond to the Q-factor value. The positions and values of the Q-factor maxima were determined using an optimization algorithm, searching for the minimal k _0im that takes the real part of the wavenumber and H as variables. A comparison of the two maps indicates that in a VN grating with Q < 10⁶ the breaking of up-down mirror symmetry by the presence of the substrate turns the BICs present in the membrane into qBICs (for examples of modes distributions in VN grating see Figure S2 in the Supplementary Materials). In the example presented in Figure 2, the presence of the substrate with a refractive index of n _s = 2.5 sets the diffraction regime in the range n _s ⁻¹ = 0.4 < L/λ. For n _s ⁻¹ > L/λ only the 0th diffraction order is emitted towards the superstrate and substrate. However, vertical symmetry breaking introduces different conditions for destructive interference in the far field in both the superstrate and the substrate. These conditions cannot be fulfilled simultaneously, contributing to light dissipation. In the range n _s ⁻¹ < L/λ all the modes emit higher than 0th diffraction orders towards the substrate, contributing to open additional emission channels besides the 0th diffraction order. Both mechanisms, breaking the up–down mirror symmetry and opening additional leakage channels, contribute to the absence of true BICs in the VN grating, as discussed in [13, 14]. The qBICs with the largest Q-factors are observed in the case of low-order vertical modes (small n indices) and in the case of large H, which clearly increases the Q-factor of cavity by increasing cavity length. Although this tendency is shown for a specific VN configuration, it is generalized for all VN configurations considered in Section 5.

Figure 2:

Q-factor (Q) of resonances expressed by colours in the domain of the grating thickness (H) and wavelength (λ) for a grating implemented on a substrate with a refractive index of 2.5. L is the grating segment width and the duty cycle F = 0.9. Circles represent local maxima of the Q-factor. Vertical dashed lines indicate s-TE _nm mode cutoffs for m = 2 and m = 4.

Figure 3(a) provides a closer inspection of the evolution of the dispersion curve of an arbitrarily selected s-TE₀₄ mode. Grey lines and dark red points indicate membrane dispersion curves and BICs, respectively. Coloured lines represent dispersion curves and Q-factor in the case of the VN grating. Although the curves relate to a specific mode, the behaviour shown in Figure 3(a) is representative of the dispersion curves for all s-TE _nm modes. As can be clearly seen, breaking the vertical symmetry eliminates anticrossings from the dispersion curve, due to reduced coupling between the modes in the VN grating (this issue is discussed in greater detail in the Supplementary Materials S1). However, a slight fluctuation in the intersections with s-TE _n2 modes remains. Although avoided crossing vanishes, the corresponding maximum Q-factor remains in the vicinity of the crossing with s-TE _n2 modes. In the case of the membrane, the corresponding Q-factor maximum is infinite and indicates an FW BIC. In the case of the VN grating, the position of the maximum is very close to that of the FW BIC in the membrane. However, its Q-factor is reduced to a finite value, indicating a quasi-FW (qFW) BIC. The BICs in the membrane that are not positioned in the vicinity of the avoided crossing are IB BICs. Breaking the vertical symmetry of the grating also reduces their Q-factor, turning them into quasi-IB (qIB) BICs. Numbers (1)–(5) indicate the resonant wavelengths and H/L of the VN grating for which the distribution of the modes is illustrated in Figure 4. Distributions numbered (2) and (4) indicate the qFW BIC and qIB BICs, respectively. As both configurations are positioned outside the substrate-subwavelength regime, the light distribution reveals a typical checkerboard pattern in the substrate. In both cases, this indicates the presence of at least two diffraction orders emitted towards substrate. On the air side, the uniform distribution of light intensity indicates zeroth diffraction order emission.

Figure 3:

Dispersion curves of symmetric modes in the VN grating (coloured curves) and the membrane (grey curves) (a). The two sloping curves in (a) represent s-TE₀₄ modes in both configurations. The nearly horizontal curves represent s-TE _n2 modes that are leaky in the case of the VN grating. Dark red circles in grey curves represent BICs in the membrane. Colours in the dispersion curves of VN grating correspond to the Q-factor value. This map is a magnification of an arbitrarily chosen section of the maps presented in Figure 2; (b) Q-factor versus etching depth (H/L) for the s-TE₀₄ mode in the membrane (black line) and VN grating (red line) with Friedrich–Wintgen (FW) and interference-based (IB) BICs and qBICs. Numbers (1)–(5) indicate the parameters of the VN grating and corresponding Q-factors of the mode illustrated in Figure 4. (c) The ratio (η) of the electromagnetic field energy in the cavity relative to the light energy in the substrate (blue line and η _s in the text) and air (red line and η _a in the text). The grey line indicates the Q-factor function for the VN grating, which is the same as in b) (red line). FW and IB quasi-BICs are indicated as qF and qI.

Figure 4:

Lateral profiles of the electric field (black line in top panels) and light intensity distributions (bottom panels) of the s-TE₀₄ mode within a single segment of VN grating. Numbers (1) to (5) correspond to the grating configurations indicated by the same numbers in Figure 3(a) and (b). The profiles of the electric field are cross-sections through the light intensity maximum of the modes. In the top panels, blue lines represent the profile of the refractive index in the grating and grey dashed lines indicate 0 of the electric field. In the bottom panels, light intensity is presented on a logarithmic scale of colours.

Figure 3(b) compares Q-factors along the dispersion curve of the s-TE₀₄ mode in the membrane and in the VN grating for a broad range of H/L. As can be seen, the qFW BICs in the VN grating form at nearly the same H/L as the FW BICs in the membrane. The difference in the refractive index of the substrate modifies the VN and membrane dispersion curves marginally. Therefore, the dispersion curve intersections do not change their positions significantly in the H/L–L/λ plane when the two configurations are compared. A greater difference in positions of IB and qIB BICs is observed. Figure 3(c) enables a more in-depth examination of the mechanism of qBIC formation in the VN grating illustrating the ratio of the electromagnetic field energy in the cavity relative to the light energy in the substrate (η _s) and air (η _a) calculated far from the cavity. Both η _s and η _a are superimposed on the Q-factor function for the VN grating. The figure indicates a strong correlation between the positions of the qBIC and η _s maxima. Moreover, η _s is significantly smaller than η _a, revealing that the main leakage channel of the electromagnetic field from the cavity leads through the substrate, where the energy flow cannot be completely inhibited due to the existence of two diffraction orders. A comparison of η _a and the membrane Q-factor in Figure 3(b) (black line) shows that the positions of the η _a maxima and membrane BICs coincide very closely. However, not all η _a maxima in the VN grating diverge to infinity (as occurs in the membrane), indicating that completely destructive air-side interference is hindered in configurations with broken up-down mirror symmetry.

4 Laterally antisymmetric modes

The zeroth diffraction order is not emitted by the antisymmetric modes a-TE _n2, a-TE _n4, and a-TE _n6. On the other hand, only the zeroth diffraction order can be emitted in the subwavelength regime of the membrane (L < λ). Therefore, any emission of antisymmetric modes in the VS grating is prohibited; making those modes bound states [16]. Implementing a substrate with refractive index n _s modifies the substrate-subwavelength condition (L/λ < n _s ⁻¹) in which SP BICs exist [14]. Modes that fulfil the condition n _s ⁻¹ < L/λ < 1 emit the nonzero diffraction order into the substrate, becoming dissipative resonances. Figure 5 illustrates the dispersion curves of a-TE _nm modes with even m in the grating implemented on a substrate with n _s = 2.5, in two configurations differing in F. The distributions of the electric field and light intensity for the selected modes in the grating configuration with F = 0.9 are illustrated in Figure S4 in the Supplementary Materials. The zeros of the electric field of the modes on the axes of the grating period symmetry indicate their antisymmetric distributions. The substrate-subwavelength condition (L/λ < n _s ⁻¹) is below the long wavelength limit of the a-TE _n4 mode ( 1 n s < 2 n g eff ). Therefore, only a-TE _n2 can be an SP BIC in this configuration.

Figure 5:

Q-factors of a-TE modes indicated by colours for the VN grating implemented on a substrate with a refractive index of 2.5 and F = 0.7 (a) and F = 0.9 (b). Q-factor functions depicted in the domain of the wavelength (λ) and the height of the grating (H). Both are normalised with respect to the length of the grating segment (L). Large dark red points represent infinite values corresponding to BICs. qBICs positioned in the dissipative regime are indicated by large points in other colours.

The substrate-subwavelength condition is equivalent to the cutoff condition of an a-TE _n2 mode. Hence, the a-TE _n2 modes with wavelengths shorter than the cutoff limit become leaky. On the other hand, as long as n g eff > n s , an a-TE _n2 mode can always be in a bound state within a certain wavelength range. Different values for F induce a change in the effective index of the grating ( n g eff ), affecting the number of modes observed in the range L < λ. As a consequence, a-TE _n2 and a-TE _n4 are present for F = 0.7 (Figure 5(a)), whereas a-TE _n6 is additionally observed for F = 0.9 (Figure 5(b)). If we compare the Q-factors for the two grating configurations of a-TE _n4, it will be noticed that the average values are lower in the case of F = 0.7 (predominantly colour blue in the a-TE _n4 dispersion curves) in comparison to F = 0.9 (predominantly green). This relates to stronger coupling of the grating modes with the continuum in the case of smaller F, which is enabled by larger air slits in the grating. Surprisingly, the local maxima of the Q-factors present in the dispersion curves of the a-TE _n4 modes reveal the opposite tendency. In the case of F = 0.9, the Q-factors of the qBICs scarcely reach the level of 10¹² and are usually at the level of 10¹⁰. However, in the case of F = 0.7 the local maxima of the Q-factors are more than 10¹² and a significant number of the maxima reach values exceeding the numerical capabilities of computers, indicating infinite values and the presence of FW or IB BICs in the VN grating. This example shows the possibility of true BICs appearing in structures with broken up-down mirror symmetry.

In the VN configuration with n _s = 2.5 and F = 0.7, when n _s ⁻¹ < L/λ < 2n _s ⁻¹ the presence of a true BIC can be explained by the existence of a single leakage channel related to the emission of the first diffraction order towards the substrate. The light emitted towards the air is prohibited for L < λ. Figure 6(a) shows the intersections of the a-TE₁₄ and aTE_n2 modes. Panels (1), (3), and (5) in Figure 7 confirm the existence of a single emission channel towards the substrate related to the first diffraction order. As expected [33], when the real parts of the wavelengths of two modes cross and their Q-factors are close, strong mode repulsion occurs in the imaginary part of the wavenumber, in the vicinity of the crossing. This mechanism is manifested as the cancelation of light emission towards the substrate and the appearance of BICs, as shown in panels (2) and (4) of Figure 7 (additionally confirmed by Figure S5 in Supplementary Materials). The BICs are positioned in the proximity of the crossings with the a-TE _n2 modes. Every second BIC relates to avoided crossings in the membrane with F = 0.7, as illustrated by the grey curves in Figure 6(a). This suggests that every second BIC is of the FW-type and the others are IB-type.

Figure 6:

Dispersion curves for antisymmetric modes with F = 0.7 in the VN grating (coloured curves) and in the membrane (grey curves) (a). Colours in the dispersion curves correspond to the Q-factor values. Sloping curves represent an a-TE₀₄ mode and nearly horizontal curves represent a-TE _n2 modes. (b) Q-factor versus the stripe height (H/L) for the a-TE₀₄ mode in VN gratings where F = 0.7 (black curve) and F = 0.9 (red curve), with Friedrich–Wintgen (FW) and interference-based (IB) BICs and qBICs. Numbers (1)–(5) indicate structures and corresponding modes illustrated in Figure 7.

Figure 7:

y-Directional profiles of the electric field (black line in top panels) and light intensity distributions (bottom panels) for an a-TE₀₄ mode within a single segment of the VN grating in the y–z plane. Numbers (1)–(5) correspond to the grating configurations indicated by the same numbers in Figure 6(b). The profiles of the electric field are cross-sections through the light intensity maximum of the modes. In the top panels, blue lines represent the profile of the refractive index in the grating and grey dashed lines indicate 0 of the electric field. In the bottom panels, light intensity is presented on a logarithmic scale of colours.

Figure 6(b) compares the Q-factors of the a-TE₀₄ mode for two configurations with F = 0.7 (black) and F = 0.9 (red). It confirms that weaker coupling with the substrate in the case of F = 0.9 results in Q-factors in the range of 10⁵–10⁶ in the minima of the Q-factor function. The Q-factors of the a-TE _n2 modes are at the level of 10²–10³ (Figures 6(a) and 5(b)), which creates a larger difference between the imaginary wavenumbers of a-TE₁₄ and a-TE _n2 modes in comparison to F = 0.7 (see Figure 5(a)). As a result, no true BICs are indicated in the configuration with F = 0.9.

5 Influence of the substrate refractive index on Q-factor

The refractive index contrast between the grating and the substrate is an important design parameter, as it determines the materials from which the grating and the substrate can be fabricated. Figures 8 and 9 show maps of Q-factors in the domain of L/λ and the refractive index of the substrate (n _s) for different values of F. Each map is composed of points produced by searching for the Q-factor maxima for given n _s in the H/L range from 0 to 3 and in the L/λ range from 0.2 to 1. No information on the H/L corresponding to Q-factor maxima is displayed in the maps. As an example, the L/λ and Q-factors of all the qBICs indicated by coloured circles in Figure 2 are implemented in Figure 8(f) along the red dashed line, corresponding to the refractive index n _s = 2.5. The same procedure is applied to all considered n _s and mode symmetries. In Figures 8 and 9 the points representing larger Q-factors overlap lower values. The dashed black lines in Figures 8(f) and 9(f) represent the borders of regions in which particular TE _nm modes are confined in the grating. The numbers in the regions enclosed by the dashed black lines indicate the m indices of the TE _nm modes. The hyperbolic black dashed curves show the cutoffs of these modes and the vertical black dashed lines show their long-wavelength limits (see formula (2)).

Figure 8:

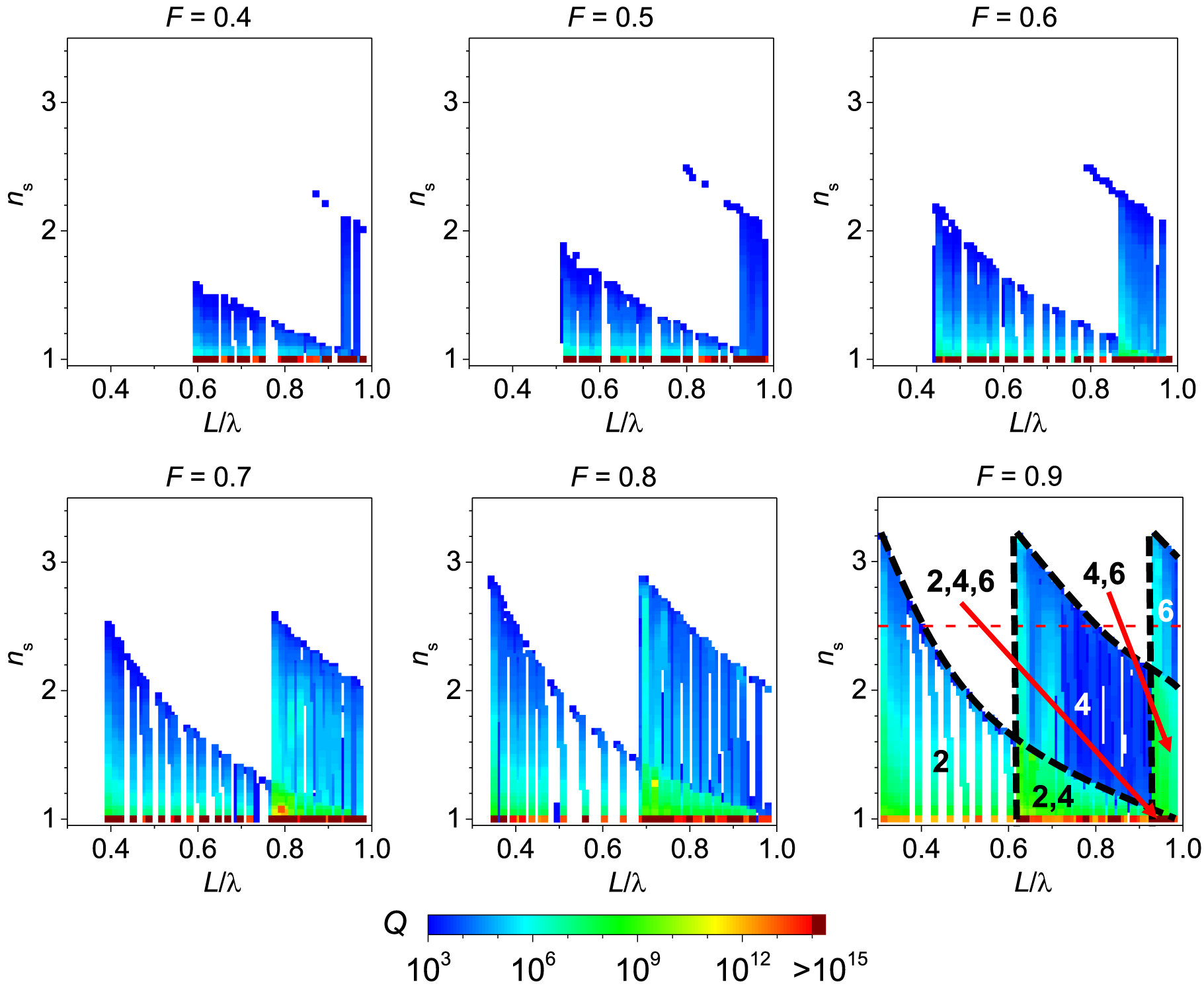
BICs (dark red) and Q-factor values of qBICs given by colours in the domain of the normalized wavelength (L/λ) and the substrate refractive index (n _s), for different duty cycle (F) values of antisymmetric modes. The dashed black lines in (f) show the regions where the groups of a-TE _nm modes indicated by the m index reach their Q-factor maxima.

Figure 9:

BICs (dark red) and Q-factor values of qBICs given by colours in the domain of the normalized wavelength (L/λ) and the substrate refractive index (n _s), for different duty cycle (F) values of antisymmetric modes. The dashed black lines in f) show the regions where the groups of a-TE _nm modes indicated by the m index reach their Q-factor maxima.

s-TE modes (Figure 8) can form BICs only in the case of the membrane and other configurations of VS gratings [11, 12] that are not analysed in this paper. Increasing the refractive index of the substrate in the VN grating qBICs reduces their Q-factors abruptly. Increasing F increases the Q-factor of qBICs by reducing the ability of the grating modes to couple with the continuum of states. Increase of F increases also mode confinement due to increase of the effective refractive index. In Figure 3(b), we showed that qFW BICs reach higher Q-factors in comparison to qIB BICs. Two mechanisms supporting the high Q-factors of symmetric modes can be observed, which were partly noticed in our analysis of Figure 2. The first relates to the occurrence of high Q-factor qBICs in the case of s-TE _nm modes with small n indices and large H. These qBICs are therefore positioned close to the long-wavelength limits. They reach Q ≈ 10⁶ (bright blue colour in Figure 8(d)–(f)) even in the case of substrate refractive indices as large as 3. The disadvantage of these configurations is the large H, which could hamper their real-world realization. Another mechanism is crossing or anticrossing in the modes inducing qFW BICs. In Figure 3(a), the appearance of a qFW BIC was associated with crossing of the dispersion curves of the s-TE₀₄ mode, which was confined in the grating, and a leaky s-TE₁₂ mode. Despite the weak overlap of the two modes, the repulsion of the imaginary parts of their wavenumbers results in a qFW BIC with a Q-factor larger than the Q-factors of neighbouring qIB BICs. In this example, we did not show the enhancement of Q-factor that occurs in the case of crossing of the dispersion curves for two modes confined in the grating. Figure 8(d)–(f) shows broad regions in the n _s–L/λ plane, where crossing between modes confined in the grating occurs (e.g. the areas marked “2, 4” and “4, 6” in Figure 9(f)). The intersections of such modes lead to much stronger repulsion than that presented in Figure 3, which induces record Q-factor values for qBICs exceeding 10¹⁰. These regions are limited in n _s as they require the cutoff for m index modes to be larger than the long wavelength limit of m + 2 index modes.

Figures 8 and 9 support our earlier observation that the spectral positions of the mode cutoffs are independent of the effective refractive index of the grating, since the hyperbolic function representing the cutoff is the same in each map representing different F. However, the long-wavelength limit of the modes shifts toward longer wavelengths as F increases. The a-TE modes reach longer wavelengths than the s-TE modes, as a consequence of zeros in the light distribution in the air slits of the a-TE modes.

The a-TE modes (Figure 9) are SP BICs when L/λ < n _s ⁻¹. This condition can be fulfilled by configurations with high values of n _s only for high values of F. We observed an SP BIC for a maximal refractive index of the substrate when n _s = 3.48, F = 0.9, and H/L = 2.3 at L/λ = 1.8. Remarkably, resonances of extremely high Q-factors exceeding the precision of numerical calculations can be found in the region n _s ⁻¹ < L/λ < 2n _s ⁻¹ where symmetry protection does not hold and only one emission channel related to the first diffraction order exists. These BICs can be found for F < 0.9 where crossings between a-TE _n4 and leaky a-TE _n2 induce strong repulsion of the imaginary parts of their wavenumbers, resulting in infinite Q-factor resonances from the a-TE _n4 modes. This tendency confirms the results presented in Figures 5(a) and 6(a). When F < 0.5, the a-TE _n4 mode remains outside the air-subwavelength region. No BICs can be observed in these configurations, except for SP BICs. When F = 0.9, only a very few non-SP BICs can be observed in the region of crossing a-TE _n4 and a-TE _n6 modes. The coexistence of a-TE _n4 and a-TE _n6 modes for F = 0.8 and 0.9 is also worth noting, due to the presence of extremely high Q-factor resonances that are mostly qFW BICs. However, these resonances are limited to the refractive indices of the substrate below 2.5. We also found a resonance of Q ≈ 6000 related to a qFW BIC that exists in the lowest refractive index contrast configuration, where n _s = 3.5 and F = 0.9. The geometrical parameters of the grating correspond to our limit value of H/L = 3 and the long-wavelength limit of the a-TE₁₂ mode L/λ = 1.8. Finally, qBICs with Q-factors of 10³ in the case of F = 0.5 can be noticed even for n _s = n _g. The origin of these low Q-factor resonances, which exist even though the waveguiding condition is not fulfilled, will be the subject of future work.

6 Example: modal characteristics of a 2D finite structure

To support the simulations of an infinite structure presented in Sections 3–5, we perform a numerical analysis of a two-dimensional subwavelength grating composed of finite number of stripes. The grating and the substrate are made from uniform materials with refractive indices of 3.52 and 2.95, respectively. These values are close to the refractive indices of GaAs and Al-rich AlGaAs in the near infra-red range. Such a combination of materials enables real-world realization of all-semiconductor structures. The refractive indices are real numbers (with a zero imaginary part), which relates to the absence of gain and internal absorption. To demonstrate the difference in the impact of BIC and qBIC on the Q-factor of a finite structure, we chose two configurations. In the first, F = 0.8, which enables a true BIC in an infinite configuration (see Figure 9(e)). In the second, F = 0.9, which provides a qBIC in an infinite structure (see Figure 9(f)). Figure 10 shows the Q-factors of modes for both configurations in the domain of the height of the grating stripes, for an arbitrarily chosen range of the resonant wavelengths. The dispersion maps of the infinite configurations are presented in Figure S6 in the Supplementary Materials.

Figure 10:

Q-factor of resonances in the domain of the VN grating thickness (H/L) and the normalized wavelength (L/λ). The VN grating is composed of 20 periods implemented on a substrate with a refractive index of 2.95 and a duty cycle F = 0.8 (a) and F = 0.9 (b). Numbers in brackets indicate the parameters of modes presented in Figure 11. Ellipses indicate dispersion curves of modes with the same light distribution within a single segment, corresponding to a-TE _n4 or s-TE _n4 modes. The dispersion maps of the infinite configuration with F = 0.9 are presented in Figure S6b, c and with F = 0.8 in Figure S6a in the Supplementary Materials.

Figure 11 illustrates the distributions of the arbitrarily chosen modes indicated by numbers in Figure 10(a). On the scale of a single segment, the intensity distribution resembles that of a TE _nm mode in the corresponding periodic structure. However, on the scale of the whole structure, another dependence is superimposed on the TE_nm distribution, which varies slowly (compared to the single-segment scale). Analogously to similar considerations concerning electronic states in low-dimensional structures in solid state physics, we name the slowly varying function the “envelope”. The distribution of a mode in a finite structure can be seen approximately as a product of the distribution of a TE _nm mode and an envelope. If we denote by p the number of zeros in the envelope function, we can denote the finite-structure mode as TE _nmp .

Figure 11:

Light intensity distribution within a VN grating composed of 20 periods for selected modes (a-TE₀₄₀ (1), a-TE₀₄₁ (2), a-TE₁₄₀ (3) and a-TE₁₄₁ (4)) in the whole grating (left column) and corresponding light distributions in the four central stripes (right column) as indicated in (1). The grating region is indicated in the left column by a white bordered rectangle, and the four central grating stripes are shown in right column. The parameters that are not shown in Figure 10 are F = 0.8, n _s = 2.95.

The dispersion lines of fundamental lateral modes (p = 0) presented in Figure 10 overlap closely with the dispersion lines of their infinite counterparts, which are depicted in Figure S6 in Supplementary Materials. Figure 10 presents the spectral range in which symmetric and antisymmetric modes can be observed (s-TE modes are absent in the spectral range presented in Figure 10(a)). Direct comparison indicates that a-TE _n4p modes reveal Q-factors 100 times higher than those of the s-TE _n4p modes in the finite structure. This is a result of the several orders of magnitude higher Q-factors of a-TE _n4 with respect to s-TE _n4, as illustrated in Figure S6 in the Supplementary Materials. Although zeroth diffraction order emission is prohibited in the case of a-TE _n4 modes in the infinite grating, it is permitted in the finite configuration since finite structures do not totally cancel the emission. Moreover, symmetric TE _nmp modes of the same n and m indices reveal decreases in the wavelength (increased energy) with increases in the index p. In the case of antisymmetric modes, this tendency is reversed, which results from the opposite signs of the effective mass of the cavity modes (see Supplementary Materials S2).

Comparison of the dispersion maps in the case of the finite structure shown in Figure 10, as well as in periodic structures (see Figure S6 Supplementary Materials), reveals a correlation between qBICs in the infinite configuration and the maxima of the Q-factors in finite configurations. In finite configurations, apart from the obviously smaller Q-factor, there is a relatively extended range of large Q-factors with respect to H. We relate this behaviour to the fact that for a qBIC occurring at a Γ−point in infinite grating, a change in the geometric parameter, e.g. H, induces the qBIC to shift beyond the Γ−point [29]. Modes in finite structures, particularly those composed of a low number of stripes, contain wavevector distributions with significantly divergent transverse wavevector component. Thus, large Q-factors can be maintained for a wide range of H, due to the presence of wavevectors whose transverse components are close to those corresponding to qBIC in an infinite structure.

Figure 12 illustrates the light intensity distribution of a-TE₀₄₀ mode in configurations with the following geometric parameters: H/L = 1.39, L/λ = 0.62, and F = 0.8 (configuration 1) which corresponds to a true BIC in an infinite structure (see Figure S6a in the Supplementary Materials). The considered structures differ with respect to the number of grating stripes. All configurations reveal emission in the vertical as well as lateral directions. However, normal emission reduces with higher numbers of stripes.

Figure 12:

Light intensity distribution on a logarithmic scale of colours for the a-TE₀₄₀ mode of a VN grating with n _s = 2.95 composed of 20 (a), 60 (b), and 100 (c) grating stripes with L/λ ≈ 0.62. The other grating parameters are F = 0.8 and H/L = 1.39. The white borders of the rectangles indicate the grating region.

Figure 13 illustrates the Q-factor of the a-TE₀₄₀ mode (black line) as a function of the number of grating stripes, in a configuration with the same geometrical parameters as in Figure 12. For the sake of comparison, Figure 13 also shows the Q-factor of the same mode in a structure with the following geometric parameters: H/L = 1.36, L/λ = 0.58, and F = 0.9 (configuration 2). In the case of the infinite configuration 2, there is a very large but finite Q-factor of 10¹² (see Figure S6c in Supplementary Materials). The calculations for finite configurations 1 and 2 were limited to the maximal size of a structure composed of ∼100 stripes. This limitation is due to computational capability. In configuration 1, Q-factors above 1000 can be achieved for structures composed of as few as 6 grating stripes, enabling very small mode volumes required for example for applications related to single photon devices. A Q-factor level above 10⁴, which is required for achieving stimulated emission [29], is achieved by configuration 1 composed of 20 stripes. Increasing the number of grating stripes increases the Q-factor nearly exponentially. When the Q-factors of the two structures are compared, configuration 1 reveals an approximately 3–5 times larger Q-factor in comparison to configuration 2, which indicates the influence of the true BIC in the infinite configuration on its finite counterpart. The ratio of the Q-factors of configuration 1 and 2 is approximately equal throughout the whole range of the investigated number of grating stripes. However, the Q-factor of configuration 2 is expected to show asymptotic behaviour when the Q-factor approaches the limit of 10¹², related to the infinite structure. The memory of the BIC is sustained in the finite structure due to reduced light emission in the vertical direction in configuration 1 with respect to configuration 2. Figure S10 in the Supplementary Materials enables qualitative comparison of light emitted vertically by configurations 1 and 2, indicating noticeably larger light emission by configuration 2 in three variants composed of 20, 60, and 100 stripes. Lateral emission, which is the second source of the cavity losses, is comparable in both configurations as their effective masses are of comparable value, as discussed in the Supplementary Materials S2.

Figure 13:

Q-factor and relative wavelength (ΔL/λ) versus the number of grating stripes for configuration 1 (black line, H/L = 1.39, L/λ ≈ 0.62 and F = 0.8) and configuration 2 (blue line, H/L ≈ 1.36, L/λ ≈ 0.58 and F = 0.9). ΔL/λ is a difference between the L/λ in the finite stripe grating and that of the infinite grating.

Possible real-world realization of BIC-based periodic cavities would entail further reduction of the Q-factor, due to effects not considered in this analysis related to material absorption, surface roughness, disorder effects, and radiation in the x direction, which limit the Q-factor to 10⁵ [34, 35]. If taken into consideration in the analysis, these effects would reduce the Q-factor of both configurations to a comparable extent. However, the ratio of Q-factors of the two analysed cavities is expected to be at the same of 3–5 level if both configurations are realized.

Finally, we examined the influence of changes in the refractive index induced by temperature variation, which reproduced the effect of temperature rising during operation of the device. We assumed a temperature dependence of 2 × 10⁻⁴ K⁻¹ for the refractive index of the grating and the substrate, which is close to the thermal dependence of the refractive index of GaAs. Increasing the temperature increased the refractive index contrast between the grating and air, which enhanced the confinement of light in the grating. Figure S11 in the Supplementary Materials indicates that a working device would remain stable under the changing thermal conditions that arise during continuous wave operation. Thermal shift of the resonant wavelength and Q-factor are insignificant in terms of the efficiency of the operating device.

7 Conclusions

In this paper, we have presented the results of an extensive numerical analysis of Fano resonance, which is responsible for the creation of BICs in one-dimensional gratings with broken up-down mirror symmetry. Such configurations are composed of a grating implemented on a substrate with a different refractive index to that of the air on the opposite side of the grating. The obvious disadvantage of such a configuration is the collapse of nonsymmetry-protected BICs (FW BICs and IB BICs), as has been explored in [13, 14]. On the other hand, a very important advantage, which may justify a compromise with regard to the collapse of BICs, is the possibility of realizing all-semiconductor configurations that in the future could enable real-world realizations of semiconductor-based electrically driven devices exploiting quasi-BICs.

We studied the formation of BICs and quasi-BICs in an infinite one-dimensional grating with a refractive index of 3.52 implemented on a substrate. The refractive index of the substrate was modified from 1 to the refractive index of the grating. The refractive index on the superstrate was kept at 1. We showed that reducing the up-down mirror symmetry leads to an abrupt collapse of BICs in the case of symmetric modes. FW and IB BICs transform to quasi-FW BICs and quasi-IB BICs, with a noticeable preponderance of quasi-FW BICs compared to quasi-IB BICs in terms of Q-factor.

Analogous analysis in the case of nonsymmetric modes indicated existence of FW and IB BICs in the structures with broken up–down mirror symmetry. Their existence can be explained by destructive interference occurring in the single emission channel, which is related to the first diffraction order being emitted towards the substrate. These BICs are present in the structures with grating duty cycles ranging from 0.5 to 0.8. They result from the repulsion of low Q-factor modes, although avoided crossing is absent.

We also performed an exemplary analysis of a finite structure composed of a finite number of grating stripes with a refractive index of 3.52 and a substrate with a refractive index of 2.95, both corresponding to the refractive indices of arsenide-based materials. In such a relatively low contrast structure, we calculated that increasing the number of grating stripes enables a nearly exponential increase in the Q-factor. We also showed the impact of the true BIC and the quasi BIC in certain infinite configurations on the Q-factor of their finite versions demonstrating 3–5 larger Q-factor in the case of true-BIC-based finite configuration. We also showed that the Q-factor of the resonance is robust against temperature changes that occur in electrically-driven semiconductor devices under continuous wave operation.

More generally, we demonstrated that in structures with broken up-down mirror symmetry not only symmetry-protected BICs can appear, as expected, but also FW and IB BICs, which had not been reported previously. The two conditions necessary to observe BICs are that the effective refractive index of the grating should be larger than the refractive index of the substrate and that the grating should be subwavelength with respect to air (or more generally with respect to the lower refractive index that surrounds the grating). This conclusion may also apply to two-dimensional gratings, as they obey analogous waveguiding phenomena. The calculations presented in this paper relate to a refractive index of the grating corresponding to narrow band gap semiconductors operating in the infrared spectrum, but the same mechanisms are expected to occur in many other materials where different refractive indices induce waveguiding in the grating.